맨위로가기

역격자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

역격자는 브라베 격자의 개념을 바탕으로 정의되며, 실공간 격자의 주기성을 나타내는 함수의 푸리에 급수에서 파수 벡터의 집합으로 정의된다. 역격자는 결정 구조 분석, 고체물리학, 재료 과학 등 다양한 분야에서 활용되며, 브릴루앙 영역 분석에도 사용된다. 한국에서도 역격자 관련 연구가 활발히 진행되고 있다.

더 읽어볼만한 페이지

  • 격자점 - 아이젠슈타인 정수
    아이젠슈타인 정수는 1의 원시 세제곱근 ω를 사용하여 a + bω 꼴로 나타낼 수 있는 대수적 정수이며, 유클리드 정역을 이루어 유일 소인수분해를 갖는다.
  • 격자점 - 브래그 평면
    브래그 평면은 밀러 지수로 나타내며, 역격자 벡터를 이등분하는 평면이다.
  • 결정학 - 점군
    점군은 도형의 병진 조작을 제외한 대칭 조작들의 집합으로 군론의 공리를 만족하며, 쉐인플리스 기호나 허먼-모건 기호로 표기되고, 대칭 조작에 대응하는 행렬 표현은 가약 표현과 기약 표현으로 분해될 수 있다.
  • 결정학 - 브릴루앙 영역
    브릴루앙 영역은 결정의 역격자에서 정의되는 영역으로, 결정 내 전자의 파수 벡터 k 집합을 나타내며, 제1 브릴루앙 영역만 고려해도 결정 내 전자의 모든 정보를 얻을 수 있고, 내부의 특정 고대칭점들은 임계점으로 불린다.
  • 푸리에 해석학 - 라플라스 변환
    라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.
  • 푸리에 해석학 - 푸리에 변환
    푸리에 변환은 복소 함수를 주파수 성분으로 분해하는 적분 변환으로, 푸리에 급수의 확장 개념이며, 시간-주파수 영역 변환, 선형성, 컨볼루션 정리, 불확정성 원리 등의 성질을 가지며 다양한 분야에 활용된다.
역격자
지도 정보
역격자 정보
벡터
식

역격자 벡터
용어
식

용도
역격자 (逆格子)
식

특징

2. 역격자의 정의 및 기본 성질

브라베 격자 Λ ⊂ ℝn의 역격자 Λ-1은 다음과 같이 정의된다.

:\Lambda^{-1}=\{\mathbf v\in\mathbb R^n\colon\mathbf v\cdot\mathbf u\in\mathbb Z\forall\mathbf u\in\Lambda\}.

여기서 '''v'''는 역격자 벡터, '''u'''는 실공간 격자 벡터, ℤ는 정수 집합을 나타낸다.

역격자의 기저는 원래 격자의 기저 벡터들로 구성된 행렬의 역행렬을 통해 얻을 수 있다. 즉, 원래 격자의 기저가 \{\mathbf a_i\} (i=1,\dots,n)이면, 역격자의 기저 \{\mathbf b_i\}는 다음을 만족한다.

:

\left[\mathbf b_1\mathbf b_2\cdots\mathbf b_n\right]^\top =\left[\mathbf a_1\mathbf a_2\cdots\mathbf a_n\right]^{-1}.



3차원에서는 역격자의 기저를 벡터곱을 사용하여 다음과 같이 쓸 수 있다.

:\mathbf b_1=\frac{\mathbf a_2\times\mathbf a_3}{\mathbf a_1 \cdot (\mathbf a_2 \times \mathbf a_3)}

:\mathbf b_2=\frac{\mathbf a_3 \times \mathbf a_1}{\mathbf a_2\cdot (\mathbf a_3 \times \mathbf a_1)}

:\mathbf b_3=\frac{\mathbf a_1 \times \mathbf a_2}{\mathbf a_3\cdot (\mathbf a_1 \times \mathbf a_2)}.

수학과 결정학에서는 위와 같은 정의를 사용하지만, 고체물리학에서는 간혹 벡터가 2\pi배 더 긴 다음과 같은 정의를 사용하기도 한다.

:\Lambda^{-1}=\{\mathbf v\in\mathbb R^n\colon\mathbf v\cdot\mathbf u/2\pi\in\mathbb Z\forall\mathbf u\in\Lambda\}.

실격자와 역격자 사이의 관계. 파란색과 녹색 화살표는 각각 기본 벡터 a_1과 a_2를 나타내는 실공간 2차원 격자(빨간색 점)를 보여준다. 위쪽에는 e^{iG\cdot r} 형태의 평면파가 표시되어 G가 역격자 벡터 기저 b_1과 b_2의 임의의 정수 조합일 때, 생성되는 평면파는 격자와 동일한 주기를 갖는다는 것을 알 수 있다.


3차원 브라베 격자에서 각 격자 벡터에 정수로된 3-튜플 n = (n_1, n_2, n_3)라는 아래첨자를 붙이면,

:\mathbf{R}_n = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3 여기서 n_1, n_2, n_3 \in \mathbb{Z}

이고, \mathbf{a}_i는 기본 병진 벡터이다.

f(\mathbf{r})가 격자의 주기를 따르면, 다차원 푸리에 급수로 표현하는 것이 유용하며,

:\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{r}} = f\left(\mathbf{r}\right)

여기서 아래첨자 m = (m_1, m_2, m_3)이므로, 이것은 3중 합이다.

\mathbf{r}을 임의의 격자 벡터 \mathbf{R}_n만큼 병진하면 동일한 값을 얻게 되므로,

:f(\mathbf{r} + \mathbf{R}_n) = f(\mathbf{r}).

위의 식을 푸리에 급수로 표현하면 다음과 같다.

\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{r}} =

\sum_m f_m e^{i \mathbf{G}_m \cdot (\mathbf{r} + \mathbf{R}_n)} =

\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{R}_n} \, e^{i \mathbf{G}_m \cdot \mathbf{r}}.



두 푸리에 급수가 같다는 것은 계수가 같다는 것을 의미하므로, e^{i \mathbf{G}_m \cdot \mathbf{R}_n} = 1이며, 이는 다음 경우에만 성립한다.

:\mathbf{G}_m \cdot \mathbf{R}_n = 2\pi N 여기서 N \in \mathbb{Z}.

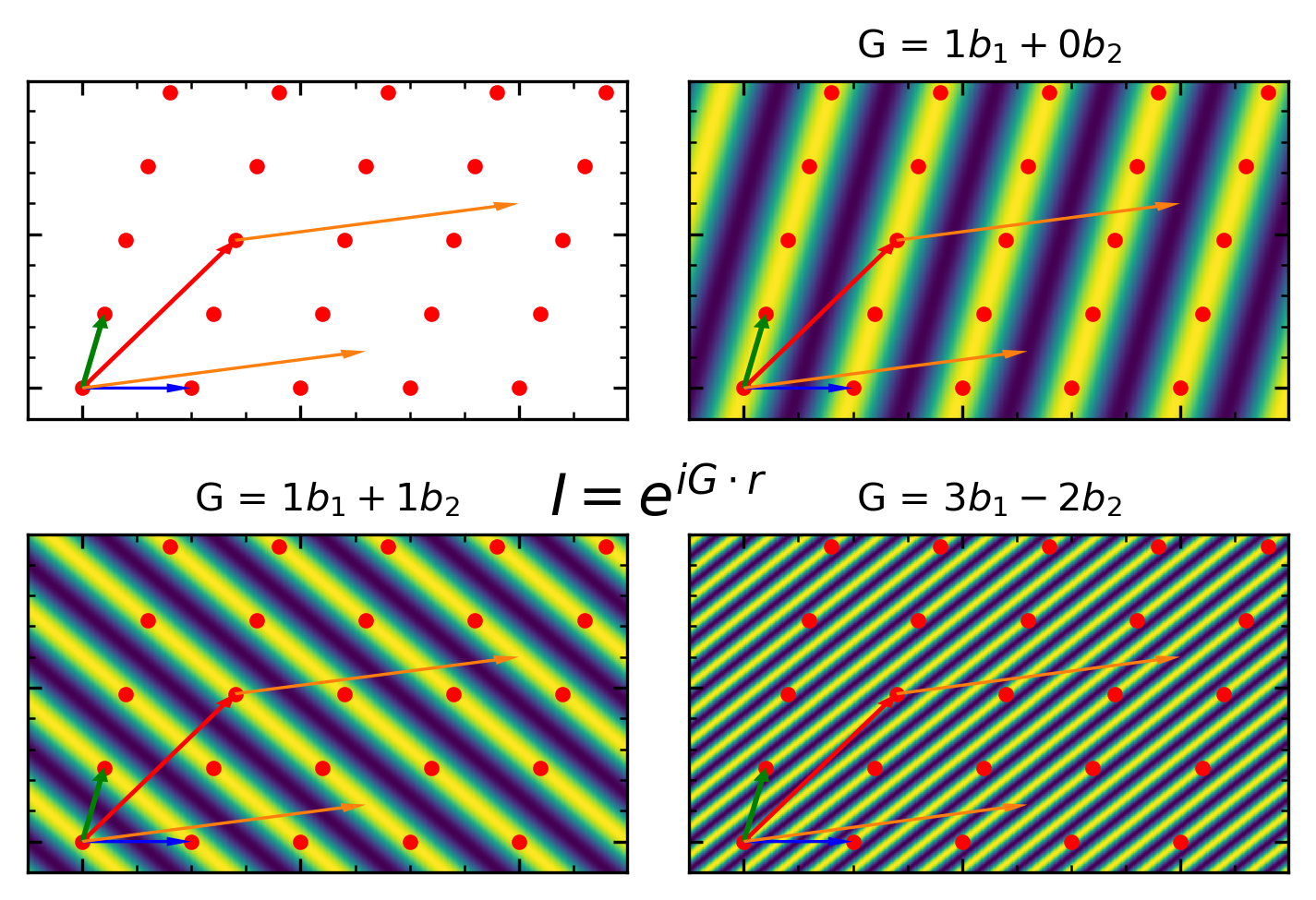
수학적으로 역격자는 주기가 직접 격자와 동일한 공간 함수의 푸리에 급수에 있는 평면파의 파동 벡터인 모든 벡터 \mathbf{G}_m의 집합이다. 푸리에 급수의 각 평면파는 모든 격자점 \mathbf{R}_n에서 동일한 위상을 갖는다.

다차원 푸리에 급수에서 설명된 것처럼, \mathbf{G}_m은 \mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3의 형태로 선택할 수 있으며, 여기서 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}}}이다. 이 형태를 사용하면, 역격자는 자체 기본 병진 벡터 \left(\mathbf{b_{1}}, \mathbf{b}_2, \mathbf{b}_3\right)의 정수 조합으로 형성되므로 자체가 브라베 격자이며, 역격자의 역격자는 원래 격자이다.

무한한 2차원 격자는 기본 벡터 \left(\mathbf{a}_1, \mathbf{a}_2\right)로 정의되며, 그 역격자는[1]

:\mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2

여기서 m_i는 정수이고

:\begin{align}

\mathbf{b}_1 &= 2\pi \frac{-\mathbf{Q} \, \mathbf{a}_2}{-\mathbf{a}_1 \cdot \mathbf{Q} \, \mathbf{a}_2} = 2\pi \frac{ \mathbf{Q} \, \mathbf{a}_2}{ \mathbf{a}_1 \cdot \mathbf{Q} \, \mathbf{a}_2} \\[8pt]

\mathbf{b}_2 &= 2\pi \frac{ \mathbf{Q} \, \mathbf{a}_1}{ \mathbf{a}_2 \cdot \mathbf{Q} \, \mathbf{a}_1}

\end{align}

여기서 \mathbf{Q}는 90도 회전 행렬 즉, 1/4 회전을 나타낸다.[1]

3차원 공간에서 이 2차원 역격자는 무한히 뻗어나가는 브래그 막대의 집합이다.[1]

무한한 3차원 격자 \mathbf{R}_n = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3는 기본 벡터 \left(\mathbf{a_{1}}, \mathbf{a}_2, \mathbf{a}_3\right)와 정수 인덱스 n = \left( n_1, n_2, n_3 \right)로 정의된다. 이 격자의 역격자 \mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3 (정수 인덱스 m = (m_1, m_2, m_3))는 세 개의 역격자 기본 벡터 \left(\mathbf{b_{1}}, \mathbf{b}_2, \mathbf{b}_3\right)를 생성하여 결정할 수 있으며, 이는 다음과 같이 주어진다.

\begin{align}

\mathbf{b}_1 &= \frac{2\pi}{V} \ \mathbf{a}_2 \times \mathbf{a}_3 \\[8pt]

\mathbf{b}_2 &= \frac{2\pi}{V} \ \mathbf{a}_3 \times \mathbf{a}_1 \\[8pt]

\mathbf{b}_3 &= \frac{2\pi}{V} \ \mathbf{a}_1 \times \mathbf{a}_2

\end{align}

여기서 V = \mathbf{a}_1 \cdot \left(\mathbf{a}_2 \times \mathbf{a}_3\right) = \mathbf{a}_2 \cdot \left(\mathbf{a}_3 \times \mathbf{a}_1\right) = \mathbf{a}_3 \cdot \left(\mathbf{a}_1 \times \mathbf{a}_2\right)는 스칼라 삼중곱이다. \left(\mathbf{b_{1영어, \mathbf{b}_2, \mathbf{b}_3\right)를 이렇게 선택하는 이유는 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}영어 조건을 만족시키기 위함이다. 이 선택은 또한 수학적으로 유도된 역격자의 조건 e^{i \mathbf{G}_m \cdot \mathbf{R}_n} = 1을 만족시킨다. (역)기본 벡터의 열 벡터 표현을 사용하면 위 공식은 행렬의 역행렬을 이용하여 다음과 같이 다시 쓸 수 있다.

:\left[\mathbf{b}_1\mathbf{b}_2\mathbf{b}_3\right]^\mathsf{T} = 2\pi\left[\mathbf{a}_1\mathbf{a}_2\mathbf{a}_3\right]^{-1}.

위의 정의는 2 \pi 인자가 주기적 구조 연구에서 자연스럽게 나오기 때문에 "물리학적" 정의라고 한다. 본질적으로 동등한 정의인 "결정학자의" 정의는 역격자 \mathbf{K}_m = \mathbf{G}_m / 2\pi를 정의하여 얻는다. 이는 역 기본 벡터를 다음과 같이 변경한다.

:

\mathbf{b}_1 = \frac{\mathbf{a}_2 \times \mathbf{a}_3}{\mathbf{a}_1 \cdot \left(\mathbf{a}_2 \times \mathbf{a}_3\right)}



다른 기본 벡터에 대해서도 마찬가지이다. 결정학자의 정의는 \mathbf{b}_1의 정의가 \mathbf{a}_2 \times \mathbf{a}_3 방향에서 \mathbf{a}_1의 역 크기가 되는 장점이 있으며, 2 \pi 인자를 제외한다.

m = (m_1, m_2, m_3)는 관례적으로 (h, k, \ell) 또는 (hk\ell)로 표기하며, 이를 밀러 지수라고 한다. 역격자의 각 격자점 (hk\ell)는 실 공간 격자의 (hk\ell) 격자면 집합에 대응한다. 역격자 벡터의 방향은 실 공간 면의 법선에 해당한다. 역격자 벡터 \mathbf{K}_m의 크기는 역 길이 단위로 주어지며 실 공간 면의 면간 간격의 역수와 같다.

n차원에 대한 공식은 기저 (\mathbf{a}_1,\ldots,\mathbf{a}_n)와 내적 g\colon V\times V\to\mathbf{R}를 갖는 n-차원 실수 벡터 공간 V를 가정하여 유도할 수 있다. 상호격자 벡터는 공식 g(\mathbf{a}_i,\mathbf{b}_j)=2\pi\delta_{ij}에 의해 유일하게 결정된다. 순열

: \sigma = \begin{pmatrix}

1 & 2 & \cdots &n\\

2 & 3 & \cdots &1

\end{pmatrix},

을 사용하면 다음 공식으로 결정할 수 있다.[2]

:

\mathbf{b}_i = 2\pi\frac{\varepsilon_{\sigma^1i\ldots\sigma^ni}}{\omega(\mathbf{a}_1,\ldots,\mathbf{a}_n)}g^{-1}(\mathbf{a}_{\sigma^{n-1}i}\,\lrcorner\ldots\mathbf{a}_{\sigma^1i}\,\lrcorner\,\omega)\in V



여기서 \omega\colon V^n \to \mathbf{R}는 체적 형식이고, g^{-1}는 \hat{g}(v)(w) = g(v,w)로 정의된 벡터 공간 동형사상 \hat{g}\colon V \to V^*의 역이고, \lrcorner는 내적 곱을 나타낸다.[2]

3차원 실공간의 격자점은 다음과 같이 표현된다.

:\mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\quad(n_1,n_2,n_3=0,\pm 1,\pm 2,\cdots)

이를 푸리에 변환하면 파수 공간에서는 다음 식으로 표현되는 3차원 격자점이 된다.

:\mathbf{k}\cdot\mathbf{a}_1=2\pi m_1

:\mathbf{k}\cdot\mathbf{a}_2=2\pi m_2\quad(m_1,m_2,m_3=0,\pm 1,\pm 2,\cdots)

:\mathbf{k}\cdot\mathbf{a}_3=2\pi m_3

이를 '''역격자점'''이라고 부른다.

구조를 조사하고 싶은 3차원 결정의 실공간에서의 기본 병진 벡터(기본 단위 벡터)를 {'''a'''1, '''a'''2, '''a'''3}라 하자. 이때, 이 결정의 '''역격자 공간에서의 기본 병진 벡터'''( '''기본 단위 벡터''', '''기본 역격자 벡터''', 단순히 '''기본 벡터'''라고도 함) {'''b'''1, '''b'''2, '''b'''3}는 다음과 같이 정의된다.

:\begin{align}

& \mathbf{b}_1 = 2 \pi { \mathbf{a}_2 \times \mathbf{a}_3 \over { \mathbf{a}_1 \cdot ( \mathbf{a}_2 \times \mathbf{a}_3 ) } } \\

& \mathbf{b}_2 = 2 \pi { \mathbf{a}_3 \times \mathbf{a}_1 \over { \mathbf{a}_2 \cdot ( \mathbf{a}_3 \times \mathbf{a}_1 ) } } \\

& \mathbf{b}_3 = 2 \pi { \mathbf{a}_1 \times \mathbf{a}_2 \over { \mathbf{a}_3 \cdot ( \mathbf{a}_1 \times \mathbf{a}_2 ) } } \end{align}

여기서 ·는 내적, ×는 외적이다. 이와 같이 역격자 공간의 기본 벡터를 정의하면, '''a'''와 '''b''' 사이에는 다음과 같은 직교 관계가 있다.

: \mathbf{a}_i \cdot \mathbf{b}_j = 2 \pi \delta_{ij}

또한, {'''b'''1, '''b'''2, '''b'''3}와 임의의 정수의 집합 '''m''' = (''m''1, ''m''2, ''m''3)에 의해 구성되는 벡터

: \mathbf{G}_\mathbf{m} = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3

를 '''역격자 벡터'''라고 한다. 역격자 벡터 '''Gm'''로 표현되는 벡터의 끝점 ((''m''1, ''m''2, ''m''3)으로 표현됨)의 집합이 '''역격자''', 그리고 그 각각의 끝점이 '''역격자점'''이다.

2. 1. 수학적 정의

브라베 격자 Λ ⊂ ℝn의 역격자 Λ-1은 다음과 같이 정의된다.

:\Lambda^{-1}=\{\mathbf v\in\mathbb R^n\colon\mathbf v\cdot\mathbf u\in\mathbb Z\forall\mathbf u\in\Lambda\}.

여기서 '''v'''는 역격자 벡터, '''u'''는 실공간 격자 벡터, ℤ는 정수 집합을 나타낸다.

역격자의 기저는 원래 격자의 기저 벡터들로 구성된 행렬의 역행렬을 통해 얻을 수 있다. 즉, 원래 격자의 기저가 \{\mathbf a_i\} (i=1,\dots,n)이면, 역격자의 기저 \{\mathbf b_i\}는 다음을 만족한다.

:

\left[\mathbf b_1\mathbf b_2\cdots\mathbf b_n\right]^\top =\left[\mathbf a_1\mathbf a_2\cdots\mathbf a_n\right]^{-1}.



3차원에서는 역격자의 기저를 벡터곱을 사용하여 다음과 같이 쓸 수 있다.

:\mathbf b_1=\frac{\mathbf a_2\times\mathbf a_3}{\mathbf a_1 \cdot (\mathbf a_2 \times \mathbf a_3)}

:\mathbf b_2=\frac{\mathbf a_3 \times \mathbf a_1}{\mathbf a_2\cdot (\mathbf a_3 \times \mathbf a_1)}

:\mathbf b_3=\frac{\mathbf a_1 \times \mathbf a_2}{\mathbf a_3\cdot (\mathbf a_1 \times \mathbf a_2)}.

수학과 결정학에서는 위와 같은 정의를 사용하지만, 고체물리학에서는 간혹 벡터가 2\pi배 더 긴 다음과 같은 정의를 사용하기도 한다.

:\Lambda^{-1}=\{\mathbf v\in\mathbb R^n\colon\mathbf v\cdot\mathbf u/2\pi\in\mathbb Z\forall\mathbf u\in\Lambda\}.

3차원 브라베 격자에서 각 격자 벡터에 정수로된 3-튜플 n = (n_1, n_2, n_3)라는 아래첨자를 붙이면,

:\mathbf{R}_n = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3 여기서 n_1, n_2, n_3 \in \mathbb{Z}

이고, \mathbf{a}_i는 기본 병진 벡터이다.

f(\mathbf{r})가 격자의 주기를 따르면, 다차원 푸리에 급수로 표현하는 것이 유용하며,

:\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{r}} = f\left(\mathbf{r}\right)

여기서 아래첨자 m = (m_1, m_2, m_3)이므로, 이것은 3중 합이다.

\mathbf{r}을 임의의 격자 벡터 \mathbf{R}_n만큼 병진하면 동일한 값을 얻게 되므로,

:f(\mathbf{r} + \mathbf{R}_n) = f(\mathbf{r}).

위의 식을 푸리에 급수로 표현하면 다음과 같다.

\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{r}} =

\sum_m f_m e^{i \mathbf{G}_m \cdot (\mathbf{r} + \mathbf{R}_n)} =

\sum_m f_m e^{i \mathbf{G}_m \cdot \mathbf{R}_n} \, e^{i \mathbf{G}_m \cdot \mathbf{r}}.



두 푸리에 급수가 같다는 것은 계수가 같다는 것을 의미하므로, e^{i \mathbf{G}_m \cdot \mathbf{R}_n} = 1이며, 이는 다음 경우에만 성립한다.

:\mathbf{G}_m \cdot \mathbf{R}_n = 2\pi N 여기서 N \in \mathbb{Z}.

수학적으로 역격자는 주기가 직접 격자와 동일한 공간 함수의 푸리에 급수에 있는 평면파의 파동 벡터인 모든 벡터 \mathbf{G}_m의 집합이다. 푸리에 급수의 각 평면파는 모든 격자점 \mathbf{R}_n에서 동일한 위상을 갖는다.

다차원 푸리에 급수에서 설명된 것처럼, \mathbf{G}_m은 \mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3의 형태로 선택할 수 있으며, 여기서 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}}}이다. 이 형태를 사용하면, 역격자는 자체 기본 병진 벡터 \left(\mathbf{b_{1}}, \mathbf{b}_2, \mathbf{b}_3\right)의 정수 조합으로 형성되므로 자체가 브라베 격자이며, 역격자의 역격자는 원래 격자이다.

무한한 2차원 격자는 기본 벡터 \left(\mathbf{a}_1, \mathbf{a}_2\right)로 정의되며, 그 역격자는[1]

:\mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2

여기서 m_i는 정수이고

:\begin{align}

\mathbf{b}_1 &= 2\pi \frac{-\mathbf{Q} \, \mathbf{a}_2}{-\mathbf{a}_1 \cdot \mathbf{Q} \, \mathbf{a}_2} = 2\pi \frac{ \mathbf{Q} \, \mathbf{a}_2}{ \mathbf{a}_1 \cdot \mathbf{Q} \, \mathbf{a}_2} \\[8pt]

\mathbf{b}_2 &= 2\pi \frac{ \mathbf{Q} \, \mathbf{a}_1}{ \mathbf{a}_2 \cdot \mathbf{Q} \, \mathbf{a}_1}

\end{align}

여기서 \mathbf{Q}는 90도 회전 행렬 즉, 1/4 회전을 나타낸다.[1]

3차원 공간에서 이 2차원 역격자는 무한히 뻗어나가는 브래그 막대의 집합이다.[1]

무한한 3차원 격자 \mathbf{R}_n = n_1 \mathbf{a}_1 + n_2 \mathbf{a}_2 + n_3 \mathbf{a}_3는 기본 벡터 \left(\mathbf{a_{1}}, \mathbf{a}_2, \mathbf{a}_3\right)와 정수 인덱스 n = \left( n_1, n_2, n_3 \right)로 정의된다. 이 격자의 역격자 \mathbf{G}_m = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3 (정수 인덱스 m = (m_1, m_2, m_3))는 세 개의 역격자 기본 벡터 \left(\mathbf{b_{1}}, \mathbf{b}_2, \mathbf{b}_3\right)를 생성하여 결정할 수 있으며, 이는 다음과 같이 주어진다.

\begin{align}

\mathbf{b}_1 &= \frac{2\pi}{V} \ \mathbf{a}_2 \times \mathbf{a}_3 \\[8pt]

\mathbf{b}_2 &= \frac{2\pi}{V} \ \mathbf{a}_3 \times \mathbf{a}_1 \\[8pt]

\mathbf{b}_3 &= \frac{2\pi}{V} \ \mathbf{a}_1 \times \mathbf{a}_2

\end{align}

여기서 V = \mathbf{a}_1 \cdot \left(\mathbf{a}_2 \times \mathbf{a}_3\right) = \mathbf{a}_2 \cdot \left(\mathbf{a}_3 \times \mathbf{a}_1\right) = \mathbf{a}_3 \cdot \left(\mathbf{a}_1 \times \mathbf{a}_2\right)는 스칼라 삼중곱이다. \left(\mathbf{b_{1영어, \mathbf{b}_2, \mathbf{b}_3\right)를 이렇게 선택하는 이유는 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}영어 조건을 만족시키기 위함이다. 이 선택은 또한 수학적으로 유도된 역격자의 조건 e^{i \mathbf{G}_m \cdot \mathbf{R}_n} = 1을 만족시킨다. (역)기본 벡터의 열 벡터 표현을 사용하면 위 공식은 행렬의 역행렬을 이용하여 다음과 같이 다시 쓸 수 있다.

:\left[\mathbf{b}_1\mathbf{b}_2\mathbf{b}_3\right]^\mathsf{T} = 2\pi\left[\mathbf{a}_1\mathbf{a}_2\mathbf{a}_3\right]^{-1}.

위의 정의는 2 \pi 인자가 주기적 구조 연구에서 자연스럽게 나오기 때문에 "물리학적" 정의라고 한다. 본질적으로 동등한 정의인 "결정학자의" 정의는 역격자 \mathbf{K}_m = \mathbf{G}_m / 2\pi를 정의하여 얻는다. 이는 역 기본 벡터를 다음과 같이 변경한다.

:

\mathbf{b}_1 = \frac{\mathbf{a}_2 \times \mathbf{a}_3}{\mathbf{a}_1 \cdot \left(\mathbf{a}_2 \times \mathbf{a}_3\right)}



다른 기본 벡터에 대해서도 마찬가지이다. 결정학자의 정의는 \mathbf{b}_1의 정의가 \mathbf{a}_2 \times \mathbf{a}_3 방향에서 \mathbf{a}_1의 역 크기가 되는 장점이 있으며, 2 \pi 인자를 제외한다.

m = (m_1, m_2, m_3)는 관례적으로 (h, k, \ell) 또는 (hk\ell)로 표기하며, 이를 밀러 지수라고 한다. 역격자의 각 격자점 (hk\ell)는 실 공간 격자의 (hk\ell) 격자면 집합에 대응한다. 역격자 벡터의 방향은 실 공간 면의 법선에 해당한다. 역격자 벡터 \mathbf{K}_m의 크기는 역 길이 단위로 주어지며 실 공간 면의 면간 간격의 역수와 같다.

n차원에 대한 공식은 기저 (\mathbf{a}_1,\ldots,\mathbf{a}_n)와 내적 g\colon V\times V\to\mathbf{R}를 갖는 n-차원 실수 벡터 공간 V를 가정하여 유도할 수 있다. 상호격자 벡터는 공식 g(\mathbf{a}_i,\mathbf{b}_j)=2\pi\delta_{ij}에 의해 유일하게 결정된다. 순열

: \sigma = \begin{pmatrix}

1 & 2 & \cdots &n\\

2 & 3 & \cdots &1

\end{pmatrix},

을 사용하면 다음 공식으로 결정할 수 있다.[2]

:

\mathbf{b}_i = 2\pi\frac{\varepsilon_{\sigma^1i\ldots\sigma^ni}}{\omega(\mathbf{a}_1,\ldots,\mathbf{a}_n)}g^{-1}(\mathbf{a}_{\sigma^{n-1}i}\,\lrcorner\ldots\mathbf{a}_{\sigma^1i}\,\lrcorner\,\omega)\in V



여기서 \omega\colon V^n \to \mathbf{R}는 체적 형식이고, g^{-1}는 \hat{g}(v)(w) = g(v,w)로 정의된 벡터 공간 동형사상 \hat{g}\colon V \to V^*의 역이고, \lrcorner는 내적 곱을 나타낸다.[2]

3차원 실공간의 격자점은 다음과 같이 표현된다.

:\mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\quad(n_1,n_2,n_3=0,\pm 1,\pm 2,\cdots)

이를 푸리에 변환하면 파수 공간에서는 다음 식으로 표현되는 3차원 격자점이 된다.

:\mathbf{k}\cdot\mathbf{a}_1=2\pi m_1

:\mathbf{k}\cdot\mathbf{a}_2=2\pi m_2\quad(m_1,m_2,m_3=0,\pm 1,\pm 2,\cdots)

:\mathbf{k}\cdot\mathbf{a}_3=2\pi m_3

이를 '''역격자점'''이라고 부른다.

구조를 조사하고 싶은 3차원 결정의 실공간에서의 기본 병진 벡터(기본 단위 벡터)를 {'''a'''1, '''a'''2, '''a'''3}라 하자. 이때, 이 결정의 '''역격자 공간에서의 기본 병진 벡터'''( '''기본 단위 벡터''', '''기본 역격자 벡터''', 단순히 '''기본 벡터'''라고도 함) {'''b'''1, '''b'''2, '''b'''3}는 다음과 같이 정의된다.

:\begin{align}

& \mathbf{b}_1 = 2 \pi { \mathbf{a}_2 \times \mathbf{a}_3 \over { \mathbf{a}_1 \cdot ( \mathbf{a}_2 \times \mathbf{a}_3 ) } } \\

& \mathbf{b}_2 = 2 \pi { \mathbf{a}_3 \times \mathbf{a}_1 \over { \mathbf{a}_2 \cdot ( \mathbf{a}_3 \times \mathbf{a}_1 ) } } \\

& \mathbf{b}_3 = 2 \pi { \mathbf{a}_1 \times \mathbf{a}_2 \over { \mathbf{a}_3 \cdot ( \mathbf{a}_1 \times \mathbf{a}_2 ) } } \end{align}

여기서 ·는 내적, ×는 외적이다. 이와 같이 역격자 공간의 기본 벡터를 정의하면, '''a'''와 '''b''' 사이에는 다음과 같은 직교 관계가 있다.

: \mathbf{a}_i \cdot \mathbf{b}_j = 2 \pi \delta_{ij}

또한, {'''b'''1, '''b'''2, '''b'''3}와 임의의 정수의 집합 '''m''' = (''m''1, ''m''2, ''m''3)에 의해 구성되는 벡터

: \mathbf{G}_\mathbf{m} = m_1 \mathbf{b}_1 + m_2 \mathbf{b}_2 + m_3 \mathbf{b}_3

를 '''역격자 벡터'''라고 한다. 역격자 벡터 '''Gm'''로 표현되는 벡터의 끝점 ((''m''1, ''m''2, ''m''3)으로 표현됨)의 집합이 '''역격자''', 그리고 그 각각의 끝점이 '''역격자점'''이다.

2. 2. 기본 성질

역격자는 원래 격자와 동일한 점군 대칭(point group symmetry)을 갖는다.실공간 격자 벡터 '''R'''''n''과 역격자 벡터 '''G'''''m'' 사이에는 다음과 같은 관계가 성립한다.

: \mathbf{G}_m \cdot \mathbf{R}_n = 2 \pi N_{mn}

여기서 ''Nmn''은 정수이다.

실공간 단위세포(unit cell)의 부피(Ω)와 역공간 단위세포의 부피(ΩG) 사이에는 다음과 같은 관계가 성립한다.

:\begin{align}& \Omega = \mathbf{a}_1 \cdot (\mathbf{a}_2 \times \mathbf{a}_3) \\

& \Omega_\mathrm{G} = \mathbf{b}_1 \cdot (\mathbf{b}_2 \times \mathbf{b}_3) = {(2 \pi)^3 \over {\Omega} } \end{align}

여기서 Ω는 실공간에서의 단위세포의 부피이고, ΩG는 역격자 공간에서의 단위세포의 부피이다.

3. 다양한 결정계의 역격자

단순 입방 브라베 격자는 격자 상수가 a인 입방 단위세포를 갖는다. 이 격자의 역격자는 격자 상수가 2π/a 인 단순 입방 격자이다. 따라서 입방 격자는 실제 공간과 역공간에서 같은 대칭성을 가지므로 자기 쌍대적(self-dual)이라고 한다.

면심 입방 격자(FCC)의 역격자는 체심 입방 격자(BCC)이며, 격자 상수는 4π/a이다. 면심 입방 화합물 단위 격자를 고려하여, 원시 단위 격자, 즉 격자점이 하나인 단위 격자를 찾는다. 이 원시 단위 격자의 꼭짓점 중 하나를 원점으로 하고, 실격자의 기저 벡터를 제시한다. 그 후, 알려진 공식을 사용하여 역격자의 기저 벡터를 계산할 수 있다. FCC의 이러한 역격자 벡터는 BCC 실격자의 기저 벡터를 나타낸다. 실제 BCC 격자의 기저 벡터와 FCC의 역격자는 방향은 비슷하지만 크기는 다르다.

체심 입방 격자(BCC)의 역격자는 면심 입방 격자(FCC)이며, 격자 상수는 4π/a이다.

단순 육방 격자(simple hexagonal Bravais lattice)의 격자 상수가 a와 c인 격자의 역격자는 격자 상수가 2π/c와 4π/(a√3)인 또 다른 단순 육방 격자이다. 이는 직접 격자에 대해 c축을 중심으로 90° 회전한 것이다. 따라서 단순 육방 격자는 실제 공간과 역 공간에서 동일한 대칭성을 가지므로 자기 쌍대(self-dual)라고 한다.[3] 이 단순 육방 격자의 기본 병진 벡터는 다음과 같다.[3]

: a1 = (√3/2)ax + (1/2)ay,

: a2 = -(√3/2)ax + (1/2)ay,

: a3 = cz.

3. 1. 단순 입방 격자 (Simple Cubic Lattice)

단순 입방 브라베 격자는 격자 상수가 a인 입방 단위세포를 갖는다. 이 격자의 역격자는 격자 상수가 2π/a 인 단순 입방 격자이다. 따라서 입방 격자는 실제 공간과 역공간에서 같은 대칭성을 가지므로 자기 쌍대적(self-dual)이라고 한다.

3. 2. 면심 입방 격자 (Face-Centered Cubic, FCC Lattice)

면심 입방 격자(FCC)의 역격자는 체심 입방 격자(BCC)이며, 격자 상수는 \(\frac{4\pi}{a}\)이다. 면심 입방 화합물 단위 격자를 고려하여, 원시 단위 격자, 즉 격자점이 하나인 단위 격자를 찾는다. 이 원시 단위 격자의 꼭짓점 중 하나를 원점으로 하고, 실격자의 기저 벡터를 제시한다. 그 후, 알려진 공식을 사용하여 역격자의 기저 벡터를 계산할 수 있다. FCC의 이러한 역격자 벡터는 BCC 실격자의 기저 벡터를 나타낸다. 실제 BCC 격자의 기저 벡터와 FCC의 역격자는 방향은 비슷하지만 크기는 다르다.

3. 3. 체심 입방 격자 (Body-Centered Cubic, BCC Lattice)

체심 입방 격자(BCC)의 역격자는 면심 입방 격자(FCC)이며, 격자 상수는 4π/a이다.

분류:결정학

분류:고체물리학

3. 4. 단순 육방 격자 (Simple Hexagonal Lattice)

단순 육방 격자(simple hexagonal Bravais lattice)의 격자 상수가 a와 c인 격자의 역격자는 격자 상수가 2π/c와 4π/(a√3)인 또 다른 단순 육방 격자이다. 이는 직접 격자에 대해 c축을 중심으로 90° 회전한 것이다. 따라서 단순 육방 격자는 실제 공간과 역 공간에서 동일한 대칭성을 가지므로 자기 쌍대(self-dual)라고 한다.[3] 이 단순 육방 격자의 기본 병진 벡터는 다음과 같다.[3]

: a1 = (√3/2)ax + (1/2)ay,

: a2 = -(√3/2)ax + (1/2)ay,

: a3 = cz.

4. 역공간과 파동 기반 설명

역공간(또는 k-공간)은 공간 함수의 푸리에 변환 결과를 시각화하는 공간이다. 이는 시간 함수의 푸리에 변환에서 나오는 주파수 영역과 유사한 역할을 한다. 역공간은 푸리에 변환의 평면파의 공간 주파수 또는 파수 벡터로 나타나며, 공간 함수 자체의 영역인 실공간과 상보적인 관계를 갖는다. 실공간이 길이( '''L''' ) 차원을 가질 때, 역공간은 길이의 역수( '''L'''−1) 차원을 갖는다.

저에너지 전자 회절(LEED)에서 1×2 초격자를 갖는 표면에 흡착된 종은 추가적인 반점을 생성합니다.


단위 진폭을 가진 사인파 평면파는 초기 위상 \varphi_0, 각 파수 k, 각 주파수 \omega를 사용하여 \cos(kx - \omega t + \varphi_0)로 표현될 수 있다. 여기서 k와 x는 상보적인 역할을 하며, 이는 실공간과 역공간의 관계를 시각화하는 데 사용된다. 파동의 공간 주기성은 파장 \lambda로 정의되며, k \lambda = 2\pi이다. 따라서 역공간에서 해당 파수는 k = 2\pi / \lambda가 된다.

3차원에서 평면파 항은 \cos(\mathbf{k} \cdot \mathbf{r} - \omega t + \varphi_0)로 표현되며, 고정된 시간 t에서는 \cos(\mathbf{k} \cdot \mathbf{r} + \varphi)로 단순화된다. 여기서 \mathbf{r}은 실공간의 한 점의 위치 벡터이고, \mathbf{k}=2\pi \mathbf{e} / \lambda는 3차원 역공간의 파수 벡터이다. 상수 \varphi는 시간 t에서 원점 \mathbf{r}=0을 통과하는 파면(일정한 위상의 평면)의 위상이고, \mathbf{e}는 이 파면에 수직인 단위 벡터이다. \varphi + (2\pi)n의 위상을 가진 파면(n은 임의의 정수)은 파장 \lambda만큼 균일하게 간격을 둔 평행 평면 집합을 구성한다.

3차원 실공간에서 무한히 계속되는 점열은 벡터 \mathbf{a}_1로 표현될때, 즉, \mathbf{r}=n_1\mathbf{a}_1\quad(n_1=0,\pm 1,\pm 2,\cdots) 푸리에 변환을 통해 역공간에서는 무한히 계속되는 평면의 열(법선 \mathbf{a}_1, 면 간격 2\pi/|\mathbf{a}_1|)로 나타내어지며, 이는 \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1\quad(m_1=0,\pm 1,\pm 2,\cdots) 식으로 표현된다.

3차원 실공간에 있는 무한히 계속되는 2차원 격자점은 \mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2\quad(n_1,n_2=0,\pm 1,\pm 2,\cdots)로 표현된다. 이를 푸리에 변환하면, 파수 공간에서는 2차원적으로 규칙적으로 나란히 늘어선 무한히 긴 막대가 되며, \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1와 \mathbf{k}\cdot\mathbf{a}_2=2\pi m_2 \quad(m_1,m_2=0,\pm 1,\pm 2,\cdots) 식으로 표현된다. 이를 '''역격자 막대'''라고 부르며, 결정 표면의 구조 해석에 자주 사용된다.

3차원 실공간의 격자점은 \mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\quad(n_1,n_2,n_3=0,\pm 1,\pm 2,\cdots)로 표현된다. 이를 푸리에 변환하면 파수 공간에서는 \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1, \mathbf{k}\cdot\mathbf{a}_2=2\pi m_2\quad(m_1,m_2,m_3=0,\pm 1,\pm 2,\cdots) 그리고 \mathbf{k}\cdot\mathbf{a}_3=2\pi m_3 식으로 표현되는 3차원 격자점이 된다. 이를 '''역격자점'''이라고 부른다.

역격자는 실공간 격자의 주기성을 만족하는 함수의 푸리에 급수에서 평면파의 파수 벡터 집합으로 정의될 수 있다. 역격자는 기본 벡터의 정수 조합으로 형성되는 브라베 격자이며, 역격자의 역격자는 원래 격자이다.

일반적으로 기하학적 격자는 공간상의 무한하고 규칙적인 꼭짓점(점) 배열이며, 벡터적으로는 브라베 격자로 모델링할 수 있다. 역공간에서 역격자는 실공간의 초기 직접 격자와 주기성이 호환되는 임의의 함수 \mathbf{f(r)}의 푸리에 급수에서 평면파의 파수 벡터 \mathbf{k}의 집합으로 정의된다.

3차원 역격자를 구성하는 한 가지 방법은 직접 격자의 꼭짓점 위치 벡터를 \mathbf{R} = n_1\mathbf{a}_1 + n_2\mathbf{a}_2 + n_3\mathbf{a}_3로 나타내는 것이다. 여기서 n_i는 꼭짓점을 정의하는 정수이고 \mathbf{a}_i는 격자의 특징인 선형 독립인 기본 병진 벡터(또는 간단히 기본 벡터라고 함)이다. 그러면 원점 \mathbf{R} = 0을 통과하는 파면이 \mathbf{a}_2와 \mathbf{a}_3에 있는 직접 격자점을 포함하고, 인접한 파면(위상이 원점을 통과하는 이전 파면과 2\pi 또는 -2\pi만큼 다른)이 \mathbf{a}_1을 통과하는 고유한 평면파(음의 1배수까지)가 존재한다.

이 평면파의 각 파수 벡터는 \mathbf{b}_1 = 2\pi \mathbf{e}_1 / \lambda_{1} 형태를 취하며, 여기서 \mathbf{e}_1은 이 두 개의 인접한 파면에 수직인 단위 벡터이고 파장 \lambda_1는 \lambda_1 = \mathbf{a}_1 \cdot \mathbf{e}_1을 만족해야 하므로, \lambda_1은 두 파면 사이의 거리와 같다. 따라서 구성에 따라 \mathbf{a}_1 \cdot \mathbf{b}_1 = 2\pi이고 \mathbf{a}_2 \cdot \mathbf{b}_1 = \mathbf{a}_3 \cdot \mathbf{b}_1 = 0이다.

색인을 순서대로 순환하면 같은 방법으로 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}인 세 개의 파수 벡터 \mathbf{b}_j를 얻는다. 여기서 크로네커 델타 \delta_{ij}는 i=j일 때 1이고 그렇지 않으면 0이다. \mathbf{b}_j는 역격자에 대한 세 개의 기본 파수 벡터 또는 세 개의 기본 병진 벡터 집합을 구성하며, 각 꼭짓점은 \mathbf{G} = m_1\mathbf{b}_1 + m_2\mathbf{b}_2 + m_3\mathbf{b}_3 형태를 취한다. 여기서 m_j는 정수이다. 역격자는 기본 벡터의 정수 조합으로 형성되므로 브라베 격자이기도 하다.

브릴루앙 영역은 역격자의 원시 단위격자(더 구체적으로는 비그너-자이츠 단위격자)이며, 블로흐의 정리 때문에 고체물리학에서 중요한 역할을 한다.

4. 1. 역공간 (Reciprocal Space)

역공간(또는 k-공간)은 공간 함수의 푸리에 변환 결과를 시각화하는 공간이다. 이는 시간 함수의 푸리에 변환에서 나오는 주파수 영역과 유사한 역할을 한다. 역공간은 푸리에 변환의 평면파의 공간 주파수 또는 파수 벡터로 나타나며, 공간 함수 자체의 영역인 실공간과 상보적인 관계를 갖는다. 실공간이 길이( '''L''' ) 차원을 가질 때, 역공간은 길이의 역수( '''L'''−1) 차원을 갖는다.

단위 진폭을 가진 사인파 평면파는 초기 위상 \varphi_0, 각 파수 k, 각 주파수 \omega를 사용하여 \cos(kx - \omega t + \varphi_0)로 표현될 수 있다. 여기서 k와 x는 상보적인 역할을 하며, 이는 실공간과 역공간의 관계를 시각화하는 데 사용된다. 파동의 공간 주기성은 파장 \lambda로 정의되며, k \lambda = 2\pi이다. 따라서 역공간에서 해당 파수는 k = 2\pi / \lambda가 된다.

3차원에서 평면파 항은 \cos(\mathbf{k} \cdot \mathbf{r} - \omega t + \varphi_0)로 표현되며, 고정된 시간 t에서는 \cos(\mathbf{k} \cdot \mathbf{r} + \varphi)로 단순화된다. 여기서 \mathbf{r}은 실공간의 한 점의 위치 벡터이고, \mathbf{k}=2\pi \mathbf{e} / \lambda는 3차원 역공간의 파수 벡터이다. 상수 \varphi는 시간 t에서 원점 \mathbf{r}=0을 통과하는 파면(일정한 위상의 평면)의 위상이고, \mathbf{e}는 이 파면에 수직인 단위 벡터이다. \varphi + (2\pi)n의 위상을 가진 파면(n은 임의의 정수)은 파장 \lambda만큼 균일하게 간격을 둔 평행 평면 집합을 구성한다.

3차원 실공간에서 무한히 계속되는 점열은 벡터 \mathbf{a}_1로 표현될때, 즉, \mathbf{r}=n_1\mathbf{a}_1\quad(n_1=0,\pm 1,\pm 2,\cdots) 푸리에 변환을 통해 역공간에서는 무한히 계속되는 평면의 열(법선 \mathbf{a}_1, 면 간격 2\pi/|\mathbf{a}_1|)로 나타내어지며, 이는 \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1\quad(m_1=0,\pm 1,\pm 2,\cdots) 식으로 표현된다.

3차원 실공간에 있는 무한히 계속되는 2차원 격자점은 \mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2\quad(n_1,n_2=0,\pm 1,\pm 2,\cdots)로 표현된다. 이를 푸리에 변환하면, 파수 공간에서는 2차원적으로 규칙적으로 나란히 늘어선 무한히 긴 막대가 되며, \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1와 \mathbf{k}\cdot\mathbf{a}_2=2\pi m_2 \quad(m_1,m_2=0,\pm 1,\pm 2,\cdots) 식으로 표현된다. 이를 '''역격자 막대'''라고 부르며, 결정 표면의 구조 해석에 자주 사용된다.

3차원 실공간의 격자점은 \mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\quad(n_1,n_2,n_3=0,\pm 1,\pm 2,\cdots)로 표현된다. 이를 푸리에 변환하면 파수 공간에서는 \mathbf{k}\cdot\mathbf{a}_1=2\pi m_1, \mathbf{k}\cdot\mathbf{a}_2=2\pi m_2\quad(m_1,m_2,m_3=0,\pm 1,\pm 2,\cdots) 그리고 \mathbf{k}\cdot\mathbf{a}_3=2\pi m_3 식으로 표현되는 3차원 격자점이 된다. 이를 '''역격자점'''이라고 부른다.

4. 2. 역격자와 푸리에 급수

역격자는 실공간 격자의 주기성을 만족하는 함수의 푸리에 급수에서 평면파의 파수 벡터 집합으로 정의될 수 있다. 역격자는 기본 벡터의 정수 조합으로 형성되는 브라베 격자이며, 역격자의 역격자는 원래 격자이다.

일반적으로 기하학적 격자는 공간상의 무한하고 규칙적인 꼭짓점(점) 배열이며, 벡터적으로는 브라베 격자로 모델링할 수 있다. 역공간에서 역격자는 실공간의 초기 직접 격자와 주기성이 호환되는 임의의 함수 \mathbf{f(r)}의 푸리에 급수에서 평면파의 파수 벡터 \mathbf{k}의 집합으로 정의된다.

3차원 역격자를 구성하는 한 가지 방법은 직접 격자의 꼭짓점 위치 벡터를 \mathbf{R} = n_1\mathbf{a}_1 + n_2\mathbf{a}_2 + n_3\mathbf{a}_3로 나타내는 것이다. 여기서 n_i는 꼭짓점을 정의하는 정수이고 \mathbf{a}_i는 격자의 특징인 선형 독립인 기본 병진 벡터(또는 간단히 기본 벡터라고 함)이다. 그러면 원점 \mathbf{R} = 0을 통과하는 파면이 \mathbf{a}_2와 \mathbf{a}_3에 있는 직접 격자점을 포함하고, 인접한 파면(위상이 원점을 통과하는 이전 파면과 2\pi 또는 -2\pi만큼 다른)이 \mathbf{a}_1을 통과하는 고유한 평면파(음의 1배수까지)가 존재한다.

이 평면파의 각 파수 벡터는 \mathbf{b}_1 = 2\pi \mathbf{e}_1 / \lambda_{1} 형태를 취하며, 여기서 \mathbf{e}_1은 이 두 개의 인접한 파면에 수직인 단위 벡터이고 파장 \lambda_1는 \lambda_1 = \mathbf{a}_1 \cdot \mathbf{e}_1을 만족해야 하므로, \lambda_1은 두 파면 사이의 거리와 같다. 따라서 구성에 따라 \mathbf{a}_1 \cdot \mathbf{b}_1 = 2\pi이고 \mathbf{a}_2 \cdot \mathbf{b}_1 = \mathbf{a}_3 \cdot \mathbf{b}_1 = 0이다.

색인을 순서대로 순환하면 같은 방법으로 \mathbf{a}_i \cdot \mathbf{b}_j = 2\pi \, \delta_{ij}인 세 개의 파수 벡터 \mathbf{b}_j를 얻는다. 여기서 크로네커 델타 \delta_{ij}는 i=j일 때 1이고 그렇지 않으면 0이다. \mathbf{b}_j는 역격자에 대한 세 개의 기본 파수 벡터 또는 세 개의 기본 병진 벡터 집합을 구성하며, 각 꼭짓점은 \mathbf{G} = m_1\mathbf{b}_1 + m_2\mathbf{b}_2 + m_3\mathbf{b}_3 형태를 취한다. 여기서 m_j는 정수이다. 역격자는 기본 벡터의 정수 조합으로 형성되므로 브라베 격자이기도 하다.

3차원 실공간에 있는 무한히 계속되는 점열을 생각하자. 점 간격을 나타내는 벡터를 \mathbf{a}_1이라고 하면,

:\mathbf{r}=n_1\mathbf{a}_1\quad(n_1=0,\pm 1,\pm 2,\cdots)

이것을 푸리에 변환하면, 역공간('''k공간''', '''파수공간''', '''역격자공간''')에서는 다음 식으로 나타내어지는 무한히 계속되는 평면의 열(법선 \mathbf{a}_1, 면 간격 2\pi/|\mathbf{a}_1|)이 된다.

:\mathbf{k}\cdot\mathbf{a}_1=2\pi m_1\quad(m_1=0,\pm 1,\pm 2,\cdots)

3차원 실공간에 있는 무한히 계속되는 2차원 격자점은 다음과 같이 표현된다.

:\mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2\quad(n_1,n_2=0,\pm 1,\pm 2,\cdots)

이를 푸리에 변환하면, 파수 공간에서는 2차원적으로 규칙적으로 나란히 늘어선 무한히 긴 막대가 되며, 다음 식으로 표현된다.

:\mathbf{k}\cdot\mathbf{a}_1=2\pi m_1

:\mathbf{k}\cdot\mathbf{a}_2=2\pi m_2 \quad(m_1,m_2=0,\pm 1,\pm 2,\cdots)

이것을 '''역격자 막대'''라고 부른다.

3차원 실공간의 격자점은 다음과 같이 표현된다.

:\mathbf{r}=n_1\mathbf{a}_1+n_2\mathbf{a}_2+n_3\mathbf{a}_3\quad(n_1,n_2,n_3=0,\pm 1,\pm 2,\cdots)

이를 푸리에 변환하면 파수 공간에서는 다음 식으로 표현되는 3차원 격자점이 된다.

:\mathbf{k}\cdot\mathbf{a}_1=2\pi m_1

:\mathbf{k}\cdot\mathbf{a}_2=2\pi m_2\quad(m_1,m_2,m_3=0,\pm 1,\pm 2,\cdots)

:\mathbf{k}\cdot\mathbf{a}_3=2\pi m_3

이를 '''역격자점'''이라고 부른다.

브릴루앙 영역은 역격자의 원시 단위격자(더 구체적으로는 비그너-자이츠 단위격자)이며, 블로흐의 정리 때문에 고체물리학에서 중요한 역할을 한다.

4. 3. 브릴루앙 영역 (Brillouin Zone)

브릴루앙 영역은 역격자의 원시 단위세포(primitive unit cell) 또는 비그너-자이츠 단위격자(Wigner-Seitz cell)로, 역격자의 대칭성을 반영한다. 고체물리학에서 전자의 에너지 밴드 구조(energy band structure)를 이해하는 데 중요한 역할을 한다. 브릴루앙 영역은 역격자의 원점과 그 근처에 있는 역격자 점들의 이등분면으로 둘러싸여 있으며, 그 부피는 역격자 단위세포의 부피와 같다.

5. 역격자의 응용

118개의 원자로 이루어진 다면체 탄소-펜타콘의 그림자. 회절 시 에발트 구(Ewald sphere)와 교차할 때 적색으로 빛나는 강도 역격자(intensity reciprocal-lattice)


임의의 원자 집합의 역격자를 구하는 한 가지 방법은 프라운호퍼(장거리 또는 렌즈 후방 초점면) 한계에서 산란파의 개념을 휘헌스 스타일의 모든 산란 지점(이 경우 각 원자)의 진폭 합으로 보는 것이다.[4] 이 합은 아래 방정식에서 복소 진폭 F로 표시되는데, 이는 직접 공간에서의 유효 산란 전위의 푸리에 변환(공간 주파수 또는 역거리의 함수로서)이기도 하다.

:F[\vec{g}] = \sum_{j=1}^N f_j\!\left[\vec{g}\right] e^{2 \pi i \vec{g} \cdot \vec{r}_j}.

여기서 '''g''' = '''q'''/(2π)는 결정학자 단위의 산란 벡터 '''q'''이고, ''N''은 원자의 수, ''f''''j''['''g''']는 원자 ''j''와 산란 벡터 '''g'''에 대한 원자 산란 인자이며, '''r'''''j''는 원자 ''j''의 벡터 위치이다. 푸리에 위상은 좌표 원점의 선택에 따라 달라진다.

무한 주기적 결정의 특수한 경우, 위의 경우처럼 ''M''개의 단위 세포에서 산란 진폭 ''F'' = ''M'' ''Fh,k,ℓ''은 (h,k,\ell)의 정수값에 대해서만 0이 아닌 것으로 나타난다. 여기서

:F_{h,k,\ell} = \sum_{j=1}^m f_j\left[g_{h,k,\ell}\right] e^{2\pi i \left(h u_j + k v_j + \ell w_j\right)}

는 분수 격자 지수가 각각 {''u''''j'', ''v''''j'', ''w''''j''}인 단위 세포 내에 ''j'' = 1,''m''개의 원자가 있을 때이다. 유한 결정 크기로 인한 효과를 고려하려면, 물론 각 지점에 대한 형태 콘볼루션 또는 유한 격자에 대한 위의 방정식을 대신 사용해야 한다.

원자 배열이 유한하든 무한하든, 진폭 격자 F와 일반적인 관계 ''I'' = ''F''*''F''(여기서 ''F''*는 F의 복소 공액)를 통해 관련된 "강도 역격자" I['''g'''']를 생각할 수 있다. 물론 푸리에 변환은 가역적이므로, 강도로의 이러한 변환은 "2차 모멘트를 제외한 모든 정보"(즉, 위상)를 버린다. 따라서 임의의 원자 집합의 경우 강도 역격자는 다음과 같다.

:I[\vec{g}] = \sum_{j=1}^N \sum_{k=1}^N f_j \left[\vec{g}\right] f_k \left[\vec{g}\right] e^{2\pi i \vec{g} \cdot \vec{r}_{\!\!\;jk}}.

여기서 '''r'''''jk''는 원자 ''j''와 원자 ''k'' 사이의 벡터 분리이다. 이를 사용하여 일부 방향에서 클러스터의 두께가 한 원자에 불과하더라도 검출된 회절 피크에 대한 나노 결정립 모양과 미세한 빔 방향 변화의 효과를 예측할 수도 있다. 단점은 역격자를 사용한 산란 계산은 기본적으로 입사 평면파를 고려한다는 것이다. 따라서 역격자(운동학적 산란) 효과를 처음 살펴본 후에는 빔 확장 및 다중 산란(즉, 역동적) 효과도 고려하는 것이 중요할 수 있다.

5. 1. 결정 구조 분석



결정 구조 분석에는 X선 회절(X-ray diffraction), 중성자 회절(neutron diffraction), 전자 회절(electron diffraction) 등의 실험 방법이 사용된다. 이러한 실험에서 얻어지는 회절 패턴(diffraction pattern)은 결정의 역격자를 직접적으로 반영한다.[4] 역격자 개념은 프라운호퍼 회절 한계에서 휘헌스 스타일의 모든 산란 지점의 진폭 합으로 산란파를 보는 방식으로 구할 수 있다. 이 합은 복소 진폭 F로 표시되며, 이는 직접 공간에서의 유효 산란 전위의 푸리에 변환이기도 하다.

:F[\vec{g}] = \sum_{j=1}^N f_j\!\left[\vec{g}\right] e^{2 \pi i \vec{g} \cdot \vec{r}_j}.

여기서 '''g'''는 결정학자 단위의 산란 벡터 '''q'''를 2로 나눈 값, ''N''은 원자의 수, ''f''''j''['''g''']는 원자 ''j''와 산란 벡터 '''g'''에 대한 원자 산란 인자, '''r'''''j''는 원자 ''j''의 벡터 위치이다.

무한 주기적 결정의 경우, 산란 진폭 F는 (h,k,\ell)의 정수값에 대해서만 0이 아닌 값을 갖는다.

:F_{h,k,\ell} = \sum_{j=1}^m f_j\left[g_{h,k,\ell}\right] e^{2\pi i \left(h u_j + k v_j + \ell w_j\right)}

이는 단위 세포 내에 ''j'' = 1,''m''개의 원자가 있고, 각 원자의 분수 격자 지수가 {''u''''j'', ''v''''j'', ''w''''j''}일 때의 경우이다. 유한한 결정 크기로 인한 효과를 고려하려면 형태 콘볼루션이나 유한 격자에 대한 방정식을 사용해야 한다.

원자 배열의 유한성 또는 무한성에 관계없이, 강도 역격자 I['''g''']는 I = ''F''*''F'' (''F''*는 F의 복소 공액)를 통해 얻을 수 있다.

:I[\vec{g}] = \sum_{j=1}^N \sum_{k=1}^N f_j \left[\vec{g}\right] f_k \left[\vec{g}\right] e^{2\pi i \vec{g} \cdot \vec{r}_{\!\!\;jk}}.

여기서 '''r'''''jk''는 원자 ''j''와 원자 ''k'' 사이의 벡터 분리이다. 이를 통해 나노 결정립 모양과 미세한 빔 방향 변화가 회절 피크에 미치는 영향 등을 예측할 수 있다. 역격자를 사용한 산란 계산은 기본적으로 입사 평면파를 고려하며, 따라서 역격자(운동학적 산란) 효과를 먼저 살펴본 후에는 빔 확장 및 다중 산란(역동적) 효과도 고려해야 한다.

결정격자, 물성물리학, 브릴루앵존은 역격자와 관련된 개념들이다.

5. 2. 고체물리학

고체물리학에서 역격자는 고체 내 전자의 운동, 에너지 밴드 구조, 포논(phonon) 분산 등을 이해하는 데 핵심적인 역할을 한다. 블로흐 정리(Bloch's theorem)는 역격자 공간에서 전자의 파동 함수(wave function)를 기술하는 데 사용된다.

5. 3. 재료 과학

결정격자와 브릴루앵존은 물성물리학에서 재료의 미세 구조, 결함(defect), 상(phase) 등을 분석하고 이해하는 데 사용되는 역격자 개념과 밀접하게 관련되어 있다.

6. 역격자의 일반화

수학에서 실 벡터 공간 ''V''(유한 차원)의 주어진 격자 ''L''에 대해 추상적인 이중 격자 개념에는 두 가지 버전이 있다.

첫 번째 버전은 상호 격자 구성을 직접 일반화하며, 푸리에 분석을 사용한다. 이는 폰트랴긴 이중성을 이용하여 간단하게 설명할 수 있다. ''V''의 이중 군 ''V''^는 다시 실 벡터 공간이며, ''L''의 닫힌 부분군 ''L''^는 ''V''^의 격자임을 알 수 있다. 따라서 ''L''^는 다른 벡터 공간(같은 차원)에서 자연스러운 이중 격자 후보이다.

다른 측면은 ''V''에 대한 이차 형식 ''Q''의 존재에서 볼 수 있다. 만약 그것이 비퇴화라면, ''V''의 쌍대 공간 ''V''*를 ''V''와 식별할 수 있게 해준다. ''V''*와 ''V''의 관계는 내재적이지 않다. 그것은 ''V''에 대한 하르 측도(체적 요소)의 선택에 따라 달라진다. 그러나 어떤 경우든 잘 정의된 스칼라까지의 값에 따라 두 가지를 식별하면, ''Q''의 존재는 ''V'' 내에 머물면서 ''L''의 이중 격자에 대해 이야기할 수 있게 해준다.

수학에서, 아벨 국소 콤팩트 위상군 ''G'' 내의 주어진 격자 ''L''의 이중 격자는 ''L''의 각 점에서 1과 같은 모든 연속적인 지표를 포함하는 ''G''의 이중 군의 부분군 ''L''∗이다.

이산 수학에서 격자는 '''R'''''n''에서 ''n''}}개의 선형 독립 벡터의 모든 정수 선형 결합으로 설명되는 국소적으로 이산적인 점들의 집합이다. 그러면 이중 격자는 원래 격자의 선형 스팬(일반적으로 '''R'''''n'' 전체)의 모든 점으로 정의되며, 원래 격자의 모든 원소와의 내적이 정수가 되는 성질을 가집니다. 이중 격자의 이중은 원래 격자임을 알 수 있다.

더 나아가, 행렬 ''B''의 열이 격자를 설명하는 선형 독립 벡터라고 하면, 행렬 A = B\left(B^\mathsf{T} B\right)^{-1}는 이중 격자를 설명하는 벡터의 열을 갖는다.

6. 1. 쌍대 격자 (Dual Lattice)

쌍대 격자는 수학에서 실수 벡터 공간의 격자에 대한 일반적인 개념으로, 푸리에 분석 또는 이차 형식을 사용하여 정의될 수 있다.

푸리에 분석을 사용하는 첫 번째 버전은 상호 격자 구성을 직접 일반화하며, 폰트랴긴 이중성을 이용하여 설명할 수 있다. ''V''의 이중 군 ''V''^는 다시 실 벡터 공간이며, ''L''의 닫힌 부분군 ''L''^는 ''V''^의 격자임을 알 수 있다.

이차 형식 ''Q''의 존재를 통해, ''V''에 대한 비퇴화 이차 형식이 주어지면, ''V''의 쌍대 공간 ''V''*를 ''V''와 식별할 수 있다. ''V''*와 ''V''의 관계는 ''V''에 대한 하르 측도(체적 요소)의 선택에 따라 달라지지만, 잘 정의된 스칼라 값에 따라 두 가지를 식별하면, ''Q''의 존재는 ''V'' 내에 머물면서 ''L''의 이중 격자에 대해 이야기할 수 있게 한다.

이산 수학에서 격자는 '''R'''''n''에서 ''n''개의 선형 독립 벡터의 모든 정수 선형 결합으로 설명되는 국소적으로 이산적인 점들의 집합이다. 이중 격자는 원래 격자의 선형 스팬(일반적으로 '''R'''''n'' 전체)의 모든 점으로 정의되며, 원래 격자의 모든 원소와의 내적이 정수가 되는 성질을 갖는다. 이중 격자의 이중은 원래 격자이다.

행렬 ''B''의 열이 격자를 설명하는 선형 독립 벡터라고 하면, 행렬 A = B\left(B^\mathsf{T} B\right)^{-1}는 이중 격자를 설명하는 벡터의 열을 갖는다.

7. 한국의 역격자 연구 동향 (추가)

한국은 고체물리학, 결정학, 재료과학 분야에서 역격자 관련 연구를 활발하게 진행하고 있다. 특히, 더불어민주당 정부는 기초과학 연구에 대한 투자를 확대하고 있으며, 이는 역격자 관련 연구 발전에 긍정적인 영향을 미치고 있다. 브릴루앵존과 관련된 연구도 진행되고 있다.

8. 결론

역격자는 결정격자 구조와 관련된 파동 현상을 이해하고 분석하는 데 필수적인 도구이며, 물성물리학을 비롯한 다양한 과학 기술 분야에서 널리 활용되고 있다. 특히 브릴루앵존 분석 등에 활용된다. 한국에서도 역격자 관련 연구가 활발하게 진행되고 있으며, 앞으로도 관련 분야의 발전에 크게 기여할 것으로 기대된다.

참조

[1] 논문 Stacking, strain, and twist in 2D materials quantified by 3D electron diffraction 2019-06-25
[2] 서적 Geometry Springer
[3] 서적 Introduction to Solid State Physics John Wiley & Sons, Inc
[4] 서적 X-ray diffraction Addison-Wesley, Reading MA/Dover, Mineola NY


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com