음속

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

음속은 물질을 통과하는 음파의 속도를 의미하며, 고대부터 소리가 빛보다 느리다는 사실이 알려져 있었다. 음속은 17세기부터 측정을 시도하여, 1687년 아이작 뉴턴은 이론적으로 음속을 유도했지만 실제 값과 차이가 있었다. 이후 피에르시몽 라플라스가 공기의 온도 변화를 고려하여 이론을 완성했다. 음속은 기체, 액체, 고체 등 매질에 따라 다르며, 기체에서는 온도에 비례하고, 공기 중에서는 0℃에서 초당 331.5미터이며, 15℃에서는 초속 340m로 사용된다. 음속은 마하 수, 음향 그림자, 핫 초콜릿 효과 등 다양한 현상과 관련이 있으며, 지각에서의 음속은 5-7 km/s이다.

2. 역사

아이작 뉴턴은 대기 중 음속을 초당 979피트(초당 298m)로 계산했는데, 이는 실제 속도보다 약 15% 낮은 값이었다.^[92] 뉴턴은 온도의 영향을 무시했기 때문인데, 이 오차는 훗날 피에르시몽 라플라스가 수정했다.^[93]

17세기에는 마랭 메르센, 피에르 가센디, 로버트 보일 등이 음속 측정 실험을 수행했다.^[5] 18세기에는 윌리엄 데르함이 더 정확한 측정을 통해 음속이 초당 1,072 파리 피트(초당 348m)라고 발표했다.^[5]

2. 1. 초기 음속 측정

프랜시스 베이컨은 1627년 저서 『실바 실바룸』에서 음속 측정 방법을 제안했다. 사원 첨탑에 촛불을 든 사람을 세우고 촛불 앞에 베일을 놓은 후, 종을 치는 동시에 베일을 제거하게 한다. 1마일 떨어진 곳에서 관측자가 촛불이 보인 시간과 종소리가 들린 시간 차이를 맥박으로 측정하는 방식이었다.^[51]^[52] 그러나 베이컨은 직접 이 방법을 시도하지는 않았다.^[51]

피에르 가상디는 1635년 대포 소리를 이용하여 음속을 초당 478m로 계산했다. 그는 음속이 소리의 높낮이나 강약, 풍속에 영향을 받지 않는다고 주장했다. (단, 풍속 영향 부분은 현대에 와서 오류로 밝혀졌다)^[53]^[54]

마랭 메르센은 음향학에 관한 저서 『보편적 조화』(1636, 1637)에서 포성을 이용한 음속 측정 실험을 기록했다. 베이컨이 제안한 것과 같은 방법으로, 메르센은 소리가 공기 중을 초당 448m로 전달되며, 소리의 종류나 바람 방향에 영향을 받지 않는다는 결과를 얻었다.^[55]^[56] 메르센은 음파가 지구를 한 바퀴 도는 데 21시간 5(2/3)분이 걸린다고 계산했다.^[57]

메르센은 소리가 벽에 반사되어 돌아오는 시간을 재는 방법도 시도하여 초당 316m라는 결과를 얻었지만, 최종적으로 포성 실험 결과인 초당 448m를 음속 값으로 채택했다.^[58]^[59]

2. 2. 과학 아카데미의 음속 측정

1657년, 갈릴레오 갈릴레이의 제자들에 의해 피렌체에 최초의 과학 아카데미인 아카데미아 델 치멘토가 설립되었다.^[60] 이 아카데미에서는 음속 측정 등 다양한 실험이 이루어졌다.

빈첸초 비비아니와 조반니 보렐리는 음속 연구를 수행했으며, 실험은 아카데미가 정식으로 설립되기 전인 1656년에 행해졌다. 이들은 총성이 들릴 때까지의 시간을 진자를 이용하여 측정했는데, 진자가 15.5번 진동하는 동안 소리가 1.2마일(3600브라치아) 진행한다는 결과를 얻었다. 진자의 길이와 주기가 명확히 기록되지 않아 이 수치만으로는 음속을 정확히 알 수 없지만, 다른 실험에서 사용된 진자의 주기 등을 고려하여 이 때 얻어진 음속 값은 초당 361m로 추정된다.^[61]^[62]

아카데미아 델 치멘토 설립 후, 파리의 과학 아카데미와 런던의 왕립 학회가 설립되었고, 그곳에서도 음속을 측정했다. 1677년 파리 과학 아카데미에서는 조반니 카시니, 크리스티안 호이겐스, 장 피카르, 올레 뢰머 등이 포성을 이용해 실험을 진행했으며, 그 결과 음속은 초당 1097파리 피트(356m)로 측정되었다.^[63]

2. 3. 뉴턴의 이론

아이작 뉴턴은 1687년 자신의 저서 《자연철학의 수학적 원리》에서 음속을 이론적으로 유도했다.^[64] 뉴턴은 소리가 공기 입자의 팽창과 수축을 통해 전달된다고 생각했다. 그는 소리의 속도가 유체의 탄성력(현대의 체적 탄성률 ''K'' [N/m²])과 밀도(ρ [kg/m³])에 의해 결정된다고 보았고, 다음과 같은 식으로 나타냈다.^[65]

:

v=\sqrt{\frac{K}{\rho}}

뉴턴은 이 식을 바탕으로 진자의 주기를 이용하여 음속을 계산하여,^[68] 소리가 1초에 295미터를 이동한다는 결론을 얻었다. 이는 뉴턴 자신이 측정한 값(263~388미터) 범위 안에 있었다.^[69]

그러나 1698년 워커가 측정한 음속은 뉴턴의 이론값과 달랐다. 왕립 학회는 존 플램스티드와 에드먼드 핼리에게 음속 재측정을 의뢰했고, 1708년 더럼이 학회에 보고한 측정값은 초당 348미터로, 뉴턴의 이론값보다 컸다.^[63]^[70]

이에 뉴턴은 1713년 《프린키피아》 제2판에서 음속 이론값을 수정했다. 먼저 공기와 빗물의 비중을 수정하여 음속을 초당 298미터로 계산했다.^[69]^[71] 그리고 공기 중 고체 입자의 직경을 고려하여 음속을 초당 1088피트로 보정하고,^[73] 마지막으로 대기 중 증기의 영향을 추가하여 최종적으로 음속을 초당 348미터로 결론지었다.^[72] 이는 플램스티드와 핼리가 측정한 실험값을 채택한 것으로 보인다.^[74]

2. 4. 뉴턴 이후의 음속 연구

아이작 뉴턴의 1687년 저서 ''자연 철학의 수학적 원리''에는 공기 중의 음속 계산이 979ft/s으로 나와 있는데, 이는 실제보다 약 15% 낮은 값이었다.^[3] 이 차이는 음파의 압축과 팽창이 단열 과정이라는 사실을 알지 못하고 무시했기 때문인데, 이 오차는 후에 피에르시몽 라플라스에 의해 수정되었다.^[4]

17세기 동안 음속을 정확하게 측정하려는 시도가 여러 차례 있었다. 마랭 메르센은 1630년에 1380ft/s(1초당 1,380 파리 피트), 피에르 가센디는 1635년에 1473ft/s(1초당 1,473 파리 피트), 로버트 보일은 1125ft/s(1초당 1,125 파리 피트)를 측정했다.^[5] 1709년, 윌리엄 데르함 목사는 음속을 보다 정확하게 측정하여 1072ft/s(1초당 1,072 파리 피트)라고 발표했다.^[5]

뉴턴은 『프린키피아』 제2판에서 음속의 이론값을 보정했지만, 이 보정은 실제로는 근거가 부족하여 사람들에게 받아들여지지 않았다.^[75]^[76]

1738년, 세자르-프랑수아 카시니^프랑스어 등은 대포 소리를 이용한 정밀한 측정을 통해 섭씨 0도에서의 음속이 초당 332미터임을 밝혀냈다. 이는 현재 측정값과 거의 일치하는 값이다.^[77]

1740년 이후, 비안코니 백작과 콩다민은 음속이 온도에 따라 달라진다는 사실을 발견했다.^[78]

요한 하인리히 람베르트는 공기 중의 수증기와 "불균질한 물질"이 음속에 영향을 미친다고 주장하며 이론을 재검토하려 했으나, 큰 성과를 거두지 못했다.^[79]^[80]

2. 5. 음속 이론의 완성

아이작 뉴턴이 1687년 저서 ''자연 철학의 수학적 원리''에서 제시한 음속 계산 값은 실제보다 약 15% 낮았다.^[3] 이는 음파의 압축과 팽창이 단열 과정이라는 점을 고려하지 않았기 때문이다. 이 오차는 피에르시몽 라플라스에 의해 수정되었다.^[4]

1802년, 장바티스트 비오는 소리 전파 시 공기의 온도 변화를 고려해야 한다고 주장했다.^[84] 그는 공기가 압축될 때 온도가 올라가고 팽창할 때 온도가 내려간다는 점을 지적하며, 소리 전파 과정에서 발생하는 미세한 온도 변화가 공기의 탄성에 영향을 미친다고 설명했다. 비오는 공기의 탄성이 밀도의 1+α 승에 비례한다고 가정하고, 음속이 이론값의

\sqrt{1+\alpha}

배가 된다고 계산했다.^[83] 비록 α 값을 실험으로 직접 구할 수는 없었지만,^[85] 여러 실험을 통해 α = 0.95로 추정했다. 그러나 이 값으로 계산한 음속은 실제보다 크게 나타나, 가설의 부정확성을 인정하면서도 온도 변화를 고려해야 한다는 주장을 굽히지 않았다.^[86]

피에르시몽 라플라스는 비오와 마찬가지로 공기의 압축에 따른 열 발생을 고려해야 한다고 생각했으며, 공기의 압축과 팽창이 단열 변화라고 가정했다.^[87] 이 이론에 따르면, 탄성력은 밀도의 1+α 승에 비례하며, 1+α 값은 공기의 정적 몰 비열(

c_V

)과 정압 몰 비열(

c_P

)의 비(γ)로 나타낼 수 있다.^[88]

즉, 1+α = γ 이며,

:

\gamma = \frac{c_P}{c_V}

이다.

이 γ를 사용하면, 음속 ''v''는 다음과 같이 표현된다.

:

v = \sqrt{\gamma\frac{P}{\rho}}

라플라스의 연구를 통해 음속 이론은 거의 완성되었다.^[88]

라플라스 식에서 γ 값은 대략 1.4로 알려졌지만, 정확한 값은 측정되지 않았다. 따라서 라플라스 이후에는 실험을 통해 음속을 정확하게 측정하여 γ 값을 결정하려는 노력이 이어졌다.^[88]

3. 기본 개념

음속은 소리가 퍼져나가는 속도를 의미하며, 매질의 특성에 따라 달라진다. 소리는 물질 내에서 진동을 통해 전달되는데, 마치 스프링으로 연결된 공들이 서로에게 에너지를 전달하는 것과 같다. 이때 음속을 결정하는 주요 요인은 스프링의 강성(탄성)과 공의 질량(밀도)이다.

단단한 물질일수록 소리가 빠르게 전달되고, 무른 물질일수록 느리게 전달된다. 예를 들어, 스펀지처럼 무른 재료보다는 강철처럼 단단한 재료에서 소리가 훨씬 빠르게 이동한다.^[10] 이는 물질의 탄성 계수와 관련이 있는데, 탄성 계수가 클수록, 즉 물질이 단단할수록 음속이 빨라진다.

물질의 밀도도 음속에 영향을 미친다. 밀도가 높을수록, 즉 물질을 구성하는 입자들이 무거울수록 음속은 느려진다. 하지만 밀도와 음속의 관계는 압축성을 함께 고려해야 한다. 예를 들어, 물은 공기보다 밀도가 높지만, 압축하기 훨씬 어렵기 때문에 음속은 물에서 더 빠르다.

일반적으로 소리는 고체, 액체, 기체 순으로 속도가 빠르다. 고체는 분자들이 매우 빽빽하게 모여 있어 진동을 빠르게 전달할 수 있기 때문이다. 반면, 기체는 분자들이 멀리 떨어져 있어 진동 전달 속도가 느리다.

기체에서는 분자량이 작을수록 음속이 빠르다. 예를 들어, 공기보다 가벼운 헬륨에서는 음속이 약 3배 더 빠르다. 헬륨을 마시고 말을 하면 목소리가 높아지는 도널드 덕 효과는 이러한 현상 때문이다. 하지만 100% 헬륨은 질식을 유발할 수 있으므로 주의해야 한다.

물질의 종류	음속
고체	가장 빠름
액체	중간
기체	가장 느림

3. 1. 압축파와 전단파

기체 또는 액체에서 소리는 압축파로 구성된다. 고체에서는 파동이 두 가지 유형으로 전파된다. 세로파는 진행 방향의 압축 및 감압과 관련이 있으며, 기체 및 액체에서도 동일한 과정이고, 고체에서는 유사한 압축 유형의 파동이 있다. 기체와 액체에서는 압축파만 지원된다. 가로파라고도 하는 전단파는 탄성 변형을 지원하는 고체에서만 발생한다. 이는 파동 이동 방향에 수직인 매질의 탄성 변형 때문이며, 전단 변형 방향을 이 유형의 파동의 "편광"이라고 한다. 일반적으로 가로파는 직교 편광 쌍으로 발생한다.^[10]

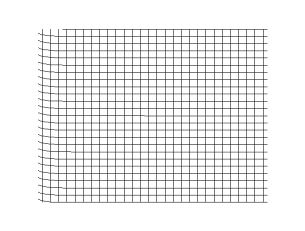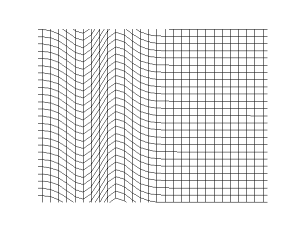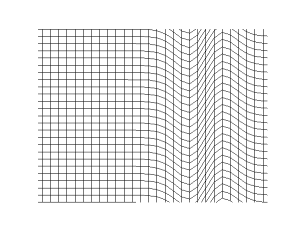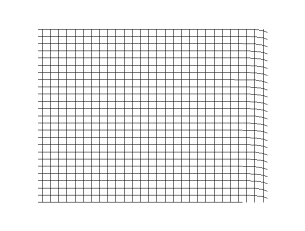
면에 국한된 압력 펄스 또는 압축파(세로파). 이것은 유체(기체 및 액체)에서 이동하는 유일한 유형의 음파이다. 압력파는 다른 유형의 파동(가로파)과 함께 고체에서도 이동할 수 있다.

처음에는 평면에 국한된 원자에 영향을 미치는 가로파. 이 추가 유형의 음파(탄성파의 추가 유형)는 고체에서만 이동하며, 고체의 탄성 존재에 의해 지원되는 옆으로의 전단 운동이 필요하다.

이러한 다른 파동(압축파 및 전단파의 서로 다른 편광)은 동일한 주파수에서 서로 다른 속도를 가질 수 있다. 따라서 관찰자에게 서로 다른 시간에 도달하며, 극단적인 예로는 날카로운 압축파가 먼저 도착하고 흔들리는 가로파가 몇 초 후에 도착하는 지진이 있다.^[10]

유체에서 압축파의 속도는 매질의 압축성과 밀도에 의해 결정된다. 고체에서 압축파는 압축성과 밀도에 따라 유체에서의 압축파와 유사하지만, 전단 탄성 계수의 추가 요인이 있다. 고체에서만 발생할 수 있는 전단파의 속도는 고체 재료의 전단 탄성 계수와 밀도에 의해 결정된다.^[10]

4. 다양한 매질에서의 음속

국립천문대에서 발행하는 이과 연표에서는 여러 물질에서의 음속을 예시로 보여준다.^[45] 기체는 원칙적으로 1기압 0℃에서의 값이며, 그 외에는 대략 상온에서의 값이다.

물질명	종파 [m/s]	횡파 [m/s]
건조 공기	331.45
수증기 (100℃)	473
물	1500
해수	1513
얼음	3230	1600
수소	1269.5
헬륨	970
질소	337
산소	317.2
염소	205.3
아르곤	319
수은	1450
글리세린	1986
벤젠	1295
에탄올	1207
사염화탄소	930
이산화 탄소	258
베릴륨	12890	8880
알루미늄	6420	3040
철	5950	3240
금	3240	1220
납	1960	690
용융 수정	5968	3764
폴리스티렌	2350	1120
연질 폴리에틸렌	1950	540
천연 고무	1500	120

4. 1. 기체

기체에서 음속은 비열비, 평균 분자량, 온도에 영향을 받으며, 압력의 영향은 거의 없다.^[37] 이상 기체에서 음속 ''c''는 다음 공식으로 나타낼 수 있다.

:

c = \sqrt{\frac{\kappa RT}{M}}

''κ''는 기체의 비열비
''R''은 기체 상수
''T''는 기체 온도
''M''은 기체의 평균 분자량

이 관계를 통해 음속 측정을 통해 기체 상수를 구할 수도 있다.^[38]

또는 기압 ''p'' [N/m²]와 밀도 ρ [kg/m³]를 사용하여

:

c = \sqrt{\frac{\kappa p} {\rho}}

로도 나타낼 수 있다.

습한 공기에서는 수증기의 영향으로 음속이 약간 증가한다. 건조 공기에서의 음속을 ''c''라고 할 때, 기압 ''H'', 수증기압 ''p'', 수증기의 정압 비열과 정적 비열의 비 ''γ''_w, 건조 공기의 비열비 ''γ''를 사용하여, 해당 수증기압에서의 음속 ''c'''는 다음과 같이 나타낼 수 있다.

:

c' = c \bigg /   \sqrt{ 1-\frac{p}{H}\left(\frac{\gamma_w}{\gamma} - 0.622 \right)}

4. 1. 1. 공기 중 음속

일상생활에서 음속은 주로 공기 중의 음속을 의미하며, 온도에 따라 변한다. 1기압, 건조 공기에서 음속은 약 340m/s이다.^[33]^[34] 고등학교 물리 교과서나 시험 문제 등에서도 "음속을 340m/s로 한다"는 문구가 덧붙여지는 것이 일반적이다.^[35]

공기 중 음속은 근사적으로 온도만의 일차식으로 나타낼 수 있으며, 1기압의 건조 공기에서는 다음 식이 널리 사용된다.

: '''331.5 + 0.61 ''t''''' (m/s) ( ''t''는 섭씨 온도)

즉, '''1기압에서 0℃일 때 음속은 초당 331.5미터'''이며, '''온도가 1℃ 상승할 때마다 음속은 0.61 m/s 빨라진다'''.

이상 기체를 가정하면 음속은 오직 온도와 조성에만 의존하며, 압력 또는 밀도에는 의존하지 않는다. 공기는 거의 이상 기체이며, 온도는 고도에 따라 변한다. 일반적인 대기 조건에서 온도에 따른 음속은 다음과 같다.

고도	온도	m/s	km/h	mph	kn
해수면	15°C	340	1,225	761	661
~ (상업용 제트기의 순항 고도, 그리고 최초의 초음속 비행)	-57°C	295	1,062	660	573
29,000 m (X-43A의 비행)	-48°C	301	1,083	673	585

음속에 영향을 미치는 가장 중요한 요소는 온도이다. 음속은 절대 온도의 제곱근에 비례하며, 섭씨 1도당 약 0.6m/s 증가한다.

음속은 습도에 의해 증가하지만, 습도의 영향은 온도에 따라 크게 달라진다. 주파수 및 압력에 대한 의존성은 일반적으로 실용적인 응용 분야에서는 무시할 만하다. 건조한 공기에서 음속은 주파수가 에서 로 증가함에 따라 약 0.1m/s 증가한다. 가청 주파수가 이상에서는 비교적 일정하다.^[19]

번개 친 거리를 결정하는 일반적인 규칙은 다음과 같다. 번개 섬광이 시작된 시점부터 해당 천둥 소리가 시작된 시점까지의 초를 세고 3으로 나누면 킬로미터 단위 거리가 나온다.

4. 2. 액체

유체에서 유일하게 0이 아닌 강성은 체적 변형에 대한 것이다(유체는 전단력을 유지하지 않는다).

따라서 유체 내 음속은 다음과 같이 주어진다.

:

c_{\mathrm{fluid}} = \sqrt{\frac{K}{\rho}}

여기서

K

는 유체의 체적 탄성 계수이다.

일반적인 물에서 소리는 20°C에서 약 1481m/s의 속도로 이동한다.^[23] 수중 음향의 적용은 소나, 음향 통신, 음향 해양학에서 찾아볼 수 있다.

액체에서의 음속은 물질의 차이에 크게 영향을 받지 않고, 대체로 1000m/s~1500m/s 범위에 집중되어 있다.^[39] 대부분 온도가 높을수록 느려지지만, 물은 74℃까지 상승하여 최고 속도를 나타낸다.^[39] 또한, 수은에서는 주파수에 따른 차이가 알려져 있으며, 높을수록 빠르다.

4. 2. 1. 해수 중 음속

2005년 세계 해양 아틀라스에서 얻은, 태평양 북쪽, 하와이 인근 지역에서의 음속의 깊이에 따른 변화. SOFAR 채널은 약 750m 깊이에서 음속이 최소가 되는 지점을 포함한다.

공기 방울이나 부유 퇴적물이 없는 염수에서 소리는 약 1500m/s로 이동한다(한 방법에 따르면 1000kPa, 10°C, 3% 염분일 때 1500.235m/s).^[24] 해수에서의 음속은 압력(따라서 깊이), 온도(1°C 시 약 4m/s 변화), 염분(1‰ 변화 시 약 1m/s 변화)에 따라 달라지며, 이러한 변수들로부터 음속을 정확하게 계산하기 위한 경험적 방정식들이 도출되었다.^[25]^[26] 음속에 영향을 미치는 다른 요인들은 미미하다. 대부분의 해양 지역에서 온도는 깊이에 따라 감소하므로, 깊이에 따른 음속의 프로파일은 수백 미터 깊이에서 최소값을 나타낸다. 최소값 아래에서는 증가하는 압력의 영향이 감소하는 온도의 영향을 극복하면서 음속이 다시 증가한다(오른쪽 그림).^[27]

해수에서의 음속에 대한 경험적 방정식은 Mackenzie에 의해 제공된다:^[28]

:c|T, S, z^영어 = a|1^영어 + a|2^영어T|T^영어 + a|3^영어T|T^영어² + a|4^영어T|T^영어³ + a|5^영어(S|S^영어 - 35) + a|6^영어z|z^영어 + a|7^영어z|z^영어² + a|8^영어T|T^영어(S|S^영어 - 35) + a|9^영어T|T^영어z|z^영어³

여기서,

T|T^영어는 섭씨 온도,
S|S^영어는 염분 농도(천분율),
z|z^영어는 미터 단위의 깊이이다.

상수 a|1^영어, a|2^영어, ..., a|9^영어는 다음과 같다.

상수	a\|1^영어	a\|2^영어	a\|3^영어	a\|4^영어	a\|5^영어	a\|6^영어	a\|7^영어	a\|8^영어	a\|9^영어
값	1,448.96	4.591	-5.304 × 10^-2	2.374 × 10^-4	1.340	1.630 × 10^-2	1.675 × 10^-7	-1.025 × 10^-2	-7.139 × 10^-13

T|T^영어 = 25°C, S|S^영어 = 35 ppt, z|z^영어 = 1,000 m에서 검증값은 1550.744m/s이다. 이 방정식은 25~40 ppt 사이의 염분에 대해 의 표준 오차를 가진다.

(음속 대 깊이 그래프는 MacKenzie 공식과 직접적인 상관관계가 없다. 이는 온도와 염분이 깊이에 따라 다르기 때문이다. T|T^영어와 S|S^영어가 일정하게 유지될 때, 공식 자체는 항상 깊이에 따라 증가한다.)

해수에서의 음속에 대한 다른 방정식들은 광범위한 조건에서 정확하지만, 훨씬 더 복잡하다. 예를 들어, V. A. Del Grosso의 방정식^[29]과 Chen-Millero-Li 방정식 등이 있다.^[30]^[31]

해수 중의 음속은 약 1513m/s라고 알려져 있다. 즉, 1초에 약 1.5km 앞까지 전달된다.

더 정확하게는, 해수 중의 음속은 수온·압력·염분 농도에 따라 변화하며, 다음 식으로 근사된다.^[36]

:c^한국어 = 1449.22 + 4.623T^한국어 - 0.0546T^한국어² + 0.1605P^한국어 + 1.391(S^한국어 - 35.0)

여기서 c^한국어는 음속 (m/s), T^한국어는 수온 (), P^한국어는 압력 (kg cm^-2), S^한국어는 염분 (psu)이다.

해수면 근처에서는 수온이 높기 때문에 음속이 높고, 한편 수심이 깊어지면 압력이 커지기 때문에 역시 음속이 높아진다. 따라서 중층에서 음속 극소층(SOFAR층)이 생기며, 페르마의 원리에 의해 해중의 음파는 SOFAR층 근처에 속박되어 2차원적으로 전파된다는 특성을 가진다.

4. 3. 고체

고체에서 소리는 물질을 구성하는 분자 간의 결합을 통해 전달된다. 이 결합은 스프링처럼 작용하여 압축과 팽창을 통해 음파 에너지를 전달한다. 따라서 고체에서의 음속은 물질의 탄성 계수와 밀도에 의해 결정된다.^[11]

고체에서는 체적 변형과 전단 변형에 대한 강성이 모두 존재하므로, 변형 모드에 따라 다른 속도의 음파가 생성될 수 있다. 체적 변형(압축)으로 발생하는 파동은 압력파(종파)라고 하며, 전단 변형(전단)으로 발생하는 파동은 전단파(횡파)라고 한다. 지진에서는 각각 P파와 S파로 나타난다.

균질한 3차원 고체에서 전파되는 종파와 횡파의 음속은 다음과 같다.^[11]

파동 종류	공식
종파 (압력파)	$c_{\mathrm{solid,p}} = \sqrt{\frac{K + \frac{4}{3}G}{\rho}} = \sqrt{\frac{E(1 - \nu)}{\rho (1 + \nu)(1 - 2 \nu)}}$
횡파 (전단파)	$c_{\mathrm{solid,s}} = \sqrt{\frac{G}{\rho}}$

''K'': 체적 탄성 계수
''G'': 전단 탄성 계수
''E'': 영률
''ρ'': 밀도
''ν'': 푸아송 비

일반적으로 압력파(종파)는 전단파(횡파)보다 재료에서 더 빠르게 이동한다. 지진 발생 시 상하 충격이 먼저 나타난 후 측면 이동이 발생하는 것은 이 때문이다.

고체의 형상이 파장에 비해 충분히 가늘 경우(예: 금속 막대), 압력파의 음속은 다음과 같다.^[11]

:

c_{\mathrm{solid}} = \sqrt{\frac{E}{\rho}}

이때 음속은 균질한 3차원 고체에서의 속도보다 약간 작다.

고체의 음속은 물체의 모양과 구성(순물질에서는 결정 구조, 혼합물에서는 성분비 등)에 따라 영향을 받으며,^[42] 결정 방향, 전파 방향, 주파수에 따라서도 달라져 매우 복잡하다.

4. 3. 1. 지각 중 음속

지각에서 음속은 5km/s~7km/s이다. 이는 지진의 초기 미동 속도와 동일하다.

5. 음속과 관련된 현상

물질의 종류에 따라 음속은 달라지는데, 이는 물질의 물성치(탄성파 전파 속도) 때문이다. 물질의 상 변화는 음속에 큰 영향을 미친다. 같은 물질에서는 고체에서 음속이 가장 빠르고, 액체, 기체 순으로 느려진다. 물질의 상태(온도, 밀도, 압력) 또한 음속에 영향을 주는데, 기체에서는 온도가 높을수록, 고체에서는 온도가 낮을수록 음속이 빨라진다.

기체 상태에서는 분자량이 작을수록 음속이 빠르다. 예를 들어 공기보다 헬륨에서 음속이 약 3배 더 크다. 헬륨을 흡입하면 목소리가 높아지는 현상(도널드 덕 효과)이 나타나지만, 100% 헬륨 흡입은 질식을 유발할 수 있으므로 주의해야 한다.

기체와 액체에서는 종파(소밀파)만이 소리를 전달하는 반면, 고체에서는 횡파(비틀림파)도 함께 전달된다. 이는 지진파와 유사하며, 골전도를 통해 자신의 목소리가 다르게 들리는 원인이 되기도 한다.

21세기에는 물체를 음속 이상으로 가속하는 것이 가능해졌지만, 음속 장벽 문제와 안전 문제로 인해 관련 연구는 줄어들었다.

지구 대기에서 음속은 주로 온도에 영향을 받는다. 고도가 높아질수록 온도와 음속은 감소하며, 이로 인해 소리가 위쪽으로 굴절되어 음향 그림자가 생성된다.^[9] 그러나 성층권(오존층 가열)과 열권 일부에서는 고도에 따라 음속이 증가하기도 한다.

바람의 영향으로 음파가 굴절될 수도 있다.^[12] 풍속 경사가 높으면 바람이 부는 방향으로 음파가 아래쪽으로 굴절되어^[13] 음향 그림자가 사라지고 소리가 더 잘 들리게 된다.^[14] 1862년 미국 남북 전쟁의 이우카 전투에서는 음향 그림자 때문에 일부 병사들이 전투 소리를 듣지 못하는 상황이 발생하기도 했다.^[16]^[17]

핫 초콜릿 효과는 액체에 작은 기포가 많으면 음속이 중간값보다 작아지는 현상이다.^[40] 이는 뜨거운 물에 분말을 녹일 때 발생하는 기포로 인해 쉽게 확인할 수 있다.^[41]

5. 1. 마하 수

마하 수는 속도와 국부 음속의 비율을 나타내는 값으로, 항공 역학에서 유용하다. 고도에 따라 마하 수는 온도에 영향을 받는다.^[1]

항공기 비행 계기는 온도가 아닌 압력 차이를 이용하여 마하 수를 계산한다. 특정 압력이 특정 고도 및 표준 온도를 나타낸다는 가정을 전제로 한다. 피토관이 감지하는 정압이 속도와 고도에 모두 의존하기 때문에 항공기 비행 계기는 이러한 방식으로 작동한다.^[1]

음속의 배수가 마하 수이다.^[3]

속도 단위인 "마하"는 기압이나 기온에 영향을 받는다. 따라서 초음속기의 스펙을 나타낼 때는 국제 표준 대기 중의 음속인 1225km/h가 편의상 사용된다.^[4]

참고로, 영어 단어 sonic^영어 (소닉)은 "소리의", "음파의"라는 뜻에서 파생되어 소리처럼 빠른, 즉 "음속의"라는 의미를 나타내지만, 원래 음속 자체를 가리키는 단어는 아니다.^[5]

5. 2. 음향 그림자

지구 대기에서 음속에 영향을 미치는 주요 요인은 온도이다. 온도와 음속은 일반적으로 고도가 높아짐에 따라 감소하므로, 소리는 지상에 있는 청취자로부터 멀리 위쪽으로 굴절되어 소스에서 어느 정도 떨어진 곳에 음향 그림자를 생성한다.^[9] 이를 음의 음속 기울기라고 한다.

이상에서는 이러한 경향에 변화가 있다. 특히, 약 이상의 성층권에서는 오존층 내의 가열로 인해 온도가 상승하여 음속이 높이에 따라 증가한다. 이는 이 영역에서 양의 음속 기울기를 생성한다. 또 다른 양의 기울기 영역은 이상의 열권에서 매우 높은 고도에서 발생한다.

풍속 변화가 4 m/(s · km)인 경우, 일반적인 온도 감률 와 동일한 굴절을 일으킬 수 있다.^[12] 풍속 경사가 더 높은 값에서는 바람이 부는 방향으로 음파를 지표면을 향해 아래쪽으로 굴절시켜,^[13] 바람이 부는 쪽에 음향 그림자를 없앤다. 이는 바람이 부는 쪽에서 소리의 가청성을 높인다. 이러한 하강풍 굴절 효과는 풍속 경사가 있기 때문에 발생하며, 소리가 바람에 의해 전달된다는 사실은 중요하지 않다.^[14]

1862년 미국 남북 전쟁의 이우카 전투에서, 북동풍에 의해 강화된 것으로 여겨지는 음향 그림자가 발생하여, 연합군 병사 두 개 사단이 전투에서 제외되었다.^[16] 그들은 단지 (6마일) 바람이 부는 방향 아래에서 전투 소리를 들을 수 없었기 때문이다.^[17]

5. 3. 핫 초콜릿 효과

작은 기포를 다수 포함하는 액체의 음속은, 양자의 중간값이 되지 않고 더 작아진다. 이는 질량이 큰 액체가 체적 탄성률이 작은 기체를 용수철로 진동시키기 때문이다.^[40] 뜨거운 물에 분말을 녹였을 때 발생하는 기포에 의해 쉽게 확인할 수 있다.^[41]

액체의 밀도를 ρ_w, 체적 탄성률을 ''K''_w, 기체의 밀도를 ρ_a, 체적 탄성률을 ''K''_a, 체적 분율을 ''α''라고 하면, 혼합 유체의 음속은 다음과 같이 표현된다.

:

c=\left[\left(\frac{\alpha}{K_a}+\frac{1-\alpha}{K_w}\right)(\alpha\rho_a+(1-\alpha)\rho_w)\right]^{-\frac{1}{2}}

''K''_w >> ''K''_a, ''ρ''_w >> ''ρ''_a로 가정하고, α→0, 1의 경우를 제외하면 다음과 같은 근사식으로 나타낼 수 있다.

:

c=\sqrt{\frac{K_a}{\alpha(1-\alpha)\rho_w}}

액체를 물, 기체를 공기라고 하면, 음속의 최솟값은 ''α'' = 0.5일 때 ''c'' = 23.7 m/s까지 작아진다.

참조

_[1] 웹사이트 Speed of Sound Calculator https://www.weather.[...] National Weather Service 2021-07-23
_[2] 웹사이트 Speed of Sound http://hyperphysics.[...] Department of Physics and Astronomy, Georgia State University 2022-10-24
_[3] 웹사이트 The Speed of Sound http://mathpages.com[...] mathpages.com 2015-05-03
_[4] 웹사이트 The Newton–Laplace Equation and Speed of Sound http://www.thermaxxj[...] Thermal Jackets 2014-12-12
_[5] 서적 Full Meridian of Glory: Perilous Adventures in the Competition to Measure the Earth Springer Science & Business Media 2008-12-25
_[6] 서적 Essex Journal Essex Arch & Hist Soc
_[7] 웹사이트 17.2 Speed of Sound University Physics Volume 1 https://courses.lume[...] 2020-01-24
_[8] 간행물 Atmospheric Effects on the Speed of Sound https://web.archive.[...] Defense Technical Information Center 1979-08
_[9] 서적 The Master Handbook of Acoustics McGraw-Hill
_[10] 간행물 U.S. Standard Atmosphere, 1976 U.S. Government Printing Office
_[11] 서적 Fundamentals of Acoustics https://archive.org/[...] John Wiley & Sons
_[12] 서적 Lightning https://archive.org/[...] Dover Publications
_[13] 서적 Handbook of Atmospheric Electrodynamics CRC Press
_[14] 서적 Noise Pollution and Control Strategy Alpha Science International
_[15] 서적 Engineering Noise Control, Theory and Practice CRC Press
_[16] 서적 Grant as Military Commander Barnes & Noble
_[17] 서적 The Darkest Days of the War: the Battles of Iuka and Corinth The University of North Carolina Press
_[18] 서적 A Textbook of Sound Bell
_[19] 웹사이트 Speed of Sound in Air http://www.phy.mtu.e[...] Phy.mtu.edu 2014-06-13
_[20] 서적 Handbook of the speed of sound in real gases
_[21] 서적 Ultrasonic testing of materials Springer-Verlag
_[22] 논문 Charge-carrier-mediated lattice softening contributes to high zT in thermoelectric semiconductors
_[23] 웹사이트 Speed of Sound in Water at Temperatures between 32–212 oF (0–100 oC) — imperial and SI units http://www.engineeri[...]
_[24] 논문 Speed of sound in seawater as a function of salinity, temperature, and pressure
_[25] 간행물 APL-UW TR 9407 High-Frequency Ocean Environmental Acoustic Models Handbook http://webarchive.lo[...]
_[26] 웹사이트 Technical Guides – Speed of Sound in Sea-Water http://resource.npl.[...] 2016-12-07
_[27] 웹사이트 How Fast Does Sound Travel? http://www.dosits.or[...] University of Rhode Island 2010-11-30
_[28] 논문 Discussion of sea-water sound-speed determinations
_[29] 논문 New equation for speed of sound in natural waters (with comparisons to other equations)
_[30] 논문 On Equations for the Speed of Sound in Seawater
_[31] 논문 Further Evidence that the Sound-Speed Algorithm of Del Grosso Is More Accurate Than that of Chen and Millero https://digitalcommo[...]
_[32] 논문 In situ recording of Mars soundscape 2022-04-01
_[33] 웹사이트 https://keisan.casio[...]
_[34] 문서 항공기 및 飞行 관련 설명에서 15℃일 때 음속 340m/s로 설명하는 것이 일반적임
_[35] 문서 수많은 물리 교과서 및 참고 자료에서 15℃일 때 음속 340m/s로 설명하는 것이 일반적임
_[36] 서적 海洋物理学概論成山堂書店
_[37] 문서 理科年表平成22年
_[38] 서적 アトキンス物理化学東京化学同人
_[39] 문서 理科年表平成22年
_[40] 서적 音と波の力学岩波書店
_[41] 간행물 The hot chocolate effect 1982-05
_[42] 문서 理科年表平成22年
_[43] 문서 理科年表平成22年
_[44] 웹사이트 社団法人日本騒音制御工学会 Dr.Noise 用語解説 http://www.ince-j.or[...]
_[45] 문서 理科年表平成22年
_[46] 서적 西條(2001)
_[47] 서적 西條(2001)
_[48] 서적 ハント(1984)
_[49] 서적 ハント(1984)
_[50] 서적 ハント(1984)
_[51] 서적 ハント(1984)
_[52] 서적 西條(2001)
_[53] 서적 早坂(1989)
_[54] 서적 ハント(1984)
_[55] 서적 ハント(1984)
_[56] 서적 西條(2001)
_[57] 서적 ハント(1984)
_[58] 서적 ハント(1984)
_[59] 서적 西條(2001)
_[60] 서적 ハント(1984)
_[61] 서적 ハント(1984)
_[62] 서적 西條(2001)
_[63] 서적 西條(2001)
_[64] 서적 ニュートン、河辺編(1971)
_[65] 서적 西條(2001)
_[66] 서적 西條(2001)
_[67] 서적 東山(2010)
_[68] 서적 ニュートン、河辺編(1971)
_[69] 서적 西條(2001)
_[70] 서적 ハント(1984)
_[71] 서적 ニュートン、河辺編(1971)
_[72] 서적 ニュートン、河辺編(1971)
_[73] 서적 ニュートン、河辺編(1971)
_[74] 서적 ニュートン、河辺編(1971)
_[75] 서적 ビオ(1988)
_[76] 서적 山本(2008)
_[77] 서적 ハント(1984)
_[78] 서적 ハント(1984)
_[79] 서적 ビオ(1988)
_[80] 서적 ビオ(1988)
_[81] 문서 命題48・定理38の「流体の弾性力がそれの圧縮され方に比例すると仮定するかぎりにおいて」の箇所
_[82] 서적 ハント(1984)
_[83] 서적 西條(2001)
_[84] 서적 ビオ(1988)
_[85] 서적 ビオ(1988)
_[86] 서적 ビオ(1988)
_[87] 서적 山本(2009)
_[88] 서적 西條(2001)
_[89] 서적 ダンネマン(1978)
_[90] 서적 ダンネマン(1978)
_[91] 서적 西條(2001)
_[92] 웹인용 The Speed of Sound http://mathpages.com[...] mathpages.com 2015-05-03
_[93] 웹인용 The Newton–Laplace Equation and Speed of Sound http://www.thermaxxj[...] Thermal Jackets 2015-05-03

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com