일률

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 단위
4. 평균 일률과 순간 일률
5. 기계적 이점
6. 관련 개념
참조

1. 개요

일률은 시간에 따른 일의 변화율, 즉 일의 시간에 대한 도함수이다. 기계적 일률은 힘과 속도의 곱으로, 전기적 일률은 전류와 전압의 곱으로 나타낼 수 있으며, 복사속도와 유사한 개념이다. 일률의 단위는 와트(W)이며, 평균 일률과 순간 일률로 구분된다. 기계적 시스템에서 입력 일률과 출력 일률이 같을 때 기계적 이점을 계산할 수 있다.

더 읽어볼만한 페이지

일률 - 방사속
방사속은 복사 에너지의 흐름률을 나타내는 물리량으로, 기호는 Φe, 단위는 와트(W)를 사용하며, 파장에 따른 방사속은 분광 방사속이라 하고 가시광선 영역에서는 광속을 사용한다.
물리학에 관한 - 전력
전력은 전압과 전류의 곱으로 계산되며, 발전소에서 생산되어 송전 및 배전을 통해 소비자에게 공급되고, 에너지 저장 기술을 통해 안정적으로 공급될 수 있으며, 산업, 상업, 가정 등 다양한 분야에서 소비된다.
물리학에 관한 - N형 반도체
N형 반도체는 전자를 주된 전하 운반체로 사용하는 반도체이다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

일률
기본 정보
단위	와트 (W)
기본 단위	kg⋅m⋅s
차원	wikidata
유도식
물리량 정보
종류	스칼라
차원	L M T
SI 단위	와트 (W)
CGS 단위	에르그 매초 (erg/s)
FPS 단위	피트 파운달 매초 (ft·pdl/s)
MKSG 단위	무게 킬로그램 미터 매초 (kgf·m/s)
FPSG 단위	피트 무게 파운드 매초 (ft·lbf/s)
플랑크 단위	플랑크 일률
고전역학
고전역학	라그랑주 역학 해밀턴 역학 루스 역학 해밀턴-야코비 방정식 아펠 방정식 쿠프만-폰 노이만 역학
언어별 명칭
영어	Power
일본어	仕事率
한국어	일률

2. 정의

일률은 시간에 따른 일의 변화율, 즉 일의 시간에 대한 도함수로 정의된다. 일반적으로 일률(''P'')은 일(''W'')을 시간(''t'')으로 나눈 값으로 표현된다.^[3]^[4]^[5]

: $P = \frac{dW}{dt}$

여기서 ''P''는 일률, ''W''는 일, ''t''는 시간이다.

힘과 속도의 곱으로도 표현될 수 있는데, 속도 '''v'''로 움직이는 물체에 힘 '''F'''가 작용하여 발생하는 기계적 일률은 다음과 같다.

: $P = \frac{dW}{dt} = \mathbf{F} \cdot \mathbf {v}$

힘이 3차원 곡선 C에서 변하는 경우 등 일반적인 상황에서도 위 공식은 유효하다.

전력은 전류와 전압의 곱으로 나타낼 수 있으며, 이는 일률과 동등한 개념이다. 전기 회로에서 전력이 소비되면, 에너지 보존 법칙에 따라 그와 동등한 일률로 다른 에너지가 생성된다.

: $P = I \times V$

복사속 또한 일률과 동등한 개념이며, 스펙트럼 밀도는 파동이 복사될 때 각 주파수 성분에서의 복사속을 의미한다.

2. 1. 기계적 일률

기계 시스템에서 일률은 힘과 운동의 결합으로 나타난다. 특히, 물체에 작용하는 힘과 물체의 속도의 곱, 또는 샤프트에 작용하는 토크와 샤프트의 각속도의 곱으로 표현된다.

기계적 일률은 일의 시간 미분으로도 설명된다. 역학에서 곡선 C를 따라 이동하는 물체에 힘 '''F'''가 한 일(일)은 다음과 같은 선적분으로 나타낼 수 있다.

W_C = \int_C \mathbf{F} \cdot \mathbf{v} \, dt = \int_C \mathbf{F} \cdot d\mathbf{x},

여기서 '''x'''는 경로 C를 정의하고 '''v'''는 이 경로를 따라 이동하는 속도이다.

힘 '''F'''가 퍼텐셜(보존적인)에서 유도된 것이라면, 기울기 정리를 적용하여(힘이 퍼텐셜 에너지의 기울기의 음수) 다음과 같은 식을 얻을 수 있다.

W_C = U(A) - U(B),

여기서 A와 B는 일이 행해진 경로의 시작과 끝 지점이다.

곡선 C를 따라 어떤 지점에서의 일률은 시간 미분으로 나타내어진다.

P(t) = \frac{dW}{dt} = \mathbf{F} \cdot \mathbf{v} = -\frac{dU}{dt}.

1차원에서는 위 식을 다음과 같이 간단하게 표현할 수 있다.

P(t) = F \cdot v.

회전 시스템에서 일률은 토크 '''τ'''와 각속도 '''ω'''의 곱으로 계산된다.

P(t) = \boldsymbol{\tau} \cdot \boldsymbol{\omega},

여기서 '''ω'''는 라디안 매 초로 측정되는 각속도이다.

\cdot

는 스칼라곱을 의미한다.

유압 액추에이터와 같은 유체 동력 시스템에서 일률은 다음과 같이 주어진다.

P(t) = pQ,

여기서 p는 파스칼 또는 N/m² 단위의 압력이고, Q는 SI 단위에서 m³/s의 체적 유량이다.

2. 2. 전기적 일률

소자에 순간적으로 전달되는 전력 ''P''는 다음과 같이 주어진다.

: ''P''(''t'') = ''I''(''t'') ⋅ ''V''(''t'')

여기서

''P''(''t'')는 순간 전력 (단위: 와트(줄/초)
''V''(''t'')는 소자 양단의 전위차(또는 전압 강하) (단위: 볼트)
''I''(''t'')는 소자를 통과하는 전류 (단위: 암페어)

소자가 시간에 따라 변하지 않는 전압 대 전류 비율을 갖는 저항이라면 다음과 같다.

: ''P'' = ''I'' ⋅ ''V'' = ''I''² ⋅ ''R'' = ''V''²/''R''

여기서

: ''R'' = ''V''/''I''

는 전기 저항 (단위: 옴)이다.

일률 ''P''는 일 ''W''과 시간 ''t''을 사용하여 다음 식으로 나타낼 수 있다.

: ''P'' = ''dW''/''dt''

전기 회로에서 전동기 등에서 전력이 소비되면, 그것과 동등한 일률로 다른 에너지가 생성된다(일이 행해진다). 이것은 전력량과 위치 에너지 및 운동 에너지의 총량은 변하지 않는다는 에너지 보존 법칙에 따른 것이다.

2. 3. 복사속

복사속은 일률과 동등한 개념이다. 스펙트럼 밀도는 파동이 복사될 때 각 주파수 성분에서의 복사속을 가리킨다. 광원에서 방출되는 복사력은 반지름 r에서의 세기 I와 관련된 식으로 표현된다.

:P(r) = I(4πr²)

3. 단위

국제단위계에서 일률의 단위는 와트(W)이며, 1초당 1줄과 같다.^[1]

다른 단위로는 영국마력(HP), 미터마력(프랑스마력, PS), Cheval Vapeur(CV)가 있다. 1마력(HP)은 745.7W이다. 1마력(PS)은 735.5W이다. 그 외에도 초당 에르그(erg/s), 분당 피트·파운드(foot-pounds), 1밀리와트를 기준으로 하는 로그 척도인 dBm, 시간당 칼로리, 시간당 BTU(BTU/h), 냉동톤(tons of refrigeration) 등이 일률의 단위로 사용된다.

4. 평균 일률과 순간 일률

Δ''W''^영어가 특정 시간 Δ''t''^영어 동안 수행된 일의 양이라면, 그 기간 동안의 평균 일률은 다음 공식으로 나타낼 수 있다.

: $P_\mathrm{avg} = \frac{\Delta W}{\Delta t}.$

이는 단위 시간당 수행된 평균 작업량 또는 변환된 에너지량이다. 문맥상 명확하다면 평균 일률을 종종 "일률"이라고 부른다.

순간 일률은 시간 간격 Δ''t''^영어가 0에 접근할 때 평균 일률의 극한값이다.

: $P = \lim_{\Delta t \to 0} P_\mathrm{avg} = \lim_{\Delta t \to 0} \frac{\Delta W}{\Delta t} = \frac{dW}{dt}.$

일률 ''P''^영어가 일정할 때, 시간 t^영어 동안 수행된 작업량은 다음과 같이 계산할 수 있다.

: $W = Pt.$

에너지 변환의 맥락에서는 ''W''^영어 대신 ''E''^영어를 사용하는 것이 더 일반적이다.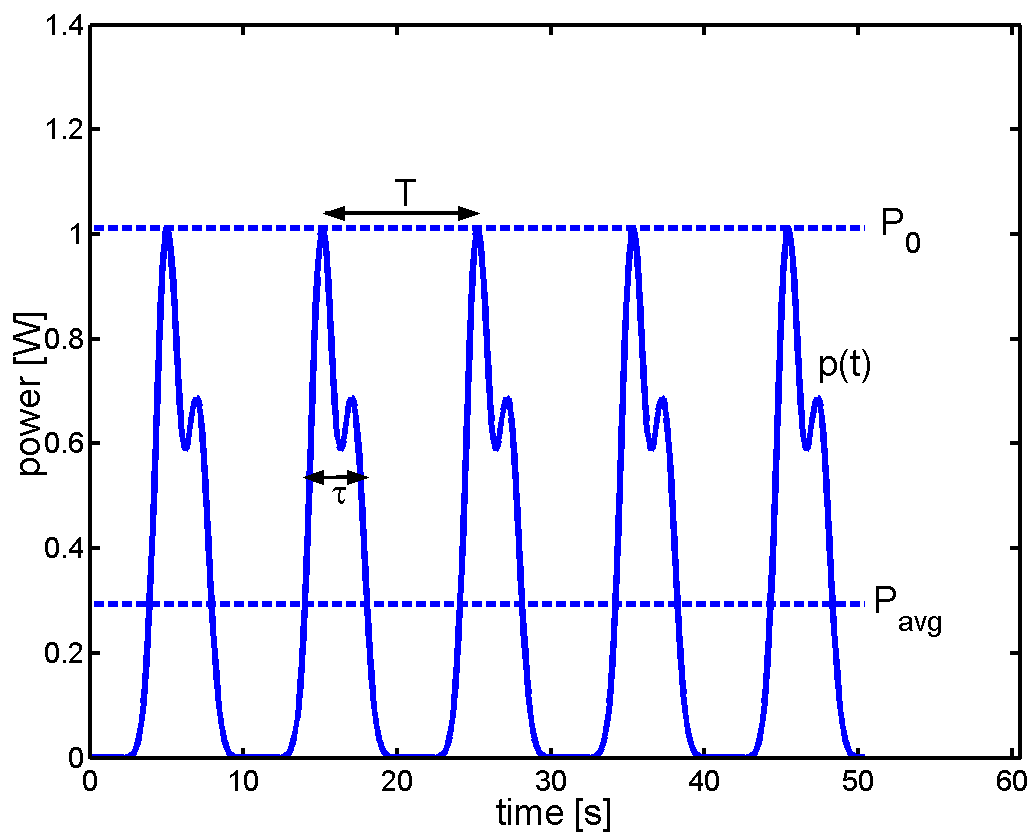

주기

T

를 갖는 주기 신호

s(t)

(예: 동일한 펄스 열)의 경우, 순간 전력

p(t) = |s(t)|^2

또한 주기

T

를 갖는 주기 함수이다. ''피크 전력''은 다음과 같이 정의된다.

:

P_0 = \max [p(t)].

그러나 피크 전력은 항상 쉽게 측정할 수 있는 것은 아니며, 계측기로 평균 전력

P_\mathrm{avg}

를 측정하는 것이 더 일반적이다. 펄스당 에너지를

:

\varepsilon_\mathrm{pulse} = \int_0^T p(t) \, dt

로 정의하면 평균 전력은

:

P_\mathrm{avg} = \frac{1}{T} \int_0^T p(t) \, dt = \frac{\varepsilon_\mathrm{pulse}}{T}.

이다.

P_0\tau = \varepsilon_\mathrm{pulse}

가 되도록 펄스 길이

\tau

를 정의하면 비율

:

\frac{P_\mathrm{avg}}{P_0} = \frac{\tau}{T}

은 같다. 이러한 비율을 펄스 열의 ''작동률(duty cycle)''이라고 한다.

5. 기계적 이점

역학적 시스템에 손실이 없다면, 입력 일률은 출력 일률과 같다. 이는 시스템의 기계적 이점에 대한 간단한 공식을 제공한다.

장치에 대한 입력 일률을 속도 vA^영어로 움직이는 지점에 작용하는 힘 FA^영어로 하고, 출력 일률을 속도 vB^영어로 움직이는 지점에 작용하는 힘 FB^영어로 한다. 시스템에 손실이 없다면,

:P = FBvB = FAvA^영어

이고, 시스템의 기계적 이점(입력 힘에 대한 출력 힘)은 다음과 같이 주어진다.

:MA = FB / FA = vA / vB^영어

회전 시스템의 경우에도 유사한 관계가 얻어진다. 여기서 TA^영어와 ωA^영어는 입력의 토크와 각속도이고, TB^영어와 ωB^영어는 출력의 토크와 각속도이다. 시스템에 손실이 없다면,

:P = TAωA = TBωB^영어

이고, 이는 기계적 이점을 생성한다.

:MA = TB / TA = ωA / ωB^영어

이러한 관계는 장치의 물리적 치수에 따라 결정되는 속도비 측면에서 장치의 최대 성능을 정의하기 때문에 중요하다. 예를 들어 기어비를 참조하라.

6. 관련 개념

전력은 전기 회로에서 일률과 동등한 개념으로, 전류와 전압의 곱으로 나타낼 수 있다. 전기 회로에서 전동기 등에서 전력이 소비되면, 에너지 보존 법칙에 따라 전력량과 위치 에너지 및 운동 에너지의 총량은 변하지 않고 그것과 동등한 일률로 다른 에너지가 생성된다.

참조

_[1] 서적 Fundamentals of Physics
_[2] 서적 The Feynman Lectures on Physics
_[3] 서적 Smithsonian Physical Tables https://books.google[...] Smithsonian Institution 1921
_[4] 학술지 Electrical Calculations for Railway Motors https://books.google[...] 1906
_[5] 학술지 Societies and Academies 1902
_[6] 웹사이트 Energy Density of Coal http://hypertextbook[...]
_[7] 웹사이트 한국물리학회 물리학용어집 https://www.kps.or.k[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com