지레

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 지레의 원리
- 2.1. 수식 표현
- 2.2. 힘점과 작용점의 명칭 문제 (일본어 위키백과 관련)
3. 지레의 역사
4. 지레의 종류
5. 복합 지레
6. 지레의 응용
참조

1. 개요

지레는 받침점을 통해 지면에 연결된 막대로, 받침점, 힘점, 작용점의 위치에 따라 1종, 2종, 3종 지레로 분류된다. 지레의 원리는 힘과 거리의 관계를 통해 작은 힘으로 큰 힘을 얻거나, 힘의 방향을 바꾸는 등 다양한 방식으로 활용되며, 아르키메데스는 지레의 원리를 최초로 수학적으로 분석했다. 지레는 단순 기계 중 하나로, 손수레, 병따개, 핀셋 등 다양한 도구와 기계에 적용되며, 복합 지레는 여러 개의 지레가 직렬로 연결되어 작동한다.

더 읽어볼만한 페이지

단순 기계 - 나사
나사는 볼트와 너트 또는 나사못을 이용하여 두 물체를 결합하는 기계 요소로, 배관 연결 및 동력 전달 장치 등 다양한 분야에서 활용되며, 미터 나사, 유니파이 나사 등 다양한 종류와 KS, ISO 등의 규격이 존재하고, 나사 곡선, 리드, 피치 등의 주요 용어를 가진다.
단순 기계 - 도르래
도르래는 밧줄과 접촉하여 회전하는 원반형 회전륜 또는 장력 전달 기구로, 힘의 방향을 바꾸거나 기계적 이득을 얻기 위해 사용되며, 건설 및 운송 분야에서 활용된다.
기계 부속품 - 밸브
밸브는 유체의 흐름을 제어하는 장치로, 다양한 크기와 작동 방식을 가지며, 산업 전반과 일상생활에서 널리 사용된다.
기계 부속품 - 크랭크축
크랭크축은 내연 기관에서 피스톤의 왕복 운동을 회전 운동으로 바꾸는 핵심 부품으로, 메인 저널, 크랭크 핀, 크랭크 암, 균형추 등으로 구성되어 엔진 성능과 효율에 중요한 역할을 하며, 자동차, 선박, 항공기 등 다양한 기계 장치에 사용된다.
도구 - 목재
목재는 수목의 목질부로, 오래전부터 연료, 건축 자재, 도구 등 다양한 용도로 사용되어 왔으며, 셀룰로오스, 헤미셀룰로오스, 리그닌으로 구성되고 수종에 따라 물성이 다르며, 다양한 형태로 가공되어 여러 분야에 활용되고 지속가능한 산림 관리와 기술 개발이 중요시되는 재료이다.
도구 - 호루라기
호루라기는 입으로 불어넣는 공기나 증기를 이용하여 소리를 내는 도구로, 스포츠 경기, 경비, 교통 정리 등 다양한 분야에서 신호 전달 및 경고 목적으로 활용되며 악기로도 사용된다.

지레
개요
지레는 한쪽 끝에서 작은 힘(노력)을 가하여 다른 쪽 끝에서 큰 힘을 작은 거리로 가할 수 있도록 사용될 수 있다.
분류	단순 기계
구성 요소	받침점 또는 회전축, 부하 및 노력
예시	시소, 병따개 등
용어
영어	Leverage
한국어	지렛대, 지레대
작동 원리
작동 원리	F₁D₁ = F₂D₂라면 정적 평형 상태가 된다.

2. 지레의 원리

지레는 받침점을 중심으로 회전하며 힘을 전달하는 도구이다. 지레의 원리는 돌림힘(torque)을 이용하여 설명할 수 있다. 돌림힘은 힘의 크기와 받침점으로부터의 거리를 곱한 값으로, 지레에서는 힘점과 작용점에 작용하는 돌림힘이 평형을 이룬다.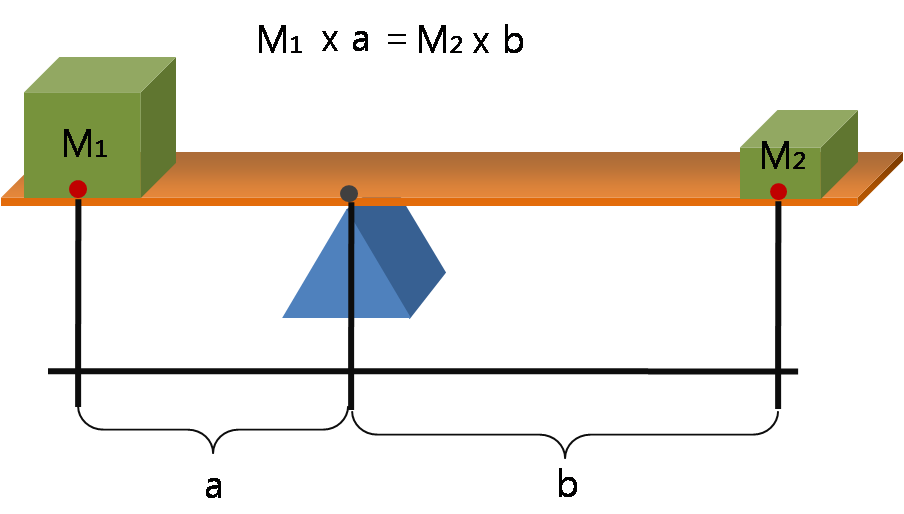

지레의 원리를 간단히 요약하면 다음과 같다.

힘점과 받침점 사이의 거리가 멀수록, 힘점에 작은 힘을 가해도 작용점에 큰 힘이 작용한다.
힘점과 받침점 사이의 거리가 가까울수록, 힘점을 조금만 움직여도 작용점은 크게 움직인다.

이러한 지레의 원리는 아르키메데스에 의해 증명되었으며,^[9] 가상일의 원리를 이용하여 설명할 수도 있다.

지레에는 받침점, 힘점, 작용점이 있다. 받침점은 고정된 지점이고, 힘점은 힘을 가하는 지점, 작용점은 힘이 작용하는 지점이다. 지레를 사용할 때는 이 세 점의 위치 관계, 특히 받침점으로부터의 거리가 중요하다. 큰 힘을 얻으려면 힘점을 받침점에서 멀리 하거나, 작용점을 받침점에 가깝게 하면 된다.

2. 1. 수식 표현

지레는 받침점을 중심으로 힘점과 작용점에 발생하는 돌림힘(torque)을 이용하는 도구이다. 돌림힘의 크기는 작용하는 힘의 크기와 회전 작용이 일어나는 거리의 곱으로 계산된다. 이상적인 지레에서는 에너지 손실이 없으므로, 지레에 가해지는 일과 지레에서 나오는 일은 같다. 따라서 출력력과 입력력의 비는 받침점에서 각 힘의 작용점까지의 거리의 비로 주어지는데, 이를 '''지레의 원리'''라고 한다.^[8]

지레의 기계적 이점은 받침점에 대한 모멘트 또는 토크 ''T''의 균형을 통해 알 수 있다.

:

T_{1} = F_{1}a,\quad

:

T_{2} = F_{2}b\!

여기서 F₁은 지레에 가해지는 입력력, F₂는 출력력이며, ''a''와 ''b''는 힘과 받침점 사이의 수직 거리이다. 토크의 모멘트는 균형을 이루어야 하므로

T_{1} = T_{2} \!

이고, 따라서

F_{1}a = F_{2}b \!

가 성립한다.

지레의 기계적 이점(MA)은 출력력과 입력력의 비로 다음과 같이 나타낼 수 있다.

:

MA = \frac{F_{2}}{F_{1}} = \frac{a}{b}.\!

이 관계식은 무게가 없고 마찰, 유연성, 마모로 인한 손실이 없는 지레의 경우, 기계적 이점은 입력력과 출력력이 지레에 적용되는 위치에서 받침점까지의 거리의 비로 계산할 수 있음을 보여준다. 지레가 수평이 아닌 다른 위치로 변하더라도 ''a''와 ''b''의 "수평" 거리(중력의 힘에 수직인 거리)가 변화(감소)하더라도 이 관계는 여전히 유효하다.

아르키메데스는 기하학적 추론을 사용하여 ''지렛대의 원리''를 증명했다.^[9] 입력 힘이 가해지는 지점(A점)에서 받침점까지의 거리 ''a''가 출력 힘이 가해지는 지점(B점)에서 받침점까지의 거리 ''b''보다 크면 지렛대는 입력 힘을 증폭시키고, 반대의 경우에는 입력 힘을 감소시킨다. 지레의 정적 분석에서 속도를 사용하는 것은 가상일의 원리를 적용한 것이다.

아르키메데스 지레, 1824년 런던에서 출판된 ''Mechanics Magazine''의 판화

지레는 받침점 ''P''를 중심으로 회전하는 강체 막대로 모델링할 수 있다. 입력력 '''F'''_''A''는 좌표 벡터 '''r'''_''A''로 위치한 점 ''A''에, 출력력 '''F'''_''B''는 '''r'''_''B''로 위치한 점 ''B''에 가해진다. 받침점 ''P''를 중심으로 한 지레의 회전은 라디안 단위의 회전각 ''θ''로 정의된다.

받침점 ''P''의 좌표 벡터를 '''r'''_''P''라고 하고, 받침점에서 입력점 ''A''와 출력점 ''B''까지의 거리를 다음과 같이 정의한다.

:

a = |\mathbf{r}_A -  \mathbf{r}_P|, \quad  b = |\mathbf{r}_B -  \mathbf{r}_P|,

받침점에서 점 ''A''와 ''B''까지의 단위 벡터 '''e'''_''A''와 '''e'''_''B''를 도입하면,

:

\mathbf{r}_A  -  \mathbf{r}_P = a\mathbf{e}_A, \quad \mathbf{r}_B -  \mathbf{r}_P = b\mathbf{e}_B.

점 ''A''와 ''B''의 속도는 다음과 같이 주어진다.

:

\mathbf{v}_A = \dot{\theta} a \mathbf{e}_A^\perp, \quad  \mathbf{v}_B = \dot{\theta} b \mathbf{e}_B^\perp,

여기서 '''e'''_''A''^⊥와 '''e'''_''B''^⊥는 각각 '''e'''_''A''와 '''e'''_''B''에 수직인 단위 벡터이다.

각도 ''θ''는 지레의 배치를 정의하는 일반화 좌표이고, 이 좌표와 관련된 일반화 힘은 다음과 같다.

:

F_\theta =  \mathbf{F}_A \cdot \frac{\partial\mathbf{v}_A}{\partial\dot{\theta}} - \mathbf{F}_B \cdot \frac{\partial\mathbf{v}_B}{\partial\dot{\theta}}= a(\mathbf{F}_A \cdot \mathbf{e}_A^\perp) - b(\mathbf{F}_B \cdot \mathbf{e}_B^\perp) = a F_A - b F_B ,

여기서 ''F''_''A''와 ''F''_''B''는 반지름 부분 ''PA''와 ''PB''에 수직인 힘의 성분이다. 가상 일의 원리는 평형 상태에서 일반화 힘이 0이라는 것을 나타낸다. 즉,

:

F_\theta = a F_A - b F_B = 0. \,\!

따라서 출력력 ''F''_''B''와 입력력 ''F''_''A''의 비, 즉 지레의 기계적 이득은 다음과 같다.

:

MA = \frac{F_B}{F_A} = \frac{a}{b},

지레에는 '''받침점''', '''힘점''', '''작용점'''이 있으며, 받침점을 중심으로 회전하는 저울이나 도르래와 축이 있을 때, 힘을 가하는 점은 힘점, 힘이 작용하는 점은 작용점이며, 보통 작용점에는 추 등의 하중이 있다. 받침점은 고정되어 힘점을 움직이면 작용점이 움직이는 구조이다.

지레를 사용할 때 중요한 것은 받침점, 힘점, 작용점의 위치 관계, 특히 그 간격이다. 큰 힘을 얻으려면 받침점에서 가능한 멀리 힘점을 두거나, 받침점에 가능한 가깝게 작용점을 두면 된다.

실험을 통해 받침점에서 힘점까지의 거리가 받침점에서 작용점까지의 거리의 2배이면 얻을 수 있는 힘은 가한 힘의 2배가 된다는 것을 알 수 있다. 이 관계를 식으로 나타내면 다음과 같다.

:

d_1 F_1=d_2 F_2

:

d_1

: 받침점과 힘점 사이의 거리

:

F_1

: 힘점에 가하는 힘

:

d_2

: 받침점과 작용점 사이의 거리

:

F_2

: 작용점에서 얻어지는 힘

위 식은 단순화하기 위해 힘점, 받침점에 작용하는 힘이 평행하다고 가정한 식이며, 원래는

d_1, d_2

는 모멘트 암(받침점에서 힘의 벡터에 내린 수선의 길이)이라는 점에 유의해야 한다. 이 모멘트 암 × 힘을 토크라고 하며, 토크의 평형이 지레의 원리의 본질이다.

2. 2. 힘점과 작용점의 명칭 문제 (일본어 위키백과 관련)

지레에는 '''받침점''', '''힘점''', '''작용점'''이 있으며, 역학에서 힘점은 물리 용어로서는 일반적으로 등장하지 않는다.^[10]

역학에서 "힘"은 벡터로 다뤄지며, 크기, 방향, 시작점을 갖는다. 이것을 힘의 세 요소라고 부르며, 특히 벡터의 시작점을 ''작용점''(또는 작용력점)이라고 부른다. 예를 들어 영어에서는 힘의 작용점을 point of application이라고 부르지만, 지레를 설명할 때는 "사람이 가하는 힘"의 ''작용점''을 point of effort, "무게가 가하는 힘"의 ''작용점''을 point of load라고 부른다.^[11] 이 두 점을 초등학교에서는 힘점, 작용점이라고 부르고 있어, 물리학을 배운 사람은 혼동하지 않도록 주의가 필요하다.

두 힘 벡터의 시작점을 다른 이름으로 부르는 이유는 지레의 분류에 필요하기 때문이다. 힘점, 작용점을 구별하지 않으면, "지레의 종류"에서 설명하는 ''제2종 지레'', ''제3종 지레''를 분류할 수 없다. 지레가 "힘을 증폭시키거나, 힘의 방향을 변경시키는" 가장 기본적인 장치로서 고대에 개발된 도구(단순 기계)이며, 힘을 전달하는 장치이기 때문에 힘 전달 장치의 입력, 출력을 구별하기 위해 힘점, 작용점이라는 다른 이름이 필요했던 것이다.

3. 지레의 역사

지레 메커니즘에 대한 가장 오래된 증거는 기원전 5000년경 고대 근동으로 거슬러 올라가는데, 당시에는 간단한 저울에 처음 사용되었다.^[3] 고대 이집트에서는 기원전 4400년경 발판이 가장 초기의 수평틀 베틀에 사용되었다.^[4] 기원전 3000년경 메소포타미아(현재의 이라크)에서는 지레 메커니즘을 사용하는 크레인과 같은 장치인 샤두프가 발명되었다.^[3] 고대 이집트에서 노동자들은 100톤이 넘는 오벨리스크를 옮기고 들어 올리는 데 지레를 사용했다. 이는 큰 블록의 오목한 부분과 지레 이외의 다른 용도로는 사용될 수 없는 취급 돌기에서 알 수 있다.^[5]

지레에 관한 가장 오래된 기록은 기원전 3세기로 거슬러 올라가며, 일반적으로 그리스 수학자 아르키메데스가 남긴 것으로 여겨진다. 그는 "내게 충분히 긴 지렛대와 받침점만 주면, 나는 지구라도 움직일 수 있다."라는 유명한 말을 남겼다. 오텀 스탠리는 삽을 최초의 지레로 간주할 수 있으며, 이는 선사 시대 여성을 지레 기술의 발명가로 위치시킨다는 주장을 한다.^[6]

아르키메데스는 고대 이탈리아 시칠리아 섬의 시라쿠사에서 태어났으며, "지렛대의 원리"를 발견하여 물리학의 한 분야로 만들었다. 이는 시라쿠사가 포에니 전쟁에 휘말렸을 때 큰 위력을 발휘했는데, 특히 투석기 등에서 그러했다. 또한 그는 "나에게 지점과 충분히 긴 지렛대만 주어진다면 지구라도 움직일 수 있다."는 전설적인 말을 남겼다고 한다.

4. 지레의 종류

지레는 받침점, 힘점, 작용점의 위치에 따라 세 가지 종류로 나뉜다. 1종 지레와 2종 지레는 작은 힘으로 큰 힘을 내거나, 큰 힘으로 넓은 범위의 일을 할 때 쓰인다. 3종 지레는 물체를 빠르게 움직이거나 정교하게 조작할 때 사용되며, 복합 지레 구조를 통해 큰 힘을 낼 수도 있다.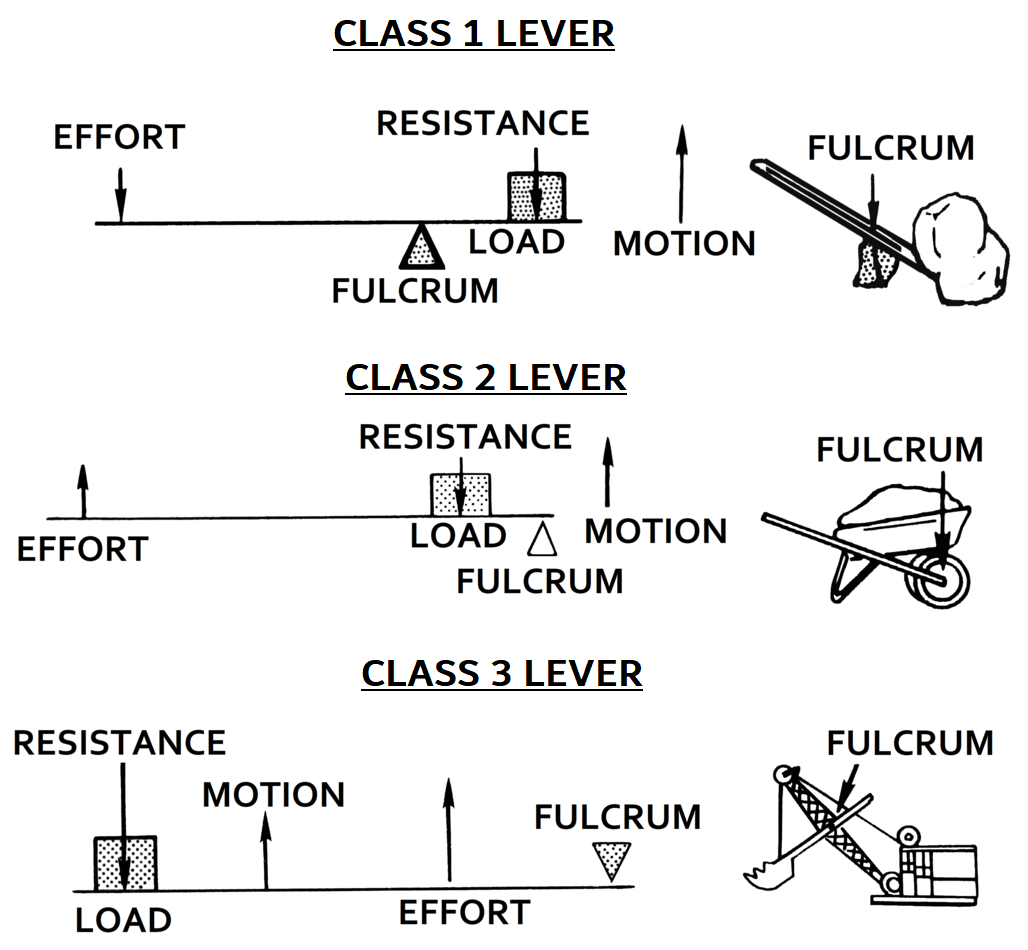

지레는 지점, 힘, 저항(또는 하중)의 상대적 위치에 따라 분류된다. 입력 힘을 "힘", 출력 힘을 "하중" 또는 "저항"이라고 부른다.^[7]

1종 지레: 지점이 힘과 저항 사이에 있다. 시소, 지렛대, 가위 등이 있다.
2종 지레: 저항이 힘과 지점 사이에 있다. 손수레, 호두까기 등이 있다.
3종 지레: 힘이 저항과 지점 사이에 있다. 핀셋, 집게 등이 있다.

이러한 지레의 종류는 "fre 123"이라는 기억법으로 설명할 수 있다. 'f'(지점)는 1종 지레, 'r'(저항)은 2종 지레, 'e'(힘)는 3종 지레에서 가운데에 위치한다.^[14]

지레는 지점, 힘점, 작용점의 위치 관계에 따라 세 종류로 분류된다. 세 점을 일직선상에 나열했을 때, 가운데가 지점이면 제1종 지레, 작용점이면 제2종, 힘점이면 제3종이라고 한다. 영어에서는 fle라고 기억하기도 한다.

지점, 힘점, 작용점이 꼭 일직선상에 있을 필요는 없다. 못뽑이가 좋은 예이다.

4. 1. 제1종 지레

받침점이 가운데에 있고 힘점과 작용점이 서로 반대쪽에 있는 지레이다. 힘점에 가하는 힘의 방향과 작용점에 가해지는 힘의 방향은 서로 반대이다. 힘점이 받침점에서 멀수록 작용점에 가해지는 힘이 커진다.^[7]

힘점과 작용점을 바꾸면 필요한 힘은 커지지만, 움직임을 크게 또는 빠르게 할 수 있다.

대표적인 1종 지레의 한 종류로, 옛날부터 거석 등을 옮기는 데에도 사용되어 왔다.

'''1종 지레의 예'''

1종 지레의 예
도구
가위
노
시소
투석기
플라이어
랜드마인
저울
장도리
못뽑이
캔따개
펜치

작은 것을 빠르고 크게 움직이는 구조로는 트레뷰셋이 있다. 추가 낙하함으로써 돌팔매를 고속으로 투척할 수 있지만, 추는 돌팔매의 수 배~수십 배의 무게가 필요하다.

4. 2. 제2종 지레

힘점과 받침점 사이에 작용점이 있는 지레이다. 병따개가 대표적인 제2종 지레로, 손잡이 부분을 위로 올리면 병뚜껑에는 큰 힘이 작용한다. 힘점이 작용점보다 받침점에서 더 멀기 때문에 힘점이 움직이는 거리는 작용점이 움직이는 거리보다 멀지만, 힘점에 가하는 힘보다 더 큰 힘이 작용점에 가해진다.

작용점을 중심에 두고, 힘점과 지점이 바깥쪽에 있는 경우도 큰 힘을 사용하기 위한 구조이다. 힘점을 왼쪽에 두면 왼쪽부터 “힘점, 작용점, 지점”의 순서가 된다. 힘점에 가한 작은 위쪽 방향의 힘은 작용점에서 큰 위쪽 방향의 힘이 된다.

이러한 원리를 이용하여 작은 힘을 큰 힘으로 바꾸어 사용할 수 있다. 이 방법을 사용하여 큰 힘을 가하는 도구에는 병따개, 호두까기, 손톱깎이, 손수레, 커터 등이 있다.

4. 3. 제3종 지레

작용점과 받침점 사이에 힘점이 있는 지레이다. 힘점에 가하는 힘보다 작은 힘이 작용점에 가해지기 때문에, 작은 힘으로 큰 힘을 내기 위해 보통 사용하는 제1종, 제2종 지레와는 다르다. 힘점이 움직이는 거리보다 작용점이 움직이는 거리가 더 크기 때문에 물체를 멀리 움직일 때 제3종 지레를 사용하는 것이 보통이다.^[7]

힘이 저항과 지점 사이에 위치한다. 저항(또는 하중)은 힘의 한쪽에 가해지고 지점은 다른 쪽에 위치한다. 힘팔이 하중팔보다 작기 때문에 지렛대의 역학적 이점은 항상 1보다 작다. 이는 속도 증배 지렛대로도 불린다.^[7]

제3종 지레의 예시는 다음과 같다.

5. 복합 지레

복합 지렛대는 여러 개의 지렛대가 직렬로 작용하는 것을 말한다. 하나의 지렛대에서 발생하는 저항이 다음 지렛대의 힘으로 작용하여, 가해진 힘이 하나의 지렛대에서 다음 지렛대로 전달된다. 복합 지렛대의 예로는 저울, 손톱깎이, 피아노 건반 등이 있다.

망치뼈(malleus), 모루뼈(incus), 등자뼈(stapes)는 중이에 있는 작은 뼈들로, 복합 지렛대로 연결되어 고막에서 달팽이관(cochlea)의 난원창으로 소리파를 전달한다. 실제 도구나 기계에는 지레의 원리를 여러 개 사용하는 것이 있다. 예를 들어 손톱깎이는 힘점, 지점, 작용점이 각각 2개씩 있다고 생각할 수 있다.^[15]

철도의 연동장치에서는 예전에 전철기나 신호기를 사람의 힘으로 움직이기 위해 거대한 레버를 지레로 이용하여 움직였다. 그 흔적으로, 전기적인 스위치 조작으로 바뀐 후에도 "지레"라고 부르는 경우가 있다.

지레의 원리는 격투기의 관절기에도 사용되고 있으며, 소림사권법에서도 중요한 원리로 여겨진다.^[16]

6. 지레의 응용

손톱깎이는 힘점, 지점, 작용점이 각각 2개씩 있는 지레의 원리를 사용한 도구이다.^[15]

철도의 연동장치에서는 과거에 전철기나 신호기를 사람의 힘으로 조작하기 위해 거대한 레버를 지레로 이용했다. 이러한 흔적 때문에 전기적인 스위치 조작으로 바뀐 후에도 "지레"라고 부르는 경우가 남아있다.

지레의 원리는 격투기의 관절기에도 사용되며, 소림사권법에서도 중요한 원리로 여겨진다.^[16]

지렛대는 건설 현장 등에서 돌이나 나무를 들어 올리거나 움직이게 하고, 석재 이음매를 맞추거나 나무 방향을 바꾸는 데 사용되는 도구의 명칭이기도 하다.^[17] 나무로 만든 목제 지렛대와 철로 만든 철제 지렛대가 있다.^[17]

지렛대를 사용하는 방법은 다음과 같다.^[17]

밀어 올리기: 지렛대를 물체 아래에 끼워 넣고, 지렛대 끝과 지면이 접하는 점을 지점으로 하여 물체를 반대쪽으로 이동시킨다.
들어 올리기: 지렛대를 물체 아래에 끼워 넣고, 지렛대 끝과 지면이 접하는 점을 지점으로 하여 물체를 들어 올린다.
튕겨 올리기: 지렛대를 물체 아래에 끼워 넣고, 각재 등의 받침목을 끼워 넣어 그것을 지점으로 하여 물체를 들어 올린다.
배 젓기: 지렛대를 사용하여 세 사람이 협력하여 물체를 조금씩 이동시킨다. 양쪽을 '튕겨 올리기'로 지지하고, 배의 노와 같은 움직임으로 밀면서 뒤에서 '밀어 올리기'로 민다.

참조

_[1] 백과사전 Lever
_[2] 웹사이트 Etymology of the word "lever" in the Online Etymological http://www.etymonlin[...] 2015-04-29
_[3] 서적 The Genius of Archimedes -- 23 Centuries of Influence on Mathematics, Science and Engineering: Proceedings of an International Conference held at Syracuse, Italy, June 8-10, 2010 Springer Science & Business Media 2010
_[4] 서적 Science and technology firsts https://archive.org/[...] Gale Research 1997
_[5] 서적 Ancient Egyptian Construction and Architecture Courier Corporation 1990
_[6] 서적 Machina Ex Dea: Feminist Perspectives on Technology Pergamon Press
_[7] 서적 Physics in Biology and Medicine Academic Press 2016-02-23
_[8] 서적 Theory of Machines and Mechanisms Oxford University Press USA
_[9] 서적 A History of Mechanical Inventions https://books.google[...] Harvard University Press (reprinted by Dover Publications 1988) 2013-04-07
_[10] 문서 小学校では力を加える点を力点、てこが力を重りに与える点を作用点としているが、作用反作用の法則により力点も作用点も外力を受け、反力を出しているという点でなんら変わりがない。そのため力学では力点・作用点をまとめて作用点（もしくは着力点）と呼ぶ。
_[11] 위키 Lever :en:Lever
_[12] 웹사이트 アーカイブされたコピー https://web.archive.[...] 2008-05-10
_[13] 위키 Fulcrum :en:Fulcrum
_[14] 위키 Lever Mnemonic :en:Lever
_[15] 웹사이트 てこを使ったさまざまな道具たち https://web.archive.[...] 2017-10-04
_[16] 서적 少林寺拳法のススメ
_[17] 웹사이트 人力による運搬組立て工法の手引 https://jflc.or.jp/m[...] 日本造園組合連合会 2019-10-16

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com