최소 상계 성질

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 최소 상계 성질
- 2.1. 실수에서의 최소 상계 성질
  - 2.1.1. 정의
- 2.2. 순서 집합으로의 일반화
  - 2.2.1. 예시: 유리수 집합
3. 증명
- 3.1. 논리적 상태
- 3.2. 코시 수열을 이용한 증명
4. 최소 상계 성질의 응용
5. 역사
참조

1. 개요

최소 상계 성질은 공집합이 아니고 상계를 갖는 실수 집합이 실수 집합 내에서 최소 상계를 갖는다는 성질이다. 이 성질은 실수와 부분 순서 집합의 상계와 최소 상계를 정의하는 데 사용되며, 유리수 집합에서는 성립하지 않는다. 최소 상계 성질은 코시 수열의 수렴과 같은 완비성 공리와 동치이며, 중간값 정리, 볼차노-바이어슈트라스 정리, 최대-최소 정리, 하이네-보렐 정리 등 실해석학의 여러 기본 정리를 증명하는 데 활용된다. 볼차노에 의해 처음 인식되었으며, 코시와 바이어슈트라스 등의 연구를 통해 중요성이 부각되었다.

더 읽어볼만한 페이지

실해석학 - 멱급수
멱급수는 실수 또는 복소수 체에서 정의되며, 수렴 영역과 반지름을 가지며 미분, 적분, 사칙연산이 가능하고 해석 함수와 관련되어 상미분 방정식의 해를 구하는 데 활용된다.
실해석학 - 디리클레 함수
디리클레 함수는 실수에서 정의되어 유리수에서 1, 무리수에서 0의 값을 가지며 모든 점에서 불연속인 함수로, 리만 적분은 불가능하지만 르베그 적분은 가능하고 함수 해석학에서 불연속 함수의 성질 연구에 사용되는 베르 함수에 속하는 예시이다.
순서론 - 스콧 위상
스콧 위상은 부분 순서 집합 위에 정의되는 위상으로, 하향 집합과 directed set의 상한에 대해 닫혀있는 집합을 닫힌 집합으로 정의하며, 컴퓨터 과학, 특히 프로그램 의미론에서 연속 함수의 개념을 일반화하고 프로그램의 계산 과정을 모델링하는 데 사용된다.
순서론 - 사전식 순서
사전식 순서는 정렬된 집합의 순서를 일반화하여 곱집합의 순서를 정의하는 데 사용되며, 단어 순서 정렬 방식과 유사하게 다양한 분야에 응용되는 수학적 개념이다.

최소 상계 성질
최소 상계 성질
정의	부분 순서 집합의 모든 비어 있지 않은 부분집합이 상계를 가지면 최소 상계를 가짐
다른 이름	최소 상계 특성, 최소 상계 속성
같이 보기
관련 개념	완비 격자 상한 하한 최대하계 성질

2. 최소 상계 성질

S^영어를 실수의 공집합이 아닌 집합이라고 하자.

실수 x^영어는 모든 s^영어 ∈ S^영어에 대해 x^영어 ≥ s^영어인 경우 S^영어에 대한 '''상계'''라고 한다.
실수 x^영어가 S^영어의 상계이고 S^영어의 모든 상계 y^영어에 대해 x^영어 ≤ y^영어인 경우 x^영어를 S^영어의 '''최소 상계''' (또는 '''상한''')라고 한다.

'''최소 상계 성질'''은 상계를 갖는 공집합이 아닌 실수 집합은 반드시 ''실수'' 내에 최소 상계를 가져야 한다고 명시한다.

2. 1. 실수에서의 최소 상계 성질

실수 집합 S가 공집합이 아니고 상계를 가질 때, S는 반드시 실수 집합 내에서 '''상한'''를 갖는다는 성질을 최소 상계 성질이라고 한다.

2. 1. 1. 정의

S^영어를 공집합이 아닌 실수의 집합이라고 하자.

모든 s^영어 ∈ S^영어에 대해 x^영어 ≥ s^영어이면, 실수 x^영어는 S^영어의 '''상계'''이다.
실수 x^영어가 S^영어의 상계이고, S^영어의 임의의 상계 y^영어에 대해 x^영어 ≤ y^영어이면, x^영어는 S^영어의 '''최소 상계''' ('''상한''')이다.

'''최소 상계 성질'''은 상계를 갖는 공집합이 아닌 실수 집합은 반드시 ''실수'' 내에 최소 상계를 가져야 한다는 것이다.

2. 2. 순서 집합으로의 일반화

"실수"를 "부분 순서 집합 X의 원소"로 바꾸어, 부분 순서 집합 X의 임의의 부분 집합에 대한 상계와 최소 상계를 정의할 수 있다. X의 상계를 갖는, 공집합이 아닌 모든 부분 집합이 X 안에 최소 상한을 가지면, X가 최소 상계 성질을 갖는다고 말한다.

2. 2. 1. 예시: 유리수 집합

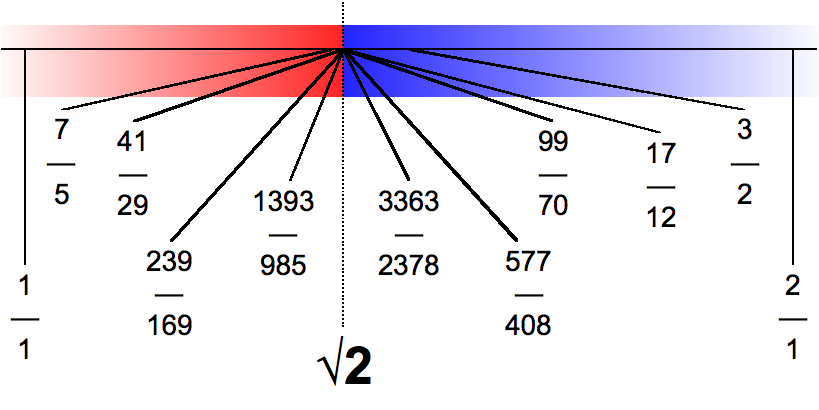
유리수 집합 '''Q'''는 통상적인 순서에서 최소 상계 성질을 만족하지 않는다. 예를 들어, 집합

:

\left\{ x \in \mathbf{Q} : x^2 \le 2 \right\} = \mathbf{Q} \cap \left(-\sqrt{2}, \sqrt{2}\right)

는 '''Q'''에서 상계를 가지지만, √2는 무리수이기 때문에 '''Q'''에서 최소 상계를 갖지 않는다. 데데킨트 절단을 이용하여 실수를 구성할 때 유리수의 특정 집합들을 최소 상계로 정의하는 데에 이를 이용한다.

'''빨강:''' 집합 $\left\{ x \in \mathbf{Q} : x^2 \le 2 \right\}$ . '''파랑:''' $\mathbf{Q}$ 내의 상계 집합

3. 증명

실수의 완비성 공리의 한 형태인 최소 상계 성질은 코시 수열의 수렴이나 축소 구간 정리와 동치이다. 이 성질의 논리적 지위는 사용된 실수의 구성에 따라 달라진다. 합성적 접근법에서는 이 성질이 일반적으로 실수에 대한 공리(최소 상계 공리 참조)로 간주된다. 구성적 접근법에서는 이 성질을 구성으로부터 직접적으로, 또는 다른 형태의 완비성의 결과로 증명해야 한다.^[1]

=== 코시 수열을 이용한 증명 ===

실수의 모든 코시 수열이 수렴한다는 가정 하에 최소 상계 성질을 증명할 수 있다. ''S''를 공집합이 아닌 실수의 부분집합이라 하고, ''S''가 상계 ''B''₁을 갖는다고 하자. ''S''가 공집합이 아니므로, ''S''의 상계가 아닌 실수 ''A''₁이 존재한다. 수열 ''A''₁, ''A''₂, ''A''₃, ... 와 ''B''₁, ''B''₂, ''B''₃, ...을 다음과 같이 귀납적으로 정의한다.

# (''A_n'' + ''B_n'') / 2 가 ''S''의 상계인지 확인한다.

# 상계라면, ''A''_''n''+1 = ''A_n'', ''B''_''n''+1 = (''A_n'' + ''B_n'') / 2 라 하자.

# 상계가 아니라면 ''s''>(''A_n'' + ''B_n'') / 2 를 만족하는 ''S''의 원소 ''s''가 존재한다. ''A''_''n''+1 = ''s'', ''B''_''n''+1 = ''B_n''라 하자.

그러면 ''A''₁ ≤ ''A''₂ ≤ ''A''₃ ≤ ⋯ ≤ ''B''₃ ≤ ''B''₂ ≤ ''B''₁ 이고 |''A_n'' - ''B_n''| → 0 (''n'' → ∞ 일 때) 이다. 이는 곧 두 수열이 코시 수열이고 같은 극한 ''L''을 가짐을 의미하는데, 이것이 곧 ''S''의 최소 상계이다.

3. 1. 논리적 상태

최소 상계 성질은 코시 수열의 수렴이나 축소 구간 정리와 같은 완비성 공리의 다른 형태와 동치이다. 이 성질의 논리적 지위는 사용된 실수의 구성에 따라 달라진다. 합성적 접근법에서는 이 성질이 일반적으로 실수에 대한 공리(최소 상계 공리 참조)로 간주된다. 구성적 접근법에서는 이 성질이 구성으로부터 직접적으로, 또는 다른 형태의 완비성의 결과로 정리로 증명되어야 한다.^[1]

3. 2. 코시 수열을 이용한 증명

실수의 모든 코시 수열이 수렴한다는 가정 하에 최소 상계 성질을 증명할 수 있다. ''S''를 공집합이 아닌 실수의 부분집합이라 하고, ''S''가 상계 ''B''₁을 갖는다고 하자. ''S''가 공집합이 아니므로, ''S''의 상계가 아닌 실수 ''A''₁이 존재한다. 수열 ''A''₁, ''A''₂, ''A''₃, ... 와 ''B''₁, ''B''₂, ''B''₃, ...을 다음과 같이 귀납적으로 정의한다.

1. (''A_n'' + ''B_n'') / 2 가 ''S''의 상계인지 확인한다.

2. 상계라면, ''A''_''n''+1 = ''A_n'', ''B''_''n''+1 = (''A_n'' + ''B_n'') / 2 라 하자.

3. 상계가 아니라면 ''s''>(''A_n'' + ''B_n'') / 2 를 만족하는 ''S''의 원소 ''s''가 존재한다. ''A''_''n''+1 = ''s'', ''B''_''n''+1 = ''B_n''라 하자.

그러면 ''A''₁ ≤ ''A''₂ ≤ ''A''₃ ≤ ⋯ ≤ ''B''₃ ≤ ''B''₂ ≤ ''B''₁ 이고 |''A_n'' - ''B_n''| → 0 (''n'' → ∞ 일 때) 이다. 이는 곧 두 수열이 코시 수열이고 같은 극한 ''L''을 가짐을 의미하는데, 이것이 곧 ''S''의 최소 상계이다.

4. 최소 상계 성질의 응용

'''R'''의 최소 상계 성질은 실해석학의 여러 기본 정리들을 증명하는 데 사용된다. 예를 들어, 중간값 정리, 볼차노-바이어슈트라스 정리, 최대-최소 정리, 하이네-보렐 정리 등이 있다.^[1]

4. 1. 중간값 정리

함수 ''f'': [''a'', ''b''] → '''R''' 가 연속 함수이고 ''f''(''a'') < 0, ''f''(''b'') > 0 이라 가정하자. 이 경우에 중간값 정리는 ''f'' 가 구간 [''a'', ''b'']에서 근을 가진다는 것을 말한다. 이는 다음 집합을 생각함으로써 증명할 수 있다.

: ''S'' = {''s'' ∈ [''a'', ''b''] : 모든 ''x'' ≤ ''s''에 대해 ''f''(''x'') < 0}.

즉, ''S''는 [''a'', ''b''] 에서 ''f''가 음의 값을 갖는 첫 부분이다. 그러면 ''b''는 ''S''의 상계이므로 최소 상계 성질에 의해 ''f''는 근을 갖는다.

4. 2. 볼차노-바이어슈트라스 정리

실해석학의 기본 정리인 볼차노-바이어슈트라스 정리는 '''R'''의 닫힌 구간 [a, b]에서 정의된 모든 실수열 xₙ은 수렴하는 부분수열을 갖는다는 것이다. 이는 다음 집합을 생각함으로써 증명할 수 있다.

: S = {s ∈ [a, b] : 무수히 많은 n에 대해 s ≤ xₙ}.

b는 S에 대한 상계이므로 S는 최소 상계 c를 갖는다. 그러면 c는 xₙ의 집적점이므로 xₙ은 c로 수렴하는 부분수열을 갖는다.

4. 3. 최대-최소 정리

''f'' : [''a'', ''b''] → '''R'''를 연속 함수, ''M'' = sup ''f'' ([''a'', ''b''])라 하자. 이때 ''f''([a,b])가 상계를 갖지 않으면 ''M'' = ∞를 의미한다. 최대-최소 정리는 ''M''이 실숫값을 갖고 ''f''(''c'') = ''M''인 ''c'' ∈ [''a'', ''b'']가 존재한다는 것을 말한다. 이는 다음 집합을 생각함으로써 증명할 수 있다.

: ''S'' = {''s'' ∈ [''a'', ''b''] : sup ''f'' ([''s'', ''b'']) = ''M''}.

만일 ''c''가 이 집합의 최소 상계이면, 연속성으로부터 ''f''(''c'') = ''M''을 얻을 수 있다.

4. 4. 하이네-보렐 정리

'''R'''의 최소 상계 성질은 실해석학의 여러 기본 정리들을 증명하는 데 사용된다.^[1]

하이네-보렐 정리는 [''a'', ''b'']를 '''R'''에서의 닫힌 구간, {''U_α''}를 [''a'', ''b'']의 열린 덮개라고 할 때, [''a'', ''b'']를 덮는 {''U_α''}의 유한 부분 덮개가 존재한다는 것을 말한다. 이는 다음 집합을 생각함으로써 증명할 수 있다.^[1]

: ''S'' = {''s'' ∈ [''a'', ''b''] : [''a'', ''s'']는 유한히 많은 ''U_α''에 의해 덮힘}

이 집합은 분명히 최소 상계 ''c''를 갖는다. 하지만 ''c'' 자신은 어떤 ''U_α''의 원소이므로 충분히 작은 δ>0에 대해 [''a'', ''c'' + ''δ'']는 유한히 많은 ''U_α''로 덮인다. 이는 곧 ''c'' + ''δ'' ∈ ''S''임을 의미하는데 이는 ''c'' = ''b''가 아니면 모순이다.^[1]

5. 역사

베르나르트 볼차노는 1817년 "두 개의 서로 반대되는 결과를 내는 두 값 사이에는 방정식의 적어도 하나의 실근이 존재한다"는 논문에서 최소 상계 성질의 중요성을 처음으로 인식하였다.^[6]^[3]

참조

_[1] 서적 completeness property 2011
_[2] 서적 Dedekind complete
_[3] 간행물 A Pedagogical History of Compactness 2015-08
_[4] 서적 completeness property 2011
_[5] 논문 The upper bound on the complexity of branch-and-bound with cardinality bound for subset sum problem http://dx.doi.org/10[...] Author(s) 2016
_[6] 논문 A Pedagogical History of Compactness 2015-08

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com