토리첼리의 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 공식
3. 조건
4. 베르누이 방정식에서의 유도
5. 실험적 검증
- 5.1. 수평 도달 거리
6. 응용
7. 한계
8. 추가 정보
참조

1. 개요

토리첼리의 정리는 비압축성, 비점성 유체가 대기압에 노출된 작은 구멍을 통해 유출될 때 유체의 속도를 계산하는 데 사용되는 공식이다. 이 정리는 베르누이 방정식에서 유도되며, 유체의 속도(v)는 중력 가속도(g)와 기준점에서의 높이(h)의 제곱근에 비례한다. 토리첼리의 정리는 물시계와 같이 유체의 흐름을 이용한 시간 측정 장치 설계에 응용되며, 용기 비우는 시간 계산 및 배출 계수와 같은 실용적인 문제에도 적용된다. 그러나 이 정리는 공기 저항과 같은 실제적인 요소를 고려하지 않으며, 배출 계수를 통해 보정될 수 있다.

더 읽어볼만한 페이지

수리학 - 홍수
홍수는 과도한 강수량, 눈 녹음, 폭풍 해일, 쓰나미 등으로 발생하는 범람 현상으로 인명 및 재산 피해, 환경 파괴를 일으키며, 기후변화로 심각성이 커짐에 따라 제방 건설, 조기 경보 시스템 구축 등 예방 대책과 취약 계층 지원이 필요하지만, 토양 비옥도 증가와 같은 긍정적인 측면도 존재한다.
수리학 - 유압구동계
유압구동계는 파스칼의 원리를 이용해 유체를 압력으로 전달하여 큰 힘을 내는 동력 전달 방식으로, 소형 펌프로 큰 힘을 낼 수 있지만, 오일 누출 등의 단점도 존재하며, 항공기 등에서는 다른 방식으로 대체되기도 한다.
유체동역학 - 항력
항력은 유체 내에서 움직이는 물체에 작용하여 물체의 운동을 방해하는 유체 저항력이며, 유체의 밀도, 물체의 속도, 기준 면적, 항력 계수 등에 의해 결정된다.
유체동역학 - 비점성 흐름
비점성 흐름은 유체 역학에서 점성을 무시할 수 있는 유체의 흐름을 의미하며, 레이놀즈 수가 무한대에 가까울 때 나타나 오일러 방정식으로 설명되고, 프란틀의 경계층 가설을 통해 실제 유체 흐름 모델링에 활용하며, 초유체는 점성이 없는 물질의 상태로 헬륨-4가 2.2K 이하로 냉각될 때 나타난다.

토리첼리의 정리
개요
이름	토리첼리의 정리
분야	유체 역학
설명	액체 수면으로부터 h의 깊이에 있는 작은 구멍에서 액체가 분출되는 속도 v는, 그 깊이에서 자유낙하하는 물체의 속도와 같다. 즉, 진공 중에서 낙하하는 물체는 속도가 점점 증가하지만, 액체는 압력 때문에 속도가 증가하지 않고 일정하게 유지된다.
상세 내용
공식	v = sqrt(2gh)
변수 설명	v: 유체의 유출 속도 g: 중력 가속도 h: 액체 표면에서 유출구까지의 높이
유도	베르누이 방정식과 연속 방정식을 사용하여 유도할 수 있다. 베르누이 방정식: P + 1/2 ρv^2 + ρgh = 일정 (P: 압력, ρ: 밀도, v: 속도, g: 중력 가속도, h: 높이) 연속 방정식: A₁v₁ = A₂v₂ (A: 단면적, v: 속도)
가정	유체는 이상 유체이다. (점성이 없고, 비압축성이다.) 유출구는 충분히 작아서 액체 표면의 속도는 0으로 간주한다. 유출구는 대기압에 노출되어 있다.
응용	수력 발전 액체 저장 탱크의 유출 속도 계산 벤투리 미터
관련 인물
관련 인물	에반젤리스타 토리첼리

2. 공식

베르누이 정리에 따르면, 비압축성 유체이고 점성을 무시할 수 있다면 수두는 일정하다.^[1]

: $\frac{p_1}{\rho_1} + \frac{{v_1}^2}{2} + g y_1 = \frac{p_2}{\rho_2} + \frac{{v_2}^2}{2} + g y_2 = \text{상수}$

여기서 $v$ 는 유체의 속도, $g$ 는 중력 가속도, $y$ 는 어떤 기준점으로부터의 높이, $p$ 는 압력, $\rho$ 는 밀도이다.

액체 표면을 첫 번째 지점, 구멍 바로 바깥쪽을 두 번째 지점으로 잡고, 액체가 비압축성이라고 가정하면 ( $\rho_1 = \rho_2 = \rho$ ), $p_1$ 과 $p_2$ 는 일반적으로 대기압이므로, $p_1 = p_2 \Rightarrow p_1 - p_2 = 0$ 이다. 또한, $y_1 - y_2$ 는 구멍으로부터 액체 표면의 높이 $h$ 와 같다.

: $\frac{{v_1}^2}{2} + g h = \frac{{v_2}^2}{2}$

연속 방정식 $v_1 A = v_2 A_A$ 를 통해 표면의 속도 $v_1$ 는 유출 속도 $v_2$ 와 관련되며, ( $A_A$ 는 구멍의 단면적, $A$ 는 용기의 단면적) $v_2$ 를 $v_A$ (A는 구멍을 의미)로 바꾸면 다음과 같다.

: $\frac{{v_A}^2}{2} \frac{A_A^2}{A^2} + g h = \frac{{v_A}^2}{2}$

: $\Rightarrow g h = \frac{{v_A}^2}{2}\left( 1 - \frac{A_A^2}{A^2} \right) .$

: $\Rightarrow {v_A} = \sqrt{ \frac{ 2 g h }{1 - \frac{A_A^2}{A^2} } } .$

구멍의 면적 $A_A$ 가 용기의 수평 단면적 $A$ 에 비해 매우 작을 때, 토리첼리의 법칙을 얻는다.^[1]

: $v_A = \sqrt{2gh}.$ ^[1]

토리첼리의 법칙은 점성 효과를 무시할 수 있을 때만 적용 가능하다.^[1]

3. 조건

토리첼리의 정리는 다음과 같은 조건에서 성립한다.

비압축성 유체(incompressible fluid): 유체의 밀도가 압력 변화에 따라 변하지 않는다고 가정한다.
비점성 유체(inviscid fluid): 유체의 점성(내부 마찰)을 무시한다.
대기(1atm : atmosphere)에 개방: 유체가 담긴 용기의 윗부분이 대기압에 노출되어 있다.
수위의 하강 속도를 무시할 정도의 작은 구멍(토출구): 구멍의 크기가 매우 작아 물이 빠져나가도 수면의 높이 변화가 거의 없다.

h₁은 기준면(수조 바닥)에서 수조 수위까지의 높이이다.
h₂는 기준면(수조 바닥)에서 토출면(작은 구멍)까지의 높이이다.
h는 토출면(작은 구멍)에서 수조 수위까지의 높이이다.

에반젤리스타 토리첼리의 『기하학 작품』(1644)에 나오는 그의 유명한 유출 공식 유도를 설명하는 그림

점성을 무시하고 비압축성 유체라는 가정 하에, 베르누이 정리는 다음과 같이 나타낼 수 있다.^[5]

:

\frac{v^2}{2} + gy + \frac{p}{\rho} = \text{constant},

여기서

v

는 유체의 속도,

g

는 중력 가속도(약 9.81 m/s²),

y

는 기준점으로부터의 높이,

p

는 압력,

\rho

는 밀도이다. 따라서 유체의 임의의 두 점에 대해 다음 식이 성립한다.

:

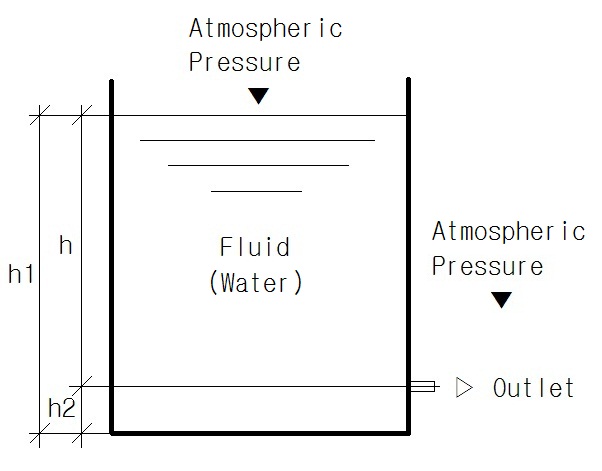
\frac{{v_1}^2}{2} + g_1 y_1 + \frac{p_1}{\rho_1} = \frac{{v_2}^2}{2} + g_2 y_2 + \frac{p_2}{\rho_2}.

첫 번째 점은 유체의 표면에서, 두 번째 점은 구멍 바로 바깥에서 취할 수 있다. 유체는 비압축성이라고 가정하므로

\rho_1

=

\rho_2

이며, 하나의 기호로 나타낼 수 있다. 또한, 구멍이 용기의 수평 단면에 비해 매우 작다면, 표면의 속도는 무시할 수 있다고 가정한다(

v_1 = 0

).

g

는 두 점에서 실질적으로 같다고 가정하므로,

g_1 = g_2 = g

이다. 따라서,

:

g y_1 + \frac{p_1}{\rho} = \frac{{v_2}^2}{2} + g y_2 + \frac{p_2}{\rho}

:

\Rightarrow v_2 = \sqrt{2 g (y_1 - y_2) + 2 (p_1 - p_2)/\rho}.

y_1 - y_2

는 구멍 위의 유체 표면의 높이

h

와 같다.

p_1

과

p_2

는 일반적으로 모두 대기압이므로,

p_1 = p_2 \Rightarrow p_1 - p_2 = 0

이다.

따라서,

:

v_2 = \sqrt{2gh}.

4. 베르누이 방정식에서의 유도

베르누이 방정식에 따르면, 비압축성 유체이고 점성을 무시할 수 있다고 가정하면, 수두는 일정하다.

: $\frac{p_1}{\rho_1} + \frac{{v_1}^2}{2} + g y_1 = \frac{p_2}{\rho_2} + \frac{{v_2}^2}{2} + g y_2 = \text{상수}$

여기서, $v$ 는 유체의 속도, $g$ 는 중력 가속도, $y$ 는 어떤 기준점으로부터의 높이, $p$ 는 압력, $\rho$ 는 밀도이다.

토리첼리의 정리를 유도하기 위해, 첫 번째 지점을 액체 표면에, 두 번째 지점을 구멍 바로 바깥쪽으로 잡는다. 액체는 비압축성이라고 가정하므로, $\rho_1$ 은 $\rho_2$ 와 같고, 둘 다 하나의 기호 $\rho$ 로 나타낼 수 있다. 압력 $p_1$ 과 $p_2$ 는 일반적으로 대기압이므로, $p_1 = p_2 \Rightarrow p_1 - p_2 = 0$ 이다. 또한, $y_1 - y_2$ 는 구멍으로부터 액체 표면의 높이 $h$ 와 같다.

: $\frac{{v_1}^2}{2} + g h = \frac{{v_2}^2}{2}$

표면의 속도 $v_1$ 는 연속 방정식 $v_1 A = v_2 A_A$ 를 통해 유출 속도 $v_2$ 와 관련될 수 있다. 여기서 $A_A$ 는 구멍의 단면적이고, $A$ 는 (원통형) 용기의 단면적이다. $v_2$ 를 $v_A$ (A는 구멍을 의미)로 바꾸면 다음과 같다.

: $\frac{{v_A}^2}{2} \frac{A_A^2}{A^2} + g h = \frac{{v_A}^2}{2}$

: $\Rightarrow g h = \frac{{v_A}^2}{2}\left( 1 - \frac{A_A^2}{A^2} \right) .$

: $\Rightarrow {v_A} = \sqrt{ \frac{ 2 g h }{1 - \frac{A_A^2}{A^2} } } .$

구멍의 면적 $A_A$ 가 용기의 수평 단면적 $A_1$ 에 비해 매우 작을 때 특수한 경우로 토리첼리의 법칙을 얻는다.

: $v_A = \sqrt{2gh}.$ ^[1]

위의 유도 과정은 점성을 무시하고 비압축성 유체라는 가정을 전제로 한다. 베르누이 정리는 다음과 같이 나타낼 수 있다.

: $\frac{v^2}{2} + gy + \frac{p}{\rho} = \text{constant},$

여기서 $v$ 는 유체의 속도, $g$ 는 중력 가속도(약 9.81 m/s²), $y$ 는 기준점으로부터의 높이, $p$ 는 압력, $\rho$ 는 밀도이다. 따라서 유체의 임의의 두 점에 대해 다음 식이 성립한다.

: $\frac{{v_1}^2}{2} + g_1 y_1 + \frac{p_1}{\rho_1} = \frac{{v_2}^2}{2} + g_2 y_2 + \frac{p_2}{\rho_2}.$

첫 번째 점은 유체의 표면에서, 두 번째 점은 구멍 바로 바깥에서 취할 수 있다. 유체는 비압축성이라고 가정하므로 $\rho_1$ = $\rho_2$ 이며, 하나의 기호로 나타낼 수 있다. 또한, 구멍이 용기의 수평 단면에 비해 매우 작다면, 표면의 속도는 무시할 수 있다고 가정한다( $v_1 = 0$ ). $g$ 는 두 점에서 실질적으로 같다고 가정하므로, $g_1 = g_2 = g$ 이다. 따라서,

: $g y_1 + \frac{p_1}{\rho} = \frac{{v_2}^2}{2} + g y_2 + \frac{p_2}{\rho}$

: $\Rightarrow v_2 = \sqrt{2 g (y_1 - y_2) + 2 (p_1 - p_2)/\rho}.$

$y_1 - y_2$ 는 구멍 위의 유체 표면의 높이 $h$ 와 같다. $p_1$ 과 $p_2$ 는 일반적으로 모두 대기압이므로, $p_1 = p_2 \Rightarrow p_1 - p_2 = 0$ 이다.

따라서,

: $v_2 = \sqrt{2gh}.$

5. 실험적 검증

분출 제트의 궤적을 결정하기 위한 실험: 수직 막대를 조정하여 제트에 거의 닿도록 한다. 실험 후 수평선과 제트의 위치 사이의 거리는 막대의 길이 조정으로 측정할 수 있다.

모든 물리 이론은 실험을 통해 검증되어야 한다. 분출 실험은 물로 채워진 원통형 용기에 여러 높이에 구멍을 뚫어 실험하는 장치로 구성된다. 이 장치는 열린 표면을 가진 액체에서 압력이 깊이에 따라 증가함을 보여주도록 설계되었다. 유체의 분출 속도는 용기 아래쪽으로 갈수록 더 빨라진다.^[2]

분출되는 제트는 아래로 향하는 포물선을 그리며, 각 포물선이 도달하는 거리는 오리피스와 표면 사이의 거리가 클수록 멀어진다. 포물선

y(x)

의 모양은 분출 속도에만 의존하며, 액체의 모든 분자가 초기 속도가 분출 속도

v_A

인 포물선 운동을 한다는 사실로부터 결정할 수 있다.

:

y(x)=-\frac{1}{2} \frac{g}{v_A^2} x^2.

이 실험 결과는 토리첼리의 정리가 매우 정확함을 확인시켜 준다.

5. 1. 수평 도달 거리

h를 오리피스(구멍)의 지면으로부터의 높이, H를 지면으로부터의 액체 기둥 높이(액체 표면의 높이)라고 할 때, 액체 제트가 액체 기둥의 바닥과 같은 높이에 도달할 때까지 이동하는 수평 거리는 다음과 같이 유도할 수 있다. 제트 흐름의 입자가 이동한 수직 높이를 h라고 하면, 낙체의 법칙에 따라 다음이 성립한다.

:

h = \frac{1}{2} gt^2 \quad \Rightarrow \quad t = \sqrt{\frac{2h}{g}},

여기서 t는 제트 입자가 오리피스에서 지면까지 낙하하는 데 걸리는 시간이다. 수평 유출 속도가 v라면, 시간 t 동안 제트 입자가 이동한 수평 거리는 다음과 같다.

:

D = vt = v \sqrt{\frac{2h}{g}}.

오리피스 위의 수위가 H-h이므로, 토리첼리의 정리에 따라 수평 유출 속도는

v = \sqrt{2g(H-h)}

이다. 따라서 두 식을 연립하면 다음을 얻는다.

:

D = 2 \sqrt{h(H-h)}.

최대 수평 범위를 제공하는 오리피스의 위치는 D를 h에 대해 미분하고 dD/dh = 0으로 놓고 풀면 구할 수 있다.

:

\frac{dD}{dh} = \frac{H - 2h}{\sqrt{h(H-h)}}.

dD/dh = 0을 풀면,

:

h^* = \frac{H}{2},

이고, 최대 범위는

:

D_{\max} = H.

이다.

6. 응용

토리첼리의 정리는 물시계 제작과 같이 일상생활에서 다양하게 응용된다. 물시계는 물의 흐름을 이용하여 시간을 측정하는 장치인데, 이 원리에는 토리첼리의 정리가 적용된다.

베르누이는 유체역학에서 이론적 예측과 실제 유출량의 차이가 수축류 형성 때문이라고 설명했다.^[2] 수축류는 유출구의 단면적을 감소시켜 배출량에 영향을 준다. 최신 실험에 따르면 유출 속도는 토리첼리의 정리에 의해 매우 정확하게 예측되며, 속도 보정 계수가 필요하지 않다.^[3]

일반적으로 배출 계수를 도입하여 배출량을 유출구의 단면적과 토리첼리의 정리를 연관시킨다. 점성이 낮은 액체가 둥근 구멍을 통해 유출될 때 배출 계수는 약 0.65 정도이다.^[4] 둥근 관이나 호스를 사용하면 0.9를 넘을 수 있으며, 직사각형 개구부의 경우 높이와 폭의 비율에 따라 최대 0.67까지 가능하다.

6. 1. 물시계 (Clepsydra)

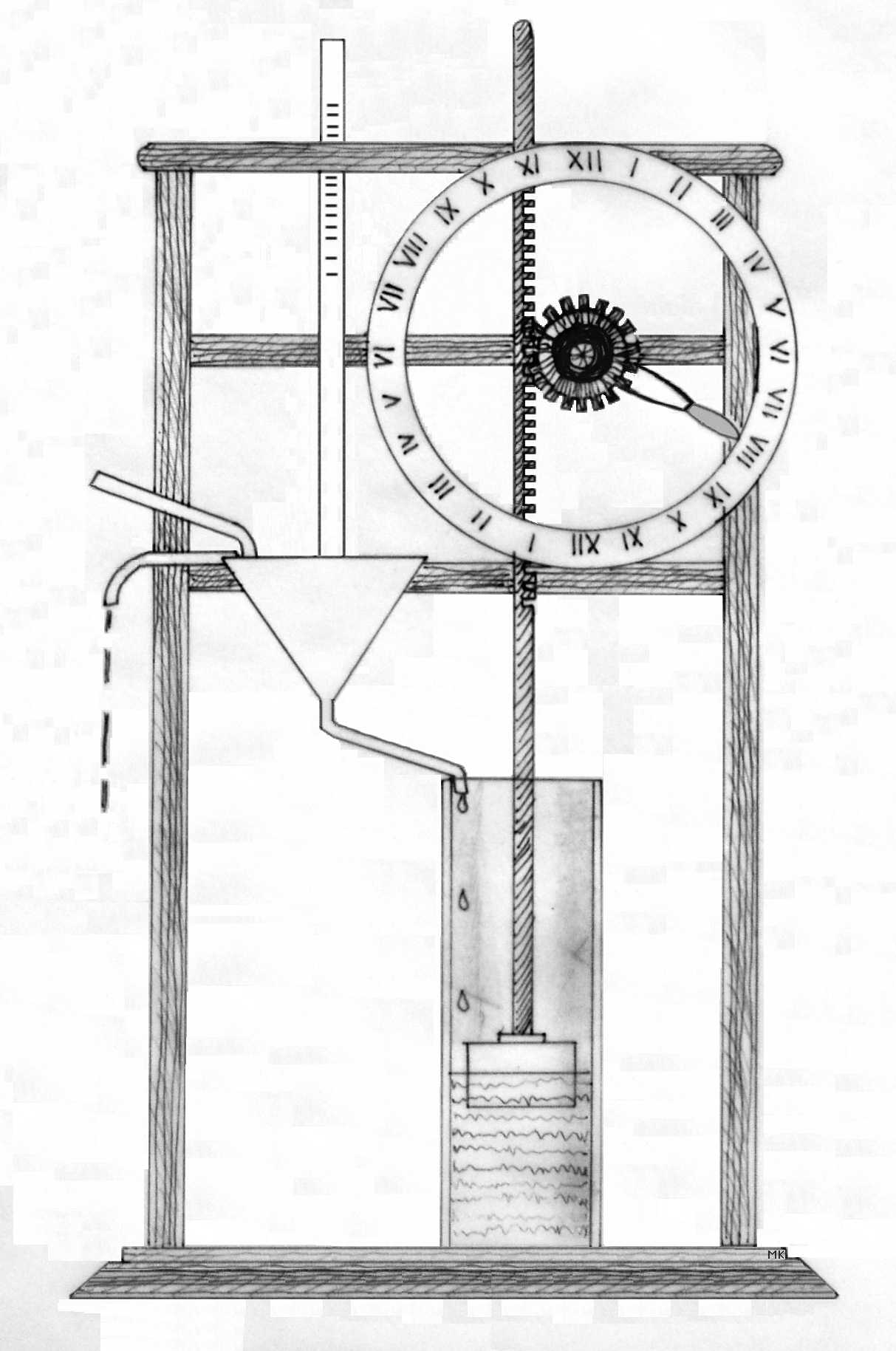
물시계(clepsydra)는 물의 흐름으로 시간을 측정하는 기구이다. 바닥에 작은 구멍이 뚫린 항아리로 구성되며, 이 구멍을 통해 물이 빠져나간다. 빠져나가는 물의 양으로 시간을 측정한다. 토리첼리의 정리에 따르면, 구멍을 통한 유출 속도는 물의 높이에 따라 달라지며, 수위가 감소함에 따라 방출량은 일정하지 않다. 간단한 해결책은 물의 높이를 일정하게 유지하는 것이다. 이는 용기에 일정한 물줄기가 흘러들어오게 하고, 넘치는 물은 상단의 다른 구멍으로 배출되도록 하여 달성할 수 있다. 따라서 높이가 일정하게 유지되면, 바닥에서 배출되는 물을 시간을 측정하기 위해 눈금이 일정하게 새겨진 원통형 용기에 모을 수 있다. 이것이 유입형 물시계이다.

또는, 용기의 모양을 신중하게 선택함으로써 용기의 수위를 일정한 비율로 감소시킬 수 있다. 용기에 남아 있는 물의 수위를 측정하여 시간을 일정한 눈금으로 측정할 수 있다. 이것은 유출형 물시계의 예이다. 물의 유출 속도는 수위가 높을수록 (압력이 더 높기 때문에) 더 높기 때문에, 수위가 높을 때 유체의 부피는 단순한 원통보다 더 커야 한다. 즉, 수위가 높을수록 반지름이 더 커야 한다. 면적이

a

인 출구 위의 수위 높이

h

에 따라 반지름

r

이 증가하게 한다. 즉,

r = f(h)

이다. 우리는 수위가 일정한 비율로 감소하게 하는 반지름, 즉

dh/dt = c

를 찾고자 한다.

주어진 수위

h

에서 물 표면적은

A = \pi r^2

이다. 물 부피의 순간적인 변화율은 다음과 같다.

:

\frac{dV}{dt} = A \frac{dh}{dt} = \pi r^2 c.

토리첼리의 정리에 따르면, 유출 속도는 다음과 같다.

:

\frac{dV}{dt} = A_A v = A_A \sqrt{2gh},

이 두 방정식에서,

:

\begin{align}A_A \sqrt{2gh} &= \pi r^2 c \\\Rightarrow \quad h &= \frac{\pi^2 c^2}{2g A_A^2} r^4.\end{align}

따라서 용기의 반지름은 높이의 네제곱근에 비례하여 변해야 한다.

r \propto \sqrt[4]{h}.

마찬가지로, 유출형 물시계의 용기 모양을 위의 사양에 따라 수정할 수 없다면, 시간을 측정하기 위해 불균일한 눈금을 사용해야 한다. 위의 비우는 시간 공식은 시간을 배출된 물의 높이의 제곱근으로 보정해야 함을 알려준다.

T \propto \sqrt{h}.

더 정확하게는,

:

\Delta t = \frac{A}{A_A} \sqrt{\frac{2}{g}} (\sqrt{h_1} - \sqrt{h_2})

여기서

\Delta t

는 수위가

h_1

의 높이에서

h_2

의 높이로 떨어지는 데 걸리는 시간이다.

6. 2. 용기 비우는 시간

단면적이

A

인 원통형 용기의 바닥에 면적

A_A

의 구멍이 있다고 가정하면, 수위 높이 변화율

dh/dt

는 일정하지 않다. 용기의 물의 부피는 용기 밖으로 배출되는 유량

\dot{V}

때문에 변한다.

:

\frac{dV}{dt} = A \frac{dh}{dt} = \dot{V} = A_A v_A = A_A \sqrt{2gh} \quad \Rightarrow \quad A \frac{dh}{\sqrt{h}} = A_A \sqrt{2g} \; dt

양변을 적분하고 정리하면 다음을 얻는다.

:

T = \frac{A}{A_A} \sqrt{\frac{2H}{g}}

여기서

H

는 초기 수위이고

T

는 모든 물을 배출하여 용기를 비우는 데 걸리는 총 시간이다.

이 공식은 몇 가지 의미를 지닌다. 단면적이

A

이고 높이가

H

이며 부피가

V = AH

인 탱크가 가득 차 있다면, 모든 물을 배출하는 데 걸리는 시간은 다음과 같다.

:

T = \frac{V}{A_A} \sqrt{\frac{2}{gH}}

이는 같은 부피로 채워진 탱크의 경우 높이가 높을수록 넓이가 넓은 탱크보다 배수 속도가 빠르다는 것을 의미한다.

마지막으로, 위의 방정식을 다시 정리하여 시간

t

의 함수로서 수위

h(t)

를 다음과 같이 결정할 수 있다.

:

h(t) = H \left(1 - \frac{t}{T} \right)^2

여기서

H

는 용기의 높이이고

T

는 위에서 제시된 배출 시간이다.

6. 3. 배출 계수 (Coefficient of discharge)

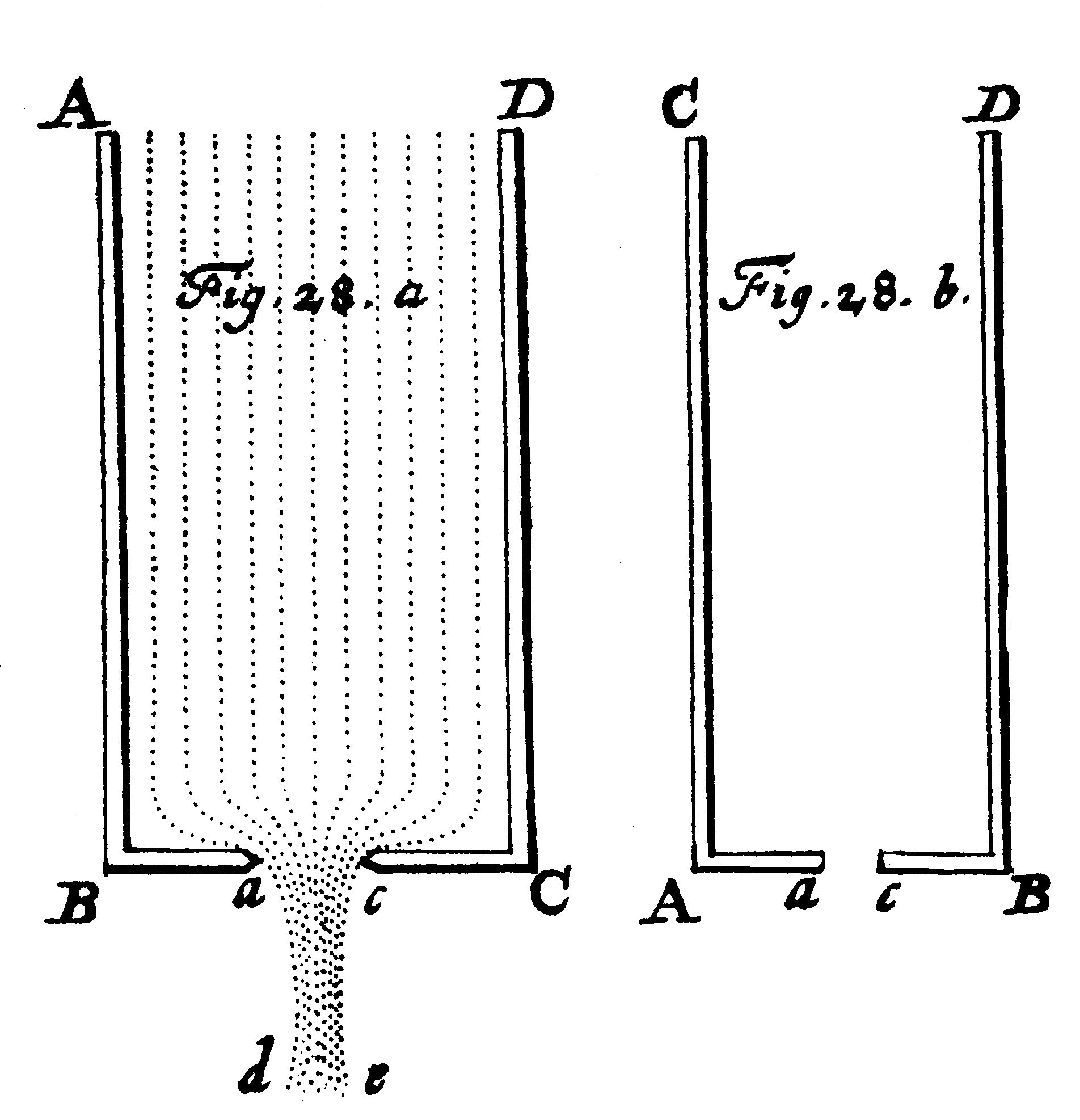
다니엘 베르누이의 『유체역학』(1738) 28번째 그림. 유속선을 따라 수축류(vena contracta)가 형성되는 모습을 보여준다.

1738년 다니엘 베르누이는 이론적 예측과 실제 유출량의 차이를 수축류의 형성 때문으로 설명했다.^[2] 수축류는 유출구의 단면적

A_A

를 수축된 단면적

A_C

로 감소시킨다. 따라서 배출량은 다음과 같이 나타낼 수 있다.

:

\dot{V} = A_C v_A = A_C \sqrt{2gh}

최신 실험(^[3] 참조)에서 배출량, 유출 속도, 수축류의 단면적을 측정한 결과, 유출 속도는 토리첼리의 정리에 의해 매우 정확하게 예측되며 속도 보정 계수가 필요하지 않음이 확인되었다.

문제는 수축류의 단면적을 어떻게 결정하는가이다. 일반적으로 배출 계수를 도입하여 배출량을 유출구의 단면적과 토리첼리의 정리와 관련짓는다.

:

{\dot {V}}_{\text{real}}=\mu A_A v_A \quad \text{with} \quad \mu = \frac{A_C}{A_A}

점성이 낮은 액체(예: 물)가 탱크의 둥근 구멍을 통해 유출될 때 배출 계수는 약 0.65 정도이다.^[4] 둥근 관이나 호스를 통해 배출하면 배출 계수는 0.9를 넘을 수 있다. 직사각형 개구부의 경우 높이-폭 비율에 따라 배출 계수는 최대 0.67까지 될 수 있다.

7. 한계

토리첼리의 정리는 점성 효과를 무시할 수 있을 때만 적용할 수 있으며, 이는 용기의 구멍을 통해 물이 흘러나오는 경우에 해당한다.^[1]

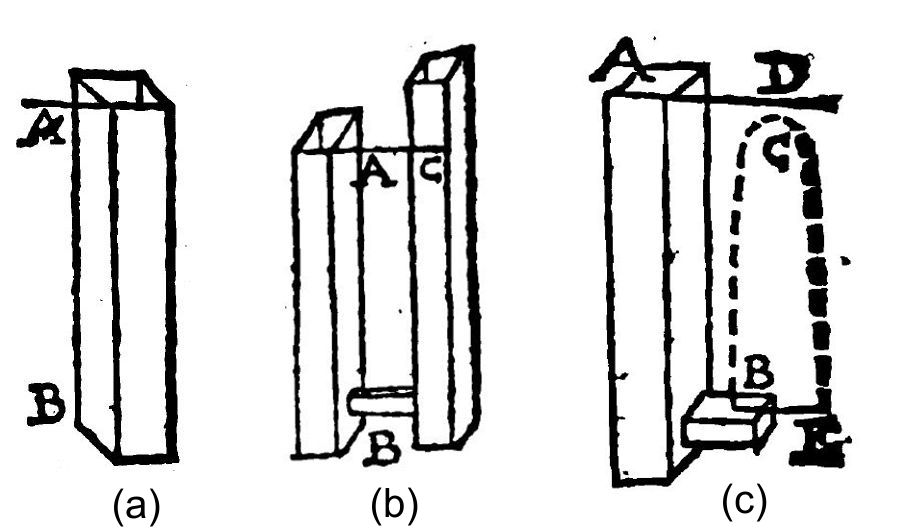
에반젤리스타 토리첼리의 원래 유도 과정은 그의 『기하학 작품』(Opera Geometrica)의 두 번째 책 'De motu aquarum'에서 찾아볼 수 있다.^[5] 그는 A 수위까지 물로 채워진 관 AB(그림 (a))로 시작하여, B 수위에 좁은 구멍을 뚫고 두 번째 수직 관 BC에 연결한다. 통하는 용기의 정수압 원리에 따라 물은 두 관 모두에서 같은 채우기 수위 AC까지 상승한다(그림 (b)). 마지막으로 관 BC를 제거하면(그림 (c)) 물은 다시 이 높이까지 상승해야 하는데, 그림 (c)에서는 AD로 명명되어 있다. 이러한 현상의 이유는 A에서 B로 떨어지는 물방울의 낙하 속도가 B에서 A로 물방울을 들어 올리는 데 필요한 초기 속도와 같다는 사실 때문이다.

그러나 이러한 실험을 수행하면 그림 (c)의 D 대신 C 높이까지만 도달하는데, 이는 제안된 이론과 모순된다. 토리첼리는 이러한 결함을 공기 저항과 하강하는 물방울이 상승하는 물방울과 충돌한다는 사실 때문이라고 설명한다.

토리첼리의 주장은 틀렸다. 자유 제트의 압력은 주변 대기압인 반면, 통하는 용기의 압력은 정수압이기 때문이다. 당시에는 압력의 개념이 알려져 있지 않았다.

8. 추가 정보

점성을 무시하고 비압축성 유체라는 가정 하에, 베르누이 정리는 다음과 같이 나타낼 수 있다.

: $\frac{v^2}{2} + gy + \frac{p}{\rho} = \text{constant},$

여기서 $v$ 는 유체의 속도, $g$ 는 중력 가속도(약 9.81m²), $y$ 는 기준점으로부터의 높이, $p$ 는 압력, $\rho$ 는 밀도이다. 따라서 유체의 임의의 두 점에 대해 다음 식이 성립한다.

: $\frac{{v_1}^2}{2} + g_1 y_1 + \frac{p_1}{\rho_1} = \frac{{v_2}^2}{2} + g_2 y_2 + \frac{p_2}{\rho_2}.$

첫 번째 점은 유체의 표면에서, 두 번째 점은 구멍 바로 바깥에서 취할 수 있다. 유체는 비압축성이라고 가정하므로 $\rho_1$ = $\rho_2$ 이며, 하나의 기호로 나타낼 수 있다. 또한, 구멍이 용기의 수평 단면에 비해 매우 작다면, 표면의 속도는 무시할 수 있다고 가정한다( $v_1 = 0$ ). $g$ 는 두 점에서 실질적으로 같다고 가정하므로, $g_1 = g_2 = g$ 이다. 따라서,

: $g y_1 + \frac{p_1}{\rho} = \frac{{v_2}^2}{2} + g y_2 + \frac{p_2}{\rho}$

: $\Rightarrow v_2 = \sqrt{2 g (y_1 - y_2) + 2 (p_1 - p_2)/\rho}.$

$y_1 - y_2$ 는 구멍 위의 유체 표면의 높이 $h$ 와 같다. $p_1$ 과 $p_2$ 는 일반적으로 모두 대기압이므로, $p_1 = p_2 \Rightarrow p_1 - p_2 = 0$ 이다.

따라서,

: $v_2 = \sqrt{2gh}.$

참조

_[1] 서적 Physics Wiley Toppan 1966
_[2] 웹사이트 Spouting cylinder fluid flow http://www.4physics.[...]
_[3] 논문 Velocity Coefficients for Free Jets from Sharp-Edged Orifices 1984
_[4] 웹사이트 Discharge of liquids (Torricelli's law) https://www.tec-scie[...] 2019-12-08
_[5] 논문 History of the Torricelli Principle and a New Outflow Theory 2016

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com