호소헤드론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
호소헤드론은 슐레플리 기호 {2, n}으로 표현되는 다면체의 한 종류로, 정다면체의 조건을 완화하여 이각형을 구면 달꼴로 표현하여 무한히 많은 종류가 존재한다. 이는 구면에서 n개의 구면 달꼴로 이루어지며, 각 달꼴은 두 꼭짓점을 공유하고 내각은 2π/n이다. 호소헤드론은 구면 타일링의 일종으로, 2n각 호소헤드론은 삼차원 이면체 대칭의 기본 삼각형을 나타내며, 사각 호소헤드론은 바이실린더 스타인메츠 다면체와 위상적으로 같다. 호소헤드론의 쌍대는 n각형 이면체이며, 깎은 n각 호소헤드론은 n각기둥이다. 극한의 경우 무한각 호소헤드론이 되며, 다차원 해석은 호소토프라고 불린다. 용어는 그리스어 "hosos"에서 유래되었으며, "원하는 만큼 많은 면을 가질 수 있다"는 의미를 담고 있다.
더 읽어볼만한 페이지
- 테셀레이션 - 준결정
준결정은 주기적인 결정 구조가 아닌 규칙적인 회절 패턴을 보이는 고체 물질이며, 댄 셰흐트만이 발견하여 2011년 노벨 화학상을 수상했으며, 다각형과 이코사헤드럴의 두 가지 유형이 존재하고, 높은 열 및 전기 저항 등의 특성을 나타낸다. - 테셀레이션 - 펜로즈 테셀레이션
펜로즈 테셀레이션은 로저 펜로즈가 발견한 비주기적 테셀레이션으로, 유한한 종류의 프로토타일로 평면을 채울 수 있으며, 초기 6개에서 2개로 줄어든 프로토타일을 사용하고 황금비와 관련되어 현대 건축 및 디자인에서 활용된다. - 다면체 - 마름모구십면체
마름모구십면체는 깎은 정이십면체에 각뿔을 붙여 만든 다면체이며, 넓은 마름모 60개와 좁은 마름모 30개로 구성되고 좁은 마름모는 황금비의 제곱과 관련된 대각선 비율을 가지며 최적 충전율은 약 0.7947이다. - 다면체 - 삼각쌍뿔
삼각쌍뿔은 6개의 정삼각형 면, 5개의 꼭짓점, 9개의 모서리를 가진 존슨 다면체이자 델타다면체로, 두 정사면체를 밑면끼리 결합한 형태이며, 분자 기하학, 색채 이론 등 다양한 분야에 응용된다. - 수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다. - 수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.
| 호소헤드론 | |
|---|---|
| 기본 정보 | |
 | |
| 유형 | 정다면체 또는 구면 타일링 |
| 오일러 지표 | 2 |
| 면 | 이각형 n개 |
| 변 | n개 |
| 꼭짓점 | 2 |
| 꼭짓점 배열 | 2n |
| 슐레플리 기호 | {2,n} |
| 위소프 기호 | n 2 2 |
| 대칭군 | Dnh, [2,n], (*22n), 4n차 |
| 회전 대칭군 | Dn, [2,n]+, (22n), 2n차 |
| 쌍대 | 정 n각형 이면체 |
| 정보 | |
| 기호 | n |
| 각 면의 각도 | |n}} |
2. 정다면체와 호소헤드론
정다면체는 슐레플리 기호 {''m'', ''n''}으로 나타낼 수 있다. 전통적인 플라톤의 다면체는 각 면이 최소 3개의 변을 가져야 한다는 조건(''m'' ≥ 3)과 각 꼭짓점에 최소 3개의 면이 만나야 한다는 조건(''n'' ≥ 3)을 만족해야 한다.
하지만 다면체를 구면 타일링으로 확장하여 생각하면, 면의 변 개수 조건(''m'' ≥ 3)을 완화할 수 있다. 구면 위에서는 변이 2개인 이각형(''m''=2)도 넓이를 가진 구면 달꼴 형태로 존재 가능하기 때문이다. 이렇게 ''m''=2 조건을 허용하여 정의되는 새로운 종류의 정다면체를 호소헤드론({2, ''n''})이라고 부른다. 호소헤드론은 구면 위에서 ''n''개의 이각형(구면 달꼴) 면이 두 꼭짓점에서 만나는 형태를 가진다.
2. 1. 정호소헤드론 족
슐레플리 기호가 {''m'', ''n''}인 정다면체에서, 다각형 면의 수 ''N''2는 다음 공식으로 주어진다::
전통적인 플라톤의 다면체는 면이 최소 세 변을 가져야 한다는 조건(''m'' ≥ 3)과 각 꼭짓점에 최소 세 면이 만나야 한다는 조건(''n'' ≥ 3) 때문에 제한된 해만 가진다.
그러나 다면체를 구면 타일링으로 간주하면, 넓이가 0이 아닌 구면 달꼴로 이각형(''m''=2) 면을 허용할 수 있다. ''m'' = 2를 허용하면 면의 수는 다음과 같이 간단해진다:
:
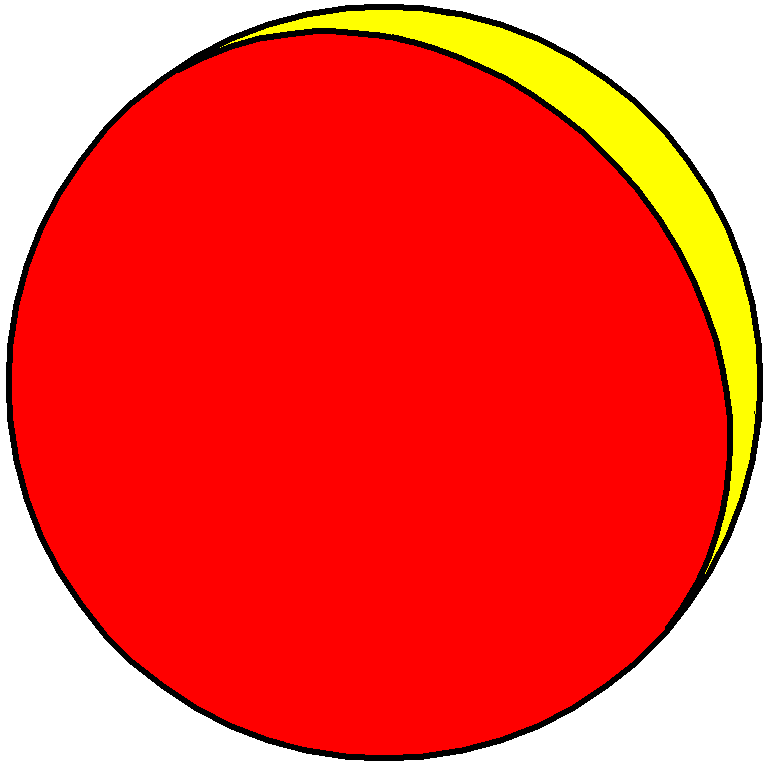
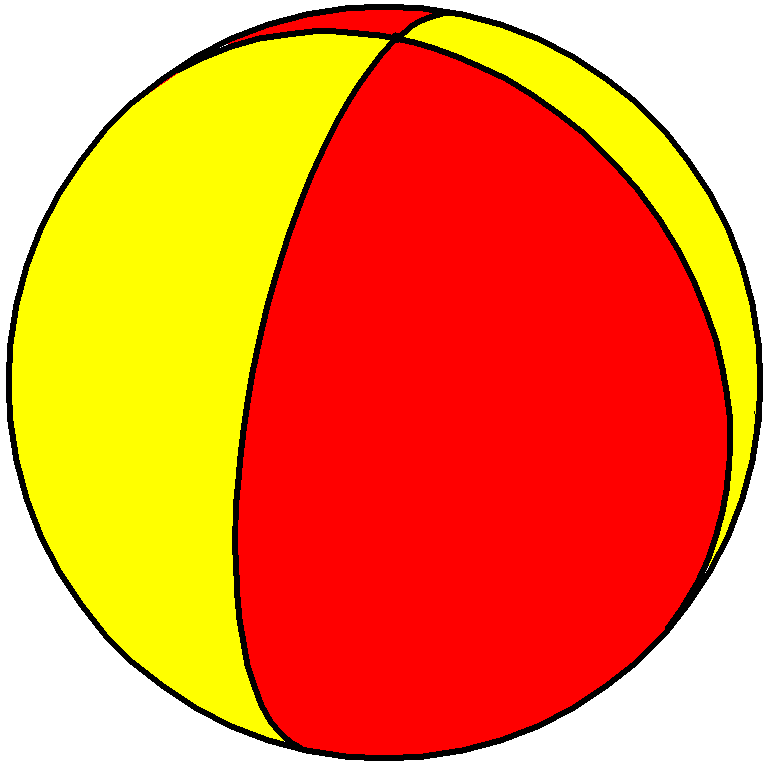
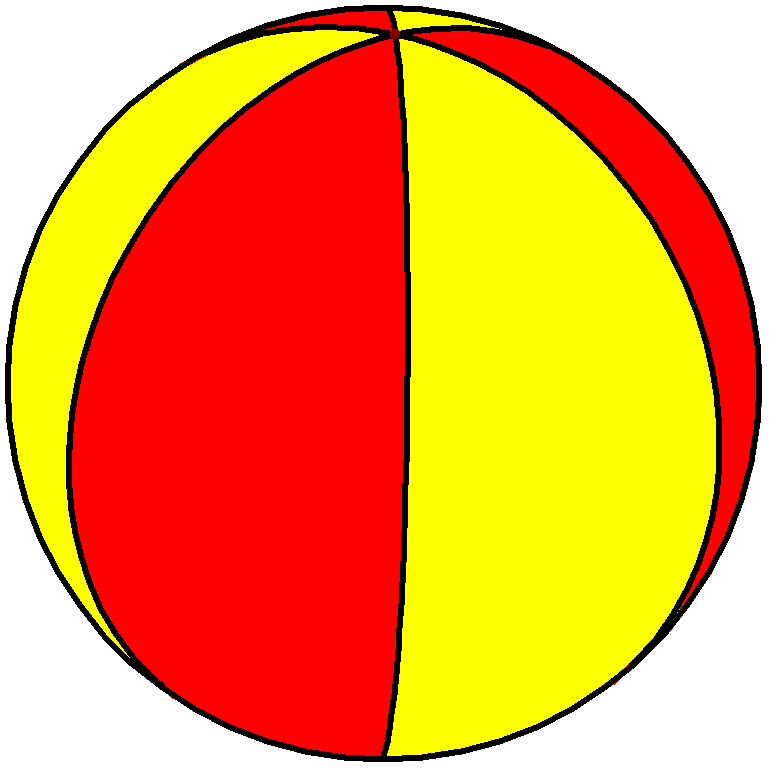
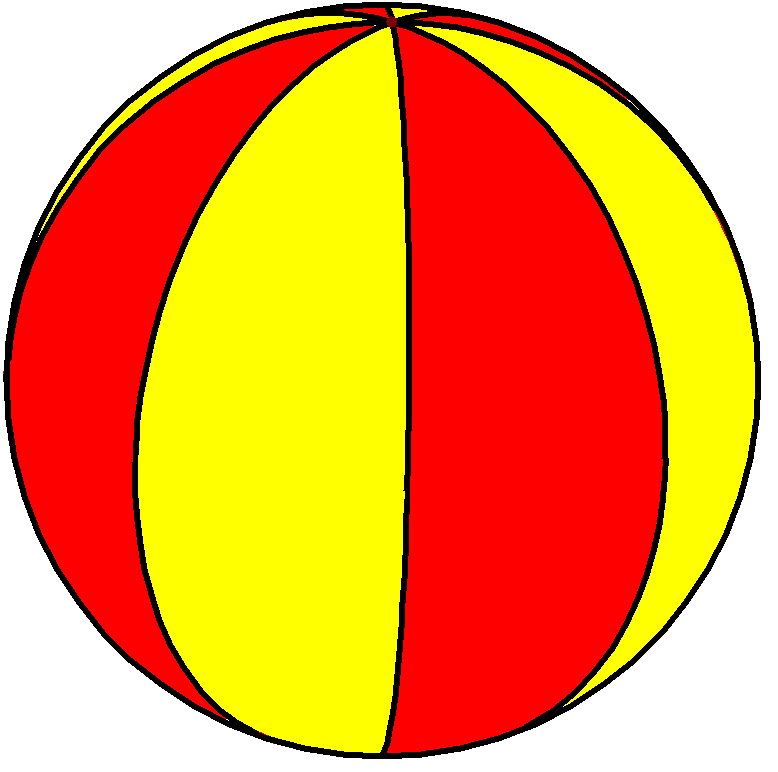
이는 호소헤드론이라는 새로운 무한한 종류의 정다면체를 정의하게 해준다. 구면 위에서 다면체 {2, ''n''}은 내부 각이 인 ''n''개의 구면 달꼴 면으로 구성되며, 이 모든 면은 두 개의 공통된 꼭짓점에서 만난다.
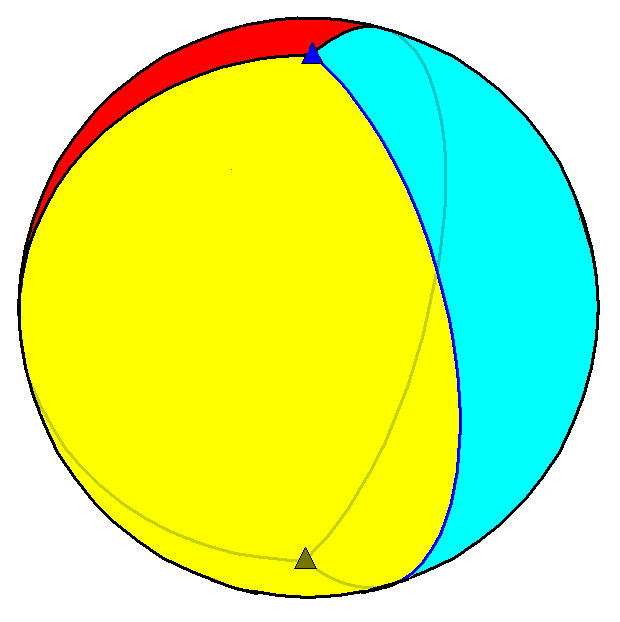
다음 표는 다양한 ''n'' 값에 따른 정호소헤드론의 종류와 관련 정보를 보여준다.
| 공간 | 구면 | 유클리드 | |||||
|---|---|---|---|---|---|---|---|
| 타일링 이름 | 일각 | 이각 | 삼각 | 사각 | 오각 | ... | 무한각 |
| 타일링 이미지 |  | -- | -- | -- | -- | ... |  |
| 슐레플리 기호 | {2,1} | {2,2} | {2,3} | {2,4} | {2,5} | ... | {2,∞} |
| 콕서터 다이어그램 | -- | -- | -- | -- | -- | ... | -- |
| 면과 변 | 1 | 2 | 3 | 4 | 5 | ... | ∞ |
| 꼭짓점 | 2 | 2 | 2 | 2 | 2 | ... | 2 |
| 꼭짓점 구성 | 2 | 2.2 | 23 | 24 | 25 | ... | 2∞ |
2''n''개의 달꼴 면으로 이루어진 2''n''-호소헤드론 {2, 2''n''}은 3차원 이면체 대칭의 기본 영역을 나타낸다. 이 대칭은 순환 대칭 C''n''v (차수 2''n'')이며, 오비폴드 표기법으로는 (*''nn''), 콕스터 표기법으로는 [''n'']으로 표기한다. 반사 영역은 거울상으로 번갈아 색칠된 달꼴로 나타낼 수 있다.
사각 호소헤드론은 서로 수직인 원기둥 두 개의 교차로 만들어지는 입체와 위상 동형이다. 이는 바이실린더 스타인메츠 다면체 또는 이중 원기둥 슈타인메츠 입체라고도 불린다.[8][3] 이러한 관계는 호소헤드론이 단순한 추상적 개념만이 아니라, 실제 3차원 공간의 물체와도 연결될 수 있는 구조임을 보여준다.
''n''각 호소헤드론 {2, ''n''}의 쌍대다면체는 ''n''각형 이면체 {''n'', 2}이다. 다면체 {2, 2}는 자기쌍대이며, 호소헤드론이면서 이면체이다.
극한의 경우, 호소헤드론은 2차원 테셀레이션인 무한각 호소헤드론이 된다.
호소헤드론의 일반적인 다차원 유사체는 '''호소토프'''라고 불린다. 슐레플리 기호 {2,''p'',...,''q''}를 갖는 정호소토프는 두 개의 꼭짓점을 가지며, 각각의 꼭짓점 도형은 {''p'',...,''q''}이다.
“호소헤드론”이라는 용어는 H.S.M. Coxeter가 제시하였다.[9] 이 용어는 그리스어 ὅσος|호소스gre("많은")에서 유래한 것으로 보이며, 이는 호소헤드론이 "원하는 만큼 많은 면을 가질 수 있다"는 개념적 특징을 반영한다.[9][4]
[1]
서적
Regular polytopes
3. Kaleidoscopic 대칭
각 달꼴을 두 개의 구면 삼각형으로 나누면 ''n''각형 쌍각뿔이 만들어지는데, 이는 차수 4''n''의 이면체 대칭 D''n''h에 해당한다.
아래 표는 특정 작은 값 ''n''에 대한 호소헤드론의 만화경 대칭을 다양한 표기법과 함께 보여준다.대칭 (차수 2n) 쇤플라이스 표기법 Cnv C1v C2v C3v C4v C5v C6v 오비폴드 표기법 (*nn) (*11) (*22) (*33) (*44) (*55) (*66) 콕스터 표기법 [n] [ ] [2] [3] [4] [5] [6] 2n-각형 호소헤드론 슐레플리 기호 {2, 2n} {2, 2} {2, 4} {2, 6} {2, 8} {2, 10} {2, 12} 번갈아 색칠된 기본 영역 
4. 스타인메츠 다면체와의 관계
5. 파생 다면체
호소헤드론은 다른 다면체처럼 깎은 다면체 변형을 통해 새로운 다면체를 만들 수 있다. 깎은 ''n''각 호소헤드론은 ''n''각기둥이다.
6. 무한각 호소헤드론
7. 호소토프
이차원 호소토프, 즉 슐레플리 기호 {2}를 가지는 도형은 이각형이다.
8. 어원
참조
[2]
서적
Abstract Regular polytopes
[3]
Mathworld
Steinmetz Solid
[4]
서적
The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English
https://archive.org/[...]
MAA
1994-01-01
[5]
서적
Regular Complex Polytopes
Cambridge University Press
[6]
서적
Regular polytopes
[7]
서적
Abstract Regular polytopes
[8]
Mathworld
Steinmetz Solid
[9]
서적인용
The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English
https://books.google[...]
MAA
1994-01-01
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com