라플라스 변환

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

라플라스 변환은 함수 f(t)를 다른 함수 F(s)로 변환하는 적분 변환의 일종이다. 모든 실수 t ≥ 0에 대해 정의되며, 복소수 s를 사용하여 적분을 통해 계산된다. 라플라스 변환은 선형성을 가지며, 미분, 적분, 컨볼루션 등의 연산을 주파수 영역에서 간단하게 표현할 수 있도록 한다. 미분방정식의 풀이나 회로 해석, 선형 시불변 시스템의 분석 등 공학 및 물리학 분야에서 널리 사용된다. 푸리에 변환, Z 변환, 멜린 변환 등 다른 변환과 밀접한 관련이 있다.

2. 정의

함수 $f(t)$ 의 라플라스 변환은 F(s)로 표기하며, 다음과 같이 정의된다.^[41]

: $F(s)= \mathcal{L}\left\{ f\right\}(s)=\int_{0^-}^\infty e^{-st} f(t)\,dt.$

여기서 $0^-$ 는 $\lim_{\epsilon \rightarrow 0+} -\epsilon$ 를 간단히 나타낸 것이고, 복소수 $s = \sigma + i \omega \,$ (σ와 ω는 실수)이다. 실제 사용 시에는 엄밀히 정확하지는 않지만 $F(s) = \mathcal{L} \left\{f(t)\right\}$ 로 표기하기도 한다.

라플라스 변환은 함수에 $e$ 를 곱한 후 푸리에 변환하는 연산이라고 생각할 수 있다(여기서 θ는 계단 함수이다).

: $F(s):=F(\sigma,\omega) = \int_{-\infty}^{\infty} \theta(t)f(t)\mathrm{e}^{-\sigma t} \mathrm{e}^{-i\omega t}\,\mathrm dt\overset{s=\sigma+i\omega}{=\!=}\int_0^{\infty} f(t)\mathrm{e}^{-st}\,\mathrm dt$

수열 $a_n$ 의 (일반형) 모함수

: $G(a_n;x)=\sum_n a_nx^n\,$

에서 $x = e^{-s}$ 로 하면,

: $G(a_n;\mathrm{e}^{-s})=\sum_n a_n \mathrm{e}^{-sn}\,$

이 된다. 여기서 합을 적분으로 바꾸면

: $G(a_t;\mathrm{e}^{-s})=\int a_t \mathrm{e}^{-st}\mathrm dt\,$

이 되고, 함수 $a_t$ 의 라플라스 변환과 일치한다. 이러한 의미에서 라플라스 변환은 모함수의 "연속형"으로 간주할 수 있다.

이러한 이유로 모함수와 라플라스 변환은 같은 종류의 성질을 만족시키는 경우가 있다. 예를 들어 모함수의 성질

: $G(a_n;x)G(b_n;x)=G(a_n*b_n;x)\,$

은 라플라스 변환의 성질

: $\mathcal{L}[f](s)\mathcal{L}[g](s)=\mathcal{L}[f*g](s)\,$

에 대응한다. 여기서 $*$ 는 컨볼루션 적분이다.

2. 1. 라플라스 변환

모든 실수 t ≥ 0에 대해 정의된 함수 f(t)의 라플라스 변환 F(s)는 다음과 같이 정의된다.^[41]

:

F(s)= \mathcal{L}\left\{ f\right\}(s)=\int_{0^-}^\infty e^{-st} f(t)\,dt.

여기서

0^-

는

\lim_{\epsilon \rightarrow 0+} -\epsilon

를 간단히 나타낸 것이고, 복소수

s = \sigma + i \omega \,

(σ와 ω는 실수)이다. 실제 사용 시에는 엄밀히 정확하지는 않지만

F(s) = \mathcal{L} \left\{f(t)\right\}

로 표기하기도 한다.^[3]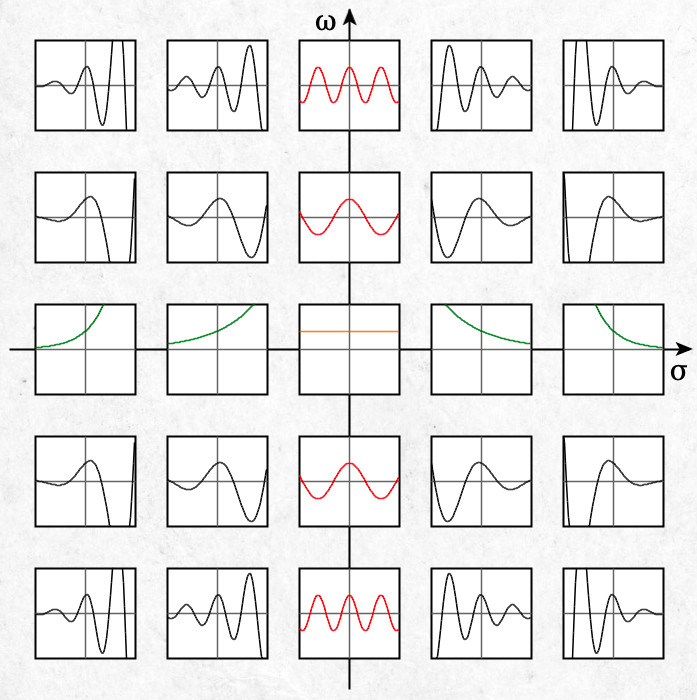

라플라스 변환의 다른 표기법은

\mathcal{L}\{f\}

이며, 종종 표기의 남용으로

F(s) = \mathcal{L}\{f(t)\}

로 표기된다.

적분의 의미는 관심 있는 함수의 종류에 따라 달라진다. 적분이 존재하기 위한 필요조건은 f가 국소적으로 적분가능해야 한다는 것이다. 무한대에서 감소하거나 지수형(

|f(t)| \le Ae^{B|t|}

)인 국소적으로 적분가능한 함수의 경우, 적분은 (적절한) 르베그 적분으로 이해할 수 있다.

유한 보렐 측도 μ의 라플라스 변환은 르베그 적분^[19]으로 정의할 수 있다.

:

\mathcal{L}\{\mu\}(s) = \int_{[0,\infty)} e^{-st}\, d\mu(t).

μ가 확률 측도, 예를 들어 디랙 델타 함수인 경우, 작용소 미적분에서 측도의 라플라스 변환은 측도가 확률 밀도 함수 f에서 나온 것처럼 종종 처리된다. 이때 혼동을 피하기 위해 다음과 같이 쓴다.

:

\mathcal{L}\{f\}(s) = \int_{0^-}^\infty f(t)e^{-st} \, dt,

여기서 하한

0^-

는

\lim_{\varepsilon \to 0^+}\int_{-\varepsilon}^\infty

의 약어이다. 이 한계는 0에 위치한 임의의 점 질량이 라플라스 변환에 의해 완전히 포착됨을 강조한다. 르베그 적분을 사용하면 이러한 극한을 취할 필요가 없지만, 라플라스-스틸체스 변환과 관련하여 더 자연스럽게 나타난다.

실수 t ≥ 0에 대해 정의된 함수 f(t)의 라플라스 변환은

:

F(s) = \int_{0}^\infty f(t)\mathrm{e}^{-st}\mathrm dt

으로 정의되는 s의 함수 F(s)이다. 여기서 s는 복소수이며, 두 실수 σ, ω를 이용하여

s = \sigma + i\omega

로 나타낼 수 있다 (i는 허수단위). 우변의 적분은 라플라스 적분이라고 불리며, 시간 영역에서 복소 평면으로의 사상이다.

함수 F(s)에서 원래 함수 f(t)를 계산하는 역라플라스 변환은

c > 0

일 때,

:

f(t) = \lim_{p\to\infty}\frac{1}{2\pi i} \int_{c-ip}^{c+ip} F(s)\mathrm{e}^{st}\,\mathrm ds

처럼 정의된다. 여기서 c는 모든 특이점의 실수부보다 큰 실수이다. 우변의 적분은 브롬위치 적분이라고 불리며, 복소 평면에서 시간 영역으로의 사상이다.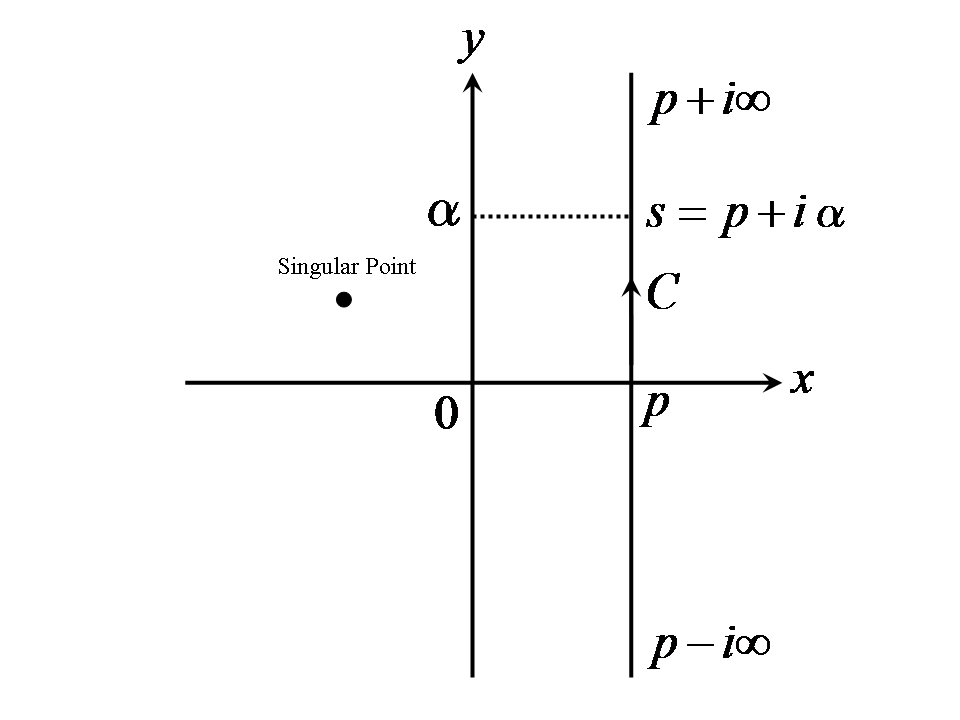

이는 복소 적분이다. 정의대로의 적분 경로에서는 계산이 어려워지지만, 폐곡선이 되도록 적분 경로를 변경하여 유수를 계산함으로써 간단하게 역라플라스 변환을 구할 수 있다. 결과적으로 복소 평면상의 모든 특이점의 유수의 총합이 된다. 여기서 f(t)를 원함수, F(s)를 상함수라고 한다.

라플라스 변환과 역라플라스 변환의 다른 표기 방법은 다음과 같다.

:

F(s) = \mathcal{L}[f(t)]

:

f(t) = \mathcal{L}^{-1}[F(s)]

이러한 기호를 사용한 사상

:

\begin{align}\mathcal{L} & \colon ~ f \mapsto F,\\\mathcal{L}^{-1} & \colon F \mapsto f\end{align}

을 각각 라플라스 변환, 역라플라스 변환이라고 부른다.

보통 라플라스 변환 및 역라플라스 변환을 할 때는 변환표를 참조하여 계산하는 경우가 많으므로, 전술한 정의식에 따라 계산하는 경우는 적다. 하지만 경우에 따라서는 정의식으로부터 계산하는 쪽이 간단한 경우도 있다. 예를 들어 역라플라스 변환을 할 때 부분분수분해를 해야 하는 경우, 오히려 브롬위치 적분을 계산하는 쪽이 빠른 경우도 많다.

;주:

: 라플라스 변환은 함수 f(t)에

eθ(t)

를 곱한 후 푸리에 변환하는 연산이라고 생각할 수 있다(여기서 θ(t)는 계단 함수이다).

:

F(s):=F(\sigma,\omega) = \int_{-\infty}^{\infty} \theta(t)f(t)\mathrm{e}^{-\sigma t} \mathrm{e}^{-i\omega t}\,\mathrm dt\overset{s=\sigma+i\omega}{=\!=}\int_0^{\infty} f(t)\mathrm{e}^{-st}\,\mathrm dt

2. 2. 역 라플라스 변환

함수

f(t)

의 라플라스 변환을

F(s)

라 하면 다음 식을 통해

F(s)

로부터

f(t)

를 구할 수 있다.

:

f(t) = \frac1{2\pi i}\int_{a-i\infty}^{a+i\infty}F(s)e^{st}\,ds,\quad i = \sqrt{-1}.

하지만 보통 위의 계산을 직접 하기 보다는 이미 알려져 있는 라플라스 변환들을 이용해 역변환을 구하는 것이 쉽다. 예를 들어

:

F(s) = \frac1{s^2 + 3s + 2},

로

F(s)

가 주어져 있는 경우 부분분수 분해를 통해

:

F(s) = \frac1{s^2 + 3s + 2} = \frac1{s + 1} - \frac1{s + 2},

를 얻게되고 라플라스 변환의 선형성으로부터

f(t)

는 다음과 같다.

:

\begin{align}f(t)&= \mathcal{L}^{-1}\left\{\frac1{s + 1}\right\} - \mathcal{L}^{-1}\left\{\frac1{s + 2}\right\} \\&= e^{-t} - e^{-2t}, \quad t \ge 0.\end{align}

라플라스 역변환은 다음 복소 적분으로 주어지는데, 이것은 브롬위치 적분, 푸리에-멜린 적분, 멜린의 역 공식등 여러 가지 이름으로 알려져 있다.

:

f(t) = \mathcal{L}^{-1}\{F\}(t) = \frac{1}{2 \pi i} \lim_{T\to\infty} \int_{\gamma - i T}^{\gamma + i T} e^{st} F(s)\, ds,

여기서

\gamma

는 적분 경로가

F(s)

의 수렴 영역에 있는 실수이다. 대부분의 응용 프로그램에서 윤곽선을 닫을 수 있으므로 유수 정리를 사용할 수 있다.

실제로는 일반적으로 표에서 얻은 함수의 알려진 변환으로 라플라스 변환을 분해하고 검사를 통해 역변환을 구성하는 것이 더 편리하다.

실수

t \ge 0

에 대해 정의된 함수

f(t)

의 역라플라스 변환은

:

f(t) = \lim_{p\to\infty}\frac{1}{2\pi i} \int_{c-ip}^{c+ip} F(s)\mathrm{e}^{st}\,\mathrm ds

처럼 정의되어 있다. 여기서 c는 모든 특이점의 실수부보다 큰 실수이다. 우변의 적분은 브롬위치 적분이라고 불린다. 이것은 복소 평면에서 시간 영역으로의 사상이다.

이는 복소 적분이다. 정의대로의 적분 경로에서는 계산이 어려워지지만, 폐곡선이 되도록 적분 경로를 변경하여 유수를 계산함으로써 간단하게 역라플라스 변환을 구할 수 있다. 결과적으로 말하면 복소 평면상의 모든 특이점의 유수의 총합이 된다. 여기서,

f(t)

를 원함수,

F(s)

를 상함수라고 한다.

역라플라스 변환은 다음과 같이도 표기된다.

:

f(t) = \mathcal{L}^{-1}[F(s)]

또한, 이러한 기호를 사용한 사상

:

\begin{align}\mathcal{L}^{-1} & \colon F \mapsto f\end{align}

의 것을 역라플라스 변환이라고 부른다.

보통, 라플라스 변환 및 역라플라스 변환을 할 때는 변환표를 참조하여 계산하는 경우가 많으므로, 전술한 정의식에 따라 계산하는 경우는 적다. 하지만 경우에 따라서는 정의식으로부터 계산하는 쪽이 간단한 경우도 있다. 예를 들어 역라플라스 변환을 할 때 부분분수분해를 해야 하는 경우, 오히려 브롬위치 적분을 계산하는 쪽이 빠른 경우도 많다.

2. 3. 양측 라플라스 변환

양측 라플라스 변환은 적분 구간을 모든 실수 영역으로 확장한 것으로, 다음과 같이 정의된다.^[20]

:

F(s) = \mathcal{L}\left\{f(t)\right\} =\int_{-\infty}^{\infty} \mathrm{e}^{-st} f(t)\,\mathrm dt

일반적으로 "라플라스 변환"이라고 할 때는 단측 또는 일방향 변환을 의미한다. 라플라스 변환은 적분 범위를 실수 전체 축으로 확장하여 양측 라플라스 변환으로 정의할 수도 있다. 이렇게 하면 일반적인 단측 변환은 단순히 변환되는 함수의 정의에 헤비사이드 계단 함수를 곱한 양측 변환의 특수한 경우가 된다.

순수 및 응용 확률론에서 라플라스 변환은 기댓값으로 정의된다. 확률밀도함수 f^영어를 갖는 확률변수 X^영어가 있다면, f^영어의 라플라스 변환은 다음 기댓값으로 주어진다.

:

\mathcal{L}\{f\}(s) = \operatorname{E}\left[e^{-sX}\right],

여기서

\operatorname{E}[r]

은 확률변수

r

의 기댓값이다.

관례적으로 이것은 확률변수 X^영어 자체의 라플라스 변환으로 불린다. s^영어를 −t^영어로 바꾸면 X^영어의 적률생성함수가 된다. 라플라스 변환은 마르코프 체인과 같은 확률 과정의 최초 통과 시간 및 재생 이론을 포함하여 확률론 전반에 걸쳐 응용된다.

특히 유용한 것은 다음과 같이 라플라스 변환을 사용하여 연속 확률변수 X^영어의 누적분포함수를 복구할 수 있다는 점이다.^[20]

:

F_X(x) = \mathcal{L}^{-1}\left\{\frac{1}{s} \operatorname{E}\left[e^{-sX}\right]\right\}(x) = \mathcal{L}^{-1}\left\{\frac{1}{s} \mathcal{L}\{f\}(s)\right\}(x).

3. 역사

라플라스 변환은 수학자이자 천문학자인 피에르-시몽 라플라스의 이름을 따서 명명되었다.^[4] 라플라스는 생성 함수를 광범위하게 연구했고(1814), 라플라스 변환의 적분 형태는 자연스럽게 발전했다.^[5]

1744년부터 레온하르트 오일러는 미분 방정식의 해를 구하기 위해 다음 형태의 적분을 연구했다.^[7]

:

z = \int X(x) e^{ax}\, dx \quad\text{ and }\quad z = \int X(x) x^A \, dx

조제프 루이 라그랑주는 오일러의 열렬한 지지자였으며, 확률 밀도 함수를 적분하는 연구에서 다음 형태의 식을 조사했는데, 이는 라플라스 변환과 유사하다.^[8]^[9]

:

\int X(x) e^{- a x } a^x\, dx,

1782년, 라플라스는 적분 자체를 방정식의 해로 사용하는 오일러의 방법을 따랐다.^[10] 1785년, 라플라스는 멜린 변환과 유사한 형태의 적분을 사용하여 차분 방정식 전체를 변환하고, 변환된 방정식의 해를 찾았다.^[11]

:

\int x^s \varphi (x)\, dx,

1809년, 라플라스는 그의 변환을 사용하여 공간에서 무한히 확산되는 해를 찾았다.^[12] 1821년 코시는 라플라스 변환에 대한 작용소 미적분을 개발했다.^[13]

베른하르트 리만은 1859년 논문 ''주어진 크기보다 작은 소수의 개수''에서 라플라스 변환을 사용했다.

히알마르 멜린은 20세기 초 라플라스 변환을 엄밀하게 연구하고 미분 방정식과 특수 함수 연구에 적용했다.^[14] 이 시대의 다른 기여자로는 마티아스 렐르흐,^[15] 올리버 헤비사이드, 토마스 브롬위치가 있다.^[16]

제2차 세계 대전 중과 그 직후, 변환의 현재 광범위한 사용(주로 공학 분야)이 이루어졌으며,^[17] 이전의 헤비사이드 작용소 미적분을 대체했다. 라플라스 변환의 장점은 구스타프 도이치에 의해 강조되었으며, 그에게 라플라스 변환이라는 이름이 붙여진 것 같다.^[18]

4. 성질

라플라스 변환은 선형성을 가지며, 미분, 적분, 컨볼루션 등의 연산을 주파수 영역에서 간단하게 표현할 수 있도록 한다.

선형성:

:

\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}

미분:

:

\mathcal{L}\{f'\} = s \mathcal{L}\{f\} - f(0)

:

\mathcal{L}\{f''\} = s^2 \mathcal{L}\{f\} - s f(0) - f'(0)

:

\mathcal{L}\left\{ f^{(n)} \right\} = s^n \mathcal{L}\{f\} - s^{n - 1} f(0) - \cdots - f^{(n - 1)}(0)

t 곱:

:

\mathcal{L}\{ t f(t)\} = -F'(s)

:

\mathcal{L}\{ t^{n} f(t) \} =(-1)^{n} F^{(n)} (s)

t 나누기:

:

\mathcal{L}\left\{ \frac{f(t)}{t} \right\} = \int_s^\infty F(\sigma)\, d\sigma

적분:

:

\mathcal{L}\left\{ \int_0^t f(\tau)\, d\tau \right\}  = \mathcal{L}\left\{ u(t) * f(t)\right\} = {1 \over s} F(s)

시간 이동:

:

\mathcal{L}\left\{ f(t - a) u(t - a) \right\} = e^{-as} F(s)

:

\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\} = f(t - a) u(t - a)

:여기서

u(t)

는 층계 함수이다.

컨볼루션:

:

\mathcal{L}\{f * g\} = \mathcal{L}\{ f \} \mathcal{L}\{ g \}

주기 함수:

:

\mathcal{L}\{ f \} = {1 \over 1 - e^{-ps}} \int_0^p e^{-st} f(t)\,dt

초기값 정리:

:

f(0^+)=\lim_{s\to \infty}{sF(s)}.

최종값 정리:

:

f(\infty)=\lim_{s\to 0}{sF(s)}

, 단

sF(s)

의 모든 극점은 좌반평면에 있다.

다음은 단측 라플라스 변환의 성질을 정리한 표이다.^[24]

단측 라플라스 변환의 성질
성질	시간 영역	s 영역	주석
주파수 영역 미분	$t f(t) \$	$-F'(s) \$	$F'(s)$ 는 $F(s)$ 의 1차 미분이다.
주파수 영역 일반 미분	$t^{n} f(t) \$	$(-1)^{n} F^{(n)}(s) \$	$F^{(n)}(s)$ 는 $F(s)$ 의 n차 미분이다.
주파수 영역 적분	$\frac{1}{t}f(t) \$	$\int_s^\infty F(\sigma)\, d\sigma \$	주파수 미분의 특성과 조건부 수렴을 이용하여 유도된다.
주파수 이동	$e^{at} f(t)$	$F(s - a) \$
시간 이동	$f(t - a) u(t - a) \$	$e^{-as} F(s) \$	$u(t)$ 는 헤비사이드 계단 함수이다.
시간 축척	$f(at)$	$\frac{1}{a} F \left ({s \over a} \right)$
곱셈	$f(t)g(t)$	$\frac{1}{2\pi i}\lim_{T\to\infty}\int_{c - iT}^{c + iT}F(\sigma)G(s - \sigma)\,d\sigma \$	적분은 $F$ 의 수렴 영역 내에 완전히 있는 수직선 $Re(\sigma) = c$ 를 따라 수행된다.^[25]
복소 공액	$f^*(t)$	$F^(s^)$
주기적 합	$f_P(t) = \sum_{n=0}^{\infty} f(t-Tn)$	$F_P(s) = \frac{1}{1-e^{-Ts}} F(s)$

4. 1. 선형성

:

\mathcal{L}\left\{a f(t) + b g(t) \right\} = a \mathcal{L}\left\{ f(t) \right\} + b \mathcal{L}\left\{ g(t) \right\}

라플라스 변환은 선형성을 가지므로, 중첩의 원리를 이용하여 계산할 수 있다. 즉, 임의의 함수 , 와 상수 , 에 대해 다음이 성립한다.

:

\mathcal{L}[af(t) + bg(t)] = aF(s) + bG(s)

역라플라스 변환도 마찬가지로 선형성을 가지며, 다음이 성립한다.

:

\mathcal{L}^{-1}[aF(s) + bG(s)] = af(t) + bg(t)

따라서, 주어진 함수를 부분분수 분해하여 각 항이 라플라스 변환 표에 있는 형태와 일치하면 변환을 구할 수 있다.^[24]

단측 라플라스 변환의 성질
성질	시간 영역	영역	주석
선형성	$a f(t) + b g(t) \$	$a F(s) + b G(s) \$	기본적인 적분 법칙을 사용하여 증명할 수 있다.

4. 2. 미분

f^영어의 도함수의 라플라스 변환은 다음과 같이 다항식의 차이로 나타난다.^[26]

1계 도함수

::

\mathcal{L}\{f'\} = s \mathcal{L}\{f\} - f(0)

2계 도함수

::

\mathcal{L}\{f''\}= s^2 \mathcal{L}\{f\} - s f(0) - f'(0)

n계 도함수

::

\mathcal{L}\left\{ f^{(n)} \right\}= s^n \mathcal{L}\{f\} - s^{n - 1} f(0) - \cdots - f^{(n - 1)}(0)

시간 t에 대한 함수 f(t)^영어에 t를 곱한 것과 t로 나눈 것의 라플라스 변환은 다음과 같다.

t를 곱한 경우

::

\mathcal{L}\{ t f(t)\}= -F'(s)

tⁿ을 곱하는 경우

::

\mathcal{L}\{ t^{n} f(t) \} =(-1)^{n} F^{(n)} (s)

t로 나눈 경우

::

\mathcal{L}\left\{ \frac{f(t)}{t} \right\} = \int_s^\infty F(\sigma)\, d\sigma

4. 3. 적분

Laplace transform^영어

\mathcal{L}\left\{ \int_0^t f(\tau)\, d\tau \right\}  = \mathcal{L}\left\{ u(t) * f(t)\right\} = {1 \over s} F(s)

이다.

\mu_n = \int_0^\infty t^nf(t)\, dt

은 함수

f

의 ''적률''이다.

f

의 처음

n

개의 적률이 절대 수렴하면, 적분 아래 미분을 반복하여

(-1)^n(\mathcal L f)^{(n)}(0) = \mu_n .

을 얻는다. 이것은 확률론에서 특히 중요한데, 확률 변수

X

의 적률은 기댓값

\mu_n=\operatorname{E}[X^n]

으로 주어지며, 다음 관계가 성립한다.

\mu_n = (-1)^n\frac{d^n}{ds^n}\operatorname{E}\left[e^{-sX}\right](0).

Laplace transform^영어의 유용한 성질 중 하나는 다음과 같다.

\int_0^\infty f(x)g(x)\,dx = \int_0^\infty(\mathcal{L} f)(s)\cdot(\mathcal{L}^{-1}g)(s)\,ds

이는

0

의 우측 근방에서

f,g

의 거동과

\infty

의 좌측 근방에서

f,g

의 감쇠율에 대한 적절한 가정 하에 성립한다. 위 공식은 부분 적분의 변형으로, 연산자

\frac{d}{dx}

와

\int \,dx

가

\mathcal{L}

과

\mathcal{L}^{-1}

로 대체된 것이다. 다음과 같은 동등한 공식을 증명할 수 있다.

\int_0^\infty(\mathcal{L} f)(x)g(x)\,dx = \int_0^\infty f(s)(\mathcal{L}g)(s)\,ds.

(\mathcal{L}f)(x)=\int_0^\infty f(s)e^{-sx}\,ds

를 대입하면 좌변은 다음과 같이 된다.

\int_0^\infty\int_0^\infty f(s)g(x) e^{-sx}\,ds\,dx,

푸비니 정리가 성립한다고 가정하면, 적분 순서를 바꾸어 원하는 우변을 얻는다.

이 방법은 실해석학의 기본적인 방법으로는 계산하기 어려운 적분을 계산하는 데 사용할 수 있다. 예를 들어,

\int_0^\infty\frac{\sin x}{x}dx = \int_0^\infty \mathcal{L}(1)(x)\sin x dx = \int_0^\infty 1 \cdot \mathcal{L}(\sin)(x)dx = \int_0^\infty \frac{dx}{x^2 + 1} = \frac{\pi}{2}.

4. 4. 시간 이동

:

\mathcal{L}\left\{ f(t - a) u(t - a) \right\} = e^{-as} F(s)

:

\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\} = f(t - a) u(t - a)

여기서

u(t)

는 층계 함수이다.

4. 5. 합성곱

함수의 컨볼루션은 라플라스 변환에서 곱(값별 곱)으로 변환된다.

:

\mathcal{L}\{f * g\} = \mathcal{L}\{ f \} \mathcal{L}\{ g \}

:

F(s) = \mathcal{L}[f(t)],\, G(s) = \mathcal{L}[g(t)]

라면

:

\mathcal{L}^{-1}[H(s)] = f(t)*g(t)

로 쓸 수도 있다.

4. 6. 주기 함수

라플라스 변환에서 주기가 p인 주기함수의 라플라스 변환은 다음과 같다.

:

\mathcal{L}\{ f \} = {1 \over 1 - e^{-ps}} \int_0^p e^{-st} f(t)\,dt

4. 7. 초기값 정리 및 최종값 정리

함수 g|g^영어의 (단측) 라플라스-스틸체스 변환은 다음과 같은 르벡-스틸체스 적분으로 정의된다.^[27]

:

\{ \mathcal{L}^*g \}(s) = \int_0^\infty e^{-st} \, d\,g(t) ~.

함수 g|g^영어는 유계 변분을 갖는다고 가정한다. g|g^영어가 f|f^영어의 원시 함수라면 다음과 같다.

:

g(x) = \int_0^x f(t)\,d\,t

g|g^영어의 라플라스-스틸체스 변환과 f|f^영어의 라플라스 변환은 일치한다. 일반적으로 라플라스-스틸체스 변환은 g|g^영어에 관련된 스틸체스 측도에 대한 라플라스 변환이다. 따라서 실제로 두 변환의 유일한 차이점은 라플라스 변환이 측도의 밀도 함수에 작용하는 것으로 간주되는 반면, 라플라스-스틸체스 변환은 그 누적 분포 함수에 작용하는 것으로 간주된다는 것이다.^[27]

라플라스 변환의 원함수의 초기값(t = 0에서의 값)과 최종값(t → ∞에서의 극한값)을 구하는 초기값 정리와 최종값 정리는 함수의 극한값을 구하는 데 유용하다.

4. 7. 1. 초기값 정리

t의 함수 f(t)가 t = 0에서 연속이라면, 다음 식이 성립한다.^[1]

:

f(0) = \lim_{t \to 0} f(t) = \lim_{s \to \infty} sF(s)

특히, f가 미분 가능할 때는 부분적분에 의해 쉽게 증명할 수 있다.^[1]

4. 7. 2. 최종값 정리

라플라스 변환의 원함수의 초기값(t = 0에서의 값)과 최종값(t → ∞에서의 극한값)을 나타내는 초기값 정리와 최종값 정리는 다음과 같다.

; 초기값 정리

: t의 함수 f(t)가 t = 0에서 연속이라면

:

f(0) = \lim_{t \to 0} f(t) = \lim_{s \to \infty} sF(s)

: 가 성립한다. 특히, f가 미분 가능할 때는 부분적분에 의해 쉽게 증명할 수 있다.

; 최종값 정리

: t의 함수 f(t)가 t → ∞에서 수렴한다면

:

f(\infty) = \lim_{t \to \infty} f(t) = \lim_{s \to 0} sF(s) \qquad s \in \Delta_0

: 가 성립한다. 단,

\Delta_0

는

s > 0

를 포함하는 각 영역이다.

5. 응용

라플라스 변환은 공학과 물리학에서 자주 사용된다. 선형 시불변 시스템의 출력은 단위 임펄스 응답과 입력 신호를 합성곱하여 계산할 수 있는데, 라플라스 공간에서는 이 계산이 곱셈으로 바뀌어 더 쉽게 풀 수 있다. 제어 이론에서 더 자세한 내용을 확인할 수 있다.^[35]

라플라스 변환은 광범위한 함수 클래스에서 역변환이 가능하며, 시스템의 입력 또는 출력에 대한 간단한 수학적/함수적 설명을 통해 시스템 동작을 분석하거나, 특정 사양에 맞춰 새로운 시스템을 합성하는 과정을 단순화한다.^[35]

또한 라플라스 변환은 미분 방정식 풀이에 사용되며, 기계 공학과 전기 공학에서 널리 활용된다. 라플라스 변환은 선형 미분 방정식을 대수 방정식으로 변환하여, 대수의 공식 규칙을 통해 해를 구할 수 있게 한다. 이후 역 라플라스 변환을 적용하여 원래의 미분 방정식을 풀 수 있다. 영국의 전기 공학자 올리버 헤비사이드는 이와 유사한 방식을 라플라스 변환 없이 처음 제안했으며, 그 결과로 얻어진 연산자 미적분은 헤비사이드 미적분으로 알려져 있다.^[35]

5. 1. 미분방정식의 풀이

라플라스 변환은 미분방정식을 대수 방정식으로 변환하여 해를 쉽게 구할 수 있게 한다. 특히, 상수 계수를 갖는 선형 상미분 방정식의 풀이에 유용하다.^[42]

함수

f(t)

의 라플라스 변환을

F(s)

라 하면, 다음 식을 통해

F(s)

로부터

f(t)

를 구할 수 있다.

:

f(t) = \frac1{2\pi i}\int_{a-i\infty}^{a+i\infty}F(s)e^{st}\,ds,\quad i = \sqrt{-1}.

하지만 보통 위의 계산을 직접 하기보다는 이미 알려져 있는 라플라스 변환들을 이용해 역변환을 구하는 것이 쉽다. 예를 들어,

:

F(s) = \frac1{s^2 + 3s + 2},

로

F(s)

가 주어져 있는 경우 부분분수 분해를 통해

:

F(s) = \frac1{s^2 + 3s + 2} = \frac1{s + 1} - \frac1{s + 2},

를 얻게 되고 라플라스 변환의 선형성으로부터

f(t)

는 다음과 같다.

:

\begin{align}f(t)&= \mathcal{L}^{-1}\left\{\frac1{s + 1}\right\} - \mathcal{L}^{-1}\left\{\frac1{s + 2}\right\} \\&= e^{-t} - e^{-2t}, \quad t \ge 0.\end{align}

다음과 같은

n

차 연립 상미분 방정식을 고려하자.

:

\dot{\mathbf{x}}(t) = \mathbf{A}\mathbf{x}(t) + \mathbf{B}\mathbf{u}(t).

양변에 라플라스 변환을 취하면

:

s\mathbf{X}(s) - \mathbf{x}(0) = \mathbf{A}\mathbf{X}(s) + \mathbf{B}\mathbf{U}(s),

이고 이를

\mathbf{X}(s)

에 관해 정리하면

:

\mathbf{X}(s) = (s\mathbf{I} - \mathbf{A})^{-1}\mathbf{x}(0) + (s\mathbf{I} - \mathbf{A})^{-1}\mathbf{B}\mathbf{U}(s),

이다. 따라서,

\mathbf{x}(t)

는 다음과 같다.^[42]

:

\mathbf{x}(t) = \exp\left[\mathbf{A}t\right]\mathbf{x}(0) + \int_{0}^{t}\exp\left[\mathbf{A}(t-\tau)\right]\mathbf{B}\mathbf{u}(\tau)\,d\tau.

5. 2. 복소 임피던스

라플라스 변환은 회로 해석에 자주 사용되며, 회로 요소를 s-영역으로 간단하게 변환할 수 있다. 회로 요소는 임피던스로 변환될 수 있으며, 이는 위상수 임피던스와 매우 유사하다.

저항기는 시간 영역과 s-영역에서 동일하다. 회로 요소에 초기 조건이 있는 경우에는 소스가 추가된다. 예를 들어, 축전기에 초기 전압이 있거나 인덕터에 초기 전류가 있는 경우, s-영역에 삽입된 소스가 이를 고려한다.

전류원과 전압원의 등가 회로는 위 그림의 변환에서 간단하게 유도된다.

5. 3. 전달 함수

선형 시불변 시스템의 전달 함수는 다음과 같이 표현된다.

H(s) = \frac{1}{(s + \alpha)(s + \beta)}.

충격 응답은 이 전달 함수의 역 라플라스 변환이다.

h(t) = \mathcal{L}^{-1}\{H(s)\}.

이 역변환을 계산하기 위해, 부분 분수 전개 방법을 사용하여 ''H''(''s'')를 다음과 같이 전개한다.

\frac{1}{(s + \alpha)(s + \beta)} = { P \over s + \alpha } + { R \over s+\beta }.

여기서 미지 상수 ''P''와 ''R''은 전달 함수의 해당 극점에 위치한 유수이다. 각 유수는 해당 특이점이 전달 함수의 전체 형태에 기여하는 상대적인 정도를 나타낸다.

유수 정리에 의해, 역 라플라스 변환은 극점과 그 유수에만 의존한다. 유수 ''P''를 구하기 위해, 방정식의 양변에 ''s'' + ''α''를 곱하면 다음을 얻는다.

\frac{1}{s + \beta} = P  + { R (s + \alpha) \over s + \beta }.

그런 다음 ''s'' = −''α''로 설정하면, ''R''의 기여는 사라지고 다음이 남는다.

P = \left.{1 \over s+\beta}\right|_{s=-\alpha} = {1 \over \beta - \alpha}.

마찬가지로, 유수 ''R''는 다음과 같이 주어진다.

R = \left.{1 \over s + \alpha}\right|_{s=-\beta} = {1 \over \alpha - \beta}.

다음을 알 수 있다.

R = {-1 \over \beta - \alpha} = - P

따라서 ''R''과 ''P''를 ''H''(''s'')의 전개된 식에 대입하면 다음을 얻는다.

H(s)  = \left(\frac{1}{\beta - \alpha} \right) \cdot \left( { 1 \over s + \alpha } - { 1  \over s + \beta }  \right).

마지막으로, 선형성과 지수 감쇠에 대한 알려진 변환을 사용하여 ''H''(''s'')의 역 라플라스 변환을 취하면 다음을 얻는다.

h(t) = \mathcal{L}^{-1}\{H(s)\} = \frac{1}{\beta - \alpha}\left(e^{-\alpha t} - e^{-\beta t}\right),

이는 시스템의 충격 응답이다.

컨벌루션 성질을 사용하여 동일한 결과를 얻을 수도 있다. 전달 함수가 와 인 필터들의 직렬 연결로 시스템을 보는 것처럼, 다음의 역변환은

H(s) = \frac{1}{(s + \alpha)(s + \beta)} = \frac{1}{s+\alpha} \cdot \frac{1}{s + \beta}

\mathcal{L}^{-1}\! \left\{ \frac{1}{s + \alpha} \right\} * \mathcal{L}^{-1}\! \left\{\frac{1}{s + \beta} \right\} = e^{-\alpha t} * e^{-\beta t} = \int_0^t e^{-\alpha x}e^{-\beta (t - x)}\, dx = \frac{e^{-\alpha t}-e^{-\beta t}}{\beta - \alpha}.

이다.

5. 4. 통계 역학

통계역학에서 상태밀도

g(E)

의 라플라스 변환은 분배함수를 정의한다.^[36] 즉, 정준 분배함수

Z(\beta)

는 다음과 같이 주어진다.

:

Z(\beta) = \int_0^\infty e^{-\beta E}g(E)\,dE

그리고 역변환은 다음과 같이 주어진다.

:

g(E) = \frac{1}{2\pi i} \int_{\beta_0-i\infty}^{\beta_0+i\infty} e^{\beta E}Z(\beta) \, d\beta

6. 다른 변환과의 관계

라플라스 변환은 푸리에 변환, Z 변환, 멜린 변환 등 다른 적분 변환과 밀접하게 관련되어 있다. 이들은 근본적으로 동일한 주제를 다루지만, 각각 다른 관점과 특징적인 문제들을 가진다.^[29]^[30]^[1]

라플라스 변환은 모함수의 "연속형"으로 생각할 수 있다. 수열 $\{a_n\}$ 의 모함수 $G(a_n;x)=\sum_n a_nx^n$ 에서 $x = e^{-s}$ 로 치환하면, $G(a_n;\mathrm{e}^{-s})=\sum_n a_n \mathrm{e}^{-sn}$ 이 된다. 여기서 합을 적분으로 바꾸면 $G(a_t;\mathrm{e}^{-s})=\int a_t \mathrm{e}^{-st}\mathrm dt$ 가 되는데, 이는 함수 $a_t$ 의 라플라스 변환과 일치한다.

이러한 관계 때문에 모함수와 라플라스 변환은 유사한 성질을 가진다. 예를 들어 모함수의 성질 $G(a_n;x)G(b_n;x)=G(a_n*b_n;x)$ 은 라플라스 변환의 성질 $\mathcal{L}[f](s)\mathcal{L}[g](s)=\mathcal{L}[f*g](s)$ 에 대응된다. 여기서 $*$ 는 컨볼루션 적분을 의미한다.

6. 1. 푸리에 변환

푸리에 변환은 (특정 조건 하에서) 양측 라플라스 변환의 특수한 경우이다. 주된 차이점은 함수의 푸리에 변환이 실수 변수(주파수)의 복소 함수인 반면, 함수의 라플라스 변환은 복소 변수의 복소 함수라는 것이다. 라플라스 변환은 일반적으로 t ≥ 0인 t의 함수 변환으로 제한된다. 이 제한의 결과로, 함수의 라플라스 변환은 s 변수의 해석 함수이다. 푸리에 변환과 달리, 분포의 라플라스 변환은 일반적으로 잘 정의된 함수이다.

형식적으로, 아래에 설명된 조건이 충족될 때, 푸리에 변환은 허수 인수 s = iω를 갖는 양측 라플라스 변환을 평가하는 것과 같다.^[29]^[30]

\begin{align}\hat{f}(\omega) &= \mathcal{F}\{f(t)\} \\[4pt]&= \mathcal{L}\{f(t)\}|_{s = i \omega}  =  F(s)|_{s = i \omega} \\[4pt]&= \int_{-\infty}^\infty e^{-i \omega t} f(t)\,dt~.\end{align}

이 푸리에 변환 규약( 다른 규약)에는 역 푸리에 변환에 1/2π의 계수가 필요하다. 라플라스 변환과 푸리에 변환 사이의 이러한 관계는 종종 신호 또는 동적 시스템의 주파수 스펙트럼을 결정하는 데 사용된다.

위의 관계는 F(s)의 수렴 영역(ROC)이 허수 축 σ = 0을 포함하는 경우에만 성립한다.

예를 들어, 함수 f(t) = cos(ω₀t)는 ROC가 Re(s) > 0인 라플라스 변환 F(s) = s/(s² + ω₀²)를 갖는다. s = iω₀은 F(s)의 극이므로, F(s)에 s = iω를 대입하면 디랙 델타 함수 δ(ω ± ω₀)에 비례하는 항을 포함하는 f(t)u(t)의 푸리에 변환이 생성되지 않는다.

그러나, 다음 형태의 관계

\lim_{\sigma\to 0^+} F(\sigma+i\omega) = \hat{f}(\omega)

는 훨씬 더 약한 조건 하에서 성립한다. 예를 들어, 측도의 약한 극한( 약 위상 참조)으로 이해하면 위의 예에서 이것이 성립한다. 경계에서 함수의 라플라스 변환의 극한과 푸리에 변환을 관련짓는 일반적인 조건은 팔리-위너 정리의 형태를 취한다.

6. 2. Z 변환

일방향 또는 단측 Z 변환은 이상적으로 샘플링된 신호의 라플라스 변환으로, 다음과 같은 치환을 통해 얻어진다.

:z^영어 = e^sT^영어

여기서 T = 1/f_s^영어는 샘플링 간격(시간 단위, 예: 초)이고 f_s^영어는 샘플링률(초당 샘플 수 또는 헤르츠)이다.

다음과 같이 정의하자.

:Δ_T(t)^영어 = ∑_n=0^∞ δ(t - nT)^영어

이는 샘플링 임펄스 열(또는 디랙 빗이라고도 함)이고,

:x_q(t)^영어 = x(t)Δ_T(t) = x(t)∑_n=0^∞ δ(t - nT)^영어

: = ∑_n=0^∞ x(nT)δ(t - nT) = ∑_n=0^∞ x[n]δ(t - nT)^영어

는 연속 시간 x(t)^영어의 샘플링된 표현이다.

:x[n]^영어 = x(nT)^영어.

샘플링된 신호 x_q(t)^영어의 라플라스 변환은 다음과 같다.

:X_q(s) = ∫_0^-^∞ x_q(t)e^-st dt^영어

: = ∫_0^-^∞ ∑_n=0^∞ x[n]δ(t - nT)e^-st dt^영어

: = ∑_n=0^∞ x[n]∫_0^-^∞ δ(t - nT)e^-st dt^영어

: = ∑_n=0^∞ x[n]e^-nsT^영어.

이는 이산 함수 x[n]^영어의 단측 Z 변환의 정확한 정의이다.

:X(z) = ∑_n=0^∞ x[n]z^-n^영어

z^영어 → e^sT^영어를 치환하면 된다.

마지막 두 방정식을 비교하면 단측 Z 변환과 샘플링된 신호의 라플라스 변환 간의 관계를 알 수 있다.

:X_q(s) = X(z)|_z=e^sT^영어.

Z 변환과 라플라스 변환의 유사성은 시간척도 미적분 이론에서 더 자세히 설명된다.

6. 3. 멜린 변환

멜린 변환과 그 역변환은 간단한 변수 변환을 통해 양측 라플라스 변환과 관련이 있다.^[1]

Mellin transform^영어

:

G(s) = \mathcal{M}\{g(\theta)\} = \int_0^\infty \theta^s g(\theta) \, \frac{d\theta} \theta

에서

\theta = e^{-t}

로 설정하면 양측 라플라스 변환을 얻는다.^[1]

참조

_[1] 논문 Electronic Signals and Systems Macmillan Education UK
_[2] 웹사이트 Differential Equations – Laplace Transforms https://tutorial.mat[...] 2020-08-08
_[3] 웹사이트 Laplace Transform https://mathworld.wo[...] 2020-08-08
_[4] 간행물 Théorie analytique des Probabilités https://archive.org/[...] 1814
_[5] 서적 Probability theory : the logic of science Cambridge University Press 2003
_[6] 간행물 Œuvres Complètes https://books.google[...] 1820
_[7] 논문
_[8] 논문
_[9] 논문
_[10] 논문
_[11] 논문
_[12] 논문
_[13] 논문 Electromagnetic Theory January 2008
_[14] 서적 Transients in Linear Systems studied by the Laplace Transform Wiley 1942
_[15] 논문 Sur un point de la théorie des fonctions génératrices d'Abel 1903
_[16] 논문 Normal coordinates in dynamical systems https://zenodo.org/r[...] 1916
_[17] 서적 Transients in Linear Systems studied by the Laplace Transform Wiley 1942
_[18] 서적 Theorie und Anwendung der Laplacesche Transformation Springer 1937
_[19] 논문
_[20] 기타
_[21] 서적 Operational Calculus https://books.google[...] Elsevier 2014-07-14
_[22] 논문
_[23] 논문
_[24] 논문
_[25] 논문
_[26] 웹사이트 Where the Laplace Transform comes from https://www.youtube.[...] 2008-11-07
_[27] 논문
_[28] 서적 Mathematics for the physical sciences Addison-Wesley
_[29] 서적 Introduction to the theory of Fourier integrals Clarendon Press
_[30] 논문
_[31] 서적 Mathematical methods for physics and engineering Cambridge University Press
_[32] 서적 Feedback systems and control McGraw-Hill
_[33] 서적 Mathematical Handbook of Formulas and Tables McGraw-Hill
_[34] 웹사이트 http://mathworld.wol[...]
_[35] 논문
_[36] 서적 Statistical mechanics https://archive.org/[...] Butterworth-Heinemann
_[37] 논문 I. Continuum spectra and brightness contours
_[37] 논문 II. Three-dimensional models
_[38] 서적 Introduction to Probability Theory, volume II
_[39] 서적 Introduction to Probability Theory, volume II
_[40] 논문 An extension of Landau's theorem in the analytic theory of numbers
_[41] 서적 Advanced Engineering Mathematics https://archive.org/[...] John Wiley & Sons
_[42] 서적 Linear System Theory and Design http://books.google.[...] Oxford University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com