지수 분포

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 응용
5. 통계적 추론
- 5.1. 모수 추정
- 5.2. 베이즈 추론
6. 난수 생성
참조

1. 개요

지수 분포는 0부터 무한대까지의 값을 가지며, 확률 밀도 함수가 λe^-λx로 주어지는 확률 분포이다. 척도 모수 θ = 1/λ를 사용하여 1/θ e^-x/θ로 표현할 수도 있다. 지수 분포는 사건 발생 사이의 시간, 제품의 수명, 대기열 이론 등 다양한 분야에 적용되며, 무기억성을 갖는 유일한 연속 확률 분포이다. 지수 분포의 주요 성질로는 기댓값이 1/λ이고 분산이 1/λ²라는 점, 그리고 쿨백-라이블러 발산, 최대 엔트로피 분포, 다른 분포와의 관계 등이 있다. 통계적 추론에서는 최대 우도 추정, 베이즈 추론 등을 통해 모수를 추정하며, 역변환 표본 추출과 같은 방법을 사용하여 난수를 생성할 수 있다.

2. 정의

지수 분포는 양의 실수 구간 `(0, ∞)`에서 정의되며, 모수 `''λ'' > 0`에 대해 확률 밀도 함수는 다음과 같다.

: $f(x; \lambda) = \lambda e^{-\lambda x}$

이때, 누적 분포 함수는 다음과 같다.

: $F(x; \lambda) = 1 - e^{-\lambda x}$

척도 모수 `''θ'' = 1/''λ''`를 사용하면 확률 밀도 함수를 다음과 같이 표현할 수도 있다.

: $f(x; \theta) = \frac{1}{\theta} e^{-x/\theta}$

2. 1. 확률 밀도 함수

지수분포의 확률 밀도 함수는 다음과 같이 정의된다.

:

f(x; \lambda) = \begin{cases}\lambda e^{-\lambda x} & x \ge 0 \\0 &  x < 0\end{cases}

여기서 ''λ'' > 0는 분포의 모수이며, 종종 율 매개변수(rate parameter)라고 불린다. 확률변수 ''X''는 구간 [0, ∞)에서 정의된다. 만약 확률 변수 ''X''가 이 분포를 따른다면, ''X'' ~ Exp(''λ'')라고 표기한다.

단위 계단 함수 ''H''(''x'')를 이용하면 다음과 같이 표현할 수도 있다.

:

f(x; \lambda) = \lambda e^{-\lambda x}H(x)

지수 분포는 무한 분할 가능성을 가진다.

이 분포의 누적 분포 함수는 다음과 같다.

:

F(x; \lambda) = 1 - e^{-\lambda x} \quad (x \ge 0)

척도 모수(scale parameter) ''θ'' = 1/''λ''를 사용하면 확률 밀도 함수를 다음과 같이 동등하게 정의할 수도 있다.

:

f(x; \theta) = \frac{1}{\theta} e^{-x/\theta} \quad (x \ge 0)

여기서 ''θ''는 척도 모수이다.

2. 2. 누적 분포 함수

지수 분포는 구간

(0, \infty)

에서 정의되며, 양수 값을 가지는 모수

\lambda

(

\lambda > 0

)에 대해 확률 밀도 함수는 다음과 같다.

:

f(x; \lambda) = \lambda e^{-\lambda x}

이때 누적 분포 함수는 다음과 같이 주어진다.

:

F(x;\lambda) = \begin{cases}1-e^{-\lambda x} & x \ge 0, \\0 & x < 0.\end{cases}

이는 단위 계단 함수

H(x)

를 사용하여 다음과 같이 표현할 수도 있다.

:

F(x; \lambda) = (1 - e^{-\lambda x})H(x)

2. 3. 척도 모수

지수 분포는 때때로 척도 모수

\beta = 1/\lambda

의 관점에서 매개변수화되기도 하며, 이 값은 분포의 기댓값(평균)과 같다. 이때 확률 밀도 함수(PDF)와 누적 분포 함수(CDF)는 다음과 같다.

f(x;\beta) = \begin{cases}\frac{1}{\beta} e^{-x/\beta} & x \ge 0, \\0 & x < 0.\end{cases} \qquad\qquadF(x;\beta) = \begin{cases}1- e^{-x/\beta} & x \ge 0, \\0 & x < 0.\end{cases}

참고로, 지수 분포는 양의 실수 구간

(0, \infty)

를 지지 집합(support)으로 가지며, 비율 모수(rate parameter)

\lambda > 0

를 사용하여 다음과 같이 정의되기도 한다.

확률 밀도 함수(PDF):

:

f(x; \lambda) = \lambda e^{-\lambda x}

누적 분포 함수(CDF):

:

F(x; \lambda) = 1 - e^{-\lambda x}

척도 모수를

\theta = 1/\lambda

로 표기할 경우, 확률 밀도 함수는 다음과 같이 표현할 수도 있다.

:

f(x; \theta) = \frac{1}{\theta} f(x/\theta; 1) = \frac{1}{\theta} e^{-x/\theta}

3. 성질

지수 분포는 여러 가지 중요한 통계적 성질을 가진다. 대표적으로 기댓값과 분산이 모수 ''λ''와 간단한 관계( $1/\lambda$ 및 $1/\lambda^2$ )를 가지며, 표준 편차는 기댓값과 같다. 중앙값은 $\frac{\ln(2)}{\lambda}$ 로 계산되며 항상 기댓값보다 작다.

지수 분포의 가장 독특한 성질 중 하나는 무기억성(Memorylessness)이다. 이는 특정 시점까지 사건이 발생하지 않았다는 정보가 앞으로 남은 대기 시간의 분포에 영향을 주지 않음을 의미한다. 이 성질 때문에 고장률이 일정한 시스템을 모델링하는 데 자주 사용된다.

또한, 지수 분포는 특정 분위수 값을 가지며, 쿨백-라이블러 발산을 통해 다른 지수 분포와의 정보량 차이를 측정할 수 있다. 주어진 평균값에 대해 최대 엔트로피를 가지는 연속 확률 분포이기도 하다.^[5]

마지막으로 지수 분포는 감마 분포, 라플라스 분포, 파레토 분포, 와이블 분포, 기하 분포 등 다양한 다른 확률 분포들과 밀접한 관계를 맺고 있으며, 여러 분포의 극한 형태나 특수한 경우로 나타나기도 한다.

3. 1. 기댓값과 분산

확률변수 ''X''가 빈도(율 모수) ''λ''를 모수로 갖는 지수분포를 따른다면, 기댓값(평균)은 다음과 같다.

:

\operatorname{E}[X] = \frac{1}{\lambda}

이는 단위 시간당 사건이 ''λ''회 발생할 경우, 사건 발생 간격의 평균 시간이 ''1/λ''임을 의미한다. 예를 들어, 시간당 평균 2통의 전화를 받는다면, 다음 전화가 걸려올 때까지 기다리는 시간의 기댓값은 0.5시간, 즉 30분이다.

분산은 다음과 같다.

:

\operatorname{Var}[X] = \frac{1}{\lambda^2}

따라서 표준 편차는 기댓값(평균)과 같은 ''1/λ''이다.

지수 분포는 때때로 척도 모수 ''β'' = 1/''λ''를 사용하여 나타내기도 하는데, 이 경우 ''β''는 기댓값(평균)과 같다.^[22]

:

E(X)=\beta , \ \ \ V(X)=\beta^2

''X''의 ''n''차 적률(

n\in\mathbb{N}

)은 다음과 같다.

:

\operatorname{E}\left[X^n\right] = \frac{n!}{\lambda^n}

''X''의 ''n''차 중심 적률(

n\in\mathbb{N}

)은 다음과 같다.

:

\mu_n = \operatorname{E}\left[(X - \operatorname{E}[X])^n\right] = \frac{!n}{\lambda^n} = \frac{n!}{\lambda^n}\sum^n_{k=0}\frac{(-1)^k}{k!}

여기서 !''n''은 ''n''의 서브팩토리얼이다.

''X''의 중앙값은 다음과 같다.

:

\operatorname{m}[X] = \frac{\ln(2)}{\lambda}

여기서 ln은 자연 로그를 나타낸다. 지수 분포에서는 항상 중앙값이 평균보다 작다 (

\operatorname{m}[X] < \operatorname{E}[X]

). 평균과 중앙값의 절대 차이는 다음과 같다.

:

\left|\operatorname{E}\left[X\right] - \operatorname{m}\left[X\right]\right| = \frac{1 - \ln(2)}{\lambda} \approx \frac{0.30685}{\lambda}

이 값은 표준 편차 ''1/λ''보다 작다.

3. 2. 중앙값

''X''의 중앙값은 다음과 같다.

\operatorname{m}[X] = \frac{\ln(2)}{\lambda} < \operatorname{E}[X],

여기서 ln은 자연 로그를 나타낸다. 따라서 평균과 중앙값의 절대 차이는 다음과 같다.

\left|\operatorname{E}\left[X\right] - \operatorname{m}\left[X\right]\right| = \frac{1 - \ln(2)}{\lambda} < \frac{1}{\lambda} = \operatorname{\sigma}[X],

이는 중앙값-평균 부등식과 일치한다.

3. 3. 무기억성

지수 분포를 따르는 확률 변수 ''T''는 다음과 같은 무기억성(Memorylessness)이라는 중요한 성질을 만족한다.

\Pr \left (T > s + t \mid T > s \right ) = \Pr(T > t), \qquad \forall s, t \ge 0.

이는 어떤 사건이 발생하기까지 기다리는 시간을 ''T''라고 할 때, 특정 시간 ''s''까지 그 사건이 발생하지 않았다는 조건 하에서 앞으로 ''t'' 시간 이상 더 기다려야 할 조건부 확률이, 처음부터 ''t'' 시간 이상 기다릴 확률과 같다는 의미이다. 즉, 과거의 기다린 시간은 미래의 기다릴 시간에 영향을 주지 않는다. 예를 들어, 어떤 부품의 수명이 지수 분포를 따를 때, 이 부품이 30시간 동안 고장 나지 않았다고 해서 앞으로 10시간 이상 더 작동할 확률은, 새 부품이 처음부터 10시간 이상 작동할 확률과 동일하다.

이 성질은 지수 분포의 누적 분포 함수의 여집합(생존 함수)을 이용하여 다음과 같이 확인할 수 있다.

\begin{align}\Pr\left(T > s + t \mid T > s\right)&= \frac{\Pr\left(T > s + t \cap T > s\right)}{\Pr\left(T > s\right)} \\[4pt]&= \frac{\Pr\left(T > s + t \right)}{\Pr\left(T > s\right)} \\[4pt]&= \frac{e^{-\lambda(s + t)}}{e^{-\lambda s}} \\[4pt]&= e^{-\lambda t} \\[4pt]&= \Pr(T > t).\end{align}

무기억성을 갖는 확률 분포는 이산 확률 분포 중에서는 기하 분포가 유일하며, 연속 확률 분포 중에서는 지수 분포가 유일하다.

따라서 지수 분포는 고장률(Hazard rate)이 시간에 따라 변하지 않고 일정한 시스템이나 현상을 모델링하는 데 사용된다. 즉, 지수 분포는 고장률이 상수인 유일한 연속 확률 분포이다.

3. 4. 분위수

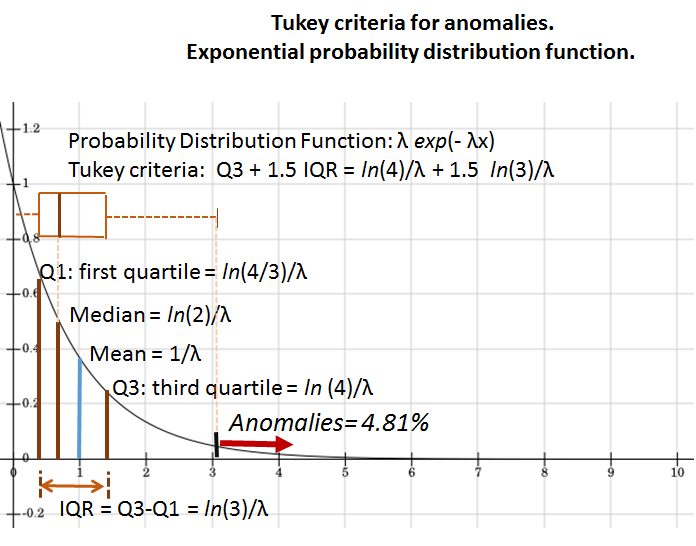
Tukey anomaly criteria for exponential probability distribution function. — 지수 확률 밀도 함수에 대한 터키 이상치 기준.

Exp(''λ'')에 대한 분위 함수 (역 누적 분포 함수)는 다음과 같다.

F^{-1}(p;\lambda) = \frac{-\ln(1-p)}{\lambda}, \quad 0 \le p < 1

따라서 사분위수는 다음과 같다.

제1사분위수: $\frac{\ln(4/3)}{\lambda}$
중앙값: $\frac{\ln(2)}{\lambda}$
제3사분위수: $\frac{\ln(4)}{\lambda}$

결과적으로 사분위 범위는

\frac{\ln(3)}{\lambda}

이다.

3. 5. 쿨백-라이블러 발산

모수

\lambda_0

를 가지는 "참" 지수 분포에서 모수

\lambda

를 가지는 "근사" 지수 분포까지의 방향 쿨백-라이블러 발산 (단위: 내트)은 다음과 같다.

\begin{align}\Delta(\lambda_0 \parallel \lambda)&= \mathbb{E}_{\lambda_0}\left( \log \frac{p_{\lambda_0}(x)}{p_\lambda(x)}\right)\\&= \mathbb{E}_{\lambda_0}\left( \log \frac{\lambda_0 e^{\lambda_0 x}}{\lambda e^{\lambda x}}\right)\\&= \log(\lambda_0) - \log(\lambda) - (\lambda_0 - \lambda)E_{\lambda_0}(x)\\&= \log(\lambda_0) - \log(\lambda) + \frac{\lambda}{\lambda_0} - 1.\end{align}

여기서

E_{\lambda_0}(x)

는 모수

\lambda_0

를 가지는 지수 분포의 기댓값이며, 그 값은

1/\lambda_0

이다.

3. 6. 최대 엔트로피 분포

모든 연속 확률 분포 중에서 지표가 [0, ∞)이고 평균이 ''μ''인 경우, ''λ'' = 1/''μ''인 지수 분포가 가장 큰 미분 엔트로피를 갖는다. 즉, E[''X'']가 고정되어 있고 0보다 크거나 같은 확률 변수 ''X''에 대한 최대 엔트로피 확률 분포이다.^[5]

3. 7. 다른 분포와의 관계

''X''₁, ..., ''X''_''n''을 각각 비율 모수 ''λ''₁, ..., ''λ_n''를 갖는 독립 확률 변수인 지수 분포 변수라고 하자. 이 변수들의 최솟값

\min\left\{X_1, \dotsc, X_n \right\}

역시 지수 분포를 따르며, 그 비율 모수는

\lambda = \lambda_1 + \dotsb + \lambda_n

이다. 이는 각 변수가 특정 값 ''x''보다 클 확률, 즉 여누적 분포 함수

\Pr(X_i > x) = e^{-x\lambda_i}

를 이용하여 확인할 수 있다.

\begin{align}\Pr\left(\min\{X_1, \dotsc, X_n\} > x\right) &= \Pr\left(X_1 > x, \dotsc, X_n > x\right) \\&= \prod_{i=1}^n \Pr\left(X_i > x\right) \\&= \prod_{i=1}^n \exp\left(-x\lambda_i\right) = \exp\left(-x\sum_{i=1}^n \lambda_i\right)\end{align}

최솟값을 갖는 변수의 인덱스 ''k'' (즉,

X_k

가 최솟값인 경우)는 다음과 같은 확률을 갖는 범주형 분포를 따른다.

\Pr\left(X_k = \min\{X_1, \dotsc, X_n\}\right) = \frac{\lambda_k}{\lambda_1 + \dotsb + \lambda_n}

반면, 최댓값

\max\{X_1, \dotsc, X_n\}

는 일반적으로 지수 분포를 따르지 않는다 (모든 ''λ_i''가 0이 아닌 경우).^[6]

독립인 두 지수 변수 ''X''₁ (모수 λ₁)과 ''X''₂ (모수 λ₂)의 합 ''Z'' = ''X''₁ + ''X''₂의 확률 밀도 함수는 각 변수의 확률 밀도 함수의 컨볼루션으로 계산된다.

f_Z(z) = \begin{cases}\dfrac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1} \left(e^{-\lambda_1 z} - e^{-\lambda_2 z}\right) & \text{ if } \lambda_1 \neq \lambda_2 \\[4 pt]\lambda^2 z e^{-\lambda z} & \text{ if } \lambda_1 = \lambda_2 = \lambda.\end{cases}

만약 두 변수의 비율 모수가 같다면(λ₁ = λ₂ = λ), 합의 분포는 형태 모수 2, 비율 모수 λ인 얼랑 분포가 되며, 이는 감마 분포 Gamma(2, λ)의 특수한 경우이다. 일반적으로, ''n''개의 독립적이고 동일한 Exp(λ) 지수 확률 변수의 합은 얼랑 분포 Erlang(''n'', λ) 또는 감마 분포 Gamma(''n'', λ)를 따른다.^[9]

지수 분포는 다른 여러 확률 분포와 다음과 같은 관계를 갖는다.

''X'' ~ 라플라스(μ, β⁻¹) 이면, |''X'' − μ| ~ Exp(β)이다.^[8]
''X'' ~ 파레토(1, λ) 이면, log(''X'') ~ Exp(λ)이다.^[8]
''X'' ~ SkewLogistic(θ) 이면, $\log\left(1 + e^{-X}\right) \sim \operatorname{Exp}(\theta)$ 이다.
''X_i'' ~ ''U''(0, 1) (독립 동일 분포) 이면, $\lim_{n \to \infty}n \min \left(X_1, \ldots, X_n\right) \sim \operatorname{Exp}(1)$ 이다.
지수 분포는 베타 분포의 스케일링된 극한이다: $\lim_{n \to \infty} n \operatorname{Beta}(1, n) = \operatorname{Exp}(1).$
지수 분포는 3형 피어슨 분포의 특수한 경우이다.
지수 분포는 형태 모수 α = 1을 갖는 감마 분포 Gamma(1, λ)와 동일하다.^[8]
''X'' ~ Exp(λ)이고 ''X''_''i'' ~ Exp(λ_''i'')일 때 여러 변환 관계가 성립한다.
스케일링: $kX \sim \operatorname{Exp}\left(\frac{\lambda}{k}\right)$ (단, k > 0). 지수 분포는 양수 인자에 의한 스케일링에 대해 닫혀있다.
1 + ''X''는 벤크탄더와이블(λ, 1)를 따른다.
''ke^X'' ~ 파레토(''k'', λ).^[8]
''e^−X'' ~ 베타(λ, 1).^[8]
(1/k)''e''^''X'' ~ 멱법칙(''k'', λ)
$\sqrt{X}$ 는 레일리 분포 $\operatorname{Rayleigh} \left(\frac{1}{\sqrt{2\lambda}}\right)$ 를 따른다.^[8]
''X''는 와이블 분포 $\operatorname{Weibull}\left(\frac{1}{\lambda}, 1\right)$ 와 같다.^[8]
$X^2$ 는 와이블 분포 $\operatorname{Weibull}\left(\frac{1}{\lambda^2}, \frac{1}{2}\right)$ 를 따른다.^[8]
μ − β log(λ''X'') ∼ 검벨(μ, β).
''X''의 정수 부분 $\lfloor X\rfloor$ 는 0, 1, 2, ...에서 값을 갖는 기하 분포 Geometric $\left(1-e^{-\lambda}\right)$ 를 따른다.
''X''의 올림 $\lceil X\rceil$ 는 1, 2, 3, ...에서 값을 갖는 기하 분포 Geometric $\left(1-e^{-\lambda}\right)$ 를 따른다.
''X'' ~ Exp(λ) 이고 ''Y'' ~ 얼랑(''n'', λ) (또는 감마 $\left(n, \frac{1}{\lambda}\right)$ )이면, $\frac{X}{Y} + 1$ 은 파레토(1, ''n'')를 따른다.
만약 지수 분포의 모수 λ 자체가 감마(k, θ) (형태, 척도 모수)를 따르는 확률 변수라면, ''X''의 주변 분포는 로맥스(k, 1/θ)가 된다. 이는 감마 혼합의 한 예이다.
독립적인 ''X''₁ ~ Exp(λ₁)과 ''X''₂ ~ Exp(λ₂)에 대해, λ₁''X''₁ − λ₂''X''₂는 라플라스(0, 1)를 따른다.
''X''₁, ..., ''X_n''이 동일한 모수 λ를 갖는 독립 지수 변수일 때:
합의 스케일링된 값 $2 \lambda \sum_{i=1}^n X_i$ 는 자유도 2''n''인 카이제곱 분포 $\chi^2_{2n}$ 를 따른다.
두 변수의 차 ''X''_''i'' − ''X''_''j''는 라플라스(0, λ⁻¹)를 따른다.
독립적인 경우, 두 변수의 비율 $\frac{X_i}{X_i + X_j}$ 는 U(0, 1)을 따른다.
만약 모수가 다를 수 있는 경우 (''X_i'' ~ Exp(λ_i), ''X_j'' ~ Exp(λ_j)), 비율 $Z = \frac{\lambda_i X_i}{\lambda_j X_j}$ 는 확률 밀도 함수 $f_Z(z) = \frac{1}{(z + 1)^2}$ 를 갖는다.
''X'' ~ Exp(1) (표준 지수 분포)일 때:
$\mu - \beta\log\left(\frac{e^{-X}}{1 - e^{-X}}\right)$ 는 로지스틱(μ, β)를 따른다.
독립적인 ''X_i'', ''X_j'' ~ Exp(1)에 대해 $\mu - \beta\log\left(\frac{X_i}{X_j}\right)$ 역시 로지스틱(μ, β)를 따른다.
''μ'' − σ log(''X'')는 GEV(μ, σ, 0)를 따른다.
만약 ''Y''가 감마 $\left(\alpha, \frac{\beta}{\alpha}\right)$ 를 따르면, $\sqrt{XY}$ 는 K-분포 K(α, β)를 따른다.
''X'' ~ Exp(1/2)이면, ''X''는 자유도 2인 카이제곱 분포 $\chi^2_2$ 와 같다. 이를 이용하면, 일반적인 Exp(λ)는 $\frac{1}{2\lambda} \chi_2^2$ 분포와 같고, 독립 동일 분포 Exp(λ) 변수 ''n''개의 합은 $\frac{1}{2\lambda }\chi_{2n}^2$ 분포를 따른다.
만약 $X \sim \operatorname{Exp}\left(\frac{1}{\lambda}\right)$ 이고, 주어진 ''X''에 대해 ''Y''가 푸아송(X)를 따른다면, ''Y''의 주변 분포는 기하 $\left(\frac{1}{1 + \lambda}\right)$ 이다.
호이트 분포는 지수 분포와 아크사인 분포로부터 유도될 수 있다.
지수 분포는 모수 $\kappa$ 가 0으로 갈 때 ''κ''-지수 분포의 극한 형태이다.
지수 분포는 모수 $\alpha = 1$ 및 $\nu = 1$ 일 때 κ-일반화 감마 분포의 극한 형태이다.

지수 분포와 밀접하게 관련된 다른 분포들은 다음과 같다.

초지수 분포: 확률 밀도 함수가 여러 지수 분포 밀도 함수의 가중 합으로 표현되는 분포.
저지수 분포: 여러 (독립이지만 동일 분포일 필요는 없는) 지수 확률 변수들의 합의 분포.^[8]
ex가우시안 분포: 지수 분포 변수와 정규 분포 변수의 합의 분포.

독립적이고 동일한 지수 분포를 따르는 확률 변수의 합은 얼랑 분포를 따른다. 얼랑 분포의 형상 모수를 1로 하면 지수 분포와 일치한다. 또한 자유도 2의 카이제곱 분포는 비율 모수 ''λ'' = 1/2 (척도 모수 ''θ'' = 2)의 지수 분포와 일치한다. 와이블 분포에서 형상 모수 ''m'' = 1로 놓은 특수한 경우이기도 하다.

4. 응용

지수 분포는 사건 발생률이 일정한 푸아송 과정에서, 한 사건이 발생하고 다음 사건이 발생하기까지 걸리는 시간을 설명하는 데 자연스럽게 사용된다. 예를 들어, 매 시간 평균 2번의 지진이 발생하는 지역에서 다음 지진이 일어나기까지 걸리는 시간을 모델링하는 데 쓰일 수 있다.

또한, 지수 분포는 이산적인 베르누이 시행 횟수를 다루는 기하 분포의 연속적인 버전으로 생각할 수 있다. 기하 분포가 특정 상태 변화가 일어나기까지 필요한 시도 횟수를 설명한다면, 지수 분포는 연속적인 과정에서 상태 변화가 일어나기까지 걸리는 시간을 설명한다.

현실 세계에서는 사건 발생률이 항상 일정하지는 않다. 예를 들어, 하루 중 시간대에 따라 전화 통화 수신율은 달라진다. 하지만 평일 오후 2시부터 4시처럼 비교적 발생률이 일정한 특정 시간 구간에 집중한다면, 지수 분포는 다음 전화가 걸려올 때까지의 시간을 근사적으로 모델링하는 데 유용하게 쓰일 수 있다. 이러한 가정 하에 지수 분포를 적용할 수 있는 다른 예시는 다음과 같다.

방사성 입자가 붕괴하기까지 걸리는 시간 또는 가이거 계수기가 방사선을 감지하여 딸깍거리는 소리 사이의 시간 간격
전화 교환대에서 한 통화가 끝나고 다음 통화가 걸려올 때까지의 시간
금융 분야의 신용 위험 모델링에서, 기업이 채무 불이행(디폴트) 상태에 이르기까지 걸리는 시간

지수 분포는 단위 길이당 특정 사건이 발생할 확률이 일정한 경우에도 사용될 수 있다. 예를 들면 다음과 같다.

DNA 가닥에서 돌연변이가 발생하는 지점 사이의 거리
특정 도로 구간에서 발생하는 로드킬 지점 사이의 거리

대기열 이론에서는 은행 창구 직원이나 콜센터 상담원 등이 고객 한 명에게 서비스를 제공하는 데 걸리는 시간을 모델링할 때 지수 분포를 자주 사용한다. (고객의 도착 자체는 도착 간격이 독립적이고 동일하게 분포되어 있다면 푸아송 분포로 모델링하는 경우가 많다.) 여러 개의 독립적인 단계를 순서대로 거쳐야 하는 프로세스의 총 소요 시간은 얼랑 분포를 따르는데, 이는 여러 독립적인 지수 분포 변수들의 합으로 나타나는 분포이다.

신뢰성 이론 및 신뢰성 공학 분야에서도 지수 분포가 널리 활용된다. 특히, 지수 분포는 메모리 없음 속성을 가지기 때문에, 제품 수명 주기를 나타내는 배스텁 곡선에서 고장률이 일정한 구간(우발 고장 구간)을 모델링하는 데 적합하다. 또한, 시스템 내 여러 부품의 고장률을 단순히 더하여 전체 시스템의 고장률을 계산할 수 있다는 점에서 모델링에 편리함을 제공한다. 하지만 지수 분포는 제품이나 생명체의 전체 수명을 모델링하기에는 한계가 있다. 왜냐하면 실제로는 초기(초기 고장)와 말기(마모 고장)에 고장률이 더 높게 나타나는 경향이 있기 때문이다.

물리학에서는 일정한 중력장 내에서 고정된 온도와 압력을 가진 기체를 관찰할 때, 기체 분자들이 존재하는 높이 분포가 기압 공식으로 알려진 근사적인 지수 분포를 따른다. 이것은 아래에 언급된 엔트로피 속성의 결과이다.

수문학에서는 지수 분포는 일 강우량 및 하천 방류량의 월별 및 연간 최대 값과 같은 변수의 극값을 분석하는 데 사용된다.^[16]

파란색 그림은 이항 분포를 기반으로 하는 90% 신뢰 벨트도 표시하여 연간 최대 1일 강우량에 지수 분포를 맞는 예시를 보여준다. 강우 데이터는 누적 빈도 분석의 일부로 플로팅 위치로 표시된다.

수술실 관리에서 전형적인 작업 내용이 없는 수술 범주(응급실에서 모든 유형의 수술을 포함)의 수술 기간 분포 예측에 활용된다.

5. 통계적 추론

아래에서는 확률 변수 ''X''가 비율 모수 λ를 갖는 지수 분포를 따른다고 가정한다. 이때, $x_1, \dotsc, x_n$ 은 ''X''로부터 얻은 ''n''개의 독립 표본이며, 표본 평균은 $\bar{x}$ 로 나타낸다. 이러한 설정을 바탕으로 모수 λ에 대한 다양한 통계적 추론 방법을 적용할 수 있다.

5. 1. 모수 추정

λ에 대한 최대 우도 추정량은 다음과 같이 구성된다.

변수에서 추출된 독립적이고 동일하게 분포된 표본 ''x'' = (''x''₁, ..., ''x''_''n'')이 주어졌을 때, λ에 대한 우도 함수는 다음과 같다.

L(\lambda) = \prod_{i=1}^n\lambda\exp(-\lambda x_i) = \lambda^n\exp\left(-\lambda \sum_{i=1}^n x_i\right) = \lambda^n\exp\left(-\lambda n\overline{x}\right),

여기서

\overline{x} = \frac{1}{n}\sum_{i=1}^n x_i

는 표본 평균이다.

우도 함수의 로그의 도함수는 다음과 같다.

\frac{d}{d\lambda} \ln L(\lambda) =\frac{d}{d\lambda} \left( n \ln\lambda - \lambda n\overline{x} \right) =\frac{n}{\lambda} - n\overline{x}\ \begin{cases}> 0, & 0 < \lambda < \frac{1}{\overline{x}}, \\[8pt]= 0, & \lambda = \frac{1}{\overline{x}}, \\[8pt]< 0, & \lambda > \frac{1}{\overline{x}}.\end{cases}

결과적으로, 율 모수(rate parameter)에 대한 최대 우도 추정량은 다음과 같다.

\widehat{\lambda}_\text{mle} = \frac{1}{\overline{x}} = \frac{n}{\sum_i x_i}

이것은

\lambda

의 불편 추정량이 아니지만,

\overline{x}

는

1/\lambda

(분포의 기댓값)의 불편 추정량^[10]이자 최대 우도 추정량(MLE)^[11]이다.

\widehat{\lambda}_\text{mle}

의 편향(bias)은 다음과 같다.

B \equiv \operatorname{E}\left[\left(\widehat{\lambda}_\text{mle} - \lambda\right)\right] = \frac{\lambda}{n - 1}

이는 편향이 보정된 최대 우도 추정량

\widehat{\lambda}^*_\text{mle} = \widehat{\lambda}_\text{mle} - B

을 얻게 한다.

평균 제곱 오차(MSE)를 근사적으로 최소화하는 추정량은 (참고: 편향-분산 트레이드오프) 표본 크기 ''n''이 2보다 크다고 가정할 때, 최대 우도 추정량에 수정 계수를 곱하여 다음과 같이 구할 수 있다.

\widehat{\lambda} = \left(\frac{n - 2}{n}\right) \left(\frac{1}{\bar{x}}\right) = \frac{n - 2}{\sum_i x_i}

이 추정량은 역감마 분포

\text{Inv-Gamma}(n, \lambda)

의 평균과 분산으로부터 유도된다.^[12]

5. 2. 베이즈 추론

지수 분포의 켤레 사전 분포는 감마 분포이며, 지수 분포는 감마 분포의 특수한 경우이다. 감마 확률 밀도 함수는 다음과 같은 매개변수화를 사용하는 것이 유용하다.

\operatorname{Gamma}(\lambda; \alpha, \beta) = \frac{\beta^{\alpha}}{\Gamma(\alpha)} \lambda^{\alpha-1} \exp(-\lambda\beta).

사후 분포 ''p''는 위에 정의된 우도 함수와 감마 사전 분포를 사용하여 다음과 같이 표현할 수 있다.

\begin{align}p(\lambda) &\propto L(\lambda) \Gamma(\lambda; \alpha, \beta) \\&= \lambda^n \exp\left(-\lambda n\overline{x}\right) \frac{\beta^{\alpha}}{\Gamma(\alpha)} \lambda^{\alpha-1} \exp(-\lambda \beta) \\&\propto \lambda^{(\alpha+n)-1} \exp(-\lambda \left(\beta + n\overline{x}\right)).\end{align}

이제 사후 밀도 ''p''는 누락된 정규화 상수를 제외하고 지정되었다. 이는 감마 확률 밀도 함수의 형태를 가지므로, 정규화 상수를 채워 넣으면 다음과 같은 사후 분포를 얻을 수 있다.

p(\lambda) = \operatorname{Gamma}(\lambda; \alpha + n, \beta + n\overline{x}).

여기에서 하이퍼파라미터 ''α''는 사전 관측치의 수로, ''β''는 사전 관측치의 합으로 해석할 수 있다. 사후 평균은 다음과 같다.

\frac{\alpha + n}{\beta + n\overline{x}}.

6. 난수 생성

지수 분포를 따르는 변량을 생성하는 개념적으로 간단한 방법은 역변환 표본 추출을 이용하는 것이다. 균등 분포를 따르는 (0, 1) 구간의 난수 변량 ''U''가 주어졌을 때, 변량

$T = F^{-1}(U)$

은 지수 분포를 따른다. 여기서 ''F''^-1는 다음과 같이 정의되는 분위 함수이다.

$F^{-1}(p)=\frac{-\ln(1-p)}{\lambda}$

''U''가 (0, 1)에서 균등 분포를 따르면, 1 − ''U'' 역시 같은 분포를 따르므로, 실제 계산에서는 더 간단히 다음과 같이 지수 변량을 생성할 수 있다.

$T = \frac{-\ln(U)}{\lambda}$

지수 변량을 생성하는 다른 방법들은 Knuth^[20]와 Devroye^[21]에 의해 논의되었으며, 정렬 과정 없이 미리 정렬된 지수 변량 집합을 빠르게 생성하는 방법도 존재한다.^[21]

참조

_[1] 웹사이트 7.2: Exponential Distribution https://stats.libret[...] 2024-10-11
_[2] 웹사이트 Exponential distribution {{!}} mathematics {{!}} Britannica https://www.britanni[...] 2024-10-11
_[3] 웹사이트 Exponential Distribution https://mathworld.wo[...] 2024-10-11
_[4] 간행물 Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation http://uryasev.ams.s[...] Springer 2023-02-27
_[5] 간행물 Maximum entropy autoregressive conditional heteroskedasticity model http://www.wise.xmu.[...] Elsevier 2011-06-02
_[6] 웹사이트 The expectation of the maximum of exponentials http://www.stat.berk[...] 2016-12-13
_[7] arXiv Entropy of the sum of two independent, non-identically-distributed exponential random variables 2016
_[8] 간행물 Univariate Distribution Relationships https://www.math.wm.[...] 2008-02
_[9] 서적 Fundamentals of Applied Probability and Random Processes https://books.google[...] Academic Press
_[10] 서적 Applied Multivariate Statistical Analysis https://books.google[...] Pearson Prentice Hall 2012-08-10
_[11] 웹사이트 NIST/SEMATECH e-Handbook of Statistical Methods http://www.itl.nist.[...]
_[12] 간행물 A Bayesian Look at Classical Estimation: The Exponential Distribution
_[13] 서적 Introduction to probability and statistics for engineers and scientists https://books.google[...] Associated Press
_[14] 간행물 Power Law Distribution: Method of Multi-scale Inferential Statistics https://www.academia[...]
_[15] 웹사이트 Cumfreq, a free computer program for cumulative frequency analysis http://www.waterlog.[...]
_[16] 서적 Frequency and Regression Analysis https://archive.org/[...] Chapter 6 in: Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands
_[17] 간행물 Frequentist predictions intervals and predictive distributions
_[18] 간행물 Predictive Likelihood: A Review
_[19] 논문 Universal Models for the Exponential Distribution http://www.emakalic.[...]
_[20] 서적 The Art of Computer Programming Addison–Wesley
_[21] 서적 Non-Uniform Random Variate Generation http://luc.devroye.o[...] Springer-Verlag
_[22] 보고서 指数分布 http://www.an.econ.k[...] ""
_[23] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com