맨위로가기

양자 순간 이동

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

양자 순간 이동은 양자 정보를 한 위치에서 다른 위치로 전송하는 기술로, 큐비트라는 2 상태 계를 통해 정보를 잃지 않고 전달한다. 이 과정은 얽힌 양자 상태 또는 벨 상태를 생성하여, 발신자가 큐비트를 준비하고 얽힌 입자 중 하나와 결합하여 얽힌 양자 상태를 변경하는 방식으로 진행된다. 1993년 이론이 제안된 이후, 1997년 이산 변수 양자 순간이동 실험 성공을 시작으로, 거리와 기술적 측면에서 꾸준히 발전해왔다. 양자 순간 이동은 다차원 시스템, 논리 게이트, 그리고 이미 정보를 가진 시스템 간의 정보 전송으로 일반화되었으며, 양자 정보 처리와 양자 컴퓨터의 발전에 기여할 것으로 기대된다.

더 읽어볼만한 페이지

  • 순간이동 - 큐비트
    큐비트는 양자 정보의 기본 단위로, 0과 1의 중첩 상태를 동시에 가질 수 있으며, 양자 컴퓨터에서 양자 논리 게이트를 통해 조작되고, 양자 얽힘을 활용한 응용이 가능하다.
  • 순간이동 - 필라델피아 실험
    필라델피아 실험은 1943년 미국 해군이 실시했다는 도시전설로, 알베르트 아인슈타인의 통일장 이론을 바탕으로 선박을 레이더에 보이지 않게 만드는 실험이었으나, 해군은 부인하고 있으며, 칼 M. 앨런의 편지를 통해 알려져 대중문화에서 음모론 소재로 활용된다.
  • 양자 컴퓨팅 - 위상 양자 컴퓨터
    위상 양자 컴퓨터는 애니온의 꼬임 상태를 이용하여 양자 정보를 저장하고 처리하는 양자 컴퓨터로, 2차원 공간에서 준입자인 애니온의 특성을 활용하며, 양자 회로 모델 등과 계산 능력이 동일하지만 특정 알고리즘에 유리하고 실험적 확인은 논쟁 중에 있다.
  • 양자 컴퓨팅 - 양자 프로그래밍
    양자 프로그래밍은 양자 컴퓨터 제어 및 양자 알고리즘 구현을 위한 프로그래밍 방식으로, 양자 명령어 집합과 양자 소프트웨어 개발 키트 및 프로그래밍 언어를 통해 양자 컴퓨팅 연구 및 개발을 지원한다.
  • 양자정보과학 - 양자 컴퓨터
    양자 컴퓨터는 양자역학적 현상을 이용하여 정보를 처리하는 컴퓨터로, 큐비트를 통해 0과 1을 동시에 표현하여 특정 연산에서 기존 컴퓨터보다 빠른 속도를 보이며 암호 해독, 신약 개발 등 다양한 분야에 혁신을 가져올 것으로 기대된다.
  • 양자정보과학 - 벨 부등식
    벨 부등식은 양자역학과 국소적 숨은 변수 이론의 모순을 보이는 부등식으로, 실험 결과는 벨 부등식의 위반을 통해 양자역학의 비국소성을 시사하며 양자 정보 과학에 중요한 함의를 가진다.
양자 순간 이동
개요
이름양자 순간 이동
분야양자 정보 이론
관련 개념양자 얽힘, 양자 게이트, 양자 회로
응용 분야양자 컴퓨팅, 양자 통신
설명
정의양자 상태를 한 위치에서 다른 위치로 전송하는 과정
특징전송되는 양자 상태에 대한 완벽한 복사본 생성
원본 양자 상태는 파괴됨
양자 복제 불가능성 정리 위배 X
원리양자 얽힘 이용
고전적인 통신 채널과 양자 채널 필요
과정


역사
최초 제안1993년 찰스 베넷, 질 브라사드 등에 의해 제안
실험적 구현1997년 디르크 보우미스터 그룹이 최초로 실험적 구현 성공
추가 연구2004년 원자 수준의 양자 순간 이동 성공 (뉴욕 타임스 기사 참조: 과학자, 커크 선장이 아닌 원자를 순간 이동시키다)
2017년 지상-위성 간 양자 순간 이동 성공 (Nature 논문 참조: 지상-위성 양자 순간 이동)
응용
양자 컴퓨팅양자 컴퓨터 내부의 정보 전송 및 처리
양자 통신안전한 정보 전송 (양자 암호)
양자 네트워크양자 정보를 공유하고 처리하는 네트워크 구축
추가 정보
관련 연구두-준위 시스템과 네-준위 시스템 간의 양자 정보 전송 (Photonics Research 논문 참조: 두-준위 및 네-준위 양자 시스템 간의 양자 정보 전송)

2. 원리

양자 순간 이동에 사용되는 기본 구성 요소 다이어그램


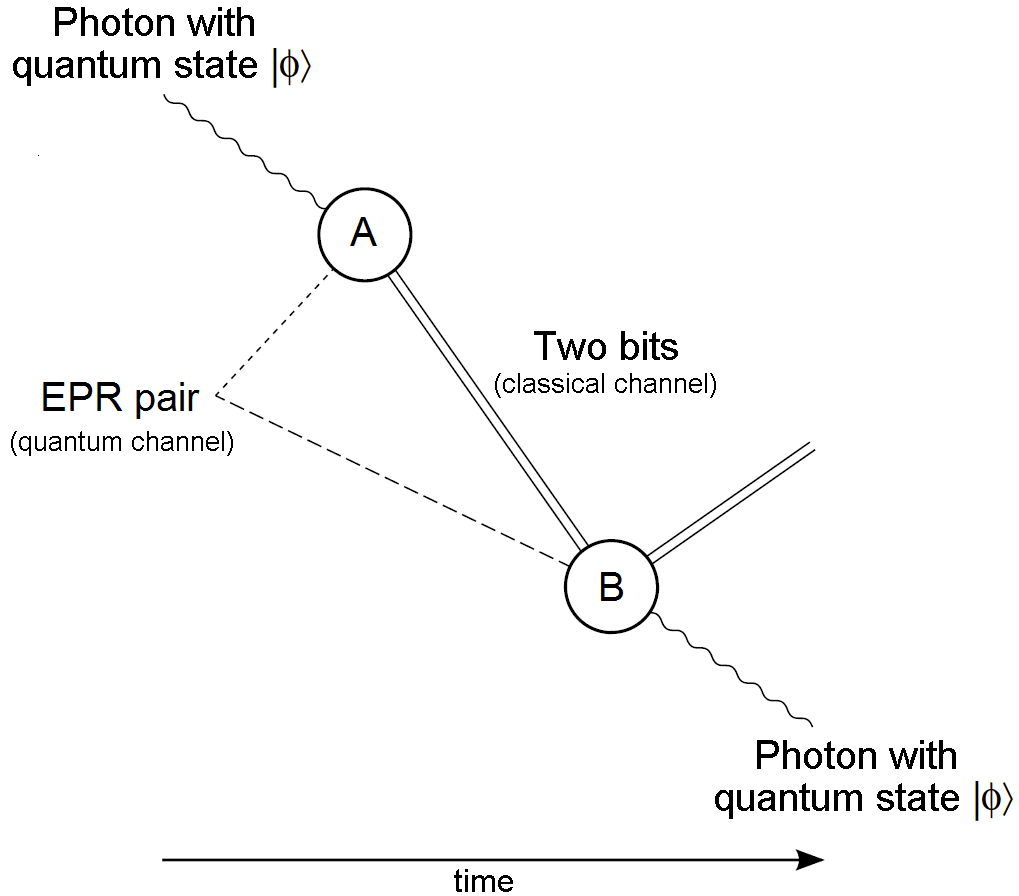
양자 순간 이동은 EPR 쌍이라는 양자 얽힘 관계에 있는 두 입자를 이용한다. 가장 간단한 예는 광자의 편광(Polarization)을 이용한 1 큐비트 전송이다.

광자 0의 편광에 관한 양자 상태 |\psi\rangle_0 (1큐비트)를 A에서 B로 전송하는 경우를 생각해 보자. 여기서, |V\rangle_0는 광자 0의 수직 편광 상태, |H\rangle_0는 광자 0의 수평 편광 상태를 나타낸다.

: |\psi\rangle_0 = \alpha|V\rangle_0 + \beta|H\rangle_0

''α'' 및 ''β''는 중첩의 계수이다.

어떤 광자 1과 광자 2가 EPR 쌍으로서 다음과 같은 양자 얽힘 관계에 있다고 가정한다.

:|\Phi^+\rangle = \frac{1}{\sqrt{2}} ( |V\rangle_1 |V\rangle_2 + |H\rangle_1 |H\rangle_2)

이 식은 광자 1과 광자 2의 편광 상태가 평행함을 의미한다.

A는 광자 0과는 별도로 EPR 쌍의 광자 2개(광자 1, 광자 2)를 생성하고 광자 2를 B에게 보낸다. A는 광자 1을 전송하고 싶은 양자 상태 |\psi\rangle_0에 있는 광자 0과 함께 벨 측정을 한다. 그 결과를 B에게 알리면, B는 광자 2에 특정 조작을 하여 |\psi\rangle_0를 광자 2에 재현할 수 있다.

편의상 |V\rangle,|H\rangle를 |0\rangle, |1\rangle으로 표기한다. 벨 측정은 벨 기저에 대한 사영 측정을 가리키며, 2준위계의 벨 기저는 다음 4가지이다.

:|\Phi^+\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle),

:|\Phi^-\rangle = \frac{1}{\sqrt{2}} (|00\rangle - |11\rangle),

:|\Psi^+\rangle = \frac{1}{\sqrt{2}} (|01\rangle + |10\rangle),

:|\Psi^-\rangle = \frac{1}{\sqrt{2}} (|01\rangle - |10\rangle).

초기 3개 광자의 상태는 다음 상태 벡터로 표현된다.

: |\psi\rangle_0\otimes |\Phi^+\rangle_{12} = (\alpha |0\rangle_0 + \beta|1\rangle_0) \otimes \frac{1}{\sqrt{2}} (|0\rangle_1 \otimes |0\rangle_2 + |1\rangle_1 \otimes |1\rangle_2).

벨 기저를 사용하여 01을 나타내면 다음과 같다.

:|0\rangle \otimes |0\rangle = \frac{1}{\sqrt{2}} (|\Phi^+\rangle + |\Phi^-\rangle),

:|0\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}} (|\Psi^+\rangle + |\Psi^-\rangle),

:|1\rangle \otimes |0\rangle = \frac{1}{\sqrt{2}} (|\Psi^+\rangle - |\Psi^-\rangle),

:|1\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}} (|\Phi^+\rangle - |\Phi^-\rangle).

이를 대입하면 다음과 같아진다.

:

\begin{align}

|\psi\rangle_0\otimes |\Phi^+\rangle_{12}

=\frac{1}{2} \Big[

&|\Phi^+\rangle_{01} \otimes (\alpha |0\rangle_2 + \beta|1\rangle_2)

+|\Phi^-\rangle_{01} \otimes (\alpha |0\rangle_2 - \beta|1\rangle_2) \\

&|\Psi^+\rangle_{01} \otimes (\beta |0\rangle_2 + \alpha|1\rangle_2)

+|\Psi^-\rangle_{01} \otimes (-\beta |0\rangle_2 + \alpha|1\rangle_2)

\Big].

\end{align}



광자 0, 1에 대해 벨 측정을 수행하면, 측정 결과에 따라 광자 2의 상태가 다음 4가지 중 하나로 확정된다.

:\alpha |0\rangle_2 + \beta|1\rangle_2

:\alpha |0\rangle_2 - \beta|1\rangle_2

:\beta |0\rangle_2 + \alpha|1\rangle_2

:-\beta |0\rangle_2 + \alpha|1\rangle_2

A는 B에게 벨 측정 결과를 전달하고(고전 채널), B는 측정 결과에 따라 광자 2에 대해 파울리 연산자를 수행한다.

  • |\Phi^+\rangle_{01}의 경우: 아무것도 수행하지 않는다.
  • |\Phi^-\rangle_{01}의 경우: \sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix}
  • |\Psi^+\rangle_{01}의 경우: \sigma_x = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix}
  • |\Psi^-\rangle_{01}의 경우: \sigma_z \sigma_x = i \sigma_y = \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix}.


최종적인 B가 가진 광자 2의 상태는 \alpha |0\rangle_2 + \beta|1\rangle_2 가 되고, 광자 0의 양자 상태를 재현할 수 있다. 벨 측정을 수행함으로써 원래 광자 0의 양자 상태는 소멸했지만, 광자 2에 나타난 것처럼 보인다.

2. 1. 큐비트와 양자 상태

양자 정보 이론에서 큐비트는 비트의 양자역학적 형태로, 0과 1의 값을 동시에 가질 수 있는 가장 간단한 정보 단위이다.[70] 큐비트는 2차원 복소수 값 벡터 공간(힐베르트 공간)을 사용하여 표현할 수 있다.

광자의 편광 상태를 예로 들면, 큐비트는 수직 편광(|V\rangle)과 수평 편광(|H\rangle)의 중첩(Superposition)으로 표현될 수 있다. 이를 브라-켓 표기법으로 나타내면 다음과 같다.

:|\psi\rangle_0 = \alpha|V\rangle_0 + \beta|H\rangle_0

여기서 \alpha와 \beta는 중첩의 계수를 나타낸다.

2. 2. EPR 쌍과 양자 얽힘

EPR 쌍은 두 입자가 서로 얽혀 있어, 한 입자의 상태를 측정하면 다른 입자의 상태도 즉시 결정되는 관계를 말한다.

차일링거 연구단은 카나리아 제도의 라 팔마와 테네리페 섬 사이에서 143km가 넘는 거리에서 실험을 진행했다. 이 실험에는 주파수 비상관 편광 얽힘 광자 쌍 소스, 초저잡음 단일 광자 검출기, 얽힘 보조 클록 동기화 등이 사용되었다.[94]

:|\Psi^-\rangle_{23}=\frac{1}{\surd2}((|H\rangle_2|V\rangle_3)-(|V\rangle_2|H\rangle_3))

이 실험에서 라 팔마는 엘리스, 테네리페는 밥에 비유할 수 있다. 엘리스와 밥은 위에서 언급한 얽힌 상태를 공유하며, 광자 2는 엘리스에게, 광자 3은 밥에게 있다. 제3자인 찰리는 일반화된 편광 상태에서 엘리스에게 순간 이동될 광자 1(입력 광자)을 제공한다.

:|\phi\rangle_1=\alpha|H\rangle_1+\beta|V\rangle_1

여기서 복소수 \alpha와 \beta는 엘리스나 밥에게는 알려지지 않았다.

엘리스는 벨 상태 측정(BSM)을 수행하여 두 광자를 무작위로 네 개의 벨 상태 중 하나에 투영하는데, 각 상태는 25%의 확률을 갖는다. 광자 3은 입력 상태 |\phi\rangle 위로 사영된다. 엘리스는 고전 채널을 통해 BSM의 결과를 밥에게 전송하며, 밥은 해당 단일 연산을 적용하여 광자 3을 광자 1의 초기 상태로 얻을 수 있다. 밥은 |\psi^-\rangle_{12} 상태를 감지하면 아무것도 할 필요가 없다. |\psi^+\rangle_{12} 상태가 감지되면 밥은 수평 및 수직 구성 요소 사이에 \pi의 페이즈 이동을 광자 3에 적용해야 한다.[94]

차일링거 연구단의 실험 결과, 평균 충실도(이상적인 순간 이동 상태와 측정된 밀도 행렬의 중첩)는 0.863이고 표준 편차는 0.038이었다. 실험 중 링크 감쇠는 강한 바람과 급격한 온도 변화로 인해 28.1 dB와 39.0 dB 사이였다. 양자 자유 공간 채널의 높은 손실에도 불구하고 평균 충실도는 고전적 한계인 2/3를 넘었다. 따라서 차일링거 연구단은 143km 거리에서 양자 순간 이동을 성공적으로 시연했다.[94]

광자의 양자 순간 이동 다이어그램


:|\Phi^+\rangle = \frac{1}{\sqrt{2}} ( |V\rangle_1 |V\rangle_2 + |H\rangle_1 |H\rangle_2)

위 식은 광자 1과 광자 2의 편광 상태가 평행함을 의미한다.

2. 3. 양자 순간이동 과정



양자 순간 이동에는 몇 가지 필수 자원이 필요하다. 우선, 두 개의 고전 비트를 전송할 수 있는 통신 채널이 있어야 한다. 또한, 큐비트의 얽힌 벨 상태를 생성하고 이를 두 개의 서로 다른 위치에 분배하는 수단, 벨 상태 큐비트 중 하나에서 벨 측정을 수행하고, 얽힘 쌍의 다른 큐비트의 양자 상태를 조작하는 수단도 필요하다. 물론, 순간 이동될 양자 상태 |\phi \rangle를 가진 입력 큐비트도 있어야 한다.

양자 순간 이동 프로토콜은 다음과 같이 진행된다.[72]

1. 벨 상태가 생성되어, 하나의 큐비트는 위치 A로, 다른 큐비트는 위치 B로 전송된다.

2. 위치 A에서 벨 상태 큐비트와 순간 이동할 큐비트 |\phi \rangle에 대한 벨 측정이 수행된다. 이 측정은 네 가지 가능한 결과 중 하나를 산출하며, 이는 두 개의 고전적인 정보 비트로 인코딩될 수 있다. 위치 A의 두 큐비트는 모두 폐기된다.

3. 고전 채널을 사용하여 두 비트가 A에서 B로 전송된다.

4. 위치 A에서 수행된 측정 결과에 따라, 위치 B의 벨 상태 큐비트는 네 가지 가능한 상태 중 하나에 있게 된다. 이 중 하나는 원래 양자 상태 |\phi \rangle와 동일하고, 나머지 세 개는 밀접하게 관련되어 있다. 실제로 얻은 상태의 정보는 두 개의 고전 비트로 인코딩되어 위치 B로 전송된다. 그런 다음 위치 B의 벨 상태 큐비트는 세 가지 방법 중 하나로 수정되거나, 전혀 수정되지 않아 순간 이동을 위해 선택된 큐비트의 상태 |\phi \rangle와 동일한 큐비트가 된다.

위 프로토콜은 큐비트가 개별적으로 주소 지정 가능하다는 가정을 하고 있다. 즉, 큐비트가 구별 가능하고 물리적으로 레이블이 지정되어 있음을 의미한다. 그러나 파동 함수의 공간적 중첩으로 인해 두 개의 동일한 큐비트를 구별할 수 없는 상황이 있을 수 있다. 이 조건에서는 큐비트를 개별적으로 제어하거나 측정할 수 없다. 그럼에도 불구하고, 초기 벨 상태가 필요 없이 두 개의 독립적으로 준비된 큐비트를 활용하여 위에서 설명한 것과 유사한 순간 이동 프로토콜을 (조건부로) 구현할 수 있다. 이는 구별할 수 없는 두 큐비트의 파동 함수에 의해 공유되는 분리된 영역 A와 B에서 수행되는 공간적으로 국소화된 측정을 통해 큐비트의 내부 자유도(예: 스핀 또는 편광)를 처리함으로써 이루어질 수 있다.[72]

2004년에는 비엔나의 다뉴브 강을 가로질러 총 600미터에 달하는 양자 순간 이동 실험이 진행되었다. 800m 길이의 광섬유 전선이 다뉴브강 아래의 공공 하수 계에 설치되어 온도 변화 및 기타 환경 영향에 노출되었다. 앨리스는 입력 광자인 광자 b와 얽힌 광자 쌍(광자 c와 d)의 일부인 광자 c에 대해 공동 벨 상태 측정(BSM)을 수행해야 한다. 밥의 수신 광자인 광자 d는 앨리스가 관찰한 상태에 따라 달라지는 위상 회전을 제외하고 입력 광자 b에 대한 모든 정보를 포함한다. 이 실험은 앨리스의 입력 광자를 정확하게 복제하기 위해 빠른 전기 광학 변조기가 있는 고전적인 마이크로웨이브 채널을 통해 앨리스의 측정 결과를 보내는 능동 피드포워드 시스템을 구현했다. 45°에서 선형 편광 상태에서 얻은 순간 이동 충실도는 0.84에서 0.90 사이로 다양했으며, 이는 고전적 충실도 한계인 0.66을 훨씬 상회한다.[73]

순간 이동 프로토콜은 수학적으로 다양하게 표현할 수 있다. 각 양자 상태를 간단하고 직접적으로 보여주는 방법은 다음과 같다.

순간 이동 프로토콜은 앨리스가 밥에게 전달하려는 양자 상태, 즉 큐비트 |\psi\rangle로부터 시작한다. 이 큐비트는 브라-켓 표기법으로 다음과 같이 표현할 수 있다.

:|\psi\rangle_C = \alpha |0\rangle_C + \beta|1\rangle_C.

여기서 아래 첨자 ''C''는 이 상태를 아래의 ''A'' 및 ''B''와 구별하기 위해 사용된다.

다음으로, 프로토콜은 앨리스와 밥이 최대로 얽힌 상태를 공유하도록 요구한다. 이 상태는 앨리스와 밥 사이의 상호 합의에 의해 미리 고정되며, 다음 네 가지 벨 상태 중 하나일 수 있다.

:|\Phi^+\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_{B} + |1\rangle_A \otimes |1\rangle_{B}) ,

:|\Psi^+\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_{B} + |1\rangle_A \otimes |0\rangle_{B}) ,

:|\Psi^-\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_{B} - |1\rangle_A \otimes |0\rangle_{B}) .

:|\Phi^-\rangle_{AB} = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_{B} - |1\rangle_A \otimes |1\rangle_{B}) ,

여기서는 앨리스와 밥이 상태 |\Phi^+\rangle_{AB} 를 공유한다고 가정한다. 앨리스는 쌍의 입자 중 하나를 얻고, 다른 입자는 밥에게 전달된다. 얽힌 상태의 첨자 ''A''와 ''B''는 각각 앨리스와 밥의 입자를 가리킨다.

이 시점에서 앨리스는 두 개의 입자(순간 이동하려는 입자 ''C''와 얽힌 쌍 중 하나인 ''A'')를 가지고 있고, 밥은 하나의 입자 ''B''를 가지고 있다. 전체 계에서 이 세 입자의 상태는 다음과 같다.

: |\psi\rangle_C\otimes|\Phi^+\rangle_{AB} = (\alpha |0\rangle_C + \beta|1\rangle_C)\otimes\frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B + |1\rangle_A \otimes |1\rangle_B) .

그런 다음 앨리스는 자신이 소유한 두 입자에 대해 벨 기준(네 개의 벨 상태)에서 국소적 측정을 수행한다. 측정 결과를 명확히 하기 위해 앨리스의 두 큐비트 상태를 벨 기저의 중첩으로 표현한다. 이는 다음 항등식을 통해 가능하다.

:|0\rangle \otimes |0\rangle = \frac{1}{\sqrt{2}} (|\Phi^+\rangle + |\Phi^-\rangle),

:|0\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}} (|\Psi^+\rangle + |\Psi^-\rangle),

:|1\rangle \otimes |0\rangle = \frac{1}{\sqrt{2}} (|\Psi^+\rangle - |\Psi^-\rangle),

그리고

:|1\rangle \otimes |1\rangle = \frac{1}{\sqrt{2}} (|\Phi^+\rangle - |\Phi^-\rangle).

| \psi\rangle_C \otimes\ |\Phi^+\rangle_{AB}에 대한 표현을 확장하고, 위 항등식을 ''A''와 ''C'' 첨자를 가진 큐비트에 적용하면,

\alpha \frac{1}{\sqrt{2}} |0\rangle_C \otimes |0\rangle_A \otimes |0\rangle_B =

\alpha \frac{1}{2}(|\Phi^+\rangle_{CA} + |\Phi^-\rangle_{CA}) \otimes |0\rangle_B,

와 같은 결과를 얻고, 다른 항들도 유사하게 전개된다. 유사한 항들을 결합하면, ''A'', ''B'', ''C''의 총 세 입자 상태는 다음 네 항의 중첩이 된다.[96]

:

\begin{align}

| & \psi\rangle_C \otimes\ |\Phi^+\rangle_{AB} \ = \\

\frac{1}{2} \Big \lbrack

\ & |\Phi^+\rangle_{CA} \otimes (\alpha |0\rangle_B + \beta|1\rangle_B)

\ + \ |\Phi^-\rangle_{CA} \otimes (\alpha |0\rangle_B - \beta|1\rangle_B) \\

\ + \ & |\Psi^+\rangle_{CA} \otimes (\alpha |1\rangle_B + \beta|0\rangle_B)

\ + \ |\Psi^-\rangle_{CA} \otimes (\alpha |1\rangle_B - \beta|0\rangle_B) \Big \rbrack . \\

\end{align}



아직 어떤 연산도 수행되지 않았으므로, 세 입자는 모두 동일한 총 상태에 있다. 위의 과정은 단지 계의 앨리스 부분에 대한 기저 변경일 뿐이다. 실제 순간 이동은 앨리스가 두 큐비트 A, C를 벨 기준으로 측정할 때 발생한다.

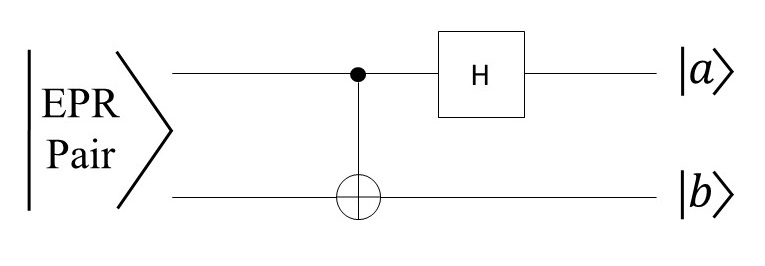
4개의 벨 상태 (그림의 EPR 쌍) 중 하나를 4개의 2큐비트 계산 기본 상태 중 하나로 매핑하는 간단한 양자 회로. 회로는 CNOT 게이트와 아다마드 연산으로 구성된다. 출력에서 a와 b는 0 또는 1의 값을 갖는다.


:|\Phi^+\rangle_{CA}, |\Phi^-\rangle_{CA}, |\Psi^+\rangle_{CA}, |\Psi^-\rangle_{CA}.

앨리스의 측정 결과에 따라, 세 입자 상태는 다음 네 가지 상태 중 하나로 붕괴된다.

  • |\Phi^+\rangle_{CA} \otimes (\alpha |0\rangle_B + \beta|1\rangle_B)
  • |\Phi^-\rangle_{CA} \otimes (\alpha |0\rangle_B - \beta|1\rangle_B)
  • |\Psi^+\rangle_{CA} \otimes (\alpha |1\rangle_B + \beta|0\rangle_B)
  • |\Psi^-\rangle_{CA} \otimes (\alpha |1\rangle_B - \beta|0\rangle_B)


앨리스의 두 입자는 이제 네 개의 벨 상태 중 하나에서 서로 얽혀 있으며, 원래 앨리스와 밥의 입자 간에 공유되었던 얽힘은 끊어진다. 밥의 입자는 위 네 가지 중첩 상태 중 하나를 취하며, 이는 순간 이동될 상태와 유사하다.

앨리스의 벨 측정 결과는 계가 위 네 가지 상태 중 어느 상태에 있는지 알려준다. 앨리스는 고전 채널을 통해 이 결과를 밥에게 보낼 수 있으며, 두 개의 고전적 비트로 네 가지 결과 중 어떤 것을 얻었는지 전달할 수 있다.

밥은 앨리스로부터 메시지를 받은 후 자신의 입자가 어떤 상태에 있는지 알고, 이 정보를 사용하여 입자에 단일 작업을 수행하여 원하는 상태 \alpha |0\rangle_B + \beta|1\rangle_B로 변환한다.

  • 앨리스가 |\Phi^+\rangle_{CA}를 얻었다고 하면, 밥은 자신의 큐비트가 이미 원하는 상태임을 알고 아무것도 하지 않는다. (항등 연산)
  • 메시지가 |\Phi^-\rangle_{CA}를 나타내면, 밥은 파울리 행렬에 의해 주어진 단일 양자 게이트를 통해 큐비트를 보낸다.


:\sigma_3 = \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix}

  • 앨리스의 메시지가 |\Psi^+\rangle_{CA}에 해당하면, 밥은


:\sigma_1 = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix}

게이트를 적용한다.

  • 나머지 경우, 적절한 게이트는 다음과 같다.


: \sigma_3 \sigma_1 = - \sigma_1 \sigma_3 = i \sigma_2 = \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix}.

이로써 순간 이동이 완료된다. 위 세 개의 게이트는 큐비트의 블로흐 구에서 적절한 축(X, Y, Z)에 대한 π 라디안(180°) 회전에 해당한다.

몇 가지 중요한 점은 다음과 같다.

  • 이 작업 후 밥의 큐비트는 |\psi\rangle_B= \alpha |0\rangle_B + \beta|1\rangle_B 상태가 되고, 앨리스의 큐비트는 얽힌 상태의 정의되지 않은 부분이 된다. 순간 이동은 큐비트를 복사하지 않으므로, 복제 불가능성 정리와 일치한다.
  • 물질이나 에너지의 이동은 없다. 앨리스의 입자가 밥에게 물리적으로 이동된 것이 아니라, 상태만 전송되었다. "순간 이동"이라는 용어는 양자 역학적 입자의 구별 불가능성을 반영한다.
  • 순간 이동되는 큐비트마다 앨리스는 밥에게 두 가지 고전 정보를 보내야 한다. 이 두 비트는 순간 이동되는 큐비트에 대한 완전한 정보를 전달하지 않는다. 도청자가 두 비트를 가로채더라도, 밥이 원하는 상태를 복구하기 위해 무엇을 해야 하는지 알 수 있지만, 밥이 소유한 얽힌 입자와 상호작용할 수 없다면 이 정보는 쓸모가 없다.

2. 4. 벨 측정과 상태 변화

벨 측정을 통해 광자 0과 광자 1의 상태는 4가지 벨 기저 중 하나로 결정된다.[96] 이에 따라 광자 2의 상태도 4가지 중첩 상태 중 하나로 확정된다.

:

\begin{align}

| & \psi\rangle_C \otimes\ |\Phi^+\rangle_{AB} \ = \\

\frac{1}{2} \Big \lbrack

\ & |\Phi^+\rangle_{CA} \otimes (\alpha |0⟩_B + \beta|1⟩_B)

\ + \ |\Phi^-\rangle_{CA} \otimes (\alpha |0⟩_B - \beta|1⟩_B) \\

\ + \ & |\Psi^+\rangle_{CA} \otimes (\alpha |1⟩_B + \beta|0⟩_B)

\ + \ & |\Psi^-\rangle_{CA} \otimes (\alpha |1⟩_B - \beta|0⟩_B) \Big \rbrack . \\

\end{align}



수행되는 작업이 없었기 때문에 세 입자는 모두 여전히 동일한 총 상태에 있다. 위의 내용은 계의 엘리스 부분(광자 0, 1)에 대한 기저 변경일 뿐이며, 실제 순간 이동은 앨리스가 벨 기준으로 두 큐비트 A, C를 측정할 때 발생한다.[96]

앨리스의 (국소적) 측정 결과는 세 입자 상태가 다음 네 가지 상태 중 하나로 붕괴될 것이라는 것이다(각각을 얻을 확률이 동일함).[96]

  • |\Phi^+\rangle_{CA} \otimes (\alpha |0⟩_B + \beta|1⟩_B)
  • |\Phi^-\rangle_{CA} \otimes (\alpha |0⟩_B - \beta|1⟩_B)
  • |\Psi^+\rangle_{CA} \otimes (\alpha |1⟩_B + \beta|0⟩_B)
  • |\Psi^-\rangle_{CA} \otimes (\alpha |1⟩_B - \beta|0⟩_B)


엘리스의 두 입자는 이제 4개의 벨 상태 중 하나에서 서로 얽혀있으며 원래 엘리스와 밥의 입자 간에 공유되었던 얽힘은 이제 끊어졌다. 밥의 입자는 위에 표시된 네 가지 중첩 상태 중 하나를 취한다. 밥의 큐비트는 순간 이동할 상태와 유사한 상태에 있으며, 밥의 큐비트에 대해 가능한 네 가지 상태는 순간 이동할 상태의 단일 이미지이다.[96]

2. 5. 파울리 연산

밥은 엘리스로부터 메시지를 받은 후, 자신의 입자가 네 가지 상태 중 어느 상태에 있는지 알게 된다. 이 정보를 사용하여 밥은 자신의 입자에 다음과 같은 단일 연산 (파울리 연산)을 수행하여 입자를 원하는 상태 \alpha |0\rangle_B + \beta|1\rangle_B로 변환한다.

  • 엘리스가 그녀의 결과를 |\Phi^+\rangle_{CA}로 나타내면, 밥은 자신의 큐비트가 이미 원하는 상태에 있음을 알고 아무것도 하지 않는다. 이것은 항등 연산자인 사소한 단일 연산에 해당한다.
  • 메시지가 |\Phi^-\rangle_{CA}로 나타내는 경우, 밥은 상태를 복구하기 위해 파울리 행렬에 의해 주어진 단일 양자 게이트를 통해 자신의 큐비트를 보낼 것이다.


:\sigma_3 = \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix}

  • 엘리스의 메시지가 |\Psi^+\rangle_{CA}에 해당하는 경우, 밥은 그의 큐비트에


:\sigma_1 = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix}

게이트를 적용한다.

  • 마지막으로, 나머지 경우에 대해 적절한 게이트는 다음과 같이 지정된다.


: \sigma_3 \sigma_1 = - \sigma_1 \sigma_3 = i \sigma_2 = \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix}.

따라서 순간 이동이 달성된다. 위에서 언급한 세 개의 게이트는 큐비트의 블로흐 구 그림에서 적절한 축(X, Y 및 Z)에 대한 π 라디안(180°)의 회전에 해당한다.

광자를 이용한 양자 순간이동 실험의 경우에도, B씨는 A씨에게 벨 측정의 결과를 고전 채널을 통해 전달받고, 그 결과에 따라 광자2에 대해 다음과 같은 파울리 연산자를 각각 수행한다.

  • |\Phi^+\rangle_{01}의 경우: 아무것도 수행하지 않는다.
  • |\Phi^-\rangle_{01}의 경우: \sigma_z = \begin{bmatrix} 1 & 0 \\ 0 & -1\end{bmatrix}
  • |\Psi^+\rangle_{01}의 경우: \sigma_x = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix}
  • |\Psi^-\rangle_{01}의 경우: \sigma_z \sigma_x = i \sigma_y = \begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix}

3. 실험 결과 및 기록

1993년 찰스 베넷 등이 양자 순간이동 이론을 처음 제안했다.[63] 1997년 안톤 차일링거가 이끄는 인스브루크 대학교 그룹이 처음으로 이산 변수 양자 순간이동 실험에 성공했으나,[9] 특정 조건에서만 순간이동이 일어나는 한계가 있었다.[9] 1998년 캘리포니아 공과대학교의 후루사와 아키라 그룹은 무조건적인 연속 변수 양자 순간이동에 성공했다.[65]

이후 양자 순간이동 거리는 점차 늘어났다. 1998년에는 초기 예측을 검증했고,[9] 2004년에는 광섬유를 이용해 600m,[73] 이후 16km,[74] 97km[94]로 늘어났다. 2012년에는 카나리아 제도의 두 천문대 사이에서 143km 야외 실험에 성공했다.[94] 2015년에는 초전도 나노선 검출기를 이용하여 광섬유를 통해 102km 거리에 도달했다.[75] 물질계의 경우 기록 거리는 21m이다.[76]

2004년에는 5광자 얽힘을 이용한 "개방형" 순간이동이 시연되었고,[77] 두 큐비트 복합 상태 순간이동도 실현되었다.[78] 2011년에는 최대 10MHz 대역폭까지 빛의 파동 패킷 순간이동을 시연했다.[79][80] 2013년에는 하이브리드 기술을 이용한 "완전 결정론적" 양자 순간이동이 보고되었다.[81] 2014년에는 양자 순간이동을 이용한 신뢰할 수 있는 데이터 전송 방법이 발표되었다.[82][83] 2015년에는 중국과학기술대학 연구진이 양자 입자의 다중 자유도를 순간이동시키는 실험을 수행했다.[84][85][86] 2016년에는 6.5km 떨어진 두 독립 소스를 이용한 양자 순간이동이 시연되었고,[87] 같은 해 캘거리 대학교 연구진은 6.2km 거리에서 양자 순간이동을 시연했다.[88] 2020년에는 44km 거리에서 90% 이상의 충실도를 가진 양자 순간이동이 달성되었다.[89][90]

2016년 8월 16일, 중화인민공화국 연구팀은 세계 최초의 양자 통신 위성인 묵자 위성을 발사했고,[59] 같은 해 8월 26일 지상-우주 간 양자 통신 시험에 성공했다.[60][61] 2017년 7월, 정보통신연구기구는 초소형 위성을 이용한 지상-우주 양자 통신에 성공했다.[62] 2021년 5월, 이화학연구소 등 공동 연구팀은 확률적 순간이동에 성공했다.[63]

4. 비기술적 요약

양자 순간 이동은 정보를 잃지 않고 양자 정보를 한 위치에서 다른 위치로 전송하는 기술이다. 송신자는 전송할 정보(큐비트)와 얽힌 입자 쌍 중 하나를 결합하여 측정하고, 그 결과를 수신자에게 고전 채널을 통해 전달한다. 수신자는 이 정보를 바탕으로 원래의 양자 정보를 복원할 수 있다. 양자 순간 이동은 정보가 얽힘 상태의 일부가 되면서 "파괴"되므로 복제 불가능성 정리를 위반하지 않는다.[70]

양자 순간 이동을 위해서는 큐비트가 전송될 수 있도록 얽힌 양자 상태 또는 벨 상태가 생성되어야 한다. 얽힘은 두 개 이상의 개별 입자를 하나의 공유 양자 상태로 생성하거나 배치하여 별개의 물리적 계 사이에 통계적 상관 관계를 부여한다. 하나의 입자가 움직이면 다른 입자도 함께 움직이며, 얽힌 입자가 하나의 양자 상태로 작용하게 된다.

발신자는 큐비트에서 입자(또는 정보)를 준비하고 중간 상태의 얽힌 입자 중 하나와 결합하여 얽힌 양자 상태를 변경한다. 얽힌 입자의 변화된 상태는 얽힌 상태의 변화를 측정할 분석기로 보내진다. "변경" 측정을 통해 수신자는 발신자가 가지고 있던 원래 정보를 다시 생성하여 다른 위치에 있는 두 사람 사이에서 정보를 순간 이동하거나 운반할 수 있다.[71]

양자 채널은 모든 양자 정보 전송에 사용되는 통신 메커니즘이며 순간 이동에 사용되는 채널이다. 그러나 양자 채널 외에도 기존 채널을 사용하여 양자 정보를 "보존"하기 위해 큐비트를 동반해야 한다. 기존 채널이 필요하기 때문에 순간 이동 속도는 빛의 속도보다 빠를 수 없다.

5. 양자 순간 이동 프로토콜의 일반화

양자 순간이동 프로토콜은 큐비트뿐만 아니라 다차원 시스템(큐디트)으로 일반화될 수 있다. 베넷(Bennett) 등의 초기 논문에서는 이미 큐디트에 대한 일반화를 논의했으며,[1] 두 큐비트의 최대 얽힘 상태를 두 큐디트의 최대 얽힘 상태로 대체하고, 벨 측정은 최대 얽힘 직교 기저에 의해 정의된 측정으로 대체하는 방식을 제시했다. 이러한 일반화는 2001년에 베르너(Werner)에 의해 더 자세히 논의되었다.[48]

무한 차원 연속 변수 양자 정보를 이용한 일반화도 가능하다.[49] 이는 무조건 작동하는 최초의 순간 이동 실험으로 이어졌다.[50]

다중 얽힘 상태를 사용하면 발신자가 여러 수신자에게 정보를 순간 이동시키거나, 모든 수신자에게 동일한 상태를 보내 얽힘의 양을 줄일 수 있다.[51] 또한 다자간 상태를 순간 이동시키거나,[52] 수신 측에서 정보를 추출하기 위해 협력해야 하는 방식으로 단일 상태를 전송하는 것도 가능하다.[53]

5. 1. 논리 게이트 순간이동

일반적으로 혼합 상태 ρ가 전송될 수 있으며, 순간이동 중에 선형 변환 ω가 적용되어 양자 정보 처리가 가능하다. 이는 양자 정보 처리의 기본 구성 요소 중 하나이다.

일반적인 순간 이동 방식은 다음과 같이 설명할 수 있다. 세 가지 양자 계가 관련되어 있다. 시스템 1은 앨리스가 순간 이동시키려는 (알려지지 않은) 상태 ''ρ''이다. 시스템 2와 3은 앨리스와 밥에게 각각 분배된 최대 얽힘 상태 ''ω''에 있다. 그러면 전체 시스템은 다음과 같은 상태에 있다.

:\rho \otimes \omega.

성공적인 순간 이동 과정은 다음을 만족하는 LOCC 양자 채널 Φ이다.

:(\operatorname{Tr}_{12} \circ \Phi ) (\rho \otimes \omega) = \rho\,

여기서 Tr12는 시스템 1과 2에 대한 부분 추적 연산이고, \circ는 맵의 합성을 나타낸다. 이것은 슈뢰딩거 그림에서 채널을 설명한다.

하이젠베르크 묘사에서 수반 사상을 사용하면 성공 조건은 다음과 같다. 밥의 계에서 관찰 가능한 모든 ''O'' 에 대해,

:\langle \Phi(\rho \otimes \omega)| I \otimes O \rangle = \langle \rho | O \rangle.

I \otimes O에서 텐서 인자는 12 \otimes 3이고 \rho \otimes \omega에서는 1 \otimes 23이다.

제안된 채널 \Phi는 보다 명시적으로 설명될 수 있다. 순간 이동을 시작하기 위해 엘리스는 소유하고 있는 두 개의 하위 계(1과 2)에서 국소적 측정을 수행한다. 국소적 측정이 ''영향을'' 미친다고 가정한다.

: {F_i} = {M_i ^2}.

측정이 ''i'' 번째 결과를 등록하면 전체 상태가 다음으로 축소된다.

: (M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I).

(M_i \otimes I)에서 텐서 인자는 12 \otimes 3이고 \rho \otimes \omega에서는 1 \otimes 23이다. 그런 다음 밥은 해당 국소적 연산 \Psi_i을 계 3에 적용한다. 결합된 계에서 이것은 다음과 같이 설명된다.

: (Id \otimes \Psi_i)(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I).

여기서 ''Id''는 복합 계 1 \otimes 2의 항등사상이다.

따라서 채널 \Phi는 다음과 같이 정의된다.

: \Phi (\rho \otimes \omega) = \sum_i (Id \otimes \Psi_i)(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I)

\Phi는 LOCC의 정의를 만족함을 주목하라. 위에서 언급한 바와 같이, 밥의 계에서 관찰 가능한 모든 ''O'' 에 대해 등식

: \langle \Phi(\rho \otimes \omega), I \otimes O \rangle = \langle \rho, O \rangle

이 성립한다. 방정식의 왼쪽은 다음과 같다.

:

\sum_i \langle (Id \otimes \Psi_i)(M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I), \; I \otimes O \rangle



:

= \sum_i \langle (M_i \otimes I)(\rho \otimes \omega)(M_i \otimes I), \; I \otimes \Psi_i ^*(O)\rangle



여기서 Ψ ''i*''는 하이젠베르크 그림에서 Ψ ''i'' 의 adjoint이다. 모든 물체가 유한 차원이라고 가정하면

: \sum_i \operatorname{Tr} \; (\rho \otimes \omega)(F_i \otimes \Psi_i^*(O)).

순간 이동의 성공 기준은 다음과 같은 표현이 있다.

: \sum_i \operatorname{Tr} \; (\rho \otimes \omega)(F_i \otimes \Psi_i ^*(O)) = \operatorname{Tr} \; \rho \cdot O.

6. 현상에 대한 국소적 설명

데이비드 도이치와 패트릭 헤이든은 양자 역학의 다세계 해석을 통해 양자 순간이동에 대한 국소적 설명을 제시했다. 이들의 논문에 따르면, 앨리스가 밥에게 보내는 두 비트는 양자 상태의 순간이동을 가능하게 하는 "국소적으로 접근할 수 없는 정보"를 포함한다. 즉, "고전적인 채널을 통해 흐르는 양자 정보의 능력, 결맞음에서 살아남는 것은 양자 순간 이동의 기초이다."[108]

7. 추가 발전

양자 순간 이동은 논리 게이트 배열을 통해 결함 허용 양자 계산과 관련된 오류를 개선할 수 있다. D. 고테스만과 I. L. 추앙의 실험에 따르면 환경적 오류로부터 보호를 강화하는 "클리포드 계층"[55] 게이트 배열이 존재한다. 게이트 시퀀스가 계산에 필요한 자원을 덜 요구하기 때문에 클리포드 계층을 사용하면 더 높은 오류 임계값을 허용할 수 있다. 양자 컴퓨터에서 더 많은 게이트를 사용할수록 더 많은 노이즈가 발생하지만, 논리 전달에서 게이트 배열과 순간 이동을 사용하면 이러한 양자 네트워크에서 컴파일되는 "트래픽"을 줄여 노이즈를 감소시킬 수 있다.[56] 양자 컴퓨터에 사용되는 큐비트가 많을수록 게이트 배열에 더 많은 레벨이 추가되며, 게이트 배열의 대각화 정도가 달라진다. 고차원 분석은 클리포드 계층의 더 높은 레벨 게이트 배열을 포함한다.[57]

정보 손실을 줄이기 위해 중간 얽힘 상태의 순도를 고려해야 한다. 개발된 보호 방법에는 일반적인 이산 변수 대신 연속 변수 정보를 사용하여 중첩된 코히어런트 중간 상태를 생성하는 것이 포함된다. 여기에는 수신된 정보의 위상 변화를 주고, 선호하는 상태(홀수 또는 짝수 코히어런트 상태)를 사용하여 수신 시 혼합 단계를 추가하는 과정이 포함된다. 이러한 상태는 "송신자의 고전 정보에 조건화"되어 원래 전송된 정보를 포함하는 2모드 상태를 생성한다.[58]

이미 양자 정보를 가지고 있는 시스템 간의 정보 순간 이동에 대한 개발도 있었다. Feng, Xu, Zhou 등의 실험에서 광학 큐비트-큐쿼트 얽힘 게이트를 사용함으로써 큐비트 가치의 정보를 이미 가진 광자에 큐비트 순간 이동이 가능하다는 것을 입증했다.[2] 이는 이전에 저장된 정보를 기반으로 계산을 수행하여 과거 계산을 개선할 수 있으므로 계산 가능성을 증가시킬 수 있다.

8. 같이 보기


  • 큐디트
  • 연속 변수 양자 정보

참조

[1] 논문 Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels 1993-03-29
[2] 논문 Quantum information transfer between a two-level and a four-level quantum systems
[3] 웹사이트 Scientists Teleport not Kirk but an Atom https://www.nytimes.[...] 2004-06-17
[4] 논문 Visualizing quantum mechanics in an interactive simulation – Virtual Lab by Quantum Flytrap
[5] 논문 Deterministic quantum teleportation of atomic qubits 2004
[6] 논문 Advances in quantum teleportation
[7] 논문 Indistinguishability of Elementary Systems as a Resource for Quantum Information Processing
[8] 논문 Experimental quantum entanglement and teleportation by tuning remote spatial indistinguishability of independent photons 2020
[9] 논문 Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels 1998-02-09
[10] 논문 Quantum teleportation across the Danube 2004-08-18
[11] 논문 Experimental free-space quantum teleportation 2010-05-16
[12] 논문 Quantum teleportation over 143 kilometres using active feed-forward 2012-09-05
[13] 논문 Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors 2015-10-20
[14] 논문 Efficient Teleportation between Remote Single-Atom Quantum Memories
[15] 논문 Experimental demonstration of five-photon entanglement and open-destination teleportation
[16] 논문 Experimental quantum teleportation of a two-qubit composite system
[17] 논문 Teleportation of Nonclassical Wave Packets of Light 2011-04
[18] 웹사이트 Quantum teleporter breakthrough http://www.unsw.edu.[...] The University Of New South Wales 2011-04-17
[19] 논문 Deterministic quantum teleportation of photonic quantum bits by a hybrid technique 2013-08-14
[20] 뉴스 Scientists Report Finding Reliable Way to Teleport Data https://www.nytimes.[...] 2014-05-29
[21] 논문 Unconditional quantum teleportation between distant solid-state quantum bits 2014-05-29
[22] 웹사이트 Two quantum properties teleported together for first time http://physicsworld.[...] 2015-02-27
[23] 논문 Quantum teleportation of multiple degrees of freedom of a single photon 2015-02-26
[24] 논문 Long distance quantum teleportation 2018
[25] 논문 Quantum teleportation with independent sources and prior entanglement distribution over a network 2016-09-19
[26] 논문 Quantum teleportation across a metropolitan fibre network 2016-09-19
[27] 논문 Teleportation Systems Toward a Quantum Internet 2020-12-04
[28] 웹사이트 Researchers Achieve First "Sustained" Long Distance Quantum Teleportation https://futurism.com[...] 2021-06-06
[29] 웹사이트 Quantum teleportation between atomic systems over long distances http://phys.org/news[...] 2013-06-13
[30] 논문 Deterministic quantum teleportation between distant atomic objects 2013-06-02
[31] 논문 Deterministic teleportation of a quantum gate between two logical qubits
[32] 논문 Experimental quantum teleportation 1997-12-01
[33] 논문 Deterministic quantum teleportation with atoms 2004-06
[34] 논문
[36] 논문 Noisy quantum teleportation: An experimental study on the influence of local environments https://link.aps.org[...] 2014-10-28
[37] 논문 Advances in quantum teleportation https://www.nature.c[...] 2015-10
[38] 논문 Optimal Extraction of Information from Finite Quantum Ensembles https://link.aps.org[...] 1995-02-20
[39] 논문 Optimal minimal measurements of mixed states http://dx.doi.org/10[...] 1999-07-01
[40] 논문 Bell's inequalities versus teleportation: What is nonlocality? https://link.aps.org[...] 1994-02-07
[41] 논문 Finite-temperature detection of quantum critical points: A comparative study https://link.aps.org[...] 2024-06-14
[42] 논문 Challenges in certifying quantum teleportation: Moving beyond the conventional fidelity benchmark https://link.aps.org[...] 2024-03-22
[43] 논문 Quantum Picturalism
[44] 간행물 Applications of negative dimensional tensors Academic Press
[45] 서적 Explorations in Quantum Computing Springer
[46] 서적 Quantum Computation and Quantum Information Cambridge University Press
[47] 보고서 The logic of entanglement 2004
[48] 논문 All teleportation and dense coding schemes 2001
[49] 논문 Teleportation of Continuous Quantum Variables https://resolver.cal[...] 1998-01-26
[50] 논문 Unconditional Quantum Teleportation
[51] 논문 Multiparty teleportation 2000
[52] 논문 Teleportation and Dense Coding with Genuine Multipartite Entanglement
[53] 논문 Quantum teleportation using three-particle entanglement 1998
[54] 논문 Information Flow in Entangled Quantum Systems 1999
[55] 논문 Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations 1999-11
[56] 논문 Quantum teleportation of physical qubits into logical code-spaces 2020-09-07
[57] 논문 Efficient quantum gate teleportation in higher dimensions
[58] 논문 High success standard quantum teleportation using entangled coherent state and two-level atoms in cavities 2021-09-27
[59] 웹사이트 中国、世界初の量子通信衛星を軌道に https://jp.wsj.com/a[...] THE WALL STREET JOURNAL 2016-08-16
[60] 웹사이트 量子衛星「墨子号」、地上拠点との通信ルートが開通 http://j.people.com.[...] 인민망 2016-08-31
[61] 웹사이트 中国の量子通信衛星チームが米科学賞受賞 https://www.newsweek[...] Newsweek 2019-02-18
[62] 웹사이트 超小型衛星による量子通信の実証実験に世界で初めて成功 https://www.nict.go.[...] 정보통신연구기구 2017-07-11
[63] 웹사이트 半導体量子ビットの確率的テレポーテーションに成功 https://www.riken.jp[...] 리켄 2021-05-06
[64] 논문 Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky–Rosen Channels
[65] 논문 Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels
[66] 논문 Experimental quantum teleportation
[67] 논문 Quantum information transfer between a two-level and a four-level quantum systems
[68] 웹인용 Scientists Teleport not Kirk but an Atom https://www.nytimes.[...]
[69] 논문 Ground-to-satellite quantum teleportation https://www.nature.c[...]
[70] 논문 Deterministic quantum teleportation of atomic qubits
[71] 논문 Advances in quantum teleportation
[72] 논문 Indistinguishability of Elementary Systems as a Resource for Quantum Information Processing
[73] 논문 Quantum teleportation across the Danube 2004-08-18
[74] 논문 Experimental free-space quantum teleportation 2010-05-16
[75] 논문 Quantum teleportation over 100 km of fiber using highly efficient superconducting nanowire single-photon detectors 2015-10-20
[76] 논문 Efficient Teleportation between Remote Single-Atom Quantum Memories
[77] 논문 Experimental demonstration of five-photon entanglement and open-destination teleportation
[78] 논문 Experimental quantum teleportation of a two-qubit composite system
[79] 논문 Teleportation of Nonclassical Wave Packets of Light 2011-04
[80] 웹인용 Quantum teleporter breakthrough http://www.unsw.edu.[...] The University Of New South Wales 2011-04-17
[81] 논문 Deterministic quantum teleportation of photonic quantum bits by a hybrid technique 2013-08-14
[82] 뉴스 Scientists Report Finding Reliable Way to Teleport Data https://www.nytimes.[...] 2014-05-29
[83] 논문 Unconditional quantum teleportation between distant solid-state quantum bits 2014-05-29
[84] 웹인용 Two quantum properties teleported together for first time http://physicsworld.[...] 2015-02-27
[85] 논문 Quantum teleportation of multiple degrees of freedom of a single photon 2015-02-26
[86] 논문 Long distance quantum teleportation 2018
[87] 논문 Quantum teleportation with independent sources and prior entanglement distribution over a network 2016-09-19
[88] 논문 Quantum teleportation across a metropolitan fibre network 2016-09-19
[89] 논문 Teleportation Systems Toward a Quantum Internet 2020-12-04
[90] 웹인용 Researchers Achieve First "Sustained" Long Distance Quantum Teleportation https://futurism.com[...] 2021-06-06
[91] 웹인용 Quantum teleportation between atomic systems over long distances http://phys.org/news[...] 2013-06-13
[92] 논문 Deterministic quantum teleportation between distant atomic objects 2013-06-02
[93] 논문 Deterministic teleportation of a quantum gate between two logical qubits
[94] 논문 Quantum teleportation over 143 kilometres using active feed-forward 2012-09-05
[95] 논문 Deterministic quantum teleportation with atoms https://www.nature.c[...] 2004
[96] 서적 Quantum Computation and Quantum Information Cambridge University Press
[97] 논문 Quantum Picturalism
[98] 문서 Applications of negative dimensional tensors Academic Press
[99] 서적 Explorations in Quantum Computing Springer
[100] 서적 Quantum Computation and Quantum Information Cambridge University Press
[101] 문서 The logic of entanglement http://web.comlab.ox[...]
[102] 논문 All teleportation and dense coding schemes 2001
[103] 논문 Teleportation of Continuous Quantum Variables https://authors.libr[...]
[104] 논문 Unconditional Quantum Teleportation https://semanticscho[...]
[105] 논문 Multiparty teleportation 2000
[106] 저널 Teleportation and Dense Coding with Genuine Multipartite Entanglement
[107] 저널 Quantum teleportation using three-particle entanglement 1998
[108] 저널 Information Flow in Entangled Quantum Systems 1999
[109] 저널 Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations 1999-11
[110] 저널 Quantum teleportation of physical qubits into logical code-spaces 2020-09-07
[111] 저널 Efficient quantum gate teleportation in higher dimensions
[112] 저널 High success standard quantum teleportation using entangled coherent state and two-level atoms in cavities 2021-09-27


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com