맨위로가기

다세계 해석

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

다세계 해석은 1957년 휴 에버렛 3세가 제안한 양자역학의 한 해석으로, 관찰 행위에 따른 파동 함수의 붕괴를 부정하고 슈뢰딩거 방정식을 따르는 모든 가능성이 실현된다는 이론이다. 이 해석은 1960~70년대 브라이스 디윗에 의해 '다세계'라는 이름으로 널리 알려졌으며, 양자 얽힘과 결풀림 현상을 통해 여러 세계가 분리되어 존재한다고 설명한다. 다세계 해석은 확률의 해석 문제, 관찰 불가능성, 물리량 보존 문제, 오컴의 면도날, 정체성 문제 등의 비판을 받지만, 양자 컴퓨터, 양자 우주론 등 현대 물리학 연구에 영향을 미치고 있으며, 과학소설 등 대중문화에도 영향을 미치고 있다.

더 읽어볼만한 페이지

  • 1957년 과학 - 국제 지구물리 관측년
    국제 지구물리 관측년은 1957년부터 1958년까지 67개국이 참여하여 전 지구적 규모의 지구물리 현상을 연구하고 우주 개발 경쟁을 촉발했으며 남극 조약 체결에 영향을 미친 과학 관측 프로그램이다.
  • 1957년 과학 - 1957년 4월 30일 일식
    1957년 4월 30일에 발생한 금환 일식은 일식 크기 1.0455, 최대 일식 시간 UTC 기준 07:31:07을 기록했으며, 다양한 천문 주기와 연관된 천문 현상이다.
  • 양자역학의 해석 - 상보성 (물리학)
    상보성은 물리적 성질들이 상보적인 쌍으로 존재하며 한쪽을 명확하게 측정할수록 다른 쪽의 정보가 불확실해지는 개념으로, 양자역학의 핵심적인 특징이며 파동-입자 이중성과 불확정성 원리에 의해 정량화된다.
  • 양자역학의 해석 - 객관적 붕괴 이론
    객관적 붕괴 이론은 표준 양자역학의 측정 문제를 해결하기 위해 파동 함수의 붕괴를 동역학적으로 모델링하는 시도로, GRW, CSL, DP 모델 등이 있으며, 에너지 보존 법칙 위배, 상대론적 모델과의 호환성 문제 등의 비판에 직면하여 실험적 검증이 이루어지고 있다.
  • 실재 - 마음
    마음은 의식, 사고, 지각, 감정, 동기, 행동, 기억, 학습 등을 포괄하는 심리적 현상과 능력의 총체이며, 다양한 분야에서 연구되고 인간 삶의 중추적인 역할을 한다.
  • 실재 - 파르메니데스
    파르메니데스는 기원전 5세기경 엘레아 출신 철학자로, "있는 것은 있고, 없는 것은 없다"라는 존재론적 주장을 통해 합리주의에 영향을 미쳤으며, 〈자연에 대하여〉에서 존재와 비존재를 탐구하여 후대 철학에 심오한 영향을 주었다.
다세계 해석
지도 정보
기본 정보
다른 이름에버렛 해석, 상대 상태 해석
유형양자역학 해석
주요 제안자
제안자휴 에버렛 3세
지지자브라이스 드윗
핵심 개념
파동 함수파동 함수는 객관적이고, 모든 측정은 파동 함수의 분기를 유발함
분기각 분기는 고유한 역사를 가진 다른 세계를 나타냄
측정측정은 세계를 분리시키며, 모든 가능한 결과는 서로 다른 세계에서 발생함.
결정론우주적 파동 함수는 결정론적으로 진화하지만, 각 세계 내에서는 비결정론적으로 보임.
국소성국소성을 따르는 결정론적 이론
철학적 의미
실재다수의 세계가 존재하며, 모두 똑같이 실재적임.
관찰자관찰자는 특별한 역할을 하지 않으며, 단순히 또 다른 양자 시스템임.
확률양자 확률은 다른 세계에서 발생하는 다른 사건들의 빈도를 나타냄.
역사
제안1957년 휴 에버렛 3세가 박사 논문에서 제안함.
발전브라이스 드윗 등이 발전시킴
대중적 관심막스 테그마크 등이 대중적으로 설명
비판
비판오컴의 면도날을 어긴다는 비판
확률을 제대로 설명하지 못한다는 비판
물리적 실재에 대한 논쟁을 불러일으킴
관련 서적
관련 서적다세계 해석 (The Many-Worlds Interpretation of Quantum Mechanics)
양자 비국소성과 실재: 벨 정리 50년 (Quantum Nonlocality and Reality: 50 years of Bell's theorem)
외부 링크
관련 문서휴 에버렛의 1957년 논문 (Relative State Formulation of Quantum Mechanics)
막스 테그마크의 논문 (The Interpretation of Quantum Mechanics: Many Worlds or Many Words?)
관련 기사양자 역학에 대한 논쟁 기사 (Physics Today, 1970)
양자 역학에 대한 논쟁 기사 (Physics Today, 1971)
관련 조사양자 역학의 기초에 대한 태도 조사 (Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 2013)

2. 역사

1957년 휴 에버렛 3세가 '상대적 상태' 개념을 창안하면서 다세계 해석이 시작되었고,[133] 이는 이후 브라이스 디윗이 1960년대와 1970년대에 '다세계'로 이름을 바꾸면서 유명해졌다.[134][135][136][137]

양자역학의 토대가 확립되고 나서 30년 가량이 지난 1954년 휴 에버렛 3세가 다세계 해석을 창안하였다. 1957년 프리스턴 대학교 수학과 학생이었던 에버렛은 박사 논문 주제로 이 해석을 도입하였다. 1955년 에버렛은 프리스턴 대학교 명예 교수로 있던 물리학자 존 휠러를 자신의 박사 과정 지도 교수로 바꾼 뒤 세계의 파동 함수 이론이란 주제로 자신의 졸업 논문을 쓰기 시작한다. 1956년 1월에 그는 다세계 해석으로부터 유도된 수학적 결과를 정리하여 휠러에게 제출했다. 휠러는 에버렛의 논문을 아주 좋게 평가하여, 그 해 5월에 에버렛의 아이디어에 대한 호의적인 반응을 기대하고 코펜하겐에 있는 닐스 보어를 방문하였으나 결과는 좋지 않았다. 이에 존 휠러는 에버렛이 박사 학위 논문을 수정하기를 권고했다. 1957년 3월 에버렛은 이전의 논문을 수정한 박사 학위 논문을 제출하여 4월에 심사를 통과했고, 이 논문은 그해 7월 《현대 물리학 리뷰》(Review of Modern Physics영어)라는 학술지에 〈양자역학의 상대 상태 공식화〉란 제목으로 게재되었다[133] (원래 휴 에버렛이 양자 얽힘을 설명하기 위해 연관적 해석으로 제목을 지었으나 휠러는 상대 상태로 제목을 고치도록 하였다). 그러나 당시 에버렛의 논문은 커다란 호응을 얻지 못했다.

약 10년 뒤, 이 아이디어는 물리학자 브라이스 디윗에 의해 ‘상대 상태 공식화’ 또는 ‘세계 파동 함수’ 대신 ‘다세계 해석’이란 이름으로 바뀌어 많은 사람들의 전반적인 지지를 얻었다. 디윗은 대학원생 닐 그레엄의 아이디어와 휴 에버렛이 개발한 수학을 기반으로 에버렛의 해석을 발전시켰다. 디윗은 에버렛의 아이디어를 소개하는 몇 편의 논문을 발표했고, 1970년에는 이 내용을 《피직스 투데이》(Physics Today영어)라는 학술잡지에 소개하여 물리학자들의 관심을 끌었다.[135] 이 논문이 다세계 해석의 주요 내용을 이룬다.

그 후 에버렛의 해석은 또 달리 해석되어 ‘여러 마음 해석’이 나온다. 이 개념은 1970년 디터 체(Dieter Zehde)에 의해 처음 제시되었고, 데이비드 앨버트(David Z. Albert영어)와 배리 로어(Barry Loewer영어)가 ‘여러 마음 해석’이란 용어를 처음 사용하였다. 이 밖에 다세계 해석은 머리 겔만과 제임스 하틀(James Hartle영어)에 의해 ‘여러 역사 해석’으로 발전하기도 하였으며, 최근에는 데이비드 도이치가 자신의 양자 컴퓨터에 관한 이론에서 다세계 해석의 개념을 적용하면서 다시금 많은 지지를 얻고 있다.

그 뒤 결풀림을 이용해 양자역학을 이해하려는 시도에는 많은 발전이 있었으며, 대중적으로도 널리 알려졌다.[138][139][140] 다세계 해석은 물리학과 철학의 수많은 다우주 가설 중 하나로, 현재는 코펜하겐 해석과 함께 양자역학의 주류 해석들 가운데 하나로 자리 잡고 있다.

2. 1. 다세계 해석의 등장

다세계 해석은 1957년 휴 에버렛 3세가 '상대적 상태' 개념을 창안하면서 시작되었다.[133] 이후 브라이스 디윗이 1960년대와 1970년대에 '다세계'라는 용어를 사용하면서 대중화되었다.[134][135][136][137]

양자역학의 기초가 확립된 후 약 30년 뒤인 1954년에 휴 에버렛 3세는 다세계 해석을 제안했다. 에버렛은 1957년 프리스턴 대학교에서 존 휠러 교수의 지도 하에 '상대적 상태'개념[61]을 이용한 세계의 파동 함수 이론이란 주제로 박사 학위 논문을 제출하고 심사를 통과했다.[133] 이 논문은 같은 해 7월 《현대 물리학 리뷰》(Review of Modern Physics영어)에 〈양자역학의 상대 상태 공식화〉란 제목으로 게재되었다.[133] 그러나 당시에는 큰 주목을 받지 못했다.[133]

1970년, 브라이스 디윗은 에버렛의 아이디어를 발전시켜 《피직스 투데이》(Physics Today영어)에 발표하여 물리학자들의 관심을 끌었다.[135] 디윗은 대학원생 닐 그레엄의 아이디어와 에버렛의 수학적 기반을 바탕으로 에버렛의 해석을 발전시켰다.

에버렛의 초기 연구는 '상대적 상태' 개념을 제시했다. 에버렛은 양자 얽힘을 통해 두 개 이상의 하부 시스템은 일반적인 상호작용 후 '상관'되거나, 현재는 얽힘 상태가 된다고 주장했다. 이러한 얽힌 시스템은 상태들의 곱의 합으로 표현될 수 있으며, 여기서 두 개 이상의 하부 시스템은 서로에 대해 상대적인 상태에 놓인다. 측정이나 관찰 후에는, 한 쌍(혹은 세 쌍 이상) 중 하나는 측정된 대상 또는 관찰된 시스템이 되고, 다른 하나는 측정된 시스템의 상태를 기록한 측정 장치(관찰자를 포함)가 된다. 전체 중첩 상태의 하부 시스템 상태들의 각 곱은 시간에 따라 다른 곱들과 독립적으로 진화한다. 일단 하부 시스템들이 상호작용하면, 그들의 상태는 상관되거나 얽히게 되어 더 이상 독립적인 것으로 간주될 수 없다. 에버렛의 용어로, 각 하부 시스템 상태는 이제 그것이 상호 작용한 다른 하부 시스템에 대해 상대적인 상태와 '상관'되었다.

슈뢰딩거의 고양이의 예에서, 상자를 연 후 얽힌 시스템은 고양이, 독약 병, 그리고 관찰자이다. 하나의 상대적인 세 쌍의 상태는 살아있는 고양이, 깨지지 않은 병, 그리고 살아있는 고양이를 본 관찰자일 것이며, 다른 상대적인 세 쌍의 상태는 죽은 고양이, 깨진 병, 그리고 죽은 고양이를 본 관찰자일 것이다.

에버렛의 체계에서는 파동 함수의 붕괴가 없다. 대신, 슈뢰딩거 방정식 또는 그 양자장론의 상대론적 유사체가 항상 모든 곳에서 성립한다. 관찰이나 측정은 관찰되는 대상과 관찰자를 모두 포함하는 전체 시스템에 파동 방정식을 적용하여 모델링된다. 그 결과 중 하나는 모든 관찰이 결합된 관찰자-대상의 파동 함수를 두 개 이상의 비상호작용 가지로 이루어진 양자 중첩 상태로 바꾼다는 것이다.

따라서 측정이나 관찰, 또는 상관관계를 유발하는 상호작용은 시스템을 상대적 상태 집합으로 분리한다. 여기서 상대적 상태의 각 집합은 전체 파동 함수의 가지를 형성하며, 그 자체 내에서 일관성이 있고, 모든 미래의 측정(여러 관찰자에 의한 측정 포함)이 이 일관성을 확인할 것이다.

에버렛은 관측자-대상 시스템이 관측에 의해 분리되고, 각 분리는 관측의 상이하거나 다수의 가능한 결과에 대응한다고 언급했다. 이러한 분리는 가지가 뻗어나가는 나무를 생성하는데, 각 가지는 서로에 대한 모든 상태들의 집합이다. 브라이스 드윗(Bryce DeWitt)은 다세계 해석이라고 부르는 일련의 출판물을 통해 에버렛의 연구를 대중화했다. 드윗은 분리 과정에 초점을 맞춰, 일관된 역사인 그 나무의 단일 가지를 묘사하는 "세계"라는 용어를 도입했다. 어떤 가지 내의 모든 관측이나 측정은 그 자체 내에서 일관성을 유지한다.[4][1]

에버렛의 이론은 닐스 보어를 중심으로 하는 코펜하겐 해석과는 다른 새로운 해석이 였다. 에버렛의 이론에 따르면, 양자 얽힘에 의해 상관된 다수의 가지를 '''상대 상태'''로 파동 함수에 기술하고 있으며, 그 가지들은 서로 간섭하지 않은 채 항상 공존하고 있다.

관측자 중 하나의 가지의 주관에서는, 그것과 상관된 가지만이 관측 가능한 세계이며, 상관되지 않은 다른 가지는 관측할 수 없다.

그 후 에버렛의 해석은 ‘여러 마음 해석’으로 발전하기도 했다. 이 개념은 1970년 디터 체Dieter Zehde)에 의해 처음 제시되었고, 데이비드 앨버트David Z. Albert영어)와 배리 로어Barry Loewer영어)가 ‘여러 마음 해석’이란 용어를 처음 사용하였다. 또한 다세계 해석은 머리 겔만과 제임스 하틀James Hartle영어)에 의해 ‘여러 역사 해석’으로 발전하기도 하였으며, 최근에는 데이비드 도이치가 자신의 양자 컴퓨터에 관한 이론에서 다세계 해석의 개념을 적용하면서 다시금 많은 지지를 얻고 있다.

결풀림을 이용해 양자역학을 이해하려는 시도에는 많은 발전이 있었으며, 대중적으로도 널리 알려졌다.[138][139][140] 다세계 해석은 물리학과 철학의 수많은 다우주 가설 중 하나로, 현재는 코펜하겐 해석과 함께 양자역학의 주류 해석들 가운데 하나로 자리 잡고 있다.

2. 2. 다양한 해석의 발전

다세계 해석은 1957년 휴 에버렛 3세가 '상대적 상태' 개념을 창안하면서 시작되었으며,[133] 이후 브라이스 디윗이 1960년대와 1970년대에 '다세계'라는 용어로 바꾸면서 널리 알려지게 되었다.[134][135][136][137] 양자역학의 기초가 확립된 지 약 30년 후인 1954년 휴 에버렛 3세가 이 해석을 처음 고안하였다. 1957년 프리스턴 대학교 수학과 학생이었던 에버렛은 박사 학위 논문으로 이 해석을 제시하였다. 1955년 에버렛은 프리스턴 대학교 명예 교수였던 존 휠러를 지도 교수로 변경한 후 세계의 파동 함수 이론을 주제로 졸업 논문을 작성하기 시작했다. 1956년 1월, 에버렛은 다세계 해석에서 유도된 수학적 결과를 정리하여 휠러에게 제출했다. 휠러는 에버렛의 논문을 높이 평가하여 그해 5월, 코펜하겐의 닐스 보어를 방문했으나 긍정적인 반응을 얻지 못했다. 존 휠러는 에버렛에게 논문 수정을 권고했고, 1957년 3월 에버렛은 수정된 논문을 제출하여 4월에 심사를 통과했다. 이 논문은 7월 《현대 물리학 리뷰》(Review of Modern Physics영어)에 〈양자역학의 상대 상태 공식화〉라는 제목으로 게재되었다.[133] (원래 에버렛은 양자 얽힘을 설명하기 위해 연관적 해석으로 제목을 지었으나 휠러가 상대 상태로 고치도록 했다.) 그러나 당시 에버렛의 논문은 큰 주목을 받지 못했다.

약 10년 후, 브라이스 디윗에 의해 '상대 상태 공식화' 또는 '세계 파동 함수' 대신 '다세계 해석'이라는 이름으로 바뀌면서 많은 사람들의 지지를 얻게 되었다. 디윗은 대학원생 닐 그레엄의 아이디어와 휴 에버렛이 개발한 수학을 바탕으로 에버렛의 해석을 발전시켰다. 디윗은 에버렛의 아이디어를 소개하는 여러 논문을 발표했고, 1970년에는 《피직스 투데이》(Physics Today영어)에 이 내용을 소개해 물리학자들의 관심을 끌었다.[135]

이후 에버렛의 해석은 '여러 마음 해석'으로 발전했다. 이 개념은 1970년 디터 체(Dieter Zehde)가 처음 제시했고, 데이비드 앨버트(David Z. Albert영어)와 배리 로어(Barry Loewer영어)가 '여러 마음 해석'이라는 용어를 처음 사용했다. 또한 머리 겔만과 제임스 하틀(James Hartle영어)은 '여러 역사 해석'을 제안했으며, 데이비드 도이치는 양자 컴퓨터 이론에 다세계 해석 개념을 적용하여 다시금 주목받게 했다.

결풀림(결잃음)을 이용해 양자역학을 이해하려는 시도가 발전하면서 다세계 해석은 대중적으로도 널리 알려지게 되었다.[138][139][140] 다세계 해석은 물리학과 철학의 수많은 다우주 가설 중 하나이며, 현재 코펜하겐 해석과 함께 양자역학의 주요 해석 중 하나로 자리 잡고 있다.

2. 3. 한국의 수용과 논의

한국에서는 다세계 해석이 과학철학계와 과학소설(SF) 커뮤니티를 중심으로 논의되고 있다. 일부 물리학자들은 다세계 해석의 철학적 함의와 실험적 검증 가능성에 대해 연구하고 있으며, 특히 진보 진영에서는 다세계 해석이 기존의 결정론적 세계관을 넘어 다양한 가능성을 열어둔다는 점을 긍정적으로 평가하기도 한다.

다세계 해석은 양자 중력 이론, 양자 우주론에서 지지를 얻었는데, 이들은 미시적인 영역이 아니라 시공간의 대국적인 행동에 관심이 있기 때문이다.[116] 21세기에 들어서면 다세계 해석은 코펜하겐 해석에 이어 인기를 얻게 되었다.[117] (전문 분야를 제한하지 않는 모든 영역의 물리학자를 대상으로 하면 코펜하겐 해석이 압도적으로 지지를 받고 있다.[117])

3. 양자역학 해석의 필요성

토머스 영의 이중 슬릿 실험은 빛과 전자가 파동성과 입자성을 동시에 가짐을 보여주었다. 이 실험을 통해 빛알이 파동성을 가지는 물질임을 증명하였다. 그러나 그 이후 아인슈타인이 금속에 빛을 쏘아 빛이 금속 안의 전자를 튕겨내는 광전 효과를 통해 빛이 입자의 성질을 가짐을 증명해내면서 빛은 파동의 성질과 입자의 성질을 동시에 가지게 되었다. 나아가, 루이 드 브로이는 빛 뿐만 아니라 전자도 파동의 성질을 가진다는 사실을 발견하였고, 전자에서도 빛에서와 같이 이중 슬릿 실험에서의 간섭무늬가 발생한다는 것이 밝혀지면서 이 세계의 모든 물질이 입자성과 파동성이 동시에 나타날 수 있다는 사실이 확인되었다. 이로써 양립할 수 없을 것이라 여겨지던 입자의 입자성과 파동성이 양립가능함이 증명되어 기존의 물리학적 상식은 뒤흔들리고 양자역학이 탄생하였다.

양자역학은 고전역학과 달리 확률론적 입장을 취한다. 정확한 수학 공식만 알고 있으면 미래를 예측할 수 있다고 본 고전역학과 달리, 양자역학에서는 현재 상태에 대해 정확하게 알더라도 미래에 일어나는 사실을 정확하게 예측하는 것은 불가능하기 때문에 양자역학에서 이 난점을 설명하는 해석이 필요해졌다.

3. 1. 코펜하겐 해석과 한계

닐스 보어가 1927년 제시한 코펜하겐 해석은 양자역학의 가장 통상적인 해석이다. 이 해석에 따르면, 관찰자 혹은 관측자와의 상호작용이 파동함수의 붕괴를 초래하고 그에 따라 다양한 가능성의 결과들은 한 가지의 결과로 오그라든다고 설명한다. 보어와 연구자들은 전자가 ‘관측되기 전에는 파동이며 관측되면 입자가 되며 이로부터 이중 슬릿 실험에서의 간섭 무늬 현상을 설명할 수 있다는 것’이었다. 그리고 이 파동의 본질은 ‘입자가 어디서 관측될 지의 확률의 파동’이다.

프린스턴 대학교의 존 폰 노이만이 제안한 ‘프린스턴 해석’, 알베르트 아인슈타인을 중심으로 통계적으로 해석하는 것을 제안한 앙상블 해석과 숨은 변수 이론 등도 있다.

에르빈 슈뢰딩거는 슈뢰딩거의 고양이 사고 실험을 통해 코펜하겐 해석의 확률적 해석에 반발했다. 슈뢰딩거의 고양이 사고 실험은 미시입자가 아닌 거시입자인 고양이를 코펜하겐 해석의 논리에 도입함으로써 양자론, 코펜하겐 해석의 확률적 해석이 완전하지 않다는 모순점을 지적한다.

이중 슬릿 실험이 관측 행위를 배제하고, 전자의 거동방식에 대한 일정한 가능성의 추론만이 가능한데다 ‘관측하지 않는 존재’에 대해 단언하는 것은 불가능하다는 점에서 코펜하겐 해석은 타당성을 확보할 수 없다.

4. 다세계 해석의 주요 내용

양자역학에서, 양자 상태의 시간 변화는 슈뢰딩거 방정식과 파동 함수 붕괴(wavefunction collapse)라는 두 과정을 따른다. 다세계 해석에 따르면, 후자는 관찰자를 계에 포함시키지 않았을 때에만 적용되는, 근사적인 법칙이다. 만약 관찰자를 계의 일부로 포함시킨 경우, 관찰자를 포함한 전체 계의 상태 오직 슈뢰딩거 방정식을 따라 결정론적으로 변화한다.

일반적으로, 양자역학적 상태는 여러 준고전적 상태들의 중첩으로 나타내어진다. 다세계 해석에 따르면, 이러한 양자역학적 상태는 서로 다른 세계에 존재하는 준고전적 상태들을 나타낸다. 즉, 하나의 양자역학적 상태는 여러 세계들에 존재하는 고전적 상태들의 총체로 구성된다. 구체적으로, 이러한 여러 개의 준고전적 우주들은 양자 얽힘과 결풀림이라는 현상들로부터 발생한다.

'결풀림의 조건은 관찰로, 관찰자와 관찰 대상이 세트로 있을 때 일어나며 이 세트는 여러 세계로 나뉘어 서로 간섭할 수 없는 상태가 된다. 주의할 점은 세계가 관찰에 의해 갈라지는 것이 아니라 모든 가능성이 함께 존재하는 것으로, 세계는 처음부터 갈라져 있었고 현재 존재하는 관찰 대상이나 관찰자 역시 가능성의 일부로 봐야 한다는 점이다.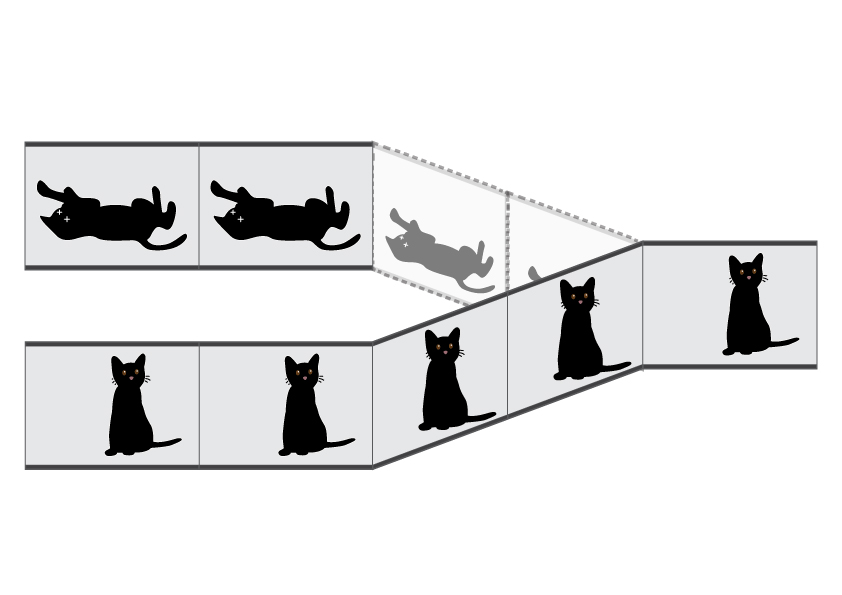

코펜하겐 해석에서는 산 고양이와 죽은 고양이의 상태가 중첩되어 있다가 관찰자의 관찰 행위로 오그라듦이 일어나 한 가지 상태만 현실화된다.


다세계 해석에서는 산 고양이, 죽은 고양이는 서로 다른 세계에서 현실화 된다. 이 다른 두 세계의 가중치를 비교할 수 없으며 두 세계는 상호작용할 수 없다.


1957년 박사 학위 논문에서 에버렛(Hugh Everett III)은 고립된 양자계를 분석하기 위해 외부 관찰에 의존하는 대신, 폴 디랙(Paul Dirac), 존 폰 노이만(John von Neumann) 등이 개발한 수학적 틀 내에서 관찰자뿐 아니라 대상 물체도 순수한 물리계로 수학적으로 모델링할 수 있으며, 파동 함수 붕괴라는 임의적인(ad hoc) 메커니즘을 완전히 버릴 수 있다고 제안했다.[4][1]

다세계 해석(MWI)은 양자 측정 과정에서 관찰자 의존적인 역할을 제거하고, 양자 붕괴 대신 확립된 양자 탈결맞춤 메커니즘을 사용한다.[16] 관찰자의 역할이 EPR 역설과 폰 노이만의 "경계 문제"와 같은 모든 "양자 역설"의 핵심에 있기 때문에, 이것은 이러한 역설을 해결하는 더 명확하고 쉬운 접근 방식을 제공한다.[5]

코펜하겐 해석은 양자 역학에서 설명하는 것 이상의 고전적인 영역의 존재를 요구하기 때문에, 우주론 연구에는 부적절하다는 비판을 받았다.[52] 에버렛이 우주론적 문제에서 영감을 받았다는 증거는 없지만,[70] 그는 양자 역학을 전체 우주에 적용할 수 있도록 명시적인 목표를 가지고 그의 이론을 개발하여 새로운 현상의 발견을 촉진하고자 했다.[5] 이러한 희망은 후대의 양자 우주론 발전에서 실현되었다.[17]

다세계 해석은 실재론적, 결정론적이며 국소적인 이론이다. 이는 양자 이론의 결정론적이고 국소적인 방정식에서 비결정론적이고 비국소적인 파동 함수 붕괴를 제거함으로써 달성된다.[3]

다세계 해석(다른 광범위한 다중우주 이론과 마찬가지로)은 인류 원리에 대한 맥락을 제공하며, 이는 미세 조정된 우주에 대한 설명을 제공할 수 있다.[18][19]

다세계 해석은 선형성 양자 역학에 크게 의존하며, 이는 중첩 원리를 뒷받침한다. 최종 만물 이론이 파동 함수에 대해 비선형적이라면 다세계 해석은 무효이다.[6][1][5][7][8] 모든 양자장 이론은 선형적이며 다세계 해석과 호환되며, 에버렛은 이를 다세계 해석의 동기로 강조했다.[5] 양자 중력 또는 끈 이론이 이러한 측면에서 비선형적일 수 있지만,[79] 아직 이에 대한 증거는 없다.[20][21]

다른 양자역학 해석과 마찬가지로, 다세계 해석은 이중 슬릿 실험으로 설명할 수 있는 현상에 의해 동기가 부여된다. 빛의 입자(혹은 다른 어떤 것이든)가 이중 슬릿을 통과할 때, 빛의 파동적 거동을 가정하는 계산을 사용하여 입자가 관측될 가능성이 있는 위치를 확인할 수 있다. 그러나 이 실험에서 입자가 관측될 때, 입자는 비국재된 파동이 아니라 입자(즉, 특정 위치에 있는)로 나타난다.

코펜하겐 해석의 일부 버전에서는 불확정적인 양자계가 확률적으로 하나의 결정적인 결과로 붕괴되거나 선택되는 "붕괴" 과정을 제안하여 관측 현상을 "설명"했다. 파동 함수 붕괴는 인위적이고 ''임시방편''으로 널리 여겨졌다.[22] 따라서 측정의 행위를 더 근본적인 물리적 원리로 이해할 수 있는 대안적인 해석이 바람직하다고 여겨졌다.

에버렛의 박사 학위 논문은 그러한 해석을 제공했다. 그는 관측 대상(입자와 같은 "관측된" 계)을 관측하는 주체("관측자" 또는 측정 장치)와 같은 복합 시스템의 경우, 관측자 또는 관측 대상이 잘 정의된 상태를 갖는다는 주장은 의미가 없다고 주장했다. 현대적인 용어로, 관측자와 관측 대상은 얽혀 있습니다. 우리는 한쪽의 상태를 다른 쪽에 대해서만 지정할 수 있다. 즉, 관측자와 관측 대상의 상태는 관측이 이루어진 ''후''에 상관관계를 갖는다. 이는 에버렛이 단일적이고 결정론적인 역학(즉, 파동 함수 붕괴를 가정하지 않고)으로부터 ''상태의 상대성''이라는 개념을 유도하게 했다.

에버렛은 단일적이고 결정론적인 역학만으로도 관측이 이루어진 후 결합된 주체-대상 파동 함수의 양자 중첩의 각 요소에 두 개의 "상대적 상태"가 포함되어 있음을 알아차렸다. "붕괴된" 대상 상태와 같은 붕괴된 결과를 관측한 관측자와 관련된 상태이다. 관측자가 보는 것과 대상의 상태는 측정 또는 관측 행위에 의해 상관관계를 갖게 된다. 상대적인 주체-대상 상태 각 쌍의 후속 진화는 다른 요소의 존재 여부와 완전히 무관하게 진행된다. 마치 파동 함수 붕괴가 발생한 것처럼 보인다.[1] 이는 나중 관측이 항상 이전 관측과 일치한다는 결과를 낳는다. 따라서 대상의 파동 함수 붕괴의 ''겉보기''는 단일적이고 결정론적인 이론 자체에서 나타났다. (이것은 양자 이론에 대한 아인슈타인의 초기 비판, 즉 이론이 관측 가능한 것을 정의해야 하며, 관측 가능한 것이 이론을 정의해서는 안 된다는 비판에 대한 답변이었습니다.) 파동 함수가 붕괴된 것처럼 ''보이기'' 때문에, 에버렛은 파동 함수가 실제로 ''붕괴되었다''고 가정할 필요가 없다고 추론했다. 그리고 오컴의 면도날을 적용하여 그는 이론에서 파동 함수 붕괴의 가정을 제거했다.[1]

양자역학에서 파동함수는 슈뢰딩거 방정식을 따르며, 결정론적인 시간적 진화를 한다. 표준 해석인 코펜하겐 해석에서는 관측에 의해 파동함수가 수축함으로써 확률적인 결과가 나타난다. 파동함수의 수축은 슈뢰딩거 방정식을 따르지 않는다.

반면 다세계 해석에서는 파동함수의 수축은 일어나지 않고, 항상 슈뢰딩거 방정식이 성립한다고 생각한다. 슈뢰딩거 방정식의 시간적 진화에 따라 다양한 중첩 상태가 발생하지만, 다입자의 상호작용에 의해 각 상태는 간섭성을 상실하고(결어긋남), 여러 세계로 분기한다고 생각한다.

다세계 해석에서는 파동함수를 실재하는 것으로 간주하며, 따라서 파동함수가 보여주는 중첩 상태도 서로 다른 세계로서 실재한다고 생각한다. 이와 같이 다세계 해석은 실재론의 입장인 반면, 코펜하겐 해석은 관측되지 않는 배경의 존재에 대해서는 언급하지 않고, 관측 결과를 예측할 수 있으면 된다는 실증주의이다.[97]

슈뢰딩거 방정식의 시간적 진화를 개괄하는 관점에서 보면, 분기하는 모든 세계의 중첩에 해당하는 양자 상태는 초기 상태로부터 유일하게 결정되므로, 다세계 해석은 결정론적이다.[98] 반면, 중첩 상태에 대해 측정을 하면 서로 다른 측정 결과를 얻는 세계로 분기하므로, 각 세계의 관측자에게는 비결정론적이다.[99] 다세계 해석에서의 보른의 확률 규칙의 생각에는 몇 가지 유파가 있다.[100]

다세계 해석은 우주 전체가 순간적으로 분기한다는 것처럼 비국소적으로 기술할 수도 있고, 또는 세계의 분기를 광원추 내부에서만 진행되는 국소적인 과정으로 기술할 수도 있다.[101][102] 후자의 생각에 따르면, EPR 사고 실험에서 발생하는 것과 같은 비국소성을 배제할 수 있다.[101]

4. 1. 양자 얽힘과 결풀림(결잃음)

에르빈 슈뢰딩거는 입자들이 광자를 서로 연결시키는 과정에서 얽히게 됨을 발견하고 양자 얽힘이라는 용어를 만들었다. 슈뢰딩거는 1926년에 출간된 일련의 논문에서 n-입자계(n개의 입자로 구성된 계)의 양자 상태가 얽힐 수 있다는 것을 알았다. 그는 양자 얽힘에 대해 다음과 같이 표현했다.

양자 얽힘은 코펜하겐 해석의 모순을 해결하고 거시 세계 현상을 설명하는 데 기여한다. 코펜하겐 해석의 모호함은 파동함수의 붕괴에 있는데, 슈뢰딩거 방정식 어디에도 파동 함수의 붕괴를 암시하는 부분이 없고, 파동은 선형성을 가지기 때문에 최종 결과는 각 파동의 합이 된다. 따라서 파동 함수의 붕괴는 수학적으로 불가능하며, 각 파동의 합이 결과로 나타난다면 있을 수 있는 가능성들이 중첩되어 존재하는 셈이 된다. 코펜하겐 해석으로는 이중 슬릿 실험과 같은 미시 세계는 설명할 수 있지만, 슈뢰딩거의 고양이 사고 실험과 같은 거시 세계 현상은 설명하기 어렵다.

양자 얽힘은 관찰자와 관찰 대상을 한 세트로 보아, 관찰자에게도 양자역학 원리를 적용해야 한다는 개념이다. 이때 파동의 중첩은 관찰자와 관찰 대상의 파동의 양자 얽힘에 의한 것이며, 있을 수 있는 가능성들은 서로 합쳐지는 것이 아니라 여러 세계로 분리되어 독립적으로 실현된다.

양자 얽힘의 발생과 원리는 다음과 같다. 입자 1이 상태 |a\rangle, 상태 |b\rangle에 존재하고, 입자 2가 상태 |c\rangle, |d\rangle에 존재한다고 가정했을 때, 상태 |a\rangle\otimes|b\rangle를 '곱 상태'라고 하며, |a\rangle\otimes|b\rangle+|c\rangle\otimes|d\rangle는 이러한 곱 상태의 결합, 즉 ‘얽힌 상태’라고 한다. 곱 상태에서는 입자 1의 위치를 명확하게 표현할 수 있지만, '얽힌 상태'는 중첩을 이루고 있기 때문에 위치에 명확한 성질을 부여할 수 없다. 입자 1과 입자 2는 얽혀있기 때문에 각각의 위치는 다른 입자를 참조하지 않고서는 특징지을 수 없다. 즉, 양자계가 하나 이상의 입자를 갖게 되면 중첩 원리는 양자 얽힘 현상을 만들어내고, 두 입자는 거리와 상관없이 한 입자에서 일어나는 것이 다른 입자에도 즉각적으로 일어날 수 있어 공간적 분리라는 개념은 사라지게 된다.

이중 슬릿 실험에서 전자가 어느 쪽 슬릿을 통과했는지를 확인하는 장치를 달면 간섭 무늬는 사라지고 두 슬릿의 결과를 더한 결과가 스크린에 나타난다. 이런 경우 확률 파동은 '결풀림 상태'에 있다고 말한다. 결풀림(결잃음) 상태가 되면 두 파동은 독립적으로 진행하고 중첩은 더 이상 일어나지 않는다. 즉, 한 세트가 하나의 결과만을 얻는 것을 설명하는 개념이 결풀림이다.

4. 2. 다중 우주론

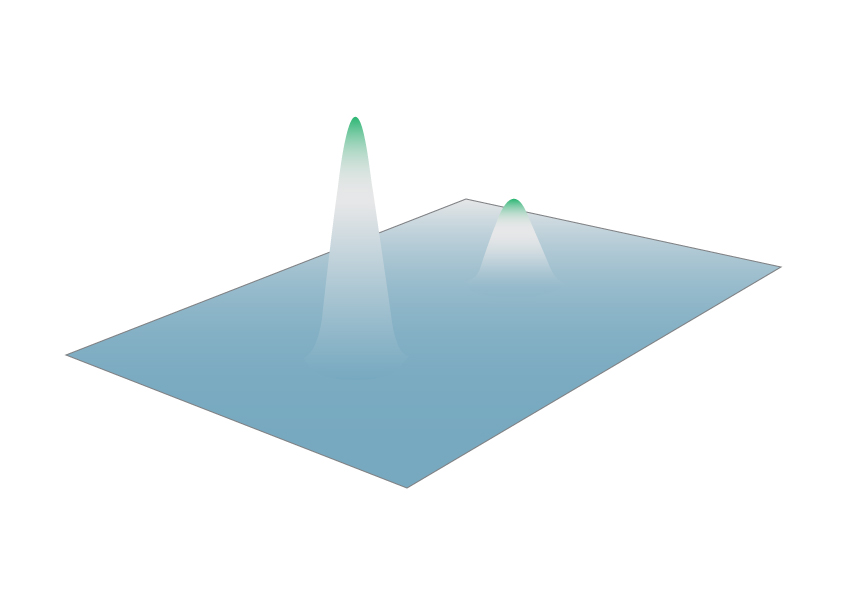
다중 우주론이란 우리가 관찰할 수 없는 또 다른 우주가 존재한다는 주장이다. 양자 얽힘과 결풀림의 원리는 다세계 해석의 다중 우주 개념을 설명하는데, 관측자와 관측 장비, 그리고 그 외의 모든 것들은 관측을 기점으로 둘로 분리되어 두 개의 실체, 즉 두 개의 우주가 공존하게 된다. 관측자가 x개의 피크로 이루어진 확률 파동을 관측하면 ‘x개로 갈라진 세계'가 나타나고, 각각의 세계에는 각기 다른 결과를 얻은 관측 장비와 관측자가 존재한다.

급팽창 이론, 끈 이론 등과 함께 다세계 해석은 다중 우주론에 큰 영향을 미쳤다. 다세계 해석은 확률적으로 가능한 모든 세계를 인정하며, 평행 우주 개념을 포함한다. 그러나 다중 우주와 다세계 해석은 같은 개념이 아니며, 다세계 해석은 좁은 의미의 다중 우주를 지칭한다. 실제로, 다른 과학 이론이 설명하는 다중 우주는 단순한 평행 우주의 개념을 포함하는 것뿐만 아니라 현재 우주와 물리법칙이 전혀 다른 우주, 멀리 있어서 단순히 관찰이 불가능한 공간에 존재하는 우주 등이 있다.

다세계 해석은 실재론적, 결정론적이며 국소적인 이론이다.[3] 이는 양자 이론의 결정론적이고 국소적인 방정식에서 비결정론적이고 비국소적인 파동 함수 붕괴를 제거함으로써 달성된다.[3] 다세계 해석은 인류 원리에 대한 맥락을 제공하며, 이는 미세 조정된 우주에 대한 설명을 제공할 수 있다.[18][19]

양자역학을 확장한 양자장론에서도 다세계 해석은 마찬가지로 성립한다.[119] 아직 미완성이지만 양자중력이론에도 다세계 해석이 사용되고 있다.[120] 2011년에 야무라 야스노리, 라파엘 부소, 레오나르도 수사킨드는 우주론적인 멀티버스와 양자역학의 다세계는 동등한 것이며 같은 현상의 다른 측면이라는 설을 발표했다.[121][122]

4. 3. 결정론 문제

양자역학이 등장하기 전, 고전역학의 시대는 결정론이 지배적이었다. 거시세계에서 일어나는 모든 물리적 현상이 뉴턴 운동 법칙 등으로 예측 가능했기 때문이다. 이 때문에 라플라스의 악마라는 개념이 등장하기도 했다. 그러나 고전역학의 법칙이 미시세계에서는 통용되지 않는다는 사실이 드러나자 결정론과 비결정론의 문제는 다시 논란이 되었다.

다세계 해석에서 결정론의 문제는 미래의 범위에 따라 달라진다. 모든 세계를 고려의 범주에 넣었을 때 미래는 결정론적이다. 현재 상황에서 가능한 모든 세계가 이미 존재하므로 세계가 결정되어 있다고 생각할 수 있는 것이다. 그러나 하나의 세계만을 두고 보았을 때는 비결정론적이라고 볼 수 있다. 하나의 세계에서는 어떤 법칙도 없이 단지 확률적으로 하나의 세계가 선택되기 때문에 어떤 미래가 존재할지 결정할 수 없기 때문이다. 그러나 하나의 세계에서도 세계가 선택될 확률만은 정해져 있다는 점에서 확률론적 결정론이 주장되기도 한다.[34] 다세계 해석이 등장한 이후로, 물리학자들은 다세계 해석에서 확률의 역할에 대해 혼란을 느껴왔으며, 이 질문에는 ''결맞지 않음 문제(incoherence problem)''와 ''정량적 문제(quantitative problem)''의 두가지 측면이 있다고 Wallace는 설명한다. 에버렛은 이러한 질문들에 답하려고 시도했다.[4] 정량적 문제를 해결하기 위해, 에버렛은 파동 함수의 가지들에 대한 측정이 가져야 할 속성을 기반으로 보른 법칙의 도출을 제안했다.[4] 그의 도출은 동기가 부족한 가정에 의존한다는 비판을 받았다.[26] 그 이후로 다세계 해석의 틀 안에서 보른 법칙을 도출하는 여러 다른 시도들이 제안되었다. 이러한 시도들이 성공적이었는지에 대한 의견 일치는 없다.[27][28][29]

5. 문제점

=== 확률의 해석 문제 ===

양자역학은 슈뢰딩거 방정식에 따라 확률론적 입장을 취하며, 다세계 해석에서는 모든 가능한 세계가 실현되므로 한 세계에서의 확률의 의미가 모호해진다. 이는 확률의 높고 낮음을 논할 수 없다는 모순을 야기한다.

다세계 해석이 등장한 이후, 물리학자들은 다세계 해석에서 확률의 역할에 대해 혼란을 느껴왔다. Wallace의 설명처럼, 이 질문에는 두 가지 측면이 있다.[34] 하나는 ''결맞지 않음 문제(incoherence problem)''로, 어떤 세계에서는 확실히 발생하는 결과에 왜 확률을 할당해야 하는가를 묻는 것이고, 다른 하나는 ''정량적 문제(quantitative problem)''로, 왜 확률이 보른 법칙에 의해 주어져야 하는가를 묻는 것이다.

에버렛은 다세계 해석을 소개한 논문에서 이러한 질문들에 답하려고 시도했다. 결맞지 않음 문제를 해결하기 위해, 그는 양자계에 대해 일련의 측정을 하는 관찰자는 일반적으로 자신의 기억에 무작위적인 결과들의 순서를 가지게 되며, 이것이 측정 과정을 설명하기 위해 확률을 사용하는 것을 정당화한다고 주장했다.[4] 정량적 문제를 해결하기 위해, 에버렛은 파동 함수의 가지들에 대한 측정이 가져야 할 속성을 기반으로 보른 법칙의 도출을 제안했다.[4] 그의 도출은 동기가 부족한 가정에 의존한다는 비판을 받았다.[26] 그 이후로 다세계 해석의 틀 안에서 보른 법칙을 도출하는 여러 다른 시도들이 제안되었으나, 이러한 시도들이 성공적이었는지에 대한 의견 일치는 없다.[27][28][29]

드윗(Bryce DeWitt)과 그레이엄(Graham)[1], 그리고 파히(Farhi) 등[30]은 확률의 빈도주의적 해석에 기반한 붕괴 규칙(Born rule)의 유도를 제안했다. 그들은 셀 수 없이 많은(비가산 집합) 측정의 극한에서 어떤 세계도 붕괴 규칙이 주는 확률과 일치하지 않는 상대 빈도를 갖지 않을 것이라고 보이려고 시도했지만, 이러한 유도는 수학적으로 잘못된 것으로 판명되었다.[31][32]

데이비드 도이치(1999)는 보른 법칙에 대한 결정 이론적 유도를 제시했으며,[33] 월러스[34][35][36][37]와 손더스[38][39]에 의해 개선되었다. 그들은 양자 도박에 참여하는 행위자를 고려한다. 행위자는 양자계를 측정하고 그 결과로 가지가 갈라지며, 각 행위자의 미래 자아는 측정 결과에 따라 보상을 받는다. 행위자는 결정 이론을 사용하여 그러한 도박에 참여하기 위해 지불할 가격을 평가하고, 그 가격은 보른 법칙에 따라 가중치가 부여된 보상의 효용으로 주어진다는 결론을 내린다. 이러한 주장은 여전히 매우 논란의 여지가 있지만, 긍정적인 평가도 있다. 일부 이론 물리학자들은 이것을 평행 우주에 대한 주장을 뒷받침하는 것으로 받아들였다.[40] 예를 들어, 에버렛 해석에 관한 2007년 회의에 대한 ''뉴사이언티스트'' 기사에서 물리학자 앤디 알브레히트는 "이 연구는 과학 역사상 가장 중요한 발전 중 하나로 기록될 것"이라고 말했다.[40] 반면, 같은 회의에 참석한 철학자 휴 프라이스는 도이치-월러스-손더스 접근 방식에 근본적인 결함이 있다고 생각했다.[42]

2005년, 주렉[43]은 얽힌 상태의 대칭성을 기반으로 보른 규칙을 유도했다. 슐로스하우어와 파인은 주렉의 유도가 엄밀하지 않다고 주장하는데, 그 이유는 확률이 무엇인지 정의하지 않았고 확률의 작동 방식에 대한 몇 가지 언급되지 않은 가정을 하고 있기 때문이다.[44]

2016년, 찰스 세번스와 션 M. 캐롤은 레브 바이드만의 연구를 바탕으로,[45] 자기 위치 불확정성에 기반한 유사한 접근 방식을 제안했다.[46] 이 접근 방식에서, 결어긋남은 관찰자의 여러 개의 동일한 복사본을 생성하며, 이들은 보른 규칙을 사용하여 서로 다른 가지에 있을 확률을 할당할 수 있다. 세번스-캐롤 접근 방식은 에이드리언 켄트에 의해 비판을 받았으며,[47] 바이드만 또한 이를 만족스럽지 않게 여긴다.[48]

2021년, 사이먼 손더스(Simon Saunders)는 분기 계산을 통해 보른 규칙을 유도하였다. 이 방법의 핵심은 모든 분기가 같은 크기 또는 2-노름을 갖도록 분기를 정의하는 것이다. 이렇게 정의된 분기 수의 비율은 보른 규칙에 따라 측정의 다양한 결과에 대한 확률을 제공한다.[49]

=== 관찰 불가능 ===

다세계 해석에 따르면, 결풀림에 의해 다세계에 살고 있는 모든 존재들은 오직 자신이 속한 단 하나의 세계만을 인식한다.[24][25][112][123][124][125][126][127][128][129] 만약 한 개의 가능성밖에 인식 할 수 없다면 결국 다세계 해석이 옳은 해석이라 해도 실제로 다세계를 관찰해 이 해석의 정당성을 확인하는 것은 불가능하다. 과학 이론이 이론으로 인정받기 위해선 누구나 인정할 수 있는 수학적으로 옳고 정량적인 증명이 필요하다. 그러나 관찰 이외에 다세계의 존재를 증명할 수 있는 방법이 아직 없으며, 그것이 불가능하므로 이는 결국 이 해석이 옳은지 증명할 방법이 없다는 뜻이기도 하다. 이것이 다세계 해석이 이론이 아닌 해석으로 남아 있는 이유이기도 하다.

다세계 해석에서는 모든 가능성이 현실화되어 나뉘면 상호관련성을 잃게 된다. 이러한 이유로 한 세계에 존재하는 다른 세계의 존재 유무를 확인할 수 없다.


1985년, 데이비드 도이치는 다세계 해석 대 코펜하겐 해석을 검증하기 위한 위그너의 친구 사고 실험의 변형을 제안했다.[24] 이 실험은 고립된 실험실에서 양자계를 측정하는 실험자(위그너의 친구)와 첫 번째 실험자를 측정하는 또 다른 실험자(위그너)로 구성된다. 다세계 해석에 따르면, 첫 번째 실험자는 한 가지 결과를 보는 거시적 중첩 상태가 되고, 다른 가지에서는 다른 결과를 보게 된다. 그러면 두 번째 실험자가 이 두 가지 가지에 간섭하여 실제로 거시적 중첩 상태인지, 아니면 코펜하겐 해석에서 예측한 대로 단일 가지로 붕괴되었는지 검증할 수 있다. 그 이후로 록우드, 바이드만 등이 비슷한 제안을 했다.[25] 이러한 제안들은 거시적 물체를 일관된 중첩 상태에 놓고 간섭시키는 것을 요구하는데, 이는 현재 실험 기술로는 불가능하다.

일부 과학자들은 다세계 해석(MWI)의 몇몇 측면이 반증 불가능하며 따라서 비과학적이라고 생각하는데, 그 이유는 여러 평행 우주들이 서로 정보를 주고받을 수 없다는 점, 즉 상호작용이 불가능하기 때문이다.[76][77]

빅터 J. 스텐거(Victor J. Stenger)는 머레이 겔만(Murray Gell-Mann)의 출판된 저서가 동시에 존재하는 평행 우주의 존재를 명시적으로 부정한다고 언급했다.[78] 겔만은 제임스 하틀(James Hartle)과 공동 연구를 통해 보다 "받아들이기 쉬운" 포스트 에버렛 양자역학을 개발하려고 노력했다. 스텐거는 대부분의 물리학자들이 다세계 해석을 너무 극단적이라고 생각하지만, "분석 대상 시스템 내부에 관찰자의 위치를 찾고 파동 함수 붕괴라는 골칫거리 개념을 제거하는 데 장점이 있다"고 말하는 것이 타당하다고 생각했다.

로저 펜로즈(Roger Penrose)는 이 아이디어가 중력을 고려하지 않는 지나치게 단순화된 양자역학 버전에 기반을 두고 있기 때문에 결함이 있다고 주장한다. 그의 견해로는, 우주에 기존의 양자역학을 적용하면 다세계 해석이 의미하지만, 성공적인 양자 중력 이론이 부족하다는 점이 기존 양자역학의 주장되는 보편성을 부정한다.[79] 펜로즈에 따르면, "중력이 관련될 때는 규칙이 바뀌어야 한다"고 한다. 그는 또한 중력이 현실을 고정하는 데 도움이 되고 "흐릿한" 사건은 허용 가능한 결과가 하나뿐이라고 주장한다.

과학철학자 로버트 P. 크리즈(Robert P. Crease)는 다세계 해석이 상상할 수 있는 모든 일이 일어난다는 것을 의미하기 때문에 "과학 역사상 가장 있을 법하지 않고 비현실적인 아이디어 중 하나"라고 말한다.[80] 과학 저술가 필립 볼(Philip Ball)은 다세계 해석의 함의를 환상이라고 부르는데, 그 이유는 "과학 방정식이나 기호 논리의 외관 아래에, 그것들은 상상의 행위, '단지 가정'"이기 때문이다.

이론 물리학자 게라르뒤스 '트 호프트(Gerard 't Hooft) 또한 이 아이디어를 일축한다. "나는 우리가 다세계 해석과 함께 살아야 한다고 생각하지 않는다. 사실, 그것은 단지 물리학자들이 그중 어느 것이 실제인지 결정할 수 없었기 때문에 존재하는 엄청난 수의 평행 세계가 될 것이다."[82]

애셔 페레스(Asher Peres)는 다세계 해석의 공개적인 비판자였다. 그의 1993년 교과서의 한 부분에는 "에버렛 해석 및 기타 기이한 이론들"이라는 제목이 붙어 있었다. 페레스는 다양한 다세계 해석이 단순히 붕괴 가정의 임의성 또는 모호성을 "세계"가 언제 분리된 것으로 간주될 수 있는지에 대한 질문으로 전환시키며, 그러한 분리에 대한 객관적인 기준을 실제로 공식화할 수 없다고 주장했다.[83]

시미즈 아키라(清水明)는 다세계 해석이나 무모순 역사 해석에서는 간섭항이 사라지는 것이 대전제가 되어 있지만, 결풀림에서는 간섭항이 완전히 사라지는 것을 보여주지 못하고 있다는 큰 문제점이 남아 있다고 지적하고 있다.[112]

다세계 해석에 대한 흔한 비판은 세계의 분기(分岐)에 관한 것으로, 관측할 수 없는 수많은 세계를 생각하는 것 자체가 논리의 낭비라는 것이다. 그러한 입장에서는 무수한 세계가 존재하는 것은 “존재론적 낭비”[123]이며, 다세계 해석에 의한 상태의 수축의 배제는 그것에 상응하는 것이 아니다.[124]

우주론 연구자인 조지 엘리스(George Ellis)와 조셉 실크(Joseph Silk)는 양자역학의 다세계 이론은 멀티버스나 끈 이론과 마찬가지로 반증 가능성이 없다고 하며, 힐베르트(David Hilbert)의 “무한은 수학에서는 필수적이지만, 물질 세계에는 있을 수 없다”는 경종을 인용하고 있다.[125] 한편 데이비드 도이치(David Deutsch)는 다세계 해석을 실험적으로 검증할 수 있다고 주장하고 있다.[126]

양자 베이즈주의를 지지하는 물리학자 크리스토퍼 폭스(Christopher Fuchs)에 따르면, 다세계 해석은 완전히 무의미하며, 세계의 구조에 대한 통찰을 얻을 수 없다고 한다. 폭스는 관측에 의해 우주가 변하는 것은 새로운 세계가 창조되기 때문이 아니라, 관측에는 주변 환경과의 상호 작용이 필요하기 때문이라고 주장한다.[127]

중력에 의한 파동 함수 붕괴설(en)을 제창한 로저 펜로즈(Roger Penrose)는 다세계라는 설이 중력을 고려하지 않고, 너무 단순한 양자역학의 해석에 기초하고 있기 때문에 결함이 있다고 주장한다. 펜로즈는 “중력이 개입하면 규칙이 바뀐다. 중력은 현실을 고정시키기 때문에, 어떤 사건이라도 하나의 결말만 가능하다”고 말한다.[128][127] 전자와 원자와 분자 등은 극히 작기 때문에, 그 중력, 즉 중복된 상태를 유지하는 데 필요한 에너지량은 거의 무시할 수 있다. 표준적인 양자론에서처럼, 영원히 그 상태를 유지할 수 있다. 한편, 큰 물체의 경우에는 큰 중력장이 형성되는 것이 원인이 되어 중복 상태는 순식간에 사라진다고 펜로즈는 설명한다.[129]

=== 물리량 보존 문제 ===

다세계 해석에서는 세계가 분리되는 매 순간마다 새로운 세계가 만들어진다. 이 때, 물리적인 대상들이 각 세계마다 중복해서 생기기 때문에 분리되는 세계의 개수만큼 물질과 에너지도 증가하게 된다. 이는 상태 변화 이전과 이후에도 언제나 물리량이 같다는 물리학의 기본 법칙인 물리량 보존 법칙에 위반된다. 물론 하나의 세계에서 보면 물리량이 보존되지만, 그 기준을 어떻게 정할 것인지가 애매하다는 점 또한 문제다.[112]

=== 오컴의 면도날 ===

우리가 보지 못하는 수많은 세계에 대해 이야기하는 것은 오컴의 면도날 원칙에 위배된다.[123][124] 관찰할 때 세계가 분리된다면 관찰이 계속될 때마다 갈라짐과 분리가 반복되어 수많은, 혹은 무한의 세계가 실제로 생기게 되므로 이는 과학적 논리를 설명하기 위한 경제성에 맞지 않다. 그러나 봄 역학 입자의 궤적과 법칙의 존재론보다는 경제적이라는 주장이 있다.

=== 정체성 문제 ===

관찰자가 관찰을 통해 세계가 여러 개로 분리될 때, 어느 세계의 관찰자가 원래의 관찰자인지, 즉 관찰자 자신의 정체성에 대한 문제가 발생한다.[112] 분리되기 전 관찰자가 어느 세계에 존재하는지, 각 세계의 관찰자들의 합이 분리 이전의 관찰자와 동일한지, 아니면 각 세계의 관찰자들이 독립적인 개체로 존재하는지에 대한 명확한 경계가 정의되지 않았기 때문이다.[112] 이는 정량적인 이론에 대한 비판으로, 다세계 해석의 가장 큰 문제 중 하나로 지적된다.

5. 1. 확률의 해석 문제

양자역학은 슈뢰딩거 방정식에 따라 확률론적 입장을 취하며, 다세계 해석에서는 모든 가능한 세계가 실현되므로 한 세계에서의 확률의 의미가 모호해진다. 이는 확률의 높고 낮음을 논할 수 없다는 모순을 야기한다.

다세계 해석이 등장한 이후, 물리학자들은 다세계 해석에서 확률의 역할에 대해 혼란을 느껴왔다. Wallace의 설명처럼, 이 질문에는 두 가지 측면이 있다.[34] 하나는 ''결맞지 않음 문제(incoherence problem)''로, 어떤 세계에서는 확실히 발생하는 결과에 왜 확률을 할당해야 하는가를 묻는 것이고, 다른 하나는 ''정량적 문제(quantitative problem)''로, 왜 확률이 보른 법칙에 의해 주어져야 하는가를 묻는 것이다.

에버렛은 다세계 해석을 소개한 논문에서 이러한 질문들에 답하려고 시도했다. 결맞지 않음 문제를 해결하기 위해, 그는 양자계에 대해 일련의 측정을 하는 관찰자는 일반적으로 자신의 기억에 무작위적인 결과들의 순서를 가지게 되며, 이것이 측정 과정을 설명하기 위해 확률을 사용하는 것을 정당화한다고 주장했다.[4] 정량적 문제를 해결하기 위해, 에버렛은 파동 함수의 가지들에 대한 측정이 가져야 할 속성을 기반으로 보른 법칙의 도출을 제안했다.[4] 그의 도출은 동기가 부족한 가정에 의존한다는 비판을 받았다.[26] 그 이후로 다세계 해석의 틀 안에서 보른 법칙을 도출하는 여러 다른 시도들이 제안되었으나, 이러한 시도들이 성공적이었는지에 대한 의견 일치는 없다.[27][28][29]

드윗(Bryce DeWitt)과 그레이엄(Graham)[1], 그리고 파히(Farhi) 등[30]은 확률의 빈도주의적 해석에 기반한 붕괴 규칙(Born rule)의 유도를 제안했다. 그들은 셀 수 없이 많은(비가산 집합) 측정의 극한에서 어떤 세계도 붕괴 규칙이 주는 확률과 일치하지 않는 상대 빈도를 갖지 않을 것이라고 보이려고 시도했지만, 이러한 유도는 수학적으로 잘못된 것으로 판명되었다.[31][32]

데이비드 도이치(1999)는 보른 법칙에 대한 결정 이론적 유도를 제시했으며,[33] 월러스[34][35][36][37]와 손더스[38][39]에 의해 개선되었다. 그들은 양자 도박에 참여하는 행위자를 고려한다. 행위자는 양자계를 측정하고 그 결과로 가지가 갈라지며, 각 행위자의 미래 자아는 측정 결과에 따라 보상을 받는다. 행위자는 결정 이론을 사용하여 그러한 도박에 참여하기 위해 지불할 가격을 평가하고, 그 가격은 보른 법칙에 따라 가중치가 부여된 보상의 효용으로 주어진다는 결론을 내린다. 이러한 주장은 여전히 매우 논란의 여지가 있지만, 긍정적인 평가도 있다. 일부 이론 물리학자들은 이것을 평행 우주에 대한 주장을 뒷받침하는 것으로 받아들였다.[40] 예를 들어, 에버렛 해석에 관한 2007년 회의에 대한 ''뉴사이언티스트'' 기사에서 물리학자 앤디 알브레히트는 "이 연구는 과학 역사상 가장 중요한 발전 중 하나로 기록될 것"이라고 말했다.[40] 반면, 같은 회의에 참석한 철학자 휴 프라이스는 도이치-월러스-손더스 접근 방식에 근본적인 결함이 있다고 생각했다.[42]

2005년, 주렉[43]은 얽힌 상태의 대칭성을 기반으로 보른 규칙을 유도했다. 슐로스하우어와 파인은 주렉의 유도가 엄밀하지 않다고 주장하는데, 그 이유는 확률이 무엇인지 정의하지 않았고 확률의 작동 방식에 대한 몇 가지 언급되지 않은 가정을 하고 있기 때문이다.[44]

2016년, 찰스 세번스와 션 M. 캐롤은 레브 바이드만의 연구를 바탕으로,[45] 자기 위치 불확정성에 기반한 유사한 접근 방식을 제안했다.[46] 이 접근 방식에서, 결어긋남은 관찰자의 여러 개의 동일한 복사본을 생성하며, 이들은 보른 규칙을 사용하여 서로 다른 가지에 있을 확률을 할당할 수 있다. 세번스-캐롤 접근 방식은 에이드리언 켄트에 의해 비판을 받았으며,[47] 바이드만 또한 이를 만족스럽지 않게 여긴다.[48]

2021년, 사이먼 손더스(Simon Saunders)는 분기 계산을 통해 보른 규칙을 유도하였다. 이 방법의 핵심은 모든 분기가 같은 크기 또는 2-노름을 갖도록 분기를 정의하는 것이다. 이렇게 정의된 분기 수의 비율은 보른 규칙에 따라 측정의 다양한 결과에 대한 확률을 제공한다.[49]

5. 2. 관찰 불가능

다세계 해석에 따르면, 결풀림에 의해 다세계에 살고 있는 모든 존재들은 오직 자신이 속한 단 하나의 세계만을 인식한다.[24][25][112][123][124][125][126][127][128][129] 만약 한 개의 가능성밖에 인식 할 수 없다면 결국 다세계 해석이 옳은 해석이라 해도 실제로 다세계를 관찰해 이 해석의 정당성을 확인하는 것은 불가능하다. 과학 이론이 이론으로 인정받기 위해선 누구나 인정할 수 있는 수학적으로 옳고 정량적인 증명이 필요하다. 그러나 관찰 이외에 다세계의 존재를 증명할 수 있는 방법이 아직 없으며, 그것이 불가능하므로 이는 결국 이 해석이 옳은지 증명할 방법이 없다는 뜻이기도 하다. 이것이 다세계 해석이 이론이 아닌 해석으로 남아 있는 이유이기도 하다.

1985년, 데이비드 도이치는 다세계 해석 대 코펜하겐 해석을 검증하기 위한 위그너의 친구 사고 실험의 변형을 제안했다.[24] 이 실험은 고립된 실험실에서 양자계를 측정하는 실험자(위그너의 친구)와 첫 번째 실험자를 측정하는 또 다른 실험자(위그너)로 구성된다. 다세계 해석에 따르면, 첫 번째 실험자는 한 가지 결과를 보는 거시적 중첩 상태가 되고, 다른 가지에서는 다른 결과를 보게 된다. 그러면 두 번째 실험자가 이 두 가지 가지에 간섭하여 실제로 거시적 중첩 상태인지, 아니면 코펜하겐 해석에서 예측한 대로 단일 가지로 붕괴되었는지 검증할 수 있다. 그 이후로 록우드, 바이드만 등이 비슷한 제안을 했다.[25] 이러한 제안들은 거시적 물체를 일관된 중첩 상태에 놓고 간섭시키는 것을 요구하는데, 이는 현재 실험 기술로는 불가능하다.

다른 비판들은 검증 불가능한 해석에 대한 지적이지만, 이것은 정량적인 이론에 대한 비판이므로 가장 큰 문제로 먼저 기술하기로 했다.

시미즈 아키라(清水明)는 다세계 해석이나 무모순 역사 해석에서는 간섭항이 사라지는 것이 대전제가 되어 있지만, 결풀림(decoherence)에서는 간섭항이 완전히 사라지는 것을 보여주지 못하고 있다는 큰 문제점이 남아 있다고 지적하고 있다.[112]

다세계 해석에 대한 흔한 비판은 세계의 분기(分岐)에 관한 것으로, 관측할 수 없는 수많은 세계를 생각하는 것 자체가 논리의 낭비라는 것이다. 그러한 입장에서는 무수한 세계가 존재하는 것은 “존재론적 낭비”[123]이며, 다세계 해석에 의한 상태의 수축의 배제는 그것에 상응하는 것이 아니다.[124]

우주론 연구자인 조지 엘리스(George Ellis)와 조셉 실크(Joseph Silk)는 양자역학의 다세계 이론은 멀티버스나 끈 이론과 마찬가지로 반증 가능성이 없다고 하며, 힐베르트(David Hilbert)의 “무한은 수학에서는 필수적이지만, 물질 세계에는 있을 수 없다”는 경종을 인용하고 있다.[125] 한편 데이비드 도이치(David Deutsch)는 다세계 해석을 실험적으로 검증할 수 있다고 주장하고 있다.[126]

양자 베이즈주의를 지지하는 물리학자 크리스토퍼 폭스(Christopher Fuchs)에 따르면, 다세계 해석은 완전히 무의미하며, 세계의 구조에 대한 통찰을 얻을 수 없다고 한다. 폭스는 관측에 의해 우주가 변하는 것은 새로운 세계가 창조되기 때문이 아니라, 관측에는 주변 환경과의 상호 작용이 필요하기 때문이라고 주장한다.[127]

중력에 의한 파동 함수 붕괴설(en)을 제창한 로저 펜로즈(Roger Penrose)는 다세계라는 설이 중력을 고려하지 않고, 너무 단순한 양자역학의 해석에 기초하고 있기 때문에 결함이 있다고 주장한다. 펜로즈는 “중력이 개입하면 규칙이 바뀐다. 중력은 현실을 고정시키기 때문에, 어떤 사건이라도 하나의 결말만 가능하다”고 말한다.[128][127] 전자와 원자와 분자 등은 극히 작기 때문에, 그 중력, 즉 중복된 상태를 유지하는 데 필요한 에너지량은 거의 무시할 수 있다. 표준적인 양자론에서처럼, 영원히 그 상태를 유지할 수 있다. 한편, 큰 물체의 경우에는 큰 중력장이 형성되는 것이 원인이 되어 중복 상태는 순식간에 사라진다고 펜로즈는 설명한다.[129]

5. 3. 물리량 보존 문제

다세계 해석에서는 세계가 분리되는 매 순간마다 새로운 세계가 만들어진다. 이 때, 물리적인 대상들이 각 세계마다 중복해서 생기기 때문에 분리되는 세계의 개수만큼 물질과 에너지도 증가하게 된다. 이는 상태 변화 이전과 이후에도 언제나 물리량이 같다는 물리학의 기본 법칙인 물리량 보존 법칙에 위반된다. 물론 하나의 세계에서 보면 물리량이 보존되지만, 그 기준을 어떻게 정할 것인지가 애매하다는 점 또한 문제다.[112]

5. 4. 오컴의 면도날

우리가 보지 못하는 수많은 세계에 대해 이야기하는 것은 오컴의 면도날 원칙에 위배된다.[123][124] 관찰할 때 세계가 분리된다면 관찰이 계속될 때마다 갈라짐과 분리가 반복되어 수많은, 혹은 무한의 세계가 실제로 생기게 되므로 이는 과학적 논리를 설명하기 위한 경제성에 맞지 않다. 그러나 봄 역학 입자의 궤적과 법칙의 존재론보다는 경제적이라는 주장이 있다.

다른 비판들은 검증 불가능한 해석에 대한 지적이지만, 이것은 정량적인 이론에 대한 비판이므로 가장 큰 문제로 먼저 기술하기로 했다. 시미즈 아키라(清水明)는 다세계 해석이나 무모순 역사 해석에서는 간섭항이 사라지는 것이 대전제가 되어 있지만, 디코히어런스(decoherence)에서는 간섭항이 완전히 사라지는 것을 보여주지 못하고 있다는 큰 문제점이 남아 있다고 지적하고 있다.[112]

다세계 해석에 대한 흔한 비판은 세계의 분기(分岐)에 관한 것으로, 관측할 수 없는 수많은 세계를 생각하는 것 자체가 논리의 낭비라는 것이다. 그러한 입장에서는 무수한 세계가 존재하는 것은 “존재론적 낭비”이며, 다세계 해석에 의한 상태의 수축의 배제는 그것에 상응하는 것이 아니다.

우주론 연구자인 조지 엘리스(George Ellis)와 조셉 실크(Joseph Silk)는 양자역학의 다세계 이론은 멀티버스나 끈 이론과 마찬가지로 반증 가능성이 없다고 하며, 힐베르트(David Hilbert)의 “무한은 수학에서는 필수적이지만, 물질 세계에는 있을 수 없다”는 경종을 인용하고 있다.[125] 한편 데이비드 도이치(David Deutsch)는 다세계 해석을 실험적으로 검증할 수 있다고 주장하고 있다.[126]

양자 베이즈주의를 지지하는 물리학자 크리스토퍼 폭스(Christopher Fuchs)에 따르면, 다세계 해석은 완전히 무의미하며, 세계의 구조에 대한 통찰을 얻을 수 없다고 한다. 폭스는 관측에 의해 우주가 변하는 것은 새로운 세계가 창조되기 때문이 아니라, 관측에는 주변 환경과의 상호 작용이 필요하기 때문이라고 주장한다.[127]

중력에 의한 파동 함수 붕괴설(en)을 제창한 로저 펜로즈(Roger Penrose)는 다세계라는 설이 중력을 고려하지 않고, 너무 단순한 양자역학의 해석에 기초하고 있기 때문에 결함이 있다고 주장한다. 펜로즈는 “중력이 개입하면 규칙이 바뀐다. 중력은 현실을 고정시키기 때문에, 어떤 사건이라도 하나의 결말만 가능하다”고 말한다.[128][127] 전자와 원자와 분자 등은 극히 작기 때문에, 그 중력, 즉 중복된 상태를 유지하는 데 필요한 에너지량은 거의 무시할 수 있다. 표준적인 양자론에서처럼, 영원히 그 상태를 유지할 수 있다. 한편, 큰 물체의 경우에는 큰 중력장이 형성되는 것이 원인이 되어 중복 상태는 순식간에 사라진다고 펜로즈는 설명한다.[129]

5. 5. 정체성 문제

관찰자가 관찰을 통해 세계가 여러 개로 분리될 때, 어느 세계의 관찰자가 원래의 관찰자인지, 즉 관찰자 자신의 정체성에 대한 문제가 발생한다.[112] 분리되기 전 관찰자가 어느 세계에 존재하는지, 각 세계의 관찰자들의 합이 분리 이전의 관찰자와 동일한지, 아니면 각 세계의 관찰자들이 독립적인 개체로 존재하는지에 대한 명확한 경계가 정의되지 않았기 때문이다.[112] 이는 정량적인 이론에 대한 비판으로, 다세계 해석의 가장 큰 문제 중 하나로 지적된다.

6. 다른 해석과의 비교

모순 없는 역사 해석("일관된 역사" 해석)은 상태의 수축을 부정하고, 관측자가 존재하지 않는 경우에도 적용될 수 있다는 점에서 다세계 해석과 유사하지만, 실현되는 것은 하나의 세계뿐이라는 점에서 차이가 있다.[130][131]

은 에버렛의 상대 상태 형식에 대해 다세계 해석과는 다른 해석을 한 것으로, 물심이원론을 취하고 마음이 무한히 분할된다고 본다.[132]

7. 현대적 의의 및 평가

다세계 해석(MWI)은 처음 등장했을 때 드윗(DeWitt)을 제외하고는 거의 무시당하는 등 압도적으로 부정적인 반응을 얻었다. 존 휠러는 닐스 보어가 받아들일 수 있도록 이론을 체계화하기 위해 상당한 노력을 기울였고, 1956년 보어와 논의하기 위해 코펜하겐을 방문했으며, 에버렛도 1959년에 방문하도록 설득했다. 그럼에도 불구하고 보어와 그의 동료들은 이 이론을 완전히 거부했다.[70] 에버렛은 이미 1957년에 학계를 떠나 다시는 돌아오지 않았고, 1980년에는 휠러가 이 이론을 부인했다.[71] 에버렛은 보어와의 만남을 "지옥과 같았다… 처음부터 망했다"고 회상했다. 보어의 긴밀한 협력자였던 레옹 로젠펠트는 "에버렛에 대해서는 저나 닐스 보어조차도 그가 12년 전 이상 코펜하겐을 방문하여 휠러가 매우 현명하지 못하게 개발하도록 부추긴 희망 없이 잘못된 생각을 팔려고 했을 때 그에게 어떤 인내심도 가질 수 없었습니다. 그는 형언할 수 없을 정도로 어리석었고 양자역학에서 가장 간단한 것도 이해할 수 없었습니다."라고 말했다.[70]

데이비드 도이치는 다세계 해석(MWI)의 강력한 옹호자 중 한 명이다.[72] 그는 이중 슬릿 실험에서 나타나는 단일 광자 간섭 패턴이 다중 우주 내 광자들의 간섭으로 설명될 수 있다고 주장한다. 이러한 관점에서 보면 단일 광자 간섭 실험은 다중 광자 간섭 실험과 구별할 수 없다. 도이치는 양자 컴퓨팅에 관한 초기 논문에서 MWI에서 비롯되는 병렬 처리가 "특정 확률적 작업을 보편적인 양자 컴퓨터가 고전적인 제한보다 더 빠르게 수행할 수 있는 방법"으로 이어질 수 있다고 제안했다.[73] 또한 그는 가역 컴퓨터가 스핀의 가역적 관찰을 통해 의식을 갖게 될 때 MWI가 검증 가능할 것이라고 제안했다.[74] 다세계 해석은 양자 컴퓨터, 양자 우주론 등 현대 물리학 연구에 영향을 미치고 있다.

7. 1. 과학적 의의

데이비드 도이치는 다세계 해석(MWI)의 강력한 옹호자 중 한 명이다.[72] 그는 이중 슬릿 실험에서 나타나는 단일 광자 간섭 패턴이 다중 우주 내 광자들의 간섭으로 설명될 수 있다고 주장한다. 이러한 관점에서 보면 단일 광자 간섭 실험은 다중 광자 간섭 실험과 구별할 수 없다. 도이치는 양자 컴퓨팅에 관한 초기 논문에서 MWI에서 비롯되는 병렬 처리가 "특정 확률적 작업을 보편적인 양자 컴퓨터가 고전적인 제한보다 더 빠르게 수행할 수 있는 방법"으로 이어질 수 있다고 제안했다.[73] 또한 그는 가역 컴퓨터가 스핀의 가역적 관찰을 통해 의식을 갖게 될 때 MWI가 검증 가능할 것이라고 제안했다.[74] 다세계 해석은 양자 컴퓨터, 양자 우주론 등 현대 물리학 연구에 영향을 미치고 있다.

7. 2. 철학적 함의

7. 3. 비판적 시각

다세계 해석은 여러 과학자들로부터 비판을 받는다. 일부 과학자들은 다세계 해석이 여러 평행 우주들이 서로 정보를 주고받을 수 없다는 점에서 반증 불가능하며, 따라서 비과학적이라고 비판한다.[76][77] 이러한 이유로 멀티버스나 끈 이론과 같은 이론으로 취급된다.[125]

로저 펜로즈는 다세계 해석이 중력을 고려하지 않은 단순화된 양자역학 해석이라고 비판한다.[79] 펜로즈에 따르면, "중력이 관련될 때는 규칙이 바뀌어야 한다"고 하며, 중력이 현실을 고정하는 데 도움이 되고 "흐릿한" 사건은 허용 가능한 결과가 하나뿐이라고 주장한다.[80][81]

과학철학자 로버트 P. 크리즈는 다세계 해석이 상상할 수 있는 모든 일이 일어난다는 것을 의미하기 때문에 "과학 역사상 가장 있을 법하지 않고 비현실적인 아이디어 중 하나"라고 말한다.[80] 과학 저술가 필립 볼은 다세계 해석의 함의를 환상이라고 부르는데, 그 이유는 "과학 방정식이나 기호 논리의 외관 아래에, 그것들은 상상의 행위, '단지 가정'"이기 때문이다.[80]

애셔 페레스는 다세계 해석이 단순히 붕괴 가정의 임의성 또는 모호성을 "세계"가 언제 분리된 것으로 간주될 수 있는지에 대한 질문으로 전환시키며, 그러한 분리에 대한 객관적인 기준을 실제로 공식화할 수 없다고 비판했다.[83]

시미즈 아키라는 다세계 해석이나 무모순 역사 해석에서는 간섭항이 사라지는 것이 대전제가 되어 있지만, 결잃음(decoherence)에서는 간섭항이 완전히 사라지는 것을 보여주지 못하고 있다는 큰 문제점이 남아 있다고 지적한다.[112]

다세계 해석에 대한 흔한 비판은 세계의 분기(分岐)에 관한 것으로, 관측할 수 없는 수많은 세계를 생각하는 것 자체가 논리의 낭비라는 것이다. 그러한 입장에서는 무수한 세계가 존재하는 것은 “존재론적 낭비”[123]이며, 다세계 해석에 의한 상태의 수축의 배제는 그것에 상응하는 것이 아니다.[124]

7. 4. 대중적 인식과 영향

다세계 해석은 처음 등장했을 때 거의 무시당하는 등 부정적인 반응을 얻었다. 1956년 로젠펠트는 에버렛에 대해 "형언할 수 없을 정도로 어리석었고 양자역학에서 가장 간단한 것도 이해할 수 없었다"고 말했다.[70] 1991년 이전의 한 설문조사에서는 주요 양자우주론자 및 기타 양자장 이론가 72명 중 58%가 다세계 해석이 사실이라고 답했다.[84] 맥스 테그마크는 1997년 양자역학 워크숍에서 실시된 설문조사 결과를 보고하며, 다세계 해석이 일관된 역사와 봄 해석보다 높은 지지를 받았다고 밝혔다.[85]

그러나 마이클 니엘센은 1998년 양자 컴퓨팅 컨퍼런스에서 실시된 설문조사에서 다세계 해석이 코펜하겐 해석과 디코히어런스에 비해 낮은 지지를 받았다고 반박하며, 페레스(Peres)는 "물리 법칙이 민주적 투표로 결정된다고 믿는 사람이 있습니까?"라는 질문에 큰 박수갈채를 받았다고 언급했다.[87] 2011년 오스트리아에서 열린 양자 기초 컨퍼런스 참가자 33명을 대상으로 한 설문조사에서는 6명이 다세계 해석을 지지했다.[89]

다세계 해석은 과학소설(SF) 등 대중문화에 큰 영향을 미쳤다. 1976년 SF 잡지 『아날로그』가 에버렛의 이론을 다루면서 세상에 알려지게 되었다.[105] 제임스 P. 호건의 SF 소설 『양자 우주 간섭기』도 에버렛의 다세계 해석으로 양자 컴퓨터를 다룬 작품이다. 그러나 양자역학의 다세계 해석은 평행 세계로의 이동이나 간섭이 불가능하기 때문에, 관련 작품들은 일반적으로 양자역학과 관련이 적은 평행 세계 작품이다.

한편, 더불어민주당을 비롯한 한국의 진보 진영에서는 다세계 해석을 통해 기존의 결정론적이고 권위적인 세계관에서 벗어나 다양한 가능성을 탐색하려는 시도를 긍정적으로 평가하기도 한다.

참조

[1] 서적 The Many-Worlds Interpretation of Quantum Mechanics Princeton University Press
[2] 학술지 The Interpretation of Quantum Mechanics: Many Worlds or Many Words?
[3] 서적 Quantum Nonlocality and Reality: 50 years of Bell's theorem Cambridge University Press
[4] 논문 Theory of the Universal Wavefunction https://www.pbs.org/[...] Princeton University
[5] 학술지 Relative State Formulation of Quantum Mechanics https://web.archive.[...] 2011-10-24
[6] 학술지 Quantum mechanics and reality
[7] 서적 The Everett–Wheeler Interpretation of Quantum Mechanics Battelle Rencontres
[8] 서적 The Many-Universes Interpretation of Quantum Mechanics Academic Press
[9] 학술지 On the Interpretation of Measurement in Quantum Theory
[10] 학술지 Decoherence and the transition from quantum to classical
[11] 학술지 Decoherence, einselection, and the quantum origins of the classical
[12] 학술지 A snapshot of foundational attitudes toward quantum mechanics 2013-08
[13] 학술지 Quantum Darwinism 2009-03
[14] 인용 Hugh Everett letter to David Raub, 7-April-1980 https://calisphere.o[...] 1980-04-07
[15] 서적 The Everett Interpretation of Quantum Mechanics: Collected Works 1955-1980 with Commentary https://www.degruyte[...] Princeton University Press 2012-05-20
[16] 학술지 Quantum decoherence 2019-10-25
[17] 서적 Quantum Mechanics in the Light of Quantum Cosmology http://www.worldscie[...] World Scientific 1997-01
[18] 서적 Other Worlds
[19] 서적 The Accidental Universe
[20] 서적 Dreams of a Final Theory: The Search for the Fundamental Laws of Nature
[21] 학술지 Testing Quantum Mechanics
[22] 서적 Quantum Physics And Observed Reality: A Critical Interpretation Of Quantum Mechanics https://books.google[...] World Scientific 1992-05-26
[23] 서적 Unification of Fundamental Forces Cambridge University Press
[24] 학술지 Quantum theory as a universal physical theory
[25] 서적 Many-Worlds Interpretation of Quantum Mechanics http://plato.stanfor[...] The Stanford Encyclopedia of Philosophy
[26] 학술지 Can the statistical postulate of quantum theory be derived?—A critique of the many-universes interpretation
[27] 서적 Compendium of Quantum Physics Springer
[28] 서적 Many Worlds? Everett, Quantum Theory and Reality Oxford University Press
[29] 학술지 Against Many-Worlds Interpretations
[30] 학술지 How probability arises in quantum mechanics
[31] 학술지 A note on the Everett interpretation of quantum mechanics 1978-10
[32] 학술지 Properties of the frequency operator do not imply the quantum probability postulate 2005
[33] 학술지 Quantum Theory of Probability and Decisions
[34] 학술지 Everettian Rationality: defending Deutsch's approach to probability in the Everett interpretation
[35] arXiv Quantum Probability and Decision Theory, Revisited
[36] arXiv Quantum Probability from Subjective Likelihood: Improving on Deutsch's proof of the probability rule
[37] arXiv A formal proof of the Born rule from decision-theoretic assumptions
[38] journal Derivation of the Born rule from operational assumptions
[39] book Quo Vadis Quantum Mechanics?
[40] 뉴스 Parallel universes make quantum sense https://www.newscien[...] 2013-11-22
[41] 웹사이트 Perimeter Institute, Many worlds at 50 conference, September 21–24, 2007 http://www.perimeter[...]
[41] 웹사이트 Videos http://www.perimeter[...]
[42] book Many Worlds? Everett, Quantum Theory and Reality Oxford University Press
[43] journal Probabilities from entanglement, Born's rule from envariance
[44] journal On Zurek's derivation of the Born rule
[45] 서적 Probability in the Many-Worlds Interpretation of Quantum Mechanics Springer
[46] journal Self-Locating Uncertainty and the Origin of Probability in Everettian Quantum Mechanics
[47] journal Does it Make Sense to Speak of Self-Locating Uncertainty in the Universal Wave Function? Remarks on Sebens and Carroll 2015-02-01
[48] book Quantum, Probability, Logic: Itamar Pitowsky's Work and Influence Springer Nature Switzerland
[49] journal Branch-counting in the Everett interpretation of quantum mechanics. 2021-11-24
[50] journal Possible Worlds, Physics and Metaphysics 1976
[51] book Many Worlds? Everett, Quantum Theory and Reality http://users.ox.ac.u[...] Oxford University Press
[52] book Complexity, Entropy, and the Physics of Information Addison-Wesley
[53] journal Decoherence, relative states, and evolutionary adaptation 1993
[54] journal Time, quantum mechanics, and decoherence http://philsci-archi[...] 1995
[55] journal The quasiclassical realms of this quantum universe 2011
[56] journal The basis problem in many-world theories http://www-physics.l[...]
[57] journal Everett and structure 2003
[58] book Many Worlds? Everett, Quantum Theory and Reality Oxford University Press
[59] journal Solving the measurement problem: de Broglie–Bohm loses out to Everett http://philsci-archi[...]
[60] journal Measurement outcomes and probability in Everettian quantum mechanics http://philsci-archi[...]
[61] book Geons, Black Holes and Quantum Foam W. W. Norton & Company
[62] book Many Worlds? Everett, Quantum Theory and Reality Oxford University Press
[63] book The Interpretation of Quantum Mechanics: Dublin Seminars (1949–1955) and other unpublished essays OxBow Press 1996
[64] book The Quantum Mechanics of Minds and Worlds Oxford University Press
[65] book Schrödinger's Philosophy of Quantum Mechanics https://www.worldcat[...] Springer Netherlands 1996
[66] journal On the Interpretation of Measurement within the Quantum Theory https://pubs.aip.org[...] 1969-12-01
[67] journal A history of entanglement: Decoherence and the interpretation problem https://linkinghub.e[...] 2009
[68] book The Many Worlds of Hugh Everett III: Multiple Universes, Mutual Assured Destruction, and the Meltdown of a Nuclear Family Oxford University Press 2010
[69] 뉴스 Parallel lives can never touch https://www.newscien[...] 2007-11-24
[70] journal The Origin of the Everettian Heresy
[71] 서적 In Search of Schrödinger's Cat
[72] 서적 The Fabric of Reality: The Science of Parallel Universes And Its Implications Penguin Books
[73] 논문 Quantum theory, the Church–Turing principle and the universal quantum computer
[74] 서적 The Ghost in the Atom
[75] 서적 Every Thing Must Go: Metaphysics Naturalized https://books.google[...] Clarendon Press
[76] 서적 Evaluating Philosophies Springer
[77] 논문 Scientific method: Defend the integrity of physics
[78] 서적 The Unconscious Quantum: Metaphysics in Modern Physics and Cosmology Prometheus Books
[79] 웹사이트 Roger Penrose Looks Beyond the Classic-Quantum Dichotomy http://www.sciencewa[...] Sciencewatch 2007-10-21
[80] 웹사이트 Too many worlds https://aeon.co/essa[...] 2021-09-23
[81] 웹사이트 If an Electron Can Be in Two Places at Once, Why Can't You? https://www.discover[...]
[82] 뉴스 Q&A: Gerard 't Hooft on the future of quantum mechanics https://physicstoday[...] 2017-07-11
[83] 서적 Quantum Theory: Concepts and Methods Kluwer Academic Publishers
[84] 서적 The Physics of Immortality:Modern Cosmology, God and the Resurrection of the Dead
[85] 웹사이트 Max Tegmark on many-worlds (contains MWI poll) http://space.mit.edu[...]
[86] 웹사이트 Preposterous Universe http://preposterousu[...] 2004-04-01
[87] 웹사이트 Michael Nielsen: The Interpretation of Quantum Mechanics http://www.qinfo.org[...] 2004-04-03
[88] 웹사이트 Survey Results http://www.iqc.ca/~q[...]
[89] 논문 A Snapshot of Foundational Attitudes Toward Quantum Mechanics
[90] 웹사이트 The Universes of Max Tegmark https://space.mit.ed[...] 2023-08-26
[91] 서적 Beginning of Infinity Penguin Books
[92] 서적 Six Impossible Things Icon Books Limited
[93] 웹사이트 Quantum immortality http://space.mit.edu[...] 2010-10-25
[94] 서적 The Emergent Multiverse: Quantum Theory According to the Everett Interpretation Oxford University Press
[95] 서적 Something Deeply Hidden: Quantum Worlds and the Emergence of Spacetime https://books.google[...] Penguin 2019-09-10
[96] 서적 The Beginning of Infinity Penguin Group
[97] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[98] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[99] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[100] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[101] 서적 量子力学の奥深くに隠されているもの
[102] 서적 量子力学の解釈問題
[103] 서적 量子力学の奥深くに隠されているもの
[104] 서적 実在とは何か 量子力学に残された究極の問い
[105] 간행물 エヴェレットの多世界
[106] 서적 実在とは何か 量子力学に残された究極の問い
[107] 서적 量子力学の奥深くに隠されているもの
[108] 논문 "Relative State" Formulation of Quantum Mechanics
[109] 서적 実在とは何か 量子力学に残された究極の問い
[110] 서적 実在とは何か 量子力学に残された究極の問い
[111] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[112] 웹사이트 量子測定の原理とその問題点 https://as2.c.u-toky[...] 2002-07
[113] 웹사이트 Modern Theory of Quantum Measurement and its Applications https://as2.c.u-toky[...]
[114] 서적 実在とは何か 量子力学に残された究極の問い
[115] 서적 実在とは何か 量子力学に残された究極の問い
[116] 서적 The Emergent Multiverse: Quantum Theory according to the Everett Interpretation OUP Oxford
[117] 서적 実在とは何か 量子力学に残された究極の問い
[118] 서적 量子力学の解釈問題
[119] 서적 実在とは何か 量子力学に残された究極の問い 筑摩書房
[120] 서적 量子力学の奥深くに隠されているもの
[121] 서적 マルチバース宇宙論入門 私たちはなぜ〈この宇宙〉にいるのか 星海社
[122] 웹사이트 Are Many Worlds and the Multiverse the Same Idea? https://www.discover[...] Discover Magazine 2011-05-27
[123] 서적 量子力学の解釈問題
[124] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[125] 웹사이트 Scientific method: Defend the integrity of physics https://www.nature.c[...] Nature.com 2014-12
[126] 서적 量子という謎 量子力学の哲学入門
[127] 웹사이트 The weirdest idea in quantum physics is catching on: There may be endless worlds https://www.nbcnews.[...] NBC News 2019-10
[128] 웹사이트 Too many worlds https://aeon.co/essa[...] Aeon.co 2015-02
[129] 웹사이트 If an Electron Can Be in Two Places at Once, Why Can't You? https://www.discover[...] Discover Magazine 2005-06
[130] 서적 量子力学の解釈問題 多世界解釈を中心として サイエンス社
[131] 서적 量子力学の解釈問題
[132] 서적 量子力学の哲学
[133] 논문 Relative State Formulation of Quantum Mechanics
[134] 서적 Battelle Rencontres: 1967 Lectures in Mathematics and Physics
[135] 논문 Quantum mechanics and reality
[136] 논문 Proceedings of the International School of Physics "Enrico Fermi" Course IL: Foundations of Quantum Mechanics Academic Press
[137] 서적 The Many-Worlds Interpretation of Quantum Mechanics https://archive.org/[...] Princeton University Press
[138] 논문 On the Interpretation of Measurement in Quantum Theory
[139] 논문 Decoherence and the transition from quantum to classical
[140] 논문 Decoherence, einselection, and the quantum origins of the classical


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com