푸앵카레 원판

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 정의
4. 성질
5. 다른 쌍곡 기하학 모형과의 관계
6. 해석 기하학적 구성
- 6.1. 직선 (측지선)
- 6.2. 각
7. 예술적 응용
참조

1. 개요

푸앵카레 원판은 2차원 쌍곡 기하학의 모델로, 1882년 앙리 푸앵카레에 의해 사용되어 널리 알려졌다. 푸앵카레 원판은 유클리드 평면의 단위 원판 내에서 쌍곡 기하학을 표현하며, 특히 루돌프 카르납과 한스 라이헨바흐의 철학적 논의에서 공간 기하학의 선택이 관습적이라는 가설의 증거로 사용되었다. 푸앵카레 원판에서 측지선은 원의 경계와 수직으로 교차하는 원호로 구현되며, 푸앵카레 원반은 클라인 모형, 푸앵카레 상반평면 모형, 쌍곡면 모형 등 다른 쌍곡 기하학 모델과 사영적으로 관련되어 있다. 이 모형은 M. C. 에셔의 예술 작품과 로그라이크 게임 HyperRogue 등 예술 및 게임 분야에서도 활용된다.

더 읽어볼만한 페이지

쌍곡기하학 - 무한원점
무한원점은 사영평면에서 z=0인 동차좌표로 표현되는 점들의 집합으로 무한원직선을 구성하며, 유클리드 기하학에는 없지만 사영기하학 등에서 평행선의 교점으로 정의되고 투영기하학에서 소실점과 관련되어 응용되지만 교육적 어려움을 야기한다는 비판도 있다.
쌍곡기하학 - 쌍곡선 함수
쌍곡선 함수는 삼각함수에서 파생된 함수로, 지수 함수를 사용하여 정의되며 삼각함수와 유사한 성질을 가지며 미분, 적분, 복소수까지 확장되어 사용된다.
고차원 기하학 - 끈 이론
끈 이론은 기본 입자를 점이 아닌 진동하는 끈으로 보고, 양자 중력을 포함한 기본 상호작용을 설명하려 하며, 초끈 이론, 추가 차원, M-이론과의 연관성, 그리고 실험적 검증의 어려움 등이 특징이다.
고차원 기하학 - 4차원
4차원은 한 점을 지정하는 데 4개의 독립적인 매개변수가 필요한 공간으로, 수학에서는 유클리드 공간과 민코프스키 시공간 등으로 구분되며, 물리학에서는 시공간 기술 및 여분 차원 가정에 활용되는 중요한 개념이다.

푸앵카레 원판
일반 정보
유형	기하학 모델
분야	쌍곡 기하학
차원	2차원
공간	쌍곡 평면
경계	단위 원
등거리 변환군	PSU(1,1)/{I, −I}
관련 모델
관련 모델	클라인 원반 모델 푸앵카레 반평면 모델 쌍곡면 모델 벨트라미-클라인 모델
특징
특징	등각 투영 쌍곡선은 원호로 표현됨

2. 역사

푸앵카레 원반은 앙리 푸앵카레의 이름이 붙었지만, 에우제니오 벨트라미가 최초로 도입하여 비유클리드 기하학의 일관성을 증명하는 데 사용하였다.^[10] 1854년 베른하르트 리만의 강연(1868년 출판)에서 처음 설명되었고, 1868년 벨트라미의 논문에 영감을 주었다.^[2] 앙리 푸앵카레는 1882년 이 모형을 사용했고,^[3] 1905년 ''과학과 가설''에서 발표하여 널리 알려졌다.^[4]

이후 푸앵카레 원반은 루돌프 카르납^[5]과 한스 라이헨바흐의 철학적 논의에서 중요한 증거로 사용되었다.^[6]

2. 1. 초기 연구

에우제니오 벨트라미가 최초로 도입하였으며, 이 모형으로 비유클리드 기하학의 일관성을 증명하였다.^[10] 원반 모형은 1854년 베른하르트 리만이 발표한 강연(1868년 출판)에서 처음 설명되었으며, 이는 1868년 에우제니오 벨트라미의 논문에 영감을 주었다.^[2] 앙리 푸앵카레는 1882년 쌍곡선, 포물선 및 타원 함수를 다루면서 이 모형을 사용했으며,^[3] 1905년 철학 논문인 ''과학과 가설''에서 푸앵카레가 발표한 이후 널리 알려지게 되었다.^[4] 그는 이 논문에서 푸앵카레 원반으로 알려진 세상을 묘사했는데, 이 세상의 공간은 유클리드 기하학을 따르지만, 그곳의 거주자들에게는 쌍곡 기하학의 공리를 만족하는 것처럼 보였다.

> "예를 들어, 거대한 구 안에 갇혀 있고 다음과 같은 법칙을 따르는 세계가 있다고 가정해 보자. 온도는 균일하지 않고, 중심에서 가장 높으며, 구의 가장자리로 갈수록 점차 감소하여 절대 영도에 이른다. 이 온도의 법칙은 다음과 같다.

R

을 구의 반지름,

r

을 중심으로부터 고려하는 점까지의 거리라고 할 때, 절대 온도는

R^2 - r^2

에 비례한다. 또한, 이 세계의 모든 물체는 동일한 선팽창 계수를 갖는다고 가정하므로, 어떤 물체의 선형 팽창은 절대 온도에 비례한다. 마지막으로, 다른 온도의 한 지점에서 다른 지점으로 운반된 물체는 즉시 새로운 환경과 열 평형 상태에 있다고 가정한다. ...

>

> 만약 그들이 기하학을 구성한다면, 우리의 기하학과 같지 않을 것이다. 즉, 불변 고체의 움직임을 연구하는 것이 아니라, 그들이 구별하게 될 위치의 변화를 연구하는 것이며, '비유클리드 변위'가 될 것이고, ''이것이 비유클리드 기하학''이 될 것이다. 따라서 그러한 세계에서 교육받은 우리와 같은 존재는 우리와 같은 기하학을 갖지 못할 것이다."^[4] (pp.65-68)

푸앵카레 원반은 특히 루돌프 카르납^[5]과 한스 라이헨바흐의 영향력 있는 철학적 논의에서 공간 기하학의 선택이 사실적이라기보다는 관습적이라는 가설에 대한 중요한 증거가 되었다.^[6]

2. 2. 푸앵카레의 기여

에우제니오 벨트라미가 최초로 도입하였으나, 앙리 푸앵카레의 이름이 붙어 있다.^[10] 벨트라미는 이 모형으로 비유클리드 기하학의 일관성을 증명하였다. 앙리 푸앵카레는 1882년 쌍곡선, 포물선 및 타원 함수를 다루면서 이 모형을 사용했으며,^[3] 1905년 철학 논문인 ''과학과 가설''에서 푸앵카레가 발표한 이후 널리 알려지게 되었다.^[4] 그는 이 논문에서 푸앵카레 원반으로 알려진, 유클리드 기하학을 따르지만 그곳의 거주자들에게는 쌍곡 기하학의 공리를 만족하는 것처럼 보이는 세상을 묘사했다. 푸앵카레 원반은 루돌프 카르납^[5]과 한스 라이헨바흐의 철학적 논의에서 공간 기하학의 선택이 사실적이라기보다는 관습적이라는 가설에 대한 중요한 증거가 되었다.^[6]

2. 3. 철학적 논의

원반 모형은 1854년 베른하르트 리만이 발표한 강연(1868년 출판)에서 처음 설명되었으며, 이는 1868년 에우제니오 벨트라미의 논문에 영감을 주었다.^[2] 앙리 푸앵카레는 1882년 쌍곡선, 포물선 및 타원 함수를 다루면서 이 모형을 사용했으며,^[3] 1905년 철학 논문인 ''과학과 가설''에서 푸앵카레가 발표한 이후 널리 알려지게 되었다.^[4] 그는 이 논문에서 푸앵카레 원반으로 알려진 세상을 묘사했는데, 이 세상의 공간은 유클리드 기하학을 따르지만, 그곳의 거주자들에게는 쌍곡 기하학의 공리를 만족하는 것처럼 보였다.

> "예를 들어, 거대한 구 안에 갇혀 있고 다음과 같은 법칙을 따르는 세계가 있다고 가정해 보자. 온도는 균일하지 않고, 중심에서 가장 높으며, 구의 가장자리로 갈수록 점차 감소하여 절대 영도에 이른다. 이 온도의 법칙은 다음과 같다. R을 구의 반지름, r을 중심으로부터 고려하는 점까지의 거리라고 할 때, 절대 온도는 R² - r²에 비례한다. 또한, 이 세계의 모든 물체는 동일한 선팽창 계수를 갖는다고 가정하므로, 어떤 물체의 선형 팽창은 절대 온도에 비례한다. 마지막으로, 다른 온도의 한 지점에서 다른 지점으로 운반된 물체는 즉시 새로운 환경과 열 평형 상태에 있다고 가정한다. ...

> 만약 그들이 기하학을 구성한다면, 우리의 기하학과 같지 않을 것이다. 즉, 불변 고체의 움직임을 연구하는 것이 아니라, 그들이 구별하게 될 위치의 변화를 연구하는 것이며, '비유클리드 변위'가 될 것이고, ''이것이 비유클리드 기하학''이 될 것이다. 따라서 그러한 세계에서 교육받은 우리와 같은 존재는 우리와 같은 기하학을 갖지 못할 것이다."^[4] (pp.65-68)

푸앵카레 원반은 특히 루돌프 카르납^[5]과 한스 라이헨바흐의 영향력 있는 철학적 논의에서 공간 기하학의 선택이 사실적이라기보다는 관습적이라는 가설에 대한 중요한 증거가 되었다.^[6]

3. 정의

''n''차원 '''푸앵카레 공'''은 다음과 같은 계량이 주어진 단위 열린 공이다.

: $B=\left\{x\in\mathbb R^n\colon\sum_{i=1}^nx_i^2<1\right\}$

여기에 주어진 리만 계량은 다음과 같다.

: $ds^2=4\frac{\sum_{i=1}^ndx_i^2}{1-\sum_{i=1}^nx^2}$

구체적으로, 두 점 $x,y\in B$ 사이의 거리는 다음과 같다.

: $d(x,y)=\cosh^{-1}\left(1+\frac{2\Vert x-y\Vert^2}{(1-\Vert x\Vert^2)(1-\Vert y\Vert^2)}\right)$

2차원 푸앵카레 공은 '''푸앵카레 원판'''이라고 한다.

''u'', ''v''를 통상의 유클리드 노름을 갖는 실수 ''n''차원 벡터 공간 '''R'''^''n''의 두 벡터로, 그 노름이 모두 1보다 작은 것으로 하면,

: $\delta (u, v) = 2 \frac{\lVert u-v \rVert^2}{(1-\lVert u \rVert^2)(1-\lVert v \rVert^2)}$

로 놓고 등거리 불변량을 정의할 수 있다. 여기서 ǁ⋅ǁ는 통상의 유클리드 노름이다. 따라서 이 거리 함수는

: $d(u, v) = \operatorname{ar\,\cosh} (1+\delta (u,v))$

로 쓸 수 있다. 이 거리 함수는 노름이 1보다 작은 임의의 두 벡터에 대해 정의되며, 그러한 벡터 전체가 이루는 집합을 상수 곡률 −1의 쌍곡 공간의 모델로 하는 거리 공간의 구조를 정한다. 이 모델은, 쌍곡 공간 내의 교차하는 두 직선이 이루는 각이, 이 모델에서의 각과 같다는 등각성을 갖는다.

푸앵카레 원반 모형에 부수되는 계량 텐서는

: $ds^2 = 4 \frac{\sum_i dx_i^2}{(1-\sum_i x_i^2)^2}$

로 주어진다. 여기에 ''x''_''i''는 전체 공간에서의 직교 좌표를 의미한다. 원반 모형에서의 측지선은 경계 구면 ''S''^''n''−1에 직교하는 원으로 주어진다.

4. 성질

쌍곡기하학의 개념들은 푸앵카레 공에서 다음과 같이 구현된다.

쌍곡기하학적 개념	푸앵카레 공에서의 구현
무한대	공의 경계 $\partial B$
측지선	공의 경계와 수직으로 교차하는 원호
측지선에 대한 반사	원에 대한 반전

이 리만 계량에 대한 정규 직교 프레임은 다음과 같다.

: $e_i = \frac{1}{2} \Bigl( 1 - |\mathbf x|^2 \Bigr) \frac{\partial}{\partial x^i},$

1-형식의 쌍대 코프레임은 다음과 같다.

: $\theta^i = \frac{2}{1-|\mathbf x|\vphantom{l}^2} \, dx^i.$

유클리드 평면에서 일반화된 원 (곡률이 일정한 곡선)은 직선과 원이다. 구에서, 이들은 대원 및 소원이다. 쌍곡 평면에는 원, 호로사이클, 하이퍼사이클, 측지선(또는 "쌍곡선")의 4가지 종류의 일반화된 원 또는 ''사이클''이 있다. 푸앵카레 원반 모델에서 이들은 모두 직선 또는 원으로 표현된다.

유클리드 원:

원반 내부에 완전히 있는 것은 '''쌍곡선'''이다.
원반 내부에 있고 경계에 접하는 것은 '''호로사이클'''이다.
경계와 직교하는 것은 '''쌍곡선'''이다.
경계와 비직교적으로 교차하는 것은 '''하이퍼사이클'''이다.

경계 원의 유클리드 현:

중심을 통과하는 것은 쌍곡선이고,
중심을 통과하지 않는 것은 하이퍼사이클이다.

'''원'''(평면상의 한 점에서 주어진 거리에 있는 모든 점들의 집합, 즉 중심에서 같은 거리에 있는 점들의 집합)은 원판의 경계에 닿거나 교차하지 않고 원판 내부에 완전히 포함되는 원을 의미한다. 이 모형에서 원의 쌍곡선 중심은 일반적으로 원의 유클리드 중심과 일치하지 않지만, 푸앵카레 원판의 같은 반지름 위에 위치한다. (유클리드 중심은 항상 쌍곡선 중심보다 원판의 중심에 더 가깝다.)

'''하이퍼사이클'''은 한쪽 면에 있고 주어진 선(축)으로부터 주어진 거리에 있는 평면의 모든 점의 집합이다. 경계 원을 양의 각도로 만나지만 직각은 아닌 유클리드 원호 또는 경계 원의 현이다. 하이퍼사이클의 축은 동일한 두 개의 이상점을 공유하는 쌍곡선이다. 이는 등거리 곡선이라고도 알려져 있다.

'''호로사이클'''은 모든 수선 또는 수직 측지선이 극한 평행선이고, 모두 동일한 이상점으로 점근적으로 수렴하는 곡선이다. 원반 내부에서 원반의 경계 원에 접하는 원이다. 경계 원에 닿는 점은 호로사이클의 일부가 아니며, 이상점이자 호로사이클의 쌍곡 중심이다. 또한 모든 수직 측지선이 수렴하는 점이기도 하다.

푸앵카레 원반 모형에서 호로사이클의 반대쪽 "끝"을 나타내는 유클리드 점은 경계 원에서 중심에 수렴하지만, 쌍곡 평면에서는 호로사이클의 모든 점이 중심에서 무한히 멀리 떨어져 있으며, 호로사이클의 반대쪽 끝은 연결되지 않는다.

4. 1. 측지선

쌍곡기하학에서 측지선은 푸앵카레 원반에서 원반의 경계와 직교하는 모든 유클리드 원의 호와 원반의 모든 지름으로 구성된다.^[7]

이 모델의 거리는 케일리-클라인 거리이다. 원반 내의 서로 다른 두 점 ''p''와 ''q''가 주어지면, 이들을 연결하는 고유한 쌍곡선은 경계와 두 개의 이상점 ''a''와 ''b''에서 교차한다. 점의 순서가 ''a'', ''p'', ''q'', ''b''가 되도록 레이블을 지정하면, ''p''와 ''q'' 사이의 쌍곡선 거리는 다음과 같이 정의된다.^[7]

:

d(p,q)= \ln \frac{ \left| aq \right| \, \left| pb \right| }{ \left| ap \right| \, \left| qb \right| } .

여기서 수직선은 모델에서 점 사이를 연결하는 선분의 유클리드 길이를 나타내며(원 호를 따라가지 않음), ln은 자연 로그이다.

만약 ''u''와 ''v''가 일반적인 유클리드 노름을 가진 실수 ''n''차원 벡터 공간 '''R'''^''n''의 두 벡터이고, 둘 다 노름이 1보다 작다면, 다음과 같은 등거리 불변량을 정의할 수 있다.

:

\delta (u, v) = 2 \frac{ \lVert  u - v \rVert ^2 }{ ( 1 - \lVert  u \rVert ^2 ) ( 1 - \lVert  v \rVert ^2 ) } \,,

여기서

\lVert \cdot \rVert

는 일반적인 유클리드 노름을 나타낸다. 그러면 거리 함수는 다음과 같이 표현된다.

:

\begin{align}d(u, v) &= \operatorname{arcosh} (1+\delta (u,v)) \\&=2 \operatorname{arsinh} \sqrt{\frac{\delta (u, v)}{2}}\\\,& = 2 \ln \frac{\lVert u - v \rVert + \sqrt{\lVert u\rVert^2 \lVert v \rVert^2 - 2 u \cdot v +1}}{\sqrt{ (1 - \lVert u\rVert^2)(1- \lVert v \rVert^2)}}.\end{align}

이러한 거리 함수는 노름이 1보다 작은 모든 두 벡터에 대해 정의되며, 이러한 벡터의 집합은 상수 곡률 −1의 쌍곡 공간 모델인 거리 공간이 된다. 이 모델은 쌍곡 공간에서 교차하는 두 곡선 사이의 각도가 모델의 각도와 동일하다는 등각성을 가진다.

점 중 하나가 원점이고 점 사이의 유클리드 거리가 ''r''인 경우, 쌍곡선 거리는 다음과 같이 나타낼 수 있다.

:

\ln\left(\frac{1+r}{1-r}\right) = 2 \operatorname{artanh}r

여기서

\operatorname{artanh}

는 쌍곡선 함수의 역 쌍곡선 함수이다.

두 점이 동일한 반경에 있고 점

x' = (r', \theta)

가 원점과 점

x = (r, \theta)

사이에 있는 경우, 이들의 쌍곡선 거리는 다음과 같다.

:

\ln\left( \frac{1+r}{1-r} \cdot \frac{1-r'}{1+r'} \right) = 2 ( \operatorname{artanh}r - \operatorname{artanh}r').

이는

r' = 0

인 경우, 즉 한 점이 원점인 경우의 특수한 경우로 축소된다.

두 점

P

와

Q

가 경계 원의 지름 위에 있지 않을 때, 두 점을 지나는 고유한 쌍곡선은 자와 컴퍼스를 사용하여 작도할 수 있다. 만약 P와 Q가 경계 원의 지름 위에 있다면, 그 지름이 쌍곡선이 된다.

푸앵카레 원반 모형에 부수되는 계량 텐서는 다음과 같다.

:

ds^2 = 4 \frac{\sum_i dx_i^2}{(1-\sum_i x_i^2)^2}

여기서 ''x''_''i''는 전체 공간에서의 직교 좌표를 의미한다. 원반 모형에서의 측지선은 경계 구면 ''S''^''n''−1에 직교하는 원으로 주어진다.

4. 2. 등각성

푸앵카레 원반 모형은 쌍곡 공간 내의 교차하는 두 직선이 이루는 각이 이 모델에서의 각과 같다는 등각성을 갖는다.

푸앵카레 원반 모형에 부수되는 계량 텐서는 다음과 같다.

:

ds^2 = 4 \frac{\sum_i dx_i^2}{(1-\sum_i x_i^2)^2}

여기서 ''x''_''i''는 전체 공간에서의 직교 좌표를 의미한다. 원반 모형에서의 측지선은 경계 구면 ''S''^''n''−1에 직교하는 원으로 주어진다.

4. 3. 거리 함수

''n''차원 '''푸앵카레 공'''은 다음과 같은 계량이 주어진 단위 열린 공이다.

:

B=\left\{x\in\mathbb R^n\colon\sum_{i=1}^nx_i^2<1\right\}

여기에 주어진 리만 계량은 다음과 같다.

:

ds^2=4\frac{\sum_{i=1}^ndx_i^2}{1-\sum_{i=1}^nx^2}

구체적으로, 두 점

x,y\in B

사이의 거리는 다음과 같다.

:

d(x,y)=\cosh^{-1}\left(1+\frac{2\Vert x-y\Vert^2}{(1-\Vert x\Vert^2)(1-\Vert y\Vert^2)}\right)

^[7]

2차원 푸앵카레 공은 '''푸앵카레 원판'''이라고 한다.

쌍곡선 '''직선''' 또는 측지선은 원반 내에 포함되고 원반의 경계와 직교하는 모든 유클리드 원의 호와 원반의 모든 지름으로 구성된다.

이 모델의 거리는 케일리-클라인 거리이다. 원반 내의 서로 다른 두 점 ''p''와 ''q''가 주어지면, 이들을 연결하는 고유한 쌍곡선은 경계와 두 개의 이상점 ''a''와 ''b''에서 교차한다. 점의 순서가 ''a'', ''p'', ''q'', ''b''가 되도록 레이블을 지정한다. 즉,

\left|aq\right| > \left|ap\right|

이고

\left|pb\right| > \left|qb\right|

가 되도록 한다.

그런 다음 ''p''와 ''q'' 사이의 쌍곡선 거리는 다음과 같다.

:

d(p,q)= \ln \frac{ \left| aq \right| \, \left| pb \right| }{ \left| ap \right| \, \left| qb \right| } .

수직선은 모델에서 점 사이를 연결하는 선분의 유클리드 길이를 나타낸다(원 호를 따라가지 않음). ln은 자연 로그이다.

''u''와 ''v''가 일반적인 유클리드 노름을 가진 실수 ''n''차원 벡터 공간 '''R'''^''n''의 두 벡터이고, 둘 다 노름이 1보다 작은 경우 다음과 같은 등거리 불변량을 정의할 수 있다.

:

\delta (u, v) = 2 \frac{ \lVert  u - v \rVert ^2 }{ ( 1 - \lVert  u \rVert ^2 ) ( 1 - \lVert  v \rVert ^2 ) } \,,

여기서

\lVert \cdot \rVert

는 일반적인 유클리드 노름을 나타낸다. 그런 다음 거리 함수는 다음과 같다.

:

\begin{align}d(u, v) &= \operatorname{arcosh} (1+\delta (u,v)) \\&=2 \operatorname{arsinh} \sqrt{\frac{\delta (u, v)}{2}}\\\,& = 2 \ln \frac{\lVert u - v \rVert + \sqrt{\lVert u\rVert^2 \lVert v \rVert^2 - 2 u \cdot v +1}}{\sqrt{ (1 - \lVert u\rVert^2)(1- \lVert v \rVert^2)}}.\end{align}

이러한 거리 함수는 노름이 1보다 작은 모든 두 벡터에 대해 정의되며, 이러한 벡터의 집합을 상수 곡률 −1의 쌍곡 공간의 모델인 거리 공간으로 만든다. 이 모델은 쌍곡 공간에서 교차하는 두 곡선 사이의 각도가 모델의 각도와 동일하다는 등각성을 갖는다.

점 중 하나가 원점이고 점 사이의 유클리드 거리가 ''r''인 경우에 특화하면 쌍곡선 거리는 다음과 같다.

:

\ln\left(\frac{1+r}{1-r}\right) = 2 \operatorname{artanh}r

여기서

\operatorname{artanh}

는 쌍곡선 함수의 역 쌍곡선 함수이다. 두 점이 동일한 반경에 있고 점

x' = (r', \theta)

가 원점과 점

x = (r, \theta)

사이에 있는 경우, 이들의 쌍곡선 거리는 다음과 같다.

:

\ln\left( \frac{1+r}{1-r} \cdot \frac{1-r'}{1+r'} \right) = 2 ( \operatorname{artanh}r - \operatorname{artanh}r').

이것은

r' = 0

인 경우 이전 특수 사례로 축소된다.

푸앵카레 원반 모형의 관련 계량 텐서는 다음과 같다.^[8]

:

ds^2 = 4 \frac{\sum_i dx_i^2}{\left(1-\sum_i x_i^2\right)^2} = \frac{ 4\, \lVert d \mathbf{x} \rVert \vphantom{l}^2 }{ \bigl(1 - \lVert \mathbf{x} \rVert \vphantom{l}^2 \bigr) ^2 }

여기서 ''x''_''i''는 주변 유클리드 공간의 데카르트 좌표이다.

이 리만 계량에 대한 정규 직교 프레임은 다음과 같다.

:

e_i = \frac12 \Bigl( 1 - |\mathbf x|^2 \Bigr) \frac{\partial}{\partial x^i},

1-형식의 쌍대 코프레임은 다음과 같다.

:

\theta^i = \frac2{1-|\mathbf x|\vphantom{l}^2} \, dx^i.

5. 다른 쌍곡 기하학 모형과의 관계

푸앵카레 원반 모형은 쌍곡 기하학을 나타내는 여러 모형들과 관계를 맺고 있다.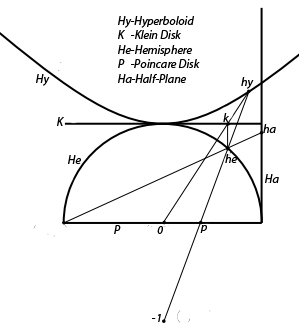

벨트라미-클라인 모형: 두 모형 모두 쌍곡 평면 전체를 원반에 투영하며, 반구 모형에 대한 투영을 통해 서로 관련된다. 클라인 원반 모형은 정사영, 푸앵카레 원반 모형은 스테레오그래픽 투영이다.
푸앵카레 상반평면 모형: 두 모형은 뫼비우스 변환으로 관련된다.
쌍곡면 모형: 푸앵카레 원반 모형은 쌍곡면 모형과 원근 투영으로 관련된다.

5. 1. [[벨트라미-클라인 모형]]

벨트라미-클라인 모형(또는 클라인 원반 모형)과 푸앵카레 원반은 모두 쌍곡 평면 전체를 원반에 투영하는 모형이다. 두 모형은 반구 모형에 대한 투영을 통해 서로 관련되어 있다. 클라인 원반 모형은 반구 모형에 대한 정사영인 반면 푸앵카레 원반 모형은 스테레오그래픽 투영이다.

클라인 원반 모형의 장점은 이 모형에서 선이 유클리드 직선 현이라는 것이다. 단점은 클라인 원반 모형이 등각이 아니라는 점이다(원과 각이 왜곡됨).

두 모형에서 동일한 선을 하나의 원반에 투영하면 두 선 모두 동일한 두 개의 이상점을 통과한다.(이상점은 동일한 위치에 유지됨) 또한, 클라인 원반 모형에서 현의 극은 푸앵카레 원반 모형에서 호를 포함하는 원의 중심이다.

푸앵카레 원반 모형의 점 (''x'',''y'')는 클라인 모형에서 로 매핑된다.

클라인 모형의 점 (''x'',''y'')는 푸앵카레 원반 모형에서 \ , \ \frac{y }{1+\sqrt{1- x^2- y^2}} \right) |(''x'', ''y'')는 푸앵카레 원반 모형에서 (x/(1 + √(1 - x^2 - y^2)), y/(1 + √(1 - x^2 - y^2)))}}로 매핑된다.

이상점의 경우

x^2 + y^2 = 1

|x^2 + y^2 = 1^영어이고 공식은

x = x \ , \ y = y

|x = x, y = y^영어가 되므로 점은 고정된다.

만약

u

|u^영어가 푸앵카레 원반 모형의 점을 나타내는 1보다 작은 노름의 벡터라면, 클라인 원반 모형의 해당 점은 다음과 같이 주어진다.

반대로, 벨트라미-클라인 모형의 점을 나타내는 1보다 작은 노름의 벡터

s

|s^영어로부터 푸앵카레 원반 모형의 해당 점은 다음과 같이 주어진다.

= \frac{\left(1-\sqrt{1-s \cdot s}\right)s}{s \cdot s}.|u = s/(1 + √(1 - s · s)) = ((1 - √(1 - s · s))s)/(s · s)}}

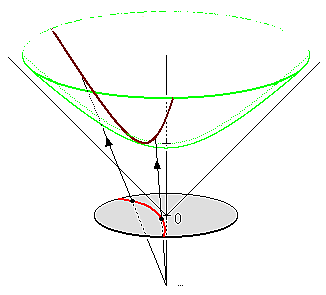
붉은 호는 원반 모형에서의 측지선이다. 이것을 녹색 쌍곡면에 투영한 것이 갈색 측지선이다.

푸앵카레 원반 모형은 클라인 모형과 마찬가지로 쌍곡면 모형과 사영적으로 관계한다. 쌍곡면 모형에서의 점을 결정하는 상반 쌍곡면 위의 점 을 초곡면 ''t'' = 0|''t'' = 0^영어 위로 사영하려면 점 을 지나는 직선과의 교점을 생각하면 된다. 이를 통해 푸앵카레 원반 모형에서의 점과의 대응이 정해진다.

쌍곡면 위의 직교 좌표계 (''t'', ''x_i'')와 평면 위의 직교 좌표계 (''y_i'') 사이의 변환 공식은

:

및

:|(t, x_i) = (1 + Σy_i^2, 2y_i)/(1 - Σy_i^2)}}

로 주어진다. 이 공식은 구면과 평면 사이의 입체 사영에 대한 공식과 대조된다.

5. 2. [[푸앵카레 상반평면 모형]]

푸앵카레 원판 모형과 푸앵카레 상반평면 모형은 뫼비우스 변환으로 관련되어 있다. 푸앵카레 원판 모형의 점을 나타내는, 노름이 1보다 작은 복소수

u \in \mathbb{D}

가 있다면, 상반평면

z \in \mathbb{H}

의 대응되는 점은 케일리 변환

C: \mathbb{H} \to \mathbb{D}

의 역변환으로 주어진다.

:

C^{-1}(u) = z = i\frac{1+u}{1-u}.

C^{-1}

에서 점

\{ 0, 1, -i, i \} \in \mathbb{D}

는

\{i, \infty, 1, -1 \} \in \mathbb{H}

로 매핑된다.

실수 좌표로 표현하면, 원반 모형의 점 (''x'',''y'')는 상반평면 모형에서

\left( \frac{2x }{x^2+ (1-y)^2} \ , \  \frac{1-x^2-y^2}{x^2+ (1-y)^2} \right) \,

로 변환된다.

상반평면 모형의 점 (''x'',''y'')는 원반 모형에서

\left( \frac{2x }{x^2+ (1+y)^2} \ , \ \frac{x^2+y^2-1}{x^2+ (1+y)^2} \right) \,

로 변환된다.

5. 3. [[쌍곡면 모형]]

푸앵카레 원반 모형은 클라인 모형과 마찬가지로 쌍곡면 모형과 원근 투영으로 관련되어 있다. 쌍곡면 모형에서 쌍곡면의 위쪽 시트에 있는 점 [''t'', ''x''₁, ..., ''x''_''n'']이 있다면, 이를 통해 쌍곡면 모형의 점을 정의할 수 있으며, [−1, 0, ..., 0]을 통과하는 선과 교차하여 평면 ''t'' = 0으로 투영할 수 있다. 그 결과가 푸앵카레 원반 모형의 해당 점이다.

데카르트 좌표계(''t'', ''x_i'')와 평면의 (''y_i'')에 대한 변환 공식은 다음과 같다.

:

y_i = \frac{x_i}{1 + t}

:

(t, x_i) = \frac {\left( 1+\sum{y_i^2},\, 2 y_i \right)} {1-\sum{y_i^2}} \,.

구와 평면 사이의 스테레오 투영에 대한 공식을 비교해 보라.

6. 해석 기하학적 구성

해석 기하학에서 기본적인 구성은 주어진 두 점을 지나는 직선을 구하는 것이다. 푸앵카레 원판 모형에서 평면 직선은 다음과 같은 형태의 원호 일부로 주어진다.

: $x^2 + y^2 + a x + b y + 1 = 0$

이는 단위원에 직교하는 원호 또는 지름을 나타내는 식의 일반형이다. 원판 내의 지름 위에 있지 않은 두 점 ''u'', ''v''가 주어졌을 때, 이 두 점을 지나는 위의 형태로 표시되는 원을 계산할 수 있으며, 그 식은 다음과 같다.

: $x^2 + y^2 + \frac{u_2(v_1^2+v_2^2)-v_2(u_1^2+u_2^2)+u_2-v_2}{u_1v_2-u_2v_1}x + \frac{v_1(u_1^2+u_2^2)-u_1(v_1^2+v_2^2)+v_1-u_1}{u_1v_2-u_2v_1}y + 1 = 0$

두 점 ''u'', ''v''가 원판의 경계상의 점이고, 지름의 양 끝점이 아니라면, 위 식은 다음과 같이 간략화된다.

: $x^2+y^2+\frac{2(u_2-v_2)}{u_1v_2-u_2v_1}x - \frac{2(u_1-v_1)}{u_1v_2-u_2v_1}y + 1 = 0$

6. 1. 직선 (측지선)

두 점 P와 Q가 경계 원의 지름 위에 있지 않을 때, 두 점을 지나는 쌍곡선(직선)은 자와 컴퍼스를 사용하여 다음과 같이 작도할 수 있다.

1. P'를 경계 원에 대한 점 P의 원반전으로 둔다.

2. Q'를 경계 원에 대한 점 Q의 반전으로 둔다.

3. M을 선분 PP'의 중점으로 둔다.

4. N을 선분 QQ'의 중점으로 둔다.

5. 점 M을 지나고 선분 PP'에 수직인 선 m을 그린다.

6. 점 N을 지나고 선분 QQ'에 수직인 선 n을 그린다.

7. 선 m과 선 n이 만나는 점을 C로 둔다.

8. 중심이 C이고 P(와 Q)를 지나는 원 c를 그린다.

9. 원판 내부에 있는 원 c의 부분이 쌍곡선이다.

만약 P와 Q가 경계 원의 지름 위에 있다면, 그 지름이 쌍곡선이다.

또 다른 방법은 다음과 같다.

1. M을 선분 PQ의 중점으로 둔다.

2. 점 M을 지나고 선분 PQ에 수직인 선 m을 그린다.

3. P'를 경계 원에 대한 점 P의 반전으로 둔다.

4. N을 선분 PP'의 중점으로 둔다.

5. 점 N을 지나고 선분 PP'에 수직인 선 n을 그린다.

6. 선 m과 선 n이 만나는 점을 C로 둔다.

7. 중심이 C이고 P(와 Q)를 지나는 원 c를 그린다.

8. 원판 내부에 있는 원 c의 부분이 쌍곡선이다.

해석 기하학에서 기본적인 구성은 주어진 두 점을 지나는 직선을 찾는 것이다. 푸앵카레 원판 모형에서 평면상의 직선은 다음 형태의 방정식을 갖는 원의 일부로 정의된다.

:

x^2 + y^2 + a x + b y + 1 = 0

이는 단위 원에 직교하는 원의 일반적인 형태이거나 지름으로 정의된다. 원반 내에 있는 지름 위에 있지 않은 두 점 ''u = (u₁,u₂)''와 ''v = (v₁,v₂)''가 주어졌을 때, 두 점을 모두 지나는 이 형태의 원에 대해 해를 구하면 다음과 같다.

:

\begin{align}x^2 + y^2 & {} + \frac{u_2(v_1^2+v_2^2+1)-v_2(u_1^2+u_2^2+1)}{u_1v_2-u_2v_1}x \\[8pt]& {} + \frac{v_1(u_1^2+u_2^2+1)-u_1(v_1^2+v_2^2+1)}{u_1v_2-u_2v_1}y + 1 = 0 \,.\end{align}

만약 점 ''u''와 ''v''가 지름의 끝점에 있지 않은 원반의 경계상의 점이라면, 위의 식은 다음과 같이 단순화된다.

:

x^2+y^2+\frac{2(u_2-v_2)}{u_1v_2-u_2v_1}x + \frac{2(v_1-u_1)}{u_1v_2-u_2v_1}y + 1 = 0

6. 2. 각

양 끝점(''이상점'')이 단위 벡터 ''u''와 ''v''로 주어지는 원호와 양 끝점이 ''s''와 ''t''인 호 사이의 각도를 계산하는 공식을 통해 푸앵카레 원판 모델에서의 각을 이해할 수 있다. 클라인 모델과 푸앵카레 원반 모델에서 이상점은 동일하므로 각 모델에 대한 공식은 동일하다.

두 모델의 선이 모두 지름인 경우, 즉 ''v'' = −''u''이고 ''t'' = −''s''인 경우, 단순히 두 단위 벡터 사이의 각도를 구하는 것이며, 각도 θ에 대한 공식은 다음과 같다.

:

\cos(\theta) = u \cdot s \,.

만약 ''v'' = −''u''이지만, ''t'' = −''s''가 아닌 경우, 공식은 외적(

\wedge

)을 사용하여 다음과 같이 된다.

:

\cos^2(\theta) = \frac{P^2}{QR},

여기서

:

P = u \cdot (s-t) \,,

:

Q = u \cdot u \,,

:

R = (s-t) \cdot (s-t) - (s \wedge t) \cdot (s \wedge t) \,.

두 현 모두 지름이 아닌 경우 일반 공식은 다음과 같다.

:

\cos^2(\theta) = \frac{P^2}{QR} \,,

여기서

:

P = (u-v) \cdot (s-t) - (u \wedge v) \cdot (s \wedge t) \,,

:

Q = (u-v) \cdot (u-v) - (u \wedge v) \cdot (u \wedge v) \,,

:

R = (s-t) \cdot (s-t) - (s \wedge t) \cdot (s \wedge t) \,.

비네-코시 항등식을 사용하고 이것들이 단위 벡터라는 사실을 이용하여 위의 식을 내적만으로 다시 쓸 수 있다.

:

P = (u-v) \cdot (s-t) + (u \cdot t)(v \cdot s) - (u \cdot s)(v \cdot t) \,.

:

Q = (1 - u \cdot v)^2 \,,

:

R = (1 - s \cdot t)^2 \,.

7. 예술적 응용

M. C. 에셔는 2차원 평면에서 무한대를 표현하는 개념을 탐구했다. 1956년경 캐나다 수학자 H.S.M. 코세터와의 논의는 에셔가 쌍곡 테셀레이션, 즉 쌍곡 평면의 정규 타일링에 관심을 갖도록 영감을 주었다. 에셔의 목판화 ''원의 극한 I–IV''는 1958년에서 1960년 사이에 이 개념을 보여주며, 마지막 작품은 1960년의 ''[https://web.archive.org/web/20120717033517/http://www.mcescher.com/Gallery/recogn-bmp/LW436.jpg 원의 극한 IV: 천국과 지옥]''이다.^[9] 브루노 에른스트에 따르면, 그중 최고는 ''원의 극한 III''이다.

에셔는 기하학자 코셰터의 조언에 따라 1958년부터 1960년까지 '''푸앵카레 원판'''을 기반으로 "원의 극한" 시리즈를 제작했다.

HyperRogue는 로그라이크 게임으로, 세계 기하학에 쌍곡 평면을 사용하며, 푸앵카레 원판 모형도 사용한다.

참조

_[1] 서적 The Road To Reality: A Complete Guide to the Laws of the Universe https://archive.org/[...] Jonathan Cape 2004
_[2] 논문 "Hyperbolic geometry: the first 150 years."
_[3] 학술지 Théorie des groupes fuchsiens 1882-12-01
_[4] 서적 Science and hypothesis http://archive.org/d[...] London W. Scott 1905
_[5] 서적 Rudolf Carnap: Early Writings: The Collected Works of Rudolf Carnap, Volume 1 https://books.google[...] Oxford University Press 2019-06-25
_[6] 서적 The Philosophy of Space and Time https://books.google[...] Courier Corporation 2012-03-13
_[7] 서적 Geometry II Springer
_[8] 웹사이트 Comparing metric tensors of the Poincare and the Klein disk models of hyperbolic geometry https://math.stackex[...] 2015-05-23
_[9] 웹사이트 Escher's Circle Limit Exploration http://euler.slu.edu[...]
_[10] 저널

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com