다각수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 페르마 다각수 정리
5. 예
- 5.1. 평면도형수
- 5.2. 입체도형수
6. 다각수와 관련된 문제
7. 역사
참조

1. 개요

다각수는 정수 m(m≥3)과 n에 대해 정의되는 수로, n번째 m각수는 Pol(m;n)으로 표기된다. 다각수는 삼각수, 정사각수, 오각수, 육각수 등으로 분류되며, 각 수는 특정 도형의 형태로 배열될 수 있는 점의 개수를 나타낸다. 다각수는 특정 공식을 통해 계산되며, 다른 다각수와의 관계, 점화식, 생성 함수 등을 갖는다. 페르마 다각수 정리는 모든 자연수가 m개의 m각수의 합으로 나타낼 수 있다는 것을 의미한다. 다각수는 펠 방정식과 관련되어 특정 다각수 집합에 모두 속하는 수를 찾는 문제로 이어진다.

더 읽어볼만한 페이지

도형수 - 세제곱수
세제곱수는 정수를 세 번 곱한 수로, 단위 길이 변을 가진 정육면체를 쌓아 더 큰 정육면체를 만들 수 있는 수이며, 모든 정수는 9개 이하의 세제곱수의 합으로 표현 가능하다는 특징이 있다.
도형수 - 삼각수
삼각수는 1부터 n까지의 자연수 합으로, n(n+1)/2로 계산되며, 삼각형 모양으로 표현되고 조합론적 문제 해결에 활용되는 수이다.
유희 수학 - 뫼비우스의 띠
"상상력" 한가 아닌 답변을 바랍니다.
유희 수학 - 암산
암산은 필기도구나 계산기 없이 머릿속으로 수를 계산하는 행위로, 두뇌 발달에 긍정적 영향을 주어 교육적으로 중요하며, 특정 직업에서는 필수적인 능력으로 여겨지고, 주판 암산, 개인 암산 기술 개발, 플래시 암산 등 다양한 방식이 존재하며 암산 대회도 개최된다.
다각형 - 폴리아몬드
폴리아몬드는 정삼각형을 이어 붙여 만든 도형으로, 삼각형 개수에 따라 n-아몬드라 불리며 조합론에서 종류와 개수를 파악하는 것이 중요하고, 평행 이동, 회전, 반사에 따라 자유형, 단면형, 고정형으로 분류되며, 폴리오미노, 폴리헥스와 유사하고 보드 게임의 구성 요소로 활용된다.
다각형 - 대각선
대각선은 다각형이나 다면체에서 서로 인접하지 않은 꼭짓점을 연결하는 선분이며, 다각형은 변의 개수에 따라, 다면체는 면의 위치에 따라 대각선의 개수와 종류가 달라지고, 기하학에서는 데카르트 곱의 부분 집합으로 정의되기도 한다.

다각수
다각수 정보
종류	정다각형에 대응하는 수
성질	수론과 조합론에서 연구 대상
일반항 공식	P(s,n) = (s-2)n(n-1)/2 + n
변수 설명	s = 변의 수 n = 순서 (n번째 다각수)
다른 이름	도형수, 형상수
예시
삼각수	1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
사각수 (제곱수)	1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ...
오각수	1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...
육각수	1, 6, 15, 28, 45, 66, 91, 120, 153, 190, ...
칠각수	1, 7, 18, 34, 55, 81, 112, 148, 189, 235, ...
팔각수	1, 8, 21, 40, 65, 96, 133, 176, 225, 280, ...
구각수	1, 9, 24, 46, 75, 111, 154, 204, 261, 325, ...
십각수	1, 10, 27, 52, 85, 126, 175, 232, 297, 370, ...
십일각수	1, 11, 30, 58, 95, 141, 196, 260, 333, 415, ...
십이각수	1, 12, 33, 64, 105, 156, 217, 288, 369, 460, ...

2. 정의

자연수 $m\ge 3$ 및 $n$ 이 주어졌을 때, $n$ 번째 ''' $m$ 각수'''( $m$ 角數, $m$ -gonal number^영어) $\operatorname{Pol}(m;n)$ 은 다음과 같이 정의된다.

: $\operatorname{Pol}(m;n)=\sum_{k=0}^{n-1}(1+(m-2)k)=\frac{n((m-2)n-(m-4))}2$

특히,

$\operatorname{Pol}(3;n)=n(n+1)/2$ 를 '''삼각수'''라고 한다.
$\operatorname{Pol}(4;n)=n^2$ 를 '''정사각수'''라고 한다.
$\operatorname{Pol}(5;n)=n(3n-1)/2$ 를 '''오각수'''라고 한다.
$\operatorname{Pol}(6;n)=n(2n-1)$ 를 '''육각수'''라고 한다.

예를 들어 숫자 10은 삼각수로 배열될 수 있지만, 정사각형으로 배열될 수 없다. 반면에 숫자 9는 정사각수로 배열될 수 있다. 36과 같은 일부 숫자는 정사각형과 삼각형 모두로 배열될 수 있다. (제곱 삼각수 참조).

만약

s

가 다각형의 변의 수라면,

n

번째

s

-각수

P(s,n)

를 구하는 공식은 다음과 같다.^[1]

:

P(s,n) = \frac{(s-2)n^2-(s-4)n}{2}

또는

:

P(s,n) = (s-2)\frac{n(n-1)}{2}+n

n

번째

s

-각수는 또한 삼각수

T_n

와 다음과 같은 관계를 가진다.^[1]

:

P(s,n) = (s-2)T_{n-1} + n = (s-3)T_{n-1} + T_n\, .

따라서:

:

\begin{align}P(s,n+1)-P(s,n) &= (s-2)n + 1\, ,\\P(s+1,n) - P(s,n) &= T_{n-1} = \frac{n(n-1)}{2}\, ,\\P(s+k,n) - P(s,n) &= k T_{n-1} = k\frac{n(n-1)}{2}\, .\end{align}

주어진

s

-각수

P(s,n) = x

에 대해, 다음 공식을 사용하여

n

을 구할 수 있다.

:

n = \frac{\sqrt{8(s-2)x+{(s-4)}^2}+(s-4)}{2(s-2)}

그리고 다음 공식을 사용하여

s

을 구할 수 있다.

:

s = 2+\frac{2}{n}\cdot\frac{x-n}{n-1}

.

P(s,n) = (s-2)T_{n-1} + n

에 6변의 경우(

s=6

)를 적용하면 다음과 같다.

:

P(6,n) = 4T_{n-1} + n

T_{n-1} = \frac{n(n-1)}{2}

이므로, 다음이 성립한다.

:

P(6,n) = \frac{4n(n-1)}{2} + n = \frac{2n(2n-1)}{2} = T_{2n-1}

이것은

n

번째 육각수

P(6,n)

가

(2n − 1)

번째 삼각수

T_{2n−1}

이기도 하다는 것을 보여준다. 따라서, 홀수 번째 삼각수를 취함으로써 모든 육각수를 찾을 수 있다.^[1]

:'''1''', 3, '''6''', 10, '''15''', 21, '''28''', 36, '''45''', 55, '''66''', ...

$s$	이름	공식	$n$										합 역수^[2]^[3]	OEIS 번호
$s$	이름	공식	1	2	3	4	5	6	7	8	9	10	합 역수^[2]^[3]	OEIS 번호
2	자연수 (선분)	$n$	1	2	3	4	5	6	7	8	9	10	∞ (발산)
3	삼각수	$\frac{n(n+1)}{2}$	1	3	6	10	15	21	28	36	45	55	2
4	정사각수	$n^2$	1	4	9	16	25	36	49	64	81	100
5	오각수	$\frac{n(3n-1)}{2}$	1	5	12	22	35	51	70	92	117	145
6	육각수	$n(2n-1)$	1	6	15	28	45	66	91	120	153	190
7	칠각수	$\frac{n(5n-3)}{2}$	1	7	18	34	55	81	112	148	189	235
8	팔각수	$n(3n-2)$	1	8	21	40	65	96	133	176	225	280
9	구각수	$\frac{n(7n-5)}{2}$	1	9	24	46	75	111	154	204	261	325
10	십각수	$n(4n-3)$	1	10	27	52	85	126	175	232	297	370
11	십일각수	$\frac{n(9n-7)}{2}$	1	11	30	58	95	141	196	260	333	415
12	십이각수	$n(5n-4)$	1	12	33	64	105	156	217	288	369	460
13	십삼각수	$\frac{n(11n-9)}{2}$	1	13	36	70	115	171	238	316	405	505
14	십사각수	$n(6n-5)$	1	14	39	76	125	186	259	344	441	550
15	십오각수	$\frac{n(13n-11)}{2}$	1	15	42	82	135	201	280	372	477	595
16	십육각수	$n(7n-6)$	1	16	45	88	145	216	301	400	513	640
17	십칠각수	$\frac{n(15n-13)}{2}$	1	17	48	94	155	231	322	428	549	685
18	십팔각수	$n(8n-7)$	1	18	51	100	165	246	343	456	585	730
19	십구각수	$\frac{n(17n-15)}{2}$	1	19	54	106	175	261	364	484	621	775
20	이십각수	$n(9n-8)$	1	20	57	112	185	276	385	512	657	820
21	이십일각수	$\frac{n(19n-17)}{2}$	1	21	60	118	195	291	406	540	693	865
22	이십이각수	$n(10n-9)$	1	22	63	124	205	306	427	568	729	910
23	이십삼각수	$\frac{n(21n-19)}{2}$	1	23	66	130	215	321	448	596	765	955
24	이십사각수	$n(11n-10)$	1	24	69	136	225	336	469	624	801	1000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
10000	미리어곤	$\frac{n(9998n-9996)}{2}$	1	10000	29997	59992	99985	149976	209965	279952	359937	449920

정수열 백과사전은 그리스어 접두사를 사용하는 용어(예: "팔각") 대신 숫자를 사용하는 용어(즉, "8각")를 사용한다.

이 표의 속성은 다음 항등식으로 표현할 수 있다.

: $2\,P(s,n) = P(s+k,n) + P(s-k,n),$ (단, $k = 0, 1, 2, 3, ..., s-3$ )

0번째 다각수는 모두 형식적으로 0으로 간주할 수 있다.

n번째 p각수를 P_p,n이라고 하면:

: $P_{p,n+1} - P_{p,n} = (p-2)n + 1\,$

이 되고, 따라서 P_p,n은 등차수열의 합

: $\begin{align} P_{p,n} &= \sum_{k=0}^{n-1} \left\{ (p-2)k+1 \right\}\\ &= \frac{1}{2} n \left[1 + \left\{ (p-2)(n-1) + 1 \right\} \right]\\ &= \frac{(p-2)n^2 - (p-4)n}{2}\end{align}$

이 된다.

이 식으로부터, 2번째 p각수는 p이고, 3번째 p각수는 3(p − 1)이라는 것을 알 수 있다.

여기서 형식적으로 "이각수" (p = 2)를 생각하면,

: $P_{2,n} = n \,$

이 되어 자연수열 자체가 된다. 이는 점을 직선상에 늘어놓는 것에 해당한다. 다만 고대 그리스의 수학자들이 직선수라고 부른 것은 직사각형으로 배열할 수 없기 때문이다.

3. 성질

임의의 자연수는 많아야 ''p''개의 ''p'' 각수의 합으로 나타낼 수 있다. 이를 다각수 정리라고 한다.^[1]
1번째 다각수는 1, 2번째 ''p'' 각수는 ''p''이다. 따라서 2 이외의 자연수는 어떤 다각수이다.
3번째 이후의 다각수는 합성수이다.
''n'' 번째 ''p'' 각수는 ''n''이 짝수이고 ''p''가 홀수일 때에 한하여, ''n''의 배수가 아니다.
''n'' 번째 ''p'' 각수와 ''n'' + 1번째 ''p'' 각수의 차이는 (''p'' − 2)''n'' + 1이다.
''n'' 번째 ''p'' 각수와 ''n'' 번째 ''p'' + 1 각수의 차이는, ''p''에 관계없이 ''n'' 만으로 결정되며, ''n'' − 1번째 삼각수와 같다.

3. 1. 점화식

m각수

\operatorname{Pol}(m;n)

에 대하여, 다음과 같은 점화식이 성립한다.

:

\operatorname{Pol}(m;n+1)=\operatorname{Pol}(m;n)+(m-2)n+1

3. 2. 생성 함수

:

\sum_{n=0}^\infty \operatorname{Pol}(m;n)x^n=\frac{x((m-3)x+1)}{(1-x)^3}

3. 3. 일반항 공식 유도

n번째 p각수 P_p,n은 등차수열의 합으로 표현 가능하다.^[1]

:

\begin{align} P_{p,n} &= \sum_{k=0}^{n-1} \left\{ (p-2)k+1 \right\}\\ &= \frac{1}{2} n \left[1 + \left\{ (p-2)(n-1) + 1 \right\} \right]\\ &= \frac{(p-2)n^2 - (p-4)n}{2}\end{align}

이 식에서 2번째 p각수는 p이고, 3번째 p각수는 3(p - 1)임을 알 수 있다.

형식적으로 "이각수" (p = 2)를 생각하면,

:

P_{2,n} = n \,

이 되어 자연수열 자체가 된다. 이는 점을 직선상에 늘어놓는 것에 해당한다. 다만 고대 그리스의 수학자들은 직사각형으로 배열할 수 없기 때문에 자연수를 직선수라고 부르지 않았다.

3. 4. 다른 다각수와의 관계

n^영어번째 육각수는 (2n^영어 - 1)번째 삼각수이다. 모든 육각수는 홀수 번째 삼각수를 취함으로써 찾을 수 있다.^[1]

:'''1''', 3, '''6''', 10, '''15''', 21, '''28''', 36, '''45''', 55, '''66''', ...

:

P(s,n) = (s-2)T_{n-1} + n = (s-3)T_{n-1} + T_n

(여기서

T_n

은 n번째 삼각수)

:

P(s,n+1)-P(s,n) = (s-2)n + 1

:

P(s+1,n) - P(s,n) = T_{n-1} = \frac{n(n-1)}{2}

:

P(s+k,n) - P(s,n) = k T_{n-1} = k\frac{n(n-1)}{2}

:

2\,P(s,n) = P(s+k,n) + P(s-k,n)

(

k = 0, 1, 2, 3, ..., s-3

)

임의의 자연수는 많아야 ''p''개의 ''p'' 각수의 합으로 나타낼 수 있다. 이를 다각수 정리라고 한다.
1번째 다각수는 1, 2번째 ''p'' 각수는 ''p''이다. 따라서 2 이외의 자연수는 어떤 다각수이다.
''n'' 번째 ''p'' 각수와 ''n'' + 1번째 ''p'' 각수의 차이는 (''p'' − 2) ''n'' + 1이다.
''n'' 번째 ''p'' 각수와 ''n'' 번째 ''p'' + 1 각수의 차이는, ''p''에 관계없이 ''n'' 만으로 결정되며, ''n'' − 1번째 삼각수와 같다.

4. 페르마 다각수 정리

임의의 자연수는 많아도 $m$ 개의 $m$ 각수의 합으로 나타낼 수 있다. 즉, 임의의 자연수 $a$ 에 대하여, 다음을 만족시키는 자연수 $n_1,\dots,n_m$ 이 존재한다.

: $a=\sum_{k=1}^m\operatorname{Pol}(m;n_k)$

이를 페르마 다각수 정리라고 한다. (만약 $m' 에 대하여 m' 개의 m 각수로 나타내려면 n_{m'+1}=\cdots=n_m=0 을 취하면 된다.)$

5. 예

예를 들어, 숫자 10은 삼각수로 배열될 수 있지만, 정사각수로는 배열될 수 없다. 반면에 숫자 9는 정사각수로 배열될 수 있다(제곱수 참조). 36과 같은 일부 숫자는 정사각형과 삼각형 모두로 배열될 수 있다 (제곱 삼각수 참조).

관례적으로, 1은 모든 변의 개수에 대해 첫 번째 다각수이다. 다각형을 다음 크기로 확대하는 규칙은 두 개의 인접한 팔을 한 점씩 연장한 다음 해당 점 사이에 필요한 추가 변을 추가하는 것이다.

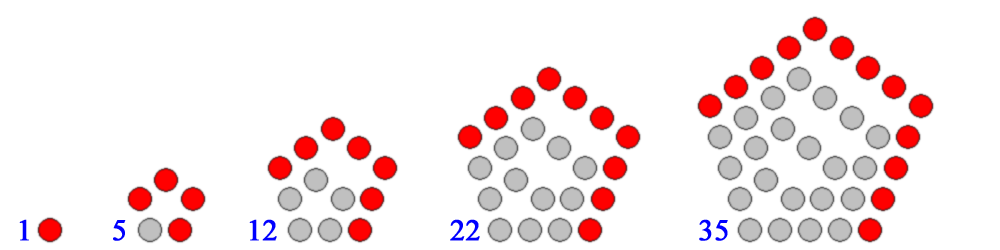
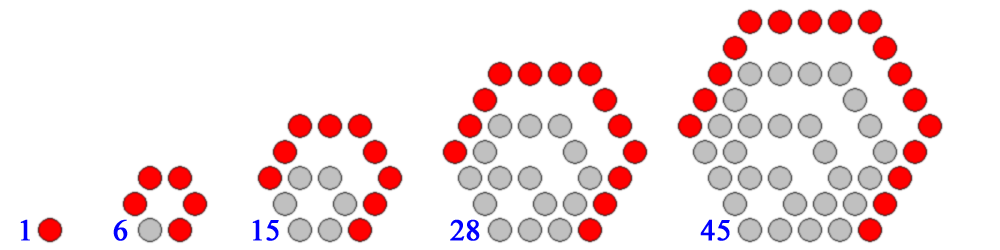
오각수 이상에서는 점을 회전대칭으로 배열하지 않는 것에 주의한다.

5. 1. 평면도형수

주어진 자연수

3\le m\le 30

에 대하여,

m

각수는 다음과 같다.

$m$	명칭	$\operatorname{Pol}(m;n)$	처음 20항 ( $0\le n\le 19$ )
3	삼각수	$n(n+1)/2$	0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, ...
4	정사각수	$n^2$	0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, ...
5	오각수	$n(3n-1)/2$	0, 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, ...
6	육각수	$n(2n-1)$	0, 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, ...
7	칠각수(heptagonal number^영어)	$n(5n-3)/2$	0, 1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403, 469, 540, 616, 697, 783, 874, ...
8	팔각수	$n(3n-2)$	0, 1, 8, 21, 40, 65, 96, 133, 176, 225, 280, 341, 408, 481, 560, 645, 736, 833, 936, 1045, ...
9	구각수(nonagonal number^영어)	$n(7n-5)/2$	0, 1, 9, 24, 46, 75, 111, 154, 204, 261, 325, 396, 474, 559, 651, 750, 856, 969, 1089, 1216, ...
10	십각수(decagonal number^영어)	$n(4n-3)$	0, 1, 10, 27, 52, 85, 126, 175, 232, 297, 370, 451, 540, 637, 742, 855, 976, 1105, 1242, 1387, ...
11	십일각수(hendecagonal number^영어)	$n(9n-7)/2$	0, 1, 11, 30, 58, 95, 141, 196, 260, 333, 415, 506, 606, 715, 833, 960, 1096, 1241, 1395, 1558, ...
12	십이각수(dodecagonal number^영어)	$n(5n-4)$	0, 1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, ...
13	십삼각수(tridecagonal number^영어)	$n(11n-9)/2$	0, 1, 13, 36, 70, 115, 171, 238, 316, 405, 505, 616, 738, 871, 1015, 1170, 1336, 1513, 1701, 1900, ...
14	십사각수(tetradecagonal number^영어)	$n(6n-5)$	0, 1, 14, 39, 76, 125, 186, 259, 344, 441, 550, 671, 804, 949, 1106, 1275, 1456, 1649, 1854, 2071, ...
15	십오각수(pentadecagonal number^영어)	$n(13n-11)/2$	0, 1, 15, 42, 82, 135, 201, 280, 372, 477, 595, 726, 870, 1027, 1197, 1380, 1576, 1785, 2007, 2242, ...
16	십육각수(hexadecagonal number^영어)	$n(7n-6)$	0, 1, 16, 45, 88, 145, 216, 301, 400, 513, 640, 781, 936, 1105, 1288, 1485, 1696, 1921, 2160, 2413, ...
17	십칠각수(heptadecagonal number^영어)	$n(15n-13)/2$	0, 1, 17, 48, 94, 155, 231, 322, 428, 549, 685, 836, 1002, 1183, 1379, 1590, 1816, 2057, 2313, 2584, ...
18	십팔각수(octadecagonal number^영어)	$n(8n-7)$	0, 1, 18, 51, 100, 165, 246, 343, 456, 585, 730, 891, 1068, 1261, 1470, 1695, 1936, 2193, 2466, 2755, ...
19	십구각수(nonadecagonal number^영어)	$n(17n-15)/2$	0, 1, 19, 54, 106, 175, 261, 364, 484, 621, 775, 946, 1134, 1339, 1561, 1800, 2056, 2329, 2619, 2926, ...
20	이십각수(Icosagonal number^영어)	$n(9n-8)$	0, 1, 20, 57, 112, 185, 276, 385, 512, 657, 820, 1001, 1200, 1417, 1652, 1905, 2176, 2465, 2772, 3097, ...
21	이십일각수(icosihenagonal number^영어)	$n(19n-17)/2$	0, 1, 21, 60, 118, 195, 291, 406, 540, 693, 865, 1056, 1266, 1495, 1743, 2010, 2296, 2601, 2925, 3268, ...
22	이십이각수(icosidigonal number^영어)	$n(10n-9)$	0, 1, 22, 63, 124, 205, 306, 427, 568, 729, 910, 1111, 1332, 1573, 1834, 2115, 2416, 2737, 3078, 3439, ...
23	이십삼각수(icositrigonal number^영어)	$n(21n-19)/2$	0, 1, 23, 66, 130, 215, 321, 448, 596, 765, 955, 1166, 1398, 1651, 1925, 2220, 2536, 2873, 3231, 3610, ...
24	이십사각수(icositetragonal number^영어)	$n(11n-10)$	0, 1, 24, 69, 136, 225, 336, 469, 624, 801, 1000, 1221, 1464, 1729, 2016, 2325, 2656, 3009, 3384, 3781, ...
25	이십오각수(icosipentagonal number^영어)	$n(23n-21)/2$	0, 1, 25, 72, 142, 235, 351, 490, 652, 837, 1045, 1276, 1530, 1807, 2107, 2430, 2776, 3145, 3537, 3952, ...
26	이십육각수(icosihexagonal number^영어)	$n(12n-11)$	0, 1, 26, 75, 148, 245, 366, 511, 680, 873, 1090, 1331, 1596, 1885, 2198, 2535, 2896, 3281, 3690, 4123, ...
27	이십칠각수(icosiheptagonal number^영어)	$n(25n-23)/2$	0, 1, 27, 78, 154, 255, 381, 532, 708, 909, 1135, 1386, 1662, 1963, 2289, 2640, 3016, 3417, 3843, 4294, ...
28	이십팔각수(icosioctagonal number^영어)	$n(13n-12)$	0, 1, 28, 81, 160, 265, 396, 553, 736, 945, 1180, 1441, 1728, 2041, 2380, 2745, 3136, 3553, 3996, 4465, ...
29	이십구각수(icosinonagonal number^영어)	$n(27n-25)/2$	0, 1, 29, 84, 166, 275, 411, 574, 764, 981, 1225, 1496, 1794, 2119, 2471, 2850, 3256, 3689, 4149, 4636, ...
30	삼십각수(triacontagonal number^영어)	$n(14n-13)$	0, 1, 30, 87, 172, 285, 426, 595, 792, 1017, 1270, 1551, 1860, 2197, 2562, 2955, 3376, 3825, 4302, 4807, ...

중심있는 평면도형수는 다음과 같다.

$m$	명칭	$\operatorname{Pol}(m;n)$	처음 20항 ( $0\le n\le 19$ )
3	중심있는 삼각수	$\frac{3n (n-1) + 2}{2}$	0, 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, …
4	중심있는 사각수	$2n (n-1) + 1$	0, 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, …
5	중심있는 오각수	$\frac{5n (n - 1) + 2}{2}$	0, 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, …
6	중심있는 육각수	$3n (n - 1) + 1$	0, 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, …
7	중심있는 칠각수	$\frac{7n (n - 1) + 1}{2}$	0, 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953, 1072, 1198, …
8	중심있는 팔각수	$(2n - 1)^2$	0, 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225, 1369, …
9	중심있는 구각수	$\frac{(3n - 2)(3n - 1)}{2}$	0, 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, …
10	중심있는 십각수	$5n (n - 1) + 1$	0, 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051, 1201, 1361, 1531, 1711, …

예를 들어 숫자 10은 삼각수로 배열될 수 있다.

그러나 10은 정사각수로 배열될 수 없다. 반면에 숫자 9는 정사각수로 배열될 수 있다(제곱수 참조).

36과 같은 일부 숫자는 정사각형과 삼각형 모두로 배열될 수 있다 (제곱 삼각수 참조).

관례적으로, 1은 모든 변의 개수에 대해 첫 번째 다각수이다. 다각형을 다음 크기로 확대하는 규칙은 두 개의 인접한 팔을 한 점씩 연장한 다음 해당 점 사이에 필요한 추가 변을 추가하는 것이다. 다음 다이어그램에서 각 추가 레이어는 빨간색으로 표시된다.

삼각수는 일련의 정삼각형 형태로 배열된 숫자들의 표현이다. 이 수들은 1, 3, 6, 10, 15, 21, 28, 36, 45, 등의 수열을 이룬다.

오각수 이상에서는 점을 회전대칭으로 배열하지 않는 것에 주의한다.

5. 2. 입체도형수

명칭	$\operatorname{Pol}(n)$	처음 20항 ( $0\le n\le 19$ )
사면체수 / 삼각뿔수	$\frac {n(n+1)(n+2)} {6}$	0, 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, 1330, …
육면체수 / 입방수	$n^3$	0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744, 3375, 4096, 4913, 5832, 6859, …
팔면체수	$\frac{n(2n^2 + 1)}{3}$	0, 1, 6, 19, 44, 85, 146, 231, 344, 489, 670, 891, 1156, 1469, 1834, 2255, 2736, 3281, 3894, 4579, …
십이면체수	${n(3n-1)(3n-2) \over 2}$	0, 1, 20, 84, 220, 455, 816, 1330, 2024, 2925, 4060, 5456, 7140, 9139, 11480, 14190, 17296, 20825, 24804, 29260, …
이십면체수	${n(5n^2-5n+2) \over 2}$	0, 1, 12, 48, 124, 255, 456, 742, 1128, 1629, 2260, 3036, 3972, 5083, 6384, 7890, 9616, 11577, 13788, 16264, …
사각뿔수	$\frac{1}{3} n^3 + \frac{1}{2} n^2 + \frac{1}{6} n$	0, 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, …
오각뿔수	$\frac{n^{2} (n + 1)}{2}$	0, 1, 6, 18, 40, 75, 126, 196, 288, 405, 550, 726, 936, 1183, 1470, 1800, 2176, 2601, 3078, 3610, …
육각뿔수	$\frac{n (n + 1) (4n - 1)}{6}$	0, 1, 7, 22, 50, 95, 161, 252, 372, 525, 715, 946, 1222, 1547, 1925, 2360, 2856, 3417, 4047, 4750, …
칠각뿔수	$\frac{n (n + 1) (5n - 2)}{6}$	0, 1, 8, 26, 60, 115, 196, 308, 456, 645, 880, 1166, 1508, 1911, 2380, 2920, 3536, 4233, 5016, 5890, …

6. 다각수와 관련된 문제

펠 방정식을 이용하여 두 다각수 집합에 모두 속하는 숫자를 찾을 수 있다.^[2] 예를 들어, 제곱수를 삼각수로 표현하면 다음과 같다.

: $\frac{n(n+1)}{2} = m^2$

위 식을 정리하면 다음과 같다.

: $(2n+1)^2 = 8m^2 + 1$

여기서 $x = 2n+1$ 이고 $y=m$ 이라면, $x^2 - 8y^2 = 1$ 이 되는데, 이는 펠 방정식의 한 형태이다. 이 방정식의 해는 무한히 많이 존재하며, 그 예시는 다음과 같다.

: $(x, y) = (3, 1), (17, 6), (99, 35), ...$

따라서, 제곱 삼각수는 다음과 같다.

:1, 36, 1225, 41616, ...

세 개 이상의 다각수 집합에 모두 속하는 숫자를 찾는 문제는 더 어렵다. 예를 들어, 오각형, 사각형, 삼각형 수의 조건을 모두 만족하는 숫자를 찾는 문제는 더욱 복잡하다.

7. 역사

일반적인 다각수는 힙시클레스()가 기원전 2세기에 처음 정의하였다.

참조

_[1] 서적 The Book of Numbers Springer Science & Business Media 2012-12-06
_[2] 웹사이트 Sums of Reciprocals of Polygonal Numbers and a Theorem of Gauss http://www.siam.org/[...] 2010-06-13
_[3] 웹사이트 Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers http://www.math.psu.[...] 2010-05-13
_[4] MathWorld Pentagonal Square Triangular Number
_[5] 서적 Elementary Number Theory in Nine Chapters Cambridge University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com