블랙-숄즈 모형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
3. 블랙-숄즈 모형의 가정 (블랙-숄즈 환경)
4. 블랙-숄즈 방정식
- 4.1. 블랙-숄즈 방정식의 유도 (일본어 위키백과 내용)
- 4.2. 블랙-숄즈 방정식의 해 (일본어 위키백과 내용)
5. 블랙-숄즈 공식
6. 옵션 그리스 문자 (The Options Greeks)
- 6.1. 주요 그리스 문자 (일본어 위키백과 내용)
7. 블랙-숄즈 모형의 확장
8. 블랙-숄즈 모형의 실제 적용 및 한계 (Black–Scholes in practice)
9. 비판 및 논평 (Criticism and comments)
10. 실무에의 응용 (일본어 위키백과 내용)
11. 발전 (일본어 위키백과 내용)
참조

1. 개요

블랙-숄즈 모형은 1973년 피셔 블랙과 마이런 숄즈가 발표한 옵션 가격 결정 모형으로, 유럽형 콜옵션과 풋옵션의 가격을 계산하는 데 사용된다. 이 모형은 주식, 채권 등 기초 자산과 무위험 자산으로 구성된 시장을 가정하며, 차익 거래 기회가 없고, 거래 비용이 없다는 등의 가정을 따른다. 블랙-숄즈 모형은 블랙-숄즈 방정식과 블랙-숄즈 공식을 통해 옵션 가격을 계산하며, 델타, 감마, 세타, 로, 베가 등의 그리스 문자를 사용하여 옵션 가격의 민감도를 측정한다. 하지만 현실과 괴리가 있다는 비판도 있으며, 변동성 스마일, 채권 옵션, 금리 곡선 등을 고려한 확장 모델이 개발되었다.

더 읽어볼만한 페이지

확률 모형 - 확률 과정
확률 과정은 시간의 흐름에 따라 변화하는 확률 변수들의 집합으로, 수학적 모델링과 다양한 분야에 응용되며, 이산 시간 또는 연속 시간, 이산 또는 연속 상태 공간으로 분류된다.
확률 모형 - 제한된 볼츠만 머신
제한된 볼츠만 머신(RBM)은 이분 그래프 구조를 가진 인공 신경망으로, 가시 유닛과 은닉 유닛 간의 연결만 존재하며, 에너지 함수와 확률 분포를 사용하여 데이터의 특징을 학습하고, 대비 발산(CD) 알고리즘으로 훈련하며, 다양한 분야에 활용된다.
1973년 경제 - 1973년 석유 파동
1973년 석유 파동은 욤키푸르 전쟁 이후 OPEC의 석유 생산량 감축과 가격 인상으로 촉발된 세계적인 에너지 위기로, 원유 가격 급등, 인플레이션, 경기 침체를 야기하며 에너지 안보의 중요성을 부각시키고 세계 경제 질서 재편에 영향을 미쳤다.
1973년 경제 - 카리브 공동체
카리브 공동체(CARICOM)는 1973년 차구아라마스 조약으로 설립된 카리브해 영어권 국가들의 정치·경제 연합체로서, 카리콤 단일 시장 및 경제(CSME) 설립을 통해 경제 통합을 추진하며 다양한 기관과 기구를 통해 회원국 간 협력을 증진하고 있다.
금융 모형 - 블랙-리터만 모형
블랙-리터만 모형은 투자자가 시장에 대한 주관적인 견해와 객관적인 시장 데이터를 결합하여 최적의 자산 배분 전략을 수립하도록 돕는 포트폴리오 이론이다.
금융 모형 - 배당할인모형
배당할인모형(DDM)은 미래 예상 배당금을 현재 가치로 할인하여 주식의 내재 가치를 평가하는 방법으로, 배당금 성장률, 요구 수익률 등을 변수로 사용하며, 고든 성장 모형이나 2단계 배당할인모형 등으로 활용 및 확장될 수 있지만, 배당금 미지급 주식이나 성장률 추정의 민감도 같은 문제점도 존재한다.

블랙-숄즈 모형
모형 개요
이름	블랙-숄즈 모형
유형	수학 모형
분야	금융 수학
목적	옵션 가격 결정 변동성 추정
역사
개발자	피셔 블랙 마이런 숄스
발표 년도	1973년
수상	마이런 숄스, 노벨 경제학상 (1997년)
가정
주가	주가는 기하 브라운 운동을 따른다.
변동성	변동성은 상수이며 알려져 있다.
이자율	이자율은 상수이며 알려져 있다.
배당	배당은 지급되지 않는다. (배당 지급 주식의 경우 모형 수정 필요)
시장	시장은 완전 시장이다. (거래 비용, 세금, 차익 거래 기회 없음)
거래	모든 옵션은 만기일에만 행사 가능하다. (유러피언 옵션)
변수
S	기초 자산의 현재 가격
K	행사가격
r	무위험 이자율
t	만기까지 남은 시간 (년 단위)
σ	기초 자산 가격의 변동성
N(x)	표준 정규 누적 분포 함수
수식
콜 옵션 가격 (C)	C = S * N(d1) - K * exp(-r * t) * N(d2)
풋 옵션 가격 (P)	P = K * exp(-r * t) * N(-d2) - S * N(-d1)
d1	(ln(S/K) + (r + (σ^2)/2) * t) / (σ * sqrt(t))
d2	d1 - σ * sqrt(t)
활용
옵션 가격 결정	유러피언 옵션의 이론적 가격 계산
변동성 추정	내재 변동성 계산
리스크 관리	델타 헤징 등 옵션 전략 활용
한계점
가정의 비현실성	변동성 불변 가정 이자율 불변 가정 배당 미지급 가정 완전 시장 가정
실제 시장과의 괴리	아메리칸 옵션에는 적용 불가 (만기일 이전 행사 가능) 거래 비용 및 세금 미고려 극단적인 시장 변동에 취약
추가 정보
관련 이론	금융공학 수리경제학 확률론
참고 문헌
주요 논문	(1973) "The Pricing of Options and Corporate Liabilities" (1973) "Theory of Rational Option Pricing"

2. 역사적 배경

루이 바슐리에는 1900년에 브라운 운동을 파생 상품 가격 결정에 적용한 최초의 연구를 발표했지만, 그의 연구는 오랫동안 주목받지 못했고 현대 시장에 적용하기에는 한계가 있었다.^[3]^[4] 1960년대에 케이스 스프렌클,^[5] 제임스 보네스,^[6] 폴 새뮤얼슨,^[7] 로버트 C. 머튼^[8] 등이 옵션 가격 결정 이론을 발전시켰다.

피셔 블랙과 마이런 숄스는 1968년에 포트폴리오의 동적 수정을 통해 증권의 예상 수익률을 제거하는 '위험 중립적 논증'을 발명했다.^[9]^[10] 블랙과 숄스는 초기에 공식(모형)을 시장에 적용하려 했으나, 위험 관리 부족으로 재정적 손실을 보았고, 이후 학계로 복귀했다.^[11] 1973년, 정치경제학 저널에 "옵션 및 기업 부채의 가격 결정"이라는 논문을 발표하며 블랙-숄즈 모형이 처음으로 소개되었다.^[12]^[13]^[14] 로버트 C. 머튼은 옵션 가격 결정 모형에 대한 수학적 이해를 확장하는 논문을 발표하고, '블랙-숄즈 옵션 가격 결정 모형'이라는 용어를 만들었다.

이 공식은 옵션 거래의 붐을 일으켰고, 시카고 옵션 거래소 및 전 세계 다른 옵션 시장의 활동에 수학적 정당성을 부여했다.^[15]

1997년 노벨 경제학상은 숄스와 머튼에게 수여되었으며, 블랙은 1995년 사망하여 수상하지 못했지만, 스웨덴 왕립 과학원에 의해 기여자로 언급되었다.^[17]

일본에서는 루이 바슐리에 이후 케이스 스프렌클(1961), 폴 새뮤얼슨(1965) 등이 기하 브라운 운동을 사용한 옵션 가격식을 도출했으나, 리스크의 시장 가격을 명시적으로 표현할 수 없어 실용성이 떨어졌다.^[62] 1965년 아서 D. 리틀에서 근무하던 피셔 블랙은 잭 트레이너의 영향을 받아 워런트 평가식 연구를 진행했고, 1969년경 블랙-숄즈 방정식의 전 단계가 되는 워런트 평가식을 도출했다. 같은 시기(1969년)에 매사추세츠 공과대학교(MIT)에 있던 마이런 숄즈와 블랙은 만나게 되었고, 숄즈의 소개로 블랙은 MIT로 직장을 옮겨 공동 연구를 시작했다. 블랙과 숄즈는 이토 기요시 등이 창시한 확률 미분 방정식 이론과 머튼과의 논의를 통해 도출된 복제 포트폴리오 개념을 사용하여 블랙-숄즈 방정식의 해를 찾는 데 성공했다. 1970년 블랙과 숄즈는 기업 금융에서의 블랙-숄즈 방정식 응용에 대한 연구 성과를 발표했지만, 머튼은 늦잠 때문에 발표를 듣지 못했다.^[55] 1970년 10월, 블랙과 숄즈는 'The Journal of Finance'에 논문 투고를 거부당했으나, 머튼 밀러와 유진 파마의 도움으로 1973년 'Journal of Political Economy'에 논문을 발표했다.^[57]

3. 블랙-숄즈 모형의 가정 (블랙-숄즈 환경)

블랙-숄즈 모형은 시장이 최소한 하나의 위험 자산(일반적으로 주식)과 하나의 안전 자산(일반적으로 머니 마켓, 현금, 채권)으로 구성되어 있다고 가정한다.

자산에 대한 가정은 다음과 같다.

무위험 자산: 무위험 자산의 수익률은 일정하며, 이를 무위험 이자율이라고 부른다.
주식: 주식 가격의 순간 로그 수익률은 표류(drift)가 있는 무한소 확률 보행이다. 더 정확하게는 기하 브라운 운동을 따르며, 이 운동의 표류 및 변동성은 일정하다고 가정한다. (표류와 변동성이 시간에 따라 변하는 경우에도, 변동성이 무작위가 아니라면 적절히 수정된 블랙-숄즈 공식을 유도할 수 있다.)
주식은 배당금을 지급하지 않는다.^[18]

시장에 대한 가정은 다음과 같다.

차익 거래 기회가 없다 (무위험 이익을 얻을 방법이 없다).
무위험 이자율로 현금의 일부를 포함하여 모든 금액을 빌리고 빌려줄 수 있다.
주식의 일부를 포함하여 모든 금액을 사고 팔 수 있다 (여기에는 공매도가 포함된다).
위의 거래에는 수수료나 비용이 발생하지 않는다 (즉, 마찰 없는 시장).

4. 블랙-숄즈 방정식

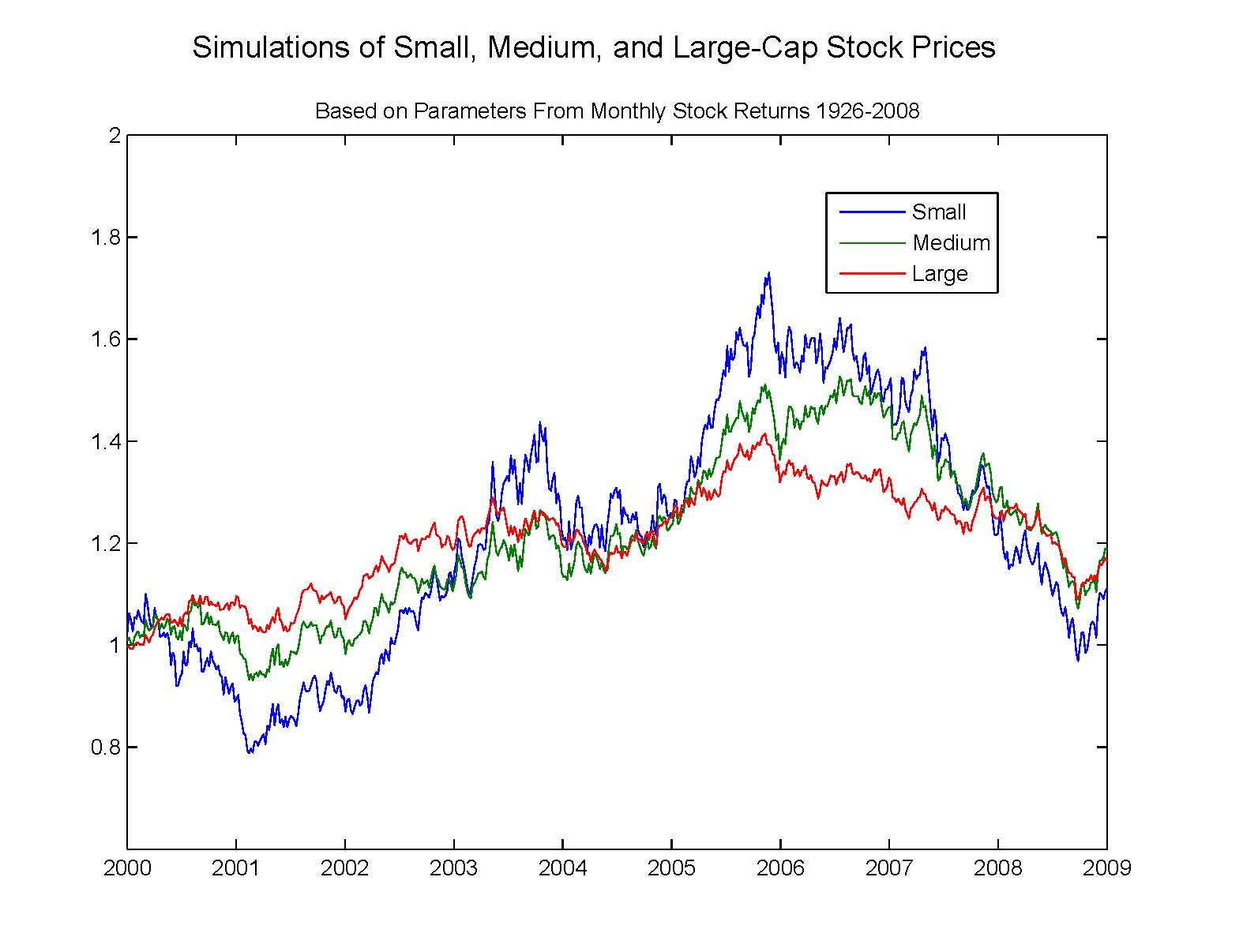
블랙-숄즈 방정식은 옵션의 가격

V(S, t)

를 설명하는 포물선 편미분 방정식이다. 여기서

S

는 기초 자산의 가격이고

t

는 시간이다.^[59]

:

\frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS\frac{\partial V}{\partial S} - rV = 0

이 방정식의 핵심적인 재무적 통찰력은 기초 자산과 은행 계좌 자산(현금)을 사고 파는 방식으로 옵션을 완벽하게 헤지하여 "위험을 제거"할 수 있다는 것이다. 이는 블랙-숄즈 공식에 의해 주어진 옵션에 대한 고유한 가격이 있음을 의미한다. 블랙-숄즈 모형에서는 차익거래가 불가능하므로 파생상품과 기초자산으로 이루어진 포트폴리오가 같은 기간의 이자 수익률과 같다고 가정한다. 따라서 위 식을 만족시키는 해가 파생상품의 가격식이 된다.

옵션 가격 평가에 대한 연구는 오랜 역사를 가지고 있다. 루이 바슐리에는 1900년에 발표된 박사 학위 논문에서 옵션 평가식을 고찰했지만^[59], 가격이 음수가 될 수 있어 비현실적이었다. 1961년 Case Sprenkle^[60], 1965년 폴 새뮤얼슨^[61]이 주가 변동에 기하 브라운 운동을 사용한 옵션 가격식을 도출했으나, 리스크의 시장 가격을 명시적으로 표현할 수 없어 실용성이 떨어졌다.^[62]

1965년 아서 D. 리틀에 취직한 피셔 블랙은 CAPM 연구로 알려진 의 영향을 받아 워런트 평가식을 연구했다. 1969년경 블랙-숄즈 방정식의 전 단계인 워런트 평가식을 도출했으나, 열전도 방정식의 일종임을 깨닫지 못해 해를 구하지 못했다. 그러나 주식 기대 수익률에 워런트 가치가 의존하지 않고, 주식 전체 리스크(변동성)가 중요함을 깨달았다.^[55]

1969년경 매사추세츠 공과대학교(MIT)의 마이론 숄즈와 알게 된 블랙은 숄즈의 소개로 MIT로 이직, 공동 연구를 통해 옵션 평가식 연구를 발전시켰다.^[55] 로버트 머튼^[64]과의 논의는 확률 미분 방정식 이론과 복제 포트폴리오 개념을 활용, 방정식 해를 찾는 데 기여했다. 1970년 여름 컨퍼런스에서 연구 성과를 발표했으나, 머튼은 늦잠으로 듣지 못했다.^[55]

1970년 10월, 블랙과 숄즈는 논문을 시카고 대학교 학술지에 투고했으나 거부되었다. 머튼 밀러와 유진 파마의 도움으로 수정, 1973년 Journal of Political Economy에 "''The Pricing of Options and Corporate Liabilities''"^[57] 논문을 발표했다.^[55] 이후 머튼의 무차익 가격 이론 논문^[58]과 블랙-숄즈 방정식의 실용성 검증으로 확고한 지위를 확립했다.^[55] 1997년 노벨 경제학상은 숄즈와 머튼에게 수여되었고, 1995년 사망한 블랙은 수상하지 못했다.

4. 1. 블랙-숄즈 방정식의 유도 (일본어 위키백과 내용)

블랙-숄즈 모형에서 만기 ''T''에 행사 가격이 ''K''인 유럽형 콜 옵션 프리미엄 ''C'' = ''C''(''S''_''t'', ''t'')가 무위험 차익 거래가 불가능한 적정 가격이 되기 위한 조건을 구한다. 구간 [0, ''T'']에서 자기 자본 충족적인 거래 전략 (''a'', ''b'')을 각 ''t'' 시점에서 다음과 같이 정의한다. 이를 '''복제 포트폴리오'''라고 한다.

:

C(S_t,t) = a_t S_t + b_t B_t

위 식 우변의 복제 포트폴리오의 자기 자금 충족성에 의해 다음 식이 유도된다.

:

dC = d\Big(a_tS_t + b_tB_t\Big) = a_t dS_t + b_t dB_t = (\mu a_t S_t + r b_t B_t)dt + \sigma a_t S_t dW_t

한편, 이토의 보조 정리에 의해 다음 식이 성립한다.

:

\begin{align} d C&= \frac{\partial C}{\partial t}dt + \frac{\partial C}{\partial S_t} dS_t+ \frac{\sigma^2}{2} S_t^2\frac{\partial^2 C}{\partial S_t^2}dt\\&= \left(\frac{\partial C}{\partial t} + \mu S_t \frac{\partial C}{\partial S_t}+ \frac{\sigma^2}{2}S_t^2 \frac{\partial^2 C} {\partial S_t^2} \right)\! dt+ \sigma S_t \frac{\partial C}{\partial S_t} dW_t\end{align}

계수를 비교하면 다음 식을 얻는다.

:

a_t = \frac{\partial C}{\partial S_t},

:

\mu a_t S_t + r b_t B_t = \frac{\partial C}{\partial t} + \mu S_t \frac{\partial C}{\partial S_t} + \frac{\sigma^2}{2}S_t^2 \frac{\partial^2 C}{\partial S_t^2}

이 식들과

C(S_t,t) = a_t S_t + b_t B_t

에서 ''a''_''t'', ''b''_''t''를 소거하면 다음 편미분 방정식을 얻는다.

:

r C = \frac{\,\partial C\,}{\partial t} + \frac{1}{2} \sigma^2 S_t^2 \frac{\,\partial^2 C\,}{\partial S_t^2}  + r S_t\frac{\partial C}{\,\partial S_t\,}

이 편미분 방정식을 '''블랙-숄즈 방정식'''(Black–Scholes equation^영어), 또는 '''블랙-숄즈 편미분 방정식'''(Black–Scholes partial differential equation^영어)이라고 한다.

4. 2. 블랙-숄즈 방정식의 해 (일본어 위키백과 내용)

다음과 같이 변수 변환을 한다.^[68]

:

\begin{align}& C(S_t, t) = e^{r(t - T)}u(S_t, t), \\& z = \frac{\log(\frac{S_t}{K}) + (r - \frac{\sigma^2}{2})(T - t)}{\sigma}, \\& s = T - t\end{align}

이는 다음과 같은 1차원 열전도 방정식(확산 방정식)의 초기값 문제가 된다.

:

\frac{\partial u}{\partial s} = \frac{1}{2}\cdot\frac{\partial^2 u}{\partial z^2}

이것을 풀어서 원래 변수로 되돌리면, 블랙-숄즈 방정식의 해는 다음과 같은 형태로 주어진다.

:

C(S_t, t) = S_t N(d_1) - Ke^{-r(T-t)} N(d_2)

단, 다음 조건에서이다.

:

N(x) =\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-\frac{y^2}{2}}dy,

:

d_1 = \frac{\log(\frac{S_t}{K}) + (r+\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}},

:

d_2 = \frac{\log(\frac{S_t}{K}) + (r-\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}

이것이 "적정 가격"이라고 불리는 이유는, 위에서 언급했듯이 주식과 채권을 사용하여 유럽형 콜 옵션을 복제할 수 있기 때문이다. 만약 콜 옵션 가격과 복제 포트폴리오의 구성 비용이 다르다면, 무한정 자금을 늘릴 수 있게 된다.^[67] 그것은 비현실적이므로 콜 옵션 가격과 복제 포트폴리오의 구성 비용은 이론적으로 일치해야 한다. 또한 여기서 ''S''_''t''는 주가라고 했지만, 실제로는 주식뿐만 아니라, 환율, 투자 신탁, 주가 지수 등의 시장성 있는 투자 상품이나 지표라면 모두 위의 논의가 성립한다.

5. 블랙-숄즈 공식

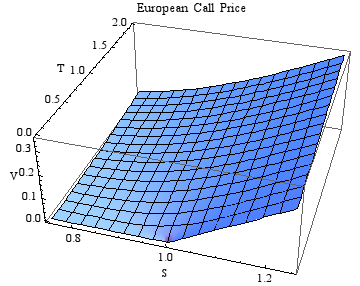
자산 가격 $S$ 와 만기까지의 시간 $T$ 에 따른 블랙-숄즈 가격 결정 방정식을 사용한 유럽형 콜옵션 평가 예시. 행사가격은 1이다.

블랙-숄즈 모형은 유럽형 풋 옵션 및 콜 옵션의 가격을 계산하며, 이 가격은 블랙-숄즈 방정식과 일치한다. 공식은 해당 터미널 및 경계 조건에 대한 방정식을 해결하여 얻을 수 있다.

:

\begin{align}& C(0, t) = 0\text{ 모든 }t\text{에 대해} \\& C(S, t) \rightarrow S - K \text{ as }S \rightarrow \infty \\& C(S, T) = \max\{S - K, 0\}\end{align}

배당금을 지급하지 않는 기초 주식에 대한 콜 옵션 가치는 블랙-숄즈 모형의 매개변수를 사용하여 다음과 같이 나타낸다.

:

\begin{align}C(S_t, t) &= N(d_+)S_t - N(d_-)Ke^{-r(T - t)} \\d_+ &= \frac{1}{\sigma\sqrt{T - t}}\left[\ln\left(\frac{S_t}{K}\right) + \left(r + \frac{\sigma^2}{2}\right)(T - t)\right] \\d_- &= d_+ - \sigma\sqrt{T - t} \\\end{align}

풋-콜 패리티를 기반으로 할인율

e^{-r(T-t)}

를 갖는 해당 풋 옵션 가격은 다음과 같다.

:

\begin{align}P(S_t, t) &= Ke^{-r(T - t)} - S_t + C(S_t, t) \\&= N(-d_-) Ke^{-r(T - t)} - N(-d_+) S_t\end{align}\,

여기서

d_\pm

는 moneyness, 내가격 (표준 편차) 척도로 해석될 수 있으며,

N(d_\pm)

는 각 numéraire, 기준 통화에서 내가격(ITM)으로 만료될 확률(''percent moneyness'')로 해석될 수 있다.^[22]

5. 1. 풋-콜 패리티 (일본어 위키백과 내용)

put-call parity^영어

동일한 기초 자산, 만기, 행사가격을 갖는 유럽형 콜옵션과 풋옵션에 대해, 콜옵션 매수와 풋옵션 매도를 결합한 포트폴리오를 고려한다. 이 포트폴리오의 가치액은 다음과 같다.

:

C(S_t, t) - P(S_t, t) = S_t - Ke^{-r(T-t)}

이는 0시점에서 주식을 1단위 매수하고, 채권을 ''Ke''^''-rT'' / ''B''₀ 단위 공매도하여 만기까지 보유하는 포트폴리오의 가치액과 항상 일치한다. 이러한 관계를 '''풋-콜 패리티'''라고 한다.^[70]

더 일반적으로, ''T'' 기를 만기로 한 액면 1원의 채권의 ''t'' 시점에서의 가격이 ''B'' ( ''t'', ''T'' ) = ''e''^{-''r'' ( ''T''-''t'' )}로 표시되므로 다음과 같이 쓸 수 있다.

:

C(S_t, t) - P(S_t, t) = S_t - KB(t,T)

이 포트폴리오의 만기에서의 페이오프는 다음과 같다.

:

C(S_T, T) - P(S_T, T) = S_T - K

이 포트폴리오의 만기에서의 페이오프는 동일 잔존 기간의 선물 가격 ''K''의 선물 계약 만기에서의 페이오프와 같다. 따라서 만기를 ''T''로 하는 ''t'' 시점에서 체결된 선물 계약의 선물 가격을 ''F'' ( ''t'', ''T'' )라고 하면, 무재정 조건에서 다음이 성립한다.

:

C(S_t, t; F(t,T)) - P(S_t, t; F(t,T)) = S_t - F(t,T)B(t,T)

유럽형 풋옵션의 이론 가격은 블랙-숄즈 방정식을 풀지 않고 풋-콜 패리티로부터 계산하는 것이 더 간단하다.

5. 2. 다른 형태 (Alternative formulation)

보조 변수를 도입하면 공식을 단순화하고 더 편리한 형태로 재구성할 수 있다. (이는 블랙 '76 공식의 특별한 경우이다.)

$D = e^{-r\tau}$ 는 할인율이다.
$F = e^{r\tau} S = \frac{S}{D}$ 는 기초 자산의 선도 가격이며 $S = DF$ 이다.

다음과 같은 풋-콜 패리티가 주어지며, 이는 다음과 같이 표현된다.

:

C - P = D(F - K) = S - D K

풋 옵션의 가격은 다음과 같다.

:

P(F, \tau) = D \left[ N(-d_-) K - N(-d_+) F \right]

5. 3. 공식의 해석 (Interpretation)

블랙-숄즈 모형의 핵심적인 해석은

d_\pm

와 두 개의 항이 나타내는 의미를 이해하는 것이다.^[22]

이 공식은 콜 옵션을 두 이진 옵션의 차이로 분해하여 해석할 수 있다. 즉, 자산형-또는-무형 콜 옵션에서 현금형-또는-무형 콜 옵션을 뺀 형태(자산형-또는-무형 콜 옵션 매수, 현금형-또는-무형 콜 옵션 매도)로 나타낼 수 있다. 콜 옵션은 만기일에 현금과 자산을 교환하지만, 자산형-또는-무형 콜 옵션은 자산만을, 현금형-또는-무형 콜 옵션은 현금만을 결과로 낸다(자산 교환 없음). 블랙-숄즈 공식은 이 두 항의 차이로 표현되며, 각 항은 이진 콜 옵션의 가치에 해당한다. 이진 옵션은 일반 콜 옵션보다 거래가 드물지만, 분석은 더 용이하다.

블랙-숄즈 공식은 다음과 같이 분해된다.

:

C = D N(d_+) F - D N(d_-) K,

여기서

D N(d_+) F

는 자산형-또는-무형 콜 옵션의 현재 가치이고,

D N(d_-) K

는 현금형-또는-무형 콜 옵션의 현재 가치를 나타낸다. ''D''는 할인율을 의미하며, 만기일이 미래이므로 이를 통해 "현재" 가치가 "미래" 가치(만기 시 가치)로 변환된다. 따라서

N(d_+) ~ F

는 자산형-또는-무형 콜 옵션의 미래 가치,

N(d_-) ~ K

는 현금형-또는-무형 콜 옵션의 미래 가치를 의미한다. 위험 중립적 관점에서 보면, 이 값들은 위험 중립 척도에서 자산과 현금의 기대값을 나타낸다.

각 항에 대한 간단한 해석은 다음과 같다.

N(d_+) F

는 옵션이 내가격으로 만료될 확률

N(d_+)

에 만기 시 기초 자산의 가치 ''F''를 곱한 값이고,

N(d_-) K

는 옵션이 내가격으로 만료될 확률

N(d_-)

에 만기 시 현금의 가치 ''K''를 곱한 값이다. 그러나 이 해석은 완전하지 않다. 두 이진 옵션이 모두 내가격 또는 외가격으로 만료될 수 있지만(현금과 자산 교환 여부),

N(d_+)

와

N(d_-)

는 같지 않기 때문이다. 실제

d_\pm

는 moneyness, 내가격 (표준 편차)의 척도로,

N(d_\pm)

는 각 numéraire, 기준 통화에서 내가격(ITM)으로 만료될 확률(''percent moneyness'')로 해석될 수 있다. 간단히 말해, 현금 옵션

N(d_-) K

의 해석은 현금 가치가 기초 자산 움직임과 독립적이므로 "확률 곱하기 가치"로 해석 가능하다. 반면

N(d_+) F

는 내가격 만료 확률과 만기 시 자산 가치가 독립적이지 않아 더 복잡하다.^[22] 더 정확하게는, 만기 시 자산 가치는 현금 관점에서 변동하지만, 자산 자체의 관점에서는 일정하므로, 기준 통화를 현금 대신 자산으로 변경하면 이 수량들은 독립적이 된다.

선물 ''F''를

d_\pm

에 사용하면,

\frac{1}{2}\sigma^2

항 대신

\left(r \pm \frac{1}{2}\sigma^2\right)\tau,

가 나타나며, 이는 (적절한 기준 통화에 대한 위험 중립 척도에서) 드리프트 요소로 해석된다. 즉,

m = \frac{1}{\sigma\sqrt{\tau}}\ln\left(\frac{F}{K}\right)

를 표준화된 내가격으로 사용하는 이유는

\frac{1}{2}\sigma^2

요소가 로그 정규 분포의 중앙값과 평균 차이 때문이며, 이는 기하 브라운 운동에 적용된 이토의 보조 정리와 동일하다. 또한,

N(d_+)

를

N(d_-)

로 대체하면 외가격 콜 옵션에서 음수 값이 나오기 때문에 단순한 해석이 부정확함을 알 수 있다.^[22]

더 자세히 보면,

N(d_+)

와

N(d_-)

항은 각각 등가 지수 마팅게일 확률 척도(기준 통화=주식) 및 등가 마팅게일 확률 척도(기준 통화=무위험 자산) 하에서 ''옵션이 내가격으로 만료될 확률''이다.^[22] 주가

S_T \in (0, \infty)

에 대한 위험 중립 확률 밀도는 다음과 같다.

:

p(S, T) = \frac{N^\prime [d_-(S_T)]}{S_T \sigma\sqrt{T}}

여기서

d_- = d_-(K)

는 위에서 정의된 값이다.

N(d_-)

는 자산 드리프트가 무위험 이자율이라고 가정할 때 콜 옵션 행사 확률이다. 그러나

N(d_+)

는 단순한 확률 해석이 어렵다.

SN(d_+)

는 만기 시 자산 가격이 행사가격보다 높다는 가정 하에 만기 시 기대 자산 가격을 무위험 이자율로 현재 가치화한 값으로 해석된다.^[21] 관련 논의 및 그래픽 표현은 실물 옵션 가치를 위한 데이터-매튜스 방법에서 확인할 수 있다.

등가 마팅게일 확률 척도는 위험 중립 확률 척도라고도 한다. 이들은 측도론적 의미에서 ''확률''이며, 실제 확률 척도 하에서 내가격 만료 실제 확률은 아니다. 실제 확률 계산에는 추가 정보, 즉 물리적 척도의 드리프트 항 또는 위험의 시장 가격이 필요하다.

6. 옵션 그리스 문자 (The Options Greeks)

그리스 문자는 파생 상품 또는 금융 포트폴리오 가치의 특정 변수 변화에 대한 민감도를 나타내는 지표이다. 이는 해당 변수에 대한 가격의 편미분 값으로 표현된다. 예를 들어, "감마"는 "델타"의 편미분이다.^[24]

그리스 문자는 금융의 수학적 이론뿐만 아니라 실제 거래에서도 중요한 역할을 한다. 금융 기관들은 거래자들이 초과해서는 안 되는 각 그리스 문자에 대한 위험 한도를 설정한다. 델타는 일반적으로 가장 큰 위험을 수반하므로 가장 중요한 그리스 문자로 간주된다. 많은 거래자들은 시장 방향에 대한 예측보다는 블랙-숄즈가 제시한 델타 중립 헤징 전략을 따르기 위해, 장 마감 시 델타를 0으로 조정한다. 또한, 거래자들은 보다 광범위한 기초 자산 가격 변동에 대해 헤지 효과를 유지하기 위해 포트폴리오의 감마를 중립화하려고 시도할 수 있다.

블랙-숄즈 모형에서 그리스 문자는 다음과 같은 닫힌 형식으로 표현된다. 이는 블랙-숄즈 공식을 미분하여 도출할 수 있다.

colspan=2 \|	콜 옵션	풋 옵션
델타	$\frac{\partial V}{\partial S}$	$N(d_+)\,$	$-N(-d_+) = N(d_+) - 1\,$
감마	$\frac{\partial^{2} V}{\partial S^{2}}$	$\frac{N'(d_+)}{S\sigma\sqrt{T - t}}\,$
베가	$\frac{\partial V}{\partial \sigma}$	$S N'(d_+) \sqrt{T-t}\,$
세타	$\frac{\partial V}{\partial t}$	$-\frac{S N'(d_+) \sigma}{2 \sqrt{T - t}} - rKe^{-r(T - t)}N(d_{-})\,$	$-\frac{S N'(d_+) \sigma}{2 \sqrt{T - t}} + rKe^{-r(T - t)}N(-d_{-})\,$
로	$\frac{\partial V}{\partial r}$	$K(T - t)e^{-r(T - t)}N( d_{-})\,$	$-K(T - t)e^{-r(T - t)}N(-d_{-})\,$

위 표에서 감마와 베가는 콜 옵션과 풋 옵션에 대해 동일한 값을 갖는다. 이는 풋-콜 패리티를 통해 확인할 수 있는데, 풋 옵션과 콜 옵션의 가격 차이는 기초 자산 가격(S)에 선형적이고 변동성(σ)에 독립적인 선물환 가격이기 때문이다. 따라서 선물환은 감마와 베가가 0이다. N'은 표준 정규 확률 밀도 함수이다.

실제 상황에서 일부 민감도는 변수의 সম্ভাব্য 변화 크기에 맞춰 조정된 용어로 표현된다. 예를 들어, 로는 종종 10,000으로 나눈 값(1 베이시스 포인트 금리 변동), 베가는 100으로 나눈 값(1% 변동성 변동), 세타는 365 또는 252(연간 달력일 또는 거래일 기준 1일 감소)로 표시된다.

"베가"는 실제 그리스 문자가 아니라는 점에 유의해야 한다. 이 명칭은 그리스 문자 뉴 (ν)를 V로 잘못 읽으면서 유래되었다.

6. 1. 주요 그리스 문자 (일본어 위키백과 내용)

블랙-숄즈 모형에서 옵션 가격의 민감도를 나타내는 지표를 '''그리크스'''(The Greeks)라고 한다.^[71] 이는 옵션 가격을 결정하는 5가지 변수(주가, 만기까지의 잔존 기간 또는 경과 시간, 행사가격, 금리, 변동성)에 대한 각각의 편미분 값으로 계산된다. 대표적인 그리스 문자는 다음과 같다.

델타(delta^영어): 주가에 대한 옵션 가격의 1차 편미분 값
감마(gamma^영어): 주가에 대한 옵션 가격의 2차 편미분 값
세타(theta^영어): 경과 시간에 대한 옵션 가격의 1차 편미분 값
로(rho^영어): 금리에 대한 옵션 가격의 1차 편미분 값
베가(vega^영어) 또는 카파(kappa^영어): 변동성에 대한 옵션 가격의 1차 편미분 값

배당이 없는 유럽형 콜 옵션에 대한 각 그리스 문자의 구체적인 형태는 다음과 같다. (기호는 이전 절과 동일)

; 델타

:

\Delta := \frac{\partial C}{\partial S_t} = N(d_1)

; 감마

:

\Gamma := \frac{\partial^2 C}{\partial S_t^2} = \dfrac{1}{\sigma S_t\sqrt{T-t}}\frac{1}{\sqrt{2\pi}}\mathrm{exp}\left\{-\frac{1}{2}d_1^2\right\}

; 세타

:

\Theta := \frac{\partial C}{\partial t} = - rKe^{-r(T-t)}N(d_2) - \dfrac{\sigma S_t}{2\sqrt{T-t}}\frac{1}{\sqrt{2\pi}}\mathrm{exp}\left\{-\frac{1}{2}d_1^2\right\}

; 로

:

\rho := \frac{\partial C}{\partial r} = (T-t)Ke^{-r(T-t)}N(d_2)

; 베가

:

\kappa := \frac{\partial C}{\partial \sigma} = S_t\sqrt{T-t}\frac{1}{\sqrt{2\pi}}\mathrm{exp}\left\{-\frac{1}{2}d_1^2\right\}

델타와 감마는 항상 양수이므로, 옵션 가치를 Y축, 기초 자산 가격을 X축으로 하는 좌표 평면에서 옵션 가치 곡선은 우상향하면서 아래로 볼록한 형태를 띤다. 세타는 음수이므로, 이 곡선은 시간이 지남에 따라 아래로 이동한다.

풋옵션이나 배당이 있는 옵션의 경우, 그리스 문자에 대한 자세한 내용은 영어 위키백과의 :en:Greeks (finance)#Formulas for European option Greeks를 참조할 수 있다.

7. 블랙-숄즈 모형의 확장

블랙-숄즈 모형은 다음과 같이 다양하게 확장될 수 있다.

변동성 및 금리 변화: 변동하는 (그러나 결정론적인) 금리와 변동성에 맞춰 모형을 확장할 수 있다.^[67]
배당금 지급: 배당금을 지급하는 금융 상품에 대한 유럽형 옵션의 가치를 평가하는 데에도 사용될 수 있다.
연속 배당 수익률: 주식에 배당이 포함되어 있더라도, 블랙-숄즈 모형은 세부적인 변경만으로 성립한다. 주가의 확률 미분 방정식 및 블랙-숄즈 방정식은 하위 섹션 "연속 배당 수익률을 지급하는 상품"에 상세히 기술되어 있다.
불연속적인 비례 배당금: 개별 비례 배당금을 지급하는 상품에 대한 옵션으로 확장할 수 있다. 관련 공식은 하위 섹션 "불연속적인 비례 배당금을 지급하는 상품"에서 확인할 수 있다.
미국형 옵션: 미국 옵션 가격을 구하는 문제는 옵션을 실행할 시간을 찾는 최적 중단 문제와 관련이 있다.
영구 풋 옵션: 미국 옵션의 한 종류인 영구 풋 옵션(Perpetual put option)은 만료 기한이 없는 옵션을 말하며, 관련 방정식은 하위 섹션 "영구 풋 옵션"을 참고할 수 있다.
이진 옵션: 블랙-숄즈 미분 방정식을 헤비사이드 함수를 경계 조건으로 풀어, 미리 정의된 행사가격 이상에서는 1단위를 지불하고 그 미만에서는 아무것도 지불하지 않는 옵션의 가격을 산출할 수 있다.^[35]
현금-또는-무형(Cash-or-nothing) 옵션: 관련 내용은 하위 섹션 "이진 옵션"에서 확인할 수 있다.
자산-또는-무형(Asset-or-nothing) 옵션: 관련 내용은 하위 섹션 "이진 옵션"에서 확인할 수 있다.
외환 (Foreign Exchange, FX): 관련 내용은 하위 섹션 "외환"에서 확인할 수 있다.
스큐 (Skew): 변동성 스큐를 고려한 블랙-숄즈 모형은 하위 섹션 "스큐"에서 확인할 수 있다.

7. 1. 연속 배당 수익률을 지급하는 상품 (Instruments paying continuous yield dividends)

지수 옵션의 경우, 배당금이 지속적으로 지급되고 배당금액이 지수 수준에 비례한다는 가정을 하는 것이 합리적이다.^[25] 시간 구간

[t, t + dt]

동안 지급되는 배당금은

qS_t\,dt

로 모델링된다. 여기서 상수

q

는 배당 수익률을 의미한다.

이러한 공식에 따르면, 블랙-숄즈 모형이 암시하는 무위험 차익 거래 가격은 다음과 같다.^[25]

:

C(S_t, t) = e^{-r(T - t)}[FN(d_1) - KN(d_2)]\,

:

P(S_t, t) = e^{-r(T - t)}[KN(-d_2) - FN(-d_1)]\,

여기서

F = S_t e^{(r - q)(T - t)}\,

는

d_1, d_2

항에 나타나는 수정된 선도 가격이다.

:

d_1 = \frac{1}{\sigma\sqrt{T - t}}\left[\ln\left(\frac{S_t}{K}\right) + \left(r - q + \frac{1}{2}\sigma^2\right)(T - t)\right]

:

d_2 = d_1 - \sigma\sqrt{T - t} = \frac{1}{\sigma\sqrt{T - t}}\left[\ln\left(\frac{S_t}{K}\right) + \left(r - q - \frac{1}{2}\sigma^2\right)(T - t)\right]

주식에 배당이 포함되어 있더라도, 블랙-숄즈 모형은 세부적인 변경만으로 성립한다. 여기서

S_t

로 표시되는 주식에는 배당이 존재하고, 그 배당은 연속적으로 지급되는 것으로 한다. 단위 시간당 배당 수익률을

q

라고 한다. 이 때, 주가의 확률 미분 방정식은 다음과 같다.^[68]

:

dS_t = \sigma S_tdW_t + (\mu - q) S_tdt

나머지는 동일한 논의를 반복함으로써 다음의 편미분 방정식을 얻는다.^[68]

:

r C = \frac{\,\partial C\,}{\partial t} + \frac{1}{2} \sigma^2 S_t^2 \frac{\,\partial^2 C\,}{\partial S_t^2} + (r-q) S_t\frac{\partial C}{\,\partial S_t\,}

경계 조건은 배당이 없는 경우와 동일하다. 이 편미분 방정식의 해는 다음과 같다.^[68]

:

C(S_t, t) = e^{-q(T-t)}S_t N(d_1) - Ke^{-r(T-t)} N(d_2)

단,

:

N(x) =\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-\frac{y^2}{2}}dy,

:

d_1 = \frac{\log(\frac{S_t}{K}) + (r-q+\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}},

:

d_2 = \frac{\log(\frac{S_t}{K}) + (r-q-\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}

이 배당 포함 블랙-숄즈 방정식은 통화 옵션에 대해서도 중요한 의미를 갖는다.

7. 2. 불연속적인 비례 배당금을 지급하는 상품 (Instruments paying discrete proportional dividends)

블랙-숄즈 모형은 개별 비례 배당금을 지급하는 상품에 대한 옵션으로 확장할 수 있다. 이는 옵션이 단일 주식에 대해 행사가 이루어지는 경우에 유용하다.

일반적인 모형은 미리 결정된 시간

t_1, t_2, \ldots, t_n

에 주가

\delta

의 비율이 지급된다고 가정한다. 그런 다음 주식의 가격은 다음과 같이 모델링된다.

:

S_t = S_0(1 - \delta)^{n(t)}e^{ut + \sigma W_t}

여기서

n(t)

는 시간

t

까지 지급된 배당금의 수이다.

이러한 주식에 대한 콜옵션 가격은 다시 다음과 같다.

:

C(S_0, T) = e^{-rT}[FN(d_1) - KN(d_2)]\,

여기서 이제

:

F = S_{0}(1 - \delta)^{n(T)}e^{rT}\,

는 배당금을 지급하는 주식의 선물 가격이다.

만약 주식에 배당이 포함되어 있더라도, 블랙-숄즈 모형은 세부적인 변경만으로 성립한다. 여기서 ''S''_''t''로 표시되는 주식에는 배당이 존재하고, 그 배당은 연속적으로 지급되는 것으로 한다. 단위 시간당 배당 수익률을 ''q''라고 한다. 이 때, 주가의 확률 미분 방정식은 다음과 같다.

:

dS_t = \sigma S_tdW_t + (\mu - q) S_tdt

따라서^영어

\mu

는 총 수익률을 나타낸다.

단, 이 주식을 보유하고 있으면 배당을 얻을 수 있으므로, 자기 자금 충족적인 포트폴리오는 다음 확률 적분 방정식을 만족한다.

:

a_tS_t + b_tB_t = a_0S_0 + b_0B_0 + \int_0^t a_s dS_s + \int_0^t b_s dB_s + \int_0^ta_s qS_sd s

나머지는 동일한 논의를 반복함으로써 다음의 편미분 방정식을 얻는다.

:

r C = \frac{\,\partial C\,}{\partial t} + \frac{1}{2} \sigma^2 S_t^2 \frac{\,\partial^2 C\,}{\partial S_t^2} + (r-q) S_t\frac{\partial C}{\,\partial S_t\,}

경계 조건은 배당이 없는 경우와 동일하다. 이 편미분 방정식의 해는 다음과 같다^[68]。

:

C(S_t, t) = e^{-q(T-t)}S_t N(d_1) - Ke^{-r(T-t)} N(d_2)

단,

:

N(x) =\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{x} e^{-\frac{y^2}{2}}dy,

:

d_1 = \frac{\log(\frac{S_t}{K}) + (r-q+\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}},

:

d_2 = \frac{\log(\frac{S_t}{K}) + (r-q-\frac{\sigma^2}{2})(T-t)}{\sigma \sqrt{T-t}}

이다.

7. 3. 미국형 옵션 (American options)

미국 옵션 가격을 구하는 문제는 옵션을 실행할 시간을 찾는 최적 중단 문제와 관련이 있다. 미국 옵션은 만료일 전에 언제든지 행사할 수 있으므로, 블랙-숄즈 모형 방정식은 다음과 같은 변분 부등식 형태가 된다.^[26]

:

\frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS\frac{\partial V}{\partial S} - rV \leq 0

여기서

V(S, t) \geq H(S)

이고,

H(S)

는 주가

S

에서의 페이오프(payoff)를 나타내며, 최종 조건은

V(S, T) = H(S)

이다.

일반적으로 이 부등식은 닫힌 형식의 해를 갖지 않는다. 하지만 배당금이 없는 미국 콜옵션은 유럽 콜옵션과 같고, Roll–Geske–Whaley 방법은 하나의 배당금이 있는 미국 콜옵션에 대한 해를 제공한다.^[27]^[28] 블랙 근사도 참고할 수 있다.

Barone-Adesi와 Whaley^[29]는 또 다른 근사 공식을 제시했다. 이 방법에서는 확률 미분 방정식을 유럽 옵션 가치와 조기 행사 프리미엄의 두 가지 구성 요소로 나누고, 몇 가지 가정을 통해 후자에 대한 해를 근사하는 이차 방정식을 얻는다. 이 해에는 조기 행사와 만기까지 보유하는 것에 대해 무차별하게 만드는 임계값

s*

을 찾는 것이 포함된다.^[30]^[31]

Bjerksund와 Stensland^[32]는 트리거 가격에 해당하는 행사 전략을 기반으로 한 근사치를 제공한다. 기초 자산 가격이 트리거 가격보다 크거나 같으면 행사하는 것이 최적이며, 그 가치는

S - X

와 같아야 한다. 그렇지 않으면 옵션은 "(i) 유럽 업-앤드아웃 콜옵션… 및 (ii) 만기일 전에 옵션이 녹아웃된 경우 녹아웃일에 받는 리베이트"로 귀결된다. 이 공식은 풋-콜 패리티를 사용하여 풋 옵션의 가치를 평가하기 위해 쉽게 수정할 수 있다. 이 근사는 계산 비용이 적게 들고 방법이 빠르며, 장기 옵션 가격 책정에 더 정확할 수 있다는 증거가 있다.^[33]

7. 3. 1. 영구 풋 옵션 (Perpetual put)

미국 옵션의 한 종류인 영구 풋 옵션(Perpetual put option)은 만료 기한이 없는 옵션을 말한다. 이러한 옵션의 경우, 시간 가치 하락이 발생하지 않으므로 블랙-숄즈 편미분방정식은 상미분방정식으로 단순화된다.^[34]

일반적인 블랙-숄즈 편미분방정식은 다음과 같이 표현된다.

:

\frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS\frac{\partial V}{\partial S} - rV = 0

여기서,

V는 옵션의 가치
S는 기초자산의 가격
t는 시간
σ는 기초자산의 변동성
r은 무위험 이자율

영구 풋 옵션의 경우, 시간 가치 하락이 없으므로 (

\frac{\partial V}{\partial t} = 0

) 위의 방정식은 다음과 같은 상미분방정식으로 단순화된다.

:

{1\over{2}}\sigma^{2}S^{2}{d^{2}V\over{dS^{2}}} + (r-q)S{dV\over{dS}} - rV = 0

여기서 q는 배당수익률이다.

이 방정식의 해는 다음과 같은 형태를 가진다.

:

V(S) = A_{1}S^{\lambda_{1}} + A_{2}S^{\lambda_{2}}

S_{-} \leq S

에 대해, 이 해를 상미분 방정식에 대입하면 다음을 얻는다.

:

\left[ {1\over{2}}\sigma^{2}\lambda_{i}(\lambda_{i}-1) + (r-q)\lambda_{i} - r \right]S^{\lambda_{i}} = 0

항을 재정렬하면 다음을 얻는다.

:

{1\over{2}}\sigma^{2}\lambda_{i}^{2} + \left(r-q - {1\over{2}} \sigma^{2}\right)\lambda_{i} - r = 0

이차 방정식을 사용하면

\lambda_{i}

에 대한 해는 다음과 같다.

:

\begin{aligned}\lambda_{1} &= {-\left(r-q-{1\over{2}}\sigma^{2} \right ) + \sqrt{\left(r-q-{1\over{2}}\sigma^{2} \right )^{2} + 2\sigma^{2}r}\over{\sigma^{2}}} \\\lambda_{2} &= {-\left(r-q-{1\over{2}}\sigma^{2} \right ) - \sqrt{\left(r-q-{1\over{2}}\sigma^{2} \right )^{2} + 2\sigma^{2}r}\over{\sigma^{2}}}\end{aligned}

S_{-}

를 옵션을 행사하는 것이 최적인 하한 행사가격 경계라고 하면, 다음 경계 조건이 적용된다.

:

V(S_{-}) = K-S_{-}, \quad V_{S}(S_{-}) = -1, \quad V(S) \leq K

여기서 K는 행사가격이다.

영구 풋옵션에 대한 유한한 해를 얻기 위해, 경계 조건이 풋의 가치에 대한 상한 및 하한 유한 경계를 의미하므로

A_{1} = 0

으로 설정해야 하며, 이는 해

V(S) = A_{2}S^{\lambda_{2}}

로 이어진다. 첫 번째 경계 조건으로부터, 다음을 알 수 있다.

:

V(S_{-}) = A_{2}(S_{-})^{\lambda_{2}} = K-S_{-} \implies A_{2} = {K-S_{-}\over{(S_{-})^{\lambda_{2}}}}

따라서, 영구 풋옵션의 가치는 다음과 같다.

:

V(S) = (K-S_{-})\left( {S\over{S_{-}}} \right)^{\lambda_{2}}

두 번째 경계 조건은 하한 행사가격 경계의 위치를 산출한다.

:

V_{S}(S_{-}) = \lambda_{2}{K-S_{-}\over{S_{-}}} = -1 \implies S_{-} = {\lambda_{2}K\over{\lambda_{2}-1}}

결론적으로,

S \geq S_{-} = {\lambda_{2}K\over{\lambda_{2}-1}}

에 대해, 영구 미국식 풋옵션의 가치는 다음과 같다.

:

V(S) = {K\over{1-\lambda_{2}}} \left( {\lambda_{2}-1\over{\lambda_{2}}}\right)^{\lambda_{2}} \left( {S\over{K}} \right)^{\lambda_{2}}

7. 4. 이진 옵션 (Binary options)

블랙-숄즈 미분 방정식을 헤비사이드 함수를 경계 조건으로 풀어내면, 미리 정의된 행사가격 이상에서는 1단위를 지불하고 그 미만에서는 아무것도 지불하지 않는 옵션의 가격을 산출할 수 있다.^[35]

일반적인 콜 옵션(또는 풋 옵션) 가격을 구하는 블랙-숄즈 공식은 콜 옵션을 자산-또는-제로 콜 옵션에서 현금-또는-제로 콜 옵션을 뺀 것으로 해석할 수 있으며, 풋 옵션도 유사하게 분해할 수 있다. 바이너리 옵션은 분석하기 더 쉬우며, 블랙-숄즈 공식의 두 항에 해당한다.

현금-또는-무형(Cash-or-nothing) 옵션:
만기 시 현물 가격이 행사가격보다 높으면 현금 1단위를 지급하는 현금-또는-무형 콜 옵션의 가치:

:

C =e^{-r (T-t)}N(d_2). \,

만기 시 현물 가격이 행사가격보다 낮으면 현금 1 단위를 지급하는 현금-또는-무형 풋 옵션의 가치:

:

P = e^{-r (T-t)}N(-d_2). \,

자산-또는-무형(Asset-or-nothing) 옵션:
만기 시 현물 가격이 행사가격보다 높으면 자산 1단위를 지급하는 자산-또는-무형 콜 옵션의 가치:

:

C = Se^{-q (T-t)}N(d_1). \,

만기에 기초 자산 가격이 행사가격보다 낮을 경우, 기초 자산 1단위를 지급하는 자산-또는-무형 풋 옵션의 가치:

:

P = Se^{-q (T-t)}N(-d_1),

7. 4. 1. 외환 (Foreign Exchange, FX)

''S''를 FOR/DOM 환율(즉, 1 단위의 외화는 S 단위의 자국 통화와 같음)로 표시하면, 만기 시 현물 가격이 행사가격보다 높거나 낮을 경우 1 단위의 자국 통화를 지급하는 것은 각각 현금-아무것도 아닌 콜옵션과 풋옵션과 정확히 같다. 마찬가지로, 만기 시 현물 가격이 행사가격보다 높거나 낮을 경우 1 단위의 외화를 지급하는 것은 각각 자산-아무것도 아닌 콜옵션과 풋옵션과 정확히 같다. 따라서 외화 이자율

r_{f}

, 자국 이자율

r_{d}

를 사용하여 다음과 같은 결과를 얻을 수 있다.

디지털 콜 (콜 FOR/풋 DOM): 현재 가치로 1 단위의 자국 통화를 지급한다.

:

C = e^{-r_{d} T}N(d_2) \,

디지털 풋 (풋 FOR/콜 DOM): 현재 가치로 1 단위의 자국 통화를 지급한다.

:

P = e^{-r_{d}T}N(-d_2) \,

디지털 콜 (콜 FOR/풋 DOM): 현재 가치로 1 단위의 외화를 지급한다.

:

C = Se^{-r_{f} T}N(d_1) \,

디지털 풋 (풋 FOR/콜 DOM): 현재 가치로 1 단위의 외화를 지급한다.

:

P = Se^{-r_{f}T}N(-d_1) \,

7. 4. 2. 스큐 (Skew)

표준 블랙-숄즈 모형은 분포의 대칭성에 의존하며 자산의 왜도를 무시한다. 하지만 시장 조성자는 모든 행사가에 걸쳐 기초 자산

\sigma

에 대한 단일 표준 편차를 사용하는 대신, 변동성이 행사가격에 따라 달라지는 변수

\sigma(K)

를 통합하여 이러한 왜도를 조정함으로써 변동성 스큐를 고려한다.^[36]^[37] 스큐는 바이너리 옵션에 일반 옵션보다 훨씬 더 큰 영향을 미치기 때문에 중요하다.

바이너리 콜 옵션은 만기가 긴 경우, 두 개의 바닐라 옵션을 사용하는 타이트 콜 스프레드와 유사하다. 행사가 ''K''에서 바이너리 현금 또는 무 옵션의 가치 ''C''를 무한히 타이트한 스프레드로 모델링할 수 있으며, 여기서

C_v

는 바닐라 유럽 콜 옵션이다.

따라서 바이너리 콜의 가치는 행사가격에 대한 바닐라 콜 가격의 미분의 음수와 같다.

변동성 스큐를 고려할 때,

\sigma

는

K

의 함수이다.

첫 번째 항은 스큐를 무시한 바이너리 옵션의 프리미엄과 같다.

\frac{\partial C_v}{\partial \sigma}

는 바닐라 콜의 베가이며,

\frac{\partial \sigma}{\partial K}

는 때때로 "스큐 기울기" 또는 단순히 "스큐"라고 불린다. 스큐가 일반적으로 음수이면, 스큐를 고려할 때 바이너리 콜의 가치는 더 높아진다.

8. 블랙-숄즈 모형의 실제 적용 및 한계 (Black–Scholes in practice)

블랙-숄즈 모형의 정규성 가정은 주식 시장 붕괴와 같은 극단적인 움직임을 포착하지 못한다.

블랙-숄즈 모형의 가정은 모두 현실과 정확히 일치하지는 않는다. 이 모형은 현실에 대한 유용한 근사치로 널리 사용되지만, 적절하게 활용하려면 그 한계를 이해해야 한다.^[38] 맹목적으로 모형을 따르면 예상치 못한 위험에 노출될 수 있다. 주요 한계점은 다음과 같다.

극단적인 움직임을 과소평가하여 꼬리 위험을 초래한다. 이는 외가격 옵션으로 헤지할 수 있다.
즉각적이고 비용이 없는 거래를 가정하여 유동성 위험을 초래하며, 이는 헤지하기 어렵다.
정상적인 프로세스를 가정하여 변동성 위험을 초래하며, 이는 변동성 헤지로 헤지할 수 있다.
연속적인 시간과 연속적인 거래를 가정하여 갭 위험을 초래하며, 이는 감마 헤지로 헤지할 수 있다.
이 모형은 깊은 외가격 옵션은 저평가하고 깊은 내가격 옵션은 과대평가하는 경향이 있다.^[39]

블랙-숄즈 모형에서는 델타 헤지를 통해 옵션을 완벽하게 헤지할 수 있다고 보지만, 실제로는 여러 다른 위험 요소들이 존재한다.

블랙-숄즈 모형을 사용한 결과는 단순화된 가정 때문에 현실 세계의 가격과 차이가 날 수 있다. 현실에서 증권 가격은 엄격한 정상 로그 정규 과정을 따르지 않으며, 무위험 이자율도 시간에 따라 변동한다. 분산은 비정상적인 것으로 관찰되어 GARCH와 같은 모형이 변동성 변화를 모델링하게 되었다. 경험적 결과와 블랙-숄즈 모형 간의 가격 불일치는 극단적인 가격 변화에 해당하는, 멀리 외가격 옵션에서 오랫동안 관찰되어 왔다.

그럼에도 불구하고 블랙-숄즈 가격 결정은 다음과 같은 이유로 실제에서 널리 사용된다.^[2]^[1]

계산이 쉽다.
특히 가격이 중요한 지점을 지날 때 가격 변화 방향을 분석할 때 유용한 근사치이다.
더 정교한 모형의 견고한 기반이 된다.
가역적이어서, 모형의 원래 결과인 가격을 입력값으로 사용하여 다른 변수 중 하나를 풀 수 있다. 이렇게 계산된 내재 변동성은 옵션 가격을 표시하는 데 사용된다.

변동성이 일정하지 않더라도, 이 모형의 결과는 위험을 최소화하기 위해 헤지를 올바른 비율로 설정하는 데 도움이 된다. 결과가 완전히 정확하지 않더라도, 조정할 수 있는 첫 번째 근사치 역할을 한다.

블랙-숄즈 모형은 일부 실패를 처리하도록 조정할 수 있다는 점에서 견고하다. 일부 매개변수(예: 변동성 또는 이자율)를 상수로 간주하는 대신, 변수로 간주하여 위험 요소를 추가한다. 이는 그리스 문자에 반영되며, 이러한 그리스 문자를 헤지하면 해당 매개변수의 비정상적인 특성으로 인한 위험을 완화한다. 그러나 꼬리 위험과 유동성 위험과 같은 다른 결함은 모형을 수정하여 완화할 수 없으며, 대신 모형 외부에서 관리된다.

이 기능을 통해 변동성을 사전에 가정하고 가격을 계산하는 대신, 이 모형을 사용하여 변동성을 풀 수 있으며, 이는 주어진 가격, 기간 및 행사가격에서 옵션의 내재 변동성을 제공한다. 주어진 기간과 행사가격 집합에 대해 변동성을 풀면, 내재 변동성 표면을 구성할 수 있다. 블랙-숄즈 모형의 이러한 적용에서, 가격 영역에서 변동성 영역으로의 좌표 변환이 얻어진다. 옵션 가격은 내재 변동성으로 표시될 수 있으며, 이는 옵션 시장에서 변동성 거래로 이어진다.

8. 1. 변동성 스마일 (The volatility smile)

블랙-숄즈 모형의 매력적인 특징 중 하나는 변동성을 제외한 모형의 매개변수(만기까지의 기간, 행사가격, 무위험 이자율, 현재 기초자산 가격)를 명확하게 관찰할 수 있다는 것이다. 다른 모든 조건이 동일할 때, 옵션의 이론적 가치는 내재 변동성의 단조 증가 함수이다.

서로 다른 행사가격과 만기를 가진 거래 옵션에 대한 내재 변동성을 계산함으로써 블랙-숄즈 모형을 검증할 수 있다. 블랙-숄즈 모형이 성립한다면, 특정 주식에 대한 내재 변동성은 모든 행사가격과 만기에 대해 동일해야 한다. 실제로는 변동성 표면(행사가격과 만기에 대한 내재 변동성의 3차원 그래프)이 평평하지 않다.

주어진 만기에 대한 내재 변동성 곡선의 전형적인 모양은 기초 자산에 따라 다르다. 주식은 왜곡된 곡선을 갖는 경향이 있다. 등가격에 비해, 내재 변동성은 낮은 행사가격에서 상당히 높고 높은 행사가격에서는 약간 낮다. 통화는 더 대칭적인 곡선을 갖는 경향이 있으며, 내재 변동성은 등가격에서 가장 낮고 양쪽 윙에서 더 높은 변동성을 보인다. 상품은 종종 주식과 반대되는 행동을 보이며, 높은 행사가격에서 더 높은 내재 변동성을 보인다.

변동성 스마일의 존재(그리고 블랙-숄즈 모형의 다른 모든 가정 위반)에도 불구하고, 블랙-숄즈 편미분 방정식과 블랙-숄즈 공식은 여전히 실무에서 광범위하게 사용된다. 일반적인 접근 방식은 변동성 표면을 시장에 대한 사실로 간주하고, 이를 기반으로 한 내재 변동성을 블랙-숄즈 평가 모형에서 사용하는 것이다. 이는 "잘못된 공식에 잘못된 숫자를 사용하여 올바른 가격을 얻는 것"으로 묘사되었다.^[40] 이러한 접근 방식은 또한 헤지 비율(그리스 문자)에 대해 사용할 수 있는 값을 제공한다. 더 발전된 모형을 사용하는 경우에도 거래자들은 블랙-숄즈 내재 변동성의 관점에서 생각하는 것을 선호하는데, 이는 서로 다른 만기, 행사가격 등의 옵션을 평가하고 비교할 수 있게 해주기 때문이다. 여기서 개발된 다양한 대체 접근 방식에 대한 논의는 도전과 비판을 참조하라.

블랙-숄즈 모형에 따른 옵션 가격에서 주가, 만기까지의 잔존 기간, 행사가격, 금리는 모두 시장에서 관측 가능하지만, 변동성만이 직접 관측 불가능하여 어떤 방법으로든 추정해야 한다. 그래서 블랙-숄즈 모형에 따른 이론상 옵션 가격이 현실 가격과 같다고 가정하고 실제 옵션의 시장 가격에서 역산된 변동성을 '''내재 변동성'''이라고 한다. 블랙-숄즈 모형이 옳다면, 모든 수준의 주가, 만기까지의 잔존 기간, 행사가격, 금리에서 내재 변동성은 같아야 하지만, 실제로 계산되는 내재 변동성은 그렇지 않다는 것이 알려져 있다.

8. 2. 채권 옵션 가치 평가 (Valuing bond options)

블랙-숄즈 모형은 채권의 액면가 수렴 현상 때문에 채권 증권에 직접 적용될 수 없다. 채권이 만기일에 도달하면 채권과 관련된 모든 가격이 알려지면서 변동성이 감소하지만, 단순한 블랙-숄즈 모형은 이러한 과정을 반영하지 못한다. 이러한 현상을 해결하기 위해 블랙 모형을 시작으로 블랙-숄즈 모형의 수많은 확장 모델이 사용되어 왔다.^[41]

8. 3. 금리 곡선 (Interest rate curve)

실제 금리는 일정하지 않으며, 만기(쿠폰 빈도)에 따라 변동하여 금리 곡선을 형성한다. 따라서 블랙-숄즈 모형에 사용할 적절한 금리는 이 곡선을 보간하여 선택할 수 있다. 또 다른 고려 사항은 금리가 시간에 따라 변동한다는 점이다. 이러한 금리 변동성은 특히 만기가 긴 옵션의 가격에 큰 영향을 미칠 수 있으며, 이는 금리와 채권 가격의 관계와 유사하게 반비례 관계를 갖는다.

8. 4. 공매도 비율 (Short stock rate)

공매도 포지션을 취하는 것은 모형의 도출에서 내포된 바와 같이, 일반적으로 비용이 발생한다. 즉, 소액의 수수료를 받고 롱 포지션의 주식을 빌려주는 것이 가능하다. 두 경우 모두, 숏 주식 차입 비용과 롱 주식 대여 수익 사이에 명백한 비대칭이 없는 한, 블랙-숄즈 모형 평가의 목적으로 지속적인 배당으로 취급될 수 있다.

9. 비판 및 논평 (Criticism and comments)

에스펜 가르더 호그와 나심 니콜라스 탈레브는 블랙-숄즈 모형이 기존에 널리 사용되던 모형을 "위험" 대신 사실상 불가능한 "동적 헤징"의 관점에서 재구성한 것에 불과하다고 주장한다.^[42] 이들은 1964년 보네스가 이미 블랙-숄즈 콜 옵션 가격 결정 방정식과 "실질적으로 동일한" 공식을 발표했다고 주장하며,^[43] 에드워드 소프 역시 1967년에 블랙-숄즈 공식을 추측했지만, 투자자들을 위해 돈을 벌기 위해 이 사실을 숨겼다고 주장한다.^[44] 에마누엘 더먼과 탈레브는 동적 헤징을 비판하며, 블랙과 숄즈 이전에 다수의 연구자들이 유사한 모형을 제시했다고 말한다.^[45] 이에 대해 폴 윌모트는 이 모형을 옹호했다.^[46]^[47]

워렌 버핏은 버크셔 해서웨이 주주들에게 보낸 2008년 서한에서 "블랙-숄즈 공식이 옵션에 대한 달러 부채를 설정하는 표준이지만, 장기적인 옵션의 가치를 평가할 때는 이상한 결과를 낳는다고 생각한다... 블랙-숄즈 공식은 금융계에서 성서와 같은 지위에 이르렀지만, 이 공식을 장기간에 걸쳐 적용하면 터무니없는 결과를 낳을 수 있다"라고 썼다.^[48]

이언 스튜어트는 2012년 저서 ''미지의 추구: 세상을 바꾼 17개의 방정식''에서^[49]^[50] 블랙-숄즈가 "엄청난 경제 성장을 뒷받침"했으며 2007년까지 "국제 금융 시스템은 연간 1Q 규모의 파생 상품을 거래했다"고 말했다. 그는 블랙-숄즈 방정식이 "거래에 대한 수학적 정당화"였으며, 2007-08년 금융 위기에 기여한 "금융적 무책임, 정치적 무능, 왜곡된 인센티브 및 느슨한 규제의 풍성한 혼합물"의 "한 가지 요소"였다고 언급했다.^[51] 그는 "방정식 자체가 진짜 문제는 아니었다"고 밝혔지만, 금융 산업에서의 남용이 문제였다고 지적했다.^[51]

블랙-숄즈 모형은 기초 자산 가격이 양수일 것을 가정한다. 기초 자산이 음수 가격을 갖는 경우, 이 모형은 직접적으로 작동하지 않는다.^[52]^[53] 기초 자산이 음수가 될 수 있는 옵션을 다룰 때, 실무자들은 바첼리에 모형^[53]^[54]과 같은 다른 모형을 사용하거나 단순히 가격에 상수 오프셋을 더할 수 있다.

10. 실무에의 응용 (일본어 위키백과 내용)

옵션의 이론 가격 산정 방식이 수학적으로 매우 명확한 형태로 제공된 것은 SPAN 증거금(SPAN, Standard Portfolio Analysis of Risk)에 결정적인 시사점을 주었다.^[72]

옵션 가격의 이론값을 얻을 수 있게 되면서 적정 프리미엄 획득이나 실제 거래 가격과의 괴리가 투자 전략으로서 차익 거래상의 이익 목표가 될 수 있다고 생각되었다. 그러나 실제로는 테일 리스크에 대한 취약성 등이 지적되고 있다. 마이런 숄스가 참여한 롱텀 캐피탈 매니지먼트의 파산으로 현실적 타당성까지 의문시되었다. 그럼에도 불구하고, 투자 중에 발생하는 이벤트의 정성 정보를 무시한 포트폴리오 전략으로서는 여전히 강력하며, 유추, 격언, 이상 현상이나 기술적 분석 등과 같은 기존의 "투자의 관행"을 넘어선 학술적 배경을 가진 것으로, 현대 포트폴리오 이론이나 자본 자산 가격 모델 등과 마찬가지로 큰 영향을 미치고 있다.

11. 발전 (일본어 위키백과 내용)

1900년 루이 바슐리에는 박사 학위 논문에서 옵션 평가식을 고찰했지만, 가격이 음수가 될 수 있어 비현실적이었다.^[59] 1961년 Case Sprenkle^[60], 1965년 폴 새뮤얼슨^[61]은 주가 변동에 기하 브라운 운동을 사용한 옵션 가격식을 도출했지만, 리스크의 시장 가격을 명시적으로 표현할 수 없어 실용성이 떨어졌다.^[62]

1965년 아서 D. 리틀에서 직장을 얻은 피셔 블랙은 CAPM 연구로 알려진 잭 트레이너의 영향을 받아 워런트 평가식을 연구했다. 1969년경 블랙-숄즈 방정식의 전 단계가 되는 워런트 평가식을 도출했다. 이는 새뮤얼슨^[63]과 로버트 머튼^[64]의 연구(머튼의 포트폴리오 문제)에 큰 영향을 받았다.^[65] 블랙은 이 방정식이 열전도 방정식의 일종임을 깨닫지 못해 해를 구하지 못했지만, 주식의 기대 수익률에 워런트 가치는 의존하지 않고, 워런트 가치를 결정하는 중요한 것은 주식 전체의 리스크(변동성)라는 것을 깨달았다.^[55]

1969년경 매사추세츠 공과대학교(MIT)의 마이론 숄즈와 블랙은 알게 되었고, 숄즈의 소개로 블랙은 MIT로 직장을 옮겼다. 블랙과 숄즈의 공동 연구로 옵션 평가식 연구는 빠르게 발전했다.^[55]

머튼과의 논의는 블랙과 숄즈의 연구에 큰 영향을 미쳤다. 이토 기요시 등에 의해 창시된 확률 미분 방정식 이론과 머튼과의 논의로 도출된 복제 포트폴리오 개념을 사용하여 블랙-숄즈 방정식의 해를 찾는 데 성공했다. 1970년 여름 컨퍼런스에서 기업 금융에서의 블랙-숄즈 방정식 응용에 대한 연구 성과를 발표했지만, 머튼은 늦잠으로 발표를 듣지 못했다.^[55]

1970년 10월, 블랙과 숄즈는 논문을 시카고 대학교가 발행하는 학술지인 Journal of Political Economy에 투고했지만, 미국 금융 학회가 발행하는 The Journal of Finance에 투고하는 것이 더 적절하다는 이유로 게재 거부되었다. 시카고 대학교의 머튼 밀러와 유진 파마의 조언을 받아 수정된 논문이 1973년 Journal of Political Economy에 발표되었다. ("''The Pricing of Options and Corporate Liabilities''"^[57])^[55]

머튼은 무차익 가격 이론의 엄밀한 이론을 전개한 논문^[58]을 발표하고, 블랙과 숄즈는 블랙-숄즈 방정식의 실용성, 데이터 적합성을 검증하여 블랙-숄즈 방정식은 확고한 지위를 확립했다.^[55] "''The Pricing of Options and Corporate Liabilities''"는 Journal of Political Economy에서 가장 많이 인용되는 논문 중 하나이다.^[66]

1997년 노벨 경제학상은 숄즈와 머튼에게 수여되었다. 블랙은 1995년 사망하여 수상하지 못했다.

블랙-숄즈 방정식은 가격 변화율의 분포가 정규 분포를 따른다는 가정을 두고 있다. 그러나 현실에서는 정규 분포가 성립하지 않는다.^[73] 이러한 비판에 대응하여, 변동성이 시간 경과에 따라 확률적으로 변동하는 확률적 변동성 모형^[74]이나, 기초 자산 가격의 불연속적인 변동을 허용하는 머튼 모형^[75] 등이 고안되었다.

참조

_[1] 웹사이트 Scholes on merriam-webster.com http://www.merriam-w[...] 2012-03-26
_[2] 서적 Investments McGraw-Hill/Irwin
_[3] 서적 Théorie de la Spéculation http://www.radio.gol[...] Annales Scientifiques de l'École Normale Supérieure 1900
_[4] 웹사이트 Black-Scholes Model History and Key Papers https://www.macropti[...] 2024-10-03
_[5] 간행물 Warrant prices as indicators of expectations and preferences. 1961
_[6] 간행물 Elements of a Theory of Stock-Option Value https://www.journals[...] 1964
_[7] 간행물 Rational Theory of Warrant Pricing https://www.proquest[...] 1965
_[8] 간행물 A Complete Model of Warrant Pricing that Maximizes Utility https://www.proquest[...] 1969
_[9] 문서 Taleb, 1997. pp. 91 and 110–111.
_[10] 문서 Mandelbrot & Hudson, 2006. pp. 9–10.
_[11] 문서 Mandelbrot & Hudson, 2006. p. 74
_[12] 문서 Mandelbrot & Hudson, 2006. pp. 72–75.
_[13] 문서 Derman, 2004. pp. 143–147.
_[14] 문서 Thorp, 2017. pp. 183–189.
_[15] 서적 An Engine, Not a Camera: How Financial Models Shape Markets https://archive.org/[...] MIT Press
_[16] 웹사이트 The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1997 https://www.nobelpri[...]
_[17] 간행물 Nobel Prize Foundation, 1997 http://nobelprize.or[...] 1997-10-14
_[18] 문서 Although the original model assumed no dividends, trivial extensions to the model can accommodate a continuous dividend yield factor.
_[19] 간행물 The Pricing of Options and Corporate Liabilities
_[20] 간행물 Theory of Rational Option Pricing
_[21] 간행물 Derivation and Interpretation of the Black–Scholes Model 2011-06-03
_[22] 웹사이트 Understanding N(d1) and N(d2): Risk-Adjusted Probabilities in the Black–Scholes Model http://www.ltnielsen[...]
_[23] 서적 Options, Futures and Other Derivatives Prentice Hall
_[24] 문서 'Martin Haugh (2016). [http://www.columbia.edu/~mh2078/QRM/BasicConceptsTechniques.pdf Basic Concepts and Techniques of Risk Management], [[Columbia University]]'
_[25] 웹사이트 Extending the Black Scholes formula http://finance.bi.no[...] 2003-10-22
_[26] 웹사이트 The Black–Scholes equation for American options http://www.lifelong-[...] 2012-05-05
_[27] 웹사이트 Extending the Black Scholes formula http://finance.bi.no[...] 2012-05-05
_[28] 웹사이트 Closed-Form American Call Option Pricing: Roll-Geske-Whaley http://www.bus.lsu.e[...] 2012-05-16
_[29] 간행물 Efficient analytic approximation of American option values https://ideas.repec.[...] 1987-06
_[30] 웹사이트 A quadratic approximation to American prices due to Barone-Adesi and Whaley http://finance.bi.no[...] 2012-06-25
_[31] 웹사이트 Approximation Of American Option Values: Barone-Adesi-Whaley http://www.bus.lsu.e[...] 2012-06-25
_[32] 문서 'Petter Bjerksund and Gunnar Stensland, 2002. [http://brage.bibsys.no/nhh/bitstream/URN:NBN:no-bibsys_brage_22301/1/bjerksund%20petter%200902.pdf Closed Form Valuation of American Options]'
_[33] 문서 '[http://www.global-derivatives.com/index.php?option=com_content&task=view&id=14 American options]'
_[34] 서적 Heard on the Street: Quantitative Questions from Wall Street Job Interviews Timothy Crack
_[35] 서적 Options, Futures and Other Derivatives Prentice Hall
_[36] 논문 Prices of state-contingent claims implicit in option prices 1978
_[37] 서적 The volatility surface: a practitioner's guide John Wiley & Sons 2006
_[38] SSRN Criticism of the Black–Scholes Model: But Why Is It Still Used? (The Answer is Simpler than the Formula 2012
_[39] journal An Empirical Examination of the Black-Scholes Call Option Pricing Model 1979-12
_[40] book Volatility and correlation in the pricing of equity, FX and interest-rate options Wiley 1999
_[41] journal The Problem with Black, Scholes et al. http://kalotay.com/s[...] 1995-11
_[42] 간행물 Option Traders Use (very) Sophisticated Heuristics, Never the Black–Scholes–Merton Formula https://ssrn.com/abs[...] 2011
_[43] 논문 Elements of a theory of stock-option value 1964
_[44] 기타 A Perspective on Quantitative Finance: Models for Beating the Market http://edwardothorp.[...] 2003
_[45] 간행물 The illusions of dynamic replication http://www.ederman.c[...] 2005-08
_[46] 웹사이트 Science in Finance IX: In defence of Black, Scholes and Merton http://www.wilmott.c[...] 2008-04-29
_[47] 기타 Derman and Taleb's The Illusions of Dynamic Replication: A Comment https://web.archive.[...] [[Boston University]] - Department of Economics 2006
_[48] 웹사이트 2008 Letter to the Shareholders of Berkshire Hathaway Inc. https://www.berkshir[...] 2009-02-27
_[49] book In Pursuit of the Unknown: 17 Equations That Changed the World https://books.google[...] Basic Books 2012-03-13
_[50] journal In Pursuit of the Unknown: 17 Equations That Changed the World
_[51] 뉴스 The mathematical equation that caused the banks to crash https://www.theguard[...] 2012-02-12
_[52] 웹사이트 The Great Switch – Negative Prices Are Forcing Traders To Change Their Derivatives Pricing Models https://www.intuitio[...] 2020-07-22
_[53] 뉴스 Traders Rewriting Risk Models After Oil's Plunge Below Zero https://www.bloomber[...] 2020-04-21
_[54] 뉴스 Switch to Bachelier Options Pricing Model - Effective April 22, 2020 - CME Group https://www.cmegroup[...] [[CME Group]]
_[55] book ファイナンス～PVとオプション～同友館 2002
_[56] Harvnb 2004
_[57] Harvnb 1973
_[58] Harvnb 1973
_[59] Harvnb 1900
_[60] Harvnb 1961
_[61] Harvnb 1965
_[62] Harvnb 2003
_[63] Harvnb 1969
_[64] Harvnb 1969
_[65] Harvnb 1989
_[66] 기타 Journal of Political Economy: Home http://www.journals.[...]
_[67] 문서 無裁定価格理論
_[68] Harvnb 2004
_[69] Harvnb 2004
_[70] Harvnb 2004
_[71] 서적
_[72] 문서 1988年にシカゴ・マーカンタイル取引所が開発したリスクベースの証拠金計算方法。
_[73] 웹사이트 野村證券｜ファットテール（証券用語解説集） https://www.nomura.c[...]
_[74] 서적
_[75] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com