포커르-플랑크 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

포커르-플랑크 방정식은 확률 과정의 확률 밀도 함수에 대한 편미분 방정식으로, 이토 확률 과정에 대응된다. 이 방정식은 물리학, 금융 공학, 생물학 등 다양한 분야에서 응용되며, 브라운 운동, 오르슈타인-울렌벡 과정 등을 포함한 여러 가지 확률 과정을 설명하는 데 사용된다. 포커르-플랑크 방정식은 콜모고로프 전진 방정식의 특수한 경우이며, 경로 적분 공식과 밀접한 관련이 있다. 이 방정식은 아드리안 다니얼 포커르와 막스 플랑크에 의해 도입되었다.

더 읽어볼만한 페이지

막스 플랑크 - 플랑크 상수
플랑크 상수는 양자론에서 에너지와 주파수의 관계를 나타내는 물리 상수이며, 흑체 복사 문제 해결을 위해 도입되었고, 2019년 SI 단위계 재정의를 통해 킬로그램을 정의하는 데 사용된다.
막스 플랑크 - 플랑크 법칙
플랑크 법칙은 물체가 방출하는 전자기파의 분광복사도를 나타내는 법칙으로, 온도가 증가함에 따라 방사 에너지가 증가하고 방출 스펙트럼의 피크가 짧은 파장으로 이동하는 현상을 설명하며, 막스 플랑크가 개발하여 열역학적 평형 상태의 방사에 대한 안정적인 분포를 보여준다.
확률 과정 - 마르코프 연쇄
마르코프 연쇄는 현재 상태가 주어졌을 때 과거와 미래 상태가 독립적인 확률 변수 순서열로, 시간 동질성, 상태 공간 유형, 시간 매개변수 유형에 따라 다양한 유형으로 분류되며 여러 분야에서 활용되는 확률적 모델링 방법이다.
확률 과정 - 브라운 운동
브라운 운동은 액체나 기체 속 미세 입자가 매질 분자와 충돌하여 불규칙하게 움직이는 현상으로, 아인슈타인과 스몰루호프스키의 이론적 설명과 페랭의 실험적 검증을 통해 원자 존재 입증에 기여했으며, 확산/랑주뱅 방정식으로 모델링되어 다양한 분야에 응용된다.
편미분 방정식 - 나비에-스토크스 방정식
나비에-스토크스 방정식은 유체의 운동을 기술하는 비선형 편미분방정식으로, 질량 및 운동량 보존 법칙에 기반하며, 해의 존재성과 매끄러움은 밀레니엄 문제이지만 다양한 유체 흐름 모델링과 수치 해석적 응용에 활용된다.
편미분 방정식 - 슈뢰딩거 방정식
슈뢰딩거 방정식은 양자역학에서 시스템의 시간적 변화를 기술하는 기본 방정식으로, 파동 함수에 대한 편미분 방정식이며, 시스템의 총 에너지를 나타내는 해밀토니안 연산자를 포함하고, 양자 상태를 기술하며, 다양한 양자역학적 현상을 설명하는 데 사용된다.

포커르-플랑크 방정식
개요
유형	편미분 방정식
분야	확률론, 물리학, 공학
관련 항목	확산 브라운 운동 랑주뱅 방정식 크라마스-모얄 방정식 채프먼-콜모고로프 방정식
일반 형태
확률 밀도 함수	P(x,t)
시간 변화율	∂P(x,t)/∂t
드리프트 계수	D₁(x,t)
확산 계수	D₂(x,t)
공간 변수	x
시간 변수	t
일반적인 1차원 포커-플랑크 방정식	∂P(x,t)/∂t = -∂/∂x [D₁(x,t)P(x,t)] + ∂²/∂x² [D₂(x,t)P(x,t)]
역사 및 배경
최초 유도	아드리안 포커 (1914년) 막스 플랑크 (1917년)
다른 이름	포커-플랑크-콜모고로프 방정식 콜모고로프 전방 방정식
설명	브라운 운동 입자의 시간적 진화 또는 더 일반적으로 마르코프 과정의 확률 밀도 함수를 설명하는 편미분 방정식

2. 정의

확률 공간 $\Omega$ 와 그 위에 정의된 위너 확률 과정 $(W_t\colon\Omega\to\mathbb R^n)_{t\in[0,\infty)}$ , 그리고 $W$ 에 대한 $\mathbb R^m$ 값의 이토 확률 과정 $\mathrm dX^i_t = f^i(t,X_t) \,\mathrm dt + g^i{}_j(t,X_t)\,\mathrm dW^j_t$ 이 주어졌다고 하자. 여기서 $f\colon \mathbb R\times\mathbb R^m \to \mathbb R^m$ 는 $x$ 에 대해 1차 연속 미분 가능 함수이고, $g\colon \mathbb R\times\mathbb R^m \to \mathbb R^n$ 는 $x$ 에 대해 2차 연속 미분 가능 함수이다.

이토 확률 과정의 분산을 나타내는 행렬 $D \colon \mathbb R \times \mathbb R^n \to \mathbb R^n$ 를 다음과 같이 정의하자.

: $D^{ij}(x,t) = \frac12\sum_k g^i{}_k(x,t) g^j{}_k(x,t)$

이 경우, 이 이토 확률 과정에 대응되는 '''포커르-플랑크 방정식'''은 함수

: $p \colon \mathbb R \times \mathbb R^m \to \mathbb R$

: $p \colon (t,x) \mapsto p(t,x)$

에 대한 다음과 같은 편미분 방정식이다.

: $\frac{\partial}{\partial t}p(t,x) + \frac\partial{\partial x^i}\left(f^i(t,x)p(t,x)\right)$

\frac\partial{\partial x^i}\frac\partial{\partial x^j}

\left(D^{ij}(t,x)p(t,x)\right) = 0

(아인슈타인 표기법을 사용하였다.)

2. 1. 1차원 포커르-플랑크 방정식

일차원 공간 ''x''에서 표준 비너 과정

W_t

에 의해 구동되고 확률 미분 방정식 (SDE)으로 설명되는 이토 미적분의 경우, 확률 변수

X_t

의 확률 밀도

p(x, t)

에 대한 포커르-플랑크 방정식은 다음과 같다.^[9]

:

\frac{\partial}{\partial t} p(x, t) = -\frac{\partial}{\partial x}\left[\mu(x, t) p(x, t)\right] + \frac{\partial^2}{\partial x^2}\left[D(x, t) p(x, t)\right].

여기서

\mu(X_t, t)

는 표류 속도,

D(X_t, t) = \sigma^2(X_t, t)/2

는 확산 계수이다.

무한소 생성기

\mathcal{L}

을 정의하고,^[10] 콜모고로프-체프먼 정리를 사용하여 콜모고로프 역방향 방정식을 유도할 수 있다.

\mathcal{L}

의 수반 연산자

\mathcal{L}^\dagger

를 사용하면 콜모고로프 순방향 방정식, 즉 포커르-플랑크 방정식을 얻을 수 있다.

이토의 보조 정리를 통해

\mathcal{L}

을 명시적으로 정의할 수 있으며, 부분 적분을 사용하여 포커르-플랑크 방정식은 다음과 같이 표현된다.

:

\partial_t p(x, t) = -\partial_x \big(\mu(x, t) \cdot p(x, t)\big) + \partial_x^2\left(\frac{\sigma(x, t)^2}{2} \, p(x,t)\right).

포커르-플랑크 방정식은 초기 분포가 알려진 문제에 사용된다. 이전 시점의 분포를 알아야 하는 경우에는 페인만-칵 공식을 사용할 수 있으며, 이는 콜모고로프 역방향 방정식의 결과이다.

이토 의미의 확률 과정은 스트라토노비치 적분 규칙 내에서 스트라토노비치 SDE로 다시 작성할 수 있다.

:

dX_t = \left[\mu(X_t, t) - \frac{1}{2} \frac{\partial}{\partial X_t}D(X_t, t)\right] \,dt + \sqrt{2 D(X_t, t)} \circ dW_t.

여기에는 노이즈가 상태에 종속되는 경우 확산 기울기 효과로 인한 추가적인 노이즈 유도 표류 항이 포함된다. 스트라토노비치 SDE의 모든 해는 이토 SDE의 해이다.

상수 확산이 있는 제로 표류 방정식은 고전적인 브라운 운동의 모델로 간주할 수 있다.

:

\frac{\partial}{\partial t} p(x, t) = D_0\frac{\partial^2}{\partial x^2}\left[p(x, t)\right].

고정 경계 조건

\{0 \leq x \leq L\}

이 추가된 경우, 이 모델은 이산 스펙트럼의 해를 가지며, 좌표-속도 위상 부피에 대한 국소적 불확실성 관계를 유도할 수 있다.^[11]

:

\Delta x \, \Delta v \geq D_0.

여기서

D_0

는 해당 확산 스펙트럼

D_j

의 최소값이고,

\Delta x

및

\Delta v

는 좌표-속도 정의의 불확실성을 나타낸다.

2. 2. 다차원 포커르-플랑크 방정식

\mathbf{X}_t

및

\boldsymbol{\mu}(\mathbf{X}_t,t)

는 차원 벡터이고,

\boldsymbol{\sigma}(\mathbf{X}_t,t)

는

N \times M

행렬이고

\mathbf{W}_t

는 ''M''차원 표준 비너 과정일 때,

\mathbf{X}_t

에 대한 확률 밀도

p(\mathbf{x},t)

는 다음과 같은 포커르-플랑크 방정식을 만족한다.

:

\frac{\partial p(\mathbf{x},t)}{\partial t} = -\sum_{i=1}^N \frac{\partial}{\partial x_i} \left[ \mu_i(\mathbf{x},t) p(\mathbf{x},t) \right] + \sum_{i=1}^{N} \sum_{j=1}^{N} \frac{\partial^2}{\partial x_i \, \partial x_j} \left[ D_{ij}(\mathbf{x},t) p(\mathbf{x},t) \right],

드리프트 벡터

\boldsymbol{\mu} = (\mu_1,\ldots,\mu_N)

과 확산 텐서

\mathbf{D} = \frac{1}{2} \boldsymbol{\sigma\sigma}^\mathsf{T}

를 사용하여, 다음과 같이 표현할 수 있다.

:

D_{ij}(\mathbf{x},t) = \frac{1}{2}\sum_{k=1}^M \sigma_{ik}(\mathbf{x},t) \sigma_{jk}(\mathbf{x},t).

만약 Itô SDE 대신에 Stratonovich SDE를 고려한다면,

:

d\mathbf{X}_t = \boldsymbol{\mu}(\mathbf{X}_t,t)\,dt + \boldsymbol{\sigma}(\mathbf{X}_t,t)\circ d\mathbf{W}_t,

포커르-플랑크 방정식은 다음과 같다:^[10]

:

\frac{\partial p(\mathbf{x},t)}{\partial t} = -\sum_{i=1}^N \frac{\partial}{\partial x_i} \left[ \mu_i(\mathbf{x},t) \, p(\mathbf{x},t) \right] + \frac{1}{2} \sum_{k=1}^M \sum_{i=1}^{N} \frac{\partial}{\partial x_i} \left\{ \sigma_{ik}(\mathbf{x},t)  \sum_{j=1}^{N} \frac{\partial}{\partial x_j} \left[  \sigma_{jk}(\mathbf{x},t) \, p(\mathbf{x},t) \right] \right\}

2. 3. 스트라토노비치 SDE와 포커르-플랑크 방정식

3. 성질

이토 확률 과정의, 시간 t에서의 확률 밀도 함수 p(t,x)는 포커르-플랑크 방정식을 따른다.

일반적으로, 포커르-플랑크 방정식은 일반적인 콜모고로프 전진 방정식의 특수한 경우이다.^[12]

: $\partial_t \rho = \mathcal{A}^*\rho$

여기서 선형 연산자 $\mathcal{A}^*$ 는 마르코프 과정의 무한소 생성자에 대한 에르미트 수반이다.^[12]

3. 1. 콜모고로프 전진 방정식과의 관계

일반적으로, 포커르-플랑크 방정식은 일반적인 콜모고로프 전진 방정식의 특수한 경우이다.^[12]

:

\partial_t \rho = \mathcal{A}^*\rho

여기서 선형 연산자

\mathcal{A}^*

는 마르코프 과정의 무한소 생성자에 대한 에르미트 수반이다.^[12]

4. 방정식의 유도

5. 응용

5. 1. 물리학

플라스마 물리학에서, 입자 종

s

의 분포 함수,

p_s (\mathbf{x},\mathbf{v},t)

는 확률 밀도 함수를 대신한다. 이에 해당하는 볼츠만 방정식은 다음과 같다.

\frac{\partial p_s}{\partial t} + \mathbf{v} \cdot \boldsymbol{\nabla} p_s + \frac{Z_s e}{m_s} \left( \mathbf{E} + \mathbf{v} \times \mathbf{B} \right) \cdot \boldsymbol{\nabla}_v p_s = -\frac{\partial}{\partial v_i} \left(p_s \langle\Delta v_i\rangle\right) + \frac{1}{2} \frac{\partial^2}{\partial v_i \, \partial v_j} \left(p_s \langle\Delta v_i \, \Delta v_j\rangle\right),

여기서 세 번째 항은 로렌츠 힘에 의한 입자 가속도를 포함하며, 오른쪽에 있는 포커-플랑크 항은 입자 충돌의 영향을 나타낸다. 양

\langle\Delta v_i\rangle

와

\langle\Delta v_i \, \Delta v_j\rangle

는 단위 시간 동안 다른 모든 입자 종과의 충돌로 인해

s

유형의 입자가 겪는 평균 속도 변화이다.^[13] 충돌을 무시하면 볼츠만 방정식은 Vlasov 방정식으로 축소된다.

5. 2. 금융 공학

수학 금융에서 변동성 스마일을 국소 변동성을 통해 옵션 모델링을 할 때, 시장 옵션 시세에서 얻은 확률 밀도와 일치하는 확산 계수

{\sigma}(\mathbf{X}_t,t)

를 도출하는 문제가 발생한다. 이 문제는 포커-플랑크 방정식의 역문제이다.^[19]^[20] 옵션 시장에서 추론한 옵션 기초 자산 ''X''의 밀도 f(x,t)가 주어지면, ''f''와 일치하는 국소 변동성

{\sigma}(\mathbf{X}_t,t)

를 찾는 것을 목표로 한다. Dupire (1994, 1997)는 비모수적 해법으로 일반화하여 해결했다. Brigo와 Mercurio (2002, 2003)는 혼합 모형에서 주어진 포커-플랑크 방정식의 해와 일치하는 특정 국소 변동성

{\sigma}(\mathbf{X}_t,t)

를 통해 매개변수 형태의 해법을 제안했다.^[21]^[22] Fengler (2008),^[23] Gatheral (2008),^[24] 및 Musiela와 Rutkowski (2008)에서도 관련 정보를 얻을 수 있다.^[25]

5. 3. 생물학

5. 4. 기타

6. 예시

위너 확률 과정 $W_t$ 는 $f = 0$ , $g^i{}_j = \delta^i_j$ 인 이토 확률 과정이다. 이 경우 포커르-플랑크 방정식은 다음과 같다.

: $\frac{\partial}{\partial t}p(t,x) = \frac12 \Delta p(t,x)$

이는 $\mathbb R^m$ 위의 열 방정식이다. 표준 스칼라 비너 과정은 확률 미분 방정식 $dX_t = dW_t.$ 에 의해 생성되는데, 여기서 드리프트 항은 0이고 확산 계수는 1/2이다. 따라서 이에 해당하는 포커르-플랑크 방정식은 다음과 같다.

$\frac{\partial p(x,t)}{\partial t} = \frac{1}{2} \frac{\partial^2 p(x,t)}{\partial x^2},$

이는 확산 방정식의 가장 간단한 형태이다. 초기 조건이 $p(x,0) = \delta(x)$ 인 경우 해는 다음과 같다.

$p(x,t) = \frac{1}{\sqrt{2 \pi t}}e^{-{x^2}/({2t})}.$

오르슈타인-울렌벡 과정은 다음과 같이 정의되는 과정이다.

: $dX_t = -a X_t \, dt + \sigma \, dW_t.$

여기서 $a>0$ 이다. 물리적으로, 이 방정식은 유체와 같은 매질에서 움직이는 속도 $V_t$ 를 가진 질량 $m$ 의 입자는 운동에 저항하는 마찰력을 경험하며, 그 크기는 입자의 속도 $-a V_t$ 에 비례하는 것으로 근사할 수 있다는 점을 통해 동기를 부여할 수 있다. 여기서 $a = \mathrm{상수}$ 이다. 매질의 다른 입자들은 입자와 충돌하면서 입자를 무작위로 움직이게 하는데, 이 효과는 백색 잡음 항 $\sigma (d W_t/dt)$ 로 근사할 수 있다. 뉴턴의 제2법칙은 다음과 같이 쓸 수 있다.

: $m \frac{dV_t}{dt}=-a V_t +\sigma \frac{dW_t}{dt}.$

단순화를 위해 $m = 1$ 로 놓고, 표기법을 $V_t\rightarrow X_t$ 로 변경하면 $dX_t = -a X_t dt + \sigma dW_t$ 와 같은 형식이 된다.

이에 해당하는 포커르-플랑크 방정식은 다음과 같다.

: $\frac{\partial p(x,t)}{\partial t} = a \frac{\partial}{\partial x}\left(x \,p(x,t)\right) + \frac{\sigma^2}{2} \frac{\partial^2 p(x,t)}{\partial x^2},$

정상 상태 해( $\partial_t p = 0$ )는 다음과 같다.

: $p_{ss}(x) = \sqrt{\frac{a}{\pi \sigma^2}} e^{-{ax^2}/{\sigma^2}}.$

과감쇠된 랑제뱅 방정식 $dx_t = -\frac{1}{k_\text{B}T} (\nabla_x U)dt + dW_t$ 는 $\partial_t p = \frac 1 2 \nabla\cdot \left(\frac{p}{k_\text{B}T} \nabla U + \nabla p\right)$ 을 제공한다. 볼츠만 분포 $p(x) \propto e^{- U(x)/k_\text{B} T}$ 는 평형 분포이며, $U$ 가 충분히 빠르게 증가한다고 가정하면(즉, 포텐셜 우물이 입자를 가둘 만큼 충분히 깊으면) 볼츠만 분포는 유일한 평형 상태이다.

1차원 브라운 역학은 단순하다.^[16]^[17] 선형 포텐셜 $U(x) = cx$ 에서, 해당 스몰루초프스키 방정식은 다음과 같다.

$\partial_t P(x,t| x_0, t_0) = \partial_x D (\partial_x + \beta c) P(x,t| x_0, t_0)$

여기서 확산 상수 $D$ 는 공간과 시간에 걸쳐 일정하다. 경계 조건은 확률이 $x \rightarrow \pm \infin$ 에서 0으로 수렴하도록 하며, 초기 조건은 동일한 위치에서 시작하는 입자 앙상블 $P(x,t|x_0,t_0)= \delta (x-x_0)$ 이다.

$\tau = D t$ 및 $b = \beta c$ 로 정의하고 좌표 변환 $y = x +\tau b ,\ \ \ y_0= x_0 + \tau_0 b$ 을 적용하고, $P(x, t, |x_0, t_0) = q(y, \tau|y_0, \tau_0)$ 를 사용하면 스몰루초프스키 방정식은 다음과 같이 변환된다.

$\partial_\tau q(y, \tau| y_0, \tau_0) =\partial_y^2 q(y, \tau| y_0, \tau_0)$

이는 자유 확산 방정식이며, 해는 다음과 같다.

$q(y, \tau| y_0, \tau_0)= \frac{1}{\sqrt {4 \pi (\tau - \tau_0)}} e^{ -\frac{(y-y_0)^2}{4(\tau-\tau_0)} }$

그리고 원래 좌표로 다시 변환하면, 다음과 같은 결과를 얻는다.

$P(x, t | x_0, t_0)= \frac{1}{\sqrt{4 \pi D (t - t_0)}} \exp {\left[{ -\frac{(x-x_0+ D \beta c(t-t_0))^2}{4D(t-t_0)}} \right]}$

브라운 운동 시뮬레이션은 시스템에 대한 랑제뱅 방정식으로 시작하여 완성되었다.^[16]^[17]

$m\ddot{x} = - \gamma \dot{x} -c + \sigma \xi(t)$

여기서 $\gamma$ 는 마찰항, $\xi$ 는 입자에 작용하는 변동력, $\sigma$ 는 변동의 진폭이다. 평형 상태에서 마찰력은 관성력보다 훨씬 크므로 ( $\left| \gamma \dot{x} \right| \gg \left| m \ddot{x} \right|$ ), 랑제뱅 방정식은 다음과 같이 간략화된다.

$\gamma \dot{x} = -c + \sigma \xi(t)$

시뮬레이션에서 변동력 $\xi(t)$ 는 가우시안 분포를 따르며, 진폭은 $\sigma = \sqrt{2\gamma k_\text{B} T}$ 이다. 랑제뱅 방정식을 다시 쓰면,

$\frac{dx}{dt}=-D \beta c + \sqrt{2D}\xi(t)$

여기서 $D = \frac{k_\text{B}T}{\gamma}$ 는 아인슈타인 관계이다. 이 방정식의 적분은 오일러-마루야마 방법을 사용하여 수행되었다.

6. 1. 위너 과정

위너 확률 과정

W_t

는

f = 0

,

g^i{}_j = \delta^i_j

인 이토 확률 과정이다. 이 경우 포커르-플랑크 방정식은 다음과 같다.

:

\frac{\partial}{\partial t}p(t,x) = \frac12 \Delta p(t,x)

이는

\mathbb R^m

위의 열 방정식이다. 표준 스칼라 비너 과정은 확률 미분 방정식

dX_t = dW_t.

에 의해 생성되는데, 여기서 드리프트 항은 0이고 확산 계수는 1/2이다. 따라서 이에 해당하는 포커르-플랑크 방정식은 다음과 같다.

\frac{\partial p(x,t)}{\partial t} = \frac{1}{2} \frac{\partial^2 p(x,t)}{\partial x^2},

이는 확산 방정식의 가장 간단한 형태이다. 초기 조건이

p(x,0) = \delta(x)

인 경우 해는 다음과 같다.

p(x,t) = \frac{1}{\sqrt{2 \pi t}}e^{-{x^2}/({2t})}.

6. 2. 오르슈타인-울렌벡 과정

오르슈타인-울렌벡 과정은 다음과 같이 정의되는 과정이다.

:

dX_t = -a X_t \, dt + \sigma \, dW_t.

여기서

a>0

이다. 물리적으로, 이 방정식은 유체와 같은 매질에서 움직이는 속도

V_t

를 가진 질량

m

의 입자는 운동에 저항하는 마찰력을 경험하며, 그 크기는 입자의 속도

-a V_t

에 비례하는 것으로 근사할 수 있다는 점을 통해 동기를 부여할 수 있다. 여기서

a = \mathrm{상수}

이다. 매질의 다른 입자들은 입자와 충돌하면서 입자를 무작위로 움직이게 하는데, 이 효과는 백색 잡음 항

\sigma (d W_t/dt)

로 근사할 수 있다. 뉴턴의 제2법칙은 다음과 같이 쓸 수 있다.

:

m \frac{dV_t}{dt}=-a V_t +\sigma \frac{dW_t}{dt}.

단순화를 위해

m = 1

로 놓고, 표기법을

V_t\rightarrow X_t

로 변경하면

dX_t = -a X_t dt + \sigma dW_t

와 같은 형식이 된다.

이에 해당하는 포커르-플랑크 방정식은 다음과 같다.

:

\frac{\partial p(x,t)}{\partial t} = a \frac{\partial}{\partial x}\left(x \,p(x,t)\right) + \frac{\sigma^2}{2} \frac{\partial^2 p(x,t)}{\partial x^2},

정상 상태 해(

\partial_t p = 0

)는 다음과 같다.

:

p_{ss}(x) = \sqrt{\frac{a}{\pi \sigma^2}} e^{-{ax^2}/{\sigma^2}}.

6. 3. 열역학 평형 상태의 볼츠만 분포

과감쇠된 랑제뱅 방정식

dx_t = -\frac{1}{k_\text{B}T} (\nabla_x U)dt + dW_t

는

\partial_t p = \frac 1 2 \nabla\cdot \left(\frac{p}{k_\text{B}T} \nabla U + \nabla p\right)

을 제공한다. 볼츠만 분포

p(x) \propto e^{- U(x)/k_\text{B} T}

는 평형 분포이며,

U

가 충분히 빠르게 증가한다고 가정하면(즉, 포텐셜 우물이 입자를 가둘 만큼 충분히 깊으면) 볼츠만 분포는 유일한 평형 상태이다.

6. 4. 1차원 선형 포텐셜

1차원 브라운 역학은 단순하다.^[16]^[17] 선형 포텐셜

U(x) = cx

에서, 해당 스몰루초프스키 방정식은 다음과 같다.

\partial_t P(x,t| x_0, t_0) = \partial_x D (\partial_x + \beta c)  P(x,t| x_0, t_0)

여기서 확산 상수

D

는 공간과 시간에 걸쳐 일정하다. 경계 조건은 확률이

x \rightarrow \pm \infin

에서 0으로 수렴하도록 하며, 초기 조건은 동일한 위치에서 시작하는 입자 앙상블

P(x,t|x_0,t_0)= \delta (x-x_0)

이다.

\tau = D t

및

b = \beta c

로 정의하고 좌표 변환

y = x +\tau b ,\ \ \ y_0= x_0 + \tau_0 b

을 적용하고,

P(x, t, |x_0, t_0) = q(y, \tau|y_0, \tau_0)

를 사용하면 스몰루초프스키 방정식은 다음과 같이 변환된다.

\partial_\tau q(y, \tau| y_0, \tau_0) =\partial_y^2 q(y, \tau| y_0, \tau_0)

이는 자유 확산 방정식이며, 해는 다음과 같다.

q(y, \tau| y_0, \tau_0)= \frac{1}{\sqrt {4 \pi (\tau - \tau_0)}} e^{ -\frac{(y-y_0)^2}{4(\tau-\tau_0)} }

그리고 원래 좌표로 다시 변환하면, 다음과 같은 결과를 얻는다.

P(x, t | x_0, t_0)= \frac{1}{\sqrt{4 \pi  D (t - t_0)}} \exp {\left[{ -\frac{(x-x_0+ D \beta c(t-t_0))^2}{4D(t-t_0)}} \right]}

브라운 운동 시뮬레이션은 시스템에 대한 랑제뱅 방정식으로 시작하여 완성되었다.^[16]^[17]

m\ddot{x} = - \gamma \dot{x} -c + \sigma \xi(t)

여기서

\gamma

는 마찰항,

\xi

는 입자에 작용하는 변동력,

\sigma

는 변동의 진폭이다. 평형 상태에서 마찰력은 관성력보다 훨씬 크므로 (

\left| \gamma \dot{x} \right| \gg \left| m \ddot{x} \right|

), 랑제뱅 방정식은 다음과 같이 간략화된다.

\gamma \dot{x} = -c + \sigma \xi(t)

시뮬레이션에서 변동력

\xi(t)

는 가우시안 분포를 따르며, 진폭은

\sigma = \sqrt{2\gamma k_\text{B} T}

이다. 랑제뱅 방정식을 다시 쓰면,

\frac{dx}{dt}=-D \beta c + \sqrt{2D}\xi(t)

여기서

D = \frac{k_\text{B}T}{\gamma}

는 아인슈타인 관계이다. 이 방정식의 적분은 오일러-마루야마 방법을 사용하여 수행되었다.

7. 계산 및 해법

브라운 운동은 Langevin 방정식을 따르는데, 이는 여러 다른 확률적 힘에 대해 풀 수 있으며, 그 결과가 평균화된다([분자동역학]에서 정준 앙상블).^[18] 그러나 이러한 계산 집약적인 접근 방식 대신, 포커르-플랑크 방정식을 사용하여 시간이 0일 때 $\mathbf{v}_0$ 에서 운동을 시작할 때 입자가 구간 $(\mathbf{v}, \mathbf{v} + d\mathbf{v})$ 내의 속도를 가질 확률 $p(\mathbf{v}, t)\,d\mathbf{v}$ 를 고려할 수 있다.^[18]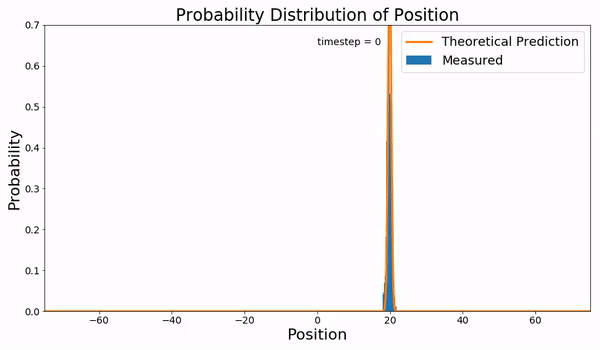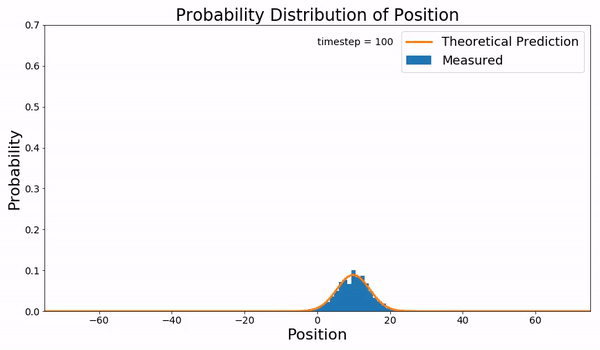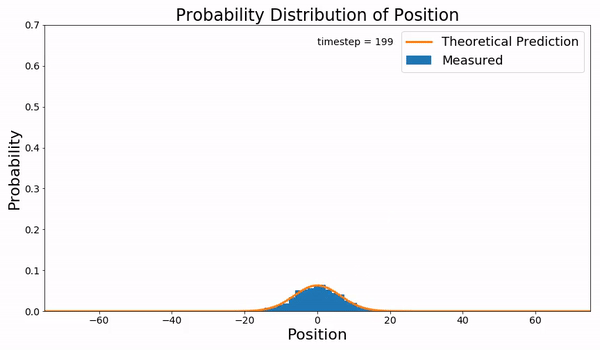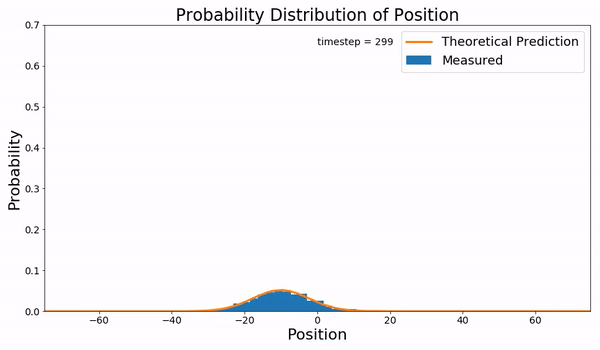

Fokker–Planck 방정식의 해와 비교한 1차원 선형 퍼텐셜 내 입자에 대한 브라운 동역학 시뮬레이션

편미분 방정식인 포커르-플랑크 방정식은 특수한 경우에만 해석적으로 풀 수 있다.^[18] 슈뢰딩거 방정식과의 형식적인 유사성을 통해 양자역학에서 알려진 고급 연산자 기술을 사용하여 여러 경우에 대한 해를 구할 수 있다.^[18] 또한 포커르-플랑크 방정식이 모든 공간 변수에 대한 2차 편미분 방정식을 포함하는 과감쇠 역학의 경우, 방정식을 쉽게 수치적으로 풀 수 있는 마스터 방정식 형태로 작성할 수 있다.^[18]

많은 응용 분야에서, 정상 상태 확률 분포

p_0(x)

에만 관심이 있으며, 이는

\frac{\partial p(x,t)}{\partial t} = 0

으로부터 찾을 수 있다.

평균 최초 통과 시간과 분할 확률의 계산은 포커르-플랑크 방정식과 밀접하게 관련된 상미분 방정식의 해로 축소될 수 있다.

8. 경로 적분과의 관계

모든 포커르-플랑크 방정식은 경로 적분과 동일하다. 경로 적분 공식은 장론 방법을 적용하기 위한 훌륭한 출발점이며, 임계 동역학에서 사용된다.^[26]

경로 적분의 유도는 양자역학에서와 유사한 방식으로 가능하다. 한 변수 $x$ 를 가진 포커르-플랑크 방정식에 대한 유도는 다음과 같다. 먼저 델타 함수를 삽입한 다음 부분 적분한다.

$\begin{align}\frac{\partial }{\partial t} p{\left( x', t\right)}& = - \frac{\partial }{\partial x'} \left[ D_1(x',t) p(x',t) \right] + \frac{\partial^2 }{\partial {x'}^2} \left[ D_2(x',t) p(x',t) \right] \\[1ex]& = \int_{-\infty}^{\infty} dx\left[ \left( D_{1}{\left( x,t\right)} \frac{\partial }{\partial x} + D_2{ \left( x,t\right)} \frac{\partial^2}{\partial x^2}\right) \delta{\left( x' -x\right)} \right] p(x,t).\end{align}$

여기서의 $x$ -미분은 $p(x,t)$ 가 아닌 $\delta$ -함수에만 작용한다. 시간 간격 $\varepsilon$ 에 대해 적분하면,

$p(x', t + \varepsilon) =\int_{-\infty}^\infty \, \mathrm{d}x\left(\left( 1+\varepsilon \left[ D_1(x,t) \frac \partial {\partial x} + D_2(x,t) \frac{\partial^2}{\partial x^2}\right]\right) \delta(x' - x) \right) p(x,t)+O(\varepsilon^2).$

푸리에 적분

$\delta{\left( x' - x\right)} = \int_{-i\infty}^{i\infty} \frac{\mathrm{d} \tilde{x}}{2\pi i} e^{\tilde{x} {\left( x - x'\right)}}$

을 $\delta$ -함수에 대해 삽입하면,

$\begin{align}p(x', t+\varepsilon) & = \int_{-\infty}^\infty \mathrm{d}x \int_{-i\infty}^{i\infty} \frac{\mathrm{d}\tilde{x}}{2\pi i} \left(1+\varepsilon \left[ \tilde{x} D_1(x,t) +\tilde{x}^2 D_2(x,t) \right] \right) e^{\tilde{x} (x - x')}p(x,t) +O(\varepsilon^2) \\[5pt]& =\int_{-\infty}^\infty \mathrm{d}x \int_{-i\infty}^{i\infty} \frac{\mathrm{d}\tilde{x}}{2\pi i}\exp \left( \varepsilon \left[ -\tilde{x}\frac{(x'- x) }\varepsilon + \tilde{x} D_1(x,t) +\tilde{x}^2 D_2(x,t) \right] \right) p(x,t) +O(\varepsilon^2).\end{align}$

이 방정식은 $p(x', t+\varepsilon)$ 을 $p(x,t)$ 의 함수로 표현한다. $(t'-t)/\varepsilon$ 번 반복하고 $\varepsilon \rightarrow 0$ 의 극한을 취하면 작용이

$S=\int \mathrm{d}t\left[ \tilde{x} D_1 (x,t) +\tilde{x}^2 D_2 (x,t) -\tilde{x}\frac{\partial x}{\partial t} \right].$

인 경로 적분을 얻는다. $x$ 에 켤레인 변수 $\tilde{x}$ 는 "응답 변수"라고 불린다.^[27]

형식적으로는 동일하지만, 서로 다른 문제는 포커르-플랑크 방정식 또는 경로 적분 공식에서 더 쉽게 해결될 수 있다. 예를 들어 평형 분포는 포커르-플랑크 방정식에서 더 직접적으로 얻을 수 있다.

9. 역사

아드리안 다니얼 포커르(Adriaan Daniël Fokker^nl, 1887〜1972)와 막스 플랑크가 도입하였다.

참조

_[1] 서적 Statistical Physics: statics, dynamics and renormalization https://books.google[...] World Scientific
_[2] 논문 Die mittlere Energie rotierender elektrischer Dipole im Strahlungsfeld https://zenodo.org/r[...]
_[3] 논문 Über einen Satz der statistischen Dynamik und seine Erweiterung in der Quantentheorie https://biodiversity[...]
_[4] 논문 Über die analytischen Methoden in der Wahrscheinlichkeitstheorie
_[5] 서적 An Introduction to Dynamics of Colloids https://books.google[...] Elsevier
_[6] 서적 Stochastic Processes Springer
_[7] 간행물 N. N. Bogolyubov and statistical mechanics
_[8] 간행물 Fokker–Planck equations generated in perturbation theory by a method based on the spectral properties of a perturbed Hamiltonian
_[9] 서적 The Fokker–Planck Equation: Methods of Solution and Applications 1996-01-01
_[10] 서적 Stochastic Processes in Polymeric Fluids Springer-Verlag 1996-01-01
_[11] 논문 Clustering and Uncertainty in Perfect Chaos Systems
_[12] 서적 Stochastic Processes and Applications : Diffusion Processes, the Fokker-Planck and Langevin Equations Springer
_[13] 논문 Fokker–Planck Equation for an Inverse-Square Force https://escholarship[...]
_[14] 웹사이트 Smoluchowski Diffusion Equation https://www.ks.uiuc.[...] 2000-01-01
_[15] 웹사이트 The Brownian Dynamics Method Applied https://www.ks.uiuc.[...] 2000-01-01
_[16] 웹사이트 Brownian Dynamics https://www.ks.uiuc.[...] 2020-05-18
_[17] 웹사이트 The Brownian Dynamics Method Applied https://www.ks.uiuc.[...] 2020-05-18
_[18] 논문 Physically consistent numerical solver for time-dependent Fokker–Planck equations
_[19] 간행물 Pricing with a Smile
_[20] 간행물 Pricing and Hedging with Smiles Cambridge University Press
_[21] 논문 Lognormal-Mixture Dynamics and Calibration to Market Volatility Smiles
_[22] 논문 Alternative asset-price dynamics and volatility smile
_[23] 서적 Semiparametric Modeling of Implied Volatility Springer Verlag
_[24] 서적 The Volatility Surface Wiley and Sons
_[25] 서적 Martingale Methods in Financial Modelling Springer-Verlag
_[26] 서적 Quantum field theory and critical phenomena Clarendon Press
_[27] 논문 On a Lagrangean for Classical Field Dynamics and Renormalization Group Calculation of Dynamical Critical Properties

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com