내부자기동형사상

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 켤레류
3. 성질
4. 내부 자기 동형 군과 외부 자기 동형 군
- 4.1. 유한 p-군의 비내부 자기 동형
5. 군의 유형
6. 환의 경우
7. 리 대수의 경우
8. 확장
참조

1. 개요

내부자기동형사상은 군 G의 원소 g에 대해 x ↦ gxg⁻¹로 정의되는 자기동형사상이다. 내부자기동형사상 전체는 내부자기동형군을 형성하며, 이는 자기동형군의 정규 부분군이다. 내부자기동형사상은 켤레와 관련이 있으며, 켤레는 군의 원소 x를 a⁻¹xa 형태로 변환하는 연산이다. 내부자기동형군의 존재 여부와 수는 군에서 교환 법칙의 위반 정도를 나타낸다. 또한, 내부자기동형사상은 환 및 리 대수에서도 정의되며, 환의 경우 단위원을 사용하여, 리 대수의 경우 수반 사상을 사용하여 정의된다.

2. 정의

군 $G$ 의 원소 $g$ 에 대해, '''내부자기동형사상'''은 다음과 같이 정의된다.^[1]

: $G\to G$

: $x\mapsto gxg^{-1}$

즉, $g$ 에 의한 (오른쪽) 켤레는 다음과 같은 함수이다.

: $\begin{align}\varphi_g\colon G&\to G \\\varphi_g(x)&:= g^{-1}xg\end{align}$

이 함수는 $G$ 의 자기사상이며, $\varphi_{g^{-1}}$ 라는 역함수를 가지므로 단사 함수이자 전사 함수이다. 따라서, $\varphi_g$ 는 자기동형사상이다. 내부 자기 동형사상은 켤레에서 발생하는 모든 자기 동형사상이다.^[1]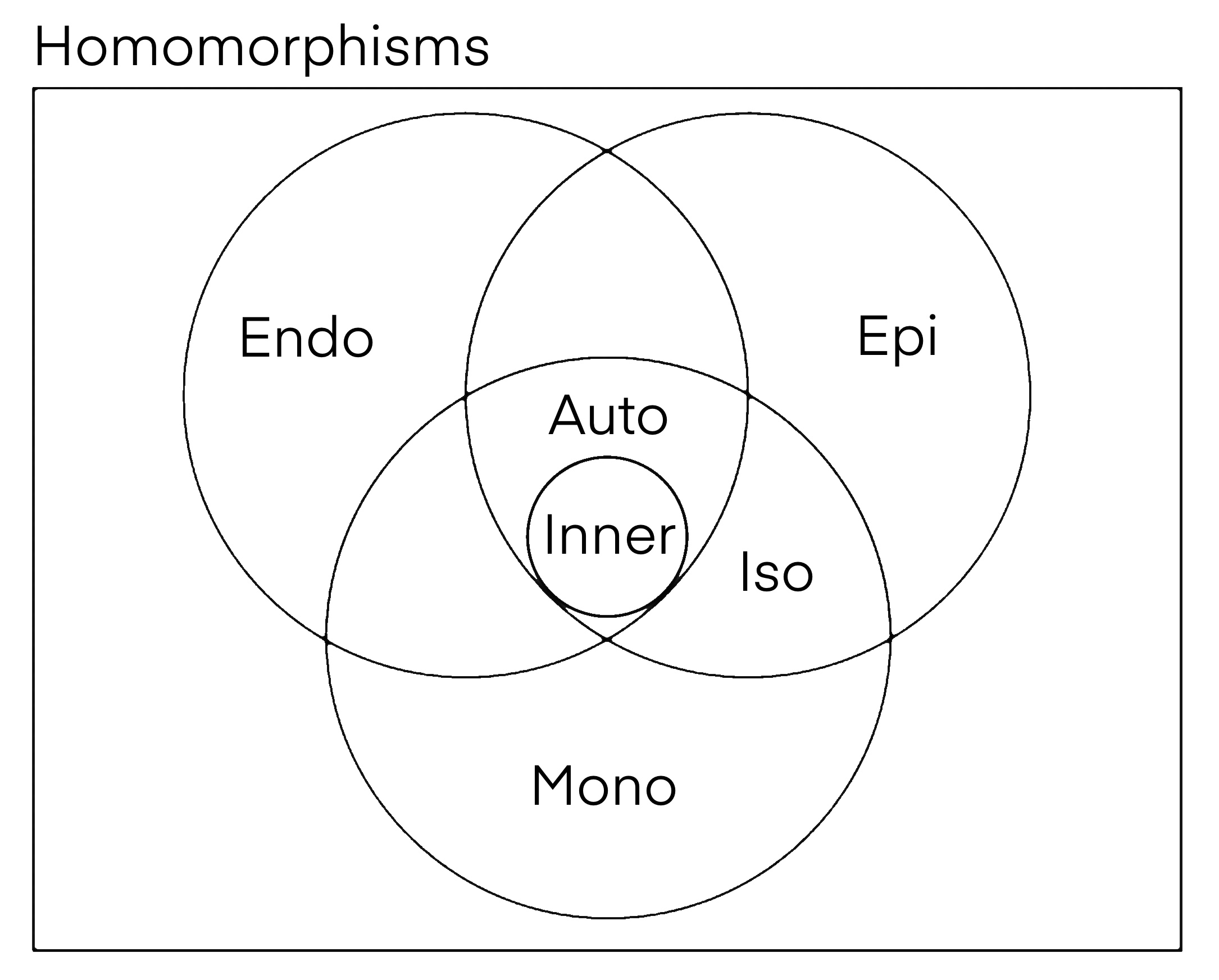

g^{-1}xg

는

x^g

로 지수적으로 표기되기도 한다. 이는 켤레의 합성이

\left(x^{g_1}\right)^{g_2} = x^{g_1g_2}

와 같은 항등식을 만족하기 때문이다.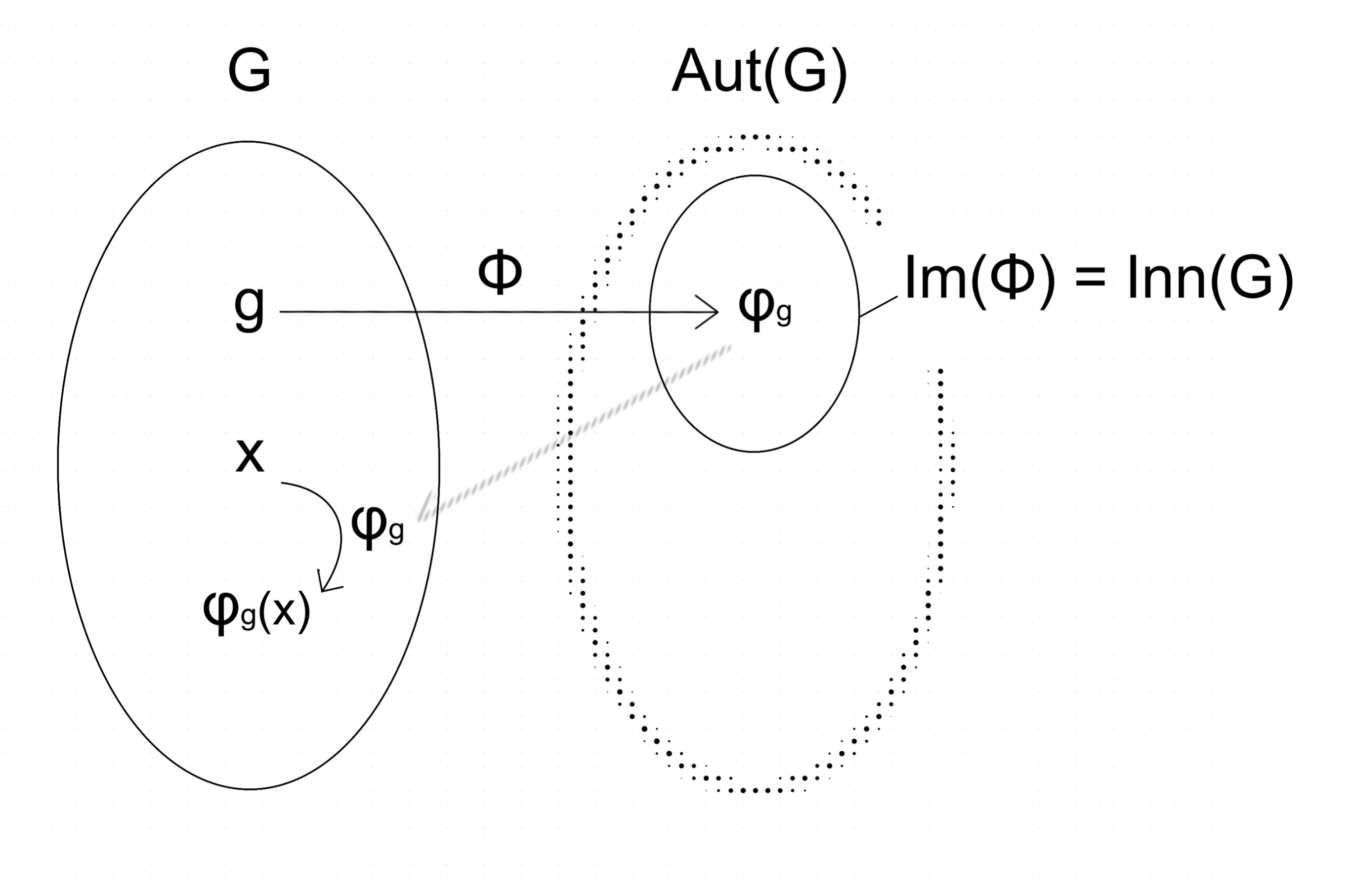

군

G

의 내부자기동형군

\operatorname{Inn}(G)

는

G

위의 내부자기동형사상들이 이루는 군이다.

\operatorname{Inn}(G)

는 자기동형군

\operatorname{Aut}(G)

의 정규 부분군이다.

항등 사상이 아닌 내부 자기 동형의 존재와 개수는 군에서 교환 법칙이 성립하지 않음을 측정하는 것과 같다. 즉,

a^{-1}xa = x

("

a

에 의한 공액은

x

를 바꾸지 않는다")라는 명제와

ax = xa

("

a

와

x

는 가환이다")는 서로 동치이다.

2. 1. 켤레류

군에서 원소

x, y \in G

가 서로 켤레(conjugate)라는 것은

gxg^{-1} = y

를 만족하는

g \in G

가 존재한다는 것을 의미한다. 서로 켤레 관계는 군 위의 동치 관계이다.

군의 원소

x \in G

의 '''켤레류'''(-類, conjugacy class^영어) 또는 '''공액류'''(共軛類)는 다음과 같은 집합이다.

:

\operatorname{Cl}(x)=\{gxg^{-1}\colon g\in G\}

이는

G

위의 켤레 관계에 대한 동치류이다. 즉, 군을 분할한다. 또한, 켤레류는 내부자기동형사상이 유도하는 군의 작용의 궤도이다.

원소

x

를 고정했을 때,

a^{-1}xa

를

x

의

a

에 의한 '''공액'''(conjugate)이라 하고,

x

를

a^{-1}xa

로 변환하는 것(

x \mapsto a^{-1}xa

)을

x

의

a

에 의한 '''공액 변환'''(conjugation) 또는 '''닮음 변환'''(similarity transformation)이라고 한다.

a

에 대해

a^{-1}xa

형태로 쓸 수 있는 원소를

x

의 '''공액 원소'''(conjugate element)라고 한다.^[5]

3. 성질

내부자기동형군은 자기동형군의 정규 부분군이다.

: $\operatorname{Inn}(G)\trianglelefteq\operatorname{Aut}(G)$

이에 대한 몫군

: $\operatorname{Out}(G)=\operatorname{Aut}(G)/\operatorname{Inn}(G)$

를 외부자기동형군이라고 한다.

군의 원소를 그에 대한 내부자기동형사상에 대응시키는 군 준동형

: $G\to\operatorname{Aut}(G)$

: $g\mapsto g{-}g^{-1}$

의 상은 내부자기동형군이며, 핵은 군의 중심이다. 따라서 다음 동형이 성립한다.

: $\operatorname{Inn}(G)\cong G/Z(G)$

이 군 준동형은 군의 작용으로 볼 때, 그 궤도는 켤레류이며, 안정자군은 중심화 부분군이다. 따라서 다음과 같은 항등식이 성립하며, 이를 '''켤레류 방정식'''(class equation^영어)이라고 한다.

: $|G|=|Z(G)|+\sum_{i=1}^n|\!\operatorname{Cl}(x_i)|$

즉,

: $|G|=|Z(G)|+\sum_{i=1}^n|G:C_G(x_i)|$

여기서

$\operatorname{Cl}(x_i)$ 는 크기 1 이상의 켤레류들이다.
$C_G(x_i)$ 는 중심화 진부분군들이다.
$Z(G)$ 는 중심이다. 중심의 원소일 조건은 켤레류가 한원소 집합일 조건 및 중심화 부분군이 $G$ 일 조건과 동치이다.

4. 내부 자기 동형 군과 외부 자기 동형 군

군 $G$의 원소 $g$에 대한 내부자기동형사상은 $x \mapsto gxg^{-1}$로 정의되는 함수 $G \to G$이다. 군 $G$의 모든 내부자기동형사상들의 집합은 군을 이루며, 이를 $G$의 내부자기동형군이라 하고 $\operatorname{Inn}(G)$로 표기한다. 내부자기동형군은 자기동형군 $\operatorname{Aut}(G)$의 정규 부분군이다.

내부자기동형군 $\operatorname{Inn}(G)$는 자기동형군 $\operatorname{Aut}(G)$의 정규 부분군이므로, 몫군 $\operatorname{Out}(G) = \operatorname{Aut}(G) / \operatorname{Inn}(G)$를 정의할 수 있으며, 이를 외부자기동형군이라고 한다.

군 $G$의 원소를 그에 대응하는 내부자기동형사상으로 보내는 군 준동형 $G \to \operatorname{Aut}(G)$, $g \mapsto g{-}g^{-1}$을 생각하면, 이 준동형사상의 상(image)은 내부자기동형군 $\operatorname{Inn}(G)$이고, 핵(kernel)은 군의 중심 $Z(G)$이다. 따라서, 다음 동형이 성립한다.

:$\operatorname{Inn}(G) \cong G/Z(G)$

$g$에 의한 (오른쪽) 켤레는 $\varphi_g(x) := g^{-1}xg$ 와 같이 정의되는 함수이며, 이는 $G$의 자기사상이다. 내부 자기 동형사상은 켤레에서 발생하는 모든 자기 동형사상이다.^[1]

오른쪽 켤레는 $x^g$ 와 같이 지수적으로 표기되기도 한다. 두 내부 자기동형사상의 합성은 다시 내부 자기동형사상이며, 이 연산에 의해 $G$의 모든 내부 자기동형사상의 집합 Inn($G$)는 군을 이룬다.

외부 자기동형군은 $G$의 자기동형사상 중 내부 자기동형사상이 아닌 것의 수를 측정한다. 모든 비내부 자기동형사상은 Out($G$)의 자명하지 않은 원소를 생성하지만, 서로 다른 비내부 자기동형사상들은 Out($G$)의 동일한 원소를 생성할 수 있다.

$a$에 의한 $x$의 켤레가 $x$를 변경하지 않는다는 것은 $a$와 $x$가 서로 교환 가능하다는 것과 같다. 즉,

:$a^{-1}xa = x \iff xa = ax.$

따라서 항등 사상이 아닌 내부 자기동형사상의 존재 여부와 수는 군 (또는 환)에서 교환 법칙이 성립하지 않는 정도를 측정하는 척도라고 할 수 있다.

4. 1. 유한 p-군의 비내부 자기 동형

볼프강 가슈츠(Wolfgang Gaschütz)의 결과에 따르면, G^영어가 유한 비가환 -군이면, G^영어는 내적이 아닌 p^영어-거듭제곱 차수의 자기동형사상을 갖는다.^[1]

모든 비가환 p^영어-군 G^영어가 차수 p^영어의 자기동형사상을 갖는지 여부는 미해결 문제이다.^[1] 이 질문은 G^영어가 다음 조건 중 하나를 만족할 때 긍정적인 답을 갖는다.^[1]

# G^영어는 2류 멱영군이다.^[1]

# G^영어는 정규 p^영어-군이다.^[1]

# 는 강력한 p^영어-군이다.^[1]

# G^영어의 중심, Z^영어의 중앙화 부분군 , 의 프라티니 부분군에 대하여, 는 와 같지 않다.^[1]

5. 군의 유형

군의 내부 자기동형사상군 Inn(''G'')가 아벨군인 것과 ''G''가 아벨 군인 것은 동치이다.^[4]

Inn(''G'')은 군의 중심에 대한 기본적인 결과에 의해 자명할 때에만 순환군이 된다.^[4]

그 반대로 내부 자기동형에 의해 모든 자기동형이 소진되는 경우도 있다. 자기동형이 내부 자기동형뿐이고 중심이 자명한 군을 완전군이라고 한다.^[4] ''n''이 2 또는 6이 아닐 때 ''n''차 대칭군은 complete이다. ''n'' = 6일 때는 대칭군은 단 하나의 비자명한 외부 자기동형의 종류를 가진다. ''n'' = 2일 때는 대칭군은 아벨 군이므로 중심은 자명하지 않고, 외부 자기동형을 갖지 않음에도 불구하고 complete가 아니다.^[4]

완전군 ''G''의 내부 자기동형군이 단순군일 때, ''G''를 준단순군이라고 한다.^[4]

6. 환의 경우

환 ''R''과 단위 ''u'' ∈ ''R''이 주어졌을 때, ƒ(''x'') = ''u''⁻¹''xu''로 정의되는 사상은 ''R''의 환 자기 동형 사상이다. 이러한 형태의 환 자기 동형 사상을 ''R''의 내부 자기 동형 사상이라고 한다. ''R''의 내부 자기 동형 사상 전체는 ''R''의 자기 동형 사상군의 정규 부분군을 이룬다.

7. 리 대수의 경우

리 대수의 자기동형사상은 $Ad_g$ 형태일 때 내부 자기동형사상이라고 한다. 여기서 $Ad$는 리 군의 원소에 대한 수반 사상이고, $g$는 리 대수가 $\mathfrak{g}$인 리 군의 원소이다. 리 대수의 내부 자기동형사상 개념은 리 군의 내부 자기동형사상 개념과 호환되는데, 리 군의 내부 자기동형사상은 해당 리 대수의 고유한 내부 자기동형사상을 유도한다는 의미이다.

8. 확장

가 환 의 가역원군이면, 위의 내부 자기 동형 사상은 행렬환 의 가역원군에 의해 환 위의 사영선 위로 확장될 수 있다. 특히, 고전군의 내부 자기 동형 사상은 그런 방식으로 확장될 수 있다.^[1]

''G''가 환 ''A''의 단위군으로 생성될 때, ''G'' 위의 내부 자기 동형 사상을 행렬환 M₂(''A'')의 단위군에 의해 ''A'' 위의 사영 직선 위의 사상으로 확장할 수 있다.^[1]

참조

_[1] 서적 Abstract algebra Wiley 2004
_[2] 서적 Abstract Algebra Springer
_[3] 서적 Algebra Springer-Verlag
_[4] 간행물 A characterization of inner automorphisms https://www.ams.org/[...] American Mathematical Society
_[5] 웹사이트 Conjugate Element http://mathworld.wol[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com