배스 확산 모형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

배스 확산 모형은 1969년 프랭크 배스가 개발한, 제품이나 서비스의 시장 확산 과정을 설명하는 수학적 모형이다. 이 모형은 혁신 계수(p)와 모방 계수(q)를 사용하여 신규 채택자 수의 변화를 예측하며, 제품의 최대 판매량 시점과 신규 채택자 곡선의 변곡점을 계산하는 데 활용된다. 배스 모형은 지수 분포, 로지스틱 분포, 감마/이동된 곰페르츠 분포의 특수한 경우이며, 일반화된 배스 모형과 연속적인 세대 확장 모형 등 다양한 확장 형태로 발전했다. 온라인 소셜 네트워크의 성장률 추정에도 사용되며, p와 q 값의 범위와 해석을 통해 시장의 특성을 파악할 수 있다. 마케팅 분야에서 널리 인용되며, 다양한 제품과 서비스의 시장 수용 예측에 활용되고 있다.

더 읽어볼만한 페이지

제품 수명 주기 관리 - 프로젝트 매니저
프로젝트 매니저는 프로젝트의 성공적인 완수를 위해 계획 수립, 이해 관계자 관리, 위험 관리, 예산 관리 등을 수행하며, 다양한 산업 분야에서 전문 지식과 기술을 요구한다.
제품 수명 주기 관리 - 컴퓨터 지원 제조
컴퓨터 지원 제조(CAM)는 컴퓨터 소프트웨어를 사용하여 제조 공정을 제어하고 자동화하는 기술로, 설계 데이터를 기반으로 공작 기계 작동을 위한 NC 데이터를 생성하며 다양한 가공 방식과 차원을 지원한다.
응용수학 - 확률
확률은 사건의 가능성을 수치화한 개념으로, 도박에서 시작되어 수학적으로 발전했으며, 다양한 해석과 요소, 응용 분야를 가지며 양자역학, 사회 현상 등에도 적용된다.
응용수학 - 수리사회학
수리사회학은 수학적 모델과 방법론을 활용하여 사회 현상을 분석하는 사회학 분야로, 사회 네트워크 분석을 통해 사회 구조를 규명하고 빅데이터 분석 및 예측에 기여하며 그 중요성이 인정받고 있다.
혁신 - 마음
마음은 의식, 사고, 지각, 감정, 동기, 행동, 기억, 학습 등을 포괄하는 심리적 현상과 능력의 총체이며, 다양한 분야에서 연구되고 인간 삶의 중추적인 역할을 한다.
혁신 - 행위자 연결망 이론
행위자 연결망 이론은 1980년대 프랑스에서 개발된 사회학 이론으로, 인간과 비인간 행위자 간의 관계를 분석하여 과학 기술 혁신 및 지식 창출 과정을 이해하며, 다양한 분야에 적용된다.

배스 확산 모형
개요
이름	배스 확산 모형
고안자	프랭크 배스
발표 년도	1969년
유형	마케팅 모델
목적	신제품의 확산 예측
적용 분야	내구재, 기술, 패션 등
관련 개념	혁신 수용 이론, 네트워크 효과, 입소문 마케팅
모형 설명
기본 가정	잠재적 구매자는 혁신자와 모방자로 나뉜다. 시간의 흐름에 따라 구매가 확산된다. 시장 규모는 고정되어 있다.
변수	p: 혁신 계수 (innovation coefficient) q: 모방 계수 (imitation coefficient) m: 시장 잠재 규모 (market potential) N(t): 시점 t까지의 누적 채택자 수 S(t): 시점 t에서의 판매량
방정식	S(t) = m * (p + q * N(t)/m) * (1 - N(t)/m)
의미	혁신자: 외부 영향(광고, 홍보 등)에 의해 제품을 구매하는 소비자 모방자: 다른 사람의 영향을 받아 제품을 구매하는 소비자 p가 높을수록 초기 채택률이 높고, q가 높을수록 후기 채택률이 높다.
활용
신제품 예측	신제품 출시 후 판매량을 예측하여 마케팅 전략 수립에 활용
마케팅 전략	혁신자와 모방자에게 적합한 마케팅 메시지 개발 제품 확산 속도를 높이기 위한 전략 수립
투자 결정	신제품의 성공 가능성을 예측하여 투자 결정에 활용
장점 및 단점
장점	비교적 간단한 모형으로 이해하기 쉽다. 적은 데이터로도 비교적 정확한 예측이 가능하다. 다양한 산업 분야에 적용 가능하다.
단점	시장 환경 변화를 반영하기 어렵다. 경쟁 제품의 영향을 고려하지 않는다. 장기적인 예측에는 한계가 있다.
추가 정보
관련 연구	배스 확산 모형을 확장하거나 개선한 다양한 연구 존재
참고 자료	Bass, F. M. (1969). A new product growth model for consumer durables. Management Science, 15(5), 215-227. Bass, F. M. (2004). Comments on "A New Product Growth for Model Consumer Durables": The Bass Model. Management Science, 50(12), 1833-1840.

2. 모형의 공식

배스 확산 모형은 시간에 따른 신제품 또는 혁신의 채택률을 설명하는 모델로, 다음과 같은 기본 수식으로 표현된다.^[2]

: $\frac{f(t)}{1-F(t)} = p + q F(t)$

여기서 $\ f(t)$ 는 특정 시점 $\ t$ 에서의 채택률 변화(신규 채택자 비율), $\ F(t)$ 는 시점 $\ t$ 까지의 누적 채택자 비율을 나타낸다. $\ p$ 는 외부 영향(광고 등)에 의한 채택 계수(혁신 계수)이며, $\ q$ 는 내부 영향(구전 효과 등 이미 채택한 사람의 영향)에 의한 채택 계수(모방 계수)이다. 이 식은 아직 제품을 채택하지 않은 사람들의 채택률이 혁신적 요인( $\ p$ )과 모방적 요인( $\ q F(t)$ )의 합으로 결정됨을 나타낸다.

이 기본 공식을 바탕으로 상미분 방정식 형태의 표현, 시간에 따른 신규 채택자 수( $\ s(t)$ ) 예측, 판매량이 최대가 되는 시점( $\ t^*$ ) 및 신규 채택자 곡선의 변곡점( $\ t^{**}$ ) 등을 유도할 수 있으며, 이에 대한 자세한 내용은 하위 섹션에서 다룬다.

2. 1. 기본 공식

\frac{f(t)}{1-F(t)} = p + q F(t)

^[2]

여기서 각 변수는 다음과 같다.

$\ F(t)$ : 시간 $\ t$ 까지 제품을 채택한 사람들의 누적 비율 (설치 기반 비율)
$\ f(t)$ : 채택률의 변화율, 즉 시간 $\ t$ 에서의 채택 확률 밀도 함수. $\ f(t)= F'(t)$
$\ p$ : 혁신 계수 (외부 영향 계수). 아직 제품을 채택하지 않은 사람이 광고 등 외부 요인에 의해 채택할 확률.
$\ q$ : 모방 계수 (내부 영향 계수). 아직 제품을 채택하지 않은 사람이 이미 채택한 사람과의 상호작용(구전 효과 등)을 통해 채택할 확률.

이 관계는 상미분 방정식으로 다음과 같이 표현할 수 있다.

\frac{dF}{dt} = p (1-F) + q F (1-F) = (1-F)(p+qF)

시간

\ t

에서의 판매량(또는 신규 채택자 수)

\ s(t)

는 채택률

\ f(t)

에 총 시장 잠재력

\ m

을 곱한 값이다. 즉,

\ s(t) = m f(t)

이다. 초기 조건

\ F(0)=0

을 적용하면, 시간

\ t

에서의 신규 채택자 수는 다음과 같이 주어진다.

\ s(t) = m \frac{dF}{dt} = m \frac{p(p+q)^2 e^{-(p+q)t}}{(p + q e^{-(p+q)t})^2}

^[2]

(원본 소스에서는

\ s(t)=m{ \frac{(p+q)^2}{p}} \frac{e^{-(p+q)t}}{(1+\frac{q}{p}e^{-(p+q)t})^2}

^[2] 로 표현되었으나, 두 식은 동일하다.)

신규 채택자

\ s(t)

는 혁신자(

\ s_n(t)

)와 모방자(

\ s_i(t)

)로 나눌 수 있다.

혁신자 수: $\ s_n(t) = m p (1-F(t))$
모방자 수: $\ s_i(t) = m q F(t) (1-F(t))$

따라서

\ s(t) = s_n(t) + s_i(t)

이다.

채택률이 최고조에 달하는 시간, 즉 판매량이 최대가 되는 시간

\ t^*

는 다음과 같다.

\ t^* = \frac{\ln(q/p)}{p+q}

^[2]

(단,

\ q > p

이어야

\ t^* > 0

이다. 만약

\ q \le p

이면 채택률은

\ t=0

에서 최대가 되고 이후 계속 감소한다.)

신규 채택자 수 곡선

\ s(t)

의 변곡점이 나타나는 시간

\ t^{**}

는 다음과 같다.

\ t^{**} = \frac{\ln(q/p) - \ln(2 \pm \sqrt{3})}{p+q}

^[4]

이는 최대 판매량 시간

\ t^*

를 기준으로 다음과 같이 표현할 수도 있다.

\ t^{**} = t^* \pm \frac{\ln(2 + \sqrt{3})}{p+q}

^[4]

최대 판매량 시간(

\ t^*

)과 변곡점 시간(

\ t^{**}

)은 모두 양수여야 의미를 가진다. 만약 계산된

\ t^*

가 음수이면, 판매량은

\ t=0

이후 지속적으로 감소하며 별도의 최고점을 갖지 않는다. 또한,

\ p

와

\ q

의 값에 따라 신규 채택자 곡선은 두 개의 변곡점을 갖거나, 하나만 갖거나, 아예 갖지 않을 수도 있다.

2. 2. 상미분 방정식 표현

:

\frac{f(t)}{1-F(t)} = p + q F(t)

^[2]

여기서 각 변수는 다음을 의미한다:

$\ F(t)$ : 설치 기반 비율 (특정 시점까지 제품을 채택한 사람들의 비율)
$\ f(t)$ : 설치 기반 비율의 변화율, 즉 $\ f(t)= F'(t)$ (새롭게 제품을 채택하는 사람들의 비율 변화)
$\ p$ : 혁신 계수 (외부 영향, 예: 광고에 의해 제품을 채택하는 비율)
$\ q$ : 모방 계수 (내부 영향, 예: 이미 제품을 사용하고 있는 사람들의 영향을 받아 채택하는 비율)

이를 상미분 방정식으로 표현하면 다음과 같다.

:

\frac{dF}{dt} = p (1-F) + q (1-F) F = (1-F)(p+qF) = p - F(p-q) - qF^2.

시간

\ t

에서의 판매량(또는 신규 채택자 수)

\ s(t)

는 설치 기반의 변화율

\ f(t)

에 전체 시장 잠재력

\ m

을 곱한 값이다. 초기 조건

\ F(0)=0

(시간 0에서는 채택자가 없음)을 가정하면 다음과 같은 식을 얻는다.

:

\ s(t)=mf(t)

:

\ s(t)=m{ \frac{(p+q)^2}{p}} \frac{e^{-(p+q)t}}{(1+\frac{q}{p}e^{-(p+q)t})^2}

^[2]

판매량

\ s(t)

는 혁신에 의한 판매량

\ s_n(t)

와 모방에 의한 판매량

\ s_i(t)

의 합으로 나눌 수 있다.

$\ s_n(t):= m p (1-F(t))$ : 시간 $\ t$ 에서의 혁신자 수 (외부 영향으로 구매)
$\ s_i(t):= m q (1-F(t))F(t)$ : 시간 $\ t$ 에서의 모방자 수 (내부 영향, 즉 다른 사용자의 영향을 받아 구매)

판매량이 최대가 되는 시간

\ t^*

는 다음과 같다.

:

\ t^*=\frac{\ln q - \ln p}{p+q}

^[2]

신규 채택자 수 변화율(판매량 곡선의 기울기)이 최대가 되는 변곡점 시간

\ t^{**}

는 다음과 같다.

\ t^{**}=\frac{\ln (q/p ) - \ln ( 2 \pm \sqrt { 3 }))}{p+q}

^[4]

또는 최대 판매량 시간

\ t^*

를 이용하여 다음과 같이 표현할 수도 있다.

\ t^{**}= t^{*}  \pm \frac{\ln ( 2 + \sqrt { 3 }))}{p+q}

^[4]

최대 판매량 시간

\ t^*

와 변곡점 시간

\ t^{**}

는 모두 양수여야 의미를 가진다. 만약

\ t^*

가 음수이면, 판매량은 제품 출시 직후부터 계속 감소하며 별도의 최대 지점을 갖지 않는다. 또한,

\ p

와

\ q

값에 따라 신규 채택자 곡선은 변곡점을 하나만 가지거나 아예 갖지 않을 수도 있다.

2. 3. 신규 채택자 수

:

\frac{f(t)}{1-F(t)} = p + q F(t)

^[2]

여기서 각 변수는 다음을 의미한다.

$\ F(t)$ : 설치 기반 비율
$\ f(t)$ : 설치 기반 비율의 변화율 ( $\ f(t)= F'(t)$ )
$\ p$ : 혁신 계수
$\ q$ : 모방 계수

이를 상미분 방정식으로 표현하면 다음과 같다.

:

\frac{dF}{dt} = p (1-F) + q (1-F) F = (1-F)(p+qF) = p - F(p-q) - qF^2.

시간

\ t

에서의 판매량(또는 신규 채택자 수)

\ s(t)

는 설치 기반의 변화율

\ f(t)

에 궁극적인 시장 잠재력

\ m

을 곱한 값이다. 초기 조건

\ F(0)=0

하에서 다음과 같이 표현할 수 있다.

:

\ s(t)=mf(t)

:

\ s(t)=m{ \frac{(p+q)^2}{p}} \frac{e^{-(p+q)t}}{(1+\frac{q}{p}e^{-(p+q)t})^2}

^[2]

신규 채택자 수

\ s(t)

는 시간

\ t

에서의 혁신자 수

\ s_n(t)

와 모방자 수

\ s_i(t)

의 합으로 분해할 수 있다.

혁신자 수: $\ s_n(t):= m p (1-F(t))$
모방자 수: $\ s_i(t):= m q (1-F(t))F(t)$

최대 판매량이 발생하는 시간

\ t^*

는 다음과 같다.

:

\ t^*=\frac{\ln q - \ln p}{p+q}

^[2]

신규 채택자 곡선의 변곡점이 발생하는 시간

\ t^{**}

는 다음과 같이 두 가지 형태로 표현할 수 있다.

\ t^{**}=\frac{\ln (q/p ) - \ln ( 2 \pm \sqrt { 3 }))}{p+q}

^[4]

또는 최대 판매량 시간

\ t^*

를 이용하여 다음과 같이 나타낼 수도 있다.

\ t^{**}= t^{*}  \pm \frac{\ln ( 2 + \sqrt { 3 }))}{p+q}

^[4]

최대 판매량 시간

\ t^*

와 변곡점 시간

\ t^{**}

는 양수여야 의미를 가진다. 만약

\ t^*

가 음수이면, 판매량은 최댓값을 가지지 않고 제품 도입 시점부터 계속 감소한다. 또한,

\ p

와

\ q

값에 따라 신규 채택자 곡선은 변곡점을 하나만 가지거나 아예 가지지 않을 수도 있다.

2. 4. 최대 판매량 및 변곡점

최대 판매량 시간

\ t^*

:

:

\ t^*=\frac{\ln q - \ln p}{p+q}

^[2]

신규 채택자 곡선

\ t^{**}

의 변곡점 시간:

\ t^{**}=\frac{\ln (q/p ) - \ln ( 2 \pm \sqrt { 3 }))}{p+q}

^[4]

또는 다른 형식으로(최대 판매량과 관련하여):

\ t^{**}= t^{*} \pm \frac{\ln ( 2 + \sqrt { 3 }))}{p+q}

^[4]

최대 시간과 변곡점 시간은 양수여야 한다. 만약

\ t^*

가 음수이면, 판매량은 최대값을 갖지 않고 도입 이후 계속 감소한다. 또한,

\ p

와 ''

\ q

''의 값에 따라 신규 채택자 곡선(0에서 시작)이 변곡점을 한 개만 갖거나 아예 갖지 않는 경우도 있다.

3. 모형의 가정 및 변수 설명

배스 확산 모형은 시장 내 잠재적 채택자의 수가 고정되어 있으며, 시간이 지남에 따라 혁신 제품이나 아이디어를 채택하는 과정을 설명한다. 이 모형은 크게 두 가지 주요 요인을 통해 확산 과정을 설명하는데, 하나는 광고와 같은 외부적 요인에 의한 혁신 효과이고, 다른 하나는 이미 제품을 채택한 사람들의 입소문과 같은 내부적 상호작용에 의한 모방 효과이다.^[5]

모형의 핵심 변수는 다음과 같다.

혁신 계수 (p): 아직 제품을 채택하지 않은 사람이 대중 매체나 광고 등 외부 정보에 영향을 받아 제품을 채택할 확률을 나타낸다. 이는 주로 제품 출시 초기에 중요한 역할을 한다.
모방 계수 (q): 아직 제품을 채택하지 않은 사람이 이미 제품을 사용하고 있는 다른 사람과의 상호작용(예: 입소문)을 통해 제품을 채택할 확률을 나타낸다. 이는 시간이 지남에 따라 채택자 수가 증가하면서 중요성이 커진다.

이 두 계수는 특정 제품이나 서비스가 시장에 얼마나 빠르고 넓게 퍼져나갈지를 예측하는 데 사용된다.

3. 1. 혁신 계수 (p)

계수

p

는 혁신 계수, 외부 영향 또는 광고 효과라고 불린다.^[5]

시간

t

를 연 단위로 측정할 때

p

의 전형적인 값은 다음과 같다:^[5]

$p$ 의 평균값은 0.03이며, 일반적인 범위는 0.01에서 0.03 사이인 것으로 밝혀졌다.

3. 2. 모방 계수 (q)

계수

\ q

는 모방 계수(coefficient of imitation), 내부 영향(internal influence) 또는 입소문 효과(word-of-mouth effect)라고 불린다.

시간

\ t

를 연 단위로 측정할 때

\ q

의 전형적인 값은 다음과 같다:^[5]

$\ q$ 의 평균값은 0.38이며, 일반적인 범위는 0.3에서 0.5 사이인 것으로 밝혀졌다.

4. 모형의 유도

배스 확산 모형은 제품 또는 서비스의 수용에 대한 위험률 $\lambda(t)$ 를 다음과 같이 정의할 수 있다고 가정하여 유도된다:

$\lambda(t) = {f(t)\over{S(t)}} = p + q[1-S(t)]$

여기서 $f(t)$ 는 확률 밀도 함수이고 $S(t) = 1-F(t)$ 는 생존 함수이며, $F(t)$ 는 누적 분포 함수이다. 생존 분석의 기본 정의로부터 다음을 알 수 있다:

$f(t) = -{dS\over{dt}} \implies \lambda(t) = -{1\over{S}}{dS\over{dt}}$

따라서, 생존 함수에 대한 미분 방정식은 다음과 같다:

${dS\over{S[p + q(1-S)]}} = -dt$

항의 적분 및 재배열을 통해 다음 식을 얻는다:

${S\over{p+q(1-S)}} = Ae^{-(p+q)t}$

모든 생존 함수는 $S(0) = 1$ 이어야 하므로, 이는 $A = p^{-1}$ 임을 의미한다. 이 조건을 적용하면 생존 함수는 다음과 같다:

$S(t) = {e^{-(p+q)t} + {q\over{p}}e^{-(p+q)t}\over{1 + {q\over{p}} e^{-(p+q)t} }}$

마지막으로, $F(t) = 1-S(t)$ 라는 관계를 사용하여, 제품 수용에 대한 배스 확산 모형을 다음과 같이 얻는다:

$F(t) = {1 - e^{-(p+q)t}\over{1 + {q\over{p}} e^{-(p+q)t} }}$

5. 모형의 확장

기본적인 배스 확산 모형은 다양한 제품의 시장 확산 패턴을 설명하는 데 널리 사용되지만, 현실 세계의 모든 복잡한 요소를 반영하지는 못한다. 예를 들어, 제품 가격의 변화, 경쟁 제품의 등장, 마케팅 활동의 영향, 또는 기술의 빠른 세대 교체와 같은 변수들은 확산 과정에 큰 영향을 미칠 수 있다.

이러한 한계를 극복하고 모형의 설명력과 예측력을 높이기 위해, 기존 배스 모형을 확장하려는 다양한 연구가 진행되었다. 주요 확장 방향은 다음과 같다.

외부 변수 통합: 가격 변화나 광고와 같은 마케팅 전략이 확산 속도에 미치는 영향을 모형에 포함시키려는 시도이다. 이는 일반화된 배스 모형에서 다루어진다.
세대 간 확산: 스마트폰이나 게임 콘솔처럼 여러 세대에 걸쳐 제품이 출시되는 경우, 이전 세대 제품의 확산이 다음 세대 제품의 확산에 미치는 영향을 고려하는 모형이다. 이는 연속적인 세대 확장 모형에서 살펴볼 수 있다.

이 외에도 시장 내 경쟁 구도, 지리적 확산 패턴 등 다양한 요인을 고려한 확장 모형들이 연구되고 있다. 이러한 확장 모형들은 특정 상황에 더 적합한 분석 도구를 제공하며, 기업의 신제품 출시 전략 수립 등에 활용될 수 있다.

5. 1. 일반화된 배스 모형 (가격 변수 고려)

기존 배스 확산 모형은 가격 책정이나 광고와 같은 다양한 관리 의사 결정 변수가 존재함에도 불구하고, 거의 모든 제품 도입 사례의 데이터에 잘 들어맞는 경향을 보인다. 이는 이러한 의사 결정 변수들이 확산 곡선을 시간적으로 앞당기거나 늦출 수는 있지만, 곡선 자체의 기본적인 모양은 대체로 유사하게 유지된다는 것을 의미한다.

배스 모형을 확장하려는 여러 시도가 있었는데, 그중 프랭크 배스(Frank Bass), 트리치 크리슈난(Trichy Krishnan), 디팩 자인(Dipak Jain)이 1994년에 개발한 모형은 특정 조건 하에서 기존 배스 모형으로 단순화될 수 있는 일반화된 형태를 제시한다.^[6] 이들은 가격 변화율 및 기타 외부 요인의 영향을 포함하기 위해 다음과 같은 일반화된 배스 모형 수식을 제안했다.

:

\frac{f(t)}{1-F(t)} = (p + {q}F(t)) x(t)

여기서

\ x(t)

는 시간에 따른 가격 변화율이나 마케팅 활동 등 외부 변수의 영향을 나타내는 함수이다.

기존 배스 모형은 해석적인 해(analytic solution)를 구할 수 있는 경우가 많지만, 이 일반화된 배스 모형은

\ x(t)

함수의 복잡성 때문에 일반적으로 해석적인 해를 갖지 않는다. 따라서 실제 적용 시에는 수치적인 방법(numerical method)을 사용하여 해를 구해야 한다.

이 모형에 대해 Orbach (2016)는 연속적인 시간 흐름을 가정하는 경우와 이산적인 시간 단위(예: 월별, 연도별)로 나누어 분석하는 경우에 사용되는 혁신 계수(p)와 모방 계수(q)의 값이 완벽하게 동일하지 않을 수 있음을 지적했다.^[7] p값이 0.01~0.03, q값이 0.2~0.4 범위인 일반적인 경우에는 연속 시간 모형과 이산 시간 모형의 예측 결과가 매우 유사하게 나타난다. 하지만 p와 q값이 이 범위를 벗어나는 경우에는 두 방식 간의 예측 결과가 상당히 달라질 수 있으므로 주의가 필요하다.

5. 2. 연속적인 세대 확장

기술 제품은 세대를 거듭하며 성공을 거둔다. 존 노턴과 프랭크 배스는 1987년에 지속적인 반복 구매가 이루어지는 제품의 판매에 대한 모델을 확장했다.^[8] 3세대에 대한 공식은 다음과 같다:

:

S_{1,t} = F(t_1) m_1 (1-F(t_2))

:

S_{2,t} = F(t_2) (m_2 + F(t_1) m_1 ) (1-F(t_3))

:

S_{3,t} = F(t_3) (m_3 + F(t_2) (m_2 + F(t_1) m_1 ))

여기서

$m_i = a_i M_i$
$M_i$ 는 ''i''번째 세대 제품의 최종 채택자 수의 증가분이다.
$a_i$ 는 ''i''번째 세대 제품 채택자들의 평균 (지속적인) 반복 구매율이다.
$t_i$ 는 ''i''번째 세대 제품이 출시된 이후의 시간이다.
$F(t_i) = \frac{1-e^{-(p+q)t_i}}{1+\frac{q}{p} e^{-(p+q)t_i}}$

p와 q의 값은 일반적으로 연속적인 세대 간에 동일한 것으로 밝혀졌다.

6. 다른 확산 모형과의 관계

배스 확산 모형은 특정 조건 하에서 다른 분포 모형의 형태를 띤다. 모형의 매개변수 q가 0일 때는 지수 분포로, p가 0일 때는 로지스틱 분포로 축소된다. 또한 배스 모형은 감마/이동된 곰페르츠 분포(G/SG)의 특수한 경우로 간주되기도 한다.^[9]

6. 1. 지수 분포

배스 확산 모형의 특수한 경우 중 하나로, q=0일 때 모형은 지수 분포로 축소된다.

6. 2. 로지스틱 분포

배스 확산 모형의 특수한 경우 중 하나로, 모형의 매개변수 p가 0일 때 로지스틱 분포로 축소된다.

6. 3. 감마/이동된 곰페르츠 분포(G/SG)

배스 모형은 감마/이동된 곰페르츠 분포(G/SG)의 특수한 경우이다. Bemmaor^[9] (1994)

7. 온라인 소셜 네트워크에서의 활용

온라인 소셜 네트워크(및 기타 가상 커뮤니티)가 최근(2007년 초 기준) 빠르게 성장하면서 배스 확산 모형의 사용이 늘어났다. 배스 확산 모형은 이러한 소셜 네트워크의 규모와 성장률을 추정하는 데 사용된다. Christian Bauckhage 등의 연구^[10]에 따르면, 배스 모형은 Weibull 분포나 이동 Gompertz 분포와 같은 다른 모형들보다 미래 예측에 있어 더 비관적인 경향을 보인다.

8. p, q 모수의 범위와 해석

배스 확산 모형에서 확산 속도와 패턴을 결정하는 중요한 두 가지 변수는 혁신 계수(''p'')와 모방 계수(''q'')이다. 혁신 계수 ''p''는 광고 등 외부 영향에 의해 자발적으로 제품을 채택하는 비율을 나타내며, 모방 계수 ''q''는 이미 제품을 채택한 사람들의 입소문이나 영향력에 의해 추가적으로 채택하는 비율을 의미한다.^[2]

초기 배스(1969년)의 연구에서는 ''p''와 ''q''의 상대적 크기에 따라 확산 양상이 달라짐을 보였다. 성공적인 신제품은 초기 채택 이후 입소문 효과가 커지는 ''p'' < ''q''의 S자형 확산 곡선을 따르는 경향이 있으며, 반대로 출시 초기에 판매가 집중되고 빠르게 감소하는 경우는 ''p'' > ''q''로 나타날 수 있다.^[2]

그러나 후속 연구들은 ''p''와 ''q''의 값이 음수가 될 수 있는 경우까지 고려하며 모형의 설명력을 확장했다. 자인 외(1995년)는 시딩 전략을 통해 초기 사용자를 확보할 경우, 제품 자체의 초기 매력도가 낮거나(예: 높은 가격, 사용 어려움) 채택 장벽이 있어 ''p'' 값이 음수(-)가 되더라도 특정 조건 하에서는 확산이 시작될 수 있음을 보였다.^[11] 이는 사용자 증가에 따른 외부 효과나 불확실성 감소로 제품 가치가 상승할 수 있기 때문이다.

또한, 몰도반과 골덴버그(2004년)는 부정적인 입소문(WOM) 효과나 채택자 증가에 따른 편익 감소(예: 특정 서비스의 혼잡 증가)를 반영하여 ''q'' 값이 음수(-)가 될 수 있음을 제시했다.^[12] ''q''가 음수일 경우, 시장은 특정 조건(p < -q) 하에서 잠재 수요 전체에 도달하지 못하고 일정 수준(-p/q)에서 포화될 수 있다.

오르바흐(2022년)는 이러한 다양한 가능성을 종합하여, ''p''와 ''q'' 값의 조합에 따라 달라지는 확산 양상을 보여주는 확장된 (p, q) 공간 지도를 제시했다.^[13] 이 지도는 단순히 자발적으로 확산되는 경우(p>0, q>0) 외에도, 확산에 초기 장벽이 있는 경우(음수 ''p''), 확산을 위해 외부 자극이 필요한 경우, 또는 신규 채택에 대한 저항(음수 ''q'')으로 인해 시장이 완전 채택에 이르지 못하고 안정화되는 다양한 시나리오를 포괄적으로 설명한다.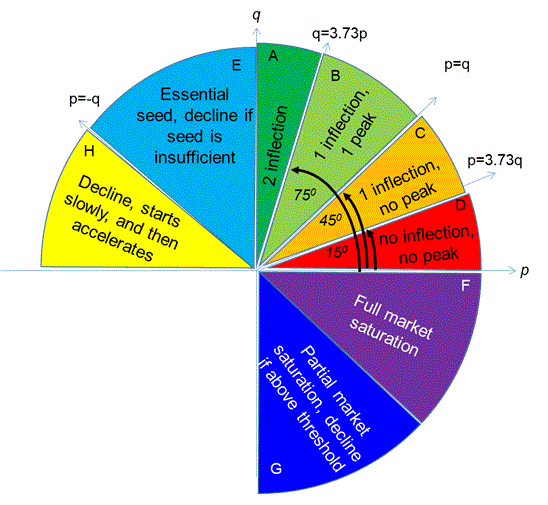

8. 1. p > q 와 p < q 의 구분

배스(1969년)^[2]는 혁신 계수(''p'')와 모방 계수(''q'')의 상대적 크기에 따라 확산 패턴을 구분했다.

''p'' < ''q'': 초기 판매가 서서히 증가하다가 정점을 찍고 감소하는 경우이다. 이는 성공적인 신제품에서 흔히 나타나는 S자형 확산 곡선에 해당하며, 초기 혁신가들의 채택 이후 모방자들의 입소문 효과가 더 크게 작용하는 상황을 나타낸다.
''p'' > ''q'': 제품 출시 직후 판매량이 가장 높고 이후 점차 감소하는 경우이다. 이는 혁신 효과가 모방 효과보다 훨씬 커서 초기 수요가 빠르게 집중되고 이후 추가 확산이 미미한 상황을 의미한다.

자인 외(1995년)^[11]는 시딩(seeding, 초기 사용자 확보 전략)의 영향을 분석하며 ''p'' 값이 음수인 경우를 탐구했다. ''p''가 음수라는 것은 초기 채택에 대한 장벽(예: 높은 가격, 사용의 어려움)이 존재함을 시사할 수 있다. 그러나 시딩을 통해 초기 사용자 비율 F(0)가 특정 조건(p + qF(0) > 0 이고 F(0) > -p/q)을 만족하면, 음수 ''p''에도 불구하고 확산이 시작될 수 있다. 이는 다른 사용자들이 제품을 채택함에 따라 외부 효과가 발생하거나 제품에 대한 불확실성이 감소하면서 잠재 고객에게 제품의 매력이 증가하기 때문이다.

몰도반과 골덴버그(2004년)^[12]는 부정적인 입소문 효과를 고려하여 ''q'' 값이 음수가 될 수 있음을 보였다. 음수 ''q''는 제품 자체에 대한 불만족보다는, 채택자가 증가함에 따라 오히려 제품 사용의 이점이 감소하는 상황(예: 특정 서비스의 혼잡 증가)을 나타낼 수 있다. 예를 들어, 기차의 예약 좌석 수가 늘어나면 비예약 칸의 혼잡이 줄어들어 좌석 확보 가능성이 높아지므로, 굳이 예약 좌석을 구매할 유인이 감소하는 경우가 이에 해당한다. 음수 ''q''일 때 시장의 최종 포화 수준은 ''p''와의 관계에 따라 달라진다.

''p'' > -''q'': 시장은 결국 잠재 수요의 100%에 도달한다.
''p'' < -''q'': 시장은 장기적으로 잠재 수요의 -p/q 수준에서 포화된다.

오르바흐(2022년)^[13]는 이러한 다양한 경우를 종합하여 (''p'',''q'') 공간에서 각 영역별 확산 양상을 정리하고 시각화했다. 아래 지도는 확산이 자발적으로 일어나는 영역(p>0, q>0) 외에도, 확산에 장벽이 있거나(음수 ''p''), 외부 자극이 필요하거나, 신규 채택에 대한 저항(음수 ''q'')으로 인해 시장이 완전 채택에 이르지 못하고 특정 수준에서 안정화될 수 있는 다양한 시나리오를 보여준다.

8. 2. 시딩(Seeding) 전략과 음수 p

배스 모형에서 혁신 계수 ''p''는 외부 영향(예: 광고)에 의한 초기 채택률을 나타낸다. 일반적으로 ''p''는 양수 값을 가지지만, 특정 조건에서는 음수 값을 가질 수도 있다.^[2]

자인(Zain) 등(1995년)은 시딩(seeding) 전략이 확산에 미치는 영향을 연구했다.^[11] 시딩은 초기에 의도적으로 특정 사용자 그룹에게 제품을 보급하여 확산을 유도하는 마케팅 전략이다. 연구에 따르면, 시딩 전략을 사용할 경우 특정 조건 하에서는 혁신 계수 ''p''가 음수 값을 갖더라도 제품 확산이 시작될 수 있다. 이 조건은 ''p'' + ''q''F(0) > 0이며, 이는 마케터가 초기 시딩 규모 F(0)를 -''p''/''q''보다 크게 설정해야 함을 의미한다.^[11]

''p'' 값이 음수라는 것이 반드시 해당 제품이 가치가 없거나 결함이 있음을 의미하지는 않는다.^[11] 오히려 초기 사용자가 거의 없을 때 제품 채택에 대한 가격 장벽이 높거나, 사용 방법을 배우기 어렵거나(학습 곡선), 네트워크 효과가 약해 효용이 낮은 경우에 나타날 수 있다. 하지만 다른 사용자들이 점차 제품을 채택함에 따라 외부 효과가 발생하거나 제품에 대한 불확실성이 감소하면서 제품의 가치가 증가하고, 더 많은 잠재 고객에게 매력적인 선택지가 될 수 있다.^[11]

오르바흐(Orbach, 2022년)는 ''p''와 ''q'' 값에 따른 다양한 확산 양상을 (''p'',''q'') 공간에 시각화하여 제시했다.^[13] 이 확장된 공간 지도는 ''p''가 음수인 경우(확산 장벽 존재)와 ''q''가 음수인 경우(신규 채택자에 대한 기존 채택자의 저항) 등, 기존의 단순한 확산 모델을 넘어선 다양한 시장 상황을 설명한다. 특히 음수 ''p'' 영역은 확산을 시작하기 위해 시딩과 같은 외부적인 "자극"이 필요한 시장 상황을 나타낸다.

8. 3. 부정적 입소문(WOM)과 음수 q

배스 모형에서 혁신 계수 ''p''와 모방 계수 ''q''의 상대적 크기는 제품 확산 패턴에 영향을 미친다. 배스(1969년)는 주기적인 판매량이 초기에 증가했다가 감소하는 경우(''p''<''q'')와 출시 직후부터 판매량이 계속 감소하는 경우(''p>q'')를 구분했다.^[2] 성공적인 제품은 일반적으로 ''p''<''q''의 패턴을 보인다.

자인 외(1995년)는 초기 구매자를 확보하는 시딩(seeding) 전략의 영향을 연구했다.^[11] 이 연구에 따르면, ''p'' 값이 음수(-)인 경우에도 특정 조건(p + qF(0) > 0) 하에서 시딩 전략(시드 크기 F(0) > -p/q)을 사용하면 확산이 시작될 수 있다. 음수 ''p'' 값은 제품 자체가 쓸모없다는 의미보다는, 초기 사용자가 적을 때 가격이나 사용 노력 등 채택에 대한 장벽이 높다는 것을 시사할 수 있다. 다른 사용자들이 제품을 채택함에 따라 외부 효과가 발생하거나 불확실성이 줄어들면 제품의 가치가 증가하여 더 많은 잠재 고객에게 매력적인 선택지가 될 수 있다.

몰도반과 골덴버그(2004년)는 부정적인 입소문(WOM) 효과를 모형에 통합하여 모방 계수 ''q''가 음수(-)가 될 가능성을 제시했다.^[12] 음수 ''q''는 반드시 채택자들이 제품 구매에 실망하거나 불만족한다는 의미는 아니다. 오히려 더 많은 사람이 제품을 채택함에 따라 개별 사용자에게 돌아가는 이점이 감소하는 상황을 설명할 수 있다. 예를 들어, 기차 통근 수요가 일정 수준일 때, 좌석을 확보하려는 사람들은 예약 티켓을 구매할 수 있다. 하지만 예약 좌석 판매가 늘어날수록 비예약 칸의 혼잡도가 줄어들어 빈 좌석을 찾을 가능성이 높아지고, 이는 결과적으로 예약 좌석 구매의 매력을 떨어뜨릴 수 있다. 음수 ''q''를 갖는 경우, 비누적 판매 곡선은 ''q''=0일 때와 유사하게 나타나지만, 누적 판매 곡선은 다른 양상을 보인다. 만약 p > -q 라면, 시장은 결국 양수 ''q''의 경우처럼 잠재 수요의 100%에 도달한다. 그러나 p < -q 라면, 시장은 장기적으로 잠재 수요의 -p/q 수준에서 포화 상태에 이르게 된다.

오르바흐(2022년)는 ''p''와 ''q'' 값에 따른 다양한 확산 양상을 종합적으로 분석했다.^[13] 그는 기존의 양수 ''p'', ''q'' 영역(자발적 확산)을 넘어, 확산에 장벽이 있는 경우(음수 ''p''), 확산을 시작하기 위해 외부 자극이 필요한 경우, 또는 신규 채택에 대한 기존 채택자들의 저항(음수 ''q'')으로 인해 시장이 완전 채택에 이르지 못하고 특정 수준에서 안정화될 수 있는 경우까지 포함하여 확장된 (''p'',''q'') 공간을 제시했다.

8. 4. 확장된 p-q 공간 지도

배스(1969년)는 초기에 주기적인 판매가 증가했다가 감소하는 경우(성공적인 제품의 일반적인 판매 주기)인 ''p''<''q''와, 제품 출시 이후 판매량이 지속적으로 감소하는 경우(판매 정점 없음)인 ''p>q''를 구분했다.^[2] 이후 연구들은 ''p''와 ''q'' 값이 음수가 되는 경우까지 고려하여 모형을 확장했다.

자인 외(1995년)는 시딩(seeding) 전략이 확산에 미치는 영향을 연구했다.^[11] 이들은 시딩을 통해 초기 구매자 집단 F(0)가 특정 조건(F(0) > -p/q)을 만족하면, 혁신 계수 ''p''가 음수일지라도 확산이 시작될 수 있음을 보였다. 음수 ''p'' 값은 반드시 제품 자체가 쓸모없다는 의미는 아니다. 예를 들어, 초기 사용자가 거의 없을 때는 제품 사용에 대한 가격 장벽이나 사용법 습득의 어려움이 클 수 있다. 그러나 점차 많은 사람들이 제품을 채택함에 따라 외부 효과가 발생하거나 제품에 대한 불확실성이 줄어들면서 제품의 가치가 증가하고, 더 많은 잠재 고객에게 매력적인 선택지가 될 수 있다.

몰도반과 골덴버그(2004년)는 부정적인 입소문(WOM, Word-of-Mouth) 효과를 모형에 통합하여 모방 계수 ''q''가 음수가 될 가능성을 제시했다.^[12] 음수 ''q'' 역시 제품에 대한 실망이나 불만족만을 의미하는 것은 아니다. 오히려 더 많은 사람이 제품을 채택함에 따라 제품 사용으로 얻는 이점이 감소하는 상황을 설명할 수 있다. 예를 들어, 특정 노선의 기차 통근에서 좌석 확보를 위해 예약 티켓을 구매하는 경우를 생각해보자. 예약 좌석 판매가 늘어날수록 비예약 칸의 혼잡도는 줄어들고, 비예약 칸에서도 좌석을 찾을 확률이 높아진다. 이는 결국 예약 좌석 구매의 매력을 감소시키는 효과를 가져온다. 음수 ''q''를 갖는 경우, 비누적 판매 곡선(특정 시점의 판매량)은 ''q''=0인 경우와 유사한 패턴을 보일 수 있다. 하지만 누적 판매 곡선은 다른 양상을 보인다. 만약 p > -q 라면, 시장은 결국 잠재 수요의 100%에 도달하지만, p < -q 인 경우에는 장기적으로 시장이 잠재 수요의 -p/q 수준에서 포화 상태에 이르게 된다.

오르바흐(2022년)는 이러한 논의들을 종합하여 확장된 (''p'',''q'') 공간 지도를 제시했다.^[13] 이 지도는 ''p''와 ''q'' 값의 조합에 따라 확산 양상이 어떻게 달라지는지를 보여준다. 기존의 자발적 확산이 일어나는 영역(p>0, q>0)을 넘어, 확산이 초기 장벽에 부딪히는 영역(음수 ''p''), 확산을 시작하기 위해 외부적인 "자극"(예: 시딩)이 필요한 영역, 또는 신규 채택에 대한 기존 채택자들의 저항(음수 ''q'')으로 인해 시장이 완전 채택에 이르지 못하고 특정 수준에서 안정화되는 영역 등을 구분하여 설명한다.

9. 모형의 의의 및 영향

이 모형은 마케팅 분야에서 가장 많이 인용되는 경험적 일반화 중 하나로 꼽힌다. 1969년 ''Management Science''에 발표된 논문 "A New Product Growth for Model Consumer Durables"는 2023년 8월 기준으로 Google Scholar에서 약 11,352회 인용되었다.^[14]

이 모형은 마케팅 및 경영 과학 분야에 상당한 영향을 미쳤다. 2004년에는 ''Management Science'' 창간 50년 역사상 가장 많이 인용된 논문 10편 중 하나로 선정되었으며,^[3] 5위를 기록했다. 이는 목록에 포함된 유일한 마케팅 분야 논문이었고, 같은 해 12월호 ''Management Science''에 재수록되기도 했다.^[3]

배스 모형은 본래 내구 소비재의 확산을 설명하기 위해 개발되었으나, 이후 그 적용 범위가 크게 확장되었다. 유형 및 무형의 의료 제품,^[15]^[16] 금융 상품,^[17] 그리고 다양한 소비재, 산업재, 서비스의 시장 수용을 예측하는 데에도 널리 활용되고 있다. 예를 들어, Sultan 등(1990)은 배스 모형을 213개 제품 범주에 적용하여 분석했는데, 여기에는 다양한 가격대의 내구 소비재뿐만 아니라 모텔과 같은 서비스나 잡종 옥수수 종자와 같은 산업 및 농업 제품도 포함되었다.^[18]

참조

_[1] 학술지 Comments on "A New Product Growth for Model Consumer Durables": The Bass Model
_[2] 학술지 A new product growth for model consumer durables
_[3] 간행물 2004-12
_[4] 학술지 Determination of Adopter Categories by Using Innovation Diffusion Models http://dx.doi.org/10[...] 1990
_[5] 학술지 Diffusion of new products: Empirical generalizations and managerial uses
_[6] 학술지 Why the Bass Model Fits without Decision Variables 1994
_[7] 학술지 Parametric analysis of the Bass model 2016-04-27
_[8] 학술지 A Diffusion Theory Model of Adoption and Substitution for Successive Generations of High-Technology Products 1987
_[9] 서적 Research Traditions in Marketing Kluwer Academic Publishers
_[10] arXiv Strong Regularities in Growth and Decline of Popularity of Social Media Services
_[11] 학술지 An approach for determining optimal sampling for the diffusion of a new product 1995
_[12] 학술지 Cellular automata modeling of resistance to innovations: Effects and solutions 2004
_[13] 서적 Forecasting the Dynamics of Market and Technology Ariel University Press
_[14] 웹사이트 Google Scholar https://scholar.goog[...]
_[15] 학술지 Forecasting the Maturation of Electronic Health Record Functions Among US Hospitals: Retrospective Analysis and Predictive Model 2018-08-07
_[16] 학술지 Nation-scale adoption of new medicines by doctors: an application of the Bass diffusion model 2012-08-10
_[17] Citation Voluntary, Occupational Pensions http://dx.doi.org/10[...] OECD 2006-05-03
_[18] 학술지 A Meta-Analysis of Applications of Diffusion Models http://dx.doi.org/10[...] 1990-02

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com