오일러-라그랑주 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 역사
4. 증명
5. 뉴턴 역학과의 관계
- 5.1. 일반화 좌표
6. 다양한 분야로의 확장
- 6.1. 라그랑주 역학
- 6.2. 해밀턴 역학
7. 일반화
참조

1. 개요

오일러-라그랑주 방정식은 변분법을 사용하여 범함수의 정류점을 찾는 데 사용되는 편미분 방정식이다. 레온하르트 오일러와 조제프루이 라그랑주가 1750년대에 타우토크론 문제 연구를 위해 개발했다. 이 방정식은 라그랑주 역학, 해밀턴 역학, 심플렉틱 기하학, 리만 기하학 등 다양한 분야에서 활용되며, 뉴턴 역학을 일반화한 것으로 볼 수 있다. 고계 도함수, 여러 함수, 여러 변수를 포함하는 경우로 확장될 수 있으며, 장 이론에서도 중요한 역할을 한다.

2. 정의

$\mathcal C^1$ 미분 가능 다양체 $X$ 와 그 접다발 $TX$ 를 생각한다. 유한한 닫힌 구간 $[a,b]\subset\mathbb{R}$ 와, 연속미분가능 다발 사상 $L(t,x,v)\in\mathbb R$ , $t\in[a,b]$ , $x\in X$ , $v\in T_xX$ 를 생각한다. $L(t,x,v)$ 의 두 번째와 세 번째 변수를 미분하여 도함수 다발 사상 $L_x(t,x,v)\in T_x^*X$ 와 $L_v(t,x,v)\in T_x^*X$ 를 정의할 수 있다. 임의의 연속미분가능함수 $q\colon[a,b]\to X$ 를 정의역으로 하는 범함수

: $S[q]=\int_a^bL(t,q(t),q'(t))\;dt$

를 정의할 수 있다. 여기서 $q'$ 는 $q$ 의 도함수 $q'(t)\in T_{q(t)}X$ 를 뜻한다. 주어진 경계조건

: $q(a)=x_a\in X$

: $q(b)=x_b\in X$

아래 $S[q]$ 의 정류점을 찾는 변분문제를 생각할 수 있다. 이 변분문제의 해 $q_0$ 는 다음 방정식

: $L_x(t,q_0,q'_0)=\frac{d}{dt}\left(L_v(t,q_0(t),q'_0(t))\right)\in T_{q(t)}^*X$

을 만족한다. 이를 '''오일러-라그랑주 방정식'''이라고 부른다.

(X, L)을 자유도 n인 실수 역학계라 하자. 여기서 X는 배위 공간이고, L = L(t, q(t), v(t))는 매끄러운 실수값 함수인 라그랑주량이다. q(t) ∈ X이고, v(t)는 n차원 "속도 벡터"이다.

q(a) = xₐ이고 q(b) = xբ인 매끄러운 경로 q: [a, b] → X의 집합을 P(a, b, xₐ, xբ)라 하자. 작용 함수 S: P(a, b, xₐ, xբ) → ℝ은 다음과 같이 정의된다.

$S[\boldsymbol q] = \int_a^b L(t,\boldsymbol q(t),\dot{\boldsymbol q}(t))\, dt.$

경로 q ∈ P(a, b, xₐ, xբ)가 S의 정상점이 되는 것은 다음과 같은 경우이고, 그 경우에만 가능하다.

: $\frac{\partial L}{\partial q^i}(t,\boldsymbol q(t),\dot{\boldsymbol q}(t))-\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot q^i}(t,\boldsymbol q(t),\dot{\boldsymbol q}(t)) = 0,\quad i = 1, \dots, n.$

여기서 q̇(t)는 q(t)의 시간에 대한 도함수이다.

3. 역사

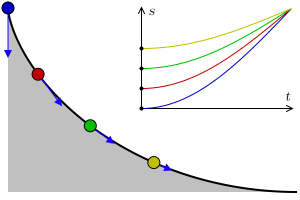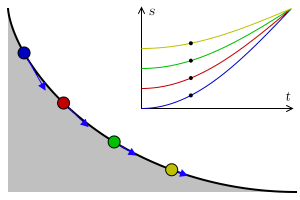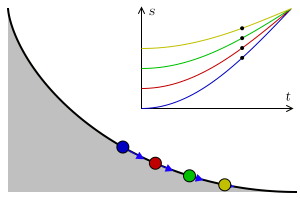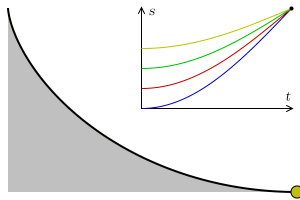
레온하르트 오일러와 조제프루이 라그랑주가 1750년대에 타우토크론 문제(등시강하곡선 문제)를 연구하면서 오일러-라그랑주 방정식을 개발하였다.

타우토크론 문제는 가중치가 있는 입자가 출발점에 관계없이 고정된 시간에 고정된 지점으로 낙하하는 곡선을 결정하는 문제이다.

라그랑주는 1755년에 이 문제를 해결하고 그 해결책을 오일러에게 보냈다. 두 사람은 이 방법을 더욱 발전시켜 역학에 적용했고, 이는 라그랑주 역학의 공식화로 이어졌다. 이들의 서신은 궁극적으로 1766년 오일러가 만든 변분법으로 이어졌다.^[3]

4. 증명

1차원 오일러-라그랑주 방정식의 유도는 변분법의 기본정리에 기반한다.^[4]

경계 조건 f(a) = c, f(b) = d를 만족하고, 다음 범함수 ''J''를 최대 또는 최소로 만드는 함수 ''f''를 찾는다고 가정한다.

: $J = \int_a^b F(x,f(x),f'(x))\, dx. \,\!$

여기서 ''F''는 연속적인 편미분값을 가진다고 가정한다.

''f''가 상대 범함수를 최대 또는 최소로 만든다면, ''f''에 매우 작은 변화를 가했을 때 ''J''의 값은 늘거나(''f''가 ''J''를 최소화할 때) 줄 수 있다(''f''가 ''J''를 최대화할 때).

''f''에 매우 작은 변화를 준 함수 ''g''_ε(''x'') = ''f''(''x'') + εη(''x'')를 도입한다. 여기서 η(''x'')는 η(''a'') = η(''b'') = 0을 만족하는 미분 가능한 함수이다. ''f'' 대신 ''g''를 넣은 ''J''는 다음과 같은 함수가 된다.

: $J(\epsilon) = \int_a^b F(x,g_\epsilon(x), g_\varepsilon'(x) )\, dx. \,\!$

''J''를 ''ε''에 대해 미분한 전미분을 구하면 다음과 같다.

: $\frac{\mathrm{d} J}{\mathrm{d} \varepsilon} = \int_a^b \frac{\mathrm{d}F}{\mathrm{d}\epsilon}(x,g_\varepsilon(x), g_\varepsilon'(x) )\, dx.$

전미분의 정의에 의해 다음 식이 유도된다.

: $\frac{\mathrm{d}F}{\mathrm{d}\epsilon} = \frac{\partial F}{\partial x}\frac{\partial x}{\partial \varepsilon} + \frac{\partial F}{\partial g_\varepsilon}\frac{\partial g_\varepsilon}{\partial \varepsilon} + \frac{\partial F}{\partial g'_\varepsilon}\frac{\partial g'_\varepsilon}{\partial \varepsilon} = \eta(x) \frac{\partial F}{\partial g_\varepsilon} + \eta'(x) \frac{\partial F}{\partial g_\varepsilon'}.$

따라서,

: $\frac{\mathrm{d} J}{\mathrm{d} \epsilon} = \int_a^b \left[\eta(x) \frac{\partial F}{\partial g_\varepsilon} + \eta'(x) \frac{\partial F}{\partial g_\varepsilon'} \, \right]\,dx.$

''ε'' = 0 이면 ''g''_''ε'' = ''f'' 이고, ''f'' 가 ''J''를 극값으로 만드는 부분이므로, ''J'''(0) = 0 이 된다. 즉,

: $J'(0) = \int_a^b \left[ \eta(x) \frac{\partial F}{\partial f} + \eta'(x) \frac{\partial F}{\partial f'} \,\right]\,dx = 0.$

두 번째 항에 부분적분을 적용하면 다음과 같다.

: $0 = \int_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx + \left[ \eta(x) \frac{\partial F}{\partial f'} \right]_a^b.$

''η''에 대한 경계값 조건을 이용하면,

: $0 = \int_a^b \left[ \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'} \right] \eta(x)\,dx. \,\!$

변분법의 기본정리를 적용하면, 오일러-라그랑주 방정식을 얻는다.

: $0 = \frac{\partial F}{\partial f} - \frac{d}{dx} \frac{\partial F}{\partial f'}.$

5. 뉴턴 역학과의 관계

오일러-라그랑주 방정식은 뉴턴 역학을 일반화 좌표로 확장한 것으로 볼 수 있다. 뉴턴 역학에서 라그랑지안은 운동 에너지와 퍼텐셜 에너지의 차이로 주어지며, 오일러-라그랑주 방정식은 뉴턴의 운동 방정식과 동등하다.

3차원 데카르트 좌표계 $\boldsymbol{x}=(x,y,z)$ 에서 시간 미분 $\dot{\boldsymbol{x}} = \boldsymbol{v} = (v_x, v_y, v_z)$ 는 속도를 나타낸다. 퍼텐셜이 속도에 의존하지 않는다고 가정하면, 라그랑지안 L은 운동 에너지와 퍼텐셜의 차이, 즉

$L(\boldsymbol{x}, \boldsymbol{v}, t)=\frac{m}{2}({v_x}^2+{v_y}^2+{v_z}^2) -V(\boldsymbol{x})$

로 표현된다. 이때 라그랑주의 운동 방정식은

$m\dot{\boldsymbol{v}} = -\nabla V(\boldsymbol{x})$

가 되며, 이는 뉴턴의 운동 방정식과 일치한다.

일반화 운동량 $p_i = \frac{\partial L}{\partial \dot{q}_i}$ 을 사용하면, 오일러-라그랑주 방정식은 $\dot{p}_i = \frac{\partial L}{\partial q_i}$ (일반화 운동량의 미분 = 일반화 힘) 형태로 표현된다. 이는 뉴턴 방정식의 "운동량의 미분 = 힘"을 일반화한 것이다.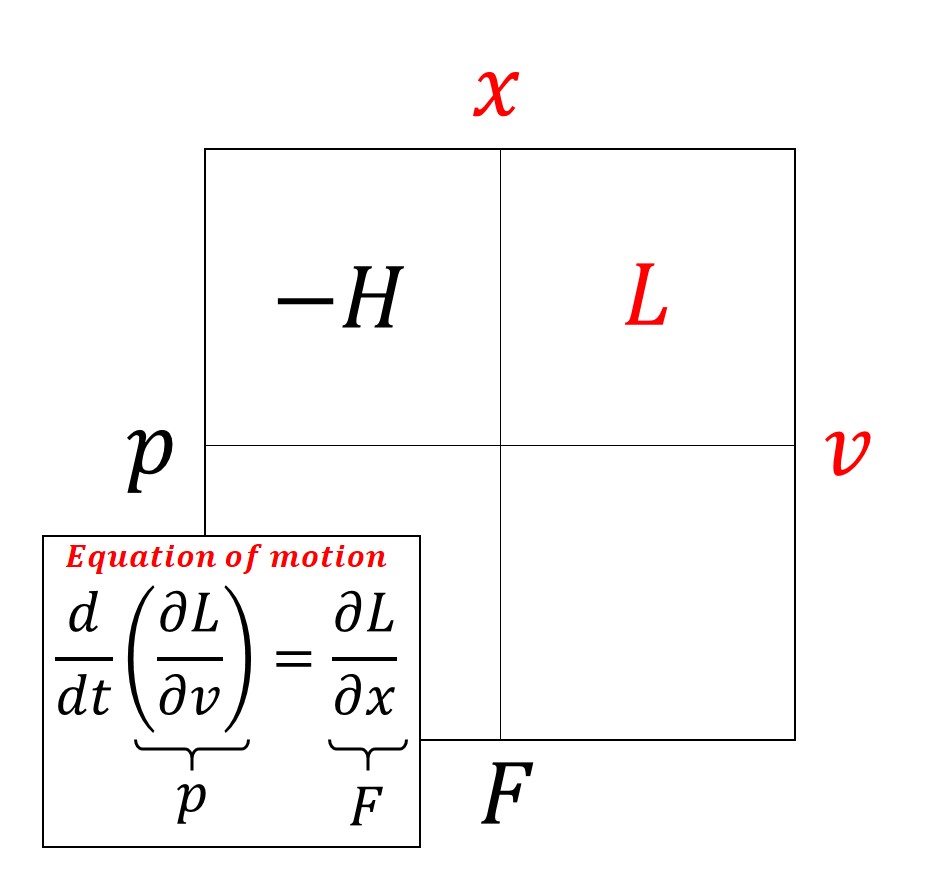

5. 1. 일반화 좌표

오일러-라그랑주 방정식은 데카르트 좌표계를 사용하는 뉴턴의 운동 방정식과 달리, 임의의 좌표( '''일반화 좌표''' )를 사용할 수 있다는 장점이 있다.^[4]

예를 들어 단진자의 운동을 기술할 때, 뉴턴 방정식에서는 세로축과 가로축 방향의 두 변수(데카르트 좌표)가 필요하여 식이 복잡해진다. 하지만 오일러-라그랑주 방정식을 사용하면 단진자의 각도라는 하나의 변수(일반화 좌표)만으로 운동을 기술할 수 있어 더 간단한 방정식을 얻을 수 있다. (단진자의 길이는 일정하다고 가정) 물론 뉴턴 방정식으로 식을 세운 후 극좌표로 변환하여 같은 결과를 얻을 수도 있지만, 오일러-라그랑주 방정식은 이러한 변환 없이 처음부터 각도에 대한 방정식을 직접 얻을 수 있다는 장점이 있다.^[4]

6. 다양한 분야로의 확장

오일러-라그랑주 방정식은 물리학의 여러 분야에서 중요한 작용의 최소 원리에서 유도된다. 이 원리에 따르면, 물리 현상은 라그랑지안(운동 에너지와 퍼텐셜 에너지의 차이)의 시간 적분인 작용을 최소화하는 방향으로 움직인다. 오일러-라그랑주 방정식은 이러한 작용의 최소 원리를 만족하는 물체의 궤적을 변분법을 통해 구하는 과정에서 유도된다.^[8]

작용의 최소 원리는 뉴턴 역학(광학의 페르마의 원리까지 거슬러 올라간다)에서 발견되었지만, 전자기학, 상대성이론 등 다른 분야에서도 적용된다.^[9] 따라서 이러한 분야에서도 오일러-라그랑주 방정식과 유사한 방정식을 만들 수 있으며, 이 방정식들은 해당 분야의 기본 방정식과 동일하다.

뉴턴 역학의 경우, 라그랑지안을 르장드르 변환하여 해밀토니안(에너지)을 얻고, 오일러-라그랑주 방정식을 해밀토니안을 사용하여 다시 쓰면 해밀턴의 정준 방정식을 얻는다. 그러나 뉴턴 역학 이외의 분야에서는 라그랑지안-해밀토니안 변환이 쉽지 않다.

새로운 물리학 분야를 연구할 때, 라그랑지안이나 해밀토니안을 정의하면, 오일러-라그랑주 방정식이나 정준 방정식에 해당하는 방정식을 공식화할 수 있어, 미지의 영역에서 기본 방정식을 유도하는 강력한 도구가 된다.

6. 1. 라그랑주 역학

오일러-라그랑주 방정식은 1750년대에 오일러와 라그랑주가 타우토크론 문제 연구와 관련하여 개발되었다. 이 문제는 가중치가 있는 입자가 출발점에 관계없이 고정된 시간에 고정된 지점으로 낙하하는 곡선을 결정하는 문제이다.^[3]

라그랑주는 1755년에 이 문제를 해결하고 그 해결책을 오일러에게 보냈다. 두 사람 모두 라그랑주의 방법을 더욱 발전시켜 역학에 적용했고, 이는 라그랑주 역학의 공식화로 이어졌다. 그들의 서신은 궁극적으로 1766년 오일러 자신이 만든 용어인 변분법으로 이어졌다.^[3]

라그랑주 역학에서 함수

u_i

는 '''일반화 좌표'''

q_i

이며, 그 변수는 시간 t이다. 일반화 좌표의 차원 f를 계의 (역학적인) 자유도라고 한다. 함수 F는 '''라그랑지안''' L이 그 역할을 한다. 오일러-라그랑주 방정식은 다음과 같다.

:

\frac{\partial L}{\partial q_i}(q(t), \dot{q}(t), t)

\frac{d}{dt} \left(

\frac{\partial L}{\partial\dot{q}_i}(q(t), \dot{q}(t), t)\right) =0

여기서 점은 시간에 대한 미분을 나타낸다. 이 식을 특히 '''라그랑주의 운동 방정식'''이라고 부르기도 한다.

'''일반화 운동량'''은 다음과 같이 정의된다.

:

p_i(q(t), \dot{q}(t), t)= \frac{\partial L}{\partial\dot{q}_i}(q(t), \dot{q}(t), t)

이것을 사용하면 오일러-라그랑주 방정식은 다음과 같이 다시 쓸 수 있다.

:

\dot{p}_i =\frac{\partial L}{\partial q_i}(q(t), \dot{q}(t), t)

위 식의 우변을 '''일반화 힘'''이라고 부르면, 위 방정식은 「일반화 운동량의 미분 = 일반화 힘」을 의미한다.

뉴턴 방정식은 「운동량의 미분 = 힘」이었으므로, 오일러-라그랑주 방정식은 뉴턴 방정식을 일반화 좌표로 확장한 것이라고 볼 수 있다.

6. 2. 해밀턴 역학

라그랑지안을 르장드르 변환하면 해밀토니안(에너지에 대응하는 함수)을 얻을 수 있으며, 오일러-라그랑주 방정식은 해밀턴의 정준 방정식으로 다시 쓸 수 있다.^[8] 이 방정식들은 뉴턴 역학의 기본 방정식 중 하나이다. 오일러-라그랑주 방정식이나 정준 방정식으로 기술한 뉴턴 역학을 해석역학이라고 한다. 뉴턴 역학 이외의 분야에서는 라그랑지안에서 해밀토니안으로(혹은 그 역) 쉽게 변환할 수 있는 것은 아니다.

7. 일반화

오일러-라그랑주 방정식은 여러 변수를 갖는 함수, 여러 함수, 그리고 함수의 고계 도함수를 포함하는 경우 등 다양하게 일반화될 수 있다.
여러 함수와 여러 변수의 경우

여러 개의 함수와 여러 개의 변수가 있는 경우, 오일러-라그랑주 방정식은 각 함수에 대한 편미분 항을 포함하는 연립 방정식 형태로 확장된다.^[5]
예를 들어, m개의 함수 $f_1, \dots, f_m$과 n개의 변수 $x_1, \dots, x_n$이 있다면, 각 함수 $f_i$에 대한 오일러-라그랑주 방정식은 다음과 같다.

:

\frac{\partial \mathcal{L}}{\partial f_i} - \sum_{j=1}^{n} \frac{\partial}{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{i,j}}\right) = 0_i

여기서 $\mathcal{L}$은 라그랑지언이고, $f_{i,j} := \cfrac{\partial f_i}{\partial x_j}$ 이다.

7. 1. 고계 도함수를 포함하는 경우

범함수가 함수의 고계 도함수를 포함하는 경우, 오일러-라그랑주 방정식은 고계 도함수에 대한 편미분 항을 포함하는 형태로 확장된다.

함수형식

:

I[f] = \int_{x_0}^{x_1} \mathcal{L}(x, f, f', f'', \dots, f^{(k)})~\mathrm{d}x ~;~~f' := \cfrac{\mathrm{d}f}{\mathrm{d}x}, ~f'' := \cfrac{\mathrm{d}^2f}{\mathrm{d}x^2}, ~f^{(k)} := \cfrac{\mathrm{d}^kf}{\mathrm{d}x^k}

의 정류값은 다음의 오일러-라그랑주 방정식을 통해 얻을 수 있다.^[5]

:

\cfrac{\partial \mathcal{L}}{\partial f} - \cfrac{\mathrm{d}}{\mathrm{d} x}\left(\cfrac{\partial \mathcal{L}}{\partial f'}\right) + \cfrac{\mathrm{d}^2}{\mathrm{d} x^2}\left(\cfrac{\partial \mathcal{L}}{\partial f''}\right) - \dots +(-1)^k \cfrac{\mathrm{d}^k}{\mathrm{d} x^k}\left(\cfrac{\partial \mathcal{L}}{\partial f^{(k)}}\right)  = 0

단, 함수 자체뿐만 아니라 처음

k-1

개의 도함수에 대해 고정된 경계 조건이 주어져야 한다. 최고차 도함수

f^{(k)}

의 끝점 값은 유동적이다.

두 변수 '''x'''₁과 '''x'''₂에 의존하는 미지 함수 '''f'''가 하나 있으며, 함수가 '''f'''의 '''n'''차까지의 고계도함수에 의존하는 경우, 즉

:

\begin{align}I[f] & = \int_{\Omega} \mathcal{L}(x_1, x_2, f, f_{1}, f_{2}, f_{11}, f_{12}, f_{22},\dots, f_{22\dots 2})\, \mathrm{d}\mathbf{x} \\& \qquad \quadf_{i} := \cfrac{\partial f}{\partial x_i} \; , \quadf_{ij} := \cfrac{\partial^2 f}{\partial x_i\partial x_j} \; , \;\; \dots\end{align}

이면, 오일러-라그랑주 방정식은 다음과 같다.^[5]

:

\begin{align}\frac{\partial \mathcal{L}}{\partial f}& - \frac{\partial}{\partial x_1}\left(\frac{\partial \mathcal{L}}{\partial f_{1}}\right)

\frac{\partial}{\partial x_2}\left(\frac{\partial \mathcal{L}}{\partial f_{2}}\right)

+ \frac{\partial^2}{\partial x_1^2}\left(\frac{\partial \mathcal{L}}{\partial f_{11}}\right)+ \frac{\partial^2}{\partial x_1\partial x_2}\left(\frac{\partial \mathcal{L}}{\partial f_{12}}\right)+ \frac{\partial^2}{\partial x_2^2}\left(\frac{\partial \mathcal{L}}{\partial f_{22}}\right) \\& - \dots+ (-1)^n \frac{\partial^n}{\partial x_2^n}\left(\frac{\partial \mathcal{L}}{\partial f_{22\dots 2}}\right) = 0\end{align}

이는 다음과 같이 간략하게 나타낼 수 있다.

:

\frac{\partial \mathcal{L}}{\partial f} +\sum_{j=1}^n \sum_{\mu_1 \leq \ldots \leq \mu_j} (-1)^j \frac{\partial^j}{\partial x_{\mu_{1}}\dots \partial x_{\mu_{j}}} \left( \frac{\partial \mathcal{L} }{\partial f_{\mu_1\dots\mu_j}}\right)=0

여기서

\mu_1 \dots \mu_j

는 변수의 개수를 나타내는 지표이며, 이 경우 1부터 2까지의 값을 가진다.

f_{12} = f_{21}

과 같이 동일한 편도함수를 여러 번 세는 것을 방지하기 위해

\mu_1 \dots \mu_j

지표에 대한 합은

\mu_1 \leq \mu_2 \leq \ldots \leq \mu_j

에 대해서만 계산된다.

7. 2. 여러 함수와 여러 변수의 경우

여러 개의 함수와 여러 개의 변수가 있는 경우, 오일러-라그랑주 방정식은 다음과 같이 확장된다.^[5]

:

\begin{align}\frac{\partial \mathcal{L}}{\partial f_1} - \sum_{j=1}^{n} \frac{\partial}{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{1,j}}\right) &= 0_1 \\\frac{\partial \mathcal{L}}{\partial f_2} - \sum_{j=1}^{n} \frac{\partial}{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{2,j}}\right) &= 0_2 \\\vdots \qquad \vdots \qquad &\quad \vdots  \\\frac{\partial \mathcal{L}}{\partial f_m} - \sum_{j=1}^{n} \frac{\partial}{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{m,j}}\right) &= 0_m.\end{align}

여기서

f_{i,j} := \cfrac{\partial f_i}{\partial x_j}

이다. 이것은 각 함수

f_i

에 대한 편미분 항을 포함하는 연립 방정식 형태이다. 즉, 여러 변수

x_1, \dots, x_n

과 여러 함수

f_1, \dots, f_m

에 대해, 각 함수

f_i

에 대한 오일러-라그랑주 방정식이 시스템을 이룬다.

7. 3. 장 이론

위에서는 오일러-라그랑주 방정식의 물리학적 측면을 설명했지만, 방정식 자체는 물리학과 무관하게 정식화할 수 있으므로, 먼저 물리학적 배경에서 벗어나 방정식을 설명하고, 그 후에 방정식의 뉴턴 역학적 해석을 설명한다.

C¹급 함수

: u^영어: R|d^영어 → R|f^영어;

: x^영어 = (x|1^영어, …, x|d^영어) ↦ u^영어(x) = (u|1^영어(x), …, u|f^영어(x))

를 생각한다.

: F^영어: R|f^영어 × R|fd^영어 × R|d^영어 → R^영어;

: (v, m, x) ↦ F^영어(v,m,x)

라고 할 때, '''오일러-라그랑주 방정식'''은 u(x)^영어에 대한 다음과 같은 연립 편미분 방정식이다.

:

\right )= 0 \quad (i=1, \ldots, f)

여기서 는 x에 대한 편미분

:

을 나타낸다.

일반적으로는 기호를 간략하게 사용하여 위의 방정식을

:

과 같이 표기하는 경우가 많다. 이 표기에서는 F에 대입되는 값으로서의 u|i^영어, ∂|μ^영어u|i^영어가 F의 변수로서의 v|i^영어, m|i,μ^영어와 혼용되고 있다.

더 나아가 벡터 표기를 사용하여 f개의 식을 일괄적으로

:

\right )= 0}}

으로 나타낼 수도 있다.

참조

_[1] 서적 An introduction to the calculus of variations Courier Dover Publications
_[2] 서적 Classical Mechanics Addison Wesley
_[3] 웹아카이브 A short biography of Lagrange http://numericalmeth[...] 2007-07-14
_[4] harvnb
_[5] 서적 Methods of Mathematical Physics Interscience Publishers, Inc
_[6] 서적 Calculus of Variations with Applications to Physics and Engineering https://archive.org/[...] McGraw-Hill
_[7] 서적 Classical Dynamics: A contemporary approach https://www.cambridg[...] Cambridge University Press 2023-09-12
_[8] 문서 뉴턴의 운동 방정식, 맥스웰 방정식, 아인슈타인 방정식
_[9] 문서 라그랑지안에 대한 설명
_[10] 문서 변분학의 기본 보조정리, Fundamental lemma of calculus of variations

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com