파스칼의 원리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 중력장 내 유체 기둥
3. 파스칼의 원리 계산
- 3.1. 유압 장치의 원리
4. 응용
5. 현대적인 표현
- 5.1. 식으로 나타내기
- 5.2. 정수압 평형
6. 파스칼의 통 실험
7. 도출
참조

1. 개요

파스칼의 원리는 밀폐된 비압축성 유체 내에서 압력 변화가 유체의 모든 방향으로 동일하게 전달되며, 압력에 의한 힘은 유체를 둘러싸는 벽면에 직각으로 작용한다는 원리이다. 이는 유체 정역학의 기본 원리로, 중력장 내 유체 기둥의 압력 차이를 수학적으로 표현하며, 관성 및 점성 항이 없는 나비에-스토크스 방정식의 특정 경우로 볼 수 있다. 파스칼의 원리는 유압 장치, 유압 잭, 유압 브레이크 등 힘을 증폭시키는 다양한 장치에 응용되며, 자동차 리프트, 아르테시안 우물, 스쿠버 다이빙 등 다양한 분야에서 활용된다. 또한, 파스칼의 원리는 유체의 유동성에서 유도되며, 정수압 평형 및 파스칼의 통 실험과 같은 개념과 관련된다.

더 읽어볼만한 페이지

유체정역학 - 수압
수압은 정지하거나 운동하는 물이 물체에 가하는 압력으로, 정지 시에는 깊이에 비례하는 무게, 운동 시에는 속도 제곱에 비례하는 운동 에너지로 결정되며, 힘의 전달 및 압력 단위로도 활용된다.
유체정역학 - 유체 정역학
유체 정역학은 정지 유체의 압력과 힘을 연구하는 학문으로, 아르키메데스와 파스칼의 발견을 통해 발전했으며, 댐 건설이나 잠수함 설계, 혈관 내 압력 등 다양한 분야에 응용된다.
블레즈 파스칼 - 파스칼 (단위)
파스칼(Pa)은 1 뉴턴의 힘이 1제곱미터의 면에 수직으로 가해질 때 작용하는 압력을 나타내는 SI 유도 단위이며, 블레즈 파스칼의 이름을 따서 명명되었고 다양한 분야에서 사용된다.
블레즈 파스칼 - 파스칼 정리
파스칼 정리는 원뿔 곡선 위의 여섯 점으로 이루어진 육각형의 대변 연장선들이 한 직선에서 만나는 기하학적 정리로, 블레즈 파스칼이 발견했으며 사영 기하학에서 중요한 역할을 하고 다양한 관련 정리와 원뿔 곡선 문제 해결에 활용된다.

파스칼의 원리
개요
분야	유체역학
내용	밀폐된 용기 안의 유체에 가해진 압력은 유체의 모든 부분과 용기의 벽에 같은 크기로 전달된다.
상세 내용
정의	밀폐된 유체의 어떤 지점에서든 압력 변화가 발생하면 유체의 모든 지점과 용기 벽에 변함없이 전달된다.
응용	유압 프레스 유압 브레이크 유압 리프트

2. 정의

파스칼의 원리는 다음과 같이 정의된다.

: 밀폐된 비압축성 유체 내의 임의의 지점에서 압력 변화는 유체 전체의 모든 방향으로 동일하게, 감소 없이 전달되며, 압력에 의한 힘은 유체를 둘러싸는 벽면에 직각으로 작용한다.

2. 1. 중력장 내 유체 기둥

균일한 중력장 내 유체 기둥(예: 유압 프레스)에서 두 지점 간의 압력 차이는 다음 공식으로 표현할 수 있다.

\Delta p = \rho g \cdot\Delta h\,

여기서 각 기호는 다음을 의미한다.

$\Delta p$ : 유체 정역학적 압력 차이 (SI 단위계에서 파스칼(Pa) 단위). 이는 유체 기둥 내 두 지점 간의 압력 차이이며, 유체의 무게 때문에 발생한다.
$\rho$ : 유체 밀도 (SI 단위계에서 kg/m³ 단위).
$g$ : 중력 가속도 (일반적으로 지구 해수면에서의 중력 가속도인 약 m/s² 사용).
$\Delta h$ : 측정 지점 위의 유체 높이 또는 유체 기둥 내 두 지점 간의 고도 차이 (m 단위).

이 공식은 두 지점 사이의 압력 변화가 그 사이 유체의 무게 때문에 생긴다는 것을 직관적으로 보여준다. 또는 중력 때문에 액체의 단위 부피당 위치 에너지가 변하면서 압력 변화가 생긴다고 해석할 수도 있다. 중요한 점은 높이에 따른 압력 변화는 다른 추가적인 압력과는 관계가 없다는 것이다. 따라서 파스칼의 원리는 "유체의 한 지점에 가해진 압력 변화는 유체 전체에 걸쳐 감소 없이 그대로 전달된다"고 설명할 수 있다.

이 공식은 관성과 점성 항을 무시한 나비에-스토크스 방정식의 특수한 경우에 해당한다.^[7]

3. 파스칼의 원리 계산

유압 장치에서 밀폐된 유체에 가해진 압력은 파스칼의 원리에 따라 유체의 모든 부분과 용기 벽면에 동일하게 전달된다. 단면적이 각각 $S_A$ , $S_B$ 인 두 피스톤으로 이루어진 유압 장치에서, 한쪽 피스톤에 가해진 압력( $P_A$ )과 다른 쪽 피스톤에 전달되는 압력( $P_B$ )은 같다.

$P_A = \frac{F_A}{S_A}$

이고, 파스칼 원리에 따라 $P_A = P_B$ 이므로,

$\frac{F_A}{S_A} = \frac{F_B}{S_B}$

가 성립한다. 여기서 $F_A$ 와 $F_B$ 는 각 피스톤에 작용하는 힘이다. 이 관계식으로부터 한쪽 피스톤에 가해지는 힘( $F_A$ )을 알면 다른 쪽 피스톤이 받는 힘( $F_B$ )을 계산할 수 있다.

$F_B = F_A \times \frac{S_B}{S_A}$

이 식은 두 피스톤의 단면적 비율( $S_B/S_A$ )에 따라 힘이 증폭되거나 감소될 수 있음을 보여준다. 즉, 출력 피스톤의 단면적( $S_B$ )이 입력 피스톤의 단면적( $S_A$ )보다 크면 작은 힘으로 큰 힘을 얻을 수 있고, 반대로 작으면 큰 힘이 작은 힘으로 변환된다.^[16]

한편, 균일한 중력장 내에 있는 유체 기둥(예: 유압 프레스 내부)의 경우, 유체 자체의 무게로 인해 발생하는 압력 차이는 다음과 같이 계산할 수 있다.

$\Delta p = \rho g \cdot\Delta h\,$

여기서 각 기호는 다음을 의미한다.

기호	의미	SI 단위
$\Delta p$	유체 정역학적 압력 변화량	파스칼 (Pa)
$\rho$	유체 밀도	kg/m³
$g$	중력 가속도	m/s²
$\Delta h$	유체 높이 차이	미터 (m)

이 공식은 두 지점 사이의 압력 차이가 그 사이 유체의 무게에 의해 결정된다는 것을 보여준다. 또한, 중력장에서 유체의 단위 부피당 위치 에너지 변화가 압력 변화를 일으킨다고 해석할 수도 있다. 중요한 점은 이 높이에 따른 압력 변화( $\Delta p$ )는 외부에서 추가로 가해지는 압력과는 별개라는 것이다. 따라서 파스칼의 원리는 "유체 내의 한 지점에 가해진 압력 변화는 유체 전체에 걸쳐 세기가 줄어들지 않고 그대로 전달된다"고 설명할 수 있다.

이 공식은 관성과 점성 효과를 무시할 수 있는 경우의 나비에-스토크스 방정식에서 유도될 수 있다.^[7]

3. 1. 유압 장치의 원리

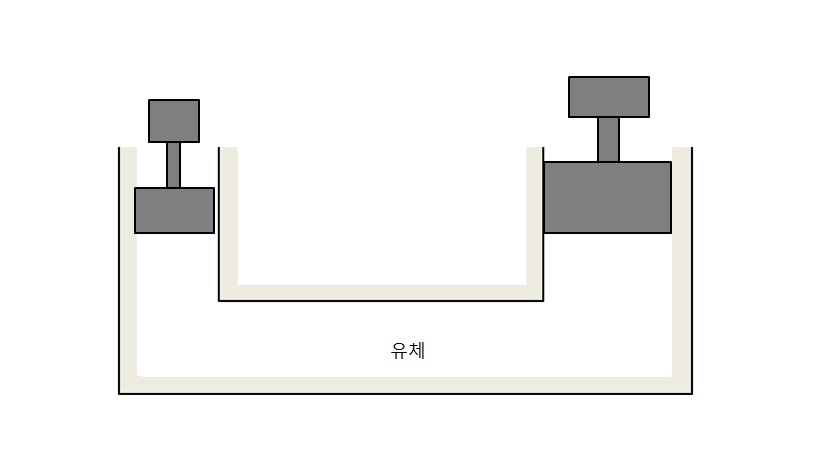
유압 장치는 단면적이 다른 관이 서로 연결되어 있고, 각 관의 끝은 피스톤으로 막혀 압력을 가할 수 있도록 만들어진 장치이다. 이 장치 내부에는 무게를 무시할 수 있는 유체가 가득 채워져 있다.

왼쪽 그림과 같은 유압 장치에서 단면적이

S_A

인 왼쪽 피스톤에

F_A

의 힘을 가하면, 유체에 가해지는 압력

P_A

는 다음과 같다.

P_A=\frac{F_A}{S_A}

파스칼의 원리에 따르면, 밀폐된 유체 내의 한 지점에 가해진 압력은 유체의 모든 부분과 용기의 벽까지 그 세기가 감소하지 않고 전달된다. 따라서 단면적이

S_B

인 오른쪽 피스톤에 전달되는 압력

P_B

도 왼쪽 피스톤에 가해진 압력

P_A

와 같다.

P_A=P_B=\frac{F_B}{S_B}=\frac{F_A}{S_A}

결과적으로 오른쪽 피스톤이 받는 힘

F_B

는 다음과 같이 계산된다.

F_B=F_A\times\frac{S_B}{S_A}

이 식을 통해 유압 장치에서 출력되는 힘(

F_B

)이 입력된 힘(

F_A

)에 두 피스톤의 단면적 비율(

S_B/S_A

)을 곱한 값과 같다는 것을 알 수 있다. 즉, 입력 피스톤의 단면적(

S_A

)을 작게 하고 출력 피스톤의 단면적(

S_B

)을 크게 만들수록, 작은 힘을 입력하여 훨씬 큰 힘을 얻을 수 있다.^[16]

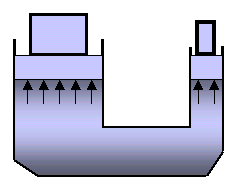
예를 들어, 오른쪽 피스톤의 단면적(

A_2

)이 왼쪽 피스톤의 단면적(

A_1

)보다 50배 넓다고 가정하자 (

\frac{A_2}{A_1} = 50

). 만약 왼쪽 피스톤에 1 뉴턴(N)의 힘(

F_1 = 1N

)을 가하면, 이 힘에 의해 발생한 추가 압력이 유체를 통해 오른쪽 피스톤으로 전달된다. 오른쪽 피스톤은 이 압력에 의해 위쪽으로

F_2 = F_1 \frac{A_2}{A_1} = 1N \times 50 = 50N

의 힘을 받게 된다. 이는 입력된 힘보다 50배 큰 힘이다. 여기서 힘과 압력의 차이를 이해하는 것이 중요하다. 압력 자체는 유체 전체에 동일하게 전달되지만, 힘은 압력이 작용하는 면적에 비례하여 커지기 때문이다.

이처럼 유압 장치는 힘을 증폭시키는 데 사용될 수 있다. 이론적으로는 피스톤의 단면적 비율을 조절하여 힘을 원하는 만큼 증폭시킬 수 있다. 파스칼의 원리는 유압 프레스와 같은 장치의 기본적인 작동 원리이다.

유압 장치가 힘을 증폭시킨다고 해서 에너지 보존 법칙을 위반하는 것은 아니다. 힘이 증가하는 대신, 피스톤이 움직이는 거리가 줄어들기 때문이다. 앞선 예시에서 작은 피스톤이 100cm 아래로 움직이면, 큰 피스톤은 그 거리의 1/50인 2cm만 위로 움직인다. 입력 측에서 한 일(입력 힘 × 작은 피스톤 이동 거리)과 출력 측에서 얻은 일(출력 힘 × 큰 피스톤 이동 거리)은 이론적으로 같다. 이는 지레와 같은 다른 단순 기계에서도 볼 수 있는 원리이다.

유압 장치의 대표적인 응용 사례로는 정비소에서 흔히 볼 수 있는 자동차 리프트(유압 잭)가 있다. 공기 압축기로 생성된 압축 공기가 저장된 오일에 압력을 가하고, 이 오일이 피스톤으로 압력을 전달하여 무거운 자동차를 들어 올린다. 또한, 대부분의 자동차에 사용되는 유압 브레이크 시스템도 브레이크 페달을 밟는 작은 힘을 증폭시켜 바퀴를 효과적으로 제동하는 데 파스칼의 원리를 이용한다.^[8]

4. 응용

파스칼의 원리는 밀폐된 유체의 한 부분에 가해진 압력이 유체의 모든 부분과 용기의 벽까지 그 세기가 줄어들지 않고 동일하게 전달된다는 원리이다. 이 원리를 이용하면 작은 힘으로 훨씬 큰 힘을 만들어낼 수 있어 다양한 기계 장치에 응용된다.

대표적인 예로 유압 프레스가 있으며, 이는 파스칼의 원리를 이용하여 힘을 증폭시키는 기본적인 장치이다. 또한, 정비소에서 흔히 볼 수 있는 자동차 리프트(유압 잭)나 대부분의 자동차에 사용되는 유압 브레이크 시스템 역시 이 원리를 활용하여 작은 조작력으로 무거운 물체를 들어 올리거나 강력한 제동력을 얻는다.

이 외에도 파스칼의 원리는 다양한 분야에서 찾아볼 수 있다. 무거운 하중을 다루는 거의 모든 건설 기계의 유압 피스톤 작동에 필수적이며, 아르테시안 우물, 물탱크, 댐의 설계에도 이 원리가 고려된다. 스쿠버 다이버가 물속 깊이에 따라 경험하는 수압의 증가(수심 10m당 약 100 kPa 증가) 역시 파스칼의 원리로 설명할 수 있다.^[8] 정적인 유체뿐만 아니라 연속적인 흐름이 있는 가스 리프트와 같은 장치에도 파스칼의 원리가 적용된다.

4. 1. 유압 잭

유압 잭은 파스칼의 원리를 이용하여 작은 힘으로 무거운 물체를 들어 올리는 대표적인 장치이다. 이는 밀폐된 유체의 한 부분에 가해진 압력이 유체의 모든 부분과 용기의 벽까지 그 세기가 줄어들지 않고 전달된다는 원리에 기반한다.

이 원리는 물을 채우고 양 끝에 다른 크기의 피스톤을 설치한 U자관으로 설명할 수 있다. 왼쪽의 작은 피스톤(면적

A_1

)에 힘(

F_1

)을 가하면, 이로 인해 발생하는 압력(

p_1 = \frac{F_1}{A_1}

)이 유체를 통해 오른쪽의 큰 피스톤(면적

A_2

)에 그대로 전달된다(

p_2 = p_1

). 따라서 큰 피스톤에는

F_2 = p_2 \times A_2 = p_1 \times A_2 = \frac{F_1}{A_1} \times A_2

만큼의 힘이 작용하게 된다. 이를 정리하면 두 피스톤에 작용하는 힘의 비율은 면적의 비율과 같다는 것을 알 수 있다:

\frac{F_2}{F_1} = \frac{A_2}{A_1}

예를 들어, 큰 피스톤의 면적(

A_2

)이 작은 피스톤의 면적(

A_1

)보다 50배 넓다면(

\frac{A_2}{A_1} = 50

), 작은 피스톤에 1 뉴턴의 힘(

F_1 = 1N

)만 가해도 큰 피스톤에는 50배 증폭된 50 뉴턴의 힘(

F_2 = 50N

)이 발생한다. 이처럼 유압 장치는 피스톤의 면적비를 조절하여 힘을 효과적으로 증폭시킬 수 있다.

정비소에서 흔히 볼 수 있는 자동차 리프트가 바로 유압 잭의 대표적인 예이다. 공기 압축기로 공기에 압력을 가하면, 이 압력이 밀폐된 관을 통해 저장된 오일로 전달된다. 오일은 다시 이 압력을 넓은 면적의 리프트 피스톤으로 전달하여, 상대적으로 작은 압력으로도 무거운 자동차를 쉽게 들어 올릴 수 있게 한다.

유압 잭으로 힘을 크게 증폭시킬 수 있지만, 이는 에너지 보존 법칙을 위배하지 않는다. 힘이 증폭되는 대신, 피스톤이 움직이는 거리는 그만큼 줄어들기 때문이다. 작은 피스톤을 100cm 아래로 누르면, 면적비가 50배인 큰 피스톤은 그 1/50인 2cm만 위로 올라간다. 즉, 작은 피스톤에 가한 일(

W_1 = F_1 \times d_1

)과 큰 피스톤이 한 일(

W_2 = F_2 \times d_2

)은 이론적으로 같다(

W_1 = W_2

). 이는 지레와 같은 다른 단순 기계들과 동일한 원리이다.

이러한 힘 증폭 원리는 유압 잭 외에도 자동차의 브레이크 시스템 등 다양한 분야에서 활용된다. 브레이크 페달을 밟는 작은 힘이 유압 시스템을 통해 증폭되어 바퀴의 회전을 효과적으로 멈추게 한다.

4. 2. 유압 브레이크

유압 브레이크는 파스칼의 원리를 이용하여 작은 힘으로 큰 제동력을 얻는 장치이다. 밀폐된 유체(주로 브레이크 오일)의 한 부분에 가해진 압력은 유체의 모든 부분과 용기의 벽에 같은 크기로 손실 없이 전달된다는 원리를 이용한다.

자동차의 브레이크 시스템에서 운전자가 브레이크 페달을 밟으면, 이 힘은 브레이크 마스터 실린더의 작은 피스톤에 압력을 가하게 된다. 이 압력은 브레이크액이라는 유압 작동유를 통해 각 바퀴에 있는 더 큰 면적의 피스톤(캘리퍼 또는 휠 실린더 내부)으로 전달된다.

파스칼의 원리에 따르면 압력(

p

)은 힘(

F

)을 그 힘이 작용하는 면적(

A

)으로 나눈 값(

p = \frac FA

)과 같다. 브레이크 시스템 내에서 유체 압력은 거의 동일하게 전달되므로(

p_1 = p_2

), 마스터 실린더의 작은 피스톤(면적

A_1

, 작용 힘

F_1

)과 바퀴 쪽의 큰 피스톤(면적

A_2

, 작용 힘

F_2

) 사이에는 다음과 같은 관계가 성립한다:

\frac{F_1}{A_1} = \frac{F_2}{A_2}

이 식을 정리하면 바퀴 쪽 피스톤에 작용하는 힘

F_2

는 다음과 같이 계산할 수 있다:

F_2 = F_1 \frac{A_2}{A_1}

바퀴 쪽 피스톤의 면적(

A_2

)이 마스터 실린더 피스톤의 면적(

A_1

)보다 훨씬 크기 때문에(

A_2 > A_1

), 운전자가 브레이크 페달을 밟는 작은 힘(

F_1

)은 면적의 비율(

\frac{A_2}{A_1}

)만큼 증폭되어 매우 큰 제동력(

F_2

)으로 나타난다. 이 큰 힘이 브레이크 패드를 디스크나 드럼에 밀착시켜 마찰력을 발생시키고, 이를 통해 자동차 바퀴의 회전을 효과적으로 멈추게 된다. 예를 들어, 바퀴 쪽 피스톤의 총 면적이 마스터 실린더 피스톤 면적의 10배라면, 운전자가 페달에 가한 힘의 10배에 해당하는 제동력이 각 바퀴에 전달될 수 있다.

이렇게 힘이 크게 증폭되는 대신, 에너지 보존 법칙에 따라 작은 피스톤이 움직이는 거리보다 큰 피스톤이 움직이는 거리는 면적비에 반비례하여 줄어든다. 즉, 큰 힘을 얻는 대가로 피스톤의 작동(이동) 거리는 짧아지는 것이다. 이는 지레와 같은 간단한 기계에서 힘의 이득을 얻으면 거리에서 손해를 보는 원리와 같다. 오늘날 대부분의 자동차에 장착된 제동 시스템은 이러한 유압 원리를 핵심적으로 활용하여 안전한 제동을 가능하게 한다.

4. 3. 기타 응용 분야

파스칼의 원리는 다양한 분야에서 응용된다.

대부분의 자동차 제동 시스템에서 힘을 증폭하는 데 사용된다. 브레이크 페달을 밟는 작은 힘을 증폭시켜 바퀴의 회전을 효과적으로 멈춘다.
정비소에서 흔히 볼 수 있는 자동차 리프트(유압 잭) 역시 파스칼의 원리를 이용한다. 공기 압축기로 생성된 압력이 오일을 통해 피스톤으로 전달되어 무거운 자동차를 들어 올린다.
무거운 하중을 다루는 거의 모든 건설 기계에는 유압 피스톤이 장착되어 있다.
아르테시안 우물, 물탱크, 댐 건설 등에도 파스칼의 원리가 적용된다.
스쿠버 다이버는 수압 변화를 이해하기 위해 이 원리를 알아야 한다. 해수면의 대기압(약 100kPa)에서 시작하여 수심이 10m 깊어질 때마다 압력이 약 100kPa씩 증가한다.^[8]
정적인 유체뿐만 아니라, 연속적인 흐름이 있는 가스 리프트와 같은 오일 리프트 장치에도 파스칼의 원리가 응용될 수 있다.

5. 현대적인 표현

파스칼의 원리는 현대적으로 다음과 같이 표현할 수 있다.^[14]

정지 유체에서 미소 면으로 서로 접촉한 두 개의 미소 유체 요소 A, B를 생각한다. 유체 요소 A가 접촉면을 통해 유체 요소 B로부터 받는 힘(접촉력)의 방향은 접촉면에 수직이며, 힘의 크기는 접촉면의 방향에 관계없이 면적에 비례한다.

이는 정지한 유체 내부의 아주 작은 면(미소 면)을 통해 두 유체 요소가 서로 힘을 주고받을 때, 그 힘(접촉력)은 항상 면에 수직으로 작용한다는 의미이다. 또한 이 힘의 크기는 면의 방향과 관계없이 오직 면적에만 비례한다. 이때 힘의 크기와 면적 사이의 비례 상수가 바로 압력이다. 정의에 따라 압력의 크기는 면의 방향에 의존하지 않지만, 유체 내 위치에 따라서는 달라질 수 있다.

5. 1. 식으로 나타내기

파스칼의 원리를 식으로 나타내면 다음과 같다.

:

\delta \boldsymbol{F} = -p\, \boldsymbol{n}\, \delta S

$\delta \boldsymbol{F}$ : 접촉력 벡터
$p$ : 비례 상수
$\delta S$ : 접촉면의 면적
$\boldsymbol{n}$ : 접촉면의 단위 법선 벡터(A→B 방향)

여기서 음(-)의 부호는 유체 요소 A를 압축하는 방향을 양(+)으로 취했기 때문에 붙는다. 비례 상수

p

는 압력을 의미한다. 정의에 따라 압력의 크기는 면의 방향에 의존하지 않지만, 위치에 따라서는 변할 수 있다.

5. 2. 정수압 평형

파스칼의 원리는 정지 유체 내에서 힘이 어떻게 작용하는지를 설명한다. 정지 상태에 있는 유체 내부에서 서로 맞닿아 있는 아주 작은 두 유체 요소 A와 B를 생각한다. 유체 요소 A가 접촉면을 통해 유체 요소 B로부터 받는 힘, 즉 접촉력은 항상 접촉면에 수직 방향으로 작용한다. 이 힘의 크기는 접촉면의 방향과는 관계없이 면적에 비례한다고 표현한다.^[14]

이 관계를 수식으로 나타내면 다음과 같다.

:

\delta \boldsymbol{F} = -p\, \boldsymbol{n}\, \delta S

여기서 각 기호는 다음을 의미한다.

$\delta \boldsymbol{F}$ : 접촉력을 나타내는 벡터
$p$ : 비례 상수, 즉 압력
$\delta S$ : 접촉면의 면적
$\boldsymbol{n}$ : 접촉면에서 A에서 B 방향을 향하는 단위 법선 벡터

수식의 음(-) 부호는 힘의 방향을 유체 요소 A를 압축하는 방향으로 정의했기 때문이다. 여기서 비례 상수

p

가 바로 압력이다. 압력의 크기는 정의상 면의 방향에 따라 달라지지 않지만, 유체 내의 위치에 따라서는 변할 수 있다.

이제 부피가

\delta V

인 아주 작은 유체 덩어리(

\Omega

)를 생각한다. 이 유체 덩어리의 표면(

\partial \Omega

) 전체에 작용하는 모든 접촉력의 합력

\boldsymbol{\mathit{F}}

는 가우스의 정리를 이용하여 다음과 같이 유도할 수 있다.^[13]

:

\begin{align}\boldsymbol{F}&\equiv \oint_{\partial \Omega} \mathrm{d} \boldsymbol{F}\\&= - \oint_{\partial \Omega} p\, \boldsymbol{n}\,\mathrm{d}S\\&= - \int_{\Omega} \nabla p\, \mathrm{d}V\\&= -\nabla p\, \delta V\end{align}

이는 유체 덩어리에 작용하는 압력에 의한 총 힘이 압력 기울기(

\nabla p

)와 부피(

\delta V

)의 곱에 음수를 취한 값과 같음을 의미한다.

만약 유체의 밀도를

\rho

라고 하고, 유체에 작용하는 단위 질량당 외력(예: 중력)을

\boldsymbol{f}

라고 하면, 정지 상태의 유체에서는 압력에 의한 힘과 외력이 평형을 이룬다. 이를 정수압 평형이라고 하며, 다음 방정식으로 표현된다.

:

\nabla p + \rho \boldsymbol{\mathit{f}} = 0

이는 유체 정역학의 기본 방정식이다. 이 식은 정지 유체 내에서 압력 기울기(

\nabla p

)가 밀도(

\rho

)와 단위 질량당 외력(

\boldsymbol{f}

)의 곱과 평형을 이룬다는 것을 의미한다.

만약 외부에서 작용하는 힘(

\boldsymbol{f}

)을 무시할 수 있다면, 위 식은

-\nabla p=0

이 된다. 이는 압력의 기울기가 0이라는 뜻이므로, 유체 내 모든 지점에서 압력이 일정하다는 결론을 얻는다. 즉,

유체가 용기를 누르는 압력은 위치에 관계없이 같다.
유체의 한 지점에 압력을 가하면, 이 압력은 유체 전체로 전달되어 멀리 떨어진 지점까지 영향을 미친다.

는 파스칼 원리의 원래 내용과 일치한다.

6. 파스칼의 통 실험

아메데 기유맹 (1872)의 ''자연의 힘''에 실린 파스칼의 통 실험 그림

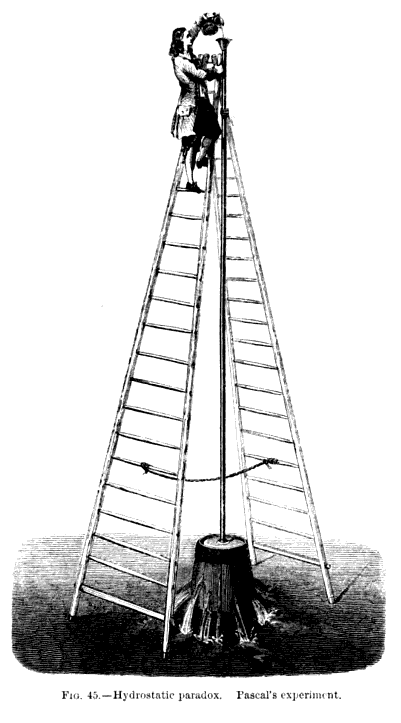
'파스칼의 통'은 1646년 블레즈 파스칼이 수행했다고 전해지는 유체 정역학 실험이다.^[9] 이 실험에서 파스칼은 물이 채워진 통에 (다른 부분은 밀봉한 채) 길고 수직인 관을 삽입했다. 수직 관에 물을 부었을 때, 높아진 유체 정압으로 인해 통이 터졌다.^[9]

하지만 이 실험은 블레즈 파스칼의 저서 어디에도 언급되지 않았다. 19세기 프랑스 저자들이 파스칼에게 귀속시킨 일화일 수 있으며, 당시 이 실험은 crève-tonneau|크레브-토노^프랑스어 (대략 "통 파괴자"라는 의미)로 알려졌다.^[10] 그럼에도 불구하고, 이 실험은 많은 초등 물리 교과서에서 파스칼의 실험으로 소개되고 있다.^[11]

7. 도출

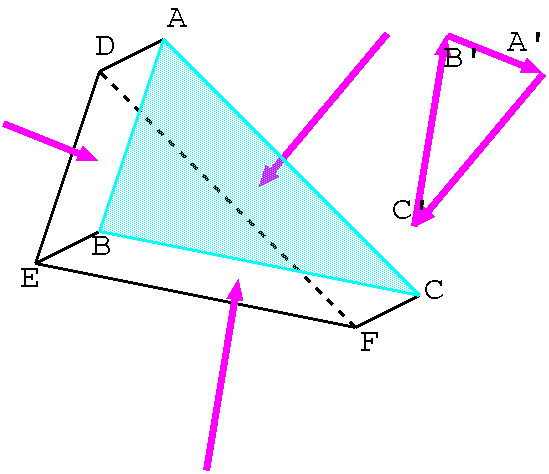
힘이 평형을 이루므로 벡터를 순서대로 연결하면 닫힌다(힘의 삼각형 A'B'C'). 힘은 측면에 수직이므로 90도 회전된 힘의 삼각형 각 변은 측면에 평행하다. 따라서 힘의 삼각형은 △ABC와 닮음이 된다.

파스칼의 원리는 유체의 정의, 즉 "정지 상태에서는 전단 응력이 발생하지 않는 연속체"라는 특징(유동성)에서 유도할 수 있다.

전단 응력이 발생하지 않기 때문에, 정지한 유체 내부의 임의 단면에 작용하는 힘은 항상 그 면에 수직이다. 또한, 단위 면적당 작용하는 힘의 크기인 압력은 면의 방향과 관계없이 동일하다는 것을 다음과 같이 설명할 수 있다.

정지된 유체 내부에 아주 작은 삼각 기둥 모양의 영역을 가정해보자. 이 삼각 기둥의 표면에 작용하는 모든 압력에 의한 힘의 총합은 0이 되어야 한다 (힘의 평형). 두 개의 삼각형 밑면(ABC와 DEF)에 작용하는 힘은 크기가 같고 방향이 반대이므로 서로 상쇄된다. 세 개의 옆면에 작용하는 힘들은 밑면에 평행한 평면 위에서 힘의 삼각형을 이룬다. 이 힘의 삼각형은 밑면 삼각형 ABC와 닮음 관계에 있으므로, 각 힘의 크기는 대응하는 옆면의 면적에 비례한다. 따라서 단위 면적당 힘인 압력은 어느 면에서나 같은 크기를 갖는다.^[15]

이처럼 파스칼의 원리와 압력이라는 개념은 유체가 가진 기본적인 성질인 유동성에서 비롯된다.

참조

_[1] 웹사이트 Pascal's principle - Definition, Example, & Facts http://www.britannic[...] 2018-05-09
_[2] 웹사이트 Pascal's Principle and Hydraulics https://www.grc.nasa[...] 2018-05-09
_[3] 웹사이트 Pressure http://hyperphysics.[...] 2018-05-09
_[4] 서적 How Things Work: The Physics of Everyday Life John Wiley & Sons
_[5] 문서 Blaise Pascal, Traitez de l'Equilibre des Liqueurs (Treatise on the Equilibrium of Fluids), Paris, 1663.
_[6] 문서 MacTutor Biography
_[7] 서적 Elementary Fluid Dynamics Oxford University Press
_[8] 간행물 The diving "Law-ers": A brief resume of their lives http://archive.rubic[...] 2011-06-14
_[9] 서적 Treatise on hydraulics https://archive.org/[...] J. Wiley
_[10] 문서 perhaps first in an educational context; the attribution is found under this name in A. Merlette, L'encyclopédie des écoles, journal de l'enseignement primaire et professionnel (1863) https://books.google[...] 2017-02-06
_[11] 서적 see e.g. E. Canon-Tapia in: Thor Thordarson (ed.) Studies in Volcanology https://books.google[...]
_[12] 문서 ここでの「圧力」は容器に垂直で圧縮する向きの「力」という意味であり、本来の「圧力」(単位面積当たりの力の法線成分)ではない。
_[13] 웹사이트 液体の平衡及び空気の質量の測定についての論述 1663年ブレーズ・パスカル(1623-1662) https://www.kanazawa[...] 2020-07-01
_[14] 서적 弾性体と流体力学岩波書店 1983-09-14
_[15] 서적 流れ学岩波全書 1967-05-30
_[16] 서적 토목기사 과년도 - 수리수문학 성안당 2015

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com