슈뢰딩거 방정식
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
슈뢰딩거 방정식은 양자역학의 기본 방정식으로, 파동 함수를 통해 양자 시스템의 시간적 변화를 설명한다. 이 방정식은 고전적인 해밀토니안 연산자를 양자화하여 얻으며, 시간 의존적, 시간 독립적 형태로 나뉜다. 슈뢰딩거 방정식은 선형성이 특징이며, 변수 분리, 근사 해법 등을 통해 풀 수 있다. 이 방정식은 입자의 에너지 준위 양자화, 터널 효과 등 양자역학적 현상을 예측하며, 조화 진동자, 수소 원자 등 다양한 시스템에 적용된다. 또한, 밀도 행렬을 이용한 표현과 상대론적 양자역학, 양자장론과의 관계를 갖는다. 슈뢰딩거 방정식의 해석은 코펜하겐 해석, 다세계 해석 등 다양한 양자역학 해석에 따라 달라진다.
파동 함수 에 대한 슈뢰딩거 방정식은 다음과 같다.
파동 함수 에 대한 슈뢰딩거 방정식은 다음 라그랑지언으로부터 유도할 수 있다.
1905년, 알베르트 아인슈타인은 광전 효과를 설명하기 위해 광자의 에너지 E와 진동수 ν 및 플랑크 상수 h 사이의 관계를 E = hν 로 나타내었다. 1924년 루이 드 브로이는 광자뿐만 아니라 모든 입자가 대응되는 파동함수 를 가진다는 드 브로이 가설을 발표하고, 파동의 파장 λ와 입자의 운동량 p에 대해 p = h / λ 의 관계식을 제안했으며, 이 관계식이 특수 상대성 이론 및 아인슈타인이 제안한 식과 일관됨을 보였다. 즉, E = hν는 광자뿐만 아니라 모든 입자에 대해 성립한다는 것이다.[72]
파동 함수 에 대한 슈뢰딩거 방정식은 다음과 같다.[72]
슈뢰딩거 방정식은 다음과 같은 중요한 성질을 가진다.
2. 정의
:
해밀토니언 연산자 는 고전적 해밀토니언에 해당하는 연산자로, 후자를 양자화하여 얻는다. 는 폴 디랙의 브라-켓 표기를 사용해 나타낸, 슈뢰딩거 묘사에서의 힐베르트 공간의 상태 벡터이다. 이를 파동 함수 로 나타낼 수 있다. (파동 함수에 대한 해석은 코펜하겐 해석을 참조하라.)
해밀토니언 연산자 는 보통 미분 연산자이다. 예를 들어, 퍼텐셜 속에 있는, 질량이 인 비상대론적 입자의 경우 해밀토니언은 다음과 같은 2차 미분 연산자이다.
:
즉, 슈뢰딩거 방정식은 다음과 같은 2차 편미분 방정식이 된다.
:
입자의 총 에너지 ''E''는 운동 에너지 ''T''와 퍼텐셜 에너지 ''V''의 합이다. 이 합은 고전역학에서 해밀토니안 ''H''를 나타내는 데에도 자주 사용된다.
:
명시적으로, 1차원 입자에 대해 위치를 ''x'', 질량을 ''m'', 운동량을 ''p'', 위치와 시간 ''t''에 따라 변하는 퍼텐셜 에너지를 ''V''(''x'', ''t'')라고 하면 다음과 같다.
:
3차원에서는 위치 벡터 '''r'''과 운동량 벡터 '''p'''가 사용된다.
:
이 형태는 임의의 일정 수의 입자 집합까지 확장할 수 있다. 즉, 계의 총 에너지는 모든 입자의 운동 에너지와 계의 퍼텐셜 에너지를 더한 것이며, 해밀토니안이기도 하다. 그러나 입자 간에는 상호작용(다체 문제)이 있을 가능성이 있으므로, 계의 퍼텐셜 에너지 ''V''는 모든 입자의 공간적 배치의 변화 또는 시간에 따라 변한다. 일반적으로 계의 퍼텐셜 에너지는 각 입자가 가지는 위치 에너지의 합이 아니라, 모든 입자의 공간 위치의 함수이다. 명시적으로 쓰면 다음과 같다.
:
3. 라그랑지언과 이차 양자화
:
예를 들어, 퍼텐셜 속에 있는, 질량이 인 비상대론적 입자의 경우 슈뢰딩거 라그랑지언은 다음과 같다.
:
여기서 두 번째 표현은 전미분항(total derivative)을 무시하고 쓴 것이다.
이 라그랑지언을 고전적 가환 또는 반가환 장의 라그랑지언으로 여겨, 양자장론으로 이차 양자화시킬 수 있다. 이 경우, 외부 배경장 속에서 움직이는, 임의의 수의 비상대론적 보손 또는 페르미온을 나타내는 양자장론을 얻는다. 또한, 이 경우 비선형 상호작용항을 추가할 수 있다. 예를 들어, 그로스-피타옙스키 방정식이 이러한 꼴이다.
4. 역사
위 식들을 각진동수 와 파수 및 를 이용해 표현하면, E = ħω 및 '''p'''와 '''k'''를 벡터로 표현하면 '''p''' = ħ'''k''' 가 된다.
에르빈 슈뢰딩거는 평면파의 위상을 복소 위상인자로 나타내었다.
:
그리고 그는
:
이므로
:
이며, 마찬가지로
:
이므로
:
이고, 따라서
:
및 각 방향의 부분들을 더하면
:
이 성립함을 알았다.
이를 총 에너지 E와 질량 m 및 위치에너지에 대한 고전역학적 공식
: (단순히 총 에너지를 운동 에너지와 위치 에너지의 합으로 나타낸 것)
에 대입하여, 당시에 슈뢰딩거가 얻었던 위치에너지가 주어진 3차원 공간 상의 단일입자에 대한 공식에 도달한다.
:
막스 플랑크(Max Planck)의 빛의 양자화(흑체 복사 참조) 이후, 알베르트 아인슈타인(Albert Einstein)은 플랑크의 양자를 광자, 즉 빛의 입자로 해석하고, 광자의 에너지는 그 진동수에 비례한다는 것을 제안했는데, 이는 파동-입자 이중성의 초기 신호 중 하나였다. 에너지와 운동량은 특수 상대성 이론에서 진동수와 파수와 같은 방식으로 관련되어 있으므로, 광자의 운동량 은 그 파장 에 반비례하거나, 파수 에 비례한다는 결론이 나왔다.
루이 드 브로이(Louis de Broglie)는 이것이 전자와 같이 질량을 가진 입자를 포함한 모든 입자에 대해 참이라고 가정했다. 그는 물질파가 그 입자와 함께 전파된다고 가정하여 전자가 정상파를 형성한다는 것을 보였다. 즉, 원자핵 주위의 전자의 회전 진동수는 특정한 이산적인 값만 허용된다는 것이다.[34] 이러한 양자화된 궤도는 이산적인 에너지 준위에 해당하며, 드 브로이는 보어 모델의 에너지 준위 공식을 재현했다. 보어 모델은 다음과 같은 각운동량 의 양자화 가정에 기반을 두었다.
:
드 브로이에 따르면, 전자는 파동으로 설명되며, 전자 궤도의 둘레에는 정수 배의 파장이 들어맞아야 한다.
:
이 접근 방식은 기본적으로 반지름 의 원형 궤도를 따라 일차원적으로 전자파를 제한했다.
1921년, 드 브로이 이전에 시카고 대학교의 아서 C. 룬(Arthur C. Lunn)은 상대론적 에너지-운동량 4-벡터의 완성을 기반으로 하는 동일한 주장을 사용하여 현재 드 브로이 관계식이라고 하는 것을 유도했다.[35][36] 드 브로이와 달리, 룬은 현재 슈뢰딩거 방정식으로 알려진 미분 방정식을 공식화하고 수소 원자에 대한 에너지 고유값을 계산했다. 카멘(Kamen)에 따르면, 이 논문은 ''Physical Review''에 게재되지 않았다.[37]
드 브로이의 아이디어를 바탕으로 물리학자 피터 데바이(Peter Debye)는 입자가 파동처럼 행동한다면 어떤 종류의 파동 방정식을 만족해야 한다는 즉흥적인 논평을 했다. 데바이의 발언에 영감을 받아 슈뢰딩거는 전자에 대한 적절한 3차원 파동 방정식을 찾기로 결정했다. 그는 윌리엄 로완 해밀턴(William Rowan Hamilton)의 역학과 광학의 유추에 따라, 광학의 파장이 0에 가까워질수록 역학계와 유사해진다는 관찰에 착안했다. 즉, 광선의 궤적은 페르마의 원리를 따르는 선명한 궤적으로 변하고, 이는 최소 작용의 원리의 유추이다.[38]
그가 찾은 방정식은[39]
:
이다.
그 당시 아놀드 조머펠트(Arnold Sommerfeld)는 보어 모델을 수정하여 상대론적 보정을 추가했다.[40][41] 슈뢰딩거는 상대론적 에너지-운동량 관계를 사용하여 현재 클라인-고르돈 방정식으로 알려진 것을 쿨롱 포텐셜(단위: 자연 단위)에서 구했다.
:
그는 이 상대론적 방정식의 정상파를 찾았지만, 상대론적 보정은 조머펠트의 공식과 일치하지 않았다. 실망한 그는 계산을 중단하고 1925년 12월 산장에서 은둔했다.[42]
산장에서 슈뢰딩거는 이전의 비상대론적 계산이 출판할 만큼 새로운 것이라고 판단하고, 상대론적 보정 문제는 미래에 남겨두기로 결정했다. 수소에 대한 미분 방정식을 푸는 데 어려움이 있었지만(그는 수학자 친구 헤르만 바일(Hermann Weyl)의 도움을 요청했다[43]), 슈뢰딩거는 1926년에 발표한 논문에서 그의 비상대론적 파동 방정식이 수소의 올바른 스펙트럼 에너지를 생성한다는 것을 보였다.[43][44] 슈뢰딩거는 수소 원자의 전자를 프로톤에 의해 생성된 퍼텐셜 우물 에서 움직이는 파동 으로 취급하여 수소 스펙트럼 계열을 계산했다. 이 계산은 보어 모델의 에너지 준위를 정확하게 재현했다.
슈뢰딩거 방정식은 의 거동을 자세히 설명하지만, 그 ''본질''에 대해서는 아무것도 말하지 않는다. 슈뢰딩거는 의 실수 부분을 전하 밀도로 해석하려고 시도했고, 그 다음 논문에서 의 절댓값 제곱이 전하 밀도라고 수정했다. 그러나 이러한 접근 방식은 성공적이지 못했다. 1926년, 이 논문이 발표된 지 불과 며칠 후, 막스 보른(Max Born)은 를 확률 진폭으로 해석하는 데 성공했는데, 이는 절댓값 제곱이 확률 밀도와 같다.[45] 나중에 슈뢰딩거 자신은 이 해석을 다음과 같이 설명했다.[48]
5. 관련 방정식
:
해밀토니언 연산자 는 고전적 해밀토니언에 해당하는 연산자로, 후자를 양자화하여 얻는다. 는 폴 디랙의 브라-켓 표기를 사용해 나타낸, 슈뢰딩거 묘사에서의 힐베르트 공간의 상태 벡터이다. 이를 파동 함수 로 나타낼 수 있다.
상대론적 효과를 고려하면, 슈뢰딩거 방정식은 스핀에 따라 클라인 고든 방정식이나 디랙 방정식 따위로 일반화된다. 이들은 비상대론적인 극한에서 슈뢰딩거 방정식으로 수렴한다.
응집물질물리학에서 보스-아인슈타인 응축을 나타내기 위해 사용하는 그로스-피타옙스키 방정식은 슈뢰딩거 방정식에 사승 상호작용을 추가한 것이다.
슈뢰딩거 그림에서 양자계의 상태 벡터 및 파동 함수의 시간적 변화는 '''시간에 의존하는 슈뢰딩거 방정식'''에 의해 기술된다.[65]
:
여기서 는 허수 단위, 는 시간에 관한 미분, 는 디랙 상수이다.[66] 는 계 전체의 역학적 에너지를 나타내는 연산자로, '''해밀토니안'''이다.[67]
해밀토니안을 자기수반이 아닌 일반적인 선형 연산자 로 대체한 방정식도 슈뢰딩거 방정식이라고 불린다.
:
슈뢰딩거 방정식은 비상대론적인 방정식이며, 상대론적 영역에 대해 그대로 적용할 수 없다. 하지만, 디랙 방정식을 변형함으로써 상대론적인 해밀토니안을 얻을 수 있으며, 형식적으로 슈뢰딩거 방정식과 유사한 형태로 나타낼 수 있다.
6. 성질
폴 디랙,[6] 데이비드 힐베르트,[7] 존 폰 노이만,[8] 헤르만 바일[9]이 개발한 양자역학의 수학적 공식화에 따르면, 양자역학적 시스템의 상태는 분리 가능하고 복소 적인 힐베르트 공간 에 속하는 벡터 로 정의한다.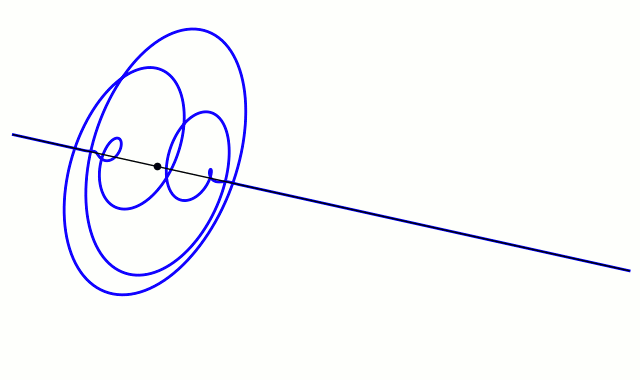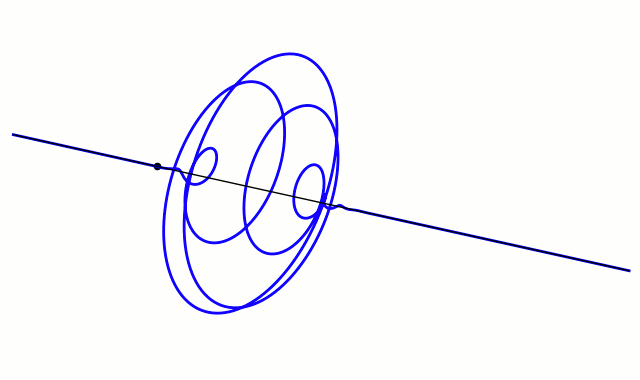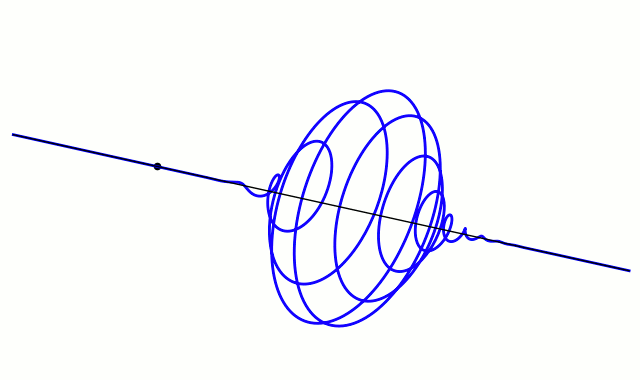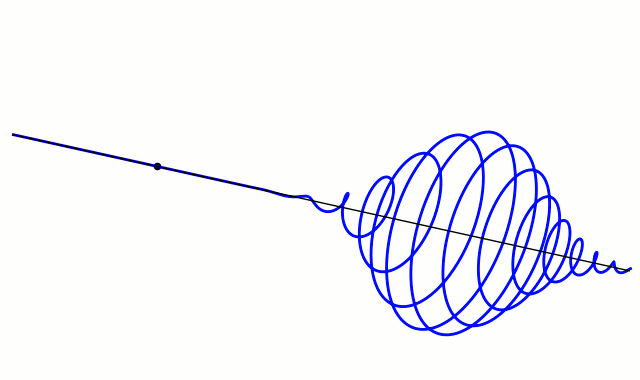
6. 1. 선형성
슈뢰딩거 방정식은 선형 미분 방정식이므로, 두 상태 벡터 와 가 해라면, 이 두 상태 벡터의 임의의 선형 결합도 해가 된다.[12]
여기서 a와 b는 임의의 복소수이다. 더 나아가, 이 합은 임의의 수의 상태 벡터로 확장될 수 있다. 이러한 성질 덕분에 양자 상태의 중첩이 슈뢰딩거 방정식의 해가 될 수 있다.
일반적으로, 슈뢰딩거 방정식의 일반적인 해는 상태의 기저에 대한 가중합을 취하여 찾을 수 있다. 자주 사용되는 선택은 시간에 무관한 슈뢰딩거 방정식의 해인 에너지 고유 상태의 기저이다. 이 기저에서, 시간에 의존하는 상태 벡터 는 다음과 같은 선형 결합으로 쓸 수 있다.
여기서 은 복소수이고 벡터 는 시간에 무관한 방정식 의 해이다.
가장 간단한 파동 함수는 평면파이다.
:
여기서 *A*는 평면파의 진폭, '''k'''는 파수 벡터, ω는 각진동수를 나타낸다. 일반적으로 순수한 평면파만으로 물리계를 기술할 수는 없지만, 중첩의 원리가 성립하므로 모든 파는 사인 평면파의 중첩으로 만들어진다. 슈뢰딩거 방정식이 선형이라면, 평면파의 선형결합도 해로 허용된다. 따라서 중첩의 원리가 성립한다면, 슈뢰딩거 방정식은 선형 미분 방정식이어야 한다.
파수 '''k'''가 불연속적인 경우, 평면파의 중첩은 단순히 여러 파수를 갖는 평면파의 합으로 표현된다.
:
파수 '''k'''가 연속적인 경우에는 합이 아니라 적분으로 표현되며, 파동 함수 Ψ( '''r''' , *t* )는 파수 공간 파동 함수의 푸리에 변환이 된다.
:
여기서 *d*3'''k''' = *dkx dky dkz*는 파수 공간에서의 미소 체적이며, 적분은 파수 공간 전체에 걸쳐 이루어진다. 운동량 파동 함수 Φ('''k''')가 피적분 함수로 나타나는 것은 위치 파동 함수와 운동량 파동 함수가 서로 푸리에 변환이기 때문이다.
6. 2. 유니터리성
해밀토니안 가 일정하면, 슈뢰딩거 방정식의 해는 다음과 같다.[11]
여기서 연산자 는 시간 진화 연산자로 알려져 있으며, 유니터리 연산자이다. 즉, 힐베르트 공간의 벡터들 사이의 내적을 보존한다.[12] 유니터리성은 슈뢰딩거 방정식에 따른 시간 진화의 일반적인 특징이다. 초기 상태가 라면, 나중 시간 에서의 상태는 어떤 유니터리 연산자 에 대해 다음과 같이 주어진다.
반대로, 가 에 의해 매개변수화된 유니터리 연산자의 연속적인 집합이라고 가정하자. 일반성을 잃지 않고[13] 매개변수화는 이 항등 연산자이고, 모든 에 대해 가 되도록 선택할 수 있다. 그러면 는 매개변수 에 따라 다음과 같은 방식으로 의존한다.
여기서 는 자기수반 연산자이며, 집합의 ''생성자''라고 한다. 해밀토니안은 (자연 단위에서 1로 설정될 플랑크 상수의 인자를 제외하고) 바로 이러한 생성자이다.
생성자가 에르미트 연산자임을 확인하기 위해, 라고 하면, 다음을 얻는다.
따라서 가 유니터리 연산자가 되려면, 1차 근사에서 그 도함수가 에르미트 연산자여야 한다.[14]
6. 3. 기저 변환
폴 디랙,[6] 데이비드 힐베르트,[7] 존 폰 노이만,[8] 그리고 헤르만 바일[9]이 개발한 양자역학의 수학적 공식화에 따르면, 양자역학적 시스템의 상태는 분리 가능 복소 힐베르트 공간 에 속하는 벡터 로 정의된다. 이 벡터는 힐베르트 공간의 내적에서 정규화되어 을 만족한다. 힐베르트 공간의 성질은 시스템에 따라 달라지는데, 예를 들어 위치와 운동량을 설명하는 힐베르트 공간은 제곱 적분 가능 함수 공간이고, 단일 양성자의 스핀 힐베르트 공간은 2차원 복소 벡터 공간 이다.[5]
위치, 운동량, 에너지, 스핀과 같은 물리량은 힐베르트 공간에 작용하는 자기 수반 작용소인 가측량으로 표현된다. 파동 함수는 가측량의 고유 벡터 (고유 상태)가 될 수 있으며, 관련된 고유값은 해당 고유 상태에서 가측량의 값에 해당한다. 일반적인 양자 상태는 고유 상태의 선형 결합 (양자 중첩)이다. 가측량을 측정하면 보른 규칙에 따라 확률적으로 고유값 중 하나가 결과로 나타난다. 고유값 가 축퇴되지 않으면 확률은 이고, 는 관련된 고유 벡터이다. 고유값이 축퇴되면 확률은 이고, 는 관련된 고유 공간에 대한 투영 연산자이다.
운동량 고유 상태는 무한히 넓은 단색파로 제곱 적분 가능하지 않다. 위치 고유 상태는 디랙 델타 분포로 제곱 적분 가능하지 않고 함수가 아니다. 따라서 둘 다 힐베르트 공간에 속할 수 없다. 물리학자들은 힐베르트 공간 외부의 요소로 구성된 고유 상태를 "일반화된 고유 벡터"로 간주하며, 계산 편의를 위해 사용되지만 물리적 상태를 나타내지는 않는다.[10][2] 위치 공간 파동 함수 는 상태 벡터 와 위치 고유 상태 의 내적으로 표현된다.
슈뢰딩거 방정식은 벡터-연산자 방정식으로서 켓의 임의의 완전한 기저를 갖는 힐베르트 공간에서 유효한 표현을 갖는다. 물리적 힐베르트 공간 외부에 있는 "기저"도 계산 목적으로 사용된다. 비상대론적 스핀 없는 입자에 대한 '위치 공간'과 '운동량 공간' 슈뢰딩거 방정식은 다음과 같다. 힐베르트 공간은 3차원 유클리드 공간에서 복소수 제곱 적분 가능 함수의 공간이며, 해밀토니안은 운동량 연산자의 제곱에 비례하는 운동 에너지 항과 퍼텐셜 에너지 항의 합이다.
3차원 위치 벡터를 , 3차원 운동량 벡터를 로 나타내면, 위치 공간 슈뢰딩거 방정식은 다음과 같다.
운동량 공간 상대방정식은 파동 함수와 퍼텐셜의 푸리에 변환을 포함한다.
함수 와 는 로부터 다음과 같이 유도된다.
여기서 와 는 힐베르트 공간에는 속하지 않지만, 공간의 모든 원소와 잘 정의된 내적을 갖는다.
정준 양자화에서 고전 변수 와 는 정준 교환 관계를 만족하는 자기 수반 연산자 와 로 바뀐다.
이는 다음을 의미한다.
위치 공간 표현에서 운동량 연산자 의 작용은 이고, 는 이계도함수가 되며, 3차원에서는 라플라시안 이 된다.
정준 교환 관계는 위치 및 운동량 연산자가 서로의 푸리에 켤레임을 의미한다. 따라서 위치 의존성으로 정의된 함수는 푸리에 변환을 통해 운동량 함수로 변환 가능하다. 고체물리학에서 슈뢰딩거 방정식은 운동량 함수에 대해 작성되는데, 블로흐 정리가 주기적 결정 격자 퍼텐셜이 이산 역격자 벡터 에 대해 를 와 결합하도록 보장하기 때문이다. 점에서 브릴루앵 영역의 다른 점들과 독립적으로 각 브릴루앵 영역의 점에서 운동량 공간 슈뢰딩거 방정식을 푸는 것이 편리하다.
6. 4. 확률 흐름
슈뢰딩거 방정식은 국소적 확률 보존과 일치한다.[2] 정규화된 파동 함수는 시간에 따라 진화한 후에도 정규화된 상태를 유지한다. 행렬 역학에서 이는 시간 진화 연산자가 유니터리 연산자임을 의미한다.[15] 클라인-고르돈 방정식과는 달리, 파동 함수의 재정의된 내적은 시간에 무관할 수 있지만, 파동 함수의 절댓값 제곱의 전체 부피 적분은 시간에 무관할 필요는 없다.[16]
비상대론적 양자역학에서 확률에 대한 연속 방정식은 다음과 같이 나타낼 수 있다.
여기서 는 확률 전류 또는 확률 플럭스(단위 면적당 유량)이다.
파동 함수가 로 표현된다면, 여기서 는 파동 함수의 복소 위상을 나타내는 실수 함수이다. 그러면 확률 플럭스는 다음과 같이 계산된다.
따라서, 파동 함수의 위상의 공간적 변화는 파동 함수의 확률 플럭스를 특징짓는다고 할 수 있다. 항이 속도의 역할을 하는 것처럼 보이지만, 위치와 속도의 동시 측정은 불확정성 원리를 위반하기 때문에 한 점에서의 속도를 나타내지는 않는다.[15]
파동 함수에 물리적 의미를 부여하려면, 파동 함수의 공간 부분이 2차 적분 가능해야 한다.
:
적분 가능성 조건은 파동 함수에 적절한 경계 조건을 부과함으로써 만족된다. 일반적으로 파동 함수의 규격화 조건
:
을 만족하는 것이 비물리적인 해가 아닌 해로 채택된다.
파동 함수의 규격화 조건은 닫힌 양자계에서의 전역적인 확률 보존 법칙으로 해석된다. 확률 해석에 기반한 일반적인 양자론에서는 시간이 진행되어도 확률이 보존되어야 한다. 즉, 어떤 경우에도 모든 사건의 확률의 합계는 100% (= 1)이 되어야 한다. 이 사실과 보른의 규칙에 의한 확률 계산 방법(상태 벡터와 그 쌍대 벡터의 곱)으로부터, 상태 벡터의 시간 진행은 유니터리 변환이어야 함을 알 수 있다. 슈뢰딩거 방정식을 풀면 "상태 벡터의 시간 진행은 유니터리 변환이다"라는 것이 유도된다. 따라서 양자계의 시간 진행에 대한 기본적인 요구(원리)는 슈뢰딩거 그림으로 기술하는 경우, 이 슈뢰딩거 방정식을 채택하여 출발하는 경우가 많다. 하지만 다른 "시간 진행 연산자가 만족해야 하는 조건"을 기본적인 요구로 하여 출발하는 경우도 있다.
6. 5. 변수 분리
변수분리법을 이용하여 방정식을 풀면, 공간 부분과 시간 부분의 곱으로 된 다음 형태의 해를 찾는 것을 의미한다.[17]
여기서 는 계를 구성하는 입자(들)의 모든 공간 좌표의 함수이고, 는 시간만의 함수이다. 에 대한 이 식을 시간에 의존하는 좌변에 대입하면 는 위상 인자임을 알 수 있다.
이러한 유형의 해를 ''정상 상태''라고 부르는데, 그 이유는 보른 규칙을 통해 확률 밀도를 계산할 때 상쇄되는 위상 인자만 시간에 의존하기 때문이다.[11]
전체 파동 함수의 공간 부분은 다음을 만족한다.[18]
여기서 에너지 는 위상 인자에 나타난다.
이는 시간에 무관한 퍼텐셜에서 임의의 수의 입자와 임의의 수의 차원으로 일반화된다. 시간에 무관한 방정식의 정상파 해는 서로 다른 에너지의 확률 분포 대신, 특정 에너지를 갖는 상태이다. 물리학에서 이러한 정상파를 "정상 상태" 또는 "에너지 고유 상태"라고 부르고, 화학에서는 "원자 궤도함수" 또는 "분자 궤도함수"라고 부른다. 에너지 고유 상태의 중첩은 에너지 준위 사이의 상대적 위상에 따라 그 성질이 변한다. 에너지 고유 상태는 기저를 형성한다. 임의의 파동 함수는 이산적인 에너지 상태의 합 또는 연속적인 에너지 상태에 대한 적분, 또는 더 일반적으로 측정에 대한 적분으로 쓸 수 있다. 이것은 수학에서의 스펙트럼 정리이며, 유한 차원 상태 공간에서는 에르미트 행렬의 고유 벡터의 완전성을 나타내는 것에 불과하다.
변수분리법은 시간에 무관한 슈뢰딩거 방정식에도 유용한 방법이 될 수 있다. 예를 들어, 문제의 대칭성에 따라 직교 좌표축을 분리할 수 있다.
또는 극좌표와 각좌표를 분리할 수 있다.
7. 예시
슈뢰딩거 방정식의 구체적인 형태는 적절한 퍼텐셜을 결정함으로써 얻을 수 있다. 퍼텐셜은 입자에 수반되는 기본적인 변수의 함수로 주어지지만, 일반적으로 퍼텐셜의 변수는 물리량의 연산자이며 일반적인 의미의 함수와는 다르다. 퍼텐셜의 변수가 되는 물리량은 예를 들어 입자의 위치, 스핀등이 있다. 퍼텐셜에는 외부에서 미치는 상호작용과 대상으로 하는 양자계의 입자 사이에 작용하는 상호작용, 두 가지가 있다. 고전론과 마찬가지로 단일 입자의 퍼텐셜은 다체간 퍼텐셜을 어떤 의미로 평균화한 것이라고 생각할 수 있다. 예를 들어 원자핵 및 내각 전자에서 외각 전자에 미치는 쿨롱 상호작용은, 원자핵과 내각 전자의 운동이 외각 전자의 운동에 거의 영향을 받지 않는다면, 원자핵과 내각 전자와 관련된 퍼텐셜의 변수는 고정되고 이체간 퍼텐셜을 단일 입자의 퍼텐셜로 대체할 수 있다. 다체간 퍼텐셜의 예로 가장 기본적인 것은 입자간의 쿨롱 상호작용 및 스핀 상호작용이다. 응용상에서는 유한 퍼텐셜 우물이나 레너드-존스 퍼텐셜 등도 이용된다.
입자계의 해밀토니안은 전술한 퍼텐셜 외에 일반적으로 입자의 운동 에너지가 더해진 것이다. 구체적인 해밀토니안에서 파동 함수를 얻으려면, 물리량의 교환 관계에 따라 물리량 연산자의 표현을 정하고, 얻어진 해밀토니안을 슈뢰딩거 방정식에 적용하여 그 해를 구한다.
예를 들어, 다음 방정식은 위치 연산자를 곱셈 연산자로 한 경우의 단일 입자 퍼텐셜에 대한 단일 입자의 운동을 나타낸다.
:
은 물체의 질량, 는 퍼텐셜 에너지, 는 라플라시안, 는 위치 표시의 파동 함수이다. 해밀토니안에 미분 연산자가 포함되어 있기 때문에, 이것은 선형 편미분 방정식이다. 확산 방정식이기도 하지만, 열전도 방정식과는 달리 시간 미분 부분에 허수 단위가 있기 때문에 파동 방정식이라고도 할 수 있다.
시간에 의존하는 슈뢰딩거 방정식을 시간과 공간에 대해 변수분리하면, 파동함수의 공간 부분에 대한 방정식으로서 해밀토니안의 고유값 방정식을 얻을 수 있다. 이 고유값 방정식을 시간에 무관한 슈뢰딩거 방정식이라고 한다.
:
여기서 는 파동함수의 공간 부분, 는 에너지 고유값이다. 시간에 무관한 슈뢰딩거 방정식의 해는 에너지 고유상태라고 불린다.
해밀토니안의 에르미트성으로부터, 에너지 고유상태는 서로 직교한다. 서로 직교하는 상태 사이에서는 전이가 일어나지 않으므로, 고유상태는 안정된 상태로 존재할 수 있다. 공간 부분이 해밀토니안의 고유상태인 파동함수는 양자계의 정상 상태에 대응하며, 정상 상태의 파동함수 또는 간단히 정상 상태라고 불린다. 원자나 분자에 속박된 전자의 파동함수에 대해서는, 원자 궤도함수나 분자 궤도함수와 같이, 고전 모형의 용어를 빌려 '''궤도'''(orbital)라고 부르기도 한다.
정상 상태의 파동함수의 시간 의존 부분은 다음과 같은 지수 함수로 표현된다.
:
슈뢰딩거 방정식의 변수 분리 해는 특별한 정상 상태의 파동함수가 되지만, 해의 선형성으로부터 일반적인 파동함수를 몇몇 정상 상태의 선형 결합으로 나타낼 수 있다.
:
여기서 는 로 표시된 에너지 고유값, 는 대응하는 고유상태, 는 각 정상 상태의 확률적인 가중치를 나타내는 복소수이다.
시간에 무관한 슈뢰딩거 방정식에 대해, 자기장이 없는 단일 입자계의 해밀토니안
:
을 주면 다음과 같다.
:
상기 해밀토니안은 퍼텐셜 을 구체적으로 정의하고 있지 않지만, 실제로 다룰 때는 퍼텐셜을 구체적인 함수로 정의하거나, 어떤 의미에서 성질이 좋은 함수임을 요구할 필요가 있다.
어떠한 상호작용도 받지 않는 입자를 자유 입자라고 한다. 자유 입자에 대한 해밀토니안에는 퍼텐셜 항이 없으므로 (), 1차원 계의 슈뢰딩거 방정식은 다음과 같다.
:
자유 입자의 에너지 고유값 는 해밀토니안이 운동 에너지 연산자에 대응하기 때문에, 입자가 가지는 운동 에너지에 대응한다. 에너지 고유값의 양음에 따라 슈뢰딩거 방정식의 해의 거동은 크게 다르다.
에너지 고유값이 양의 경우 (), 자유 입자의 슈뢰딩거 방정식의 해는 진동 해가 된다 (는 임의 상수).
:
한편, 에너지 고유값이 음의 경우 (), 자유 입자의 슈뢰딩거 방정식의 해는 지수 해가 된다.
:
지수 해는 무한원에서 발산 등에 의해 물리적인 요구를 만족시키지 않기 때문에, 비물리적인 해로 취급된다. 그러나 터널링 효과처럼, 부분적으로 파동 함수가 지수적인 거동을 하는 것은 허용된다.
자유 입자의 슈뢰딩거 방정식은, 예를 들어 금속 내의 전도 전자의 운동이나, 무한원에서 평탄한 퍼텐셜을 갖는 계에서 퍼텐셜의 구속을 벗어난 입자의 거동을 조사하는 등에 응용된다.
7. 1. 상자 속 입자
1차원 포텐셜 에너지 상자 속 입자는 구속 조건이 에너지 준위의 양자화로 이어지는 가장 수학적으로 간단한 예시이다. 상자는 특정 영역 ''내부''에서는 포텐셜 에너지가 0이고 ''외부''에서는 무한대의 포텐셜 에너지를 갖는 것으로 정의된다.[19] 1차원 상자 속 입자에 대한 시간에 무관한 슈뢰딩거 방정식은 다음과 같다.
미분 연산자를 다음과 같이 정의하면
위 방정식은 고전적인 운동 에너지 유사체를 연상시킨다.
여기서 상태 는 입자의 운동 에너지와 일치하는 에너지 를 갖는다.
상자 속 입자에 대한 슈뢰딩거 방정식의 일반적인 해는 다음과 같다.
또는 오일러 공식에서,
무한 포텐셜 상자의 벽은 과 에서 가 0이어야 하므로, 와 의 값을 결정한다. 따라서 에서,
이고, 이다. 에서,
가 놈 1을 갖는다는 가정과 모순되므로 는 0일 수 없다. 따라서 이므로, 은 의 정수배여야 한다.
에 대한 제약 조건은 에너지 준위에 대한 제약 조건을 의미하며, 다음을 얻는다.
유한 포텐셜 우물은 무한 포텐셜 우물 문제를 유한한 깊이의 포텐셜 우물로 일반화한 것이다. 유한 포텐셜 우물 문제는 파동 함수가 우물 벽에서 0으로 고정되지 않기 때문에 무한 입자-상자 문제보다 수학적으로 더 복잡하다. 파동 함수는 우물 외부 영역에서 0이 아니므로 더 복잡한 수학적 경계 조건을 만족해야 한다. 직사각형 포텐셜 장벽 문제는 양자 터널링 효과에 대한 모델을 제공하며, 플래시 메모리와 주사 터널링 현미경과 같은 현대 기술의 성능에 중요한 역할을 한다.
7. 2. 조화 진동자
조화 진동자에 대한 슈뢰딩거 방정식은 다음과 같다.
:
여기서 는 변위이고 는 각진동수이다. 이 방정식은 진동하는 원자, 분자,[20] 격자 내의 원자 또는 이온[21] 등 다양한 다른 계를 근사적으로 설명하는 데 사용될 수 있으며, 평형점 근처의 다른 퍼텐셜을 근사하는 데에도 사용된다. 또한 양자역학에서 섭동 방법의 기초이기도 하다.
위치 공간에서의 해는 다음과 같다.
:
여기서 이고, 함수 는 차 에르미트 다항식이다.
고유값은 다음과 같다.
:
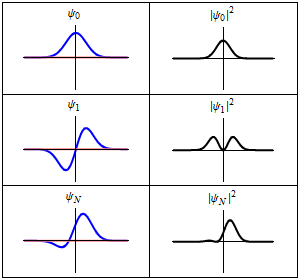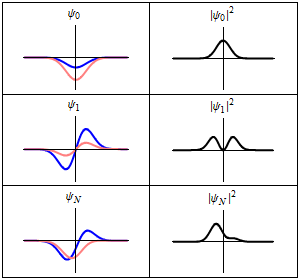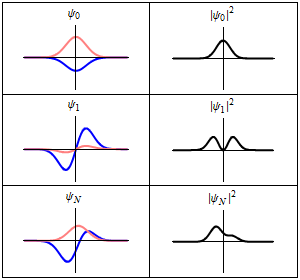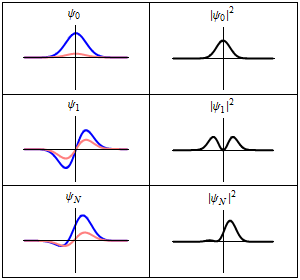
인 경우를 바닥 상태라고 하며, 그 에너지를 영점 에너지라고 하고, 파동 함수는 가우스 분포이다.[22]
상자 속 입자와 마찬가지로 조화 진동자는 슈뢰딩거 방정식의 일반적인 특징인 결합 고유 상태의 에너지가 불연속적이라는 것을 보여준다.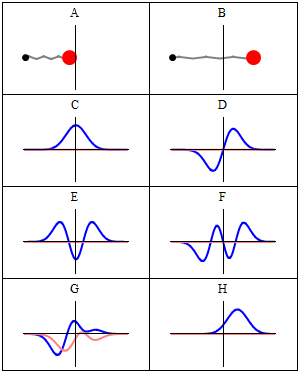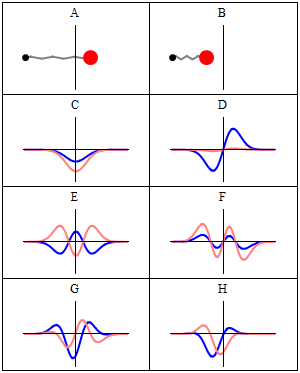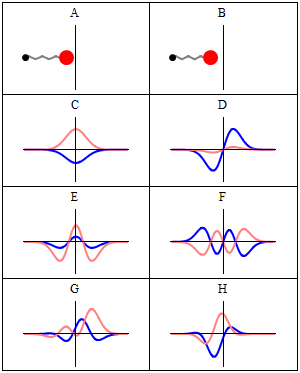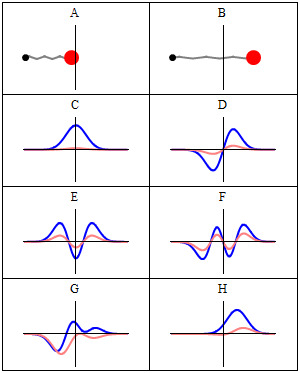
7. 3. 수소 원자
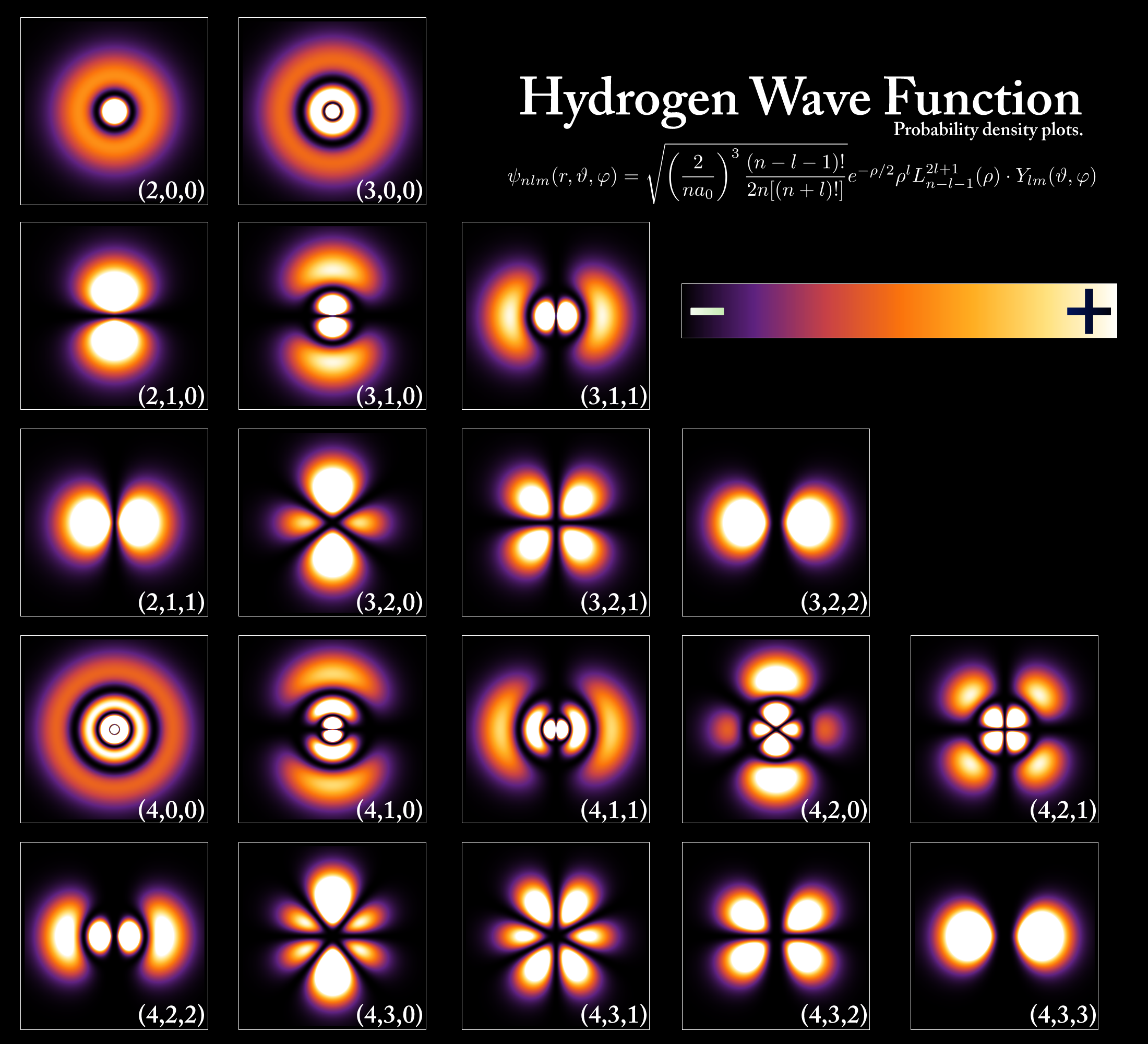
수소 원자(또는 수소 유사 원자)의 전자에 대한 슈뢰딩거 방정식은 다음과 같다.
:
여기서 는 전자 전하량, 은 핵에 대한 전자의 위치, 는 상대 위치의 크기이고, 퍼텐셜 항은 쿨롱 상호작용에 기인하며, 는 진공 유전율이다.
:
는 질량 인 수소 원자핵(단순히 양성자)와 질량 인 전자의 2체 환산 질량이다. 퍼텐셜 항에 음의 부호가 있는 것은 양성자와 전자가 서로 반대 전하를 띠기 때문이다. 전자 질량 대신 환산 질량을 사용하는 것은 전자와 양성자가 함께 공통 질량 중심 주위를 공전하고 2체 문제를 구성하기 때문이다. 여기서는 전자의 운동이 주로 관심 대상이므로, 등가적인 1체 문제는 환산 질량을 사용하는 전자의 운동이다.
수소 원자에 대한 슈뢰딩거 방정식은 변수 분리법으로 풀 수 있다.[23] 이 경우 구면 좌표계가 가장 편리하다. 따라서,
:
여기서 R은 방사 함수이고 는 차수 와 위수 의 구면 조화 함수이다. 이것은 슈뢰딩거 방정식이 정확하게 풀린 유일한 원자이다. 다전자 원자는 근사 방법이 필요하다. 해의 집합은 다음과 같다.[24]
:
여기서
8. 근사 해법
일반적으로 물리적으로 흥미로운 상황에 대해서는 슈뢰딩거 방정식을 정확하게 풀 수 없다. 따라서 변분법과 WKB 근사와 같은 기법을 사용하여 근사해를 얻는다. 또한, 정확하게 풀 수 있는 문제에 대한 작은 수정으로 문제를 다루는 방법, 즉 섭동 이론을 사용하는 것도 일반적이다.
일반적인 방법은 다음과 같다.
특수한 경우의 방법은 다음과 같다.
- List of quantum-mechanical systems with analytical solutions
- 하트리-포크 방정식과 포스트-하트리-포크 방법
9. 준고전적 극한
고전역학과 양자역학을 비교하는 간단한 방법은 기대값 위치와 기대값 운동량의 시간 변화를 살펴봄으로써 고전역학에서 일반적인 위치와 운동량의 시간 변화와 비교하는 것이다.[49] 양자 기대값은 에렌페스트 정리를 만족한다. 퍼텐셜 에서 움직이는 1차원 양자 입자의 경우, 에렌페스트 정리는 다음과 같다.
:
첫 번째 방정식은 고전적인 움직임과 일치하지만, 두 번째는 그렇지 않다. 만약 쌍 가 뉴턴의 제2법칙을 만족하려면, 두 번째 방정식의 우변은 여야 하는데, 이는 일반적으로 와 다르다. 그러나 양자 조화 진동자의 경우, 는 선형이므로 이러한 구분이 사라진다. 이 특별한 경우에는 기대값 위치와 기대값 운동량이 고전 궤적을 정확하게 따른다.
일반적인 시스템의 경우, 파동 함수가 어떤 점 주변에 매우 집중되어 있다면, 와 는 거의 같아진다. 둘 다 와 거의 같기 때문이다. 이 경우, 기대값 위치와 기대값 운동량은 파동 함수가 위치에서 매우 국한된 상태로 유지되는 한, 고전 궤적에 매우 가깝게 유지된다.
일반적인 형태의 슈뢰딩거 방정식
:
은 해밀턴-야코비 방정식
:
과 밀접한 관련이 있다. 여기서 는 고전적인 작용이고 는 해밀토니안 함수(연산자가 아님)이다.[49] 여기서 에 대한 일반화 좌표 (해밀턴-야코비 방정식에서 사용됨)는 데카르트 좌표계의 위치로 로 설정할 수 있다.
:
를 대입하고, 여기서 는 확률 밀도이며, 슈뢰딩거 방정식에 대입한 다음 결과 방정식에서 의 극한을 취하면 해밀턴-야코비 방정식이 나온다.
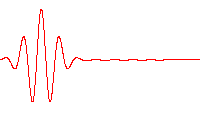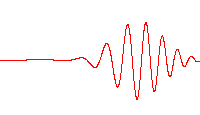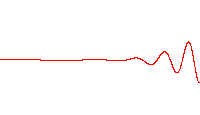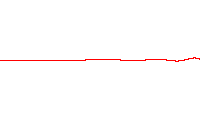
슈뢰딩거는 위치가 r 근처이고 파수 벡터가 k 근처인 파동 패킷을 나타내는 해는, k(따라서 속도)의 퍼짐이 r의 퍼짐을 현저히 증가시키지 않을 정도로 충분히 짧은 시간 내에, 고전역학에서 결정되는 궤적을 그린다고 주장했다.
주어진 k의 퍼짐에 대해, 속도의 퍼짐은 플랑크 상수에 비례하기 때문에, 플랑크 상수를 0으로 근사할 때, 고전역학의 방정식은 양자역학에서 유도된다고 말해진다. 그 극한이 어떻게 취해지는지, 그리고 어떤 상황에서인지에 대한 세심한 주의가 필요하다.
단파장 극한은 플랑크 상수를 0으로 근사하는 것과 동일하다. 왜냐하면 이것은 파동 패킷의 국소화를 극한까지 강화하여 입자를 특정 위치에 국소화시키기 때문이다(위 그림 참조). 하이젠베르크의 불확정성 원리를 위치와 운동량에 적용하면, 위치의 불확정성과 운동량의 불확정성의 곱은 ħ → 0에 따라 0이 된다.
:
여기서 σ는 측정량의 표준편차이며, 위치 x와 운동량 px(y와 z에 대해서도 마찬가지)가 이 극한에서만 임의의 정밀도로 알려질 수 있음을 시사한다.
슈뢰딩거 방정식과 해밀턴-야코비 방정식의 관계는 다음과 같다.
- 입자의 운동(슈뢰딩거 방정식의 (단파장) 파동 패킷 해로 설명됨)은 운동의 해밀턴-야코비 방정식으로 설명된다.
- 슈뢰딩거 방정식은 파동 함수를 포함하므로, 그 파동 패킷 해는 (양자) 입자의 위치가 파면에 애매하게 퍼져 있음을 나타낸다. 반대로, 해밀턴-야코비 방정식은 정확한 위치와 운동량을 가진 (고전적인) 입자에 적용되며, 대신 모든 시간에 위치와 운동량(궤적)이 결정론적이고 동시에 알 수 있다.
10. 밀도 행렬
파동 함수는 양자 시스템과 그 거동을 설명하는 유일한 방법은 아니다. 시스템의 준비가 불완전하게 알려져 있거나 조사 중인 시스템이 더 큰 전체의 일부인 경우 밀도 행렬을 대신 사용할 수 있다.[49] 밀도 행렬은 양의 준정부호 연산자이며 그 트레이스는 1과 같다. ("밀도 연산자"라는 용어도 특히 기저가 되는 힐베르트 공간이 무한 차원일 때 사용된다.) 모든 밀도 행렬의 집합은 볼록하며, 극점은 힐베르트 공간의 벡터에 투영되는 연산자이다. 이들은 파동 함수의 밀도 행렬 표현이며, 디랙 표기법에서 다음과 같이 쓸 수 있다.
파동 함수에 대한 슈뢰딩거 방정식과 유사한 밀도 행렬의 방정식은 다음과 같다.[25][26]
여기서 대괄호는 교환자를 나타낸다. 이 방정식은 폰 노이만 방정식, 리우빌-폰 노이만 방정식 또는 밀도 행렬에 대한 슈뢰딩거 방정식으로도 알려져 있다.[49] 해밀토니안이 시간에 무관하다면 이 방정식은 쉽게 풀려 다음과 같은 결과를 얻는다.
일반적으로 유니터리 연산자 가 특정 시간 간격 동안 파동 함수의 진화를 설명한다면, 같은 간격 동안 밀도 행렬의 시간 진화는 다음과 같이 주어진다.
밀도 행렬의 유니터리 진화는 그 폰 노이만 엔트로피를 보존한다.[49]
11. 상대론적 양자역학과 양자장론
알베르트 아인슈타인이 광전 효과를 설명하기 위해 광자의 에너지와 진동수 및 플랑크 상수 사이의 관계를 제시하고, 루이 드 브로이는 모든 입자가 파동함수를 가진다는 드 브로이 가설을 발표하면서, 에르빈 슈뢰딩거는 이 개념들을 바탕으로 1925년 슈뢰딩거 방정식을 발표하였다.[72] 슈뢰딩거 방정식은 비상대론적이므로 특수상대론과는 맞지 않아, 이를 일반화하여 스핀에 따라 클라인 고든 방정식이나 디랙 방정식 등을 얻을 수 있으며, 이들은 비상대론적인 극한에서 슈뢰딩거 방정식으로 수렴한다.
슈뢰딩거 방정식은 응집물질물리학에서 보스-아인슈타인 응축을 나타내기 위해 비선형 항을 추가하여 사용될 수 있다. 예를 들어 그로스-피타옙스키 방정식은 슈뢰딩거 방정식에 사승 상호작용을 추가한 형태이다.
슈뢰딩거 방정식의 형태는 물리적 상황에 따라 다르며, 가장 일반적인 형태는 시간에 따라 변화하는 시스템을 설명하는 시간에 따른 슈뢰딩거 방정식이다.[11]
상대성이론과 양자역학을 결합하기 위해 비상대론적 에너지 방정식 대신 상대론적 에너지-운동량 관계식을 사용하여 파동 방정식을 구성한다. 클라인-고르돈 방정식과 디랙 방정식이 그 예시이다. 클라인-고르돈 방정식은 질량을 가진 스핀이 없는 입자에 적용되며, 디랙 방정식은 스핀- 입자에 대해 참이며, 해는 스피너장이다.
일반적으로 일반 슈뢰딩거 방정식에 대입할 해밀토니안은 위치 및 운동량 연산자뿐만 아니라 스핀 행렬의 함수이기도 하다. 또한, 상대론적 파동 방정식의 해는 복소수 값 스피너장이다.
초기 형태의 디랙 방정식은 단일 양자 입자에 대한 방정식이며, 이는 입자 수가 고정되지 않은 상대론적 양자역학에서는 제한적이다. 양자장론(QFT)에서는 포크 공간을 도입하여 이 문제를 해결한다.[32] 그러나 슈뢰딩거 방정식은 특정 시간 축을 선택하기 때문에 이론의 로렌츠 불변성이 명확하지 않아, 다른 방식으로 공식화되기도 한다.[33] 뉴턴의 운동 방정식과 마찬가지로, 슈뢰딩거 방정식에서 시간을 다루는 방식은 상대론적 기술로 만들기에는 부적절하다.
12. 해석
막스 플랑크(Max Planck)의 빛의 양자화(참조: 흑체 복사) 이후, 알베르트 아인슈타인(Albert Einstein)은 플랑크의 양자를 광자, 즉 빛의 입자로 해석하고, 광자의 에너지는 그 진동수에 비례한다는 것을 제안했는데, 이는 파동-입자 이중성의 초기 신호 중 하나였다. 에너지와 운동량은 특수 상대성 이론에서 진동수와 파수와 같은 방식으로 관련되어 있으므로, 광자의 운동량 은 그 파장 에 반비례하거나, 파수 에 비례한다는 결론이 나왔다.[34]
:
:여기서 는 플랑크 상수이고 는 환산 플랑크 상수이다.
루이 드 브로이(Louis de Broglie)는 이것이 전자와 같이 질량을 가진 입자를 포함한 모든 입자에 대해 참이라고 가정했다. 그는 물질파가 그 입자와 함께 전파된다고 가정하여 전자가 정상파를 형성한다는 것을 보였다. 즉, 원자핵 주위의 전자의 회전 진동수는 특정한 이산적인 값만 허용된다는 것이다.[34] 이러한 양자화된 궤도는 이산적인 에너지 준위에 해당하며, 드 브로이는 보어 모델의 에너지 준위 공식을 재현했다. 보어 모델은 다음과 같은 각운동량 의 양자화 가정에 기반을 두었다.[34]
:
드 브로이에 따르면, 전자는 파동으로 설명되며, 전자 궤도의 둘레에는 정수 배의 파장이 들어맞아야 한다.[34]
:
이 접근 방식은 기본적으로 반지름 의 원형 궤도를 따라 일차원적으로 전자파를 제한했다.[34]
1921년, 드 브로이 이전에 시카고 대학교의 아서 C. 룬(Arthur C. Lunn)은 상대론적 에너지-운동량 4-벡터의 완성을 기반으로 하는 동일한 주장을 사용하여 현재 드 브로이 관계식이라고 하는 것을 유도했다.[35][36] 드 브로이와 달리, 룬은 현재 슈뢰딩거 방정식으로 알려진 미분 방정식을 공식화하고 수소 원자에 대한 에너지 고유값을 계산했다. 카멘(Kamen)에 따르면, 이 논문은 ''Physical Review''에 게재되지 않았다.[37]
드 브로이의 아이디어를 바탕으로 물리학자 피터 데바이(Peter Debye)는 입자가 파동처럼 행동한다면 어떤 종류의 파동 방정식을 만족해야 한다는 즉흥적인 논평을 했다. 데바이의 발언에 영감을 받아 슈뢰딩거는 전자에 대한 적절한 3차원 파동 방정식을 찾기로 결정했다. 그는 윌리엄 로완 해밀턴(William Rowan Hamilton)의 역학과 광학의 유추에 따라, 광학의 파장이 0에 가까워질수록 역학계와 유사해진다는 관찰에 착안했다. 즉, 광선의 궤적은 페르마의 원리를 따르는 선명한 궤적으로 변하고, 이는 최소 작용의 원리의 유추이다.[38]
그가 찾은 방정식은[39]
:
그 당시 아놀드 조머펠트(Arnold Sommerfeld)는 보어 모델을 수정하여 상대론적 보정을 추가했다.[40][41] 슈뢰딩거는 상대론적 에너지-운동량 관계를 사용하여 현재 클라인-고르돈 방정식으로 알려진 것을 쿨롱 포텐셜(단위: 자연 단위)에서 구했다.
:
그는 이 상대론적 방정식의 정상파를 찾았지만, 상대론적 보정은 조머펠트의 공식과 일치하지 않았다. 실망한 그는 계산을 중단하고 1925년 12월 산장에서 정부인과 은둔했다.[42]
산장에서 슈뢰딩거는 이전의 비상대론적 계산이 출판할 만큼 새로운 것이라고 판단하고, 상대론적 보정 문제는 미래에 남겨두기로 결정했다. 수소에 대한 미분 방정식을 푸는 데 어려움이 있었지만(그는 수학자 친구 헤르만 바일(Hermann Weyl)의 도움을 요청했다[43]), 슈뢰딩거는 1926년에 발표한 논문에서 그의 비상대론적 파동 방정식이 수소의 올바른 스펙트럼 에너지를 생성한다는 것을 보였다.[43][44] 슈뢰딩거는 수소 원자의 전자를 프로톤에 의해 생성된 퍼텐셜 우물 에서 움직이는 파동 으로 취급하여 수소 스펙트럼 계열을 계산했다. 이 계산은 보어 모델의 에너지 준위를 정확하게 재현했다.
슈뢰딩거 방정식은 의 거동을 자세히 설명하지만, 그 ''본질''에 대해서는 아무것도 말하지 않는다. 슈뢰딩거는 의 실수 부분을 전하 밀도로 해석하려고 시도했고, 그 다음 논문에서 의 절댓값 제곱이 전하 밀도라고 수정했다. 그러나 이러한 접근 방식은 성공적이지 못했다. 1926년, 이 논문이 발표된 지 불과 며칠 후, 막스 보른(Max Born)은 를 확률 진폭으로 해석하는 데 성공했는데, 이는 절댓값 제곱이 확률 밀도와 같다.[45] 나중에 슈뢰딩거 자신은 이 해석을 다음과 같이 설명했다.[48]
슈뢰딩거 방정식은 어떤 계의 파동 함수와 그것이 시간에 따라 어떻게 동적으로 변하는지를 계산하는 방법을 제공한다. 그러나 슈뢰딩거 방정식은 파동 함수가 정확히 무엇인지에 대해 직접적으로 말해주지는 않는다. 슈뢰딩거 방정식의 의미와 그 안의 수학적 개체가 물리적 현실과 어떻게 관련되는지는 채택하는 양자역학의 해석에 달려 있다.
코펜하겐 해석으로 종종 묶이는 견해에서, 계의 파동 함수는 그 계에 대한 통계적 정보의 집합이다. 슈뢰딩거 방정식은 어떤 시간의 계에 대한 정보를 다른 시간의 정보와 관련짓는다. 슈뢰딩거 방정식으로 표현되는 시간 진화 과정은 연속적이고 결정론적이지만, 한 순간의 파동 함수를 알면 원칙적으로 모든 미래 시간에 대한 파동 함수를 계산할 수 있지만, 파동 함수는 측정 중에 불연속적이고 확률적으로 변할 수도 있다. 이러한 사고방식에 따르면, 파동 함수는 새로운 정보가 이용 가능해짐에 따라 변한다. 측정 후 파동 함수는 일반적으로 측정 전에는 알 수 없지만, 서로 다른 가능성에 대한 확률은 보른 규칙을 사용하여 계산할 수 있다.[49][50] 관계적 양자역학과 QBism과 같은 다른, 더 최근의 양자역학 해석도 슈뢰딩거 방정식에 이러한 종류의 지위를 부여한다.[53][54]
슈뢰딩거 자신은 1952년에 슈뢰딩거 방정식에 따라 진화하는 중첩의 서로 다른 항들은 "대안이 아니라 모두 실제로 동시에 일어난다"고 제안했다. 이것은 에버렛의 다세계 해석의 초기 버전으로 해석되어 왔다.[55][56] 1956년에 독립적으로 공식화된 이 해석은 양자 이론에 의해 기술된 모든 가능성이 대부분 독립적인 평행 우주로 구성된 다중 우주에서 동시에 발생한다고 주장한다.[58] 이 해석은 파동 함수 붕괴의 공리를 제거하고 슈뢰딩거 방정식에 따른 연속적인 진화만 남기므로, 측정된 계와 측정 장치, 그리고 관찰자를 포함한 모든 가능한 상태가 실제 물리적 양자 중첩으로 존재한다. 다중 우주는 결정론적이지만, 우리는 다중 우주 전체를 관찰하는 것이 아니라 한 번에 하나의 평행 우주만 관찰하기 때문에 비결정론적 행동을 확률에 따라 인지한다. 이것이 어떻게 작동하는지에 대한 것은 많은 논쟁의 대상이었다. 어떤 세계에서는 확실히 발생하는 결과에 왜 확률을 할당해야 하며, 왜 확률은 보른 규칙에 따라 주어져야 하는가?[59] 다세계 틀에서 이러한 질문에 답하는 몇 가지 방법이 제안되었지만, 그것들이 성공적인지 여부에 대한 합의는 없다.[60][61][62]
보미안 역학은 "양자 퍼텐셜"로 인한 힘을 추가하는 대가로 양자역학을 결정론적으로 만들기 위해 재구성한다. 이것은 각 물리적 계에 파동 함수뿐만 아니라 비국소적 안내 방정식에 따라 결정론적으로 진화하는 실제 위치도 부여한다. 물리적 계의 진화는 항상 슈뢰딩거 방정식과 안내 방정식에 의해 주어진다.[63]
파동 함수에 물리적 의미가 부여되려면, 파동 함수의 공간 부분이 2차 적분 가능해야 한다.
:
적분 가능성 조건은 파동 함수에 적절한 경계 조건을 부과함으로써 만족된다. 일반적으로 파동 함수의 규격화 조건
:
을 만족하는 것이 비물리적인 해가 아닌 해로 채택된다.
잘 알려져 있듯이, 파동 함수의 규격화 조건은 닫힌 양자계에서의 전역적인 확률 보존 법칙으로 해석된다. 확률 해석에 기반한 일반적인 양자론에서는 시간이 진행되어도 확률이 보존되어야 한다. 즉, 어떤 경우에도 모든 사건의 확률의 합계는 100% (= 1)이 되어야 한다. 이 사실과 보른의 규칙에 의한 확률의 구하는 방법(상태 벡터와 그 쌍대 벡터의 곱으로부터 구해짐)으로부터, 상태 벡터의 시간 진행은 유니터리 변환이어야 함을 알 수 있다. 슈뢰딩거 방정식을 풀면 "상태 벡터의 시간 진행은 유니터리 변환이다"라는 것이 유도된다. 따라서 양자계의 시간 진행에 대한 기본적인 요구( 원리)는 슈뢰딩거 그림으로 기술하는 경우, 이 슈뢰딩거 방정식을 채택하여 출발하는 경우가 많다. 하지만 다른 "시간 진행 연산자가 만족해야 하는 조건"을 기본적인 요구로 하여 출발하는 경우도 있다.
슈뢰딩거 방정식과 그 해는 물리학의 획기적인 발전을 가져왔다. 슈뢰딩거 방정식의 해는 당시에는 예상할 수 없었던 결론을 이끌어냈다.
슈뢰딩거 방정식은 물리량이 양자화된다(불연속적인 값만 나타난다)는 것을 예측한다. 예를 들어 에너지의 양자화가 있으며, 원자 내부의 전자 에너지는 항상 불연속적이다. 이것을 나타내는 것이 에너지 준위이며, 이는 원자 분광 분석으로 확인된다. 다른 예로 각운동량의 양자화가 있다. 이것은 초기의 보어의 원자 모형에서는 가정이었지만, 슈뢰딩거 방정식으로부터 도출되는 것이다.
하지만 모든 측정값이 양자화되는 것은 아니며, 예를 들어 위치나 운동량, 시간이나 에너지는 연속적인 범위의 값을 취할 수 있다.
고전역학에서는 입자가 항상 정해진 위치와 운동량의 조합을 갖는다. 이러한 값들은 뉴턴 역학과 일반 상대론에 따라 결정론적으로 변화한다. 그러나 양자역학에서는 입자가 정해진 물리량을 갖지 않고, 관측할 때마다 어떤 확률 분포에 따라 무작위로 측정 결과가 결정된다. 슈뢰딩거 방정식은 그 확률 분포를 예측하지만, 본질적으로 개별 관측의 정확한 결과를 예측할 수 없다. 불확정성 원리는 양자역학이 본래 갖는 불확실성의 유명한 예이다. 그것은 더 정확하게 입자의 위치를 확인하면 운동량이 애매해지고, 그 반대도 마찬가지임을 주장하고 있다. 슈뢰딩거 방정식은 입자의 파동 함수의 결정론적인 시간적 발전을 설명한다. 그러나 파동 함수를 정확히 알더라도, 그 파동 함수에 대해 수행되는 구체적인 관측의 결과를 결정할 수는 없다.
고전 물리학에서는 공을 천천히 산꼭대기로 굴리면 결국 공은 멈춰서 다시 굴러 내려온다. 이는 공이 산꼭대기에 도달하여 반대편으로 가는 데 필요한 에너지를 가지고 있지 않기 때문이다. 그러나 슈뢰딩거 방정식은 공이 산꼭대기에 도달할 만큼 충분한 에너지를 가지고 있지 않더라도 산 반대편에 도달할 작은 가능성이 존재한다고 예측한다. 이것이 터널 효과라고 불린다. 이는 불확정성 원리와 관련이 있다. 공이 산 이쪽에 있는 것처럼 보이더라도 그 위치는 불확실하며 반대편에서 확인될 가능성이 있다.
비상대론적인 슈뢰딩거 방정식은 파동 방정식이라고도 불리는 편미분 방정식의 일종이다. 그래서 입자는 파동처럼 행동한다고 자주 말해진다. 현대의 많은 해석에서는 이와 반대로, 양자 상태(즉, 파동)가 순수한 물리적 실재이며, 어떤 적절한 조건 하에서는 입자로서의 성질을 보인다고 여겨진다.
이중 슬릿 실험은 일반적으로 파동이 보이는, 직관적으로는 입자와 관련되지 않는 이상한 행동의 예로 유명하다. 어떤 장소에서는 두 개의 슬릿에서 온 파동이 서로 상쇄되고, 다른 장소에서는 강화되어 복잡한 간섭무늬가 나타난다. 직관적으로는 하나의 입자만을 발사했을 때는, 어느 한 슬릿만을 통과하여 두 슬릿에서 온 기여의 중첩이 되지 않기 때문에 간섭무늬는 나타나지 않을 것 같다.
그런데, 슈뢰딩거 방정식은 파동 방정식이므로, 하나의 입자만을 이중 슬릿에 발사했을 때에도 같은 간섭무늬가 “나타난다”(왼쪽 그림). 참고로, 간섭무늬가 나타나려면 실험을 반복해서 여러 번 수행해야 한다. 이렇게 간섭무늬가 나타나는 것은 각각의 전자가 “두 개”의 슬릿을 동시에 통과한다는 것을 보여준다. 직관과 반하는 일이지만, 이 예측은 정확하며, 이 생각으로 전자 회절과 중성자 회절을 잘 이해할 수 있고, 과학 및 공학에서 널리 사용되고 있다.
회절 외에도, 입자는 중첩과 간섭의 성질을 보인다. 중첩의 성질에 의해, 입자는 고전적으로는 다른 두 개 이상의 상태를 동시에 가질 수 있다. 예를 들어, 입자는 동시에 여러 개의 에너지를 가지거나, 다른 장소에 동시에 존재할 수 있다. 이중 슬릿 실험의 예에서는 두 개의 슬릿을 동시에 통과할 수 있는 것이다. 고전적인 이미지와 반하는 일이지만 이 중첩 상태는 하나의 양자 상태로 남아 있다.
13. 분류
슈뢰딩거 방정식은 그 형태에 따라 여러 종류로 분류된다.
하나의 분류는 시간 의존성으로, 시간에 의존하는 슈뢰딩거 방정식과 시간에 의존하지 않는 슈뢰딩거 방정식이 있다. '''시간에 의존하는 슈뢰딩거 방정식'''(Time-dependent Schrödinger equation; TDSE)은 파동 함수의 시간적 변화를 기술하는 방정식이며, 파동 함수의 변화 방식은 파동 함수에 작용하는 해밀토니안에 의해 결정된다. 해석역학에서 해밀토니안은 계의 에너지에 대응하는 함수였지만, 양자역학에서는 에너지 고유 상태를 결정하는 작용소이다.[64]
'''시간에 의존하지 않는 슈뢰딩거 방정식'''(Time-independent Schrödinger equation; TISE)은 해밀토니안의 고유값 방정식이다. 시간에 의존하지 않는 슈뢰딩거 방정식은 계의 에너지가 일정하게 유지되는 닫힌 계에 대한 파동 함수를 결정한다.
슈뢰딩거 방정식의 또 다른 분류로는 방정식의 선형성이 있다. 일반적으로 선형인 슈뢰딩거 방정식은 단순히 슈뢰딩거 방정식이라고 불린다. 선형인 슈뢰딩거 방정식은 동차 방정식이기 때문에, 방정식의 해가 되는 파동 함수의 선형 결합도 또한 방정식의 해가 된다.
'''비선형 슈뢰딩거 방정식'''(non-linear Schrödinger equation; NLS)은 일반적인 슈뢰딩거 방정식에서 해밀토니안에 해당하는 부분이 파동 함수 자체에 의존하는 형태의 방정식이다. 슈뢰딩거 방정식에 비선형성이 나타나는 것은 예를 들어, 여러 입자가 상호 작용하는 계에 대해, 상호 작용 포텐셜을 평균장 근사함으로써 단일 입자에 대한 포텐셜로 대체하는 것에 의한 것이다. 상호 작용 포텐셜이 구해야 할 파동 함수 자체에 의존하는 단일체 포텐셜이 되는 경우, 방정식은 비선형이 된다(자세한 내용은 예를 들어 하트리-포크 방정식, 그로스-피타예프스키 방정식 등을 참조). 본 항에서는 주로 선형인 슈뢰딩거 방정식에 대해 설명한다.
참조
[1]
서적
Introduction to Quantum Mechanics (2nd ed.)
Prentice Hall
[2]
뉴스
Physicist Erwin Schrödinger's Google doodle marks quantum mechanics work
https://www.theguard[...]
2013-08-13
[3]
논문
An Undulatory Theory of the Mechanics of Atoms and Molecules
http://home.tiscali.[...]
[4]
서적
A history of the theories of aether & electricity. 2: The modern theories, 1900 – 1926
Dover Publ
1989
[5]
서적
Mastering Quantum Mechanics: Essentials, Theory, and Applications
MIT Press
[6]
서적
The Principles of Quantum Mechanics
Clarendon Press
[7]
서적
Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology
Springer
[8]
서적
Mathematische Grundlagen der Quantenmechanik
Springer
[8]
서적
Mathematical Foundations of Quantum Mechanics
Princeton University Press
[9]
서적
The Theory of Groups and Quantum Mechanics
Dover
[9]
서적
Gruppentheorie und Quantenmechanik
S. Hirzel Verlag
[10]
서적
Quantum Theory for Mathematicians
Springer
[11]
서적
Principles of Quantum Mechanics
Kluwer Academic/Plenum Publishers
[12]
서적
Quantum Computing: A Gentle Introduction
MIT Press
2011-03-04
[13]
웹사이트
Chapter 6: Symmetries
https://courses.wash[...]
2021-01-01
[14]
서적
Modern Quantum Mechanics
Cambridge University Press
2017
[15]
서적
Modern quantum mechanics
Cambridge University Press
2021
[16]
논문
Hilbert Space Structures on the Solution Space of Klein-Gordon Type Evolution Equations
2003-01-07
[17]
논문
Student understanding of quantum mechanics at the beginning of graduate instruction
http://aapt.scitatio[...]
2008-03-01
[18]
논문
Atom optics
Elsevier BV
[19]
서적
Quantum Mechanics
John Wiley & Sons
[20]
서적
Physical Chemistry
Oxford University Press
[21]
서적
Solid State Physics
John Wiley & Sons
[22]
서적
A Modern Approach to Quantum Mechanics
University Science Books
[23]
서적
Physics for Scientists and Engineers – with Modern Physics
Freeman
[24]
서적
Introduction to Elementary Particles
https://books.google[...]
Wiley-VCH
2011-06-27
[25]
서적
The theory of open quantum systems
https://books.google[...]
Oxford University Press
[26]
서적
Statistical mechanics
https://books.google[...]
Springer
[27]
서적
Conceptual Foundations of Quantum Physics
Springer US
[28]
논문
Schrödinger representation and Casimir effect in renormalizable quantum field theory
https://dx.doi.org/1[...]
1981-07-06
[29]
논문
Functional Schrödinger equation for scalar QED
https://link.aps.org[...]
1992-03-15
[30]
서적
Quantum Field Theory of Point Particles and Strings
https://www.worldcat[...]
Perseus Books
1992
[31]
논문
The Schrödinger equation in quantum field theory
http://link.springer[...]
1994-05-01
[32]
서적
Lectures Of Sidney Coleman On Quantum Field Theory
World Scientific Publishing
2018-11-08
[33]
서적
Quantum Field Theory
https://www.worldcat[...]
Cambridge University Press
[34]
논문
Recherches sur la théorie des quanta
http://tel.archives-[...]
[35]
논문
A pioneer remembered: biographical notes about Arthur Constant Lunn
https://match.pmf.kg[...]
[36]
논문
Alan Sokal's Hoax and A. Lunn's Theory of Quantum Mechanics
[37]
서적
Radiant Science, Dark Politics
https://archive.org/[...]
University of California Press
[38]
서적
Collected papers
Friedrich Vieweg und Sohn
[39]
서적
Encyclopaedia of Physics
VHC publishers
[40]
서적
Atombau und Spektrallinien
Friedrich Vieweg und Sohn
[41]
서적
The Old Quantum Theory
https://archive.org/[...]
Pergamon Press
[42]
뉴스
The Lone Ranger of Quantum Mechanics
https://www.nytimes.[...]
2020-10-13
[43]
서적
Collected Papers on Wave Mechanics
American Mathematical Society
[44]
논문
Quantisierung als Eigenwertproblem; von Erwin Schrödinger
http://gallica.bnf.f[...]
[45]
서적
Schrödinger: Life and Thought
Cambridge University Press
[46]
서적
Philosophy of Quantum Mechanics: The interpretations of quantum mechanics in historical perspective
https://archive.org/[...]
Wiley-Interscience
[47]
논문
Schrödinger's original struggles with a complex wave function
http://aapt.scitatio[...]
2020-06-00
[48]
논문
The Present situation in Quantum Mechanics
https://www.jstor.or[...]
Proceedings of the American Philosophical Society
[49]
서적
Quantum Theory: Concepts and Methods
Kluwer
[50]
서적
The Interpretation of Quantum Mechanics
Princeton University Press
[51]
간행물
Stanford Encyclopedia of Philosophy
Metaphysics Research Lab, Stanford University
[52]
서적
Epistemological and Experimental Perspectives on Quantum Physics
Springer Science+Business Media
[53]
논문
Rovelli's World
http://link.springer[...]
2010-04-00
[54]
간행물
Stanford Encyclopedia of Philosophy
Metaphysics Research Lab, Stanford University
[55]
서적
Many Worlds? Everett, Quantum Theory and Reality
Oxford University Press
[56]
서적
The Interpretation of Quantum Mechanics: Dublin Seminars (1949–1955) and other unpublished essays
OxBow Press
1996
[57]
서적
Schrödinger's Philosophy of Quantum Mechanics
https://www.worldcat[...]
Springer Netherlands
1996
[58]
간행물
Stanford Encyclopedia of Philosophy
Metaphysics Research Lab, Stanford University
[59]
논문
Everettian Rationality: defending Deutsch's approach to probability in the Everett interpretation
[60]
논문
Can the statistical postulate of quantum theory be derived?—A critique of the many-universes interpretation
1973-00-00
[61]
서적
Compendium of Quantum Physics
Springer
[62]
서적
Many Worlds? Everett, Quantum Theory and Reality
Oxford University Press
[63]
간행물
Stanford Encyclopedia of Philosophy
Metaphysics Research Lab, Stanford University
[64]
문서
물리학의 文献において作用素は演算子とも呼ばれる。以下では作用素の意味で演算子という語を用いる。
[65]
문서
このようなベクトル空間ベクトルの記法をブラ・ケット記法と呼ぶ。 という形のベクトルをケットベクトル、 という形のベクトルをブラベクトルと呼ぶ。文献によっては状態ベクトルに対してブラ・ケット記法が用いられていないが、数学的に意味するところは同じである。
[66]
문서
誤解のおそれがない限り、単にプランク定数と呼ぶことが多い。
[67]
문서
古典論におけるハミルトニアンと区別する意味で、あるいは演算子であることを強調する意味で、ハミルトン演算子 (Hamiltonian operator) と呼ぶこともある。
[68]
문서
物理学の文献において共役演算子は を用いて示されることが多い。他に標準的な記号として で示す文献もある。
[69]
문서
ラゲールの陪多項式は文献によって異なった定義がなされる。ラゲールの陪多項式や水素原子を参照。
[70]
문서
以降の時間発展演算子の取り扱いについてはたとえば、 を参照。
[71]
서적
輻射と物質の相互作用
2002
[71]
서적
場の古典論
2008
[72]
저널
An undulatory theory of the mechanics of atoms and molecules
https://archive.org/[...]
1926-12
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

