맨위로가기

구면좌표계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

구면 좌표계는 3차원 공간의 점을 세 개의 실수로 나타내는 좌표계이다. 원점으로부터의 거리, z축과의 각도, x축과 xy평면 투영선 사이의 각도로 정의되며, 직교 좌표계, 원통 좌표계, 지리 좌표계 등 다른 좌표계와의 변환이 가능하다. 구면 좌표계는 물리학, 공학, 게임 개발 등 다양한 분야에서 구 대칭성을 가진 문제를 분석하고, 벡터 연산 및 미분, 적분에 활용된다.

더 읽어볼만한 페이지

  • 좌표계 - 데카르트 좌표계
    데카르트 좌표계는 르네 데카르트가 고안한 좌표계로, 다양한 차원의 공간에서 점의 위치를 나타내며, 2차원에서는 x축과 y축, 3차원에서는 직교하는 세 평면으로 확장되고, 고차원에서는 실수 튜플을 사용한다.
  • 좌표계 - 극좌표계
    극좌표계는 평면 위의 점을 극점으로부터의 거리 *r*과 극축으로부터의 각도 *θ*로 나타내는 2차원 좌표계로, 데카르트 좌표계와 달리 점을 무한히 많은 방식으로 표현할 수 있으며, 삼각함수를 통해 데카르트 좌표계와 상호 변환이 가능하고, 항해, 천문학, 공학 등에서 활용되며 원운동이나 궤도 운동, 방사형 대칭 시스템 모델링에 유용하다.
구면좌표계
개요
종류좌표계
차원3차원
좌표동경 (r)
편각 (θ)
방위각 (φ)
기호(r, θ, φ)
정의
동경 (r)원점으로부터의 거리 (r ≥ 0)
편각 (θ)z축으로부터의 각도 (0 ≤ θ ≤ π)
방위각 (φ)x축으로부터의 각도 (-π < φ ≤ π or 0 ≤ φ < 2π)
좌표 변환
직교 좌표계 → 구면 좌표계

구면 좌표계 → 직교 좌표계

응용
분야천문학
지리학
물리학
항해

2. 정의

구면좌표계에서 점 P의 좌표 (r, \theta, \phi)는 다음과 같이 정의된다.[1]


  • \color{Blue} r : 원점으로부터 P까지의 거리.
  • \color{Blue} \theta : z축의 양의 방향으로부터 원점과 P가 이루는 직선까지의 각.
  • \color{Blue} \phi : x축의 양의 방향으로부터 원점과 P가 이루는 직선을 xy평면에 투영시킨 직선까지의 각.


섬네일


구면좌표계에서는 좌표값에 따라 한 점을 여러 좌표가 가리키는 경우가 있으므로, 각 변수의 범위를 보통 다음과 같이 제한한다.

:r \ge 0

:0 \le \theta \le \pi

:0 \le \phi < 2\pi

고정된 원점으로부터의 반지름 거리는 "반지름", "반경선", 또는 "반경 좌표"라고도 한다. 극각은 "경사각", "천정각", "법선 각", 또는 "여위도"라고 부를 수 있다. "경사각" 대신 "고도각"을 사용할 수 있는데, 이는 기준 평면과 반경선 사이에서 위쪽으로 측정된다. 즉, 기준 평면에서 위쪽(양의 z축 방향)으로 반경선까지 측정된다. "우울각"은 고도각의 음수이다.

지리 좌표계의 표기법에 따르면, 위치는 위도, 경도, 고도(고도)로 측정된다.

3. 표기법

국제 표준 기구(ISO)의 지침(ISO 31-11)에 따라 물리학에서는 (r, \theta, \phi) 표기법을 사용한다. 여기서 r은 원점으로부터의 거리, \theta는 천정각(천정과 이루는 각도), \phi는 방위각을 나타낸다.[1]

반면, (미국의) 수학에서는 (r, \theta, \phi) 또는 (\rho, \theta, \phi) 표기법을 사용하며, \theta와 \phi의 의미가 물리학과 반대이다. 즉, \rho 또는 r은 원점으로부터의 거리, \theta는 방위각, \phi는 천정각을 의미한다.[8][1]

'''수학적 표기법'''. 구면 좌표는 일반적으로 반지름 거리 r, 방위각 \theta, 극각 \phi로 표현된다. 물리학적 표기법과 비교하여 \theta와 \phi의 의미가 바뀌어 있다.


이러한 기호의 사용과 튜플 좌표의 순서는 여러 소스와 학문 분야에서 다를 수 있다.[1] 한국의 일부 자료에서는 ISO 표기법과 다른 표기법이 혼용되어 사용될 수 있으므로, 기호의 의미를 확인하는 데 특별한 주의를 기울여야 한다.

주요 규칙[2]
좌표 집합 순서해당 지역 지리 방향
(Z, X, Y)		오른손/왼손
(r, \theta_{inc}, \phi_{az,right})(U, S, E)오른손
(r, \phi_{az,right}, \theta_{el})(U, E, N)오른손
(r, \theta_{el}, \phi_{az,right})(U, N, E)왼손



'''참고:''' 동쪽 (E), 북쪽 (N), 위쪽 (U). (U, S, E)의 경우 로컬 방위각 각도는 S에서 E로 반시계 방향으로 측정된다.

4. 다른 좌표계와의 변환

구면좌표계는 다른 3차원 좌표계와 변환될 수 있다.

구면 좌표 삼중항(또는 튜플) <math>(r,θ,φ)</math>영어는 3차원 공간의 단일 점을 지정한다. 그러나 단일 점은 무한히 많은 동등한 구면 좌표를 가질 수 있다. 각도를 변경하지 않고 각도 측정값에 완전한 회전을 여러 번 더하거나 뺄 수 있기 때문이다. 음의 반지름 거리를 사용하는 것도 가능한데, <math>(-r,θ,φ)</math>영어는 , , 모든 값에 대해 <math>(r,θ+180°,φ)</math>영어 또는 <math>(r,90°-θ,φ+180°)</math>영어와 동일하다. 또한, <math>(r,-θ,φ)</math>영어는 <math>(r,θ,φ+180°)</math>영어와 동일하다.

각 점에 대해 고유한 구면 좌표 집합을 정의하려면 각 좌표의 범위를 제한해야 한다. 일반적인 선택은 다음과 같다.


  • 반지름 거리:
  • 극각: 또는
  • 방위각: 또는


하지만 방위각 는 구간 대신 반열린 구간 또는 라디안으로 제한되기도 하는데, 이는 지리적 경도에 대한 표준 규칙이다.

극각 의 범위는 이며, 이는 고도 범위 와 같다. 지리학에서 위도는 고도에 해당한다.

이러한 제한에도 불구하고 극각(경사)이 0° 또는 180° (고도가 −90° 또는 +90°)이면 방위각은 임의적이며, 이 0이면 방위각과 극각 모두 임의적이다. 좌표를 고유하게 정의하기 위해 이 경우 임의 좌표를 0으로 설정하는 규칙을 사용하기도 한다.

구면 좌표계와 직교 좌표계, 원통 좌표계 간의 변환은 각각 하위 섹션을 참조하라.

지리 좌표계는 구면 좌표계와 유사하지만, 경사각 대신 위도를 사용하며, 범위는 에서 사이이고 적도 평면에서 북쪽으로 회전한다. 위도에서 90°를 뺀 극각은 0°에서 180°까지의 범위를 가지며 지리학에서 여위도라고 한다. 지구 또는 기타 고체 천체의 위치에서 기준 평면은 일반적으로 자전축에 수직인 평면으로 간주된다. 지구상의 특정 위치의 방위각(경도, λ영어)은 IERS 기준 자오선과 같은 기준 자오선에서 동쪽 또는 서쪽으로 도 단위로 측정된다. 따라서 경도의 범위는 에서 사이이며, "동" 또는 "서"로 표시된다.

지리학자들은 반경 거리() 대신 수직 기준 위 또는 아래의 고도를 사용하며, 이는 평균 해수면을 기준으로 할 수 있다. 필요한 경우, 반경 거리는 고도에 지구의 반지름(약 6360km})을 더하여 계산할 수 있다.

4. 1. 직교 좌표계

구면 좌표계는 3차원 공간의 점을 나타내는 좌표계 중 하나로, 직교 좌표계와 서로 변환할 수 있다.
구면 좌표계에서 직교 좌표계로 변환구면 좌표계의 점 (r, θ, φ)는 다음과 같은 공식으로 직교 좌표계 (x, y, z)로 변환할 수 있다.

  • x = r sin θ cos φ
  • y = r sin θ sin φ
  • z = r cos θ


여기서 r은 원점으로부터의 거리, θ는 z축과 이루는 각(경사각), φ는 x축과 이루는 각(방위각)이다.
직교 좌표계에서 구면 좌표계로 변환직교 좌표계의 점 (x, y, z)는 다음과 같은 공식으로 구면 좌표계 (r, θ, φ)로 변환할 수 있다.

  • r = √(x² + y² + z²)
  • θ = arccos(z / √(x² + y² + z²))
  • φ = sgn(y) arccos(x / √(x² + y²))


여기서 sgn(y)는 부호 함수로, y가 양수이면 1, 음수이면 -1, 0이면 0을 반환한다.

φ = arctan(y/x)

arctan는 (x, y)의 사분면을 고려하여 정의한다.
특이점z축 상에서는 x와 y가 모두 0이므로 φ 값이 정해지지 않는다. 또한, 원점에서는 x, y, z가 모두 0이므로 θ와 φ 값이 모두 정해지지 않는다. 이러한 특이점에서는 값을 정의할 수 없다.

4. 2. 원통 좌표계

원통 좌표 (축 반지름 ''ρ'', 방위각 ''φ'', 고도 ''z'')는 다음 공식으로 구면 좌표 (중심 반지름 ''r'', 경사 ''θ'', 방위각 ''φ'')로 변환할 수 있다.

:r=\sqrt{\rho^2+z^2}

:{\theta}=\operatorname{arctan}\frac{\rho}{z}=\operatorname{arccos}\frac{z}{\sqrt{\rho^2+z^2}}

:{\varphi}=\varphi \quad

반대로, 구면 좌표는 다음 공식으로 원통 좌표로 변환할 수 있다.

: \rho = r \sin \theta \,

: \varphi = \varphi \,

: z = r \cos \theta \,

이 공식들은 두 좌표계가 동일한 원점과 기준 평면을 가지며, 동일한 축에서 동일한 방향으로 방위각 \varphi를 측정하고, 구면 각 \theta가 원통 z 축으로부터의 경사각임을 가정한다.

4. 3. 지리 좌표계

지리 좌표계는 경사각 대신 위도를 사용하며, 범위는 이고 적도 평면에서 북쪽으로 회전한다. 위도는 지구 중심에서 측정되는 지심 위도({\psi}, q, {\varphi}', {\varphi}_{c}, {\varphi}_{g}로 표시) 또는 관찰자의 수직선에서 측정되는 측지 위도(일반적으로 {\varphi}로 표시)일 수 있다.

위도에서 90°를 뺀 극각은 0에서 180°까지의 범위를 가지며 지리학에서 여위도라고 한다.

지구 또는 기타 고체 천체의 위치에서 기준 평면은 일반적으로 자전축에 수직인 평면으로 간주된다. 지구상의 특정 위치의 방위각(경도, {\lambda}로 표시)은 IERS 기준 자오선과 같은 기준 자오선에서 동쪽 또는 서쪽으로 도 단위로 측정된다. 따라서 경도의 범위는 이며, "동" 또는 "서"로 표시된다.

지리학자들은 반경 거리({r}) 대신 수직 기준 위 또는 아래의 고도를 사용하며, 이는 평균 해수면을 기준으로 할 수 있다. 필요한 경우, 반경 거리는 고도에 지구의 반지름(약 6360±)을 더하여 계산할 수 있다.

하지만 현대 지리 좌표계는 매우 복잡하며, 단순한 공식으로 계산된 위치는 수 킬로미터의 오차가 있을 수 있다. ''위도, 경도'' 및 ''고도''의 정확한 표준 의미는 현재 세계 측지계(WGS)에 의해 정의되며, 극에서 지구의 찌그러짐(약 21km) 및 기타 세부 사항을 고려한다.

5. 벡터 연산

구면 좌표계에서 벡터 연산은 위치 벡터의 편미분을 통해 정의되는 기저 벡터들을 사용하여 표현된다.

구면 좌표 에서 위치 벡터 의 편미분을 통해 기저 벡터를 정의하면 다음과 같다.

:\boldsymbol{e}_r =\frac{\partial\boldsymbol{x}}{\partial r},~

\boldsymbol{e}_\theta =\frac{1}{r}\frac{\partial\boldsymbol{x}}{\partial\theta},~

\boldsymbol{e}_\phi =\frac{1}{r\sin\theta}\frac{\partial\boldsymbol{x}}{\partial\phi}

이 기저 벡터들은 정규 직교 기저를 이루며, 다음과 같은 성질을 갖는다.

:| \boldsymbol{e}_r |^2 =| \boldsymbol{e}_\theta |^2

=| \boldsymbol{e}_\phi |^2 =1

:\boldsymbol{e}_r\cdot \boldsymbol{e}_\theta

=\boldsymbol{e}_r\cdot \boldsymbol{e}_\phi

=\boldsymbol{e}_\theta\cdot \boldsymbol{e}_\phi =0

3차원 공간에서 벡터곱을 사용하여 구면 좌표계의 단위 벡터 간의 관계를 나타낼 수 있다.

:\boldsymbol{e}_r\times \boldsymbol{e}_\theta =\boldsymbol{e}_\phi,~

\boldsymbol{e}_\phi\times \boldsymbol{e}_r =\boldsymbol{e}_\theta,~

\boldsymbol{e}_\theta\times \boldsymbol{e}_\phi =\boldsymbol{e}_r

임의의 벡터장 는 다음과 같이 성분 표시된다.

:A_r =\boldsymbol{e}_r \cdot \boldsymbol{A},~

A_\theta =\boldsymbol{e}_\theta \cdot \boldsymbol{A},~

A_\phi =\boldsymbol{e}_\phi \cdot \boldsymbol{A}

:\boldsymbol{A} =A_r \boldsymbol{e}_r +A_\theta \boldsymbol{e}_\theta +A_\phi \boldsymbol{e}_\phi

벡터장의 미분은 다음과 같이 주어진다.

:\frac{\partial\boldsymbol{A}}{\partial r}

=\frac{\partial A_r}{\partial r} \boldsymbol{e}_r

+\frac{\partial A_\theta}{\partial r} \boldsymbol{e}_\theta

+\frac{\partial A_\phi}{\partial r} \boldsymbol{e}_\phi

:\frac{\partial\boldsymbol{A}}{\partial\theta}

=\left( \frac{\partial A_r}{\partial\theta} -A_\theta \right) \boldsymbol{e}_r

+\left( \frac{\partial A_\theta}{\partial\theta} +A_r\right) \boldsymbol{e}_\theta

+\frac{\partial A_\phi}{\partial\theta} \boldsymbol{e}_\phi

:\frac{\partial\boldsymbol{A}}{\partial\phi}

=\left( \frac{\partial A_r}{\partial\phi}


  • A_\phi\sin\theta \right) \boldsymbol{e}_r

+\left( \frac{\partial A_\theta}{\partial\phi}

  • A_\phi\cos\theta \right) \boldsymbol{e}_\theta

+\left( \frac{\partial A_\phi}{\partial\phi}

+A_r\sin\theta +A_\theta\cos\theta \right) \boldsymbol{e}_\phi



스칼라장 의 구배는

:df =(\mathrm{grad}\, f)\cdot d\boldsymbol{x}

로 정의되는 벡터장이다.

구면 좌표계에서 스칼라장 의 구배는 다음과 같다.

:\mathrm{grad}\, f =\boldsymbol{e}_r \frac{\partial f}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \frac{\partial f}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \frac{\partial f}{\partial\phi}

벡터 미분 연산자

:\nabla =\boldsymbol{e}_r \frac{\partial}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \frac{\partial}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \frac{\partial}{\partial\phi}

를 사용하면,

:\mathrm{grad}\, f =\nabla f

로 쓸 수 있다.

벡터장 의 발산은

:\boldsymbol{A}\cdot d\boldsymbol{S} =(\operatorname{div} \boldsymbol{A})\, dV

로 정의되는 스칼라장이다.

구면 좌표계에서 벡터장의 발산은 다음과 같다.

:\operatorname{div} \boldsymbol{A}

=\frac{1}{r^2} \frac{\partial(r^2A_r)}{\partial r}

+\frac{1}{r\sin\theta} \frac{\partial(A_\theta\sin\theta)}{\partial\theta}

+\frac{1}{r\sin\theta} \frac{\partial A_\phi}{\partial\phi}

벡터 미분 연산자를 사용하면

:\begin{align}

\mathrm{div}\, \boldsymbol{A} &= \nabla\cdot \boldsymbol{A} \\

&=\boldsymbol{e}_r\cdot\frac{\partial\boldsymbol{A}}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \cdot\frac{\partial\boldsymbol{A}}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \cdot\frac{\partial\boldsymbol{A}}{\partial\phi} \\

&= \left( \frac{\partial A_r}{\partial r} +\frac{2}{r} A_r\right)

+\frac{1}{r} \left( \frac{\partial A_\theta}{\partial\theta} +A_\theta\cot\theta \right)

+\frac{1}{r\sin\theta} \frac{\partial A_\phi}{\partial\phi} \\

&=\frac{1}{r^2} \frac{\partial(r^2A_r)}{\partial r}

+\frac{1}{r\sin\theta} \frac{\partial(A_\theta\sin\theta)}{\partial\theta}

+\frac{1}{r\sin\theta} \frac{\partial A_\phi}{\partial\phi}

\end{align}

로 쓸 수 있다.

5. 1. 단위 벡터

구면 좌표계의 단위 벡터


각 단위벡터의 직교좌표계 표현은 다음과 같다.

= \begin{bmatrix} \sin \theta \cos \phi \\ \sin \theta \sin \phi \\ \cos \theta \end{bmatrix}

|-

! \hat{\mathbf{\theta}}

| \frac{\frac{d\mathbf{r}}{d\theta}}{\left|\frac{d\mathbf{r}}{d\theta}\right|} = \begin{bmatrix} \cos \theta \cos \phi \\ \cos \theta \sin \phi \\ -\sin \theta \end{bmatrix}

|-

! \hat{\mathbf{\phi}}

| \frac{\frac{d\mathbf{r}}{d\phi}}{\left|\frac{d\mathbf{r}}{d\phi}\right|} = \begin{bmatrix} -\sin\phi \\ \cos\phi \\ 0 \end{bmatrix}

|}

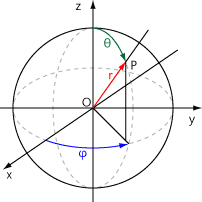
Iyanaga|이야나가영어 (1977)에서 언급한 '물리학적 표기법'에서 극좌표 \theta가 양의 z 축으로부터의 기울기라고 가정하면, (r, \theta, \varphi)에서 (r + dr, \theta + d\theta, \varphi + d\varphi)까지의 무한소 변위에 대한 선요소는 다음과 같다.

:\mathrm{d}\mathbf{r} = \mathrm{d}r\,\hat{\mathbf r} + r\,\mathrm{d}\theta \,\hat{\boldsymbol\theta } + r \sin{\theta} \, \mathrm{d}\varphi\,\mathbf{\hat{\boldsymbol\varphi}},

여기서

\hat{\mathbf{r}} \frac{\frac{d\mathbf{r}}{dr}}{\left>\frac{d\mathbf{r}}{dr}\right|}
\hat{\mathbf r}\sin \theta \cos \varphi \,\hat{\mathbf x} + \sin \theta \sin \varphi \,\hat{\mathbf y} + \cos \theta \,\hat{\mathbf z}
\hat{\boldsymbol\theta} \cos \theta \cos \varphi \,\hat{\mathbf x} + \cos \theta \sin \varphi \,\hat{\mathbf y} - \sin \theta \,\hat{\mathbf z}
\hat{\boldsymbol\varphi} - \sin \varphi \,\hat{\mathbf x} + \cos \varphi \,\hat{\mathbf y}



는 각각 r, \theta, \varphi가 증가하는 방향의 국소 직교 단위 벡터이고, \hat{\mathbf x}, \hat{\mathbf y}, \hat{\mathbf z}는 데카르트 좌표계의 단위 벡터이다.

이 오른손 좌표계로의 선형 변환은 회전 행렬이다.

:R = \begin{pmatrix}

\sin\theta\cos\varphi&\sin\theta\sin\varphi&\hphantom{-}\cos\theta\\

\cos\theta\cos\varphi&\cos\theta\sin\varphi&-\sin\theta\\


  • \sin\varphi&\cos\varphi &\hphantom{-}0

\end{pmatrix}.



이 행렬은 직교 행렬이며, 역행렬은 단순히 전치 행렬이다. 따라서 데카르트 단위 벡터는 다음과 같이 구면 단위 벡터와 관련된다.

:\begin{bmatrix}\mathbf{\hat x} \\ \mathbf{\hat y} \\ \mathbf{\hat z} \end{bmatrix}

= \begin{bmatrix} \sin\theta\cos\varphi & \cos\theta\cos\varphi & -\sin\varphi \\

\sin\theta\sin\varphi & \cos\theta\sin\varphi & \hphantom{-}\cos\varphi \\

\cos\theta & -\sin\theta & \hphantom{-}0 \end{bmatrix}

\begin{bmatrix} \boldsymbol{\hat{r}} \\ \boldsymbol{\hat\theta} \\ \boldsymbol{\hat\varphi} \end{bmatrix}

각 단위 벡터의 미분은 다음과 같다.

r에 대한 미분\theta에 대한 미분\phi에 대한 미분
\hat{r}의 미분\frac{\partial \hat{r} }{\partial r} = 0\frac{\partial \hat{r} }{\partial \theta} = \hat{\theta}\frac{\partial \hat{r} }{\partial \phi} = \sin \theta \hat{\phi}
\hat{\theta}의 미분\frac{\partial \hat{\theta} }{\partial r} = 0\frac{\partial \hat{\theta} }{\partial \theta} = -\hat{r}\frac{\partial \hat{\theta} }{\partial \phi} = \cos \theta \hat{\phi}
\hat{\phi}의 미분\frac{\partial \hat{\phi} }{\partial r} = 0\frac{\partial \hat{\phi} }{\partial \theta} = 0\frac{\partial \hat{\phi} }{\partial \phi} = -\cos \theta \hat{\theta} - \sin \theta \hat{r}


5. 2. 미분, 적분

면적 요소는 다음과 같다.

:d영어'''a''' = r2 sin θ d영어θ d영어φ

부피 요소는 다음과 같다.

:dV영어 = r2 sin θ dr d영어θ d영어φ

기울기는 다음과 같다.

:\nabla = \hat{r} \frac{\partial}{\partial r} + \hat{\theta} \frac{1}{r}\frac{\partial}{\partial \theta} + \hat{\phi}

\frac{1}{r \sin \theta}\frac{\partial}{\partial \phi}

발산은 다음과 같다.

:\nabla \cdot \mathbf{F} = \frac{1}{r^2}\frac{\partial}{\partial r} r^2 F_r + \frac{1}{r \sin \theta} \frac{\partial}{\partial \theta} \sin \theta F_\theta + \frac{1}{r \sin \theta} \frac{\partial}{\partial \phi} F_\phi

회전은 다음과 같다.

:\nabla \times F = \frac{1}{r^2 \sin \theta} \begin{vmatrix} \hat{r} & r\hat{\theta} & r \sin \theta \hat{\phi} \\ \\

{\frac{\partial}{\partial r}} & {\frac{\partial}{\partial \theta}} & {\frac{\partial}{\partial \phi}} \\

\\ F_r & rF_\theta & r\sin\theta F_\phi \end{vmatrix}

라플라시안은 다음과 같다.

:\nabla^2 = \frac{1}{r^2}\frac{\partial}{\partial r} r^2 \frac{\partial}{\partial r} + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \sin \theta\frac{\partial}{\partial \theta} + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^2}{\partial \phi^2}

(r, \theta, \varphi)에서 (r + dr, \theta + d\theta, \varphi + d\varphi)까지의 무한소 변위에 대한 선요소는 다음과 같다.

:\mathrm{d}\mathbf{r} = \mathrm{d}r\,\hat{\mathbf r} + r\,\mathrm{d}\theta \,\hat{\boldsymbol\theta } + r \sin{\theta} \, \mathrm{d}\varphi\,\mathbf{\hat{\boldsymbol\varphi}}

여기서

:\begin{align}

\hat{\mathbf r} &= \sin \theta \cos \varphi \,\hat{\mathbf x} +

\sin \theta \sin \varphi \,\hat{\mathbf y} + \cos \theta \,\hat{\mathbf z}, \\

\hat{\boldsymbol\theta} &= \cos \theta \cos \varphi \,\hat{\mathbf x} +

\cos \theta \sin \varphi \,\hat{\mathbf y} - \sin \theta \,\hat{\mathbf z}, \\

\hat{\boldsymbol\varphi} &= - \sin \varphi \,\hat{\mathbf x} +

\cos \varphi \,\hat{\mathbf y}

\end{align}

는 각각 r, \theta, \varphi가 증가하는 방향의 국소 직교 단위 벡터이고, \hat{\mathbf x}, \hat{\mathbf y}, \hat{\mathbf z}는 데카르트 좌표계의 단위 벡터이다.

미분 선요소를 증명하는 공식의 일반적인 형태는 다음과 같다.[5]

:\mathrm{d}\mathbf{r} =

\sum_i \frac{\partial \mathbf{r}}{\partial x_i} \,\mathrm{d}x_i =

\sum_i \left|\frac{\partial \mathbf{r}}{\partial x_i}\right|

\frac{\frac{\partial \mathbf{r}}{\partial x_i}}{\left|\frac{\partial \mathbf{r}}{\partial x_i}\right|} \, \mathrm{d}x_i =

\sum_i \left|\frac{\partial \mathbf{r}}{\partial x_i}\right| \,\mathrm{d}x_i \, \hat{\boldsymbol{x}}_i

즉, \mathbf r의 변화는 개별 좌표의 변화에 해당하는 개별 변화로 분해된다.

이를 현재 경우에 적용하려면, \mathbf r이 각 좌표에 따라 어떻게 변하는지를 계산해야 한다. 사용된 표기법에서,

:\mathbf{r} = \begin{bmatrix}

r \sin\theta \, \cos\varphi \\

r \sin\theta \, \sin\varphi \\

r \cos\theta

\end{bmatrix}

, x1=r, x2=θ, x3=φ 이다.

따라서,

:

\frac{\partial\mathbf r}{\partial r} = \begin{bmatrix}

\sin\theta \, \cos\varphi \\

\sin\theta \, \sin\varphi \\

\cos\theta

\end{bmatrix}=\mathbf{\hat r}, \quad

\frac{\partial\mathbf r}{\partial \theta} = \begin{bmatrix}

r \cos\theta \, \cos\varphi \\

r \cos\theta \, \sin\varphi \\

  • r \sin\theta

\end{bmatrix}=r\,\hat{\boldsymbol\theta }, \quad

\frac{\partial\mathbf r}{\partial \varphi} = \begin{bmatrix}

  • r \sin\theta \, \sin\varphi \\

\hphantom{-}r \sin\theta \, \cos\varphi \\

0

\end{bmatrix}

=

r \sin\theta\,\mathbf{\hat{\boldsymbol\varphi}}



이다.

원하는 계수는 이 벡터의 크기이다.[5]

:

\left|\frac{\partial\mathbf r}{\partial r}\right| = 1, \quad

\left|\frac{\partial\mathbf r}{\partial \theta}\right| = r, \quad

\left|\frac{\partial\mathbf r}{\partial \varphi}\right| = r \sin\theta



상수 반경 r에서 구면의 표면에서 \theta에서 \theta + d\theta까지, \varphi에서 \varphi + d\varphi까지의 면적분은 다음과 같다.

:

\mathrm{d}S_r =

\left\|\frac{\partial {\mathbf r}}{\partial \theta} \times \frac{\partial {\mathbf r}}{\partial \varphi}\right\| \mathrm{d}\theta \,\mathrm{d}\varphi =

\left|r {\hat \boldsymbol\theta} \times r \sin \theta {\boldsymbol\hat \varphi} \right|\mathrm{d}\theta \,\mathrm{d}\varphi=

r^2 \sin\theta \,\mathrm{d}\theta \,\mathrm{d}\varphi



따라서 미분 입체각은 다음과 같다.

:\mathrm{d}\Omega = \frac{\mathrm{d}S_r}{r^2} = \sin\theta \,\mathrm{d}\theta \,\mathrm{d}\varphi

극각 \theta가 상수인 표면(원점을 꼭짓점으로 하는 원뿔)에서의 표면 요소는 다음과 같다.

:\mathrm{d}S_\theta = r \sin\theta \,\mathrm{d}\varphi \,\mathrm{d}r

방위각 \varphi가 상수인 표면(수직 반평면)에서의 표면 요소는 다음과 같다.

:\mathrm{d}S_\varphi = r \,\mathrm{d}r \,\mathrm{d}\theta

r에서 r + dr, \theta에서 \theta + d\theta, \varphi에서 \varphi + d\varphi까지의 부피 요소는 편미분의 야코비 행렬의 행렬식에 의해 지정된다.

:

J =\frac{\partial(x,y,z)}{\partial(r,\theta,\varphi)}

=\begin{pmatrix}

\sin\theta\cos\varphi & r\cos\theta\cos\varphi & -r\sin\theta\sin\varphi\\

\sin\theta\sin\varphi & r\cos\theta\sin\varphi & \hphantom{-}r\sin\theta\cos\varphi\\

\cos\theta & -r\sin\theta & \hphantom{-}0

\end{pmatrix}



즉,

:

\mathrm{d}V = \left|\frac{\partial(x, y, z)}{\partial(r, \theta, \varphi)}\right| \,\mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi=

r^2 \sin\theta \,\mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi =

r^2 \,\mathrm{d}r \,\mathrm{d}\Omega



따라서, 예를 들어, 함수 f(r, \theta, \varphi)는 삼중 적분에 의해 \mathbb{R}^3의 모든 점에서 적분될 수 있다.

:\int\limits_0^{2\pi} \int\limits_0^\pi \int\limits_0^\infty f(r, \theta, \varphi) r^2 \sin\theta \,\mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi

이 시스템에서 델 연산자는 스칼라장에 대한 기울기 및 라플라시안에 대해 다음과 같은 표현을 제공한다.

:\begin{align}

\nabla f &= {\partial f \over \partial r}\hat{\mathbf r}

+ {1 \over r}{\partial f \over \partial \theta}\hat{\boldsymbol\theta}

+ {1 \over r\sin\theta}{\partial f \over \partial \varphi}\hat{\boldsymbol\varphi}, \\[8pt]

\nabla^2 f &= {1 \over r^2}{\partial \over \partial r} \left(r^2 {\partial f \over \partial r}\right) + {1 \over r^2 \sin\theta}{\partial \over \partial \theta} \left(\sin\theta {\partial f \over \partial \theta}\right)

+ {1 \over r^2 \sin^2\theta}{\partial^2 f \over \partial \varphi^2} \\[8pt]

& = \left(\frac{\partial^2}{\partial r^2} + \frac{2}{r} \frac{\partial}{\partial r}\right) f + {1 \over r^2 \sin\theta}{\partial \over \partial \theta} \left(\sin\theta \frac{\partial}{\partial \theta}\right) f + \frac{1}{r^2 \sin^2\theta}\frac{\partial^2}{\partial \varphi^2}f

\end{align}

이는 벡터장의 발산 및 회전에 대해 다음과 같은 표현을 제공한다.

:\nabla \cdot \mathbf{A}

= \frac{1}{r^2}{\partial \over \partial r}\left( r^2 A_r \right)

+ \frac{1}{r \sin\theta}{\partial \over \partial\theta} \left( \sin\theta A_\theta \right)

+ \frac{1}{r \sin \theta} {\partial A_\varphi \over \partial \varphi}

:\begin{align}

\nabla \times \mathbf{A} = {}

& \frac{1}{r\sin\theta} \left[{\partial \over \partial \theta} \left( A_\varphi\sin\theta \right)

  • {\partial A_\theta \over \partial \varphi}\right] \hat{\mathbf r} \\[4pt]

& {} + \frac 1 r \left[{1 \over \sin\theta}{\partial A_r \over \partial \varphi}

  • {\partial \over \partial r} \left( r A_\varphi \right) \right] \hat{\boldsymbol\theta} \\[4pt]

& {} + \frac 1 r \left[{\partial \over \partial r} \left( r A_\theta \right)

  • {\partial A_r \over \partial \theta}\right] \hat{\boldsymbol\varphi}

\end{align}

구면 좌표 (r, \theta, \phi)에서 직교 좌표 (x, y, z)로의 변환은

:\begin{cases}

x = r\sin\theta\, \cos\phi \\

y = r\sin\theta\, \sin\phi \\

z = r\cos\theta

\end{cases}

로 주어진다.

구면 좌표 (r, \theta, \phi)에서 직교 좌표 (x, y, z)로의 변환 식을 미분하면

:\begin{cases}

dx = \sin\theta\, \cos\phi\, dr +r\cos\theta\, \cos\phi\, d\theta -r\sin\theta\, \sin\phi\, d\phi \\

dy = \sin\theta\, \sin\phi\, dr +r\cos\theta\, \sin\phi\, d\theta +r\sin\theta\, \cos\phi\, d\phi \\

dz = \cos\theta\, dr -r\sin\theta\, d\theta

\end{cases}

를 얻고, 야코비 행렬과 야코비 행렬식은

:\begin{align}

\frac{\partial(x,y,z)}{\partial(r,\theta,\phi)}

&=\begin{pmatrix}

\sin\theta\, \cos\phi & r\cos\theta\, \cos\phi & -r\sin\theta\, \sin\phi \\

\sin\theta\, \sin\phi & r\cos\theta\, \sin\phi & r\sin\theta\, \cos\phi \\

\cos\theta & -r\sin\theta & 0

\end{pmatrix} \\

&=\begin{pmatrix}

\cos\phi & -\sin\phi & 0 \\

\sin\phi & \cos\phi & 0 \\

0 & 0 & 1

\end{pmatrix}

\begin{pmatrix}

\sin\theta & \cos\theta & 0 \\

0 & 0 & 1 \\

\cos\theta & -\sin\theta & 0

\end{pmatrix}

\begin{pmatrix}

1 & 0 & 0 \\

0 & r & 0 \\

0 & 0 & r\sin\theta

\end{pmatrix}

\end{align}

:\left| \frac{\partial(x,y,z)}{\partial(r,\theta,\phi)} \right| =r^2 \sin\theta

이 된다. 따라서 구면 좌표로 나타낸 체적소는

:dV =dx\, dy\, dz =r^2 \sin\theta\, dr\, d\theta\, d\phi

가 된다. 또한, 선소의 제곱은

:ds^2 =dx^2 +dy^2 +dz^2 =dr^2 +r^2d\theta^2 +r^2\sin^2\theta\, d\phi^2

가 된다.

표준 기저 \mathbf{e}_x, \mathbf{e}_y, \mathbf{e}_z를 사용하면, 위치 벡터의 미분은

:\begin{align}

d\boldsymbol{x} &=\boldsymbol{e}_x\, dx +\boldsymbol{e}_y\, dy +\boldsymbol{e}_z\, dz \\

&=\begin{pmatrix}

\boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z

\end{pmatrix}

\begin{pmatrix}

dx \\ dy \\ dz

\end{pmatrix} \\

&=\begin{pmatrix}

\boldsymbol{e}_x & \boldsymbol{e}_y & \boldsymbol{e}_z

\end{pmatrix}

\frac{\partial(x,y,z)}{\partial(r,\theta,\phi)}

\begin{pmatrix}

dr \\ d\theta \\ d\phi

\end{pmatrix}

\end{align}

이 되므로, 구체적으로

:\begin{cases}

\boldsymbol{e}_r =\boldsymbol{e}_x \sin\theta\, \cos\phi +\boldsymbol{e}_y \sin\theta\, \sin\phi +\boldsymbol{e}_z \cos\theta \\

\boldsymbol{e}_\theta =\boldsymbol{e}_x \cos\theta\, \cos\phi +\boldsymbol{e}_y \cos\theta\, \sin\phi -\boldsymbol{e}_z \sin\theta \\

\boldsymbol{e}_\phi =-\boldsymbol{e}_x \sin\phi +\boldsymbol{e}_y \cos\phi

\end{cases}

로 표현된다.

표준 내적을 생각하면

:| \boldsymbol{e}_r |^2 =| \boldsymbol{e}_\theta |^2

=| \boldsymbol{e}_\phi |^2 =1

:\boldsymbol{e}_r\cdot \boldsymbol{e}_\theta

=\boldsymbol{e}_r\cdot \boldsymbol{e}_\phi

=\boldsymbol{e}_\theta\cdot \boldsymbol{e}_\phi =0

이 되어, 이것들은 정규 직교 기저이다.

곡면 위의 점이 u, v로 매개변수화될 때, 면적소 벡터는

:\begin{aligned}

d\boldsymbol{S}

&=\frac{\partial\boldsymbol{x}}{\partial u}\times \frac{\partial\boldsymbol{x}}{\partial v}\, du\wedge dv \\

&=\boldsymbol{e}_r\, r^2\sin\theta\, d\theta\wedge d\phi

+\boldsymbol{e}_\theta\, r\sin\theta\, d\phi\wedge dr

+\boldsymbol{e}_\phi\, r\, dr\wedge d\theta

\end{aligned}

로 주어진다.

임의의 벡터장 \mathbf{A}는

:A_r =\boldsymbol{e}_r \cdot \boldsymbol{A},~

A_\theta =\boldsymbol{e}_\theta \cdot \boldsymbol{A},~

A_\phi =\boldsymbol{e}_\phi \cdot \boldsymbol{A}

:\boldsymbol{A} =A_r \boldsymbol{e}_r +A_\theta \boldsymbol{e}_\theta +A_\phi \boldsymbol{e}_\phi

에 의해 성분 표시된다.

벡터장의 구면 좌표에 의한 미분은

:\frac{\partial\boldsymbol{A}}{\partial r}

=\frac{\partial A_r}{\partial r} \boldsymbol{e}_r

+\frac{\partial A_\theta}{\partial r} \boldsymbol{e}_\theta

+\frac{\partial A_\phi}{\partial r} \boldsymbol{e}_\phi

:\frac{\partial\boldsymbol{A}}{\partial\theta}

=\left( \frac{\partial A_r}{\partial\theta} -A_\theta \right) \boldsymbol{e}_r

+\left( \frac{\partial A_\theta}{\partial\theta} +A_r\right) \boldsymbol{e}_\theta

+\frac{\partial A_\phi}{\partial\theta} \boldsymbol{e}_\phi

:\frac{\partial\boldsymbol{A}}{\partial\phi}

=\left( \frac{\partial A_r}{\partial\phi}

  • A_\phi\sin\theta \right) \boldsymbol{e}_r

+\left( \frac{\partial A_\theta}{\partial\phi}

  • A_\phi\cos\theta \right) \boldsymbol{e}_\theta

+\left( \frac{\partial A_\phi}{\partial\phi}

+A_r\sin\theta +A_\theta\cos\theta \right) \boldsymbol{e}_\phi



로 주어진다.

스칼라장 f(\mathbf{x}) 의 구배는

:df =(\mathrm{grad}\, f)\cdot d\boldsymbol{x}

로 정의되는 벡터장이다.

벡터 미분 연산자를

:\nabla =\boldsymbol{e}_r \frac{\partial}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \frac{\partial}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \frac{\partial}{\partial\phi}

로 정하면

:\mathrm{grad}\, f =\nabla f

로 쓸 수 있다.

벡터장 \mathbf{A}의 발산은

:\boldsymbol{A}\cdot d\boldsymbol{S} =(\operatorname{div} \boldsymbol{A})\, dV

로 정의되는 스칼라장이다.

벡터 미분 연산자를 사용하면

:\begin{align}

\mathrm{div}\, \boldsymbol{A} &= \nabla\cdot \boldsymbol{A} \\

&=\boldsymbol{e}_r\cdot\frac{\partial\boldsymbol{A}}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \cdot\frac{\partial\boldsymbol{A}}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \cdot\frac{\partial\boldsymbol{A}}{\partial\phi} \\

&= \left( \frac{\partial A_r}{\partial r} +\frac{2}{r} A_r\right)

+\frac{1}{r} \left( \frac{\partial A_\theta}{\partial\theta} +A_\theta\cot\theta \right)

+\frac{1}{r\sin\theta} \frac{\partial A_\phi}{\partial\phi} \\

&=\frac{1}{r^2} \frac{\partial(r^2A_r)}{\partial r}

+\frac{1}{r\sin\theta} \frac{\partial(A_\theta\sin\theta)}{\partial\theta}

+\frac{1}{r\sin\theta} \frac{\partial A_\phi}{\partial\phi}

\end{align}

로 쓸 수 있다.

벡터장 \mathbf{A}의 회전은

:\boldsymbol{A}\cdot d\boldsymbol{x} =(\operatorname{rot}\boldsymbol{A})\cdot d\boldsymbol{S}

로 정의되는 벡터장이다.

벡터 미분 연산자를 사용하면

:\begin{align}

\mathrm{rot}\, \boldsymbol{A} &=\nabla\times\boldsymbol{A} \\

&=\boldsymbol{e}_r\times\frac{\partial\boldsymbol{A}}{\partial r}

+\frac{\boldsymbol{e}_\theta}{r} \times\frac{\partial\boldsymbol{A}}{\partial\theta}

+\frac{\boldsymbol{e}_\phi}{r\sin\theta} \times\frac{\partial\boldsymbol{A}}{\partial\phi} \\

&=\frac{\boldsymbol{e}_r}{r\sin\theta} \left[

\frac{\partial(A_\phi\sin\theta)}{\partial\theta} -\frac{\partial A_\theta}{\partial\phi} \right]

+\frac{\boldsymbol{e}_\theta}{r} \left[

\frac{1}{\sin\theta}\frac{\partial A_r}{\partial\phi}

  • \frac{\partial(rA_\phi)}{\partial r} \right]

+\frac{\boldsymbol{e}_\phi}{r} \left[

\frac{\partial(rA_\theta)}{\partial r}

  • \frac{\partial A_r}{\partial\theta} \right]

\end{align}

가 된다.

6. 운동학

구면 좌표계에서 점 또는 입자의 위치는 다음과 같이 표현된다.[7]

:\mathbf{r} = r \mathbf{\hat r} .

이때 속도는 다음과 같다.[7]

:\mathbf{v} = \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} = \dot{r} \mathbf{\hat r} + r\,\dot\theta\,\hat{\boldsymbol\theta } + r\,\dot\varphi \sin\theta\,\mathbf{\hat{\boldsymbol\varphi}}

가속도는 다음과 같이 나타낼 수 있다.[7]

:

\begin{align}

\mathbf{a} = {} & \frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t} \\[1ex]

= {} & \hphantom{+}\; \left( \ddot{r} - r\,\dot\theta^2 - r\,\dot\varphi^2\sin^2\theta \right)\mathbf{\hat r} \\

& {} + \left( r\,\ddot\theta + 2\dot{r}\,\dot\theta - r\,\dot\varphi^2\sin\theta\cos\theta \right) \hat{\boldsymbol\theta } \\

& {} + \left( r\ddot\varphi\,\sin\theta + 2\dot{r}\,\dot\varphi\,\sin\theta + 2 r\,\dot\theta\,\dot\varphi\,\cos\theta \right) \hat{\boldsymbol\varphi}

\end{align}



각운동량은 질량 m에 대해 다음과 같이 표현된다.

: \mathbf{L} =

\mathbf{r} \times \mathbf{p} = \mathbf{r} \times m\mathbf{v} = m r^2 \left(- \dot\varphi \sin\theta\,\mathbf{\hat{\boldsymbol\theta}} + \dot\theta\,\hat{\boldsymbol\varphi }\right)



이에 해당하는 각운동량 연산자는 다음과 같다.

: \mathbf{L}= -i\hbar ~\mathbf{r} \times \nabla =i \hbar \left(\frac{\hat{\boldsymbol{\theta}}}{\sin(\theta)} \frac{\partial}{\partial\phi} - \hat{\boldsymbol{\phi}} \frac{\partial}{\partial\theta}\right).

토크는 다음과 같이 주어진다.[7]

: \mathbf{\tau} =

\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} = \mathbf{r} \times \mathbf{F} = -m \left(2r\dot{r}\dot{\varphi}\sin\theta + r^2\ddot{\varphi}\sin{\theta} + 2r^2\dot{\theta}\dot{\varphi}\cos{\theta} \right)\hat{\boldsymbol\theta} + m \left(r^2\ddot{\theta} + 2r\dot{r}\dot{\theta} - r^2\dot{\varphi}^2\sin\theta\cos\theta \right) \hat{\boldsymbol{\varphi}}



운동 에너지는 다음과 같이 표현된다.[7]

: E_k =

\frac{1}{2}m \left[ \left(\dot{r}\right)^2 + \left(r\dot{\theta}\right)^2 + \left(r\dot{\varphi}\sin\theta\right)^2 \right]


7. 응용

구면 좌표계는 구 대칭성을 가진 다양한 물리적 문제에 적용된다. 2차원 데카르트 좌표계가 평면에서 유용하듯이, 2차원 구면 좌표계는 구의 표면에서 유용하다. 예를 들어, 방정식 ''x''2 + ''y''2 + ''z''2 = ''c''2로 ''데카르트 좌표''로 설명되는 구는 간단한 방정식 ''r'' = ''c''로 ''구면 좌표''로 나타낼 수 있다.

이러한 단순성은 회전 행렬과 같은 객체를 처리할 때 유용하다. 구면 좌표는 점에 대해 어느 정도의 대칭성을 가진 시스템을 분석하는 데 유용하며, 부피 적분(구 내부), 집중된 질량 또는 전하 주변의 잠재 에너지장, 행성의 대기에서 전 세계 날씨 시뮬레이션 등이 이에 해당한다.

스피커 출력 패턴의 3차원 모델링을 통해 성능을 예측할 수 있다. 패턴이 주파수에 따라 크게 변화하므로, 다양한 주파수에서 얻은 여러 개의 극좌표 플롯이 필요하다. 극좌표 플롯은 많은 스피커가 낮은 주파수에서 전방향성을 나타내는 경향이 있음을 보여준다.

구면 좌표의 중요한 응용 분야는 많은 물리적 문제에서 발생하는 두 개의 편미분 방정식—라플라스와 헬름홀츠 방정식—에서 변수 분리를 제공한다. 이러한 방정식의 해의 각도 부분은 구면 조화 함수의 형태를 취한다. 또 다른 응용 분야는 인체 공학적 설계로, r은 고정된 사람의 팔 길이이고 각도는 팔이 뻗어 나가는 방향을 설명한다. 구면 좌표계는 또한 플레이어의 위치를 중심으로 카메라를 회전시키기 위해 3D 게임 개발에서도 일반적으로 사용된다[4].

8. 타원 좌표계

타원 좌표계도 참조

수정된 구면 좌표계를 사용하여 데카르트 좌표계에서 타원체를 다루는 것도 가능하다.

P를 다음과 같은 등위 집합으로 지정된 타원체라고 하자.

:ax^2 + by^2 + cz^2 = d.

ISO 규칙(즉, 물리학의 경우: ''반경'' , ''경사'' , ''방위각'' )에서 P의 점에 대한 수정된 구면 좌표는 다음 공식을 사용하여 데카르트 좌표계 에서 얻을 수 있다.

:\begin{align}

x &= \frac{1}{\sqrt{a}} r \sin\theta \, \cos\varphi, \\

y &= \frac{1}{\sqrt{b}} r \sin\theta \, \sin\varphi, \\

z &= \frac{1}{\sqrt{c}} r \cos\theta, \\

r^{2} &= ax^2 + by^2 + cz^2.

\end{align}

무한소 부피 요소는 다음과 같이 주어진다.

:

\mathrm{d}V = \left|\frac{\partial(x, y, z)}{\partial(r, \theta, \varphi)}\right| \, dr\,d\theta\,d\varphi =

\frac{1}{\sqrt{abc}} r^2 \sin \theta \,\mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi =

\frac{1}{\sqrt{abc}} r^2 \,\mathrm{d}r \,\mathrm{d}\Omega.



제곱근 계수는 행렬식의 속성에서 비롯되며, 상수를 열에서 빼낼 수 있다.

:

\begin{vmatrix}

ka & b & c \\

kd & e & f \\

kg & h & i

\end{vmatrix} =

k \begin{vmatrix}

a & b & c \\

d & e & f \\

g & h & i

\end{vmatrix}.


참조

[1] 웹사이트 ISO 80000-2:2019 Quantities and units – Part 2: Mathematics https://www.iso.org/[...] 2020-08-12
[2] 서적 Duffett-Smith, P and Zwart, J
[3] 웹사이트 Spherical Coordinates http://mathworld.wol[...] MathWorld 2010-01-15
[4] 웹사이트 Video Game Math: Polar and Spherical Notation https://aie.edu/arti[...] 2022-02-16
[5] 웹사이트 Line element (dl) in spherical coordinates derivation/diagram https://math.stackex[...] 2011-10-21
[6] 웹사이트 Distance between two points in spherical coordinates https://math.stackex[...]
[7] 서적 Keplerian ellipses : the physics of the gravitational two-body problem https://www.worldcat[...] 2019
[8] 문서 이러한 표시는 ''φ''가 2차원 [[극좌표]], 3차원 [[원통좌표]]의 방위각과 호환된다는 장점이 있다.


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com