맨위로가기

내접원

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

내접원은 다각형의 모든 변에 접하는 원을 의미하며, 내접원의 중심은 내심이라고 한다. 내접원을 갖는 다각형은 외접 다각형이라고 불린다. 삼각형의 경우, 세 각의 이등분선의 교점이 내심이며, 모든 삼각형은 내접원을 가진다. 사각형이 내접원을 가지려면 AB + CD = BC + DA 조건을 만족해야 하며, 연꼴, 마름모 등이 해당한다. 다각형의 내접원 반지름은 2 × 면적 ÷ 둘레로 구할 수 있다. 내접원은 다각형 내부에 포함되는 가장 큰 원이며, 내심은 모든 내각 이등분선의 교점이다. 내접원과 외접원의 관계, 내심 삼각형, 제르곤 점, 제르곤 삼각형, 애덤스 원 등 관련 개념이 존재한다.

더 읽어볼만한 페이지

  • 다각형 - 폴리아몬드
    폴리아몬드는 정삼각형을 이어 붙여 만든 도형으로, 삼각형 개수에 따라 n-아몬드라 불리며 조합론에서 종류와 개수를 파악하는 것이 중요하고, 평행 이동, 회전, 반사에 따라 자유형, 단면형, 고정형으로 분류되며, 폴리오미노, 폴리헥스와 유사하고 보드 게임의 구성 요소로 활용된다.
  • 다각형 - 대각선
    대각선은 다각형이나 다면체에서 서로 인접하지 않은 꼭짓점을 연결하는 선분이며, 다각형은 변의 개수에 따라, 다면체는 면의 위치에 따라 대각선의 개수와 종류가 달라지고, 기하학에서는 데카르트 곱의 부분 집합으로 정의되기도 한다.
  • 원 (기하학) - 대원
    구면기하학에서 대원은 구의 중심을 지나는 평면과 구의 교선으로, 유클리드 공간의 직선에 대응하며, 서로 대극점이 아닌 두 점을 잇는 최단 거리인 대원 거리를 정의하고, 자오선이나 적도처럼 항해, 천문학 등 다양한 분야에서 응용된다.
  • 원 (기하학) - 반지름
    반지름은 원의 중심에서 원 위의 점까지의 거리로, 원의 지름과 둘레, 넓이 계산에 사용될 뿐 아니라 정다각형 외접원, 그래프 이론, 극좌표계 등 다양한 분야에서 활용되며, 여러 도형의 반지름을 구하는 공식이 존재하고 한국의 교육, 건축, 디자인 분야에서도 널리 쓰인다.
  • 삼각 기하학 - 피타고라스 삼조
    피타고라스 삼조는 a² + b² = c²을 만족하는 양의 정수 세 쌍 (a, b, c)이며, 특히 서로소인 세 정수로 이루어진 경우를 원시 피타고라스 삼조라고 한다.
  • 삼각 기하학 - 페르마 점
    페르마 점은 삼각형 세 꼭짓점까지의 거리 합이 최소가 되는 점으로, 120도 이상의 각이 없는 삼각형에서는 내부에 존재하며 ∠AFB=∠BFC=∠CFA=120도를 만족하고, 120도 이상의 각이 있는 삼각형에서는 가장 큰 각의 꼭짓점이 되며, 작도를 통해 찾을 수 있고 기하중앙값, 슈타이너 나무 문제 등과 관련된다.
내접원
개요
삼각형 내접원의 작도
삼각형 내접원의 작도
정의삼각형의 세 변에 모두 접하는 원
중심내심
반지름내반지름
성질
내심삼각형의 세 내각의 이등분선의 교점
내접원의 넓이πr², 여기서 r은 내반지름
내반지름삼각형의 넓이를 s로 나누면 구할 수 있으며, s는 삼각형 둘레의 절반
공식r = A/s (A는 삼각형의 넓이, s는 반둘레)
삼각형과의 관계
정삼각형내접원은 외접원과 중심이 같고, 반지름은 외접원의 1/2
직각삼각형내반지름 r = (a + b - c)/2 (a, b는 직각변, c는 빗변)
일반적인 삼각형내접원은 삼각형의 넓이와 반둘레를 이용하여 계산 가능
사각형과의 관계
외접사각형모든 변에 접하는 원을 갖는 사각형. 마름모, 연꼴, 외접 사각형 등이 있다.
성질외접 사각형은 두 쌍의 대변의 길이의 합이 같다.
다각형과의 관계
내접다각형모든 변에 접하는 원을 갖는 다각형
정다각형모든 정다각형은 내접원을 가진다.
응용
기하학적 문제 해결삼각형, 사각형, 다각형의 성질을 이용한 문제 해결에 활용
디자인다양한 디자인 요소로 활용

2. 정의

다각형의 모든 변에 접하는 원을 이 다각형의 '''내접원'''이라고 한다. 내접원의 중심을 '''내심'''이라고 한다. 내접원을 갖는 다각형을 '''외접 다각형'''(tangential polygon, circumscribed polygon영어)이라고 한다.

3. 성질

다각형의 모든 변에 접하는 원을 이 다각형의 '''내접원'''이라고 한다. 내접원의 중심을 '''내심'''이라고 한다. 내접원을 갖는 다각형을 '''외접 다각형'''이라고 한다.

(내접원을 갖는) 다각형의 내접원은 그 내부에 포함되는 가장 큰 원이다. (내접원을 갖는) 다각형의 내심은 모든 내각 이등분선의 교점이다. (내접원을 갖는) 다각형의 내심과 모든 변 사이의 거리는 같으며, 이는 내접원의 반지름이다.

모든 삼각형과 정다각형은 내접원을 갖는다. 정삼각형의 내심은 외심, 무게 중심, 수심과 일치한다. 삼각형의 내심은 방심 삼각형의 수심이다. 포이어바흐 정리에 따르면, 삼각형의 내접원 및 세 방접원은 구점원과 접한다.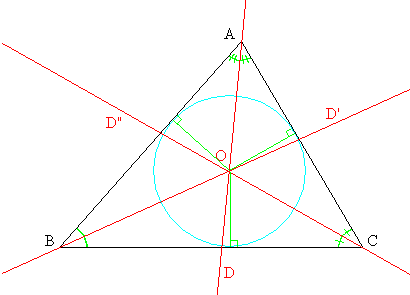

삼각형의 내접원과 각의 이등분선




변 ABC로 구성된 삼각형에 대해, A를 "해당 삼각형의 내심으로부터의 수선"과의 교점에서 분할하여 만들어지는 길이 각각의 변을 갖는 정사각형끼리의 면적차(절댓값)는, A의 길이와 "B와 C의 길이의 차(절댓값)"의 곱과 같다.


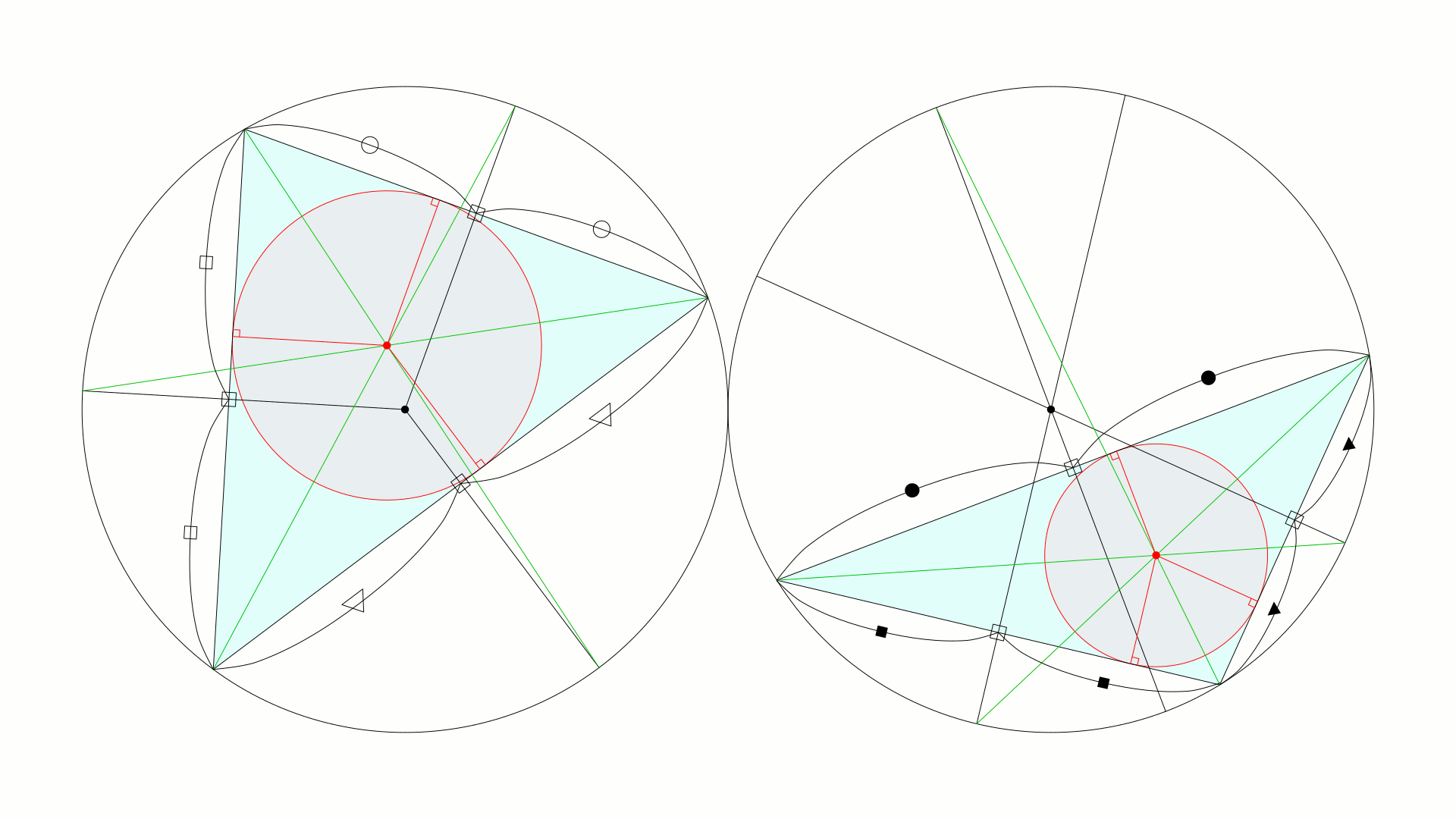
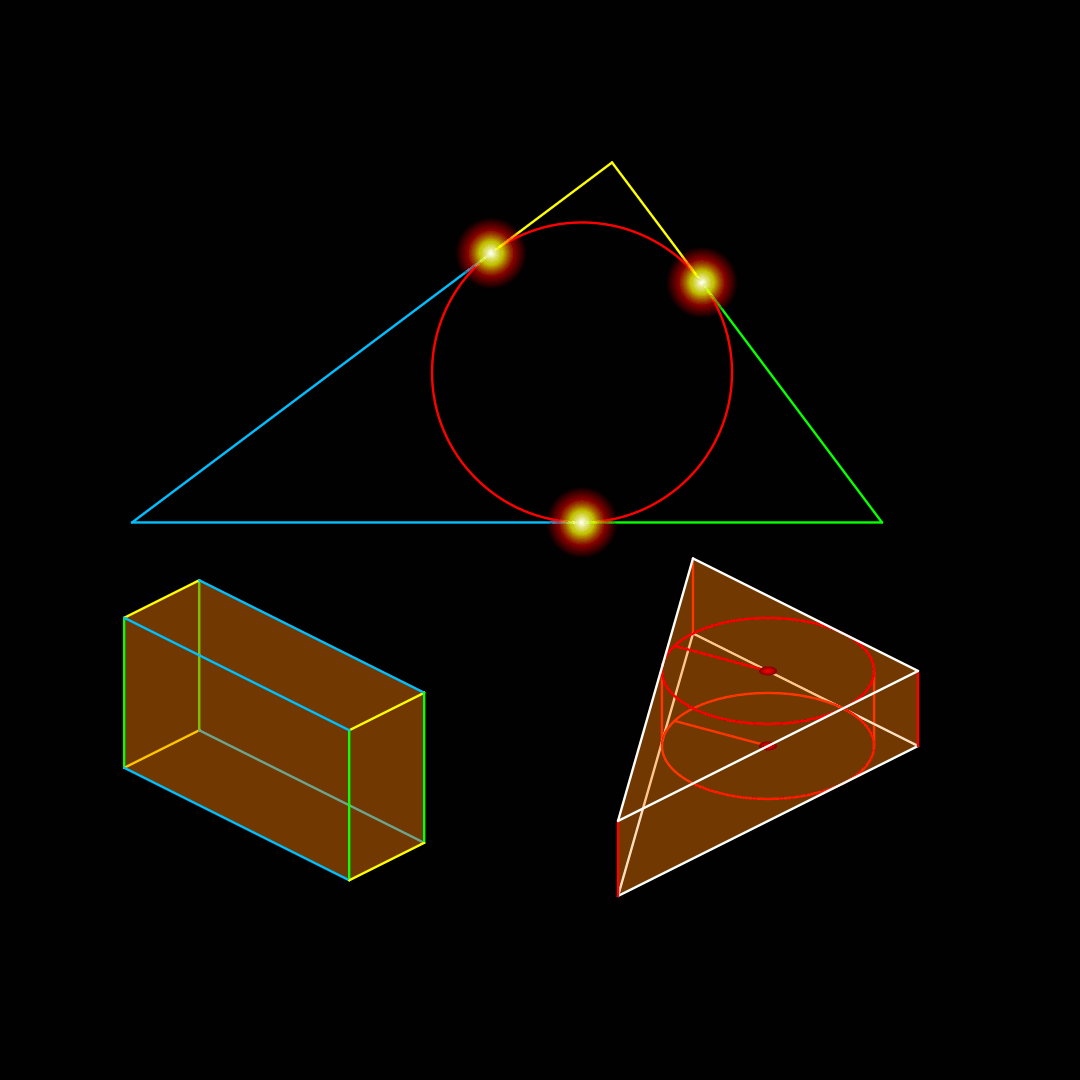
삼각형의 내접원의 반지름은, 『세 종류의 "꼭짓점부터 내접원과의 접점까지의 거리"의 변을 갖는 직육면체』와 같은 체적의 『같은 삼각형을 면으로 갖는 기둥』의 높이와 같다.


삼각형에서, 어떤 꼭짓점과 그 대변의 수직 이등분선의 연장선상에 있는 외접원(원주)과의 교점(대변에서 봐서 삼각형의 바깥쪽)을 잇는 직선은, 그 꼭짓점의 내각을 이등분하는 직선이 된다.(그림에 녹색 직선으로 표시됨. 이들의 교점은 해당 삼각형의 내접원의 중심이 된다.)

임의의 삼각형에 내접원이 존재한다. 내심은 3개의 각의 이등분선의 교점이다.

내접원 외에, 삼각형의 외부에 1변과 2변의 연장선에 접하는 원이 존재한다. 이를 방접원이라고 한다. 방접원은 하나의 삼각형에 대해 3개 존재한다.

3. 1. 반지름

(내접원을 갖는) 다각형의 내접원의 반지름 r은 넓이 S와 반둘레 s를 통해 다음과 같이 나타낼 수 있다.

:r=\frac Ss

삼각형의 세 변의 길이가 a, b, c, 반둘레가 s, 넓이가 S, 외접원의 반지름이 R, 방접원의 반지름이 r_A, r_B, r_C라고 할 때, 내접원의 반지름은 다음과 같다.

:\begin{align}r

&=\sqrt{\frac{(s-a)(s-b)(s-c)}s}\\

&=\frac{abc}{4sR}\\

&=\frac 1{\frac 1{r_A}+\frac 1{r_B}+\frac 1{r_C}}\\

&=r_A+r_B+r_C-4R

\end{align}

첫 등호는 헤론의 공식에 의한다.

다각형에 내접원이 존재하는 경우, 그 반지름은 다음과 같이 구할 수 있다.

: 반지름 = 2 × 면적 ÷ 둘레

3. 2. 접점과 중심각

삼각형 ABC영어의 내심을 I영어라고 하고, 내접원과 두 변 AC영어, BC영어의 접점을 각각 TB영어, TC영어라고 하고, 직선 AI영어와 TBTC영어의 교점을 P영어라고 할 때, BP영어는 AI영어의 수선이다.[1]

삼각형 ABC영어의 내접원의 A영어, B영어, C영어의 대변에서의 접점을 각각 TA영어, TB영어, TC영어라고 하고, 반둘레를 s영어, A영어, B영어, C영어의 대변의 길이를 각각 a영어, b영어, c영어라고 할 때, 다음이 성립한다.

  • ATB영어 = ATC영어 = s-a영어
  • BTC영어 = BTA영어 = s-b영어
  • CTA영어 = CTB영어 = s-c영어


삼각형 ABC영어의 내심 I영어와 꼭짓점들이 이루는 각의 크기는 다음과 같다.

  • = 90° + /2
  • = 90° + /2
  • = 90° + /2


3. 3. 외접원과의 관계

삼각형의 외접원과 내접원의 반지름을 각각 R, r라고 할 때, 내심 I와 외심 O 사이의 거리는 다음과 같다. (오일러 삼각형 정리)

:OI=\sqrt{R^2-2Rr}

특히 다음과 같은 부등식이 성립한다. (오일러의 부등식)

:R\ge 2r

삼각형 ABC의 내심을 I, 외접원의 호 BC의 중점 M이라고 할 때, 다음이 성립한다. (맨션 정리)

:MI=MB=MC

4. 삼각형의 내접원

임의의 삼각형에는 내접원이 존재한다. 내심은 3개의 각의 이등분선의 교점이다.

삼각형에서, 어떤 꼭짓점과 그 대변의 수직 이등분선의 연장선상에 있는 외접원(원주)과의 교점(대변에서 봐서 삼각형의 바깥쪽)을 잇는 직선은, 그 꼭짓점의 내각을 이등분하는 직선이 된다. (그림에 녹색 직선으로 표시됨. 이들의 교점은 해당 삼각형의 내접원의 중심이 된다.)

내접원 외에, 삼각형의 외부에 1변과 2변의 연장선에 접하는 원이 존재한다. 이를 방접원이라고 한다. 방접원은 하나의 삼각형에 대해 3개 존재한다.[1]

5. 사각형의 내접원

사각형에 내접원이 존재할 필요충분조건은 다음과 같다.


  • 모든 내각이 180도 이하
  • AB + CD = BC + DA

연꼴, 마름모 등이 이에 해당한다.

내접원의 중심과 두 대각선의 중점은 동일 직선상에 있다. (뉴턴의 정리)

내접원과 외접원을 모두 갖는 사각형을 쌍심 사각형이라고 한다.

6. 일반적인 다각형의 내접원

다각형에 내접원이 존재하는 경우, 그 반지름은 다음과 같이 구할 수 있다.

: 반지름 = 2 × 면적 ÷ 둘레

7. 관련 개념



임의의 삼각형에는 항상 내접원이 존재하며, 내심은 삼각형의 세 내각의 이등분선이 만나는 점이다. 삼각형의 한 변과 다른 두 변의 연장선에 동시에 접하는 원을 방접원이라고 하며, 하나의 삼각형에는 3개의 방접원이 존재한다.

사각형에 내접원이 존재하기 위한 필요충분조건은 다음과 같다.


  • 모든 내각이 180도 이하
  • AB + CD = BC + DA


연꼴이나 마름모 등이 이러한 조건을 만족하는 사각형에 해당한다.

뉴턴의 정리에 따르면, 내접원의 중심과 두 대각선의 중점은 동일한 직선 위에 놓인다.

쌍심 사각형은 내접원과 외접원을 모두 갖는 사각형을 의미한다. 다각형에 내접원이 존재하는 경우, 그 반지름은 다음과 같이 구할 수 있다.

: 반지름 = 2 × 면적 ÷ 둘레

7. 1. 내심 삼각형

삼각형 ABC의 내각 이등분선 AI₊|AIₐ|영어, BI₊|BIₐ|영어, CI₊|CIₐ|영어의 발 I₊|Iₐ|영어, I₋|IB|영어, I₌|IC|영어를 꼭짓점으로 하는 삼각형을 삼각형 ABC의 '''내심 삼각형'''(incentral triangle|인센트럴 트라이앵글|영어) I₊I₋I₌|IₐIBIC|영어라고 한다. 즉, 내심 삼각형은 내심의 체바 삼각형이다.

7. 2. 제르곤 점과 제르곤 삼각형

제르곤 점과 제르곤 삼각형


삼각형 ABC의 내접원과 꼭짓점 A, B, C의 대변의 접점을 각각 T_A, T_B, T_C라고 하자. 그렇다면 체바 정리에 따라 선분 AT_A, BT_B, CT_C는 한 점에서 만난다. 이 점을 삼각형 ABC의 '''제르곤 점'''(Gergonne point영어) X_7이라고 한다. 삼각형 ABC의 내접원의 세 접점 T_A, T_B, T_C를 꼭짓점으로 하는 삼각형을 삼각형 ABC의 '''제르곤 삼각형'''(Gergonne triangle영어), '''내촉 삼각형'''(intouch triangle영어) 또는 '''접촉 삼각형'''(contact triangle영어) T_AT_BT_C라고 한다. 즉, 제르곤 삼각형은 내심의 수족 삼각형이자 제르곤 점의 체바 삼각형이다.

제르곤 점은 제르곤 삼각형의 대칭 중점이다.[1]

7. 3. 애덤스 원

삼각형 ABC의 내접원과 꼭짓점 A, B, C의 대변의 접점을 각각 T_A, T_B, T_C라고 하고, 제르곤 점을 X_7라고 하자. 제르곤 점 X_7을 지나는, 제르곤 삼각형의 각 변 T_AT_B, T_BT_C, T_CT_A의 평행선 PS, RU, TQ와 원래 삼각형 ABC의 두 변 BC와 CA, CA와 AB, AB와 BC의 교점을 각각 P와 S, R와 U, T와 Q라고 하자. 그렇다면 이 6개의 교점은 한 원 위에 있다. 이 원을 삼각형 ABC의 '''애덤스 원'''(Adams’ circle영어)이라고 한다.[1] 애덤스 원은 내접원과 동심원이다.[1]

직선 UP와 QR, QR와 ST, ST와 UP의 교점을 각각 X, Y, Z라고 하자. 그렇다면 삼각형 ABC의 제르곤 점 X_7은 삼각형 XYZ의 대칭 중점이며, 삼각형 ABC의 애덤스 원은 삼각형 XYZ의 제1 르무안 원이다.[1]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com