맨위로가기

헤론 공식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

헤론 공식은 삼각형의 세 변의 길이를 이용하여 삼각형의 넓이를 계산하는 공식이다. 알렉산드리아의 헤론의 저서 《Metrica》에 증명이 제시되어 그의 이름이 붙었으며, 코사인 법칙, 피타고라스 정리, 삼각함수 등을 이용하여 다양한 방법으로 증명할 수 있다. 헤론 공식은 브라마굽타 공식, 브레치나이더 공식 등 사각형과 관련된 공식의 특별한 경우로 간주될 수 있으며, 케일리-멩거 행렬식을 통해 일반화된 형태로 표현할 수도 있다.

더 읽어볼만한 페이지

  • 넓이 - 피타고라스 정리
    피타고라스 정리는 직각삼각형에서 직각변의 제곱의 합이 빗변의 제곱과 같다는 정리로, a² + b² = c²으로 표현되며, 한 변의 길이를 계산하는 데 사용되고, 여러 지역에서 알려졌으나 피타고라스 학파에 의해 체계화되었다고 전해진다.
  • 넓이 - 카발리에리의 원리
    카발리에리의 원리는 평행한 두 직선 또는 평면 사이에서 일정한 조건을 만족하는 두 평면 도형 또는 입체의 면적이나 부피가 동일하다는 원리이며, 미적분학 발달 이전 시대에 중요한 역할을 했다.
  • 삼각형에 대한 정리 - 스튜어트 정리
    스튜어트 정리는 삼각형의 변과 체바 선분 사이의 관계를 나타내는 기하학 정리이며, 아폴로니우스 정리를 포함하고 코사인 법칙을 이용하여 증명한다.
  • 삼각형에 대한 정리 - 코사인 법칙
    코사인 법칙은 삼각형의 세 변 길이와 한 각의 코사인 값 사이의 관계를 나타내는 정리로, 두 변과 사잇각으로부터 제3의 변을 구하거나 세 변의 길이로 세 각을 구할 수 있으며, 직각삼각형의 경우 피타고라스 정리로 귀결된다.
헤론 공식
기본 정보
공식 명칭헤론의 공식
다른 이름헤론 공식
영어 명칭Heron's formula
사용 분야기하학, 수학
종류정리
공식 내용
변수a, b, c (삼각형의 세 변의 길이)
s (반둘레, (a+b+c)/2)
A (넓이)
공식A = √s(s-a)(s-b)(s-c)
설명삼각형의 세 변의 길이만 알면 넓이를 구할 수 있음.
역사
고안자헤론
최초 언급서기 60년 ~ 70년경
증명다양한 증명 방법 존재 (피타고라스 정리 이용 등)
활용
응용토지 측량, 건축 설계 등 다양한 분야에서 활용
관련 공식사인 법칙
코사인 법칙
다른 삼각형 넓이 공식들

2. 공식

삼각형의 세 변의 길이를 a, b, c라 하고, s영어 = (a+b+c)/2 (삼각형 둘레의 절반)라고 할 때, 삼각형의 넓이 S는 다음과 같이 표현된다.[2]

:S=\sqrt{s(s-a)(s-b)(s-c)}

s영어를 사용하지 않고, 다음과 같이 표현할 수도 있다.

:S=\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}

:S=\frac{1}{4}\sqrt{2(a^2 b^2+a^2c^2+b^2c^2)-(a^4+b^4+c^4)}

:S=\frac{1}{4}\sqrt{(a^2+b^2+c^2)^2-2(a^4+b^4+c^4)}

:S=\frac{1}{4}\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}

3. 역사

알렉산드리아의 헤론이 그의 저서 《Metrica》에서 증명을 제시하여 헤론의 공식이라는 이름이 붙여졌다. 하지만 현대 수학사학자들은 이 공식이 아르키메데스 시대 혹은 그 이전부터 알려졌을 가능성이 있다고 추정한다.[3][4][5] 친지우사오가 1247년에 쓴 《수학구장》에는 헤론의 공식과 동등한 공식이 수록되어 있다.[6]

4. 증명

헤론의 공식은 삼각법, 삼각형의 내심과 하나의 방심 이용,[7] 드 구아 정리의 특수한 경우(예각 삼각형의 특정 경우), 브라마굽타 공식의 특수한 경우(퇴화된 원내 사각형의 경우) 등 다양한 방법으로 증명할 수 있다.[8]

4. 1. 일반적인 방법 (코사인 법칙 이용)

코사인 법칙과 삼각함수의 항등식을 이용하여 증명하는 방법이다.

삼각형 ABC의 세 변을 a, b, c라고 하면, 이 삼각형의 넓이 S는

: S = \frac{1}{2} ab\sin C \cdots (1)

이다. 코사인 법칙을 이용하면

:\cos C = \frac{a^2+b^2- c^2}{2ab}

:\sin C = \sqrt{1-\cos^2 C } = \sqrt{\frac{4a^2 b^2 -(a^2 +b^2 - c^2)^2 }{4a^2 b^2}}

이다. 여기서 얻어진 \sin C의 값을 (1)에 대입하면,

:S = \frac{1}{4}\sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2}=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}

를 얻는다.

코사인 법칙을 적용하면 다음과 같다.

: \cos \gamma = \frac{a^2+b^2-c^2}{2ab}

이 증명에서 다음의 대수적 표현을 얻을 수 있다.

: \sin \gamma = \sqrt{1-\cos^2 \gamma} = \frac{\sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2 }}{2ab}.

밑변 a에 대한 삼각형의 높이는 b\sin\gamma이고, 따라서

:\begin{align}

A

&= \tfrac12 (\mbox{밑변}) (\mbox{높이}) \\

&= \tfrac12 ab\sin \gamma \\

&= \frac{ab}{4ab}\sqrt{4a^2 b^2 -(a^2 +b^2 -c^2)^2} \\

&= \tfrac14\sqrt{-a^4 - b^4 - c^4 + 2 a^2 b^2 + 2 a^2 c^2 + 2 b^2 c^2} \\

&= \tfrac14\sqrt{(a + b + c)(- a + b + c)(a - b + c)(a + b - c)} \\

&= \sqrt{

\left(\frac{a + b + c}{2}\right)

\left(\frac{- a + b + c}{2}\right)

\left(\frac{a - b + c}{2}\right)

\left(\frac{a + b - c}{2}\right)} \\

&= \sqrt{s(s-a)(s-b)(s-c)}.

\end{align}

이다.

삼각비, 코사인 법칙, 인수 분해를 이용한 증명도 가능하다.

△ABC에서, A, B, C의 대변 BC, CA, AB의 길이를 각각 a, b, c라 하고, A에서 변 BC에 내린 수선의 길이를 h라고 한다.

이 때 △ABC의 면적 S는,

:\begin{align}

S&=\frac{ah}{2}=\frac{ab}{2}\sin C=\frac{ab}{2}\sqrt{1-\cos^2C} \\

&=\frac{ab}{2}\sqrt{(1+\cos C)(1-\cos C)} \\

&=\frac{ab}{2}\sqrt{\left(1+\frac{a^2+b^2-c^2}{2ab}\right)\left(1-\frac{a^2+b^2-c^2}{2ab}\right)} \\

&=\frac{ab}{2}\sqrt{\frac{a^2+2ab+b^2-c^2}{2ab}\cdot\frac{-(a^2-2ab+b^2-c^2)}{2ab}} \\

&=\sqrt{\frac{(a+b)^2-c^2}{4}\cdot\frac{-[(a-b)^2-c^2]}{4}} \\

&=\sqrt{\frac{(a+b+c)(a+b-c)}{4}\cdot\frac{-(a-b+c)(a-b-c)}{4}} \\

&=\sqrt{\frac{a+b+c}{2}\cdot\frac{-a+b+c}{2}\cdot\frac{a-b+c}{2}\cdot\frac{a+b-c}{2}} \\

&=\sqrt{\frac{a+b+c}{2}\left(\frac{a+b+c}{2}-a\right)\left(\frac{a+b+c}{2}-b\right)\left(\frac{a+b+c}{2}-c\right)}

\end{align}

가 된다. 여기서,

:\frac{a+b+c}{2}=s

라고 하면,

:S=\sqrt{s(s-a)(s-b)(s-c)}

를 얻을 수 있다.[9]

4. 2. 다른 방법 (피타고라스 정리 이용)

오른쪽


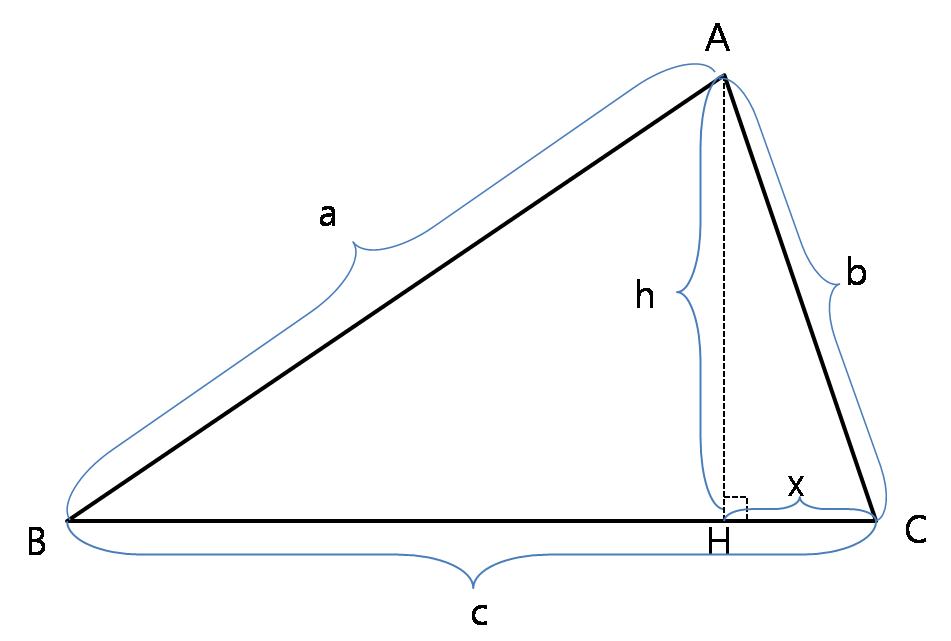
삼각형 ABC의 세 변을 a, b, c라 하고, A에서 BC에 내린 수선 AH의 길이를 h, 선분 CH의 길이를 x라 한다. 이때 각 ACB가 둔각이면 x는 음의 값을 갖는다.

피타고라스 정리에 의해 다음이 성립한다.

: x^2+h^2=b^2

: h^2 =b^2 -x^2 \cdots (2)

삼각형 AHB에 대해서도 같은 방법으로 정리하면,

: h^2 =a^2 -(c-x)^2

이를 정리하여 x에 대해 나타내면,

:x=\frac{1}{2c} (c^2 +b^2 -a^2)

이를 (2)에 대입하고 h에 대해 정리하면,

: h=\frac{1} {2c} \sqrt {(4b^2 c^2 -(c^2 +b^2 -a^2 )^2 )}

삼각형 ABC의 넓이 S는 다음과 같이 계산된다.

:S=\frac{ch}{2}= \frac {1} {2} \sqrt {4b^2 c^2 -(c^2 +b^2 -a^2 )^2}

: \therefore S=\sqrt {s(s-a)(s-b)(s-c)}

:: 단, s= \frac{a+b+c} {2}

다음 증명은 Raifaizen에 의해 주어진 것과 매우 유사하다.[10]

피타고라스 정리에 의해, b^2 = h^2 + d^2와 a^2 = h^2 + (c - d)^2이다. 이 식들을 빼면 a^2 - b^2 = c^2 - 2cd.가 된다. 이 방정식은 d를 삼각형의 변으로 표현할 수 있게 해준다.

:d = \frac{-a^2 + b^2 + c^2}{2c}.

삼각형의 높이에 대해, h^2 = b^2 - d^2.이다. 위에 주어진 공식으로 d를 대체하고 제곱차 항등식을 적용하면



\begin{align}

h^2 &= b^2-\left(\frac{-a^2 + b^2 + c^2}{2c}\right)^2 \\

&= \frac{(2bc - a^2 + b^2 + c^2)(2bc + a^2 - b^2 - c^2)}{4c^2} \\

&= \frac{\big((b + c)^2 - a^2\big)\big(a^2 - (b - c)^2\big)}{4c^2} \\

&= \frac{(b + c - a)(b + c + a)(a + b - c)(a - b + c)}{4c^2} \\

&= \frac{2(s - a) \cdot 2s \cdot 2(s - c) \cdot 2(s - b)}{4c^2} \\

&= \frac{4s(s - a)(s - b)(s -c )}{c^2}.

\end{align}



이제 이 결과를 높이로부터 삼각형의 넓이를 계산하는 공식에 적용한다.

\begin{align}

A &= \frac{ch}{2} \\

&= \sqrt{\frac{c^2}{4} \cdot \frac{4s(s - a)(s - b)(s - c)}{c^2}} \\

&= \sqrt{s(s - a)(s - b)(s - c)}.

\end{align}

4. 2. 1. 좌표평면을 이용한 증명

좌표상의 삼각형 ABC


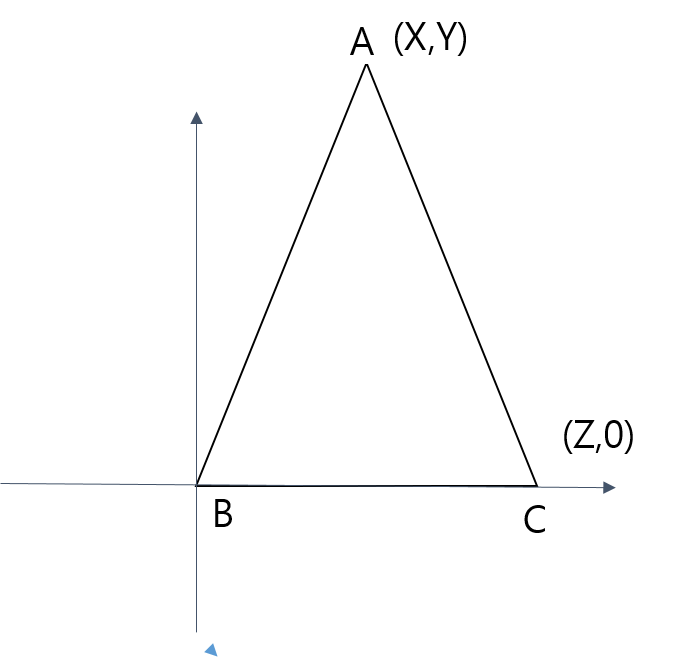
삼각형 ABC의 세 변 BC, CA, AB를 각각 a, b, c라고 하자.

오른쪽 그림처럼 B를 원점으로 하고 한 변을 X축에 놓아 좌표평면에 삼각형을 그릴 수 있다. 이때 점 C는 (Z, 0), 점 A는 (X, Y)라고 가정할 수 있다. 그러면 a=Z,b=\sqrt{(X-Z)^2+Y^2},c=\sqrt{X^2+Y^2} 이다.

이때 s=\frac{a+b+c}{2}=\frac{Z+\sqrt{(X-Z)^2+Y^2}+\sqrt{X^2+Y^2}}{2} 이다.

s-a=\frac{-Z+\sqrt{(X-Z)^2+Y^2}+\sqrt{X^2+Y^2}}{2}

s-b=\frac{Z-\sqrt{(X-Z)^2+Y^2}+\sqrt{X^2+Y^2}}{2}

s-c=\frac{Z+\sqrt{(X-Z)^2+Y^2}-\sqrt{X^2+Y^2}}{2}

\sqrt{s(s-a)(s-b)(s-c)}

=\sqrt{\frac{(-Z^2+(\sqrt{(X-Z)^2+Y^2}+\sqrt{X^2+Y^2} )^2)^2}{4}}x\sqrt{\frac{(Z^2-(\sqrt{(X-Z)^2+Y^2}-\sqrt{X^2+Y^2} )^2)^2}{4}}

=\sqrt{\frac{(2X^2+2Y^2-2XZ+2\sqrt{((X-Z)^2+Y^2)(X^2+Y^2)})}{4}} x \sqrt{\frac{(2X^2+2Y^2-2XZ-2\sqrt{((X-Z)^2+Y^2)(X^2+Y^2)})}{4}}

=\frac{\sqrt{(YZ)(YZ)}}{2}=\frac{YZ}{2}

삼각형 ABC의 넓이는 밑변인 BC와 높이를 가지고 구할 수 있다.

S=\frac{1}{2}BC\times h =\frac{1}{2}Z\times Y=\frac{YZ}{2}

=\sqrt{s(s-a)(s-b)(s-c)}

이처럼 좌표평면을 사용하면 어려운 증명이라도 계산만 복잡할 뿐, 보조선과 같은 창의적인 방식 없이도 증명할 수 있다.

4. 3. 삼각함수를 이용한 증명 (코탄젠트 법칙 이용)

, , 의 기하학적 의미. 이에 대한 자세한 내용은 코탄젠트 법칙을 참조.


삼각형의 내접원의 반지름을 r영어이라고 하면, 이 삼각형은 높이가 r영어이고 밑변이 각각 a영어, b영어, c영어인 세 개의 작은 삼각형으로 나눌 수 있다. 이 작은 삼각형들의 면적의 합은 다음과 같다.

:A = \tfrac12ar + \tfrac12br + \tfrac12cr = rs

여기서 s = \tfrac12(a + b + c)는 삼각형의 반둘레이다.

또한, 원래 삼각형은 높이가 r영어이고 밑변이 각각 s - a영어, s - b영어, s - c영어인 여섯 개의 작은 삼각형(합동인 쌍)으로 나눌 수 있다. (코탄젠트 법칙 참조) 이 작은 삼각형들의 면적의 합은 다음과 같이 나타낼 수 있다.

:\begin{align}

A &= r(s-a) + r(s-b) + r(s-c) \\

&= r^2\left(\frac{s - a}{r} + \frac{s - b}{r} + \frac{s - c}{r}\right) \\

&= r^2\left(\cot{\frac{\alpha}{2}} + \cot{\frac{\beta}{2}} + \cot{\frac{\gamma}{2}}\right) \\

&= r^2\left(\cot{\frac{\alpha}{2}} \cot{\frac{\beta}{2}} \cot{\frac{\gamma}{2}}\right)\\

&= r^2\left(\frac{s - a}{r} \cdot \frac{s - b}{r} \cdot \frac{s - c}{r}\right) \\

&= \frac{(s-a)(s-b)(s-c)}{r}.

\end{align}

위 식에서 중간 단계는 삼중 코탄젠트 항등식 \cot{\tfrac{\alpha}{2}} + \cot{\tfrac{\beta}{2}} + \cot{\tfrac{\gamma}{2}} = \cot{\tfrac{\alpha}{2}}\cot{\tfrac{\beta}{2}}\cot{\tfrac{\gamma}{2}}을 이용한 것이다. 이 항등식은 반각의 합이 \tfrac\alpha2 + \tfrac\beta2 + \tfrac\gamma2 = \tfrac\pi2이기 때문에 성립한다.

위의 두 면적 식을 결합하면 다음과 같다.

:A^2 = s(s - a)(s - b)(s - c)

따라서 헤론의 공식이 유도된다.

5. 예제

△ABC영어에서 변 a = 4, b = 13, c = 15라고 할 때, 삼각형 둘레의 절반은 s = 16 이고, s-a = 12, s-b = 3, s-c = 1이므로, 넓이는 다음과 같이 계산된다.

:\begin{align}

A &= {\textstyle \sqrt{s(s-a)(s-b)(s-c)}} \\[3mu]

&= {\textstyle \sqrt{16 \cdot 12 \cdot 3 \cdot 1 \vphantom)} } \\[3mu]

&= 24.

\end{align}

이 예에서 삼각형의 변의 길이와 넓이는 정수이므로 헤론 삼각형이다. 그러나 헤론의 공식은 변의 길이가 임의의 실수일 때도 똑같이 적용된다.

다른 예로, △ABC의 세 변의 길이를 a, b, c, 면적을 S라고 하고, a = 14, b = 13, c = 15라고 할 때, s는 다음과 같다.

:s= \frac{a+b+c}{2}= \frac{14+13+15}{2}= 21

따라서, 면적 S는 다음과 같이 계산된다.

:\begin{align}

S &= \sqrt{s(s-a)(s-b)(s-c)} = \sqrt{21 \cdot (21-14) \cdot (21-13) \cdot (21-15)} \\

&= \sqrt{21 \cdot 7 \cdot 8 \cdot 6} = 84

\end{align}

6. 수치적 안정성

헤론의 공식은 부동 소수점 연산을 사용할 때 매우 작은 각을 가진 삼각형에 대해 수치적으로 불안정하다. 안정적인 대안은 변의 길이를 a \ge b \ge c가 되도록 정렬하고 다음을 계산하는 것이다.[11][12]

:A = \tfrac14 \sqrt{\big(a + (b + c)\big) \big(c - (a - b)\big) \big(c + (a - b)\big) \big(a + (b - c)\big)}.

추가 괄호는 계산 시 수치적 안정성을 확보하기 위해 필요한 연산 순서를 나타낸다.

7. 일반화

헤론의 공식은 브라마굽타 공식(원에 내접하는 사각형의 넓이를 구하는 공식)의 특별한 경우이다. 헤론의 공식과 브라마굽타 공식은 모두 브레치나이더 공식(일반적인 사각형의 넓이를 구하는 공식)의 특별한 경우이다. 헤론의 공식은 사각형의 한 변을 0으로 설정하여 브라마굽타 공식이나 브레치나이더 공식에서 얻을 수 있다.[24][25]

헤론의 공식은 변의 길이만을 사용하여 사다리꼴의 넓이를 구하는 공식의 특수한 경우이기도 하다. 이때는 사다리꼴의 작은 평행변의 길이를 0으로 설정하여 얻는다.

데이비드 P. 로빈스는 헤론의 공식을 원에 내접하는 오각형과 육각형으로 일반화한 공식을 발견했다.[17]

구면 기하학이나 쌍곡 평면에서도 삼각형의 변의 길이를 사용하여 넓이를 구하는 공식이 존재한다.[19] 구면 삼각형의 경우, 변의 길이가 a영어, b영어, c영어이고 반둘레가 s=\tfrac12(a+b+c), 넓이가 S영어일 때 공식은 다음과 같다.



\tan^2 \frac S 4 = \tan \frac s2 \tan\frac{s-a}2 \tan\frac{s-b}2 \tan\frac{s-c}2



쌍곡 평면의 경우에는 다음 공식을 사용한다.



\tan^2 \frac S 4 = \tanh \frac s2 \tanh\frac{s-a}2 \tanh\frac{s-b}2 \tanh\frac{s-c}2.



하지만, 원에 내접하는 ''n''각형의 면적을, 그 변의 길이로부터 사칙연산과 ''k''제곱근을 취하는 연산으로 구하는 대수적인 공식은 ''n'' ≥ 5에서는 존재하지 않는 것으로 알려져 있다.

7. 1. 브라마굽타 공식

브라마굽타 공식은 원에 내접하는 사각형의 넓이를 구하는 공식으로, 헤론 공식의 일반화된 형태이다. 변의 길이가 $a, b, c, d$인 원내접 사각형의 넓이 $K$는 다음과 같다.

:$K=\sqrt{(s-a)(s-b)(s-c)(s-d)}$

여기서 $s = \tfrac12(a + b + c + d)$는 둘레의 절반이다.

원에 내접하는 사각형


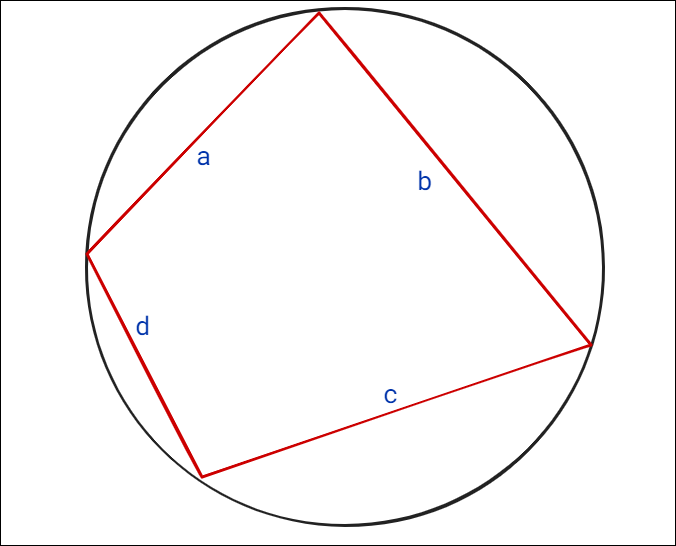
헤론 공식은 브라마굽타 공식에서 사각형의 한 변을 0으로 설정하여 얻을 수 있다.

7. 2. 브레치나이더 공식

브레치나이더 공식은 일반적인 사각형의 넓이를 구하는 공식으로, 브라마굽타 공식의 일반화된 형태이다. 헤론의 공식과 브라마굽타 공식은 모두 브레치나이더 공식의 특별한 경우이다.[24][25]

7. 3. 케일리-멩거 행렬식

케일리-멩거 행렬식을 사용하여 헤론의 공식을 다음과 같이 표현할 수 있다.[2]

-16A^2 = \begin{vmatrix}

0 & a^2 & b^2 & 1 \\

a^2 & 0 & c^2 & 1 \\

b^2 & c^2 & 0 & 1 \\

1 & 1 & 1 & 0

\end{vmatrix}.

사면체의 부피를 케일리-멩거 행렬식을 통해 나타낸 공식은 헤론의 공식의 일반화된 형태이다.

7. 4. 기타 일반화

헤론의 공식은 브라마굽타 공식의 특수한 경우로, 원내접 사각형의 넓이를 구하는 데 사용된다. 헤론의 공식과 브라마굽타 공식은 모두 브레슈나이더의 공식의 특수한 경우이다. 헤론의 공식은 사각형의 한 변을 0으로 설정하여 브라마굽타 공식 또는 브레슈나이더 공식에서 얻을 수 있다.

헤론의 공식은 변의 길이만을 사용하여 사다리꼴의 넓이를 구하는 공식의 특수한 경우이기도 하다. 이때는 사다리꼴의 작은 평행변의 길이를 0으로 설정하여 얻는다.

세 꼭짓점 사이의 거리의 제곱으로 케일리-멩거 행렬식을 사용하여 헤론의 공식을 표현하면 다음과 같다.

A = \frac{1}{4} \sqrt{- \begin{vmatrix}

0 & a^2 & b^2 & 1 \\

a^2 & 0 & c^2 & 1 \\

b^2 & c^2 & 0 & 1 \\

1 & 1 & 1 & 0

\end{vmatrix} }

이는 삼각뿔의 부피를 구하는 타르탈리아의 공식과 유사하다.

데이비드 P. 로빈스는 헤론의 공식을 원에 내접하는 오각형과 육각형으로 일반화한 공식을 발견했다.[17]

구면 기하학 또는 쌍곡 평면에서 삼각형의 변의 길이를 사용하여 삼각형의 넓이를 구하는 공식도 있다.[19] 구면 삼각형의 경우, 변의 길이가 a영어, b영어, c영어이고 반둘레가 s=\tfrac12(a+b+c), 넓이가 S영어일 때 공식은 다음과 같다.



\tan^2 \frac S 4 = \tan \frac s2 \tan\frac{s-a}2 \tan\frac{s-b}2 \tan\frac{s-c}2



쌍곡 평면의 경우에는 다음 공식을 사용한다.



\tan^2 \frac S 4 = \tanh \frac s2 \tanh\frac{s-a}2 \tanh\frac{s-b}2 \tanh\frac{s-c}2.


참조

[1] 간행물 Is a 2000-year-old formula still keeping some secrets? https://www.maa.org/[...] 2021-12-27
[2] 간행물 Some examples of the use of distances as coordinates for Euclidean geometry
[3] 간행물 A medieval proof of Heron's formula
[4] 서적 A History of Greek Mathematics Oxford University Press
[5] MathWorld Heron's Formula
[6] 서적 數學九章 (四庫全書本)
[7] 웹사이트 Personal email communication between mathematicians John Conway and Peter Doyle https://math.dartmou[...] 2020-09-25
[8] 간행물 A Symmetric 3D Proof of Heron's Formula 2020-09-14
[9] 서적 Maxima and Minima Without Calculus https://archive.org/[...] The Mathematical Association of America
[10] 간행물 A Simpler Proof of Heron's Formula
[11] 서적 Floating-Point Computation Prentice Hall 1974-05-01
[12] 웹사이트 Miscalculating Area and Angles of a Needle-like Triangle http://www.cs.berkel[...] 2000-03-24
[13] 간행물 A Heron-type formula for the triangle 2003-07
[14] 간행물 A Heron-type formula for the reciprocal area of a triangle 2005-11
[15] 간행물 A Heron-type area formula in terms of sines
[16] 간행물 Disentangling a triangle http://lagrange.math[...] 2009
[17] 간행물 Areas of Polygons Inscribed in a Circle 1994
[18] 웹사이트 What has the Volume of a Tetrahedron to do with Computer Programming Languages? http://www.cs.berkel[...]
[19] 서적 Geometry. II: Spaces of constant curvature Springer-Verlag
[20] 웹사이트 Fórmula de Herón para calcular el área de cualquier triángulo http://recursostic.e[...] 2012-06-30
[21] 간행물 ヘロンとガロワ 日本評論社 2009-11
[22] 간행물 The Volume as a Metric Invariant of Polyhedra 1998
[23] 웹사이트 Cayley-Menger Determinant http://mathworld.wol[...] 2018-06-19
[24] 문서 http://www.mathpages[...]
[25] mathpages mathpages http://www.mathpages[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com