리 미분

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
3. 정의
4. 성질
5. 일반화
6. 응용
참조

1. 개요

리 미분은 텐서장을 벡터장 방향으로 미분하는 연산으로, 1931년 브와디스와프 실레보진스키에 의해 처음 도입되었고, 다비트 판 단지흐에 의해 '리 미분'으로 명명되었다. 이는 스칼라 함수, 벡터장, 텐서장, 미분 형식, 스피너장 등 다양한 대상에 대해 정의되며, 텐서장의 변화율을 나타낸다. 리 미분은 선형 변환이며 텐서곱과 축약에 곱 규칙을 따르고, 외미분과 가환하며, 카르탕 마법 공식을 만족시키는 등 여러 성질을 갖는다. 일반 상대성이론에서 시공간 대칭성을 나타내는 킬링 벡터장을 찾는 데 활용되며, 유체역학 및 미분기하학 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

미분의 일반화 - 기울기 (벡터)
기울기(벡터)는 스칼라장의 특정 지점에서 값이 가장 빠르게 증가하는 방향과 변화율을 나타내는 벡터로, 함수의 등위면에 수직이며 크기는 해당 방향의 변화율을 나타내고, 스칼라 함수의 각 성분에 대한 편미분으로 구성되며 나블라 연산자로 표현된다.
미분의 일반화 - 야코비 행렬
야코비 행렬은 열린 집합 U에서 정의된 함수 f의 각 성분 편도함수를 요소로 가지는 행렬이며, 함수가 미분 가능할 때 전미분을 나타내고, n=m일 경우 행렬식은 함수의 동작에 대한 정보를 제공하며 다양한 분야에 응용된다.
미분 연산자 - 기울기 (벡터)
기울기(벡터)는 스칼라장의 특정 지점에서 값이 가장 빠르게 증가하는 방향과 변화율을 나타내는 벡터로, 함수의 등위면에 수직이며 크기는 해당 방향의 변화율을 나타내고, 스칼라 함수의 각 성분에 대한 편미분으로 구성되며 나블라 연산자로 표현된다.
미분 연산자 - 델 (연산자)
델 연산자는 3차원 유클리드 공간에서 편미분 연산자를 항으로 하는 벡터로 정의되며, 기울기, 발산, 회전, 라플라시안 등 다양한 연산을 표현하는 데 사용되며 전자기학, 유체역학, 양자역학 등 다양한 분야에 응용된다.
미분기하학 - 가우스 곡률
가우스 곡률은 3차원 유클리드 공간에 놓인 곡면의 두 주곡률의 곱으로, 곡면의 형태를 나타내는 지표이며 곡면 자체의 길이 측정만으로 결정되는 내재적인 값이다.
미분기하학 - 가우스의 빼어난 정리
가우스의 빼어난 정리는 곡면의 가우스 곡률이 외부 공간이 아닌 곡면 자체의 리만 계량만으로 결정된다는 정리로, 곡면의 변형 시 가우스 곡률이 보존됨을 의미하며, 지도 제작의 불가능성 증명과 고차원 리만 다양체 일반화에 응용되어 미분기하학과 일반 상대성 이론의 기초가 된다.

리 미분
개요
정의	미분기하학에서 벡터장을 따라 다른 텐서장의 변화율을 나타내는 연산
기호	ℒ (Lie derivative)
이름 유래	마리우스 리의 이름에서 유래
리 미분의 정의
스칼라 함수	벡터장 X에 대한 스칼라 함수 f의 리 미분은 단순히 방향 미분임: ℒX(f) = df(X) = X(f).
벡터장	벡터장 Y에 대한 벡터장 X의 리 미분은 리 괄호로 정의됨: ℒX(Y) = [X, Y].
텐서장	텐서장 T에 대한 리 미분은 T와 임의의 스칼라 함수 f, 벡터장 Y, 쌍대 벡터장 α에 대해 다음 항등식을 만족하는 유일한 텐서장임: ℒX(T(Y, α, ...)) = (ℒX T)(Y, α, ...) + T(ℒX Y, α, ...) + T(Y, ℒX α, ...) + ....
좌표 표현
벡터장	ℒX(Yi) = Xj∂jYi − Yj∂jXi
쌍대 벡터장	ℒX(ωi) = Xj∂jωi + ωj∂jXi
(0, 2) 텐서장	ℒX(Tij) = Xk∂kTij + Ti∂kXj + Tk∂kXi
속성
선형성	ℒX(S + T) = ℒX S + ℒX T
라이프니츠 법칙	ℒX(S ⊗ T) = (ℒX S) ⊗ T + S ⊗ (ℒX T)
축약	ℒX(ctr(T)) = ctr(ℒX T) (여기서 ctr은 임의의 축약)
미분과의 교환	ℒX(dT) = d(ℒX T) (여기서 d는 외미분)
응용
다양체 변형	다양체의 변형에 대한 벡터장의 유도를 정량화하는 데 사용됨
보존 법칙	뇌터 정리와 결합하여 보존 법칙을 찾는 데 사용됨

2. 역사적 배경

1931년에 폴란드의 수학자 브와디스와프 실레보진스키가 리 미분의 개념을 처음 도입하였다.^[16]^[17] 1932년에 다비트 판 단지흐(David van Danzig^nl)가 소푸스 리의 이름을 따 "리 미분"(Liesche Ableitung^de)으로 명명하였다.^[18]

벨기에의 물리학자 레옹 로젠펠드(Léon Rosenfeld^프랑스어)는 일반 상대성이론 연구 과정에서 리 미분과 유사한 개념을 독자적으로 도입하였다.^[19] 로젠펠드는 이를 "국소 변화"(variation locale^프랑스어)라고 불렀다.

1963년에 앙드레 리크네로비츠(André Lichnerowicz^프랑스어)가 스피너장의 리 미분을 정의하였고,^[20] 1972년에 이베트 코스만슈와르즈바크(Yvette Kosmann-Schwarzbach^프랑스어)가 이를 일반화하였다.^[21]

3. 정의

리 미분은 벡터장의 흐름(flow)을 따라 텐서장이 변화하는 비율을 나타낸다. 함수, 벡터장, 텐서장, 미분 형식 등 다양한 기하학적 객체에 대해 리 미분을 정의할 수 있다.

매끄러운 다양체 $M$ 위에 매끄러운 벡터장 $X\in\Gamma(\mathrm TM)$ 가 주어졌을 때, $X$ 방향으로의 '''리 미분'''은 임의의 매끄러운 $(p,q)$ 차 텐서장 $T$ 에 작용하여 매끄러운 $(p,q)$ 차 텐서장 $\mathcal L_XT$ 를 만드는 선형 변환이며, 다음 공리들을 만족시키는 유일한 연산이다.

(함수의 리 미분) 함수((0,0)차 텐서) $f\in\mathcal C^\infty(M;\mathbb R)$ 에 대하여, 리 미분은 벡터장의 1차 미분 연산자로의 작용과 같다.
: $\mathcal L_Xf=Xf$
(함수 외미분과의 호환) 함수 $f$ 에 대하여, 리 미분은 외미분과 가환한다.
: $\mathcal L_X(\mathrm df)=\mathrm d(\mathcal L_Xf)$
(텐서곱과의 호환) 리 미분은 텐서곱에 대하여 곱 규칙을 따른다.
: $\mathcal L_X(T_1\otimes T_2)=(\mathcal L_XT_1)\otimes T_2+T_1\otimes(\mathcal L_XT_2)$
(축약과의 호환) 리 미분은 축약에 대하여 곱 규칙을 따른다. 즉, 임의의 벡터장 $Y$ 와 $(p,q)$ 차 텐서장 $T$ 에 대하여 ( $q>0$ ),
: $\mathcal L_X(T(Y,-))=(\mathcal L_XT)(Y,-)+T(\mathcal L_XY,-)$

아인슈타인 표기법을 사용하고, 국소 좌표계

x^\mu

를 잡았을 때, 벡터

X=X^\mu\partial_\mu

방향의,

(p,q)

차 텐서

T^{\mu_1\mu_2\cdots\mu_p}_{\nu_1\nu_2\dots\nu_q}

의 '''리 미분'''은 다음과 같다.

:

\mathcal L_XT^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}=X^\rho\partial_\rho T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}-(\partial_\rho X^{\mu_1})T^{\rho\mu_2\cdots\mu_p}_{\nu_1\dots\nu_q}

\cdots-(\partial_\rho X^{\mu_p})T^{\mu_1\cdots\mu_{p-1}\rho}_{\nu_1\dots\nu_q}

+(\partial_{\nu_1}X^\rho)T^{\mu_1\cdots\mu_p}_{\rho\nu_2\dots\nu_q}+\cdots+(\partial_{\nu_q}X^\rho)T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_{q-1}\rho}

비틀림이 없는 아핀 접속

\nabla

의 경우, 위의 편미분을 공변 미분으로 치환하여도 상관없다. 리 미분은 아핀 접속에 의존하지 않는다.

:

\mathcal L_XT^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}=X^\rho\nabla_\rho T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}-(\nabla_\rho X^{\mu_1})T^{\rho\mu_2\cdots\mu_p}_{\nu_1\dots\nu_q}

\cdots-(\nabla_\rho X^{\mu_p})T^{\mu_1\cdots\mu_{p-1}\rho}_{\nu_1\dots\nu_q}

+(\nabla_{\nu_1}X^\rho)T^{\mu_1\cdots\mu_p}_{\rho\nu_2\dots\nu_q}+\cdots+(\nabla_{\nu_q}X^\rho)T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_{q-1}\rho}

3. 1. 함수의 리 미분

매끄러운 다양체

M

위의 매끄러운 벡터장

X

가 주어졌을 때, 함수((0,0)차 텐서)

f

의

X

방향으로의 리 미분은 벡터장의 1차 미분 연산자로의 작용과 같으며, 이는 단순한 미분이다. 국소 좌표계에서 다음과 같이 표현된다.

:

\mathcal L_Xf=Xf=X^\mu\partial_\mu f

다양체에서 함수

f\colon M \to {\mathbb R}

의 도함수는

x+h

가 정의되지 않아 차분 몫

\textstyle (f(x+h)-f(x))/h

이 정의될 수 없기 때문에 문제가 된다.

점

p \in M

에서 벡터장

X

에 대한 함수

f

의 리 미분은 다음과 같다.

:

(\mathcal{L}_X f) (p) = {d \over dt} \biggr|_{t=0} \bigl(f \circ \Phi^t_X\bigr)(p) = \lim_{t\to 0} \frac{f\bigl(\Phi^t_X(p)\bigr) - f\bigl(p)\bigr)}{t}

여기서

\Phi^t_X(p)

는 벡터장

X

에 의해 정의된 흐름이 시간

t

에서 점

p

를 매핑하는 점이다.

t=0

근처에서,

\Phi^t_X(p)

는 다음 1차 자율 (시간에 독립적인) 미분 방정식 시스템의 고유한 해이다.

:

\frac{d}{dt}\biggr|_t \Phi^t_X(p) = X\bigl(\Phi^t_X(p)\bigr)

여기서

\Phi^0_X(p) = p

이다.

\mathcal{L}_X f = \nabla_X f

로 설정하면 함수의 리 미분은 방향 미분과 동일시되며,

X(f):= \mathcal{L}_X f = \nabla_X f

로도 표시된다.

다음은 지역 좌표계 표기법으로 나타낸 예시이다.

스칼라장

\phi

에 대해 다음과 같다.

:

(\mathcal {L}_X \phi) = X(\phi) = X^a \partial_a \phi

.

스칼라장

\phi(x,y) = x^2 - \sin(y)

와 벡터장

X = \sin(x)\partial_y - y^2\partial_x

에 대해 해당하는 리 미분은 다음과 같다.

\begin{alignat}{3}\mathcal{L}_X\phi &= (\sin(x)\partial_y - y^2\partial_x)(x^2 - \sin(y))\\& = \sin(x)\partial_y(x^2 - \sin(y)) - y^2\partial_x(x^2 - \sin(y))\\& = -\sin(x)\cos(y) - 2xy^2 \\\end{alignat}

''M'' 위의 매끄러운 벡터장 ''X''가 ''M'' 위의 곡선족을 정의함을 보이는 것으로부터 리 미분을 정의할 수도 있다. ''M'' 위의 임의의 점 ''p''에 대해, ''M'' 위의 곡선 γ(''t'')가 존재하여, ''p'' = γ(0)이고,

:

\frac{d\gamma}{dt}(t)=X(\gamma(t))

가 성립한다. 이 1계 상미분 방정식의 해는 피카르-린델뢰프 정리(더 일반적으로는 프로베니우스 정리)에 의해 존재가 보장된다. 이때 리 미분은 다음과 같이 정의된다.

:

\mathcal{L}_Xf(p)=\frac{d}{dt}  f(\gamma(t)) \vert_{t=0}

.

3. 2. 벡터장의 리 미분

벡터장

Y

의 벡터장

X

에 대한 리 미분은 리 괄호

[X, Y]

와 같다. 리 괄호는 여러 가지로 정의될 수 있는데, 그중 두 가지는 다음과 같다.

국소 좌표계에서 $(\mathcal L_X Y)^\mu = X^\nu \partial_\nu Y^\mu - Y^\nu \partial_\nu X^\mu$ 로 표현된다. 여기서 $\partial_X$ 와 $\partial_Y$ 는 각각 ''X''와 ''Y''에 대한 방향 미분 연산이다.

벡터장을 함수에 대한 1계 미분 작용소로 보아, 두 벡터장 ''X'', ''Y''에 대해 리 괄호곱을 다음과 같이 정의할 수 있다.

:

[X,Y](f)=X(Y(f))-Y(X(f)).

이때,

[X,Y]

는 다시 벡터장이 된다.

벡터장

Y

의

X

에 관한 리 미분은 리 괄호곱

[X, Y]

와 같으므로,

:

\mathcal{L}_X Y = [X,Y]

로 정의한다.

3. 3. 텐서장의 리 미분

아인슈타인 표기법을 사용하면, 국소 좌표계

x^\mu

에서 벡터

X=X^\mu\partial_\mu

방향으로 (p,q)차 텐서

T^{\mu_1\mu_2\cdots\mu_p}_{\nu_1\nu_2\dots\nu_q}

의 리 미분은 다음과 같이 표현된다.

:

\mathcal L_XT^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}=X^\rho\partial_\rho T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}-(\partial_\rho X^{\mu_1})T^{\rho\mu_2\cdots\mu_p}_{\nu_1\dots\nu_q}

\cdots-(\partial_\rho X^{\mu_p})T^{\mu_1\cdots\mu_{p-1}\rho}_{\nu_1\dots\nu_q}

+(\partial_{\nu_1}X^\rho)T^{\mu_1\cdots\mu_p}_{\rho\nu_2\dots\nu_q}+\cdots+(\partial_{\nu_q}X^\rho)T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_{q-1}\rho}

이는 흐름에 의해 공간이 바뀌면서 텐서장이 바뀌는 비율을 나타낸다.

비틀림이 없는 아핀 접속

\nabla

을 사용하는 경우, 위의 편미분을 공변 미분으로 바꾸어도 동일한 결과를 얻는다. 리 미분은 아핀 접속에 의존하지 않는다.

:

\mathcal L_XT^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}=X^\rho\nabla_\rho T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_q}-(\nabla_\rho X^{\mu_1})T^{\rho\mu_2\cdots\mu_p}_{\nu_1\dots\nu_q}

\cdots-(\nabla_\rho X^{\mu_p})T^{\mu_1\cdots\mu_{p-1}\rho}_{\nu_1\dots\nu_q}

+(\nabla_{\nu_1}X^\rho)T^{\mu_1\cdots\mu_p}_{\rho\nu_2\dots\nu_q}+\cdots+(\nabla_{\nu_q}X^\rho)T^{\mu_1\cdots\mu_p}_{\nu_1\dots\nu_{q-1}\rho}

매끄러운 다양체

M

에 미분 가능한 (시간에 독립적인) 벡터장

X

가 주어지고,

\Phi^t_X : M \to M

가 해당 국소 흐름일 때,

\Phi^t_X

는 각

t

에 대한 국소 미분동형사상이므로 텐서장의 당김을 유도한다.

공변 텐서의 경우, 당김 사상의 다중 선형 확장으로 정의된다.

:

\left(\Phi^t_X\right)^*_p : T^*_{\Phi^t_X(p)}M \to T^*_{p}M, \qquad \left(\Phi^t_X\right)^*_p \alpha (X) = \alpha\bigl(T_p \Phi^t_X(X)\bigr), \quad \alpha \in T^*_{\Phi^t_X(p)}M, X \in T_{p}M

반공변 텐서의 경우, 미분

T_p\Phi^t_X

의 역함수를 확장한다.

:

\left(T_p\Phi^t_X\right)^{-1} : T_{\Phi^t_X(p)}M \to T_{p}M

모든

t

에 대해,

T

와 같은 종류인 텐서장

(\Phi^t_X)^* T

를 얻는다.

(r,0)

또는

(0,s)

-형 텐서장

Y

의 벡터장

X

에 대한 리 미분

{\cal L}_XY

는 점

p \in M

에서 다음과 같이 정의된다.

:

{\cal L}_X T(p) = \frac{d}{dt}\biggl|_{t=0} \left(\bigl(\Phi^t_X\bigr)^* T\right)_p = \frac{d}{dt}\biggl|_{t=0}\bigl(\Phi^t_X\bigr)^*_p T_{\Phi^t_X(p)}= \lim_{t \to 0}\frac{\bigl(\Phi^t_X\bigr)^*T_{\Phi^t_X(p)} - T_p}{t}.

결과 텐서장

{\cal L}_X T

는

T

와 같은 유형이다.

3. 4. 미분 형식의 리 미분

매끄러운 다양체

M

위의

n

차 미분 형식

\omega

는

(0,n)

차 텐서로 볼 수 있으며, 이 경우 리 미분은 다음과 같이 정의된다. 이 공식을 '''카르탕 마법 공식'''(Cartan's magic formula)이라고 한다.

:

\mathcal L_X\omega=X\lrcorner d\omega+d(X\lrcorner\omega)

여기서

\lrcorner

는 내부곱(interior product)을 나타내며, 다음과 같이 정의된다.

:

(X_1\lrcorner\omega)(X_2,\dots,X_n)=\omega(X_1,X_2,\dots,X_n)

미분 형식에 대한 리 미분은 다음과 같은 항등식들을 만족시킨다.

:

\mathcal L_X(\alpha\wedge\beta)=\mathcal L_X\alpha\wedge\beta+\alpha\wedge\mathcal L_X\beta

:

[\mathcal L_X,\mathcal L_Y]\alpha=\mathcal L_{[X,Y]}\alpha

:

[\mathcal L_X,Y\lrcorner]\alpha=[X\lrcorner,\mathcal L_Y]\alpha=[X,Y]\lrcorner\alpha

일반적인 미분 형식

\omega

에 대해서, 리 미분은

X

의 변분을 고려한 축약으로 다음과 같이 표현된다.

:

\mathcal{L}_X\omega = i_Xd\omega + d(i_X \omega).

이 공식은 '''카르탄 공식''', '''카르탄 호모토피 공식''' 또는 '''카르탄의 마법 공식'''으로도 알려져 있다.

특히, 카르탄 공식은 다음을 보여준다.

:

d\mathcal{L}_X\omega = \mathcal{L}_X(d\omega).

리 미분은 또한 다음 관계를 만족한다.

:

\mathcal{L}_{fX}\omega = f\mathcal{L}_X\omega + df \wedge i_X \omega .

3. 5. 스피너장의 리 미분

스핀 구조를 갖는 리만 다양체에서 스피너장

\psi

의 리 미분은 다음과 같이 정의된다.

:

\mathcal L_X\psi=\nabla_X\psi-\frac14(\mathrm dX^\flat)\cdot\psi

여기서

$X^\flat=g(X,-)$ 는 벡터장(=(1,0)차 텐서장) $X$ 에 대응하는 1차 미분 형식(=(0,1)차 텐서장)이다.
$\mathrm d$ 는 1차 미분 형식의 외미분이다.
$\cdot$ 은 클리퍼드 대수의 곱이다.

국소 좌표계로 표기하면 이는 다음과 같다.

:

(\mathcal L_X\psi)^i = X^\mu\nabla_\mu\psi^i - \frac1{16} \left(\nabla_\mu X_\nu - \nabla_\nu X_\mu\right) \left(\gamma^{\mu i}{}_j\gamma^{\nu j}{}_k-\gamma^{\nu i}{}_j\gamma^{\mu j}{}_k\right)\psi^k

여기서

$\mu,\nu\in\{1,\dots,\dim M\}$ 는 접다발 $\mathrm TM$ 의 지표이다.
$i,j,k\in\{1,\dots,2^{\lfloor\dim M/2\rfloor}\}$ 는 스피너 다발 $\mathrm SM$ 의 (복소수 성분) 지표이다.
$\gamma^{\mu i}{}_j$ 는 디랙 행렬이다.

스피너장의 리 미분은 리만 다양체의 리만 계량에 의존하지 않는다.

만약

X

가 킬링 벡터장이라면 (즉,

\nabla_\mu X_\nu = -\nabla_\nu X_\mu

), 이는 다음과 같이 더 간단해진다.

:

(\mathcal L_X\psi)^i = X^\mu\nabla_\mu\psi^i - \frac14(\nabla_\mu X_\nu)\gamma^{\mu i}{}_j\gamma^{\nu j}{}_k\psi^k

일반적인 시공간 벡터장(필연적으로 킬링 벡터장이 아님)에 대한 스피너의 리 미분에 대한 정의는 1971년에 이브트 코스만에 의해 이미 제안되었다.^[5] 이후, 그녀의 임시 처방을 섬유 다발에 대한 리 미분의 일반적인 틀 내에서 정당화하는 기하학적 틀이 제공되었으며,^[6] 이는 게이지 공변 필드 이론에 가장 적합한 분야로 밝혀진 게이지 자연 다발의 명시적인 맥락에서 제공되었다.^[7]

스핀 다양체에서, 즉 스핀 구조를 허용하는 리만 다양체

(M,g)

에서 스피너 장

\psi

의 리 미분은 1963년에 주어진 앙드레 리흐네로비츠의 국소 표현을 통해 무한소 등거리 변환(킬링 벡터장)에 대해 정의함으로써 정의될 수 있다:^[8]

:

\mathcal{L}_X \psi := X^{a}\nabla_{a}\psi - \frac14\nabla_{a}X_{b} \gamma^{a}\gamma^{b}\psi\, ,

여기서

\nabla_{a}X_{b} = \nabla_{[a}X_{b]}

이며,

X = X^{a}\partial_{a}

는 킬링 벡터장이라고 가정하고,

\gamma^{a}

는 디랙 행렬이다.

그 후 리흐네로비츠의 정의를 모든 벡터장(일반적인 무한소 변환)으로 확장할 수 있으며, ''일반'' 벡터장

X

에 대해 리흐네로비츠의 국소 표현을 유지하되,

\nabla_{a}X_{b}

의 반대칭 부분만 명시적으로 취한다.^[5] 1972년에 주어진 코스만의 국소 표현은 다음과 같다:^[5]

:

\mathcal{L}_X \psi := X^{a}\nabla_{a}\psi - \frac18\nabla_{[a}X_{b]}[\gamma^{a},\gamma^{b}]\psi\, = \nabla_X \psi - \frac14 (d X^\flat)\cdot \psi\, ,

여기서

[\gamma^{a},\gamma^{b}]= \gamma^a\gamma^b - \gamma^b\gamma^a

는 교환자이고,

d

는 외 미분이며,

X^\flat = g(X, -)

는 메트릭 아래에서

X

에 해당하는 듀얼 1-형식(즉, 낮춰진 인덱스 포함)이고,

\cdot

는 클리포드 곱이다.

스피너 리 미분은 메트릭에 독립적이므로, 접속에도 독립적이라는 점에 주목할 가치가 있다. 이는 코스만의 국소 표현의 오른쪽에 나타나지 않는데, 이는 오른쪽이 스핀 접속(공변 미분), 벡터장의 이중화(인덱스 낮추기) 및 스피너 다발에서 클리포드 곱을 통해 메트릭에 의존하는 것처럼 보이기 때문이다. 그러나 실제로는 그렇지 않다. 코스만의 국소 표현의 오른쪽의 양은 결합하여 모든 메트릭 및 접속 의존 항이 상쇄된다.

스피너 장의 리 미분에 대한 오랫동안 논쟁이 되어온 개념을 더 잘 이해하려면, 섬유 다발의 단면에 대한 리 미분 이론의 보다 일반적인 틀에 스피너 장의 리 미분 정의가 놓여 있으며, 스피너 경우에 대한 Y. 코스만의 직접적인 접근 방식이 코스만 올림이라고 하는 새로운 기하학적 개념의 형태로 게이지 자연 다발로 일반화된 원래 기사를 참조할 수 있다.^[9]^[10]

4. 성질

리 미분은 선형 변환이며, 텐서곱과 축약에 대해 곱 규칙을 만족시킨다. 외미분과 가환하며, 미분 형식에 대해서는 카르탕 마법 공식을 만족한다. 리 괄호에 대해 야코비 항등식을 만족한다.

함수의 리 미분: 함수((0,0)차 텐서) $f\in\mathcal C^\infty(M;\mathbb R)$ 에 대하여, 리 미분은 벡터장의 1차 미분 연산자로의 작용과 같다.
: $\mathcal L_Xf=Xf$
함수 외미분과의 호환: 함수 $f$ 에 대하여, 리 미분은 외미분과 가환한다.
: $\mathcal L_X(\mathrm df)=\mathrm d(\mathcal L_Xf)$
텐서곱과의 호환: 리 미분은 텐서곱에 대하여 곱 규칙을 따른다.
: $\mathcal L_X(T_1\otimes T_2)=(\mathcal L_XT_1)\otimes T_2+T_1\otimes(\mathcal L_XT_2)$
축약과의 호환: 리 미분은 축약에 대하여 곱 규칙을 따른다. 즉, 임의의 벡터장 $Y$ 와 $(p,q)$ 차 텐서장 $T$ 에 대하여 ( $q>0$ ),
: $\mathcal L_X(T(Y,-))=(\mathcal L_XT)(Y,-)+T(\mathcal L_XY,-)$

벡터장의 경우, 리 미분은 리 괄호가 된다.

:

\mathcal L_XY=[X,Y]

이 경우, 야코비 항등식에 따라 리 미분은 리 괄호에 대해 곱 규칙을 따른다.

:

\mathcal L_X[Y,Z]=[\mathcal L_XY,Z]+[Y,\mathcal L_XZ]

n

차 미분 형식

\omega

는

(0,n)

차 텐서로 보고 그 리 미분을 정의할 수 있다. 이 경우, 리 미분은 다음과 같이 주어지며, 이 공식을 '''카르탕 마법 공식'''(Cartan’s magic formula^영어)이라고 한다.

:

\mathcal L_X\omega=X\lrcorner d\omega+d(X\lrcorner\omega)

여기서

\lrcorner

는 내부곱(interior product^영어)을 나타낸다.

:

(X_1\lrcorner\omega)(X_2,\dots,X_n)=\omega(X_1,X_2,\dots,X_n)

미분 형식에 대하여, 리 미분은 다음과 같은 항등식들을 만족시킨다.

:

\mathcal L_X(\alpha\wedge\beta)=\mathcal L_X\alpha\wedge\beta+\alpha\wedge\mathcal L_X\beta

:

[\mathcal L_X,\mathcal L_Y]\alpha=\mathcal L_{[X,Y]}\alpha

:

[\mathcal L_X,Y\lrcorner]\alpha=[X\lrcorner,\mathcal L_Y]\alpha=[X,Y]\lrcorner\alpha

대칭 (0,2)차 텐서장

g_{\mu\nu}

(예를 들어, 리만 계량)의 경우,

:

(\mathcal L_Xg)_{\mu\nu}=X^\rho\partial_\rho g_{\mu\nu}+g_{\mu\rho}\partial_\nu X^\rho+g_{\nu\rho}\partial_\mu X^\rho

이다.

특히, 만약 리만 계량

g

로 유도되는 아핀 접속을 사용할 경우,

\nabla_\mu g_{\rho\sigma}=0

이며, 따라서

:

(\mathcal L_Xg)_{\mu\nu}=\nabla_\nu X_\mu+\nabla_\mu X_\nu

이다. 위 표현이 0이 되게 하는 벡터장

X

를

g

의 킬링 벡터장이라고 한다.

\mathcal{F}(M)

을 체에 정의된 함수의 다양체 ''M''에 대한 대수라고 하면

:

\mathcal{L}_X : \mathcal{F}(M) \rightarrow \mathcal{F}(M)

은 대수

\mathcal{F}(M)

에 대한 미분이다. 즉,

\mathcal{L}_X

는 '''R'''-선형이고

:

\mathcal{L}_X(fg) = (\mathcal{L}_Xf) g + f\mathcal{L}_Xg.

이다.

마찬가지로,

\mathcal{X}(M)

이 ''M''상의 벡터장의 집합일 때,

\mathcal{F}(M) \times \mathcal{X}(M)

에 대한 미분이다.^[4]

:

\mathcal{L}_X(fY) = (\mathcal{L}_Xf) Y + f\mathcal{L}_X Y

이것은 다음과 같이 동등한 표기법으로도 쓸 수 있다.

:

\mathcal{L}_X(f\otimes Y) = (\mathcal{L}_Xf) \otimes Y + f\otimes \mathcal{L}_X Y

여기서 텐서 곱 기호

\otimes

는 함수와 벡터장의 곱이 전체 다양체에 걸쳐 이루어진다는 사실을 강조하기 위해 사용된다.

벡터장에 대한 미분으로 간주하면

:

\mathcal{L}_X [Y,Z] = [\mathcal{L}_X Y,Z] + [Y,\mathcal{L}_X Z]

위의 식이 바로 야코비 항등식임을 알 수 있다. 따라서 리 괄호를 갖춘 ''M''상의 벡터장 공간이 리 대수를 형성한다는 중요한 결과를 얻는다.

''α''와 ''β''를 ''M''상의 두 개의 미분 형식이라고 하고, ''X''와 ''Y''를 두 개의 벡터장이라고 하면

$\mathcal{L}_X(\alpha\wedge\beta) = (\mathcal{L}_X\alpha) \wedge\beta + \alpha\wedge (\mathcal{L}_X\beta)$
$[\mathcal{L}_X,\mathcal{L}_Y]\alpha := \mathcal{L}_X\mathcal{L}_Y\alpha-\mathcal{L}_Y\mathcal{L}_X\alpha = \mathcal{L}_{[X,Y]}\alpha$
$[\mathcal{L}_X,i_Y]\alpha = [i_X,\mathcal{L}_Y]\alpha = i_{[X,Y]}\alpha,$ 여기서 ''i''는 위에 정의된 내적을 나타내며 [·,·]가 교환자 또는 리 괄호를 나타내는지 명확하다.

5. 일반화

공변 리 미분: 주다발 상에서 정의되는 리 미분의 일반화이다. 다양체 M 위의 주다발이 있고, X를 주다발의 접공간의 단면으로 공변 벡터장(수평 및 수직 성분을 가짐)으로 선택한다면, 공변 리 미분은 주다발에 대한 X에 대한 리 미분이다. 다양체 ''M'' 위에 벡터장 ''Y''가 주어져 있지만 (주다발은 아님) 주다발에 대한 접속도 있다면, 수평 성분이 ''Y''와 일치하고 수직 성분이 접속과 일치하는 주다발 위에 벡터장 X를 정의할 수 있는데, 이것이 공변 리 미분이다.

나이엔하위스-리 미분: 미분 형식을 반변 텐서장으로 확장한 일반화이다. 알베르트 니엔하위스(Albert Nijenhuis)는 접선 다발을 값으로 갖는 미분 형식의 다발 Ω^''k''(''M'', T''M'')의 임의의 단면을 따라 미분 형식의 리 미분을 정의할 수 있도록 하였다. 만약 ''K'' ∈ Ω^''k''(''M'', T''M'')이고 α가 미분 ''p''-형식이라면, ''K''와 α의 내부 곱 ''i''_''K''α를 정의하는 것이 가능하다. 니엔하위스-리 미분은 내부 곱과 외 미분의 반가환자이다.

: $\mathcal{L}_K\alpha=[d,i_K]\alpha = di_K\alpha-(-1)^{k-1}i_K \, d\alpha.$

반변 텐서장 ''K''와 ''p''차 미분 형식 α에 대해, 이들의 내부곱 ''i''_''K''α가 정의될 수 있음을 이용하여, 나이엔하이스-리 미분은 내부곱과 외미분의 반교환자로 정의된다. 나이엔하이스-리 미분은 "통상의 의미로는 더 이상 미분이 아니다"라는 주의해야 할 예외 사항이 있다는 것을 제외하고, 통상의 리 미분에서와 마찬가지의 다양한 대수적 성질을 만족한다.

6. 응용

미분기하학에서 텐서장의 미분에 대한 세 가지 주요 좌표 독립적 개념 중 하나인 리 미분은, 벡터장을 사용하여 수송 개념(리 수송)을 정의한다.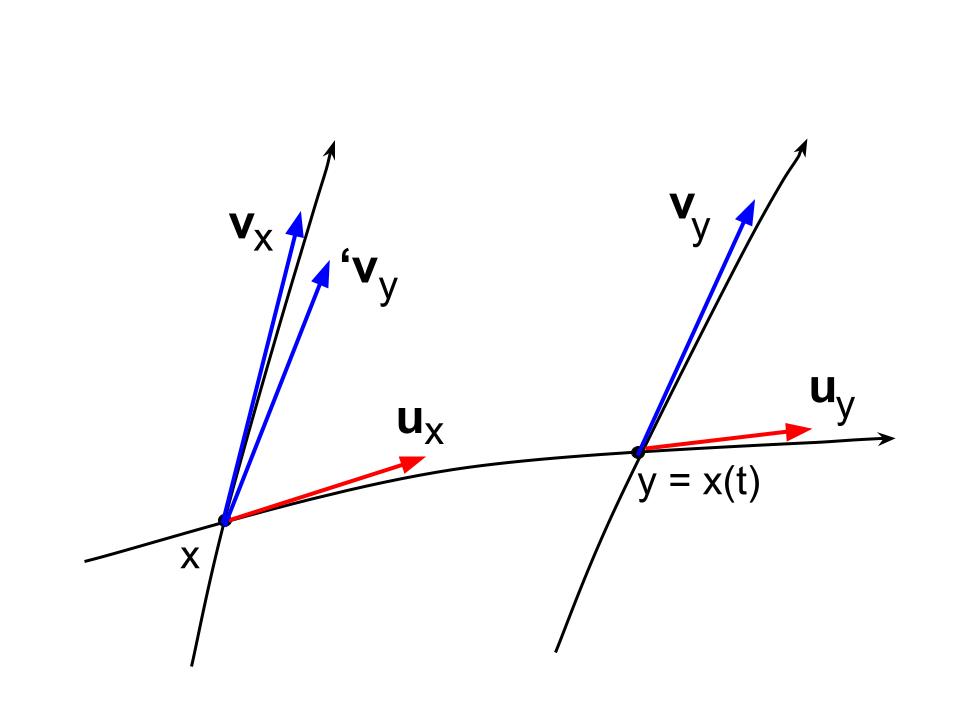

벡터 흐름장 $u$ 을 따라 점 $y$ 에서 점 $x$ 로 벡터 $v_y$ 의 리 수송.

매끄러운 벡터장은 다양체에 매끄러운 흐름을 정의하며, 이를 통해 벡터는 동일한 흐름 선상의 두 점 사이에서 수송될 수 있다. 이는 임의의 점 사이의 수송을 허용하는 접속과 대조된다.

리만 계량

g

로 유도되는 아핀 접속을 사용할 경우,

(\mathcal L_Xg)_{\mu\nu}=\nabla_\nu X_\mu+\nabla_\mu X_\nu

이다. 위 표현이 0이 되게 하는 벡터장

X

를

g

의 킬링 벡터장이라고 하며, 일반 상대성이론에서 시공간의 대칭성을 나타내는 데 활용된다.

참조

_[1] 서적 Variations, Geometry and Physics: In honour of Demeter Krupka's sixty-fifth birthday Nova Science
_[2] 저널 Sur les équations de Hamilton
_[3] 서적 The Theory of Lie Derivatives and its Applications https://archive.org/[...] North-Holland
_[4] 저널 Unification Theories: New Results and Examples 2019
_[5] 저널 Dérivées de Lie des spineurs
_[6] 서적 General Relativity: Papers in honour of J. L. Synge Clarenden Press
_[7] 서적 Natural and Gauge Natural Formalism for Classical Field Theories Kluwer Academic
_[8] 저널 Spineurs harmoniques
_[9] 서적 Proceedings of the 6th International Conference on Differential Geometry and Applications, August 28th–September 1st 1995 (Brno, Czech Republic) Masaryk University
_[10] 저널 Reductive G-structures and Lie derivatives
_[11] 저널 Sur le tenseur d'impulsion-énergie 1940
_[12] 서적 Theory of Relativity Dover 1981-07-01
_[13] 서적 https://archive.org/[...]
_[14] 서적 Natural operations in differential geometry http://www.emis.de/m[...] Springer-Verlag 2016-12-20
_[15] 저널
_[16] 저널
_[17] 서적 https://www.novapubl[...] 2016-12-07
_[18] 저널 http://www.dwc.knaw.[...]
_[19] 저널
_[20] 저널 Spineurs harmoniques http://gallica.bnf.f[...]
_[21] 저널 Dérivées de Lie des spineurs

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com