킬링 벡터장

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

킬링 벡터장은 리만 다양체에서 계량 텐서의 리 미분이 0이 되는 벡터장이다. 킬링 벡터장은 등거리 변환군의 리 대수를 형성하며, 국소 좌표계에서는 킬링 방정식으로 표현된다. 킬링 벡터장은 킬링 지평선, 킬링 텐서장, 등각 킬링 벡터장 등으로 일반화될 수 있으며, 킬링 벡터장의 개념은 1892년 빌헬름 킬링에 의해 처음 도입되었다.

더 읽어볼만한 페이지

리만 기하학 - 등각 사상
등각 사상은 각도를 보존하는 사상으로, 2차원에서는 도함수가 0이 아닌 정칙 함수인 복소 함수가 해당되며, 3차원 이상에서는 상사 변환, 등거리 변환, 특수 등각 변환 등으로 분류되어 지도 제작, 항공우주 공학 등 다양한 분야에 응용된다.
리만 기하학 - 편평도
편평도는 아직 내용이 없어 정의를 내릴 수 없는 위키백과 페이지이다.

킬링 벡터장
개요
정의	리만 다양체 위에서 미터 텐서를 보존하는 벡터장이다.
다른 이름	아이소메트리 생성자, 운동의 무한소 생성자
관련 개념
관련 개념	등거리 변환

2. 정의

일반화 리만 다양체 $(M,g)$ 가 주어졌을 때, 임의의 벡터장 $X\in\Gamma(\mathrm TM)$ 에 대하여 리 미분 $\mathcal L_Xg$ 를 정의할 수 있다. 이는 (0,2)-텐서장들의 벡터 공간 위의 선형 변환이다.

만약 $\mathcal L_Xg=0$ 이 성립한다면, $X$ 를 $(M,g)$ 의 킬링 벡터장이라고 한다. 킬링 벡터장들의 벡터 공간은 선형 변환 $X\mapsto \mathcal L_Xg$ 의 핵이다. 즉, 두 킬링 벡터장들의 합은 킬링 벡터장이며, 킬링 벡터장과 상수 스칼라의 곱 역시 킬링 벡터장이다. 킬링 벡터장은 등거리 변환군의 리 대수 $\mathfrak{isom}(M,g)$ 를 이룬다.^[18]

2. 1. 킬링 벡터장

일반화 리만 다양체

(M,g)

에서, 벡터장

X

의 리 미분이

\mathcal L_X g = 0

을 만족하면

X

를 '''킬링 벡터장'''이라고 한다.^[1] 킬링 벡터장은 등거리 변환군의 리 대수

\mathfrak{isom}(M,g)

를 이룬다.

킬링 벡터장의 조건은 공변 미분을 사용하여 다음과 같이 나타낼 수 있다.^[18]

:

\nabla_{(\mu}X_{\nu)}=0

이는 킬링 벡터장의 조건이 공변 상수 벡터장의 조건(

\nabla_\mu X_\nu=0

)을 약화시킨 것이다.

레비-치비타 접속을 사용하면 킬링 벡터장의 조건을 다음과 같이 표현할 수 있다.

:

g\left(\nabla_Y X, Z\right) + g\left(Y, \nabla_Z X\right) = 0 \,

여기서

Y

와

Z

는 임의의 벡터이다. 국소 좌표계에서는 이 조건이 킬링 방정식^[2]으로 표현된다.

:

\nabla_\mu X_\nu + \nabla_{\nu} X_\mu = 0 \,.

이 조건은 공변적 형태로 표현되므로, 한 좌표계에서 만족하면 모든 좌표계에서 성립한다.

예를 들어, 원 위의 반시계 방향으로 가리키며 각 지점에서 길이가 같은 벡터장은 킬링 벡터장이다. 이 벡터장을 따라 원의 각 점을 움직이면 단순히 원을 회전시키기 때문이다.

만약 어떤 좌표 기저

dx^{a} \,

에서 계량 텐서

g_{\mu \nu} \,

가 좌표 중 하나인

x^{\kappa} \,

에 의존하지 않는다면,

K^{\mu} = \delta^{\mu}_{\kappa} \,

는 크로네커 델타

\delta^{\mu}_{\kappa} \,

를 갖는 킬링 벡터가 된다.^[3]

2. 2. 킬링 지평선

일반화 리만 다양체

(M,g)

의 킬링 벡터장

X

가 주어졌을 때, 부분 집합

\{x\in M\colon g(X,X)|_x=0\}

을

X

의 '''킬링 지평선'''(Killing horizon^영어)이라고 한다.^[18] 이는 일반적으로 특이점을 가져 다양체가 아닐 수 있다.

3. 성질

정의에 따라, 모든 킬링 벡터장은 등각 벡터장이다.

3. 1. 리 대수 구조

일반화 리만 다양체

(M,g)

의 킬링 벡터장들의 벡터 공간은 리 대수를 이룬다. 즉, 두 킬링 벡터장의 리 괄호 역시 킬링 벡터장이다.^[14]

두 킬링 벡터장의 리 괄호는 여전히 킬링 벡터장이다. 따라서 다양체 ''M'' 위의 킬링 벡터장들은 ''M'' 위의 벡터장의 리 대수의 리 부분 대수를 형성한다. 이것은 ''M''이 완비 다양체일 경우 다양체의 등거리 변환군의 리 대수이다.

k

개의 연결 성분을 갖는,

n

차원의 일반화 리만 다양체의 킬링 리 대수의 차원은

kn(n+1)/2

이하이다.^[14]

3. 2. 위상 수학적 성질

콤팩트 리만 다양체

(M,g)

에 대하여, 다음이 성립한다.

만약 $M$ 의 리치 곡률 텐서가 음의 정부호 이차 형식이라면, 킬링 벡터장은 0 밖에 없다.
만약 모든 단면 곡률이 양수이며, $M$ 의 차원이 짝수라면, 모든 킬링 벡터장은 항상 0을 갖는다. (즉, 임의의 킬링 벡터장 $X$ 에 대하여, $X|_x=0\in\mathrm T_xM$ 인 $x\in M$ 이 존재한다.)

콤팩트 리만 다양체의 경우,

음의 리치 곡률은 자명하지 않은 (영이 아닌) 킬링 벡터장이 없음을 의미한다.
비양의 리치 곡률은 모든 킬링 벡터장이 평행함을 의미한다. 즉, 임의의 벡터장 방향으로의 공변 미분은 항등적으로 0이다.
만약 단면 곡률이 양수이고 ''M''의 차원이 짝수라면, 킬링 벡터장은 반드시 영점을 갖는다.

3. 3. 조화 함수와의 관계

일반화 리만 다양체

(M,g)

의 킬링 벡터장

X

는 다음 성질들을 갖는다.

발산이 0이다.^[14]

:

\nabla\cdot X=0

2차 공변 미분은 리만 곡률 텐서에 비례한다.^[14]

:

\nabla_\mu\nabla_\nu X_\rho=R_{\rho\nu\mu\sigma}X^\sigma

라플라스-벨트라미 연산자는 리치 곡률 텐서에 비례한다.^[14]

:

\nabla^2 X_\mu=-R_{\mu\nu}X^\nu

특히, 아인슈타인 방정식의 진공해의 경우 $X_\mu$ 의 라플라스-벨트라미 연산자는 0이다. 이는 $X_\mu$ 가 진공 맥스웰 방정식을 만족시키며, 로렌츠 게이지 조건 $\nabla\cdot X=0$ 역시 자동적으로 만족시킴을 의미한다. 이 사실을 통해 아인슈타인-맥스웰 계의 일부 해를 구할 수 있다.^[15]

만약 $X$ 가 킬링 벡터장이고 $Y$ 가 조화 벡터장이면, $g(X, Y)$ 는 조화 함수이다.

만약 $X$ 가 킬링 벡터장이고 $\omega$ 가 조화 p-형식이면, $\mathcal{L}_{X} \omega = 0$ 이다.

3. 4. 측지선에 대한 물리량의 보존

킬링 벡터장

X

와 측지선

\gamma

가 주어졌을 때,

g(X, \dot\gamma)

는 측지선을 따라 보존된다. 즉, 킬링 벡터장

X

와 측지선의 속력의 내적

g(X,\dot\gamma)

는 측지선을 따라 변하지 않는다.^[4]

이는 일반 상대성 이론에서 뇌터 정리에 따라 각 킬링 벡터장에 대응하는 보존 법칙이 존재함을 의미한다. 구체적으로, 에너지-운동량 텐서

T_{\mu\nu}

와 킬링 벡터장

X^\mu

에 대해,

T^{\mu\nu}X_\nu

는 공변 보존류가 된다.

이 보존량은 킬링 벡터와 측지선 접선 벡터 간의 계량 곱으로 표현된다. 접선 벡터가

U^a

인 아핀 매개변수화된 측지선에서 킬링 벡터

X_b

가 주어지면,

U^bX_b

는 보존된다.^[4] 즉, 측지선을 따라 다음 식이 성립한다.

:

U^a\nabla_a(U^bX_b)=0

이는 대칭성을 가진 시공간에서의 운동을 분석적으로 연구하는 데 도움을 준다.^[4]

일반 상대성 이론에서 뇌터 정리에 따르면, 각 킬링 벡터는 측지선을 따라 보존되는 양에 해당한다. 이 보존량은 킬링 벡터와 측지선 접선 벡터 간의 계량 곱이다. 동일한 아핀 매개변수

\lambda

의 측지선을 따라, 방정식

\frac d {d\lambda} ( K_\mu \frac{dx^\mu}{d\lambda} ) = 0

이 성립한다.

3. 5. 표면 중력

일반화 리만 다양체

(M,g)

의 킬링 벡터장

X

가 주어졌을 때, 킬링 지평선

\{x\in M\colon g(X,X)|_x=0\}

에 대해 표면 중력을 정의할 수 있다.^[18]

킬링 지평선의 표면 중력

\kappa

는 다음 조건을 만족시키는 함수

\kappa\colon\{x\in M\colon g(X,X)|_x=0\}\to\mathbb R

이다.

:

\partial_\mu\left(g(X,X)\right)=-2\kappa g_{\mu\nu}X^\nu

이는 다음과 같이 쓸 수도 있다.

:

X^\mu \nabla_\mu X^\nu=\kappa X^\nu

위 등식의 좌변은 일종의 "가속도"이므로,

\kappa

를 일종의 "중력장"으로 해석할 수 있다.

다음의 경우,

\kappa

는 킬링 지평선 위의 상수 함수이다.^[18]

킬링 지평선이 (민코프스키 공간의 $x\partial_t+t\partial_x$ 와 같이) 서로 교차하는 두 잎으로 구성되어 있을 때
우세 에너지 조건이 성립할 경우

3. 6. 킬링 지평선 근처의 기하

일반화 리만 다양체

(M,g)

의 킬링 벡터장

X

가 주어졌을 때, 부분 집합

\{x\in M\colon g(X,X)|_x=0\}

을

X

의 '''킬링 지평선'''(Killing horizon^영어)이라고 한다.^[18] 이는 일반적으로 특이점을 가져 다양체가 아닐 수 있다.

d+1

차원 로런츠 다양체

(M,g)

의 킬링 벡터장

X

가 주어졌다고 하자. 또한,

X

가

U\subseteq M

에서 시간꼴 벡터장이라고 하자 (즉,

g(X,X)|_x<0\qquad\forall x\in U

). 그렇다면, 다음과 같은 꼴의 국소 좌표계

(t,x^i)

를 정의할 수 있다.

:

\mathrm ds^2=-f(x)^2(\mathrm dt+\theta_i(x)\mathrm dx^i)^2+h_{ij}(x)\,\mathrm dx^i\,\mathrm dx^j

여기서

h_{ij}

는 양의 정부호 이차 형식이며,

i,j\in\{1,2,\dots,d\}

이며, 또한

f

와

\theta_i

와

h_{ij}

는

(x^1,\dots,x^d)

에만 의존하고,

t

에 의존하지 않는다. 이 경우,

h_{ij}

를 '''궤도 공간 계량'''(orbit-space metric^영어)이라고 한다.

4. 예

Killing vector field^영어의 예로는 다음과 같은 경우가 있다.

공변 상수 벡터장은 정의에 따라 킬링 벡터장이다.
원 위의 각 점에서 길이가 같고 반시계 방향으로 향하는 벡터장은 킬링 벡터장이다. 이 벡터장을 따라 원의 각 점을 움직이면 단순히 원을 회전시키는 것이기 때문이다.

쌍곡면의 경우, 푸앵카레 계량 $g = y^{-2}\left(dx^2 + dy^2\right)$ 은 $x$ 에 독립적이므로, $\partial_x$ 는 킬링 벡터장이다.

상반평면 모델에서 반원형으로 선택된 점들에 대한 킬링 벡터장. 이 킬링 벡터장은 특수 등각 변환을 생성하며, 색상은 각 지점에서 벡터장의 크기를 나타낸다.

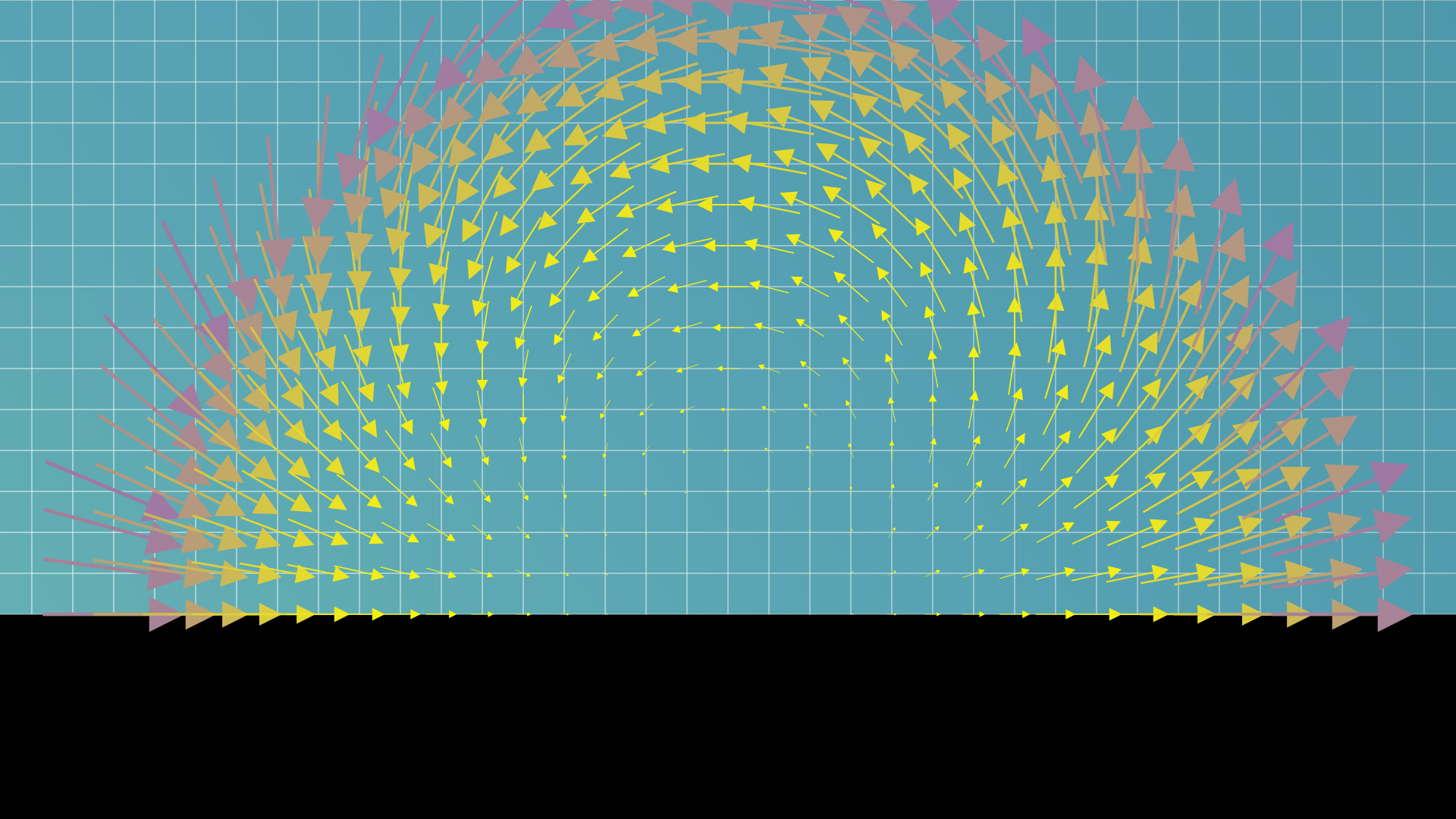
민코프스키 공간의 킬링 벡터장은 시간 이동, 세 개의 공간 이동, 세 개의 회전 생성자(작은 군), 세 개의 부스트 생성자로 이루어져 있다.
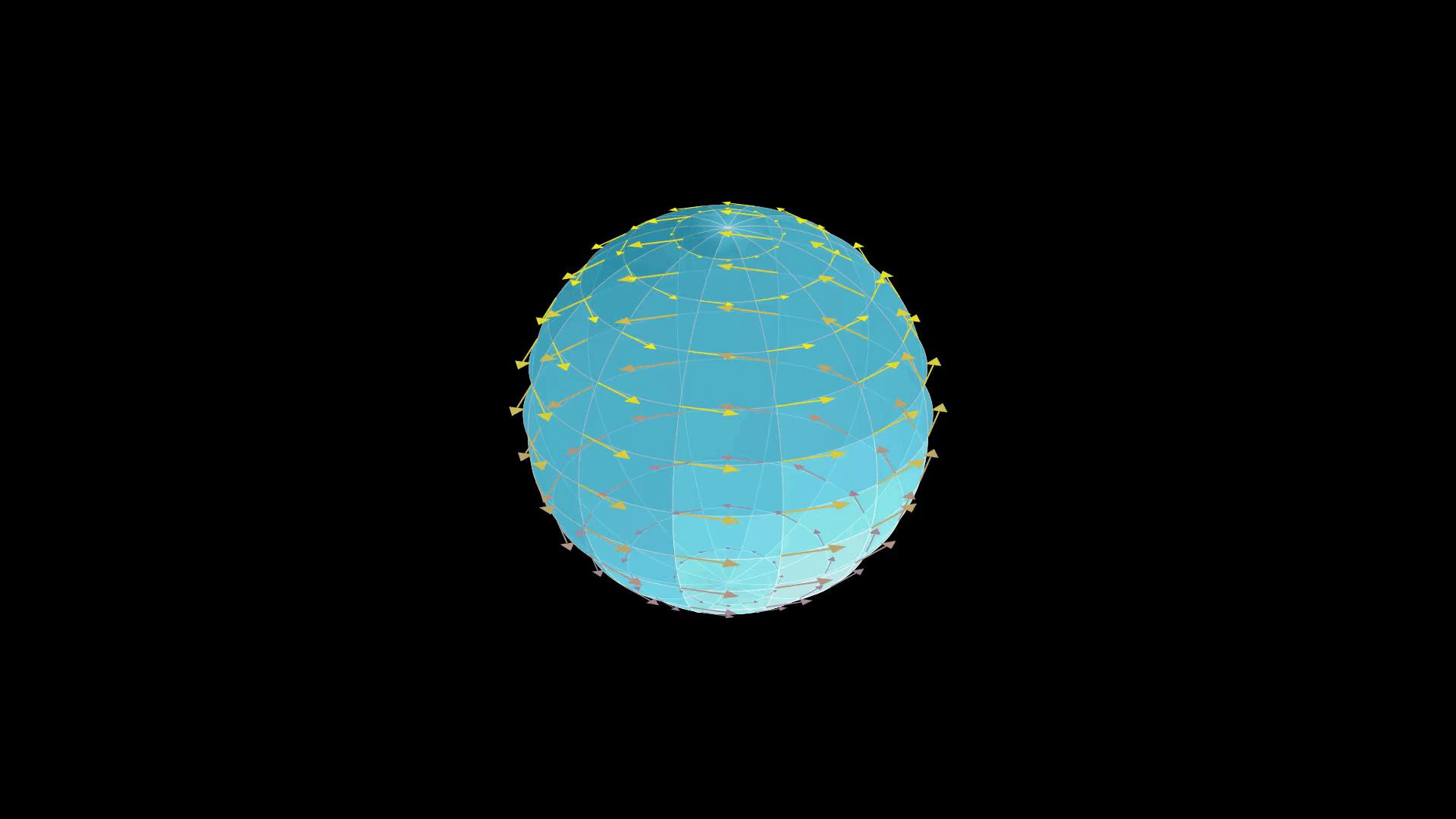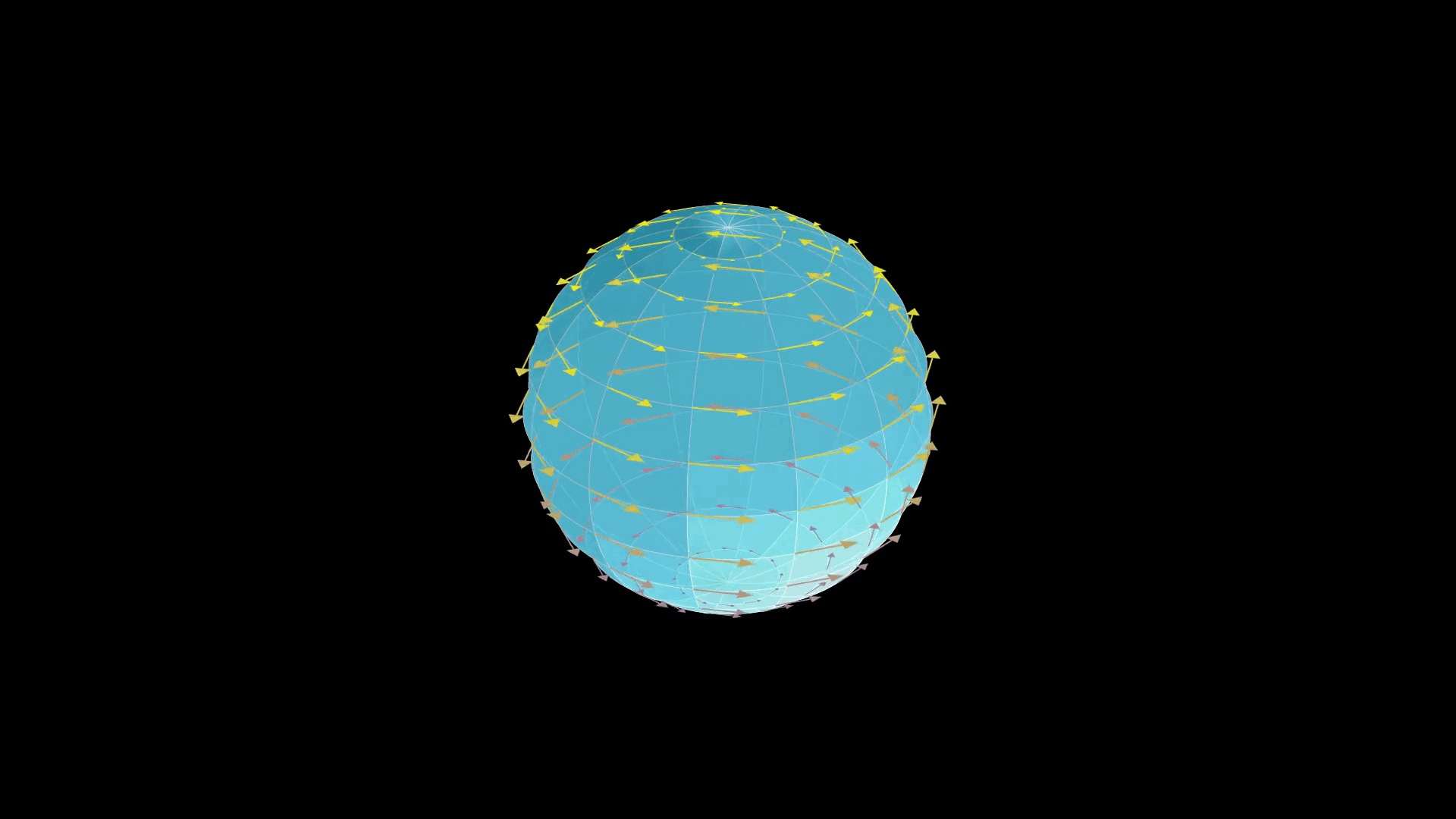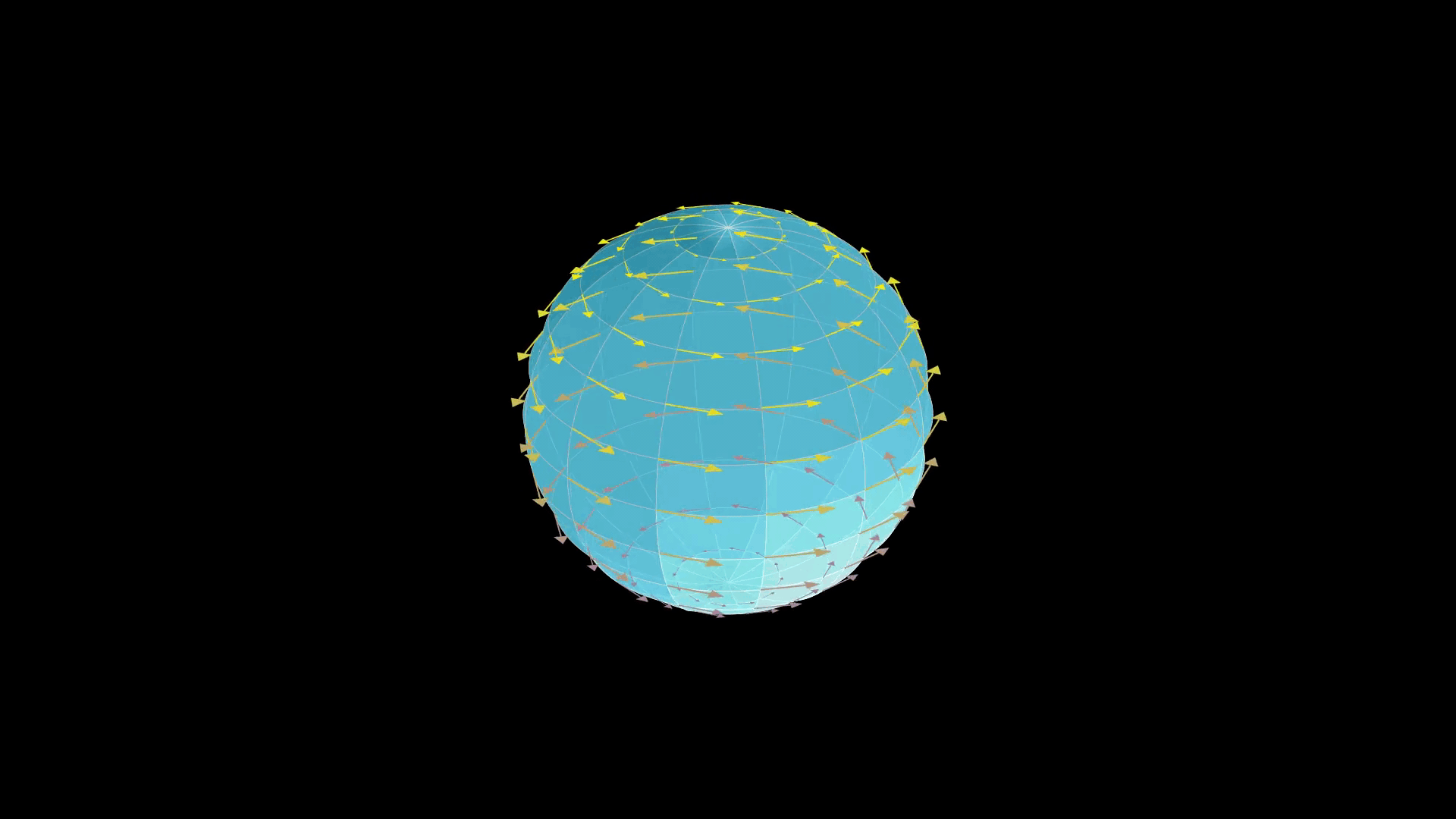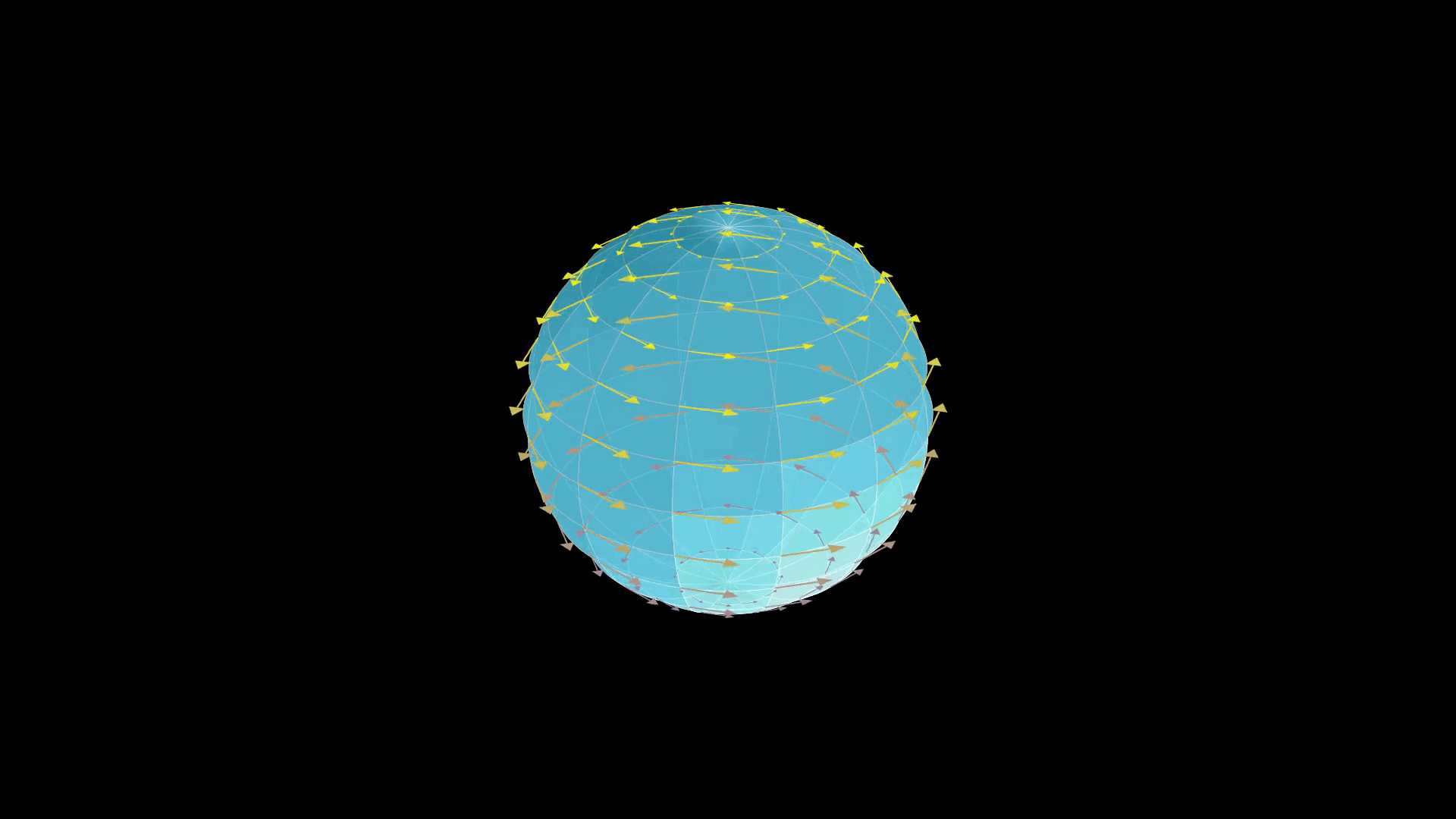
2차원 구면은 회전 대칭을 가지므로, 임의의 축을 중심으로 회전을 생성하는 킬링 벡터장을 갖는다.

구면의 킬링 벡터장. 이 킬링 벡터장은 z축 주위의 회전을 생성하며, 색상은 각 벡터의 기준점 높이를 나타낸다.

4. 1. 좌표계와 킬링 벡터장

Killing vector field^영어은 계량 텐서가 특정 좌표에 의존하지 않을 때, 해당 좌표 방향으로 정의되는 벡터장이다. 좀 더 구체적으로 설명하면, 일반화 리만 다양체

(M,g)

에서 계량 텐서

g_{\mu\nu}

의 각 성분이 특정 좌표

x^1

에 의존하지 않는다고 가정해보자. 즉,

:

\frac\partial{\partial x^1}g_{\mu\nu}=0\qquad\forall \mu,\nu\in\{1,\dots,n\}

이다.

이 경우, 벡터장

:

\frac\partial{\partial x^1}

은 Killing vector field^영어이 된다.

이는 다음과 같이 유도할 수 있다.^[1]

주어진 벡터장

X^\mu=\delta^\mu_1

에 대해,

X_\mu=g_{\mu\nu}X^\nu=g_{\mu1}

이다. 킬링 벡터장의 조건인

\nabla_{(\mu}X_{\nu)}=0

을 확인하면,

:

\nabla_\nu X_\mu+\nabla_\mu X_\nu=\partial_\nu X_\mu+\partial_\mu X_\nu-2\Gamma^\rho_{\mu\nu}X_\rho=\partial_\nu g_{\mu1}+\partial_\mu g_{\nu1} - (\partial_\nu g_{1\mu}+\partial_\mu g_{1\nu}-\partial_1g_{\mu\nu} ) = \partial_1g_{\mu\nu}

이 된다. 따라서,

\partial_1g_{\mu\nu} = 0

이므로,

\frac\partial{\partial x^1}

은 킬링 벡터장이다.

예를 들어, 쌍곡면의 경우, 푸앵카레 계량

g = y^{-2}\left(dx^2 + dy^2\right)

은

x

에 독립적이므로,

\partial_x

는 킬링 벡터장이다.

어떤 좌표 기저

dx^{a} \,

에서 계량 텐서

g_{\mu \nu} \,

가 좌표 중 하나인

x^{\kappa} \,

에 의존하지 않는다면,

K^{\mu} = \delta^{\mu}_{\kappa} \,

는 크로네커 델타

\delta^{\mu}_{\kappa} \,

를 갖는 킬링 벡터가 된다.^[3]

물리적으로, 예를 들어 계량 텐서의 어떤 성분도 시간의 함수가 아니라면, 다양체는 자동적으로 시간꼴 킬링 벡터를 갖는다는 의미를 가진다.

4. 2. 슈바르츠실트 계량

D

차원 시공간의 슈바르츠실트 계량

:

\mathrm ds^2=-\left(1-(r_0/r)^{D-3}\right)dt^2+\left(1-(r_0/r)^{D-3}\right)^{-1}\,\mathrm dr^2+r^2\,\mathrm d\Omega_{D-2}^2

에서,

\partial/\partial t

는 킬링 벡터이며, 이는 시간 변화에 대한 대칭을 나타낸다. 이에 대한 킬링 벡터는

:

g_{tt}=-1+(r_0/r)^{D-3}=0

이 되는 곳, 즉

r=r_0

이며, 이는 (일반) 사건 지평선과 일치한다.

이 밖에도, 슈바르츠실트 계량은

\mathrm{SO}(D-1)

대칭에 대응하는 킬링 벡터들을 갖는다.

4. 3. 커 계량

커 계량은 다음과 같다.

:

\mathrm ds^2 = -\left( 1 - \frac{r_0r}{\rho^2} \right) \mathrm dt^2 + \frac{\rho^2\,\mathrm dr^2}{r^2-r_0r+\alpha^2} + \rho^2\,\mathrm d\theta^2 + \left( r^2+ \alpha^2+ \frac{r_0r \alpha^2}{\rho^2} \sin^2\theta \right) \sin^2\theta\,\mathrm d\phi^2 + \frac{2r_0r\alpha \sin^2\theta }{\rho^2}\,\mathrm dt\,\mathrm d\phi

:

\rho^2=r^2+\alpha^2\cos^2\theta

이는 두 개의 킬링 벡터

\frac\partial{\partial t}

와

\frac\partial{\partial\phi}

를 가지며, 각각 시간 변화와 블랙홀 회전에 대한 대칭을 나타낸다.^[18]

\partial/\partial t

에 대응하는 킬링 지평선은

rr_0=\rho^2

의 두 해에 위치한다. 이는 2차 방정식이므로 두 해를 가지는데, 더 안쪽의 킬링 지평선은 사건 지평선이며, 더 바깥쪽의 킬링 지평선은 작용권의 경계이다.

4. 4. 민코프스키 공간

2차원 민코프스키 공간

\mathbb R^{1,1}=\{(t,x)\}

에서 킬링 벡터장

X=x\partial_t+t\partial_x

를 생각해 보자.^[18] 이 경우, 킬링 지평선은

\{(t,x)\in\mathbb R^2\colon x=\pm t\}

인데, 이는

x=t=0

에서 매끄럽지 않다.

4. 5. 2차원 구면

2차원 구면은 회전 대칭을 가지므로, 임의의 축을 중심으로 회전을 생성하는 킬링 벡터장을 갖는다. 2차원 구면(

S^2

)은 3차원 회전군 SO(3)의 작용 하에 대칭을 가질 것으로 예상된다. 즉, 유클리드 공간에 구를 임베딩하여 킬링 벡터장의 형태를 추측할 수 있다.

카르테시안 좌표

(x, y, z)

에서

\mathbb{R}^3

에 임베딩된 2차원 구면에 대한 일반적인 차트는 다음과 같다.

:

x = \sin\theta\cos\phi,\qquad y = \sin\theta\sin\phi,\qquad z = \cos\theta

여기서

\theta

는 높이를,

\phi

는

z

축을 중심으로 한 회전을 나타낸다.

표준 카르테시안 메트릭

ds^2 = dx^2 + dy^2 + dz^2

의 당김은 구면의 표준 메트릭을 제공한다.

:

ds^2 = d\theta^2 + \sin^2\theta d\phi^2

.

z

축을 중심으로 회전을 생성하는 벡터장은

\frac{\partial}{\partial\phi}

이다. 이 좌표에서 메트릭 구성 요소는 모두

\phi

에 독립적이므로,

\partial_\phi

는 킬링 벡터장이다.

x

축 및

y

축을 중심으로 하는 회전에 대한 생성자는 각각 다음과 같다.

:

X = z\partial_y - y\partial_z

:

Y = z\partial_x - x\partial_z

z

축을 중심으로 하는 회전 생성자는 다음과 같다.

:

Z = x\partial_y - y\partial_x = \sin^2\theta \,\partial_\phi

이 세 생성자의 선형 조합으로 이루어진 대수는 닫혀 있으며, 다음 관계를 따른다.

:

[X,Y] = Z \quad [Y,Z] = X \quad [Z,X] = Y.

이는 리 대수

\mathfrak{so}(3)

이다.

X

와

Y

를 구면 좌표로 표현하면 다음과 같다.

:

X = \sin^2\theta \,(\sin\phi\partial_\theta + \cot\theta\cos\phi\partial_\phi)

:

Y = \sin^2 \theta \,(\cos\phi\partial_\theta - \cot\theta\sin\phi\partial_\phi)

이 세 벡터장이 킬링 벡터장이라는 것은,

X, Y, Z

가 유클리드 공간에서 등거리 변환의 생성자이고, 구면의 메트릭이 유클리드 공간의 메트릭에서 상속되므로 등거리 변환도 상속되기 때문이다.

이 세 킬링 벡터장은 리 대수를 위한 완전한 생성자 집합을 형성하며, 유일하지 않다. 이 세 벡터장의 임의의 선형 조합은 여전히 킬링 벡터장이다.

4. 6. 평탄 공간

일반화 리만 다양체

(M,g)

가 평탄 공간, 즉 유클리드 공간 또는 유사 유클리드 공간(민코프스키 공간)인 경우, 전역 평탄 좌표를 선택하여 리만 곡률 텐서와 레비-치비타 접속이 모든 곳에서 사라지도록 할 수 있다. 이는 다음을 의미한다.

:

\partial_\mu\partial_\nu X_\rho = 0.

킬링 방정식을 통합하고 적용하면

X_\rho

에 대한 일반적인 해는 다음과 같다.

:

X^\rho = \omega^{\rho\sigma} x_\sigma + c^\rho

여기서

\omega^{\mu\nu} = -\omega^{\nu\mu}

는 반대칭이다. 적절한

\omega^{\mu\nu}

와

c^\rho

값을 선택하면, 평탄 공간의 등거리 변환에 대한 일반화된 푸앵카레 대수의 기저를 얻을 수 있다.^[18]

:

M_{\mu\nu} = x_\mu\partial_\nu - x_\nu\partial_\mu

:

P_\rho = \partial_\rho.

이들은 각각 유사 회전(회전 및 부스트)과 평행 이동을 생성하며, 각 점에서 (유사-)계량을 보존한다.

총 차원이

n

인 (유사-)유클리드 공간의 경우, 총

n(n+1)/2

개의 생성자가 있으며, 이는 평탄 공간을 최대한 대칭적으로 만든다.

5. 일반화

킬링 벡터장은 접다발 뿐만 아니라 다른 벡터 다발의 단면에 대해서도 일반화할 수 있다.^[18]

5. 1. 킬링 텐서장과 킬링 스피너장

킬링 벡터장의 개념은 접다발 대신 다른 벡터 다발의 단면에 대하여 일반화할 수 있다. 유사하게 킬링 텐서 및 킬링 스피너장을 정의할 수 있다.^[18]

예를 들어, 킬링 2-텐서장

T

는 다음을 만족한다.^[18]

:

\mathcal L_XT=0

:

\nabla_{(\mu}T_{\nu\rho)}=0

킬링 텐서장은 대칭 텐서장 ''T''로,

\nabla T

의 대칭화의 무흔적 부분이 사라진다. 킬링 텐서를 가진 다양체의 예로는 Kerr 회전 블랙홀과 FRW 우주론이 있다.^[7]

5. 2. 정칙 킬링 벡터장

켈러 다양체는 리만 구조와 더불어 복소 구조를 갖춘다. 따라서, 켈러 다양체의 대칭은 복소 구조를 보존시키는 특수한 킬링 벡터장에 의하여 주어진다. 이를 '''정칙 킬링 벡터장'''(正則Killing vector場, holomorphic Killing vector field^영어)이라고 한다.^[16]^[17] 켈러 다양체의 접다발

TM^{\mathbb C}

은 정칙적 부분

T^+M

과 반정칙적 부분

T^-M

으로 나뉜다. 정칙 킬링 벡터장은

T^+M

의 단면이다.

X^i

가 켈러 다양체

(M,g_{i\bar\jmath})

위의 정칙 킬링 벡터장이라고 하면, 킬링 방정식은 다음과 같다.

:

\nabla_iX^kg_{k\bar\jmath}+\bar\nabla_{\bar\jmath}\bar X^{\bar k}g_{\bar ki}=0

이에 따라,

X

는 국소적으로 다음과 같이 나타낼 수 있다.

:

X^i=-ig^{i\bar\jmath}\bar\partial_{\bar\jmath}D(z,\bar z)

:

\bar X^{\bar\imath}=ig^{j\bar\imath}\partial_jD(z,\bar z)

여기서

D(z,\bar z)

는 '''킬링 퍼텐셜'''(Killing potential^영어)이라고 불리는, 국소적으로 정의된 실수 함수다. 이는 운동량 사상의 한 예로 볼 수 있다.

5. 3. 등각 킬링 벡터장

일반화 리만 다양체 $(M,g)$에서, 벡터장 $X\in\Gamma(\mathrm TM)$에 대한 리 미분 $\mathcal L_Xg$는 (0,2)-텐서장들의 벡터 공간 위의 선형 변환이다. 킬링 벡터장은 $\mathcal L_Xg=0$을 만족하는 벡터장으로 정의된다.

킬링 벡터장은 $\mathcal{L}_{X} g = \lambda g$를 만족하는 등각 킬링 벡터장으로 일반화할 수 있으며, 여기서 $\lambda$는 어떤 스칼라이다. 1-매개변수 등각 사상 패밀리의 미분은 등각 킬링 벡터장이다.^[18]

5. 4. 카르탕 분해

두 킬링 벡터장의 리 괄호는 여전히 킬링 벡터장이다. 따라서 다양체

M

위의 킬링 벡터장들은

M

위의 모든 벡터장들의 리 부분 대수

\mathfrak{g}

를 형성한다. 점

p \in M

을 선택하면, 대수

\mathfrak{g}

는 두 부분으로 분해될 수 있다.

:

\mathfrak{h} = \{ X\in\mathfrak{g} : X(p) = 0 \}

:

\mathfrak{m} = \{ X\in\mathfrak{g} : \nabla X(p) = 0 \}

여기서

\nabla

는 공변 미분이다. 이 두 부분은 자명하게 교차하지만, 일반적으로

\mathfrak{g}

를 분할하지는 않는다. 예를 들어,

M

이 리만 균질 공간인 경우,

M

이 리만 대칭 공간인 경우에만

\mathfrak{g} = \mathfrak{h} \oplus \mathfrak{m}

이다.^[5]

직관적으로,

M

의 등거리 변환은 전체 공간의 부분 다양체

N

을 국소적으로 정의하며, 킬링 벡터장은 그 부분 다양체를 "따라 미끄러지는" 방법을 보여준다. 킬링 벡터장은 그 부분 다양체의 접 공간을 생성한다. 접 공간

T_pN

은 해당 지점에서 유효하게 작용하는 등거리 변환과 동일한 차원을 가져야 한다. 즉,

T_pN \cong \mathfrak{m}

이 예상된다. 그러나 일반적으로 킬링 벡터장의 수는 그 접 공간의 차원보다 크다.

이런 현상은 "추가" 킬링 벡터장이 중복되기 때문에 발생한다. 모든 필드를 함께 고려하면, 특정 지점에서의 접 공간에 대한 과잉 완전 기저를 제공하게 된다. 따라서 선형 조합을 통해 해당 지점에서 0이 되도록 만들 수 있다. 이는 2차원 구면의 킬링 벡터장의 예에서 확인할 수 있다. 3개의 킬링 벡터장이 존재하며, 주어진 지점에서 두 개는 해당 지점의 접 공간을 생성하고, 세 번째는 나머지 두 개의 선형 조합으로 표현 가능하다. 임의의 두 개를 선택하면

\mathfrak{m}

을 정의하고, 나머지 퇴화된 선형 조합은 직교 공간

\mathfrak{h}

를 정의한다.

카르탕 인볼루션은 측지선의 방향을 반사하거나 반전시키는 것으로 정의된다. 그 미분은 측지선에 대한 접선의 방향을 뒤집는다. 이는 노름이 1인 선형 연산자이며, 고유값 +1과 -1인 두 개의 불변 부분 공간을 갖는다. 이 두 부분 공간은 각각

\mathfrak{p}

와

\mathfrak{m}

에 해당한다.

점

p \in M

을 고정하고

p

를 통과하는 측지선

\gamma: \mathbb{R} \to M

을 고려하고,

\gamma(0) = p

로 둔다. 인볼루션

\sigma_p

는 다음과 같이 정의된다.

:

\sigma_p(\gamma(\lambda)) = \gamma(-\lambda)

이 맵은 인볼루션이며,

\sigma_p^2 = 1

이다. 킬링 벡터장을 따라 측지선으로 제한하면 분명히 등거리 변환이며, 이는 고유하게 정의된다.

G

를 킬링 벡터장에 의해 생성된 등거리 변환 그룹이라고 할 때, 함수

s_p: G \to G

는 다음과 같이 정의된다.

:

s_p(g) = \sigma_p \circ g \circ \sigma_p = \sigma_p \circ g \circ \sigma_p^{-1}

이 함수는

G

의 준동형사상이다. 그 미분

\theta_p: \mathfrak{g} \to \mathfrak{g}

는 다음과 같다.

:

\theta_p(X) = \left. \frac{d}{d\lambda} s_p\left(e^{\lambda X}\right) \right|_{\lambda=0}

카르탕 인볼루션은 리 대수 준동형사상이며, 모든

X, Y \in \mathfrak{g}

에 대해 다음이 성립한다.

:

\theta_p[X, Y] = \left[\theta_p X, \theta_p Y\right]

부분 공간

\mathfrak{m}

은 카르탕 인볼루션에서 홀수 패리티를 갖는 반면,

\mathfrak{h}

는 짝수 패리티를 갖는다. 즉, 점

p \in M

에서의 카르탕 인볼루션을

\theta_p

로 나타내면 다음이 성립한다.

:

\left.\theta_p\right|_{\mathfrak{m}} = -Id

:

\left.\theta_p\right|_{\mathfrak{h}} = +Id

여기서

Id

는 항등 맵이다. 이로부터 부분 공간

\mathfrak{h}

는

\mathfrak{g}

의 리 부분 대수이며, 다음이 성립한다.

:

[\mathfrak{h}, \mathfrak{h}] \subset \mathfrak{h}

짝수 및 홀수 패리티 부분 공간이므로, 리 괄호는 다음과 같이 분리된다.

:

[\mathfrak{h}, \mathfrak{m}] \subset \mathfrak{m}

:

[\mathfrak{m}, \mathfrak{m}] \subset \mathfrak{h}

위의 분해는 대칭 공간

M

의 모든 점

p \in M

에서 성립한다.^[6] 이 분해는 더 일반적인 설정에서도 성립하지만, 반드시 다양체의 모든 점에서 성립하는 것은 아니다.

대칭 공간의 특수한 경우,

T_pM \cong \mathfrak{m}

임을 명시적으로 알 수 있다. 즉, 킬링 벡터장은 대칭 공간의 전체 접 공간을 span한다. 동등하게, 곡률 텐서는 국소적으로 대칭인 공간에서 공변적으로 일정하며, 따라서 이들은 국소적으로 평행화 가능하다. 이는 카르탕-앰브로즈-힉스 정리이다.

6. 역사

빌헬름 킬링이 1892년에 도입하였다.^[19] 킬링은 킬링 벡터장에 대하여 특별한 이름을 붙이지 않았으나, 이후 1926년 저서에서 루서 팔러 아이전하트(1876~1965)가 이 조건을 "킬링 방정식"(equations of Killing|킬링 방정식^영어)이라고 지칭하였다.^[20]

참조

_[1] 서적 Riemannian Geometry and Geometric Analysis Springer-Verlag
_[2] 서적 Introduction to General Relativity https://archive.org/[...] McGraw-Hill
_[3] 서적 Gravitation W H Freeman and Company
_[4] 서적 Spacetime and Geometry: An Introduction to General Relativity https://archive.org/[...] Addison Wesley
_[5] 간행물 The index of symmetry of compact naturally reductive spaces 2014
_[6] 서적 Riemmanian Geometry and Geometric Analysis Springer
_[7] 서적 Spacetime and Geometry: An Introduction to General Relativity https://archive.org/[...] Addison Wesley
_[8] citation Analysis, Manifolds and Physics https://archive.org/[...] Elsevier
_[9] 서적 Gravitation W H Freeman and Company
_[10] 서적 An Introduction to General Relativity Spacetime and Geometry Addison Wesley
_[11] 서적 An Introduction to General Relativity Spacetime and Geometry Addison Wesley
_[12] citation Analysis, Manifolds and Physics Elsevier
_[13] 서적 현대 기하학 입문 京文社 2002
_[14] 서적 General relativity http://press.uchicag[...] University of Chicago Press 1984-06
_[15] 저널 Black hole in a uniform magnetic field 1974-09-15
_[16] 서적 Supersymmetry and supergravity Princeton University Press 1992
_[17] 서적 Supergravity http://cambridge.org[...] Cambridge University Press 2012-04
_[18] 저널 Mathematical general relativity: a sampler 2010-10
_[19] 저널 Ueber die Grundlagen der Geometrie http://resolver.sub.[...] 1892
_[20] 서적 Riemannian geometry https://archive.org/[...] Princeton University Press 1926

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com