리 지수 사상

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 구체적 정의
3. 성질
4. 예
5. 리만 기하학과의 비교
6. 로그 좌표
참조

1. 개요

리 지수 사상은 리 군의 리 대수 원소를 해당 리 군의 원소로 대응시키는 함수이다. 행렬 리 군의 경우 행렬 지수와 일치하며, 일반적인 경우 1-매개변수 부분군을 통해 정의된다. 리 지수 사상은 매끄러운 함수이며, 0에서의 미분은 항등 사상이다. 이 사상은 가환 그림을 가지며, 리 군의 성질과 관련하여 다양한 항등식을 만족한다. 리 지수 사상은 전사 함수가 아닐 수 있으며, 아벨 리 군, SU(2), SL(2;ℝ) 등 다양한 예시가 존재한다. 또한, 리만 기하학의 지수 사상과 연관되며, 로그 좌표계를 정의하는 데 사용된다.

더 읽어볼만한 페이지

리 대수 - 베유 대수
베유 대수는 체 K 위의 리 대수 g에 대하여 정의되는 미분 등급 대수이며, g의 쌍대 공간과 그 등급 이동으로 생성되는 외대수와 대칭 대수의 텐서곱으로 표현되고, 리 군의 분류 공간의 주다발의 무한소 형태를 나타내는 완전열과 관련이 있다.
리 대수 - 아핀 리 대수
아핀 리 대수는 카츠-무디 대수의 특수한 경우로, 유한 차원 단순 리 대수에 대응하는 루프 대수의 중심 확장으로 구성되며, 딘킨 도표를 통해 분류되고, 끈 이론과 2차원 등각장론 등 다양한 분야에 응용된다.
리 군 - 리 대수
리 대수는 가환환 위의 가군과 리 괄호 연산으로 구성되며 쌍선형성, 교대성, 야코비 항등식을 만족하고, 리 군 연구와 분류, 표현 이론에 중요한 역할을 한다.
리 군 - 보렐-베유-보트 정리
보렐-베유-보트 정리는 복소수 반단순 리 군의 표현론에서 층 코호몰로지를 사용하여 리 군의 기약 표현을 설명하며, 보렐-베유 정리와 보트의 일반화를 포함한다.

리 지수 사상
리 이론에서의 지수 사상
정의	리 대수에서 대응하는 리 군으로의 사상
세부 사항
유형	미분 기하학, 리 군론

2. 정의

리 군 $G$ 와 그 리 대수 $\mathfrak g$ 가 주어졌을 때, 지수 사상 $\exp\colon \mathfrak g \to G$ 는 리 대수의 원소를 리 군의 원소로 대응시키는 함수이다. 지수 사상은 리 대수의 원소 $x$ 에 대하여, $\gamma_x(0) = 1$ 이고 $\dot\gamma_x(0) = x$ 를 만족하는 유일한 군 준동형 함수 $\gamma_x\colon \mathbb R\to G$ 를 통해 정의된다. 즉, $\exp_G \colon x \mapsto \gamma_x(1)$ 이다.^[1]

행렬 리 군의 경우, 지수 사상은 행렬 지수와 일치하며, 일반적인 급수 전개로 표현할 수 있다.^[1]

2. 1. 구체적 정의

리 군

G

의 리 대수

\operatorname{Lie}(G)=\mathfrak g

가 주어졌을 때, '''지수 사상'''은

\mathfrak g

에서

G

로 가는 사상이며, 다음과 같이 여러 방법으로 정의할 수 있다.

$\exp(X) = \gamma(1)$ . 여기서 $\gamma\colon \mathbb R \to G$ 는 항등원에서의 접벡터가 $X$ 인 $G$ 의 유일한 1-매개변수 부분군이다. 연쇄 법칙에 의해 $\exp(tX) = \gamma(t)$ 이다.
평행 이동이 왼쪽 이동으로 주어지는 $G$ 위의 표준적인 왼쪽 불변 아핀 접속의 지수 사상. 즉, $\exp(X) = \gamma(1)$ 이며, 여기서 $\gamma$ 는 시작점이 항등원이고 시작 속도가 $X$ 인 유일한 측지선이다.
$G$ 의 표준적인 오른쪽 불변 아핀 접속의 지수 사상. 이는 보통 표준적인 왼쪽 불변 접속과는 다르지만, 두 접속 모두 동일한 측지선을 가지므로 동일한 지수 사상을 제공한다.
리 군-리 대수 대응을 통해 정의할 수 있다. $\mathfrak g$ 의 원소 $X$ 에 대해, $t \mapsto \exp(tX)$ 는 리 대수 준동형 $t \mapsto tX$ 에 대응하는 유일한 리 군 준동형이다.

행렬 리 군의 경우, 지수 사상은 행렬 지수와 일치하며, 다음과 같은 급수 전개로 주어진다.

:

\exp (X) = \sum_{k=0}^\infty\frac{X^k}{k!} = I + X + \frac{1}{2}X^2 + \frac{1}{6}X^3 + \dotsb

(여기서

I

는 항등 행렬이다.)

3. 성질

리 지수 사상은 매끄러운 함수이며, 그 치역은 리 군 $G$ 의 항등원을 포함하는 연결 성분 $G_1$ 의 부분 집합이다.^[2] 0에서의 미분은 항등 사상이다.^[3]

리 지수 사상은 다음 항등식들을 만족시킨다.^[2]

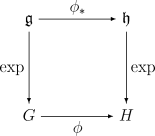
$\exp((s+t)x) = \exp(sx) \exp(tx)\qquad(s,t\in\mathbb R,\;x\in\mathfrak g)$
$\exp(-x) = \exp(x)^{-1} \qquad(x\in\mathfrak g)$
$\exp(x+y) = \exp(x)\exp(y)\qquad(x,y\in\mathfrak g,\;[x,y]=0)$

마지막 항등식에서

x

와

y

가 교환 가능하다는 가정은 중요하다.^[2]

또한, 리 군의 스스로의 리 대수 위의 딸림표현에 대하여 다음이 성립한다.^[9]

:

\operatorname{Ad}_{\exp x}(y) = \sum_{k=0}^\infty \frac1{k!}\operatorname{ad}_x^k(y) =y + [x,y] + \frac12[x,[x,y]] + \frac16[x,[x,[x,y]]] + \dotsb

리 지수 함수는 함자성을 가지며, 두 리 군 사이의 매끄러운 군 준동형

f\colon G\to H

는 리 대수 사이의 준동형

f_*\colon \operatorname{Lie}(G)\to\operatorname{Lie}(H)

를 유도한다. 다음 그림은 가환 그림이다.^[8]

리 군

G

가 다음 조건 중 하나 이상을 만족하면, 리 지수 사상은 전사 함수이다.^[5]^[6]

$G$ 는 연결 공간이며 콤팩트 공간이다.
$G$ 는 연결 공간이며 멱영군이다.
$G$ 는 $\operatorname{GL}(n;\mathbb C)$ 의, 이산군에 대한 몫군이다.

하지만, ''SL''₂('''R''')과 같이 연결되어 있지만 콤팩트하지 않은 군의 경우, 지수 사상은 전사 함수가 아닐 수 있다.^[7]

4. 예

복소 평면에서 0을 중심으로 하는 단위 원은 원군이라고 불리는 리 군이며, 1에서의 접선 공간은 복소 평면의 허수선 $\{it:t\in\mathbb R\}$ 과 동일시될 수 있다. 이 리 군에 대한 지수 사상은 다음과 같이 일반적인 복소 지수와 동일한 공식으로 주어진다.

::

it \mapsto \exp(it) = e^{it} = \cos(t) + i\sin(t),\,

사원수 $\mathbb H$ 에서, 단위 길이 사원수의 집합은 1에서의 접선 공간이 순수 허수 사원수의 공간, $\{it+ju + kv :t, u, v\in\mathbb R\}$ 와 동일시될 수 있는 리 군(특수 유니타리 군과 동형)을 형성한다. 이 리 군에 대한 지수 사상은 다음과 같다.

::

\mathbf{w} := (it+ju+kv) \mapsto \exp(it+ju+kv) = \cos(|\mathbf{w}|)1 + \sin(|\mathbf{w}|)\frac{\mathbf{w}}

.\,

: 이 맵은 순수 허수 사원수 내에서 반지름 R의 2-구면을

\{s\in S^3 \subset \mathbf{H}: \operatorname{Re}(s) = \cos(R)\}

, 반지름

\sin(R)

의 2-구면으로 보낸다 (참조: 파울리 벡터의 지수).

유한 차원 실수 벡터 공간을 ''V''라고 하고 벡터 덧셈 연산 하에서 리 군으로 볼 때, $\operatorname{Lie}(V) = V$ 는 0에서의 접선 공간과의 식별을 통해, 지수 사상

::

\operatorname{exp}: \operatorname{Lie}(V) = V \to V

:은 항등 사상이다. 즉,

\exp(v)=v

이다.

분할 복소수 평면 $z = x + y \jmath , \quad \jmath^2 = +1,$ 에서 허수선 $\lbrace \jmath t : t \in \mathbb R \rbrace$ 는 단위 쌍곡선 군 $\lbrace \cosh t + \jmath \ \sinh t : t \in \mathbb R \rbrace$ 의 리 대수를 형성한다. 지수 사상은 다음과 같다.

::

\jmath t \mapsto \exp(\jmath t) = \cosh t + \jmath \ \sinh t.

4. 1. 아벨 리 군

아벨 군 리 군

G=\mathbb R^n

의 리 지수 사상은 다음과 같이 단순한 지수 함수로 주어진다.^[1]

:

\mathfrak g=\mathbb R^n

:

\exp_G\colon\mathfrak g\to G

:

\exp_G\colon (x_1,\dotsc,x_n) \mapsto (\exp x_1,\dotsc,\exp x_n)

마찬가지로,

G=\operatorname U(1) = \{z\in\mathbb C\colon |z|=1\}

(단위 복소수의 곱셈군)가 아벨 리 군일 때, 리 지수 사상은 다음과 같다.

:

\mathfrak g = \mathrm i\mathbb R

:

\exp_G \colon \mathfrak g\to G

:

\exp_G \colon \mathrm i\theta \mapsto \exp(\mathrm i\theta)

복소 평면에서 0을 중심으로 하는 단위원은 원군이라고 불리는 리 군이며, 1에서의 접선 공간은 복소 평면의 허수선

\{it:t\in\mathbb R\}

과 동일시될 수 있다. 이 리 군에 대한 지수 사상은 다음과 같이 일반적인 복소 지수와 동일한 공식으로 주어진다.

:

it \mapsto \exp(it) = e^{it} = \cos(t) + i\sin(t),\,

4. 2. SU(2)

사원수

\mathbb H

에서 단위 길이 사원수의 집합은 1에서의 접선 공간이 순수 허수 사원수의 공간,

\{it+ju + kv :t, u, v\in\mathbb R\}

와 동일시될 수 있는 리 군(특수 유니타리 군과 동형)을 형성한다. 이 리 군에 대한 지수 맵은 다음과 같다.^[1]

:

\mathbf{w} := (it+ju+kv) \mapsto \exp(it+ju+kv) = \cos(|\mathbf{w}|)1 + \sin(|\mathbf{w}|)\frac{\mathbf{w}}

.\,

이 맵은 순수 허수 사원수 내에서 반지름 R의 2-구면을

\{s\in S^3 \subset \mathbf{H}: \operatorname{Re}(s) = \cos(R)\}

, 반지름

\sin(R)

의 2-구면으로 보낸다. (참조: 파울리 벡터의 지수)

4. 3. SL(2;ℝ)

리 군

\operatorname{SL}(2;\mathbb R)

의 리 지수 사상은 전사 함수가 아니다.^[10] 그 치역은 다음 조건들 가운데 적어도 하나를 만족시키는 2×2 실수 행렬들로 구성된다.

복소수체에서 대각화가 가능하며, 그 고윳값은 모두 실수이다.
복소수체에서 대각화가 가능하며, 그 고윳값은 모두 절댓값이 1인 복소수이다.
고윳값 1이 중복해서 등장한다.
$\operatorname{diag}(-1,-1)$ 이다.

특히, 예를 들어

\operatorname{diag}(-1,-2)\in \operatorname{SL}(2;\mathbb R)

는 리 지수 사상의 치역에 포함되지 않는다.

5. 리만 기하학과의 비교

만약 ''G''가 콤팩트이면, 왼쪽과 오른쪽 이동에 대해 불변인 리만 계량을 가지며, 이 경우 ''G''에 대한 리 군 지수 사상은 이 리만 계량의 지수 사상과 일치한다.

일반적인 ''G''의 경우에는 왼쪽과 오른쪽 이동 모두에 대해 불변인 리만 계량이 존재하지 않는다. 예를 들어, 왼쪽 이동에 대해 불변인 리만 계량은 항상 존재하지만, 좌-불변 계량에 대한 리만 기하학적 의미의 지수 사상은 일반적으로 리 군적 의미의 지수 사상과는 일치하지 않는다. 즉, ''G''가 왼쪽 불변이지만 오른쪽 불변은 아닌 계량을 갖춘 리 군인 경우, 항등원을 통과하는 측지선은 일반적으로 ''G''의 일변수 부분군이 아니다.

6. 로그 좌표

역함수 정리에 의해, 지수 함수 $\operatorname{exp} : N \overset{\sim}\to U$ 는 원점의 어떤 근방 $N \subset \mathfrak{g} \simeq \mathbb{R}^n$ 에서 리 군 $G$ 의 항등원 $e \in G$ 의 근방 $U$ 로의 미분 동형 사상이다. 그 역함수는 다음과 같다.

: $\log: U \overset{\sim}\to N \subset \mathbb{R}^n$

그리고 이것은 ''U''에 대한 좌표계이다. 이것은 로그 좌표, 지수 좌표 또는 정규 좌표와 같은 다양한 이름으로 불린다. 응용 분야에서 어떻게 사용되는지에 대한 예는 닫힌 부분군 정리를 참조하라.

참조

_[1] 서적 Complex Abelian Varieties https://www.worldcat[...] Springer Berlin Heidelberg 2004
_[2] 문서 This follows from the [[Baker-Campbell-Hausdorff formula]].
_[3] 참고
_[4] 참고
_[5] 참고
_[6] 참고
_[7] 참고
_[8] 참고
_[9] 참고
_[10] 서적 Lie Groups, Lie Algebras, and Representations: An Elementary Introduction Springer-Verlag

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com