삼각지붕
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
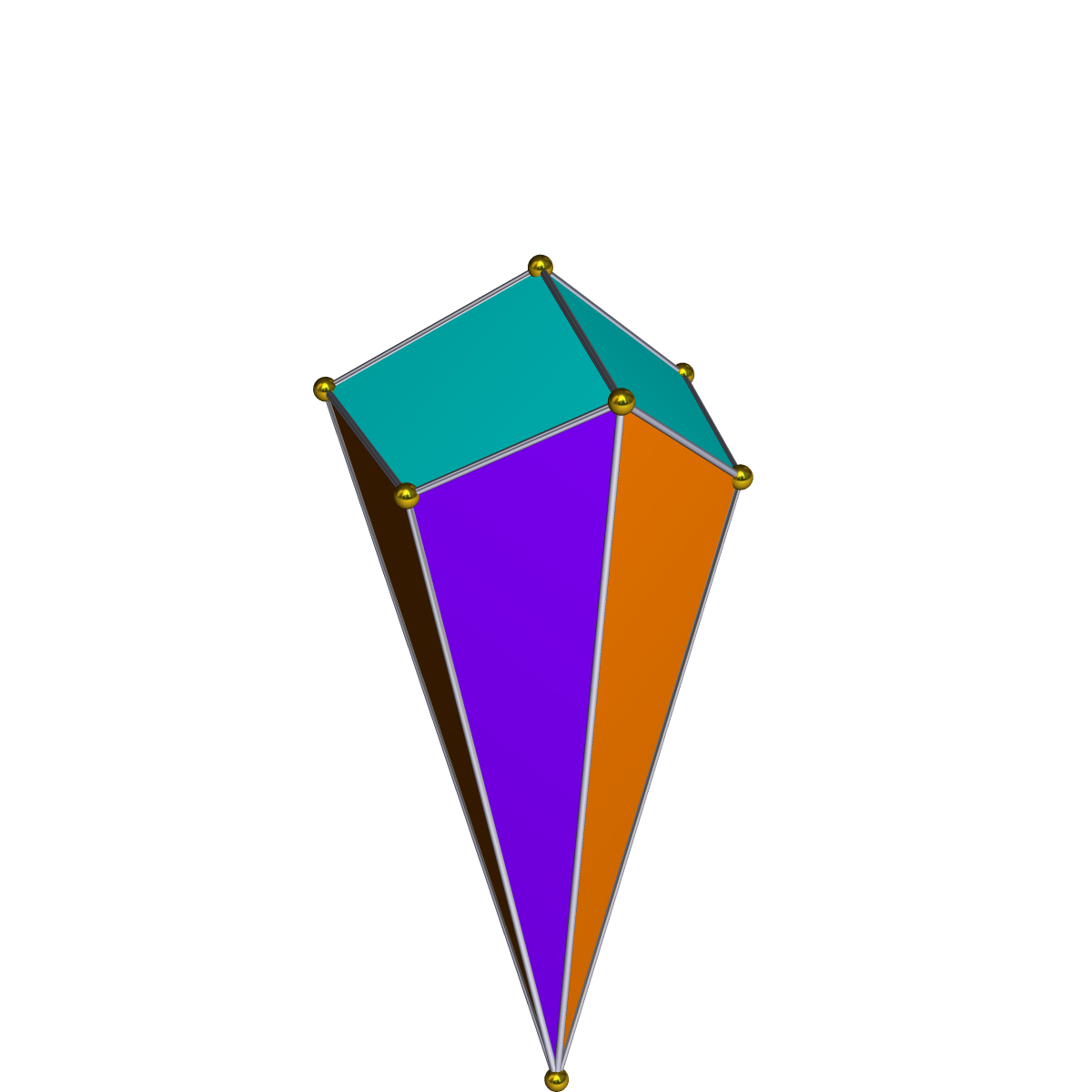
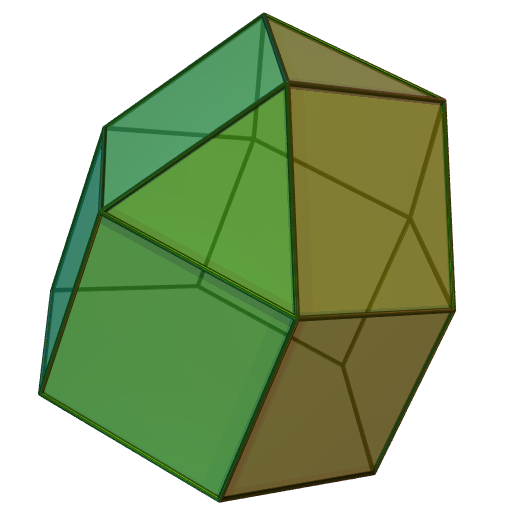
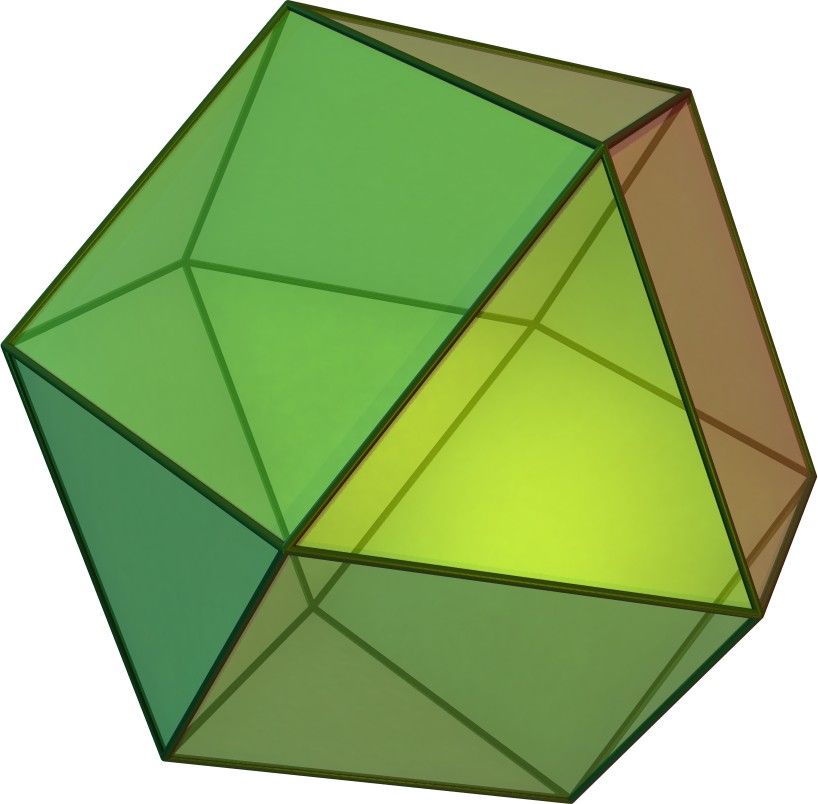
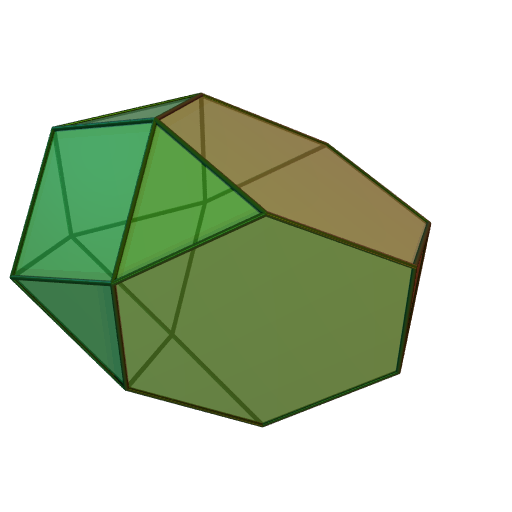
삼각지붕은 4개의 정삼각형, 3개의 정사각형, 1개의 정육각형을 면으로 가지는 다면체이다. 모든 면이 정다각형인 볼록 다면체인 존슨의 다면체 중 하나이며, 세 번째 존슨의 다면체(J₃)로 분류된다. 삼각지붕은 대칭축을 가지며, 120° 및 240° 회전 시 대칭을 이루고, 쌍대다면체는 6개의 삼각형 면과 3개의 연꼴 면으로 구성된다. 사각뿔 및/또는 정팔면체와 함께 공간 테셀레이션을 이룰 수 있으며, 다른 다면체와 결합하여 다양한 형태를 만들 수 있다.
더 읽어볼만한 페이지
- 기둥형 다면체 - 직육면체
직육면체는 6개의 직사각형 면으로 이루어진 볼록 다면체로, 모든 이면각이 직각이고 마주보는 면이 합동인 특징을 가지며, 정사각형 직육면체와 정육면체 같은 특수한 경우가 있고 부피, 표면적, 공간 대각선은 가로, 세로, 높이로 계산하며, 공간 감각과 기하학적 개념 이해에 중요한 역할을 한다. - 기둥형 다면체 - 오각지붕
오각지붕은 5개의 정삼각형, 5개의 정사각형, 1개의 정오각형, 1개의 정십각형으로 이루어진 존슨의 다면체이며, 회전 대칭을 갖고, 다양한 다면체를 구성하는 데 사용된다. - 존슨의 다면체 - 삼각쌍뿔
삼각쌍뿔은 6개의 정삼각형 면, 5개의 꼭짓점, 9개의 모서리를 가진 존슨 다면체이자 델타다면체로, 두 정사면체를 밑면끼리 결합한 형태이며, 분자 기하학, 색채 이론 등 다양한 분야에 응용된다. - 존슨의 다면체 - 오각지붕
오각지붕은 5개의 정삼각형, 5개의 정사각형, 1개의 정오각형, 1개의 정십각형으로 이루어진 존슨의 다면체이며, 회전 대칭을 갖고, 다양한 다면체를 구성하는 데 사용된다.
2. 공식
모든 면이 정다면체이고 변의 길이가 ''a''인 경우, 부피(V)와 표면적(A)은 다음과 같다:[11]
삼각 큐폴라는 4개의 정삼각형, 3개의 정사각형, 1개의 정육각형으로 이루어져 있다. 밑면은 육각형이고, 4개의 삼각형 중 하나는 꼭대기에 있다. 모든 모서리의 길이가 같으면, 정삼각형과 육각형은 정다각형이 된다.[1] 삼각형과 육각형 사이의 이각은 약 70.5°, 정사각형과 육각형 사이는 54.7°, 정사각형과 삼각형 사이는 125.3°이다.[2] 모든 면이 정다각형인 볼록 다면체는 존슨의 다면체이며, 삼각 큐폴라는 그중 하나로, 세 번째 존슨의 다면체()이다.[3]
삼각지붕의 쌍대다면체는 삼각형 면 6개와 연꼴 면 3개를 가진다.
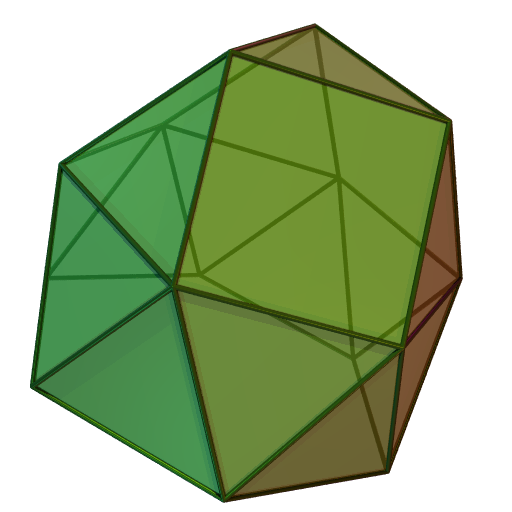
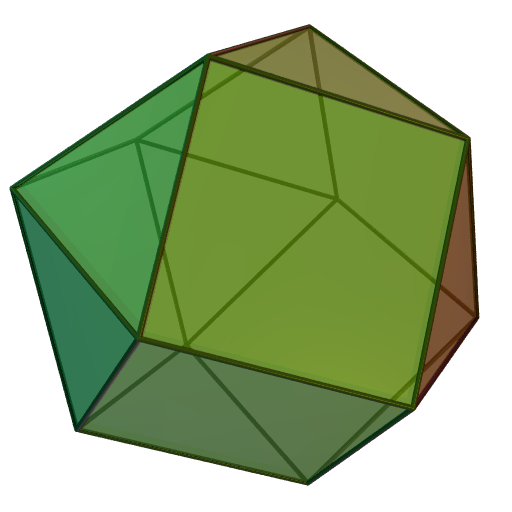
삼각지붕은 사각뿔 및/또는 정팔면체와 함께 공간 테셀레이션을 이룰 수 있다. 이는 정팔면체와 육팔면체가 공간을 채우는 것과 유사한 방식이다.[12] 삼각 돔은 깎인 정팔면체의 구성에서 반구로 간주될 수 있다.
[1]
논문
Regular-faced convex polyhedra
:
:
삼각지붕의 높이 는 다음과 같다:
:
3. 성질
를 삼각 큐폴라의 모서리 길이라고 하면, 표면적 는 다음과 같이 4개의 정삼각형, 3개의 정사각형, 1개의 육각형의 면적을 더하여 계산할 수 있다.[1]
:
높이 와 부피 는 다음과 같다:[4][1]
:
꼭대기와 밑면의 중심을 통과하는 대칭축이 있으며, 전체 회전 각도의 1/3 및 2/3 회전했을 때 대칭을 이룬다. 육각형 밑면의 이등분선을 통과하는 수직 평면에 대해서도 거울 대칭을 이룬다. 따라서 피라미드 대칭을 가지며, 순환군 의 차수는 6이다.[2]
4. 쌍대다면체
5. 관련 다면체와 벌집
삼각 돔의 밑면에 정육각기둥을 붙이면 늘린 삼각 돔(J₁₈), 정반육각기둥을 붙이면 회전 늘린 삼각 돔(J₂₂)이 된다. 삼각 돔 두 개를 밑면끼리 붙이면 동상 쌍삼각 돔(J₂₇)이 된다. 만약 밑면끼리 60° 어긋나게 붙이면 깎은 정육면체가 된다. 깎은 사면체의 밑면에 삼각 돔을 붙이면 옆면 늘린 깎은 사면체(J₆₅)가 된다.
정사각 돔, 정오각 돔은 삼각 돔에서 밑면의 변의 개수를 늘린 형태이다. 삼각지붕은 사각지붕 3개를 붙여 동일평면 상의 면을 만들 수 있지만, 동일평면 상의 면이 존재하므로 존슨의 다면체는 아니다.
참조
[2]
서적
Polyhedra
https://archive.org/[...]
Cambridge University Press
[3]
논문
2642. Unitary Construction of Certain Polyhedra
[4]
논문
Logical and Geometrical Distance in Polyhedral Aristotelian Diagrams in Knowledge Representation
2017
[5]
논문
Convex polyhedra with regular faces
[6]
논문
Area and volume of the Johnson solid
https://www.problema[...]
2020-09-08
[7]
서적
Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem
https://books.google[...]
Hindustan Book Agency
[8]
논문
Composite Concave Cupolae as Geometric and Architectural Forms
https://www.helderma[...]
[9]
서적
Introduction to Computational Origami: The World of New Computational Geometry
https://books.google[...]
Springer
[10]
인용
Convex polyhedra with regular faces
[11]
웹사이트
Triangular cupola
http://www.wolframal[...]
2010-07-20
[12]
웹사이트
http://woodenpolyhed[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com