고속 푸리에 변환

3. 정의

신호 $x\_0,\; ...,\; x\_\{N-1\}$가 복소수라고 가정할 때, DFT는 다음과 같이 정의한다.^[11]

:$f\_k\; =\; \backslash sum\_\{n=0\}^\{N-1\}\; x\_n\; e^\{-\{2\backslash pi\; i\; \backslash over\; N\}\; kn\; \}\; \backslash qquad\backslash qquad\; k\; =\; 0,\backslash dots,N-1$

$W\_N\; =\; e^\{-2\backslash pi\; i/N\}$ 을 회전자(Twiddle factor)라고 부르며, 1의 거듭제곱근(Root of unity), 단위근도 회전자의 다른 호칭이다. 이 회전자를 사용해 식을 다시 정리하면 다음과 같다.

:$f\_k\; =\; \backslash sum\_\{n=0\}^\{N-1\}\; x\_n\; W\_N^\{kn\}\; \backslash qquad\backslash qquad\; k\; =\; 0,\backslash dots,N-1$

회전자는 N에 관한 주기성으로 인해 다음과 같은 성질을 가진다.

:$W\_N^\{k+N\}=W\_N^k$

:$W\_N^\{k+N/2\}=-W\_N^k$

:$W\_a^b=W\_\{na\}^\{nb\}\backslash qquad$ (n은 자연수)

(예 1)

:$W\_4^6=W\_4^2,\backslash qquad\; W\_2^1=W\_4^2\; =W\_8^4,\backslash qquad\; W\_4^\{(k+4/2)\}=W\_4^kW\_4^2=-W\_4^k$

$x\_0,\; \backslash ldots,\; x\_\{n-1\}$을 복소수라고 할 때, DFT는 다음 공식으로 정의된다.

:$X\_k\; =\; \backslash sum\_\{m=0\}^\{n-1\}\; x\_m\; e^\{-i2\backslash pi\; k\; m/n\}\; \backslash qquad\; k\; =\; 0,\backslash ldots,n-1,$

여기서 $e^\{i\; 2\backslash pi/n\}$은 1의 n차 원시근이다.

이 정의를 직접 계산하려면 $O(n^2)$ 연산이 필요하다. 즉, n개의 출력 $X\_k$가 있으며, 각 출력은 n개 항의 합을 필요로 한다. FFT는 동일한 결과를 $O(n\; \backslash log\; n)$ 연산으로 계산하는 모든 방법을 말한다.

복소 함수 $f(x)$의 이산 푸리에 변환인 복소 함수 $F(t)$는 다음과 같이 정의된다.

:$F(t)=\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; \backslash exp\backslash left(-i\backslash frac\{2\; \backslash pi\; t\; x\}\{N\}\; \backslash right)$

이 때, $\backslash \{x\; =\; 0,\; 1,\; 2,\; ...,\; N\; -\; 1\backslash \}$을 표본점이라고 한다.

이산 푸리에 변환을

:$F(t)\; =\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; \backslash exp\backslash left(-i\backslash frac\{2\; \backslash pi\; t\; x\}\{N\}\backslash right)$

로 정의했을 때, 역변환은

:$f(x)\; =\; \backslash frac\{1\}\{N\}\; \backslash sum\_\{t=0\}^\{N-1\}\; F(t)\; \backslash exp\backslash left(i\backslash frac\{2\backslash pi\{tx\}\}\{N\}\backslash right)$

= \frac{1}{N} \overline{ \sum_{t=0}^{N-1} \overline{F(t)} \exp\left(-i\frac{2 \pi t x}{N} \right)}

가 된다.

4. 알고리즘

쿨리-튜키 알고리즘은 가장 널리 사용되는 고속 푸리에 변환(FFT) 알고리즘이다. 분할 정복 알고리즘을 사용하여 이산 푸리에 변환(DFT)를 더 작은 크기의 DFT로 분할하여 계산량을 줄인다. 일반적으로 입력 신호의 크기 ''N''이 2의 거듭제곱인 경우에 가장 효율적이지만, ''N''이 임의의 합성수일 때에도 적용 가능하다.

• '''분할(Decimation)''': 어떤 길이 ''N''인 수열을 짝수 및 홀수 인덱스로 나누는 것이다. 쿨리-튜키 알고리즘은 이 분할을 반복하여 계산량을 줄인다.^[6]
• '''다니엘슨-란초스 보조정리''': 1942년 다니엘슨과 란초스가 발견한 공식으로, 길이가 ''N''(짝수)인 이산 푸리에 변환(DFT)을 길이가 ''N/2''인 두 개의 DFT 합으로 표현할 수 있다는 것을 보여준다.
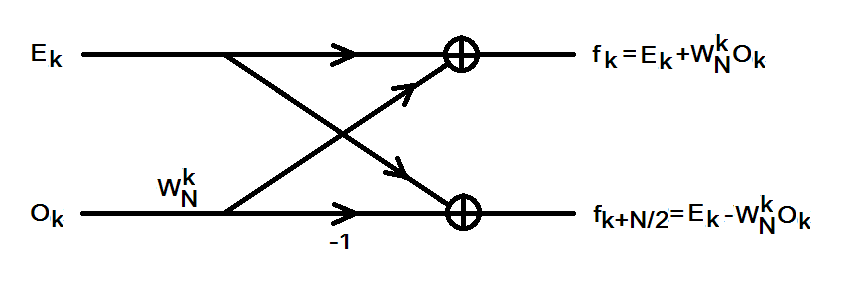
• '''역비트순(Bit-reversed Order)''': Bit reversal|비트 리버설^영어은 ''N''이 2의 거듭제곱일 때, 분할을 반복하면 입력 신호의 순서가 바뀌는 현상을 말한다. 이 순서는 이진수로 표현했을 때 비트 순서를 뒤집은 것과 같다.
• '''푸리에 행렬(Fourier Matrix)''': 회전자로 이루어진 차수(order) N의 복소 방데르몽드 행렬을 푸리에 행렬이라 한다.

• 소인수 알고리즘 (PFA)
• 브룬 FFT 알고리즘
• 레이더의 FFT 알고리즘
• 블루스타인 FFT 알고리즘 (Chirp Z-변환)
• 오들리츠코-쇤하게 알고리즘
• 고속 월시-아다마르 변환

4. 1. 쿨리-튜키 알고리즘

4. 1. 1. 분할(Decimation)

4. 1. 2. 다니엘슨-란초스 보조정리(Danielson-Lanczos Lemma)

4. 1. 3. 역비트순(Bit-reversed Order)

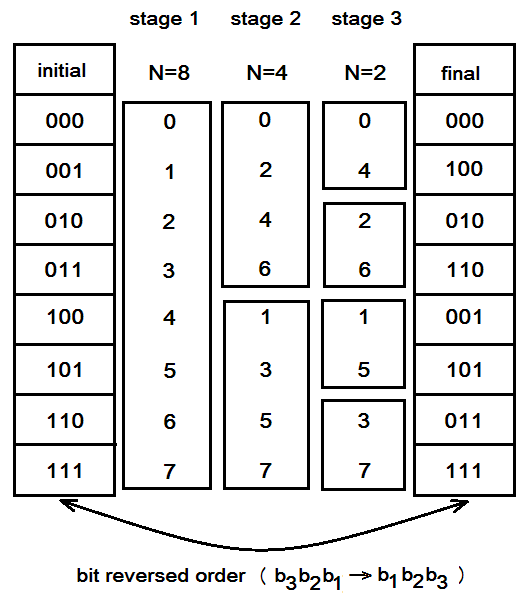
이러한 현상은 신호의 길이 ''N''이 2의 거듭제곱 (''N''=2ⁿ)일 때 항상 나타난다. 만약 계산 구조가 '''in-place''' (입력 신호 메모리 장소에 출력 값을 덮어쓰는 방식) 여야 한다는 요구 조건을 포기하면, 입력 자료와 출력 결과 모두 순서대로 나열되도록 하는 '''out-of-place''' 방식도 가능하다.

컴퓨터 상에서 버터플라이 연산은 비트 반전으로 구현할 수 있다. 일부 DSP는 비트 반전 어드레싱을 갖추고 있어 버터플라이 연산 프로그래밍을 쉽게 할 수 있도록 지원한다.

4. 1. 4. 푸리에 행렬(Fourier Matrix)

회전자로 이루어진 차수(order) N의 복소 방데르몽드 행렬

:$F\_\{jk\}\; =e^\{-2\backslash pi\; i(j-1)(k-1)/N\}$

을 푸리에 행렬(Fourier Matrix)이라고 한다.

이산 푸리에 변환(DFT)은 푸리에 행렬을 사용하여 다음과 같이 행렬 곱셈으로 표현할 수 있다.

: $$

\begin{bmatrix}f_0\\f_1\\f_2\\f_3\\.\\.\\f_{N-1}\end{bmatrix}=

\begin{bmatrix}

W^0&W^0&W^0&.&.&.&W^0\\

W^0&W^1&W^2&.&.&.&W^{N-1}\\

W^0&W^2&W^4&.&.&.&W^{2(N-1)}\\

W^0&W^3&W^6&.&.&.&W^{3(N-1)}\\

.&.&.&.&&&.&\\

.&.&.&&.&&.&\\

W^0&W^{N-1}&W^{2(N-1)}&.&.&.&W^{(N-1)^2}\\

\end{bmatrix}

\begin{bmatrix}x_0\\x_1\\x_2\\x_3\\.\\.\\x_{N-1}\end{bmatrix} \qquad \qquad \qquad (5)



여기서 $W^k=W\_N^k$는 회전자를 의미하며, 편의상 아래첨자 ''N''은 생략한다.

회전자의 주기성으로 인해 $W^0$부터 $W^\{(N-1)^2\}$까지 모두 계산할 필요 없이 $W^\{(N-1)\}$까지만 계산하면 된다.

4. 2. 기수 2 알고리즘(Radix-2 FFT Algorithm)

기수 2 알고리즘은 쿨리-튜키 FFT 알고리즘의 가장 기본적인 형태로, 신호의 길이가 2의 거듭제곱일 때 사용되며, 이산 푸리에 변환(DFT) 계산을 위해 신호를 짝수 번째와 홀수 번째로 나누는 과정을 반복한다.

1805년 카를 프리드리히 가우스는 팔라스와 유노 소행성의 궤도를 계산하기 위해 FFT와 유사한 방법을 사용했다. 1965년 제임스 쿨리와 존 튜키가 발표한 쿨리-튜키 FFT 알고리즘은 가우스의 방법과 매우 유사하며, 더 일반적인 FFT 알고리즘으로 발전했다.

프랭크 예이츠는 1932년 '상호 작용 알고리즘(interaction algorithm)'을 발표하여 아다마르 변환 및 월시 변환을 효율적으로 계산했다. 1942년 G. C. 다니엘슨과 코넬리우스 란초스는 X선 결정학을 위한 DFT 계산 알고리즘을 발표했다. 이들은 "주기성"을 이용하여 계산량을 줄이는 방법을 발견했지만, $O(n\; \backslash log\; n)$ 스케일링을 분석하지는 못했다.

쿨리와 튜키는 이 합성수이고 반드시 2의 거듭제곱일 필요가 없는 경우에도 적용할 수 있는 더 일반적인 FFT를 발표했으며, $O(n\; \backslash log\; n)$ 스케일링을 분석했다. 이 알고리즘은 소련의 핵실험 탐지 및 3차원 헬륨-3 결정의 스핀 방향 주기성 결정 등 다양한 문제에 적용되었다.

이산 푸리에 계수는 1의 원시 N 제곱근 중 하나 $W\_N$을 사용하면 다음과 같이 나타낼 수 있다.

:$F(t)\; =\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; W\_N^\{tx\}\; .$

입력 열 $x\_k$를 첨자의 짝수와 홀수로 나누어 행렬을 변형하고, 크기 N/2의 FFT 연산 결과를 사용하여 표현할 수 있으며, 크기 분할이 가능하다. 이 분할 절차를 그림으로 나타내면 나비와 같은 그림이 되기 때문에, '''버터플라이 연산'''이라고도 불린다.

right

버터플라이 연산은 컴퓨터 상에서 비트 반전으로 실현된다. DSP 중에는 이 버터플라이 연산의 프로그램을 용이하게 하기 위해 비트 반전 어드레싱을 갖춘 것이 있다.

4. 2. 1. 기수(radix)의 의미

'''기수'''(基數)는 밑 또는 기저(radix, base)라고도 불리며, 숫자 표현(진법 체계)의 기준이 되는 수이다. radix는 라틴어로 뿌리(root)라는 뜻이다.

예를 들어, 10진수의 기수는 10이다. 10¹, 10², 10³의 밑은 10이다.

거듭제곱 rⁿ의 기수는 ''r''이다. 여기서 ''n''은 지수(exponent)이다.

(예) N=2ⁿ는 기수 2(radix-2)이다. N=4ⁿ는 기수 4(radix-4)이다.

4. 2. 2. 기수 2 시분할 FFT(Radix-2 Decimation in Time FFT)

기수 2 시분할(Decimation in Time, DIT) FFT는 입력 신호를 시간 영역에서 분할하는 쿨리-튜키 FFT 알고리즘의 대표적인 예시이다.

''N''=4 일 때, 기수 2 시분할 FFT를 유도하면 다음과 같다.

$$

\begin{bmatrix}f_0\\f_1\\f_2\\f_3\end{bmatrix}=

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^1&W^2&W^3\\

W^0&W^2&W^4&W^6\\

W^0&W^3&W^6&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_1\\x_2\\x_3\end{bmatrix}



위 식에서 지수의 짝수, 홀수를 기준으로 열의 순서를 바꾸면 다음과 같이 변형된다.

$$

=

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^2&W^1&W^3\\

W^0&W^4&W^2&W^6\\

W^0&W^6&W^3&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix}



$W^4=W^0,\; \backslash quad\; W^6=W^\{2+4\}=W^\{2+0\}=W^2$ 의 관계를 이용하면

$$

=\begin{bmatrix}

W^0&W^0&W^0W^0&W^0W^0\\

W^0&W^2&W^1W^0&W^1W^2\\

W^0&W^0&W^2W^0&W^2W^0\\

W^0&W^2&W^3W^0&W^3W^2

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix}



$$

=

\begin{bmatrix}

1&0&W^0&0\\

0&1&0&W^1\\

1&0&W^2&0\\

0&1&0&W^3

\end{bmatrix}\,

\begin{bmatrix}

\begin{bmatrix}W^0&W^0\\W^0&W^2\end{bmatrix} \begin{bmatrix}x_0\\x_2\end{bmatrix}\\

\begin{bmatrix}W^0&W^0\\W^0&W^2\end{bmatrix} \begin{bmatrix}x_1\\x_3\end{bmatrix}

\end{bmatrix}



위 식의 $W^2$ 는 N=2 DFT 행렬 안에 있으므로 $W\_4^2\; \backslash rightarrow\; W\_2^1$ 로 변경해서 고쳐쓰면

$=$

\begin{bmatrix}

1&0&W_4^0&0\\

0&1&0&W_4^1\\

1&0&W_4^2&0\\

0&1&0&W_4^3

\end{bmatrix}\,

\begin{bmatrix}

\begin{bmatrix}W_2^0&W_2^0\\W_2^0&W_2^1\end{bmatrix} \begin{bmatrix}x_0\\x_2\end{bmatrix}\\

\begin{bmatrix}W_2^0&W_2^0\\W_2^0&W_2^1\end{bmatrix} \begin{bmatrix}x_1\\x_3\end{bmatrix}

\end{bmatrix}



$W\_4^2\; \backslash rightarrow\; -W\_4^0$, $W\_4^3\; \backslash rightarrow\; -W\_4^1$, $W\_2^1\; \backslash rightarrow\; -W\_2^0$ 이므로 다음과 같은 최종식을 얻는다.

$$

\begin{bmatrix}f_0\\f_1\\f_2\\f_3\end{bmatrix}=

\begin{bmatrix}

1&0&W_4^0&0\\

0&1&0&W_4^1\\

1&0&-W_4^0&0\\

0&1&0&-W_4^1

\end{bmatrix}\,

\begin{bmatrix}

\begin{bmatrix}W_2^0&W_2^0\\W_2^0&-W_2^0\end{bmatrix} \begin{bmatrix}x_0\\x_2\end{bmatrix}\\

\begin{bmatrix}W_2^0&W_2^0\\W_2^0&-W_2^0\end{bmatrix} \begin{bmatrix}x_1\\x_3\end{bmatrix}

\end{bmatrix}



따라서, ''N''=4 인 DFT는 위 식과 같이 ''N/2'' 즉, ''N''=2 인 DFT 두 개를 사용해서 계산할 수 있고, 이는 다니엘슨-란초스 보조정리가 적용됨을 행렬을 이용해 보인 것이다. 그 결과로 입력과 출력이 서로 역비트순이 됨도 알 수 있다. 아래 그림은 위 식의 결과를 나타내는 '''신호흐름도(signal flow graph)'''이며, '''나비도표(butterfly diagram)'''로도 불린다.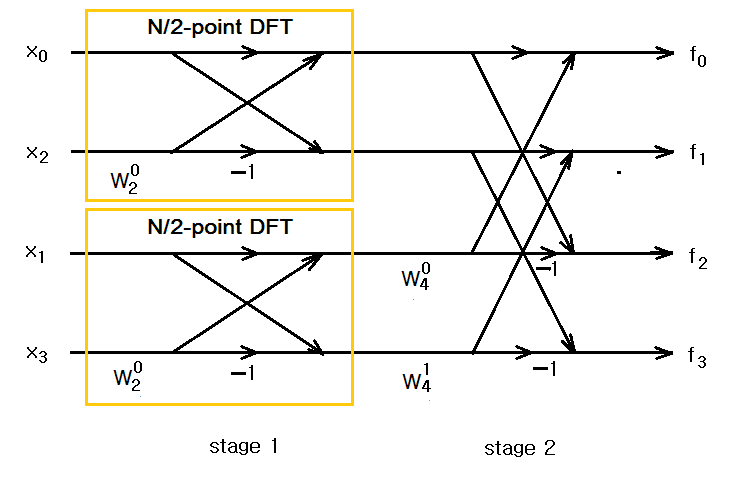

4. 2. 3. 기수 2 주파수분할 FFT(Radix-2 Decimation in Frequency FFT)

기수 2 주파수분할 FFT(Radix-2 Decimation in Frequency FFT)는 입력 신호를 주파수 영역에서 분할하는 고속 푸리에 변환(FFT) 알고리즘이다.

이산 푸리에 계수는 1의 원시 N 제곱근 중 하나 $W\_N$을 사용하면 다음과 같이 나타낼 수 있다.

:$F(t)\; =\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; W\_N^\{tx\}\; .$

예를 들어, $N\; =\; 4$일 때, $F(t)=X\_t$, $f(k)=\; x\_k$로 하면, 이산 푸리에 계수는 행렬을 사용하여 표현하면 ($W\; =\; W\_4$로 약기) 다음과 같다.

:$$

\begin{bmatrix}X_0\\X_1\\X_2\\X_3\end{bmatrix}=

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^1&W^2&W^3\\

W^0&W^2&W^4&W^6\\

W^0&W^3&W^6&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_1\\x_2\\x_3\end{bmatrix}



입력 열 $x\_k$를 첨자의 짝수와 홀수로 나누어 다음과 같이 변형한다.

:$$

\begin{align}

\begin{bmatrix}X_0\\X_1\\X_2\\X_3\end{bmatrix}

& =

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^2&W^1&W^3\\

W^0&W^4&W^2&W^6\\

W^0&W^6&W^3&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix} \\

& =

\begin{bmatrix}

W^0&W^0&W^0W^0&W^0W^0\\

W^0&W^2&W^1W^0&W^1W^2\\

W^0&W^0&W^2W^0&W^2W^0\\

W^0&W^2&W^3W^0&W^3W^2

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix}

\end{align}



($\backslash because\; W^\{k+N\}=W^k$)

그러면, 크기 2의 FFT 연산 결과를 사용하여 표현할 수 있고, 크기 분할이 가능하다.

:$\backslash begin\{bmatrix\}X\_0\backslash \backslash X\_1\backslash \backslash X\_2\backslash \backslash X\_3\backslash end\{bmatrix\}=$

\begin{bmatrix}

1&0&W^0&0\\

0&1&0&W^1\\

1&0&W^2&0\\

0&1&0&W^3

\end{bmatrix}\,

\begin{bmatrix}

W_2^0&W_2^0&0&0\\

W_2^0&W_2^1&0&0\\

0&0&W_2^0&W_2^0\\

0&0&W_2^0&W_2^1

\end{bmatrix}\,

\begin{bmatrix}

x_0\\

x_2\\

x_1\\

x_3

\end{bmatrix}



이 분할 절차를 그림으로 나타내면 나비와 같은 그림이 되기 때문에, '''버터플라이 연산'''이라고도 불린다. --

버터플라이 연산은 컴퓨터 상에서 비트 반전으로 실현된다. DSP 중에는, 이 버터플라이 연산의 프로그램을 용이하게 하기 위해, 비트 반전 어드레싱을 갖춘 것이 있다.

4. 3. 공통인수 FFT(Common-Factor FFT)

쿨리-튜키 알고리즘은 가장 널리 사용되는 고속 푸리에 변환(FFT) 알고리즘으로, 신호의 길이가 임의의 합성수일 때 사용할 수 있어 쿨리-튜키 알고리즘의 일반화된 형태로 볼 수 있다.

FFT의 원리는 N차 이산 푸리에 변환을 P차 이산 푸리에 변환과 Q차 이산 푸리에 변환으로 분해하는 것이다.^[6]

n, k를 다음과 같이 바꿔 쓴다. (단, 0 ≤ s ≤ P - 1, 0 ≤ r ≤ Q - 1 그리고 0 ≤ p ≤ P - 1, 0 ≤ q ≤ Q - 1)

:$\backslash begin\{align\}$

n &= sQ+r \\

k &= qP+p

\end{align}

N차 이산 푸리에 변환은 다음과 같다.

:$F(n)\; =\; \backslash sum\_\{k=0\}^\{N-1\}f(k)\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{nk\}\{N\}\backslash right)$

위 식에 따라 다음을 얻는다.

:$\backslash begin\{align\}$

F(n) &= F(sQ+r) = \sum_{p=0}^{P-1}\sum_{q=0}^{Q-1}f(qP+p)\exp\left(-2\pi i\frac{(qP+p)(sQ+r)}{PQ}\right) \\

&= \sum_{p=0}^{P-1}\sum_{q=0}^{Q-1}f(qP+p)\exp\left(-2\pi i\left(\frac{rq}{Q}+\frac{sp}{P}+\frac{pr}{PQ}\right)\right) \\

&= \sum_{p=0}^{P-1}\left[\exp\left(-2\pi i\left(\frac{sp}{P}+\frac{pr}{PQ}\right)\right)\sum_{q=0}^{Q-1}f(qP+p)\exp\left(-2\pi i\frac{rq}{Q}\right)\right]\end{align}

여기서,

:$f\_1(p,r)\; =\; \backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{pr\}\{PQ\}\backslash right)\backslash sum\_\{q=0\}^\{Q-1\}f(qP+p)\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{rq\}\{Q\}\backslash right)$

로 놓으면,

:$F(n)\; =\; F(sQ+r)\; =\; \backslash sum\_\{p=0\}^\{P-1\}\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{sp\}\{P\}\backslash right)f\_1(p,r)$

가 된다.

즉, F(n) = F(sQ + r)의 계산은 다음 2단계가 된다.

;단계 1: p = 0, 1, ..., P - 1 및 r = 0, 1, ..., Q - 1 에 대해

::$f\_1(p,r)=\; \backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{pr\}\{PQ\}\backslash right)\backslash sum\_\{q=0\}^\{Q-1\}f(qP+p)\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{rq\}\{Q\}\backslash right)$

:를 계산한다. 이는 Q차 이산 푸리에 변환

::$\backslash sum\_\{q=0\}^\{Q-1\}f(qP+p)\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{rq\}\{Q\}\backslash right)$

:의 실행과, 회전 인자 exp(-2πipr/PQ)의 곱셈을, 모든 p, r의 조합(PQ = N가지)에 대해 수행하는 것으로 볼 수 있다.

;단계 2: s = 0, 1, ..., P - 1 및 r = 0, 1, ..., Q - 1에 대해

::$F(sQ+r)\; =\; \backslash sum\_\{p=0\}^\{P-1\}\backslash exp\backslash left(-2\backslash pi\; i\backslash frac\{sp\}\{P\}\backslash right)f\_1(p,r)$

:를 계산한다. 여기서 우변은 r을 고정하면 P차 이산 푸리에 변환이다.

단계 1, 2는 N = PQ차 이산 푸리에 변환을 Q차 이산 푸리에 변환과 회전 인자 곱셈 실행을 통해 Q개(r = 0, 1, ..., Q - 1)의 P차 이산 푸리에 변환으로 분해한 것으로 볼 수 있다.

:N '''차 이산 푸리에 변환 문제''' ⇒ Q '''차 이산 푸리에 변환 실시''' ⇒ N/Q '''차 이산 푸리에 변환 문제로 귀착'''

특히 Q가 2 또는 4인 경우, Q차 이산 푸리에 변환은 매우 간단한 계산이 된다.

• Q = 2인 경우, exp(-2πirq/Q)는 1 또는 -1이므로, Q차 이산 푸리에 변환은 부호 반전과 덧셈만으로 계산할 수 있다.
• Q = 4인 경우, exp(-2πirq/Q)는 1, -1, i, -i 중 하나이므로, Q차 이산 푸리에 변환의 계산은 부호 반전, 실수부 허수부 교환과 덧셈만으로 계산할 수 있다.

Q = 2 또는 Q = 4인 경우의 이 부분의 Q차 이산 푸리에 변환을 '''나비 연산'''이라고 한다.

N = Q^k (P = Q^{k - 1})인 경우에는 위를 반복할 수 있으며, Q차 이산 푸리에 변환과 회전 인자 곱셈을 반복하는 것만으로 차수를 낮출 수 있고, 최종적으로 1차 이산 푸리에 변환(아무것도 하지 않는 것과 같음)까지 낮추면 F(t)를 구할 수 있다.

2의 거듭제곱 또는 4의 거듭제곱 차수의 이산 푸리에 변환은 양쪽의 성질을 이용할 수 있으며 매우 간단하게 계산할 수 있다.

Q = 2 또는 Q = 4인 경우에 계산을 종료하기까지 몇 번의 "곱셈"이 필요한지를 생각한다. 부호 반전, 실수부 허수부 교환은 "곱셈"으로 계산하지 않으면 회전 인자의 곱셈만이 "곱셈"이다. N = Q^k의 차수를 1 낮추기 위해 N번의 "곱셈"이 필요하며 차수를 k에서 0으로 낮추기 위해 그것을 k번 반복할 필요가 있으므로 "곱셈"의 수는 Nk = N log_Q N이 된다. 고속 푸리에 변환의 계산에서 시간이 걸리는 것은 "곱셈" 부분이기에 "고속 푸리에 변환에서는 계산 속도가 O(N log N)이 된다"는 것의 근거가 된다.

4. 3. 1. 기수r FFT (Radix-r FFT)

신호의 길이가 r의 거듭제곱일 때 사용하는 FFT 알고리즘으로, 기수 2 알고리즘의 일반화된 형태이다.

기수 r (radix-r) FFT는 신호의 수 N이 r의 거듭제곱, 즉 ''N=r ⁿ''인 경우에 사용된다.

• 각 단계(stage)에서 사용되는 ''N/r''-point DFT (나비, butterfly)는 동일하다.
• 기수 r FFT에서 나비는 한 단계에서 ''N/r'' 개이다.
• (예) ''N=16'' 이고 기수 ''r=2'' 이면 단계 당 나비 수는 16/2 = 8 개이다.
• FFT 나비 도표(butterfly diagram)에서 단계의 수 ''s''는 $s=\backslash log\; \_r\; N$이다.
• ''N=16'' 이고 기수 ''r=2'' 이면 단계 수 ''$s=\backslash log\; \_2\; 16\; =\; 4$''이다.
• ''N=16'' 이고 기수 ''r=4'' 이면 단계 수 ''$s=\backslash log\_\; 4\; 16\; =\; 2$''이다.
• 로그의 성질에 의해 $\backslash log\; \_4\; N=(\backslash log\; \_2\; N)/2$이므로 기수 4의 stage 수 s는 기수 2일 때보다 반으로 감소한다.
• 기수에 따른 계산 효율
• 대체적으로 기수 4는 대규모 변환에서 기수 2보다 약 20% 더 효율적이다.

기수 r 에 따른 복소수 곱셈 수

기수	stage 수 (a)	stage 내의 나비(butterfly)수 (b)	butterfly 연산 안에서의 복소수 곱셈의 수 (c)	전체 복소수 곱셈의 수 (a)x(b)x(c)
radix-2	log2N	N/2	1 (회전자 계수 중복으로 1/2만 연산)	(N/2)log2N
radix-4	log4N=(1/2)log2N	N/4	3	(3N/8)log2N

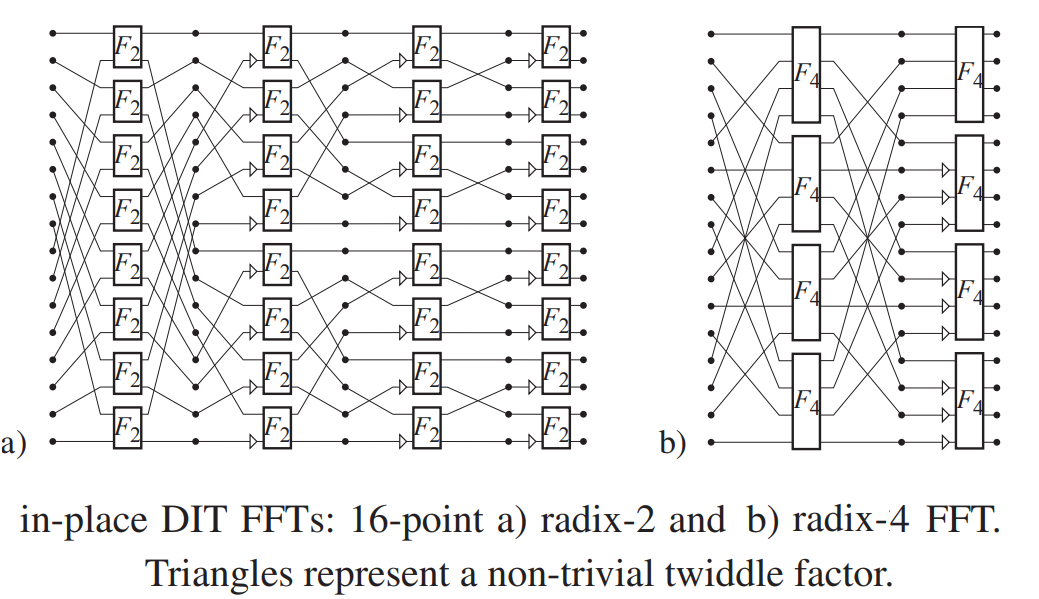
표의 결과만을 볼 때 radix-4 가 고속이 될 것 같지만, 실제로는 실장 방법에 의존한다. CPU로 실행하는 경우는 연산기가 1개 이므로, 연산 횟수가 적은 radix-4 쪽이 좀 더 고속이 될 것 같다. 그러나, FPGA로 구현하는 경우의 상충관계(trade-off)는 복잡하다. 나비연산을 복수의 연산기를 사용해 파이프라인으로 하면 radix-2와 radix-4 모두 같은 1 클럭이 되어버리므로 radix-4가 4배 고속이 될 것 같아 보이지만, 1개의 메모리에서는 1개씩 밖에 데이터를 읽을 수 없기 때문에 여기가 병목이 되어 radix-4는 4 클럭, radix-2는 2 클럭을 소요함으로 radix-4는 radix-2의 2배 밖에 빨라지지 않는다. 그래서, 보통은 메모리를 분할하여 복수의 데이터를 동시에 읽도록 고안하지만 메모리 읽기를 병렬화하는 것에 맞추어 연산기도 radix-2의 나비 연산을 4병렬화시키면, 연산기 수가 radix-4와 거의 같아져 차이가 없어진다. 그렇게 생각하면 radix-2 쪽이 병렬화 설계가 더 간단한 만큼 유리할지도 모른다.

기수 8이 사용되기도 하지만, 효율성 개선이 크지 않고 추가되는 복잡성이 상당하여(특히 하드웨어 구현의 경우) 더 긴 기수 나비는 일반적이지 않다.

4. 3. 2. 혼합 기수 FFT (Mixed-radix FFT)

혼합 기수 고속 푸리에 변환(FFT) 알고리즘은 1969년 리처드 C. 싱글턴(Richard C. Singleton)이 처음 고안한 알고리즘으로, 쿨리-튜키 알고리즘의 변종이다. 이 알고리즘은 신호의 길이가 임의의 합성수(composite number)일 때도 사용할 수 있는 보다 일반적인 알고리즘이다.

주요 특징은 다음과 같다.

• '''1) ''N≠rⁿ'' 일 때도 포함해서 일반적으로 합성수 ''N=N₁N₂'' ...''N_m'' 일 때 사용한다.'''

• ''N=2ⁿ''(즉, 기수 2)인 경우에 ''N=2, 4, 8,...''이고, ''N=4ⁿ'' 인 경우 ''N=4, 16, 64...'' 등의 갯수를 가질 수 있으나, 중간 갯수인 ''N=12'' , ''N=15'', ''N=24'' 등은 단일한 기수로는 처리할 수 없다. 따라서 서로 다른 기수가 혼합된 여러 기수를 사용해 해결한다.
• ''N=2ⁿ×q^s'' (''q=2^m>2, 1
• 예) ''N=2^(2m+1)=2¹×4^m''
• ''N=32=2¹×4²'' 즉 기수2 한 단계와 기수4 두 단계를 수행한다.

• '''2) 나비도표에 서로 다른 기수의 나비들이 존재한다.'''

4. 4. 그 외의 알고리즘

• 소인수 알고리즘 (PFA)
• 브룬 FFT 알고리즘
• 레이더의 FFT 알고리즘
• 블루스타인 FFT 알고리즘 (Chirp Z-변환)
• 오들리츠코-쇤하게 알고리즘
• 고속 월시-아다마르 변환

5. 응용

FFT는 다양한 분야에서 활용되고 있다. 신호의 주파수 성분을 분석하는 스펙트럼 분석기^[1], 통신 시스템에서 데이터를 전송하는 OFDM 변복조기^[1], 의료 영상에서 이미지를 생성하는 CT 스캐너 및 MRI^[1], 오디오 데이터를 압축하는 MP3^[1] 등에 사용된다.

대한민국에서는 5G, LTE, Wi-Fi, DSL 등 통신 시스템과 디지털 방송, 의료 영상 등 다양한 분야에서 FFT가 활용되고 있다. 금융 분야에서도 옵션 가치 평가 등에 활용될 수 있다.^[2]

• 스펙트럼 분석기
• OFDM 변복조기
• 일본 및 유럽에서 지상파 디지털 텔레비전 방송과 ADSL 등에 사용되는 변조 방식인 OFDM은 LSI화된 FFT 및 IFFT (역변환)를 각각 복조기 및 변조기로 사용한다.
• 푸리에 변환 NMR
• 핵자기 공명 (NMR) 스펙트럼을 얻기 위해 사용된다.
• CT, MRI
• 수광 소자를 360도 회전시키면서 연속 촬영한 영상을 푸리에 변환하여 회전면의 투과 영상을 합성한다.
• FFT 분석기
• 주파수 분포를 조사하기 위해 사용된다. 이전에는 하드웨어로 신호를 처리했지만, 최근에는 CPU의 성능 향상으로 소프트웨어로 처리된다. 노트북 컴퓨터와 USB로 연결하여 사용하는 것^[8]이나, 최근에는 디지털 오실로스코프에 FFT 기능을 내장한 것도 있다.
• 전파 천문학
• FX형 디지털 분광 상관기 등을 사용하여 성간 분자의 스펙트럼을 분석한다.^[9][10]

6. 계산 복잡도

DFT을 직접 계산하면 $O(n^2)$ 연산이 필요하다. 구체적으로, n개의 출력 각각은 n개 항의 합으로 계산된다.^[11] FFT는 동일한 결과를 $O(n\; \backslash log\; n)$ 연산으로 계산하는 방법이다.^[11]

예를 들어 $n=4096$개의 데이터 포인트에 대해 DFT 합을 직접 계산하면, 약 3천만 개의 연산($n^2$ 복소수 곱셈, $n(n-1)$ 복소수 덧셈)이 필요하다.^[11] 반면, n이 2의 거듭제곱인 경우 Cooley–Tukey 알고리즘을 사용하면, 약 3만 개의 연산($(n/2)\backslash log\_2(n)$ 복소수 곱셈, $n\backslash log\_2(n)$ 복소수 덧셈)만으로 동일한 결과를 얻을 수 있다. 이는 직접 계산보다 1,000배 적은 연산량이다.^[11]

이론적으로 중요한 미해결 문제는 고속 푸리에 변환의 복잡성과 정확한 연산 횟수에 대한 하한을 증명하는 것이다.^[11] DFT가 실제로 $\backslash Omega(n\; \backslash log\; n)$ 연산을 필요로 하는지는 엄밀하게 증명되지 않았지만, 이보다 낮은 복잡성을 가진 알고리즘은 알려져 있지 않다.^[11]

위노그라드의 연구에 따르면, FFT에 필요한 실수 곱셈 수의 정확한 $\backslash Theta(n)$ 하한이 알려져 있다. 2의 거듭제곱 길이 $n\; =\; 2^m$ DFT 계산에는 $4n\; -\; 2\backslash log\_2^2(n)\; -\; 2\backslash log\_2(n)\; -\; 4$개의 무리수 실수 곱셈만 필요하며, 이 횟수를 달성하는 알고리즘도 알려져 있다. 그러나 이 알고리즘은 실용적이기에는 너무 많은 덧셈을 필요로 한다.

필요한 덧셈 수에 대한 정확한 하한은 알려져 있지 않지만, 일부 제한적인 가정 하에서는 하한이 증명되었다. 파파디미트리우는 Cooley–Tukey 알고리즘의 복소수 덧셈 수 $n\; \backslash log\_2\; n$이 특정 가정 하에서 최적이라고 주장했다. 현재까지 $n\; \backslash log\_2\; n$개 미만의 복소수 덧셈을 달성하는 FFT 알고리즘은 없다.

실수 곱셈과 덧셈의 총 횟수를 최소화하는 문제도 연구되고 있지만, 정확한 하한은 증명되지 않았다. 분할-기수 FFT 알고리즘은 n > 1에 대해 $4n\backslash log\_2(n)\; -\; 6n\; +\; 8$개의 실수 곱셈과 덧셈을 필요로 했으나, 최근에는 $\backslash sim\; \backslash frac\{34\}\{9\}\; n\; \backslash log\_2\; n$으로 감소되었다.

복소수 데이터 FFT는 실수 데이터 FFT, 이산 코사인 변환, 이산 하틀리 변환 등과 밀접하게 관련되어 있어, 한 알고리즘의 개선은 다른 알고리즘의 개선으로 이어진다.

복소 함수 f(x)의 이산 푸리에 변환 F(t)는 다음과 같이 정의된다.

:$F(t)=\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; \backslash exp\backslash left(-i\backslash frac\{2\; \backslash pi\; t\; x\}\{N\}\; \backslash right)\; .$

여기서 x = {0, 1, 2, ..., N − 1}는 표본점이다.

이를 직접 계산했을 때의 시간 복잡도는 $O(N^2)$이다.

고속 푸리에 변환은 N이 2의 거듭제곱일 때 $O(N\; \backslash log\; N)$ 계산량으로 결과를 얻는 알고리즘이다. 일반적으로 N = ∏ ni 로 소인수 분해될 수 있을 때, $O(N\sum ni)$ 계산량이 된다. N이 2의 거듭제곱일 때가 가장 고속으로 계산 가능하며, 알고리즘도 단순하여 0 채우기로 차수를 조정하기도 한다.

고속 푸리에 변환을 사용하면 컨볼루션 적분 등의 계산을 빠르게 구할 수 있으며, 계산량을 $O(N^2)$에서 $O(N\; \backslash log\; N)$까지 줄일 수 있다.

이산 푸리에 계수는 1의 원시 N 제곱근 W_N = e^(-2πi/N) 를 사용하여 다음과 같이 나타낼 수 있다.

:$F(t)\; =\; \backslash sum\_\{x=0\}^\{N-1\}\; f(x)\; W\_N^\{tx\}\; .$

예를 들어 N = 4 일 때, F(t)=Xt, f(k) = xk로 하면, 이산 푸리에 계수는 행렬로 표현하면 (W = W4 로 약기) 다음과 같다.

:$$

\begin{bmatrix}X_0\\X_1\\X_2\\X_3\end{bmatrix}=

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^1&W^2&W^3\\

W^0&W^2&W^4&W^6\\

W^0&W^3&W^6&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_1\\x_2\\x_3\end{bmatrix}



입력 열 xk를 첨자의 짝수와 홀수로 나누어 변형하면 다음과 같다.

:$$

\begin{align}

\begin{bmatrix}X_0\\X_1\\X_2\\X_3\end{bmatrix}

& =

\begin{bmatrix}

W^0&W^0&W^0&W^0\\

W^0&W^2&W^1&W^3\\

W^0&W^4&W^2&W^6\\

W^0&W^6&W^3&W^9

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix} \\

& =

\begin{bmatrix}

W^0&W^0&W^0W^0&W^0W^0\\

W^0&W^2&W^1W^0&W^1W^2\\

W^0&W^0&W^2W^0&W^2W^0\\

W^0&W^2&W^3W^0&W^3W^2

\end{bmatrix}

\begin{bmatrix}x_0\\x_2\\x_1\\x_3\end{bmatrix}

\end{align}



(∵ W^(k+N)=W^k)

그러면 크기 2의 FFT 연산 결과를 사용하여 표현할 수 있고, 크기 분할이 가능하다.

:$\backslash begin\{bmatrix\}X\_0\backslash \backslash X\_1\backslash \backslash X\_2\backslash \backslash X\_3\backslash end\{bmatrix\}=$

\begin{bmatrix}

1&0&W^0&0\\

0&1&0&W^1\\

1&0&W^2&0\\

0&1&0&W^3

\end{bmatrix}\,

\begin{bmatrix}

W_2^0&W_2^0&0&0\\

W_2^0&W_2^1&0&0\\

0&0&W_2^0&W_2^0\\

0&0&W_2^0&W_2^1

\end{bmatrix}\,

\begin{bmatrix}

x_0\\

x_2\\

x_1\\

x_3

\end{bmatrix}



이 분할 절차를 그림으로 나타내면 나비 모양이 되므로, '''버터플라이 연산'''이라고 한다.

버터플라이 연산은 컴퓨터에서 비트 반전으로 구현된다. 일부 DSP는 비트 반전 어드레싱을 갖추고 있다.

7. 정확도

FFT(고속 푸리에 변환) 알고리즘은 유한 정밀도 부동 소수점 산술을 사용할 때 오류가 발생하지만, 이러한 오류는 일반적으로 매우 작다. 대부분의 FFT 알고리즘(예: 쿨리-튜키 알고리즘)은 알고리즘의 쌍별 합산 구조 덕분에 훌륭한 수치적 특성을 가진다. 쿨리-튜키 알고리즘의 상대 오차에 대한 상한은 $O(\backslash varepsilon\; \backslash log\; n)$인데, 이는 단순 DFT 공식의 $O(\backslash varepsilon\; n^\{3/2\})$에 비해 훨씬 낫다. 여기서 ε는 기계 부동 소수점 상대 정밀도를 나타낸다. 사실, 평균 제곱근 (rms) 오차는 이러한 상한보다 훨씬 더 우수하며, 쿨리-튜키의 경우 $O(\backslash varepsilon\; \backslash sqrt\{\backslash log\; n\})$이고, 단순 DFT의 경우 $O(\backslash varepsilon\; \backslash sqrt\{n\})$에 불과하다.

그러나 이러한 결과는 FFT에 사용된 트위들 인자(즉, 삼각 함수 값)의 정확도에 매우 민감하며, 부주의한 FFT 구현은 훨씬 더 나쁜 정확도를 가질 수 있다. 예를 들어, 부정확한 삼각 재귀 공식을 사용하는 경우가 그렇다. 쿨리-튜키와 같은 일부 FFT 외에도 Rader–Brenner 알고리즘은 본질적으로 덜 안정적이다.

고정 소수점 산술에서 FFT 알고리즘에 의해 축적된 유한 정밀도 오류는 더욱 심각하며, 쿨리-튜키 알고리즘의 경우 rms 오차가 $O(\backslash sqrt\{n\})$으로 증가한다. 이 정확도를 달성하려면 정밀도 손실을 최소화하기 위해 스케일링에 주의를 기울여야 하며, 고정 소수점 FFT 알고리즘은 쿨리-튜키와 같은 분해의 각 중간 단계에서 재 스케일링을 포함한다.

FFT 구현의 정확성을 확인하기 위해 무작위 입력에 대한 변환의 선형성, 임펄스 응답 및 시간 이동 속성을 확인하는 간단한 절차를 통해 $O(n\; \backslash log\; n)$ 시간에 엄격한 보장을 얻을 수 있다.

8. 다차원 FFT

다차원 DFT는 다음과 같이 정의된다.

:$X\_\backslash mathbf\{k\}\; =\; \backslash sum\_\{\backslash mathbf\{n\}=0\}^\{\backslash mathbf\{N\}-1\}\; e^\{-2\backslash pi\; i\; \backslash mathbf\{k\}\; \backslash cdot\; (\backslash mathbf\{n\}\; /\; \backslash mathbf\{N\})\}\; x\_\backslash mathbf\{n\}$

여기서 $\backslash mathbf\{n\}\; =\; \backslash left(n\_1,\; \backslash ldots,\; n\_d\backslash right)$는 ''d''차원 벡터 인덱스이고, $x\_\backslash mathbf\{n\}$은 이 인덱스를 갖는 배열이다. $n\_j\; =\; 0\; \backslash ldots\; N\_j\; -\; 1$에 대해 ''d''개의 중첩된 합으로 변환되며, 나눗셈 $\backslash mathbf\{n\}\; /\; \backslash mathbf\{N\}\; =\; \backslash left(n\_1/N\_1,\; \backslash ldots,\; n\_d/N\_d\backslash right)$는 요소별로 수행된다. 이는 ''d''개의 1차원 DFT 세트를 한 번에 한 차원씩(어떤 순서로든) 수행한 결과와 같다.

이러한 구성적 관점은 가장 일반적인 다차원 DFT 알고리즘인 '''행-열''' 알고리즘을 제공한다. 이 알고리즘은 ''d''개의 1차원 FFT 시퀀스를 수행한다. 먼저 $n\_1$ 차원을 따라 변환하고, 그다음 $n\_2$ 차원을 따라 변환하는 식으로 진행한다(어떤 순서로도 가능하다). 이 방법은 $O(n\; \backslash log\; n)$의 복잡도를 가지며, 여기서 $n\; =\; n\_1\; \backslash cdot\; n\_2\; \backslash cdots\; n\_d$는 변환된 데이터 포인트의 총 개수이다.

2차원의 경우, $x\_\backslash mathbf\{k\}$는 $n\_1\; \backslash times\; n\_2$ 행렬로 볼 수 있다. 이 알고리즘은 먼저 모든 행(또는 열)의 FFT를 수행하고, 결과로 변환된 행(또는 열)을 다른 $n\_1\; \backslash times\; n\_2$ 행렬로 함께 그룹화한 다음, 이 두 번째 행렬의 각 열(또는 행)에 대해 FFT를 수행하고, 결과를 최종 결과 행렬로 그룹화한다.

2차원 이상에서는 캐시 지역성을 위해 차원을 재귀적으로 그룹화하는 것이 유리하다. 예를 들어, 3차원 FFT는 먼저 각 고정된 $n\_1$에 대해 각 평면 "슬라이스"의 2차원 FFT를 수행한 다음, $n\_1$ 방향을 따라 1차원 FFT를 수행할 수 있다. 더 일반적으로, 점근적으로 최적 캐시 불가지론적 알고리즘은 차원을 두 그룹 $(n\_1,\; \backslash ldots,\; n\_\{d/2\})$과 $(n\_\{d/2+1\},\; \backslash ldots,\; n\_d)$로 재귀적으로 분할하여 재귀적으로 변환한다.

행-열 알고리즘 외에도 다른 다차원 FFT 알고리즘이 있지만, 모두 $O(n\; \backslash log\; n)$ 복잡성을 갖는다. 벡터-밑수 FFT 알고리즘은 각 단계에서 밑수의 벡터 $\backslash mathbf\{r\}\; =\; \backslash left(r\_1,\; r\_2,\; \backslash ldots,\; r\_d\backslash right)$로 변환 차원을 나누는 쿨리-터키 알고리즘의 일반화이다.

참조

_[1] 서적 The History of Music Production https://books.google[...] Oxford University Press 2014
_[2] 논문 A revisited and stable Fourier transform method for affine jump diffusion models 2008-10
_[3] 논문 Quantum circuit for the fast Fourier transform https://link.springe[...]
_[4] 웹사이트 Arm Performance Libraries https://www.arm.com/[...] Arm 2020-12-16
_[5] 웹사이트 Complete list of C/C++ FFT libraries https://community.vc[...] 2021-03-03
_[6] 논문 高速フーリエ変換（FFT）について http://id.nii.ac.jp/[...] 情報処理学会 1973-08
_[7] 논문 Real-valued fast Fourier transform algorithms https://doi.org/10.1[...] IEEE
_[8] 웹사이트 FFT spectrum analyzer http://www.stjapan.c[...]
_[9] 웹사이트 惑星大気の観測「SPART」 http://www.astro.s.o[...]
_[10] 웹사이트 空間FFT電波干渉計による電波天体の高速撮像 http://search.ieice.[...]
_[11] 문서 J. W. Cooley and J. W. Tukey: Math. of Comput. 19 (1965) 297.
_[12] 웹사이트 IEEE Archives: History of FFT with Cooley and Tukey http://www.ieeeghn.o[...]
_[13] 논문 1970
_[14] 문서 Carl Friedrich Gauss, "Nachlass: Theoria interpolationis methodo nova tractata", Werke band 3, 265–327 (Konigliche Gesellschaft der Wissenschaften, Gottingen, 1866). See also　M. T. Heideman, D. H. Johnson, and C. S. Burrus, "Gauss and the history of the fast Fourier transform", IEEE ASSP Magazine 1 (4), 14–21 (1984). https://books.google[...]
_[15] 웹사이트 vDSP - Accelerate - Apple Developer Documentation https://developer.ap[...] 2024-05-25
_[16] 웹사이트 AOCL-FFTW (Fastest Fourier Transform in the West) https://www.amd.com/[...] 2024-05-25
_[17] 웹사이트 Arm Performance Libraries https://developer.ar[...] 2024-05-25
_[18] 웹사이트 cuFFT https://developer.nv[...] 2024-05-25
_[19] 웹사이트 NEC Corporation of America https://www.mathkeis[...] 2024-05-25
_[20] 웹사이트 rocFFT documentation — rocFFT Documentation https://rocm.docs.am[...] 2024-05-25