맨위로가기

조합론

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

조합론은 고대부터 연구되어 온 수학의 한 분야로, 순열, 조합, 그래프 등 다양한 구조를 연구하며, 계수적 조합론, 극대 조합론, 위상수학적 조합론 등 여러 분야로 분류된다. 19세기 이후 급속도로 발전하여 대수학, 확률론, 전산학 등 다양한 분야와 관련 있으며, 정보 이론, 통계 물리학, 경제학 등 다른 분야에도 응용된다.

2. 역사



조합론의 기본 개념과 결과는 고대부터 여러 문화권에서 나타났다. 인도의 의사 수슈루타는 《수슈루타 삼히타》에서 6가지 맛의 조합으로 63가지 경우의 수가 만들어질 수 있다고 주장했다.[7][8][9] 고대 그리스의 역사가 플루타르크는 크리시푸스와 히파르코스 사이의 열거 문제에 대한 논쟁을 언급했는데, 이는 나중에 슈뢰더–히파르코스 수와 관련이 있는 것으로 밝혀졌다.

중세 시대에는 주로 유럽 문화 밖에서 연구가 계속되었다. 인도의 수학자 마하비라는 순열과 조합의 수에 대한 공식을 제공했으며,[13][14] 아브라함 이븐 에즈라는 이항 계수의 대칭성을 확립했다. 레비 벤 게르손은 1321년에 관련 공식을 제시하였다.[16] 파스칼의 삼각형은 10세기부터 알려졌으며, 중세 잉글랜드의 캠퍼놀로지는 해밀턴 사이클의 예시를 제공했다.

르네상스 시대에는 파스칼, 뉴턴, 베르누이, 오일러 등이 조합론을 발전시켰다. J.J. 실베스터와 퍼시 맥마혼은 열거 조합론과 대수적 조합론의 기초를 다졌다. 그래프 이론도 사색 문제와 관련하여 발전했다.

20세기 후반에는 조합론이 급성장하여, 여러 분야와 연결되며 발전했지만, 동시에 분야가 분열되기도 했다.

2. 1. 고대

조합론의 기초 개념은 고대 수학에서부터 시작되었다. 기원전 10세기~기원전 4세기 주나라에서 집필된 《역경》은 양(⚊) 또는 음(⚋)의 값을 가질 수 있는 6개의 효(爻)로부터 64 = 26개의 괘(卦)를 구성하였다.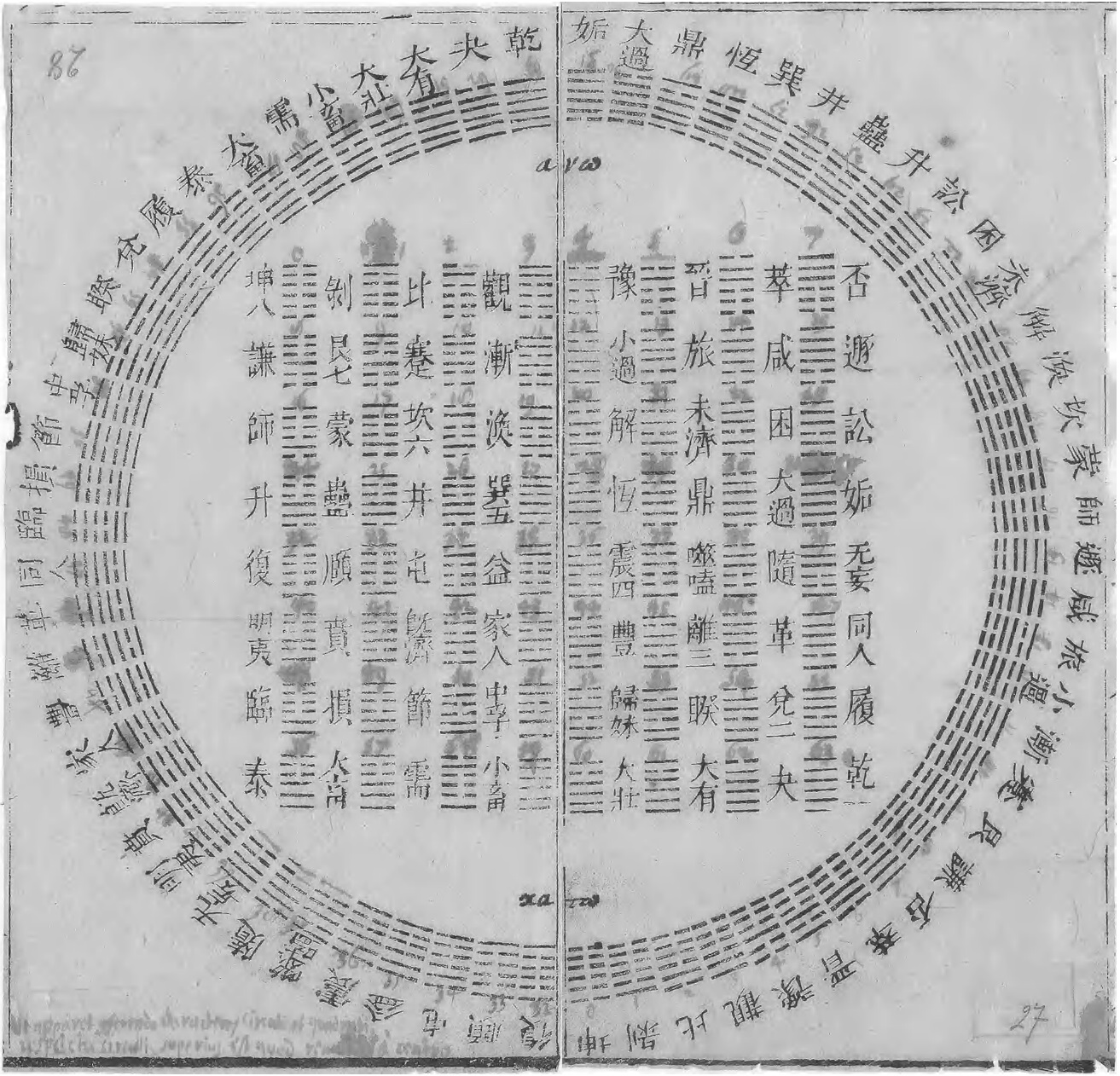
《역경》에 등장하는 64괘
기원전 6세기에 인도의 외과의사 수슈루타(सुश्रुतsa)는 의학서 《수슈루타상히타》(सुश्रुतसंहिताsa)에서, 6개의 기본 맛(단맛, 신맛, 짠맛, 쓴맛, 매운 맛, 떫은 맛)을 63 = 26 − 1가지로 조합할 수 있다고 서술하였다. 이는 6개의 원소로 만들 수 있는 집합 가운데 공집합을 제외한 것들의 가짓수이다.[7][8][9]

기원후 1세기 고대 그리스에서, 플루타르코스(46~120)는 에세이집 《윤리학》(Ἠθικά|에티카grc)의 49번째 에세이 〈잡담〉(Συμποσιακά|심포시아카grc) 8권에서 크리시포스가 10개의 기초 명제로부터 만들 수 있는 합성 명제는 100만 개를 넘는다고 하였으나, 히파르코스가 긍정적 합성 명제는 103,049개, 부정적 합성 명제는 310,952개임을 보였다고 언급했다.[28] 여기서 "긍정적 합성 명제"의 수 103,049는 10번째 슈뢰더 수(Schröder number영어) s_{10}이며, 10개의 글자로 구성된 문자열에 괄호를 삽입할 수 있는 가짓수이다.[29] "부정적 합성 명제"의 수 310,952는 10번째와 11번째 슈뢰더 수의 평균이다.[30]

2. 2. 중세

850년 경, 인도의 수학자 마하비라는 《산법 요론(要論)》(गणितसारसंग्रह|가니타사라상그라하sa)에서 순열과 조합의 수에 대한 공식을 제시하였다.[13][14]

아랍 세계에서는 중세 스페인의 랍비 아브라함 이븐 에즈라(אברהם אבן עזרא|아브라함 이븐 에즈라he, Abenezra|아베네즈라la, 1089~1167)는 이항 계수의 대칭성을 증명하였다. 1321년에 랍비 레비 벤 게르숀(לוי בן גרשום|레비 벤 게르숀he, Gersonides|게르소니데스la, 1288~1344)은 순열과 조합의 수에 대한 공식을 제시하였다.[16]

송나라의 양휘는 《구장산술》에 대한 주석인 《상해구장산법》(詳解九章算法)에서 파스칼 삼각형을 제시하였다.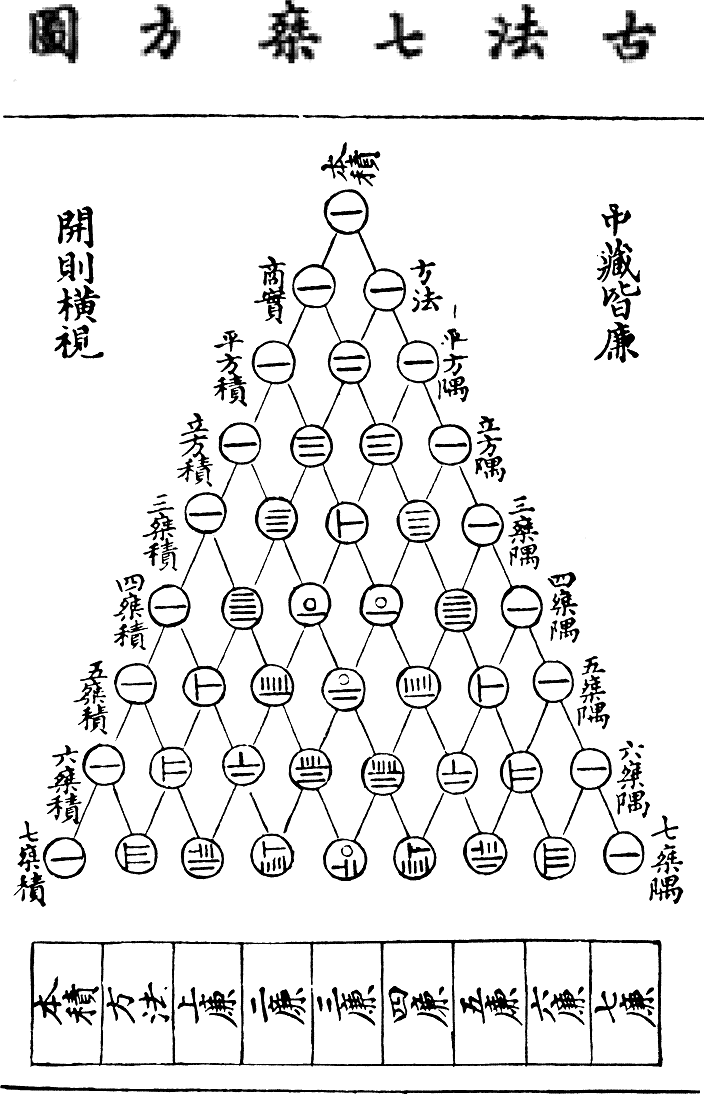

양휘가 지은 《상해구장산법》(詳解九章算法)에 수록된 파스칼 삼각형


중세 일본에는 벨 수가 최초로 등장하였다. 《겐지모노가타리》에서의 한 일화로부터 겐지코(源氏香일본어)라는 놀이가 등장했는데,[31] 이 놀이에서는 5개의 향 가운데 어떤 것들이 같은 냄새의 향인지 구별하는 것이 목표이다. 가능한 경우의 수는 5차 벨 수 B_5=52가지다.

2. 3. 근세 및 현대

블레즈 파스칼(1623~1662), 아이작 뉴턴(1643~1727), 야코프 베르누이(1655~1705) 등은 조합론을 포함한 수학 발전에 기여하였다. 파스칼은 1665년 사후 출판된 《산술 삼각형에 대하여》(Traité du triangle arithmétique프랑스어)[32]에서 파스칼 삼각형을 연구하였다. 1666년 고트프리트 라이프니츠는 《조합술에 대하여》(Dissertatio de arte combinatoriala)[33]를 출판하였는데, 이 책에서 "조합술"(ars combinatoriala)이라는 용어를 최초로 사용하였다.

레온하르트 오일러(1707~1783)는 오일러 수를 연구하였고, 쾨니히스베르크의 다리 문제를 풀어 그래프 이론을 창시하였다.

19세기 말~20세기 초 제임스 조지프 실베스터와 퍼시 알렉산더 맥메이헌은 대수적 조합론을 창시하였고, 이 시기에 그래프 이론 역시 급속히 발달하였다. 20세기 후반에는 기하학적·위상수학적 기법들이 조합론에 사용되기 시작하였다.

3. 조합론의 분류

조합론은 다루는 대상, 사용하는 기법, 목표 등에 따라 다양하게 분류할 수 있다. 조합론의 전체 범위는 보편적으로 합의된 바가 없다.[3] H.J. 라이저에 따르면, 이 분야는 매우 많은 수학적 세분 분야를 넘나들기 때문에 정의하기 어렵다.[4]

레온 미르스키는 "조합론은 공통점을 가지고 있지만 목표, 방법 및 일관성 측면에서 크게 다른 일련의 연관된 연구 분야이다."라고 말했다.[5] 조합론을 정의하는 한 가지 방법은 문제와 기법을 통해 하위 분야를 설명하는 것이다. 그러나 조합론의 범주에 일부 주제를 포함하거나 포함하지 않는 데에는 순전히 역사적인 이유도 있다.[6]

조합 수학은 이론 구축과 마찬가지로, (특히 20세기 후반 이후) 주어진 문제를 해결하는 것을 목표로 한다. 조합 수학 중 가장 오래되었고 접근하기 쉬운 것은 그래프 이론이며, 현재는 다른 다양한 분야와 연결되어 있다.

조합론적 질문의 예로, 52장의 트럼프 카드 배열은 몇 가지 방법이 있는가 하는 것이 있다. 이에 대한 답은 52! (52의 계승)이며, 이 수는 대략 8.065817517094 × 1067으로, 8 뒤에 0이 67개나 붙는 놀라운 규모이다. 이는 무량대수 (1068)에 필적할 정도로 크다.

다른 종류의 문제에는, ''n''명의 사람이 여러 그룹을 만들 때, 각 사람이 적어도 하나의 그룹에 속하고, 어떤 두 사람을 보더라도 공통적으로 정확히 하나의 그룹에 속하며, 어떤 두 그룹을 보더라도 공통의 사람이 정확히 한 명씩 있고, n-1명 이상으로 이루어진 그룹이 없는 분할이 있는가 하는 것이 있다. 답은 n에 따라 다르며, 아직 부분적인 답변만 얻어졌다.

3. 1. 다루는 대상에 따른 분류


  • '''순열'''과 '''조합''': 순서와 중복을 고려하여 대상을 배열하거나 선택하는 경우의 수를 다룬다. 이들을 세는 문제는 12정도라는 이름으로 체계화되어 있다.[3]
  • '''집합의 분할''', 특히 자연수의 분할: 집합을 서로소인 부분집합들로 나누는 방법을 연구한다.
  • '''문자열'''(word영어): 문자들의 배열을 다룬다.
  • '''부분 순서 집합''': 순서 관계가 주어진 집합을 연구한다. 특수한 경우로 전순서 집합이나 격자 등이 있다. 이들을 연구하는 분야를 순서론이라고 한다.
  • '''그래프''': 점과 선으로 연결된 조합론적 구조를 연구한다. 이들을 다루는 분야를 그래프 이론이라고 한다.
  • '''매트로이드''': 그래프를 일반화한 개념으로, 선형 독립의 개념을 추상화한 조합론적 구조를 연구한다.
  • '''유한 기하'''(finite geometry영어): 유한한 수의 점과 선으로 구성된 기하학적 공간을 연구한다.
  • '''계획'''(design영어): 통계학의 실험계획법에서 유래한 개념으로, 라틴 방진 등이 이에 속한다. 계획 이론은 유한 기하학과 코드 이론(coding theory영어)과 밀접하게 연관되어 있다.[3]

3. 2. 사용하는 기법 또는 목표에 따른 분류

조합론은 다루는 대상 대신 사용하는 기법 또는 목표로서 분류할 수도 있다.

  • '''계수적 조합론'''은 주어진 조건을 만족하는 대상의 수를 세는 것을 목표로 한다.[3]
  • '''해석적 조합론'''은 해석학적 기법을 조합론에 응용하며, 보통 주어진 대상의 정확한 수보다는 이들의 수의 점근적 공식(asymptotic formula영어)을 목표로 한다.[3] 계승의 스털링 공식이 대표적인 예이다.
  • '''극대 조합론'''은 주어진 조건을 만족시키는 대상 가운데 "가장 큰" 또는 "가장 작은" 것 따위의 문제를 다룬다.[3] 극대 그래프 이론은 그래프 이론에서 중요한 연구 분야의 하나이다. 다른 방향으로, 램지 이론도 이에 속한다.
  • '''위상수학적 조합론'''은 그래프 따위의 조합론적 구조에 위상을 주어, 보르수크-울람 정리나 호몰로지 대수학을 조합론적 문제에 응용한다.[3] 로바스 라슬로는 보르수크-울람 정리를 사용하여 크네저 그래프에 대한 크네저 추측을 증명하였다.
  • '''확률적 조합론'''에서는 무작위 이산 객체, 예를 들어 무작위 그래프에 대해 특정 속성을 가질 확률은 무엇인지, 무작위 그래프에서 삼각형의 평균 개수는 얼마인지 등의 질문을 다룬다. 확률적 방법은 또한 특정 지정된 속성을 가진 조합론적 객체의 존재를 결정하는 데 사용된다.[5]
  • '''대수적 조합론'''은 추상대수학의 방법, 특히 군론과 표현론을 다양한 조합론적 맥락에서 활용하고, 반대로 조합론적 기법을 추상대수학의 문제에 적용하는 수학의 한 분야이다.[6]

4. 관련 분야

조합론은 대수학, 확률론, 에르고딕 이론, 기하학 등 수학의 여러 분야와 밀접하게 관련되어 있다. 또한, 전산학, 통계 물리학과 같은 응용 분야에서도 중요한 역할을 한다.[26][27]

키싱 수는 부호 이론과 이산 기하학 모두와 관련이 있다.

  • '''수학'''
  • 대수학
  • 확률론
  • 에르고딕 이론
  • 기하학
  • 위상수학
  • 수론
  • 조화 해석
  • 조합 최적화: 이산적이고 조합적인 대상에 대한 최적화 연구로, 운영 과학, 알고리즘 이론, 계산 복잡도 이론과 관련된다.
  • 부호 이론: 효율적이고 신뢰할 수 있는 데이터 전송 방법을 설계하는 정보 이론의 한 분야이다. 초기에는 오류 정정 부호의 조합론적 구성을 통해 설계 이론의 일부로 시작되었다.
  • 이산 기하학(조합 기하학): 볼록 다면체 및 접촉수에 대한 초기 결과와 함께 조합론의 일부로 시작되었으며, 계산 기하학 응용 분야가 등장하면서 별도의 연구 분야로 발전했다.
  • 동역학계의 조합론적 측면: 그래프 동역학계와 같이 동역학계가 조합론적 대상에 대해 정의될 수 있다.


조합론은 확률의 기초로 응용되기도 한다. 조합의 수를 알고 각각의 개별 사건이 독립적이라면, 확률은 조합의 수로 나누어 구할 수 있다.[26][27]

참조

[1] 문서 Björner and Stanley, p. 2
[2] 서적 Combinatorial Problems and Exercises https://books.google[...] North-Holland 1979
[3] 웹사이트 What is Combinatorics? https://www.math.ucl[...] 2017-11-01
[4] 문서 Ryser 1963
[5] 간행물 Book Review https://www.ams.org/[...] 2021-02-04
[6] 서적 Discrete Thoughts https://link.springe[...] Birkhaüser 1969
[7] 저널 On the shoulders of Hipparchus https://link.springe[...] 2021-03-12
[8] 저널 Hipparchus, Plutarch, Schröder, and Hough
[9] 저널 On the Second Number of Plutarch
[10] 저널 Towards a reconstruction of Archimedes' Stomachion https://www.sciamvs.[...] 2021-03-12
[11] 저널 Arabic Traces of Lost Works of Apollonius https://www.jstor.or[...] 2021-03-26
[12] 저널 Okytokion https://grbs.library[...] 2021-03-26
[13] MacTutor
[14] 서적 Mathematics Across Cultures: The History of Non-Western Mathematics https://books.google[...] Kluwer Academic Publishers 2015-11-15
[15] 저널 The Roots of Combinatorics
[16] 간행물 Probability Theory: A Historical Sketch https://books.google[...] Academic Press 2015-01-25
[17] 저널 Ringing the Cosets
[18] 저널 Fabian Stedman: The First Group Theorist?
[19] Webarchive Journals in Combinatorics and Graph Theory http://www.math.iit.[...] 2021-02-17
[20] webarchive 2-Digit MSC Comparison http://www.math.gate[...] 2008-12-31
[21] 문서 Stinson 2003
[22] 문서 Combinatorial Cardinal Characteristics of the Continuum Springer
[23] 간행물 Successors of Singular Cardinals http://link.springer[...] Springer Netherlands 2022-08-27
[24] 웹사이트 Continuous and profinite combinatorics http://faculty.uml.e[...] 2009-01-03
[25] 웹사이트 Mathematics Subject Classification 2020 (MSC2020) https://msc2020.org 2024-01-19
[26] 문서 確率論及統計論
[27] 웹사이트 確率論および統計論 復刻版 https://iss.ndl.go.j[...] 現代工学社 2019-02-28
[28] 서적 Ἠθικά
[29] 저널 http://www-math.mit.[...]
[30] 저널
[31] 저널 The Bells: versatile numbers that can count partitions of a set, primes and even rhymes
[32] 서적 http://gallica.bnf.f[...]
[33] 서적 http://www.labirinto[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com