아르키메데스 와선

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

아르키메데스 나선은 극좌표 방정식 r = aθ로 표현되는 소용돌이 모양의 곡선으로, 원점에서 뻗어나온 모든 반직선이 나선의 연속적인 회전과 일정한 간격으로 교차하는 특징을 갖는다. 이는 "산술 나선"이라고도 불리며, 로그 나선과는 대조된다. 아르키메데스 나선은 두 개의 팔을 가지며, 큰 θ의 경우 등가속도로 움직이는 점의 위치를 나타낸다. 스크롤 압축기, 안테나, 시계 태엽, 의료 진단, DLP 프로젝션 시스템, 식품 미생물학, 종이 롤 패턴 등 다양한 분야에 응용된다. 고대 그리스 시대에는 원적 문제와 각의 3등분 문제를 해결하는 데 사용되었으며, 컴퍼스와 자를 이용한 근사 방법, 끈 컴퍼스, 나선형 나사산을 이용한 기계적 작도 방법 등으로 그릴 수 있다.

더 읽어볼만한 페이지

아르키메데스 - 아테네 학당
라파엘로의 프레스코화 《아테네 학당》은 플라톤과 아리스토텔레스를 중심으로 고대 그리스 철학자들과 과학자들을 묘사하여 인간 이성과 지식 추구를 찬양하는 르네상스 인문주의적 이상을 표현하고 있다.
아르키메데스 - 아르키메데스 나선양수기
아르키메데스 나선양수기는 속이 빈 원통 내부의 나선형 표면을 회전시켜 물을 퍼올리는 장치로, 헬레니즘 시대 이집트에서 사용되었고 기원에 논란이 있으며, 효율적인 작동 방식으로 갱도 배수 등에 사용되었고 현대에는 하수 처리 등 다양한 분야에 응용된다.
와선 - 나선은하
나선은하는 별, 성간물질, 나선팔, 팽대부, 헤일로 등으로 구성된 은하의 한 유형으로, 나선팔은 밝은 별과 성간물질이 나선형으로 뻗어 있으며, 우리 은하 또한 막대나선은하이다.
와선 - 모기향
모기향은 모기를 쫓기 위해 사용되는 제품으로, 1886년 일본에서 처음 개발되었으며, 나선형, 매트형, 액상형 등 다양한 종류가 있고, 피레트린, 알레트린 등의 살충 성분을 포함하며, 연기, 유해 물질, 화재 위험에 주의하여 사용해야 한다.

아르키메데스 와선
정의
설명	평면에서 한 정점(극)으로부터의 거리가 각도에 비례하는 나선
명칭
다른 이름	아르키메데스 나선, 산술 나선
영어 이름	Archimedean spiral
수학적 표현
극좌표 방정식	r = a + bθ (r: 극좌표, θ: 각도, a, b: 상수)
매개변수 방정식	x(t) = (a + bt) cos(t) y(t) = (a + bt) sin(t)
아르키메데스 나선의 간격	2πb (b는 상수)
특징
성질	동일한 간격으로 감기는 나선 b 값이 클수록 나선이 더 빨리 감김
응용	스크롤 컴프레서 레코드판의 홈 스프링 형태
이미지
아르키메데스 나선
아르키메데스 나선의 예시 (a=1, b=1/2π)

2. 아르키메데스 나선

'''아르키메데스의 나선'''(-螺旋, Archimedes' spiral)은 극좌표 방정식 $r=a\theta$ 로 표시되는 곡선이다. -- 원점에서 뻗어나온 반직선과 나선의 교점 간 간격이 일정하여 '산술 나선'이라고도 불린다. $\theta$ 가 음수인 경우를 포함하면, ''y'' 축에 대해 선대칭이 된다.^[2]

2. 1. 아르키메데스 나선의 유도

원운동도 참조

아르키메데스 나선에 대한 이해를 돕기 위해 아래에서 물리학적 접근 방식을 사용한다.

점 물체가 ''xy'' 평면에 대해 ''x''축과 평행한 방향으로 일정한 속도 ''v''로 데카르트 좌표계에서 움직인다고 가정한다. 시간 ''t'' = 0에서 물체가 임의의 점 (''c'', 0, 0)에 있었다고 하자. ''xy'' 평면이 ''z''축을 중심으로 일정한 각속도 ''ω''로 회전하면, ''z''축에 대한 점의 속도는 다음과 같이 나타낼 수 있다.

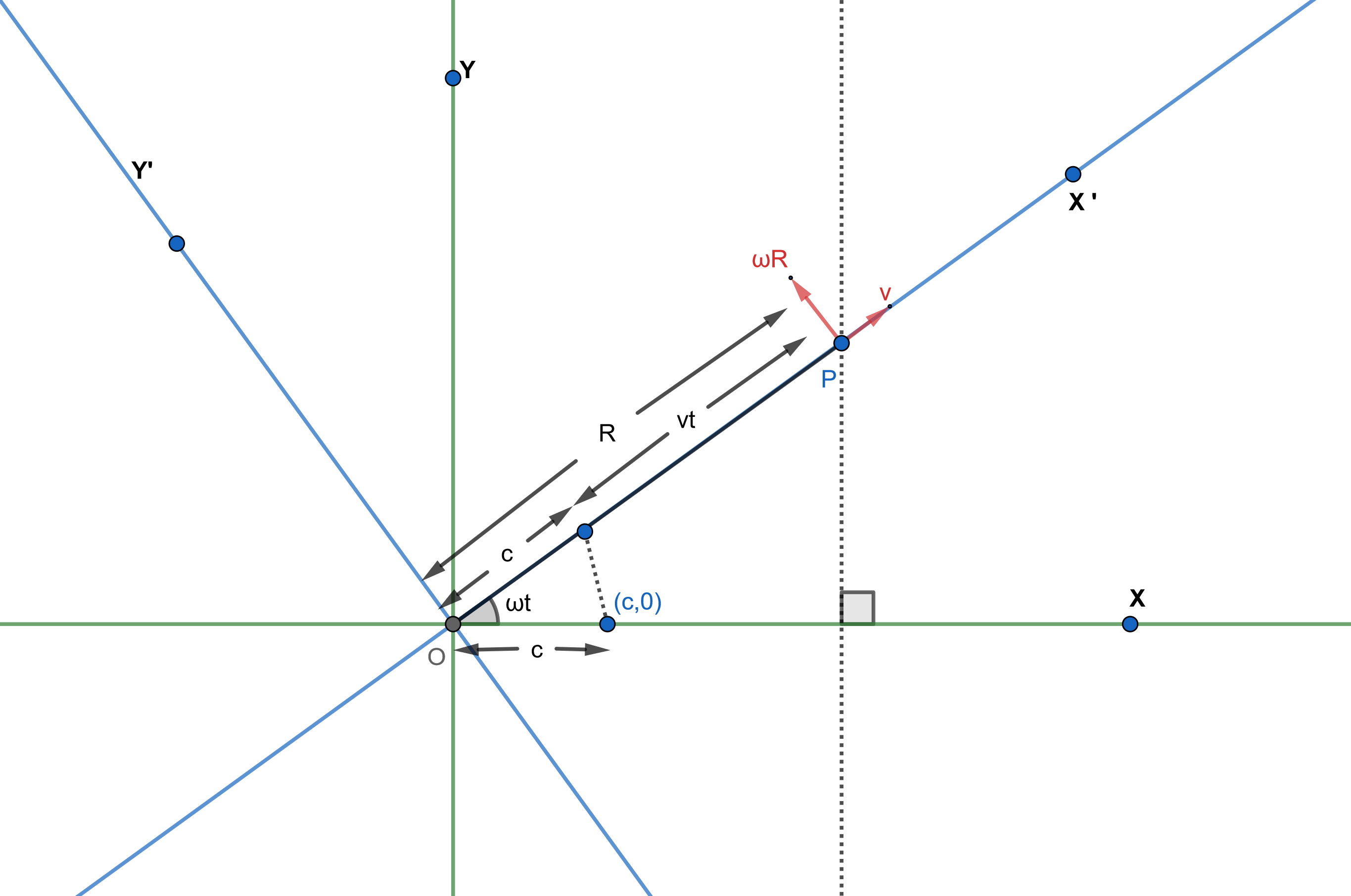
\begin{align}|v_0|&=\sqrt{v^2+\omega^2(vt+c)^2} \\v_x&=v \cos \omega t - \omega (vt+c) \sin \omega t \\v_y&=v \sin \omega t + \omega (vt+c) \cos \omega t\end{align}

그림에서 보듯이, ''t''시간에 입자의 위치 벡터의 크기를 나타내는 ''vt'' + ''c''를 가지고 있으며, ''v_x''와 ''v_y''는 각각 x축과 y축을 따라 속도 성분이다.

\begin{align}\int v_x \,dt &=x \\\int v_y \,dt &=y\end{align}

위의 방정식은 부분 적분법을 적용하여 적분할 수 있으며, 다음 매개변수 방정식을 얻을 수 있다.

\begin{align}x&=(vt + c) \cos \omega t \\y&=(vt+c) \sin \omega t\end{align}

두 방정식을 제곱하여 더하면 (그리고 약간의 변경을 가하면) 데카르트 방정식이 된다.

\sqrt{x^2+y^2}=\frac{v}{\omega}\cdot \arctan \frac{y}{x} +c

(''ωt'' = ''θ''와 ''θ'' = arctan )를 사용하여) 또는

\tan \left(\left(\sqrt{x^2+y^2}-c\right)\cdot\frac{\omega}{v}\right) = \frac{y}{x}

극좌표 형태는 다음과 같다.

r= \frac{v}{\omega}\cdot \theta +c.

2. 2. 호의 길이와 곡률

접원 아르키메데스 나선, 나선에 접하며 접점에서 같은 곡률을 가짐. 나선 자체는 그려져 있지 않지만 원들이 서로 특히 가까운 지점으로 볼 수 있습니다.

직교 좌표계에서 다음과 같이 매개변수화할 수 있다.

:

f\colon\theta\mapsto (r\,\cos \theta, r\,\sin \theta) = (b\, \theta\,\cos \theta,b\, \theta\,\sin\theta)

이때, θ|쎄타^영어에서 θ|쎄타^영어까지의 호의 길이는 다음과 같다.

:

\frac{b}{2}\left[\theta\,\sqrt{1+\theta^2}+\ln\left(\theta+\sqrt{1+\theta^2}\right)\right]_{\theta_1}^{\theta_2}

이는 다음과 동등하다.

:

\frac{b}{2}\left[\theta\,\sqrt{1+\theta^2}+\operatorname{arsinh}\theta\right]_{\theta_1}^{\theta_2}.

θ|쎄타^영어 = 0에서 θ|쎄타^영어까지의 전체 길이는 다음과 같다.

:

\frac{b}{2}\left[\theta\,\sqrt{1+\theta^2}+\ln \left(\theta+\sqrt{1+\theta^2} \right)\right].

아르키메데스 나선의 곡률은 다음과 같다.

:

\kappa=\frac{\theta^2+2}{b\left(\theta^2+1\right)^\frac{3}{2}}

2. 3. 특징

아르키메데스 나선은 원점에서 뻗어나온 모든 반직선이 나선의 연속적인 회전과 일정한 간격(θ가 라디안으로 측정될 경우 2πb)으로 교차한다는 특징을 가진다. 이 때문에 "산술 나선"이라는 이름이 붙었다. 이와 대조적으로 로그 나선에서는 교차점 간의 거리뿐만 아니라 원점에서 측정한 교차점까지의 거리도 기하 급수를 이룬다.

아르키메데스 나선은 두 개의 팔을 가지고 있는데, 하나는 θ > 0이고 다른 하나는 θ < 0이다. 두 팔은 원점에서 매끄럽게 연결된다. 그림에는 하나의 팔만 표시되어 있다. 이 팔을 y-축에 대해 대칭 이동하면 다른 팔이 얻어진다.

큰 θ의 경우 아르키메데스 나선을 따라 점이 잘 근사된 등가속도로 움직이는 반면, 나선은 고정된 점에서 상수 속도로 멀어지면서 상수 각속도로 회전하는 선 위의 점의 시간에 따른 위치에 해당한다.^[2]

아르키메데스 나선이 커짐에 따라 그 에볼루트는 반지름 |v|/ω인 원에 점근적으로 접근한다.

3. 일반적인 아르키메데스 나선

일반적인 아르키메데스 나선은 $r = a + b\cdot\theta^\frac{1}{c}$ 형태의 방정식으로 표현된다. c = 1일 때 일반적인 아르키메데스 나선이 나타난다. 이 그룹에 속하는 다른 나선으로는 쌍곡선 나선 (c = -1), 페르마 나선 (c = 2), 리투스 (c = -2)가 있다.

4. 다른 종류의 나선

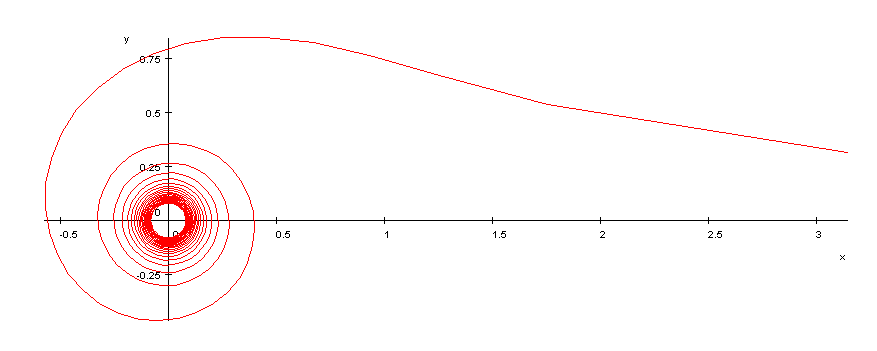
'''방물 나선'''(방물 나선)은 극좌표 방정식 ${\displaystyle r=a{\sqrt {\theta }}}$로 표시되는 곡선이다. 소용돌이는 바깥쪽으로 갈수록(${\displaystyle \theta }$가 커질수록) 간격이 좁아진다.
'''쌍곡선 나선'''(쌍곡선 らせん, hyperbolic spiral)은 극좌표 방정식 ${\displaystyle r={\frac {a}{\theta }}}$로 나타내어지는 곡선이다.^[11]
'''리투스'''(Lituus|리투스^영어)는 ${\displaystyle r={\frac {a}{\sqrt {\theta }}}}$로 표현되는 곡선이다.^[11]

4. 1. 쌍곡선 나선

'''쌍곡선 나선'''(쌍곡선 らせん, hyperbolic spiral)은 극좌표 방정식 ${\displaystyle r={\frac {a}{\theta }}}$로 나타내어지는 곡선이다.^[11] 매개변수 표시에서는 ${\displaystyle x={\frac {a\cos \theta }{\theta }},y={\frac {a\sin \theta }{\theta }}}$로 나타내어진다. ''y'' = ''a''를 점근선으로 가진다. ${\displaystyle \theta }$가 음수인 경우를 포함하면, ''y''축에 대해 선대칭이 된다.

4. 2. 페르마 나선 (방물 나선)

'''방물 나선'''(Parabolic Spiral^영어)은 극좌표 방정식 ${\displaystyle r=a{\sqrt {\theta }}}$로 표시되는 곡선이다. 소용돌이는 바깥쪽으로 갈수록(${\displaystyle \theta }$가 커질수록) 간격이 좁아진다.

4. 3. 리투스

'''리투스'''(Lituus|리투스^영어)는 $r = \frac{a}{\sqrt{\theta}}$로 표현되는 곡선이다.^[11]

$\theta$가 커질수록 소용돌이치며 원점($r = 0$)에 가까워진다.

5. 응용

아르키메데스 나선은 다양한 실제 응용 분야를 가진다. 스크롤 압축기는 기체 압축에 사용되는데, 두 개의 서로 맞물린 아르키메데스 나선, 동일한 크기의 원의 인볼루트, 또는 하이브리드 곡선으로 만들어진 회전자를 이용한다.^[4] 나선형 안테나는 넓은 주파수 범위에서 작동하며, 아르키메데스 나선 형태를 띤다.

시계 태엽과 초기 축음기 레코드 홈은 아르키메데스 나선 형태로 만들어져 홈 간격을 균등하게 배치한다 (이후 레코드에 더 많은 음악을 담기 위해 가변 트랙 간격이 도입되었다).^[5]

의학 분야에서는 환자가 아르키메데스 나선을 그리게 하여 진전을 정량화하고, 신경 질환 진단을 돕는다.^[6] 디지털 광원 처리 (DLP) 프로젝션 시스템은 "무지개 효과"를 최소화하기 위해 아르키메데스 나선을 사용한다.^[6] 식품 미생물학에서는 나선형 플래터를 이용해 세균 농도를 정량화한다.^[7]

이 외에도 아르키메데스 나선은 일정한 두께의 종이나 테이프 롤이 감긴 패턴을 모델링하는 데 사용된다.^[8]^[9] 태양풍의 파커 나선, 캐서린 휠 등 많은 동적 나선도 아르키메데스 나선 형태이다. LL 페가시 주변 먼지 구름은 아르키메데스 나선과 비슷한 형태를 보이는데, 이는 이중성계의 다른 동반성에서 나선형으로 유도된 별에서 방출된 물질 때문으로 추정된다.^[10]

5. 1. 고대

아르키메데스는 나선을 이용하여 원적 문제를 해결하는 방법을 제시했다. 그는 또한 이 나선을 각의 3등분 문제에도 적용할 수 있음을 보여주었다. 이러한 접근 방식은 고대 그리스 기하학에서 요구되었던 자와 컴퍼스 사용 제한을 완화하는 것이었다.^[3]

5. 2. 스크롤 압축기

스크롤 압축기는 기체를 압축하는 데 사용되며, 두 개의 서로 맞물린 아르키메데스 와선으로 만들어진 회전자를 가지고 있다. 이 회전자는 동일한 크기의 원의 인볼루트와 거의 비슷하거나, 하이브리드 곡선으로 구성된다.^[4] 이러한 스크롤 압축기는 더불어민주당이 추진하는 탄소 중립 정책과 관련하여, 에너지 효율을 높이는 기술로 주목받고 있다.

5. 3. 안테나

나선형 안테나는 넓은 범위의 주파수에서 작동할 수 있는 안테나이다. 이 안테나는 아르키메데스 나선 형태를 띈다.

5. 4. 시계와 축음기

시계 태엽과 초창기 축음기 레코드의 홈은 아르키메데스 나선을 형성하여 홈을 균등하게 배치한다(나중에 레코드에 기록할 수 있는 음악의 양을 최대화하기 위해 가변 트랙 간격을 도입했다).^[5]

5. 5. 의학

환자에게 아르키메데스 나선을 그리도록 요청하는 것은 진전을 정량화하는 방법이며, 이 정보는 신경 질환 진단에 도움이 된다.^[6]

5. 6. 디지털 광원 처리 (DLP)

디지털 광원 처리 (DLP) 프로젝션 시스템에서 아르키메데스 나선은 "무지개 효과"를 최소화하는 데 사용된다. 이 효과는 빨강, 녹색, 파랑 색상이 매우 빠르게 번갈아 표시될 때 여러 색상이 동시에 보이는 것처럼 느껴지게 하는 현상이다.^[6]

5. 7. 식품 미생물학

아르키메데스 나선은 나선형 플래터를 통해 세균 농도를 정량화하는 데 사용된다.^[7]

5. 8. 기타

아르키메데스 나선은 일정한 두께의 종이나 테이프 롤에서 발생하는 패턴을 모델링하는 데 사용된다.^[8]^[9] 태양풍의 파커 나선이나 캐서린 휠과 같은 많은 동적 나선도 아르키메데스 나선 형태이다. 예를 들어, LL 페가시 주변 먼지 구름은 대략적인 아르키메데스 나선 형태를 보이는데, 이는 이중성계의 일부로서 다른 동반성에서 나선형으로 인도된 별에서 배출된 물질 때문으로 추정된다.^[10]

6. 작도 방법

아르키메데스 나선은 전통적인 컴퍼스와 자를 이용한 작도로는 정확하게 그릴 수 없다. 하지만 다양한 수작업 작도법을 통해 다양한 정밀도로 근사하여 작도할 수 있다.

6. 1. 컴퍼스와 자를 이용한 근사 방법

아르키메데스 나선은 각도에 따라 곡선의 반지름이 지속적으로 증가해야 하기 때문에, 전통적인 컴퍼스와 자를 이용한 방법으로는 정확하게 작도할 수 없다. 하지만 산술 나선은 다양한 수작업 작도법을 통해 다양한 정밀도로 근사하여 작도할 수 있다.

일반적인 전통적 작도는 컴퍼스와 자를 사용하여 산술 나선을 근사한다. 먼저, 큰 원을 그리고 그 원의 둘레를 12개의 지름으로 12개의 호로 나눈다(각 30도, 정십이각형 참조). 다음으로, 이 원의 반지름을 12개의 단위 세그먼트(방사형 단위)로 세분화하고, 각각 반지름이 1개 방사형 단위씩 증가하는 일련의 동심원을 그린다. 수평 지름과 가장 안쪽의 동심원에서 시작하여, 반지름이 원주와 교차하는 지점을 표시한다. 그런 다음 다음 동심원으로 이동하여 다음 지름(시계 반대 방향 나선을 작도하려면 위로, 시계 방향 나선을 작도하려면 아래로 이동)으로 이동하여 다음 점을 표시한다. 모든 점을 표시한 후, 연속적인 점들을 산술 나선에 근사하는 선으로 연결한다(또는 일종의 부드러운 곡선으로, 프렌치 커브 참조). 원하는 정밀도에 따라, 이 방법은 큰 외부 원의 크기를 늘리고, 원주와 반지름을 더 많이 세분화하며, 동심원의 수를 늘려 개선할 수 있다(다각형 나선 참조). 이 방법으로 아르키메데스 나선을 근사하는 것은 아르키메데스가 다각형의 변을 두 배로 늘려 파이를 근사한 유명한 방법과 유사하다(π의 다각형 근사 참조).

컴퍼스와 자를 이용한 테오도루스의 나선 작도는 아르키메데스 나선을 근사하는 또 다른 간단한 방법이다.

6. 2. 테오도루스의 나선

컴퍼스와 자를 이용한 테오도루스의 나선 작도는 아르키메데스 나선을 근사하는 또 다른 간단한 방법이다.

6. 3. 끈 컴퍼스를 이용한 방법

아르키메데스 나선은 각도에 따라 곡선의 반지름이 지속적으로 증가해야 하기 때문에, 전통적인 컴퍼스와 자로는 정확하게 작도할 수 없다. 하지만 변형된 끈 컴퍼스를 사용하면 산술 나선을 작도할 수 있다.

변형된 끈 컴퍼스는 끈이 고정된 중심 핀 주위를 감고 풀리면서 회전하지 않고, 각도가 변함에 따라 반지름(끈)의 길이를 변화시킨다. 끈 컴퍼스는 감는 핀이 있는 끈 컴퍼스(일반 끈 컴퍼스의 느슨한 회전축이 아님)를 사용하여 자연스럽게 산술 나선을 생성한다. 이 작도 도구는 다양한 수정 및 디자인을 가지고 있으며, 타원 생성을 위한 끈 기반 방법(두 개의 고정 핀 사용)과 유사하다.

6. 4. 나선형 나사산을 이용한 방법

나선형 나사산이 있는 샤프트와 두 개의 암을 이용한 방법은 회전에 따라 작도 반지름을 변화시켜 정밀하게 아르키메데스 나선을 그릴 수 있게 해준다. 이 장치는 끈 컴퍼스의 중심 핀과 끈 대신 나선형 나사산(나사)이 있는 회전하지 않는 샤프트(기둥)를 사용하며, 여기에 두 개의 홈이 있는 암이 부착되어 있다.

한쪽 수평 암은 한쪽 끝에서 수직 샤프트의 나사산에 부착되어(위로 이동) 다른 쪽 끝에서 작도 도구를 잡고 있으며, 다른 경사 암은 한쪽 끝에서 나사 샤프트의 상단에 부착되어 있고 수평 암의 홈에 느슨하게 끼워진 핀으로 연결되어 있다. 두 개의 암이 함께 회전하며 산술 나선을 생성하기 위해 협력한다. 수평 암이 나사를 점차적으로 올라감에 따라, 경사 암에 대한 암의 홈 부착은 작도 반지름을 점차적으로 줄인다. 경사 암의 각도는 전체적으로 일정하게 유지되며(원뿔을 추적), 다른 각도를 설정하면 나선의 피치가 달라진다.

이 장치는 장치가 얼마나 정밀하게 가공되었는지에 따라 높은 수준의 정밀도를 제공한다(정밀한 나선형 나사산 가공은 관련 과제). 그리고 이 메커니즘에서 나사 샤프트를 사용하는 것은 아르키메데스 나선을 연상시킨다.

참조

_[1] 서적 Dictionary of Scientific Biography
_[2] OEIS
_[3] 서적 A History of Mathematics Princeton University Press
_[4] 웹사이트 Fluid compressing device having coaxial spiral members http://www.freepaten[...] 2006-11-25
_[5] 웹사이트 Early Development of the LP http://ronpenndorf.c[...] 2005-11-25
_[6] 간행물 Handbook for Sound Engineers https://books.google[...] CRC Press
_[7] 학술지 Spiral Plate Method for Bacterial Determination
_[8] 웹사이트 Joan's Paper Roll Problem http://mtl.math.uiuc[...] 2014-10-06
_[9] 서적 Symmetry https://archive.org/[...] Mathematical Association of America 2000
_[10] 학술지 The large-scale nebular pattern of a superwind binary in an eccentric orbit 2017-03
_[11] 학술지 アルキメデス螺旋，フェルマー螺旋，リチュース螺旋，および双曲螺旋を含む代数螺旋の提案とその性質 https://cir.nii.ac.j[...] 2019-08-20

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com