지프의 법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

지프의 법칙은 데이터의 순위와 빈도 사이의 관계를 설명하는 경험적 법칙으로, 다양한 현상에서 관찰된다. 이 법칙은 가장 흔한 요소가 두 번째로 흔한 요소보다 약 두 배 더 자주 나타나는 등, 요소의 빈도가 순위에 반비례한다는 것을 나타낸다. 지프의 법칙은 언어학, 사회과학, 정보과학, 자연과학 등 다양한 분야에서 발견되며, 단어 빈도, 웹 페이지 접속 빈도, 도시 인구, 소득, 음악 음표 사용 빈도, 유전자 발현량, 지진 규모, 고체 파편 크기 등에서 나타난다. 지프의 법칙은 멱법칙의 일종으로, 율-사이먼 분포, 벤포드의 법칙 등과 관련이 있으며, 최소 노력의 원리, 선호적 연결, 무작위 텍스트 생성 등 다양한 이론으로 설명된다.

2. 역사

1913년, 독일 물리학자 펠릭스 아우어바흐는 도시의 인구 규모와 그 변수의 감소 순서에 따라 정렬된 순위 사이에 반비례 관계가 있음을 관찰했다.^[10]

조지 지프가 법칙을 발표하기 이전에, 1916년 프랑스 속기사 장-밥티스트 에스투가 처음 발견하였고,^[20] 1923년 G. 듀이, 1928년 E. 콘돈에 의해 발견되었다.^[2]

1932년 조지 지프는 자연어 텍스트에서 단어 빈도에 대한 동일한 관계를 관찰했지만,^[11] 자신이 처음 제안했다고 주장하지 않았다. 지프는 수학을 좋아하지 않았으며, 같은 해 출판물에서 언어학에 대한 수학적 관여에 대해 경멸조로 이야기했다. 지프가 사용한 유일한 수학적 표현은 알프레드 J. 로트카의 1926년 출판물에서 "빌려온" 것이다.^[13]

이러한 관계는 빈도 외에도 다른 변수 및 여러 맥락에서 발생한다.^[34] 예를 들어, 기업을 규모 순으로 정렬하면 크기가 순위에 반비례한다.^[50] 개인 소득(파레토 원리^[3]), 같은 TV 채널 시청자 수,^[36] 음악의 음표,^[26] 세포 전사체 등에서도 동일한 관계가 발견된다.^[44]^[51]

1992년 생물정보학자 리 웬티안은 무작위 생성 텍스트에서도 지프의 법칙이 나타난다는 논문을 발표했다.^[17]

2. 1. 초기 발견

1913년, 독일 물리학자 펠릭스 아우어바흐는 도시의 인구 규모와 그 변수의 감소 순서에 따라 정렬된 순위 사이에 반비례 관계가 있음을 관찰했다.^[10]

조지 지프보다 먼저, 1916년 프랑스 속기사 장-밥티스트 에스투가 처음 발견하였고,^[20] 1923년 G. 듀이, 1928년 E. 콘돈에 의해 발견되었다.^[2]

자연어 텍스트에서 단어 빈도에 대한 동일한 관계는 1932년 조지 지프가 관찰했지만,^[11] 그는 자신이 처음 제안했다고 주장하지 않았다.

2. 2. 지프의 기여

독일 물리학자 펠릭스 아우어바흐는 1913년에 도시 인구 규모와 순위 사이에 반비례 관계가 있음을 발견했다.^[10]

지프의 법칙은 지프 이전에 발견되었다.^[14] 1916년 프랑스 속기사 장-밥티스트 에스투가 처음 발견했고,^[20] 1923년 G. 듀이, 1928년 E. 콘돈에 의해 발견되었다.^[2]

자연어 텍스트에서 단어 빈도에 대한 동일한 관계는 1932년 조지 지프가 관찰했지만,^[11] 그는 자신이 처음 제안했다고 주장하지 않았다. 지프는 수학을 좋아하지 않았으며, 1932년 출판물에서 언어학에 대한 수학적 관여에 대해 경멸조로 이야기했다.^[12] 지프가 사용한 유일한 수학적 표현은 알프레드 J. 로트카의 1926년 출판물에서 "빌려온" 것이다.^[13]

이러한 관계는 빈도 외에도 다른 변수 및 여러 맥락에서 발생한다.^[34] 예를 들어, 기업을 규모 순으로 정렬하면 크기가 순위에 반비례한다.^[50] 개인 소득(파레토 원리^[3]), 같은 TV 채널 시청자 수,^[36] 음악의 음표,^[26] 세포 전사체 등에서도 동일한 관계가 발견된다.^[44]^[51]

1992년 생물정보학자 리 웬티안은 무작위 생성 텍스트에서도 지프의 법칙이 나타난다는 논문을 발표했다.^[17]

2. 3. 현대적 발전

1913년, 독일 물리학자 펠릭스 아우어바흐는 도시의 인구 규모와 그 변수의 감소 순서에 따라 정렬된 순위 사이에 반비례 관계가 있음을 관찰했다.^[10]

지프의 법칙은 조지 지프보다 먼저 발견되었으며, 1916년 프랑스 속기사 장-밥티스트 에스투에 의해 처음 발견되었고, 1923년 G. 듀이, 1928년 E. 콘돈에 의해 발견되었다.^[2]

자연어 텍스트에서 단어 빈도에 대한 동일한 관계는 1932년 조지 지프에 의해 관찰되었지만,^[11] 그는 그것을 처음 제안했다고 주장한 적이 없다.

이와 같은 관계는 빈도 외에도 다른 변수 및 많은 다른 맥락에서도 발생한다는 것을 발견했다.^[34] 예를 들어, 기업을 규모 감소 순으로 정렬하면, 그 크기가 순위에 반비례하는 것을 알 수 있다.^[50] 동일한 관계는 개인 소득(여기서는 파레토 원리라고 불림^[3]), 같은 TV 채널을 시청하는 사람 수,^[36] 음악의 음표,^[26] 세포 전사체 등에서 발견된다.^[44]^[51]

1992년 생물정보학자 리 웬티안은 지프의 법칙이 무작위로 생성된 텍스트에서도 나타난다는 짧은 논문을 발표했다.^[17] 여기에는 지프의 법칙의 거듭제곱 법칙 형태가 단어를 순위별로 정렬한 결과라는 증명이 포함되어 있었다.

3. 수학적 정의

지프의 법칙은 특정 순위의 요소 빈도를 계산하는 공식으로 표현된다. 요소 수를 ''N'', 순위를 ''k'', 분포 특성 지수를 ''s''라 할 때, 순위 ''k''인 요소 빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.^[56]

: $f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}$

이 공식은 요소 발생 횟수가 독립적이고 멱법칙 분포 $p(f) = \alpha f^{-1-1/s}$ 를 따르는 무작위 변수로 나타날 때 적용된다.^[56]

영어 단어 사용 빈도의 경우, ''N''은 영어 단어 수이고, 고전적 버전의 지프 법칙에서는 지수 ''s''가 1이다. ''f''(''k'';''s'',''N'')은 ''k''번째로 많이 나타나는 단어의 빈도 비율이다.

위 식은 다음과 같이 표현 가능하다.

: $f(k;s,N)=\frac{1}{k^s H_{N,s}}$

여기서 ''H_N,s''는 ''N''번째 일반화된 조화수이다.

지프 법칙의 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포에 따라 빈도를 순위대로 정렬하면, 2위 빈도는 1위의 ½, 3위는 ⅓이 된다. ''n''위 빈도는 1위의 ¹⁄_''n''이 되지만, 빈도는 정수이므로 오차가 발생한다. 그럼에도 많은 자연 현상이 지프 법칙을 따른다.

지프 분포상 모든 관계 빈도의 합은 조화급수와 같다.

: $\sum_{n=1}^\infty \frac{1}{n}=\infty\!$

인간 언어에서 단어 빈도는 꼬리가 긴 헤비테일 분포를 가지며, ''s'' 값이 1에 가까운 지프 분포로 모델링할 수 있다.

''s''가 1보다 크면, 다음이 성립하므로 무한히 많은 단어에 법칙이 적용될 수 있다.

: $\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!$

여기서 ζ는 리만 제타 함수이다.

3. 1. 기본 형태

지프의 법칙은 데이터의 순위와 빈도를 각 축에 로그 스케일로 나타낸 그래프를 통해 쉽게 확인할 수 있다. 예를 들어, "the"라는 단어는 ''x'' = log(1), ''y'' = log(69971) 지점에 나타난다. 이 데이터를 선형 그래프로 나타내면 지프의 법칙에 잘 들어 맞는다.^[56]

변수들을 다음과 같이 정의한다.

''N'' ― 요소의 숫자
''k'' ― 요소의 순위
''s'' ― 분포의 특성을 나타내는 지수값

지프의 법칙에 따르면 ''N''개의 요소들 가운데 순위가 ''k'' 번째인 요소의 사용빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}

지프의 법칙은 각 요소들의 발생 횟수가 독립적이고 멱법칙 분포

p(f) \alpha f^{-1-1/s}

에 따라 동일하게 분포된 랜덤 변수로 나타날 때에만 적용된다.^[56]

영어 단어 사용 빈도의 경우, ''N''은 영어 단어의 개수이고, 고전적 버전의 지프의 법칙을 사용한다고 가정할 경우 지수 ''s''는 1이다. ''f''(''k'';''s'',''N'')은 ''k''번째로 많이 나타난 단어의 분수가 된다.

이를 정리하면 다음과 같다.

:

f(k;s,N)=\frac{1}{k^s H_{N,s}}

여기서 ''H_N,s''는 ''N'' 번째 일반화된 조화수이다.

지프의 법칙의 가장 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포를 따르는 빈도가 순위에 따라 정렬되어 주어졌을 때, 2위에 해당하는 빈도는 1위의 빈도의 ½이 된다. 3위의 빈도는 1위 빈도의 ⅓이 된다. 이러한 방식으로, ''n''위의 빈도는 1의 ¹⁄_''n''이 된다. 다만, 빈도는 정수이므로 2.5와 같은 수가 올 수 없기 때문에 이러한 계산과 실제 빈도 사이에는 약간의 오차가 발생한다. 그럼에도 불구하고 많은 자연 현상들이 꽤 넓은 범위에서 상당한 정확도로 지프의 법칙을 따른다.

수학적으로 지프 분포상의 모든 관계 빈도의 합은 조화급수와 동일하며 다음이 성립한다.

:

\sum_{n=1}^\infty \frac{1}{n}=\infty\!

인간의 언어에서, 단어의 사용 빈도는 꼬리가 매우 긴 헤비테일 분포를 보이며, 따라서 이는 ''s'' 값이 1에 가까운 지프 분포로 상당히 근접하게 모델링할 수 있다.

지수 ''s''가 1을 넘을 경우, 이러한 법칙이 무한히 많은 단어에 적용되는 것이 가능한데, 이것은 ''s''>1 일 때 다음이 성립하기 때문이다.

:

\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!

여기서 ζ는 리만 제타 함수이다.

Formally^영어, N개의 요소에 대한 지프 분포는 순위 k (1부터 시작)인 요소에 다음 확률을 할당한다.

:

\ f(k;N)  ~=~\begin{cases}\frac{ 1 }{\ H_N }\ \frac{1}{\ k\ }\ , &\ \mbox{ if }\ 1 \le k \le N ~, \\{} \\~~ 0 ~~ , &\ \mbox{ if }\ k < 1\ \mbox{ or }\  N < k ~.\end{cases}

여기서 H_N는 정규화 상수이다. N번째 조화수는 다음과 같다.

:

H_N \equiv \sum_{k=1}^N \frac{\ 1\ }{ k } ~.

이 분포는 때때로 1 대신 지수 s를 갖는 역제곱 법칙으로 일반화된다.^[22] 즉,

:

f(k;N,s) = \frac{1}{H_{N,s}}\,\frac{1}{k^s}

여기서 H_N,s는 일반화된 조화수이다.

:

H_{N,s} = \sum_{k=1}^N \frac{1}{k^s} ~.

일반화된 지프 분포는 지수 s가 1보다 큰 경우에만 무한히 많은 항목(N = ∞)으로 확장될 수 있다. 이 경우 정규화 상수 H_N,s는 리만 제타 함수가 된다.

:

\zeta (s) = \sum_{k=1}^\infty \frac{1}{k^s} < \infty ~.

무한 항목의 경우는 제타 분포에 의해 특징지어지며 로트카의 법칙이라고 불린다. 지수 s가 1 이하이면 정규화 상수 H_N,s는 N이 무한대로 갈 때 발산한다.

일반적인 지프의 법칙은 다음과 같이 나타낸다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N 1/n^s}

(단, N은 전체 요소의 수, k는 순위)

여기서 원래의 지프의 법칙에서는 s=1이다. 이 때 N을 무한대로 하면 분모가 수렴하지 않으므로(무한대로 발산, "조화급수" 참조), 원래의 지프의 법칙에서는 N을 유한으로 해야 한다(현실에서도 그렇게 생각되는 경우가 많다).

하지만 s가 1보다 약간이라도 큰 실수라면, N을 무한대로 해도 분모는 수렴하고(제타 함수 ζ(s)와 동일), k의 값을 무한대로 취할 수 있는 분포 함수로 할 수 있다.

3. 2. 일반화된 형태

지프의 법칙은 데이터의 순위와 빈도를 각 축에 로그 스케일로 나타낸 그래프를 통해 쉽게 확인할 수 있다. 예를 들어, "the"라는 단어는 ''x'' = log(1), ''y'' = log(69971) 지점에 나타난다. 이러한 데이터들을 선형 그래프로 나타내면 지프의 법칙에 잘 들어 맞는다.^[56]

변수들을 다음과 같이 정의한다.

''N'' ― 요소의 숫자
''k'' ― 요소의 순위
''s'' ― 분포의 특성을 나타내는 지수값

지프의 법칙에 따르면 ''N''개의 요소들 가운데 순위가 ''k'' 번째인 요소의 사용빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}

지프의 법칙은 각 요소들의 발생 횟수가 독립적이고 멱법칙 분포

p(f) \alpha f^{-1-1/s}

에 따라 동일하게 분포된 랜덤 변수로 나타날 때에만 적용된다.^[56]

영어의 단어 사용 빈도 사례에서, ''N''은 영어 단어의 개수이고, 고전적 버전의 지프의 법칙을 사용한다고 가정할 경우 지수 ''s''는 1이다. ''f''(''k'';''s'',''N'')은 ''k''번째로 많이 나타난 단어의 분수가 된다.

이를 정리하면 다음과 같다.

:

f(k;s,N)=\frac{1}{k^s H_{N,s}}

여기서 ''H_N,s''는 ''N'' 번째 일반화된 조화수이다.

지프의 법칙의 가장 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포를 따르는 빈도가 순위에 따라 정렬되어 주어졌을 때, 2위에 해당하는 빈도는 1위의 빈도의 ½이 된다. 3위의 빈도는 1위 빈도의 ⅓이 된다. 이러한 방식으로, ''n''위의 빈도는 1의 ¹⁄_''n''이 된다. 다만, 빈도는 정수이므로 2.5와 같은 수가 올 수 없기 때문에 이러한 계산과 실제 빈도 사이에는 약간의 오차가 발생하게 된다. 그럼에도 불구하고 많은 자연 현상들이 꽤 넓은 범위에서 상당한 정확도로 지프의 법칙을 따른다.

수학적으로 지프 분포상의 모든 관계 빈도의 합은 조화급수와 동일하며 다음이 성립한다.

:

\sum_{n=1}^\infty \frac{1}{n}=\infty\!

인간의 언어에서, 단어의 사용 빈도는 꼬리가 매우 긴 헤비테일 분포를 보이며, 따라서 이는 ''s'' 값이 1에 가까운 지프 분포로 상당히 근접하게 모델링할 수 있다.

지수 ''s''가 1을 넘을 경우, 이러한 법칙이 무한히 많은 단어에 적용되는 것이 가능한데, 이것은 ''s''>1 일 때 다음이 성립하기 때문이다.

:

\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!

여기서 ζ는 리만 제타 함수이다.

일반화된 지프의 법칙은 다음과 같이 나타낸다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N 1/n^s}

(단, N은 전체 요소의 수, k는 순위)

여기서 원래의 지프의 법칙에서는 s=1이다. 이 때 N을 무한대로 하면 분모가 수렴하지 않으므로(조화급수 참조), 원래의 지프의 법칙에서는 N을 유한으로 해야 한다.

하지만 s가 1보다 약간이라도 큰 실수라면, N을 무한대로 해도 분모는 수렴하고(제타 함수 ζ(s)와 동일), k의 값을 무한대로 취할 수 있는 분포 함수로 할 수 있다.

3. 3. 지프-만델브로 법칙

지프의 법칙은 데이터의 순위와 빈도를 로그 스케일로 나타낸 그래프를 통해 확인할 수 있다. 예를 들어, 단어 "the"는 ''x'' = log(1), ''y'' = log(69971) 지점에 나타나며, 이를 선형 그래프로 나타내면 지프의 법칙에 부합한다.^[56]

변수는 다음과 같이 정의한다.

''N'' ― 요소의 숫자
''k'' ― 요소의 순위
''s'' ― 분포의 특성을 나타내는 지수값

지프의 법칙에 따르면 ''N''개의 요소들 가운데 순위가 ''k'' 번째인 요소의 사용빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.^[56]

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}

이는 각 요소들의 발생 횟수가 독립적이고 멱법칙 분포

p(f) = \alpha f^{-1-1/s}

에 따라 동일하게 분포된 랜덤 변수로 나타날 때에만 적용된다.^[56]

영어 단어 빈도 사례에서 ''N''은 영어 단어의 개수이고, 고전적 버전의 지프의 법칙을 사용하면 지수 ''s''는 1이다. ''f''(''k'';''s'',''N'')은 ''k''번째로 많이 나타난 단어의 분수가 된다. 이를 정리하면 다음과 같다.

:

f(k;s,N)=\frac{1}{k^s H_{N,s}}

여기서 ''H_N,s''는 ''N'' 번째 일반화된 조화수이다.

지프의 법칙의 가장 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포를 따르는 빈도가 순위에 따라 정렬되면, 2위 빈도는 1위 빈도의 ½, 3위 빈도는 1위 빈도의 ⅓이 된다. ''n''위 빈도는 1의 ¹⁄_''n''이 되지만, 빈도는 정수이므로 오차가 발생한다. 그럼에도 많은 자연 현상들이 지프의 법칙을 따른다.

수학적으로 지프 분포상 모든 관계 빈도의 합은 조화급수와 동일하다.

:

\sum_{n=1}^\infty \frac{1}{n}=\infty\!

인간의 언어에서 단어 빈도는 꼬리가 긴 헤비테일 분포를 보이며, ''s'' 값이 1에 가까운 지프 분포로 모델링할 수 있다.

지수 ''s''가 1을 넘을 경우, 다음이 성립하므로 법칙이 무한히 많은 단어에 적용될 수 있다.

:

\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!

여기서 ζ는 리만 제타 함수이다.

일반화된 지프 분포는 다음과 같다.

:

f(k;N,s) = \frac{1}{H_{N,s}}\,\frac{1}{k^s}

여기서 ''H''_''N'',''s''는 일반화된 조화수이다.

:

H_{N,s} = \sum_{k=1}^N \frac{1}{k^s} ~.

브누아 망델브로가 제안한 지프-만델브로 법칙은 지프의 법칙을 일반화한 것으로 빈도는 다음과 같다.

:

f(k;N,q,s)=\frac{ 1 }{\ C\ }\ \frac{ 1 }{\ \left( k + q\right)^s} ~.

상수 ''C''는 ''s''에서 평가된 허위츠 제타 함수이다.

지프 분포는 변수 교환을 통해 파레토 분포에서 얻을 수 있으며,^[22] 연속 파레토 분포와 유사하여 '''이산 파레토 분포'''라고도 불린다.^[18]

율-시몬 분포의 꼬리 빈도는 다음과 같다.

:

f(k;\rho) \approx \frac{\ [\mathsf{constant}]\ }{ k^{(\rho + 1)} }

포물선 프랙탈 분포에서 빈도의 로그는 순위의 로그에 대한 이차 다항식으로, 단순 멱법칙보다 적합성을 향상시킨다.^[25] 프랙탈 차원과 마찬가지로 텍스트 분석에 유용한 지프 차원을 계산할 수 있다.^[27]

벤포드의 법칙은 지프의 법칙의 특수한 경계 사례이며,^[25] 두 법칙은 통계 물리학 및 임계 현상에서 규모 불변 함수 관계에서 파생되어 설명된다.^[23] ''s'' = 1인 지프의 법칙을 만족하는 데이터의 선두 자릿수는 벤포드의 법칙을 만족한다.

일반적인 지프의 법칙은 다음과 같다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N 1/n^s}

(단, ''N''은 전체 요소의 수, ''k''는 순위)

원래 지프의 법칙에서 ''s'' = 1이다. ''N''을 무한대로 하면 분모가 수렴하지 않으므로("조화급수" 참조), 원래 지프의 법칙에서는 ''N''을 유한으로 해야 한다.

하지만 ''s''가 1보다 약간이라도 큰 실수라면, ''N''을 무한대로 해도 분모는 수렴하고(제타 함수 ζ(''s'')와 동일), ''k''의 값을 무한대로 취할 수 있다.

4. 특성

지프의 법칙에 따르면 어떠한 자연어 말뭉치 표현에 나타나는 단어들을 그 사용 빈도가 높은 순서대로 나열하였을 때, 모든 단어의 사용 빈도는 해당 단어의 순위에 반비례한다. 가장 사용 빈도가 높은 단어는 두 번째 단어보다 빈도가 약 두 배 높으며, 세 번째 단어보다는 빈도가 세 배 높다. 예를 들어, 브라운 대학교 현대 미국 영어 표준 말뭉치의 경우, 가장 사용 빈도가 높은 단어는 영어 정관사 “the”이며 전체 문서에서 7%(약 백만 개 남짓의 전체 사용 단어 중 69,971회)를 차지한다. 두 번째로 사용 빈도가 높은 단어는 “of”로 약 3.5%(36,411회) 남짓한 빈도를 차지하며, 세 번째로 사용 빈도가 높은 단어는 “and”(28,852회)이다. 약 135개 항목의 어휘만으로 브라운 대학 말뭉치의 절반을 나타낼 수 있다.

형식적으로, N개의 요소에 대한 지프 분포는 순위 k (1부터 시작)인 요소에 다음 확률을 할당한다.

: $f(k;N) = \frac{1}{H_N} \cdot \frac{1}{k}$ (단, $1 \le k \le N$ )

여기서 H_N은 정규화 상수이며, N번째 조화수이다.

: $H_N = \sum_{k=1}^N \frac{1}{k}$

이 분포는 지수 s를 갖는 역제곱 법칙으로 일반화될 수 있다.^[22]

: $f(k;N,s) = \frac{1}{H_{N,s}} \cdot \frac{1}{k^s}$

여기서 H_N,s는 일반화된 조화수이다.

: $H_{N,s} = \sum_{k=1}^N \frac{1}{k^s}$

일반화된 지프 분포는 지수 s가 1보다 큰 경우에만 무한히 많은 항목(N = ∞)으로 확장될 수 있다. 이 경우 정규화 상수 H_N,s는 리만 제타 함수가 된다.

: $\zeta(s) = \sum_{k=1}^\infty \frac{1}{k^s} < \infty$

무한 항목의 경우는 제타 분포에 의해 특징지어지며 로트카의 법칙이라고 불린다. 지수 s가 1 이하이면 정규화 상수 H_N,s는 N이 무한대로 갈 때 발산한다.

4. 1. 경험적 검증

지프의 법칙은 언어학뿐만 아니라 도시 인구 순위, 기업 크기, 소득 순위 등 다양한 분야에서 발견된다. 도시 인구 순위 분포에서 이 현상은 1913년 독일의 펠릭스 아워바흐에 의해 처음 발견되었다.^[54]

경험적으로 특정 데이터 집합에 지프의 법칙이 적용되는지 확인하는 방법은 다음과 같다. 데이터 순위(R), 해당 데이터 값(n), 상수값(a, b)로 이루어진 로그 회귀식 R = a - b log n을 적용한다. 지프의 법칙은 b = 1일 때 성립한다. 도시 크기에 이 회귀함수를 적용하면 b = 1.07일 때 더 정확하게 들어맞는다. 지프의 법칙은 도시 크기 분포의 상위 항목에 적용되며, 전체 도시 크기 분포는 로그정규분포이며 지브라의 법칙을 따른다.^[55] 지프의 법칙과 지브라의 법칙은 로그정규분포의 꼬리가 일반적으로 파레토(지프) 분포의 꼬리와 구분되지 않기 때문에 서로 일치한다.

데이터 집합이 지프의 법칙을 따르는지 검증하기 위해, 콜모고로프-스미르노프 검정을 사용하여 경험적 분포와 가설적 멱법칙 분포 간의 적합도를 확인한다. 또한 멱법칙 분포의 (로그) 우도비를 지수 분포 또는 로그 정규 분포와 같은 다른 분포와 비교하여 테스트할 수 있다.^[4]

지프의 법칙은 항목 빈도 데이터를 그래프로 표현하여 시각화할 수 있다. 이때 그래프는 로그-로그 그래프를 사용하고, 축은 순위의 로그와 빈도의 로그를 나타낸다. 데이터가 지수 s를 가진 지프의 법칙을 따르는 정도는 그래프가 기울기가 -s인 선형 (정확히는 아핀) 함수에 근사하는 정도를 통해 알 수 있다. 지수 s=1의 경우, 빈도의 역수(단어 간 평균 간격)를 순위에 대해, 또는 순위의 역수를 빈도에 대해 그래프로 그려, 기울기가 1인 원점을 지나는 선과 비교할 수도 있다.^[19]

4. 2. 관련 법칙

지프의 법칙은 도시의 인구 순위, 기업의 크기, 소득 순위 등 언어학과 관련이 없는 여러 순위에서도 나타난다. 도시 인구 순위 분포 현상은 1913년 펠릭스 아워바흐에 의해 처음 발견되었다.^[54] 경험적으로, 특정 데이터 집합에 지프의 법칙이 적용되는지는 로그 회귀를 통해 확인 가능하다. 지프의 법칙은 로그 회귀식에서 b = 1일 때 적용된다. 도시 크기에 적용하면 b = 1.07일 때 더 정확하며, 도시 크기 분포의 상위 항목들에 적용된다. 전체 도시 크기 분포는 지브라의 법칙을 따른다.^[55] 지프의 법칙과 지브라의 법칙은 서로 일치하는데, 로그정규분포의 꼬리가 파레토 분포의 꼬리와 구분되지 않기 때문이다.

지프 분포는 변수 교환을 통해 파레토 분포에서 얻을 수 있다.^[22] 연속 파레토 분포와 유사하기 때문에 '이산 파레토 분포'라고도 불린다.^[18]

벤포드의 법칙은 지프의 법칙의 특수한 경계 사례라는 주장이 제기되었으며,^[25] 두 법칙의 연결은 통계 물리학 및 임계 현상에서 규모 불변 함수 관계에서 파생되었기 때문에 설명된다.^[23] 지프의 법칙 (s=1)을 만족하는 데이터의 선두 자릿수는 벤포드의 법칙을 만족한다.

n	벤포드의 법칙: P(n) = log₁₀(n+1)-log₁₀(n)	\frac{\log(P(n)/P(n-1))}{\log(n/(n-1))}
1	0.30103000
2	0.17609126	−0.7735840
3	0.12493874	−0.8463832
4	0.09691001	−0.8830605
5	0.07918125	−0.9054412
6	0.06694679	−0.9205788
7	0.05799195	−0.9315169
8	0.05115252	−0.9397966
9	0.04575749	−0.9462848

지프의 법칙은 멱법칙(Power law)의 일종이다. 또한, 지프 분포는 변수 변환을 통해 파레토 분포(연속 분포)와 같은 형태가 된다. 파레토 법칙은 파레토 분포의 특별한 경우에 해당하며, 80-20 법칙과도 관련이 있다. '''순위-크기 법칙'''이라고도 불린다.

5. 이론적 설명

지프의 법칙은 데이터의 순위와 빈도를 각 축에 로그 스케일로 나타낸 그래프를 통해 쉽게 확인할 수 있다. 예를 들어, "the"라는 단어는 ''x'' = log(1), ''y'' = log(69971) 지점에 나타나며, 이 데이터들을 선형 그래프로 나타내면 지프의 법칙에 잘 들어 맞는다.

변수를 다음과 같이 정의한다.

''N'' ― 요소의 숫자
''k'' ― 요소의 순위
''s'' ― 분포의 특성을 나타내는 지수값

지프의 법칙에 따르면 ''N''개의 요소들 가운데 순위가 ''k'' 번째인 요소의 사용빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}

지프의 법칙은 각 요소들의 발생 횟수가 독립적이고 멱법칙 분포

p(f) \alpha f^{-1-1/s}

에 따라 동일하게 분포된 랜덤 변수로 나타날 때에만 적용된다.^[56]

영어 단어 사용 빈도의 경우, ''N''은 영어 단어의 개수이고, 고전적 버전의 지프의 법칙을 사용한다고 가정할 경우 지수 ''s''는 1이다. ''f''(''k'';''s'',''N'')은 ''k''번째로 많이 나타난 단어의 분수가 된다. 이를 정리하면 다음과 같다.

:

f(k;s,N)=\frac{1}{k^s H_{N,s}}

여기서 ''H_N,s''는 ''N'' 번째 일반화된 조화수이다.

지프의 법칙의 가장 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포를 따르는 빈도가 순위에 따라 정렬되어 주어졌을 때, 2위에 해당하는 빈도는 1위의 빈도의 ½이 된다. 3위의 빈도는 1위 빈도의 ⅓이 된다. 이러한 방식으로, ''n''위의 빈도는 1의 ¹⁄_''n''이 된다. 다만, 빈도는 정수이므로 2.5와 같은 수가 올 수 없기 때문에 이러한 계산과 실제 빈도 사이에는 약간의 오차가 발생한다. 그럼에도 불구하고 많은 자연 현상들이 꽤 넓은 범위에서 상당한 정확도로 지프의 법칙을 따른다.

수학적으로 지프 분포상의 모든 관계 빈도의 합은 조화급수와 동일하며 다음이 성립한다.

:

\sum_{n=1}^\infty \frac{1}{n}=\infty\!

인간의 언어에서, 단어의 사용 빈도는 꼬리가 매우 긴 헤비테일 분포를 보이며, 따라서 이는 ''s'' 값이 1에 가까운 지프 분포로 상당히 근접하게 모델링할 수 있다. 지수 ''s''가 1을 넘을 경우, 이러한 법칙이 무한히 많은 단어에 적용되는 것이 가능한데, 이것은 ''s''>1 일 때 다음이 성립하기 때문이다.

:

\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!

여기서 ζ는 리만 제타 함수이다.

지프의 법칙은 대부분의 자연어는 물론 에스페란토^[29]와 토키 포나^[30]와 같은 일부 비자연어에도 적용되지만, 그 이유는 아직 잘 밝혀지지 않았다.^[16] 지프의 법칙에 대한 생성 과정에 대한 최근 검토로는 미첸마허의 "거듭제곱 법칙 및 로그 정규 분포에 대한 생성 모델의 간략한 역사"^[5]와 심킨의 "윌리스 재발명"이 있다.^[6]

5. 1. 최소 노력의 원리

최소 노력의 원리는 지프의 법칙을 설명할 수 있는 한 가지 가설이다. 지프는 언어 사용자인 화자와 청자 모두 이해에 도달하기 위해 필요 이상으로 노력하고 싶어하지 않으며, 이 과정에서 대략적으로 동일한 노력을 분배하게 되어 지프 분포가 나타난다고 제안했다.^[14]^[24]

최소 노력의 원리에 따르면, 단어는 무작위로 타이핑하는 원숭이에 의해 생성된다고 가정할 수 있다. 즉, 언어가 각 문자 키 또는 공백을 누를 확률이 고정된 채 0이 아닌 어떤 확률로, 단일 원숭이가 무작위로 타이핑하여 생성되는 경우, 원숭이가 생성한 단어(공백으로 구분된 문자열)는 지프의 법칙을 따르게 된다.^[7]

5. 2. 무작위 생성 텍스트

웬티안 리는 각 문자가 모든 문자(공백 문자 포함)의 균일 분포에서 무작위로 선택된 문서에서 길이가 다른 "단어"가 지프의 법칙의 거시적 추세(더 가능성이 높은 단어는 가장 짧고 동일한 확률을 가짐)를 따른다는 것을 보여주었다.^[17] 1959년, 비톨드 벨레비치는 잘 정의된 대규모 통계적 분포(정규 분포뿐만 아니라) 중 하나가 순위로 표현되어 테일러 급수로 확장되면, 급수의 1차 절단이 지프의 법칙을 초래한다는 것을 관찰했다. 또한, 테일러 급수의 2차 절단은 만델브로 법칙을 초래했다.^[15]^[32]

5. 3. 선호적 연결

최소 노력의 원리는 지프의 법칙을 설명하는 한 가지 가설이다. 지프는 언어 사용자들이 이해에 필요한 노력 이상을 들이고 싶어하지 않으며, 화자와 청자 간의 노력이 균등하게 분배되는 과정에서 지프 분포가 나타난다고 주장했다.^[14]^[24]

이러한 최소 노력의 원리는 단어가 무작위로 타이핑하는 원숭이에 의해 생성된다는 가정으로 설명될 수 있다. 즉, 언어가 각 문자 키나 공백을 누를 확률이 고정된 단일 원숭이에 의해 무작위로 생성된다면, 원숭이가 만들어낸 단어(공백으로 구분된 문자열)들은 지프의 법칙을 따르게 된다.^[7]

지프 분포는 항목의 값이 그 값에 비례하는 속도로 성장하는 선호적 연결 과정으로도 설명 가능하다. 이는 직관적으로 "부익부" 또는 "성공은 성공을 낳는다"는 원리와 같다. 이러한 성장 과정은 언어에서 단어 빈도 대 순위^[35]와 인구 대 도시 순위^[37]에서 지프의 법칙보다 더 잘 맞는 율-사이먼 분포를 유도한다. 율-사이먼 분포는 원래 율이 종의 인구 대 순위를 설명하기 위해 유도했으며, 사이먼이 도시에 적용했다.

아틀라스 모델을 기반으로 한 유사한 설명도 존재한다. 아틀라스 모델은 드리프트 및 분산 매개변수가 프로세스의 순위에만 의존하는 교환 가능한 양수 값 확산 과정 시스템이다. 특정 정규성 조건을 만족하는 아틀라스 모델에서는 지프의 법칙이 성립함이 수학적으로 증명되었다.^[43]^[45]

5. 4. 아틀라스 모델

확산 과정 시스템에서 드리프트 및 분산 매개변수가 프로세스의 순위에만 의존하는 교환 가능한 양수 값에 대한 아틀라스 모델을 기반으로 지프의 법칙을 설명할 수 있다. 특정 정규성 조건을 충족하는 아틀라스 모델에 대해 지프의 법칙이 성립한다는 것이 수학적으로 입증되었다.^[43]^[45]

6. 다양한 현상에서의 법칙 성립 사례

지프의 법칙은 언어학, 사회과학, 자연과학 등 다양한 분야에서 관찰되는 현상이다. 이 법칙은 특정 현상에서 빈도나 크기를 순위대로 나열했을 때, 순위와 빈도(또는 크기) 사이에 반비례 관계가 성립함을 의미한다.

지프의 법칙이 적용되는 다양한 현상
분야	내용
단어 출현 빈도 (언어 전체, 햄릿과 같은 개별 작품)
웹 페이지 접속 빈도
도시 인구 (순위-규모 법칙)
상위 3% 사람들 수입
음악 음표 사용 빈도
세포 내 유전자 발현량
지진 규모
고체 파편 크기

6. 1. 언어학

지프의 법칙에 따르면 어떠한 자연어 말뭉치 표현에 나타나는 단어들을 그 사용 빈도가 높은 순서대로 나열하였을 때, 모든 단어의 사용 빈도는 해당 단어의 순위에 반비례한다. 따라서 가장 사용 빈도가 높은 단어는 두 번째 단어보다 빈도가 약 두 배 높으며, 세 번째 단어보다는 빈도가 세 배 높다. 예를 들어, 브라운 대학교 현대 미국 영어 표준 말뭉치의 경우, 가장 사용 빈도가 높은 단어는 영어 정관사 “the”이며 전체 문서에서 7%의 빈도(약 백만 개 남짓의 전체 사용 단어 중 69,971회)를 차지한다. 두 번째로 사용 빈도가 높은 단어는 “of”로 약 3.5% 남짓(36,411회)한 빈도를 차지하며, 세 번째로 사용 빈도가 높은 단어는 “and”(28,852회)로, 지프의 법칙에 정확히 들어 맞는다. 약 135개 항목의 어휘만으로 브라운 대학 말뭉치의 절반을 나타낼 수 있다.^[54]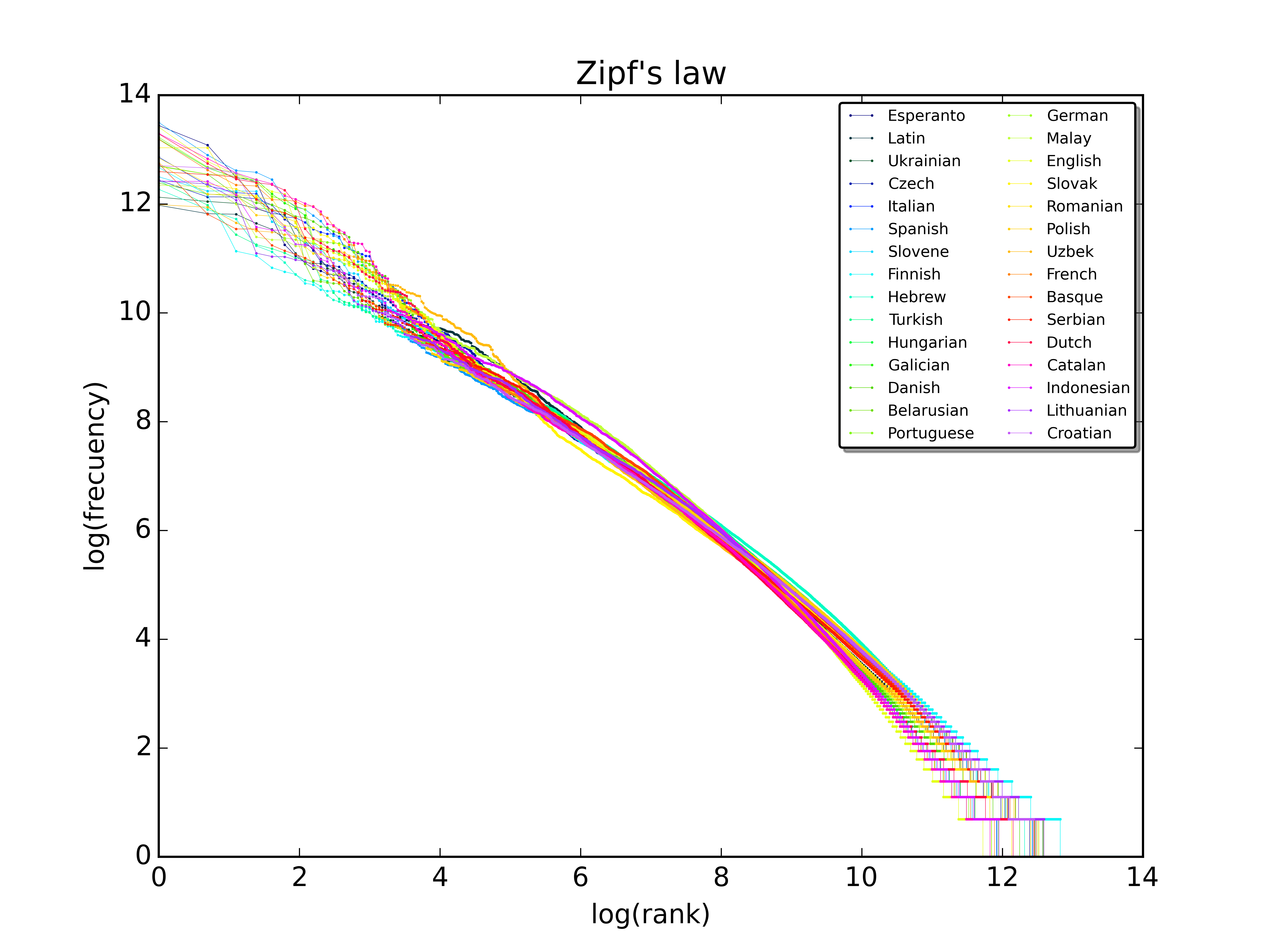

30개의 위키백과(2015년 10월 기준)의 처음 1,000만 단어에 대한 지프의 법칙 플롯(로그-로그 축척)

인간 언어의 많은 텍스트에서 단어 빈도는 대략적으로 지수가 1에 근접한 지프 분포를 따른다. 즉, 가장 흔한 단어는 n번째로 흔한 단어의 약 n배 발생한다.

자연어 텍스트의 실제 랭크-빈도 플롯은 특히 범위의 양쪽 끝에서 이상적인 지프 분포에서 어느 정도 벗어난다. 이러한 편차는 언어, 텍스트의 주제, 저자, 텍스트가 다른 언어에서 번역되었는지 여부, 사용된 맞춤법 규칙에 따라 달라질 수 있다. 샘플링 오류로 인해 어느 정도 편차가 불가피하다.

랭크가 N에 가까워지는 낮은 빈도 끝에서 플롯은 각 단어가 정수 횟수만큼만 발생할 수 있기 때문에 계단 모양을 취한다.

frame에 해당한다. 다른 설명은 대신 두 개의 세그먼트 또는 "영역"을 강조한다.]]

일부 로맨스어에서 가장 빈번한 단어 중 12개 정도의 빈도는 해당 단어가 문법적 성 및 문법적 수에 대해 굴절된 관사를 포함하기 때문에 이상적인 지프 분포에서 크게 벗어난다.

중국어, 라사 티베트어, 베트남어와 같은 많은 동아시아 언어에서 각 "단어"는 단일 음절로 구성된다. 영어의 단어는 종종 그러한 두 음절의 합성어로 번역된다. 이러한 "단어"에 대한 랭크-빈도 표는 범위의 양쪽 끝에서 이상적인 지프 법칙에서 크게 벗어난다.

영어에서도 텍스트의 큰 모음을 검토할수록 이상적인 지프 법칙으로부터의 편차가 더 분명해진다. 30,000개의 영어 텍스트 코퍼스를 분석한 결과, 약 15%의 텍스트만 지프의 법칙에 잘 맞았다. 지프의 법칙 정의를 약간 변경하면 이 비율을 50%에 가깝게 늘릴 수 있다.

이러한 경우 관찰된 빈도-랭크 관계는 다른 단어의 하위 집합 또는 유형에 대한 별도의 지프-만델브로트 법칙 분포로 보다 정확하게 모델링될 수 있다. 이것은 영어 위키백과의 처음 1,000만 단어의 빈도-랭크 플롯의 경우이다. 특히, 영어의 기능어의 닫힌 클래스의 빈도는 s가 1보다 낮을 때 더 잘 설명되는 반면, 문서 크기 및 코퍼스 크기에 따른 개방형 어휘 성장은 일반화된 조화 급수의 수렴에 대해 1보다 큰 s가 필요하다.

각 고유한 평문 단어의 각 발생이 항상 동일한 암호화된 단어로 매핑되는 방식으로 텍스트가 암호화된 경우(예: 간단한 치환 암호인 카이사르 암호 또는 간단한 코드북 암호의 경우), 빈도-랭크 분포는 영향을 받지 않는다. 반면에 동일한 단어의 개별 발생이 두 개 이상의 다른 단어로 매핑될 수 있는 경우(예: 비제네르 암호의 경우) 지프 분포는 일반적으로 고빈도 끝에서 평평한 부분을 갖는다.

지프의 법칙은 비교 가능한 말뭉치에서 텍스트의 병렬 구절을 추출하는 데 사용되어 왔다.^[38]

단어 빈도-순위 분포는 종종 저자를 특징짓고 시간이 지나도 거의 변하지 않는다. 이 특징은 저작자 귀속을 위한 텍스트 분석에 사용되어 왔다.^[46]^[47]

15세기 필사본인 보이니치 원고의 단어와 유사한 기호 그룹은 지프의 법칙을 만족하는 것으로 밝혀졌으며, 이는 텍스트가 허위일 가능성이 낮고 모호한 언어나 암호로 작성되었을 가능성이 높다는 것을 시사한다.^[41]^[33]

지프의 법칙은 언어 전체뿐만 아니라, 예를 들어 햄릿과 같은 1 작품 내에서도 성립하는 것이 나타난다.^[34]

6. 2. 사회과학

자연어 말뭉치 표현에 나타나는 단어들을 사용 빈도가 높은 순서대로 나열했을 때, 모든 단어의 사용 빈도는 해당 단어의 순위에 반비례한다는 지프의 법칙은 언어학뿐만 아니라 사회과학의 여러 분야에서도 발견된다. 도시 인구 순위, 기업 크기, 소득 순위 등 다양한 현상에서 지프의 법칙이 적용된다.^[54]

1913년 독일의 펠릭스 아우어바흐는 도시 인구 순위 분포에서 이러한 현상을 처음 발견했다.^[54] 데이터 순위(R), 해당 데이터 값(n), 상수값(a, b)로 이루어지는 로그 회귀식 R = a - b log n을 통해 특정 데이터 집합에 지프의 법칙 적용 여부를 확인할 수 있다. 지프의 법칙은 b = 1일 때 성립하며, 도시 크기에 적용하면 b = 1.07일 때 더 정확하다.^[55] 도시 크기 분포의 상위 항목에는 지프의 법칙이, 전체 분포에는 로그정규분포가 적용되며, 이는 지브라의 법칙과 일치한다.^[55]

지프의 법칙은 지프보다 먼저 1916년 프랑스 속기사 장-밥티스트 에스투에 의해 처음 발견되었고,^[20] 1923년 G. 듀이, 1928년 E. 콘돈에 의해 발견되었다.^[2]

이러한 관계는 빈도 외에도 기업 규모,^[50] 개인 소득(파레토 원리라고도 불림),^[3] TV 채널 시청자 수,^[36] 음악의 음표,^[26] 세포 전사체 등 다양한 변수 및 맥락에서 나타난다.^[44]^[51]

1992년 리 웬티안은 무작위 생성 텍스트에서도 지프의 법칙이 나타난다는 논문을 발표했다.^[17] 아우어바흐의 1913년 관찰 이후 도시 규모에 대한 지프의 법칙에 대한 상당한 연구가 진행되었으나,^[21] 최근 연구들은 도시의 지프 법칙 관련성에 이의를 제기하기도 한다.^[40]^[28]^[42]

지프의 법칙은 다양한 현상(자연 현상, 사회 현상 등)에서 성립하는 경우가 확인되고 있다.

현상	설명
단어 출현 빈도	언어 전체 및 개별 작품 (햄릿 등)
웹 페이지 접속 빈도
도시 인구	순위-규모 법칙
상위 3% 사람들 수입
음악 음표 사용 빈도
세포 내 유전자 발현량
지진 규모
고체 파편 크기

6. 3. 정보과학

지프의 법칙은 어떠한 자연어 말뭉치 표현에 나타나는 단어들을 그 사용 빈도가 높은 순서대로 나열하였을 때, 모든 단어의 사용 빈도는 해당 단어의 순위에 반비례한다는 법칙이다. 가장 사용 빈도가 높은 단어는 두 번째 단어보다 빈도가 약 두 배 높으며, 세 번째 단어보다는 빈도가 세 배 높다.

지프의 법칙은 비교 가능한 말뭉치에서 텍스트의 병렬 구절을 추출하는 데 사용되어 왔다.^[38] 로렌스 도일 등은 외계 언어 탐지, 지적 외계 생명체 탐사를 위해 지프의 법칙을 적용할 것을 제안했다.^[8]^[9]

단어 빈도-순위 분포는 종종 저자를 특징짓고 시간이 지나도 거의 변하지 않는다. 이 특징은 저작자 귀속을 위한 텍스트 분석에 사용되어 왔다.^[46]^[47]

15세기 필사본인 보이니치 원고의 단어와 유사한 기호 그룹은 지프의 법칙을 만족하는 것으로 밝혀졌으며, 이는 텍스트가 허위일 가능성이 낮고 모호한 언어나 암호로 작성되었을 가능성이 높다는 것을 시사한다.^[41]^[33]

6. 4. 자연과학

지프의 법칙에 따르면 어떠한 자연어 말뭉치 표현에 나타나는 단어들을 그 사용 빈도가 높은 순서대로 나열하였을 때, 모든 단어의 사용 빈도는 해당 단어의 순위에 반비례한다. 가장 사용 빈도가 높은 단어는 두 번째 단어보다 빈도가 약 두 배 높으며, 세 번째 단어보다는 빈도가 세 배 높다.

지프의 법칙은 도시의 인구 순위나 기업의 크기, 소득 순위 등과 같은 언어학과 관련이 없는 다른 여러 가지 순위에서도 동일하게 발견된다. 도시의 인구 순위 분포에서 발견되는 현상은 1913년 독일의 펠릭스 아우어바흐에 의해 처음 발견되었다.^[54]

지프의 법칙은 데이터의 순위와 빈도를 각 축에 로그 스케일로 나타낸 그래프를 통해 쉽게 확인할 수 있다. 예를 들어, 영어 정관사 “the”는 ''x'' = log(1), ''y'' = log(69971)인 지점에 나타날 것이다. 이 데이터들을 선형 그래프로 나타내면 지프의 법칙에 잘 들어 맞는다.

변수들을 다음과 같이 정의한다.

''N'' ― 요소의 숫자
''k'' ― 요소의 순위
''s'' ― 분포의 특성을 나타내는 지수값

지프의 법칙에 따르면 ''N''개의 요소들 가운데 순위가 ''k'' 번째인 요소의 사용빈도 ''f''(''k'';''s'',''N'')는 다음과 같다.

:

f(k;s,N)=\frac{1/k^s}{\sum_{n=1}^N (1/n^s)}

지프의 법칙은 각 요소들의 발생 횟수가 독립적이고 멱법칙 분포

p(f) \alpha f^{-1-1/s}

에 따라 동일하게 분포된 랜덤 변수로 나타날 때에만 적용된다.^[56]

지프의 법칙의 가장 단순한 예는 “¹⁄_''f'' 함수”이다. 지프 분포를 따르는 빈도가 순위에 따라 정렬되어 주어졌을 때, 2위에 해당하는 빈도는 1위의 빈도의 ½이 된다. 3위의 빈도는 1위 빈도의 ⅓이 된다. 이러한 방식으로, ''n''위의 빈도는 1의 ¹⁄_''n''이 된다. 다만, 빈도는 정수이므로 2.5와 같은 수가 올 수 없기 때문에 이러한 계산과 실제 빈도 사이에는 약간의 오차가 발생하게 된다. 그럼에도 불구하고 많은 자연 현상들이 꽤 넓은 범위에서 상당한 정확도로 지프의 법칙을 따른다.

지수 ''s''가 1을 넘을 경우, 이러한 법칙이 무한히 많은 단어에 적용되는 것이 가능한데, 이것은 ''s''>1 일 때 다음이 성립하기 때문이다.

:

\zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s}<\infty\!

여기서 ζ는 리만 제타 함수이다.

1913년, 독일 물리학자 펠릭스 아우어바흐는 도시의 인구 규모와 그 변수의 감소 순서에 따라 정렬된 순위 사이에 반비례 관계가 있음을 관찰했다.^[10]

이와 같은 관계는 빈도 외에도 다른 변수 및 많은 다른 맥락에서도 발생한다는 것을 발견했다.^[34] 예를 들어, 기업을 규모 감소 순으로 정렬하면, 그 크기가 순위에 반비례하는 것을 알 수 있다.^[50] 동일한 관계는 개인 소득(여기서는 파레토 원리라고 불림^[3]), 같은 TV 채널을 시청하는 사람 수,^[36] 음악의 음표,^[26] 세포 전사체 등에서 발견된다.^[44]^[51]

지프의 법칙이 적용되는 다양한 현상
분야	내용
단어의 출현 빈도 (언어 전체, 햄릿과 같은 개별 작품)
웹 페이지의 접속 빈도
도시의 인구 (순위-규모 법칙)
상위 3% 사람들의 수입
음악에서의 음표 사용 빈도
세포 내에서의 유전자 발현량
지진의 규모
고체가 갈라질 때의 파편의 크기

6. 5. 기타

지프의 법칙은 다양한 현상(자연 현상, 사회 현상 등)에서 성립하는 경우가 있는 것으로 확인되고 있다.

단어의 출현 빈도: 언어 전체뿐만 아니라, 햄릿과 같은 한 작품 내에서도 성립한다.
웹 페이지의 접속 빈도
도시의 인구 (도시의 순위-규모 법칙)
상위 3% 사람들의 수입
음악에서의 음표 사용 빈도
세포 내 유전자 발현량
지진의 규모
고체가 갈라질 때 파편의 크기

참조

_[1] 서적 Relative Frequency of English Speech Sounds https://archive.org/[...] Harvard University Press
_[2] 논문 Statistics of vocabulary
_[3] 서적 The Principal Problem in Political Economy 2015
_[4] 논문 Power-law distributions in empirical data
_[5] 논문 A brief history of generative models for power law and lognormal distributions 2004-01
_[6] 논문 Re-inventing Willis 2010-12
_[7] 논문 Power Laws for Monkeys Typing Randomly: The Case of Unequal Probabilities 2004-07
_[8] 논문 Why alien language would stand out among all the noise of the universe http://cosmos.nautil[...] 2016-11-18
_[9] 서적 "The Zoologist's Guide to the Galaxy: What animals on Earth reveal about aliens – and ourselves" Penguin 2021-03-16
_[10] 논문 Das Gesetz der Bevölkerungskonzentration
_[11] 서적 The Psychobiology of Language Houghton-Mifflin
_[12] 서적 Selected Studies on the Principle of Relative Frequency in Language Harvard University Press
_[13] 논문 The Unity of Nature, Least-Action, and Natural Social Science 1942
_[14] 서적 Human Behavior and the Principle of Least Effort https://archive.org/[...] Addison-Wesley
_[15] 논문 On the statistical laws of linguistic distributions http://www.csl.sri.c[...] 1959-12-18
_[16] 서적 La science et la théorie de l'information
_[17] 논문 Random Texts Exhibit Zipf's-Law-Like Word Frequency Distribution
_[18] 서적 Univariate Discrete Distributions John Wiley & Sons, Inc.
_[19] 간행물 Applications and explanations of Zipf's law http://aclweb.org/an[...] Association for Computational Linguistics
_[20] 서적 Foundations of Statistical Natural Language Processing MIT Press 1999
_[21] 논문 Zipf's Law for Cities: An Explanation 1999
_[22] 보고서 original publication http://www.parc.xero[...] Xerox Corporation
_[23] 논문 Explaining the uneven distribution of numbers in nature: The laws of Benford and Zipf 2001
_[24] 논문 Least effort and the origins of scaling in human language
_[25] 웹사이트 Factorial randomness: The laws of Benford and Zipf with respect to the first digit distribution of the factor sequence from the natural numbers http://home.zonnet.n[...] 2003-11-08
_[26] arXiv Zipf's law and the creation of musical context 2004-06-07
_[27] 논문 Fractal geometry of texts: An initial application to the works of Shakespeare 2006
_[28] 논문 Is the Zipf law spurious in explaining city-size distributions? 2006-08
_[29] 간행물 Investigating Esperanto's statistical proportions relative to other languages using neural networks and Zipf's law http://www.cs.cofc.e[...] 2006-02-13
_[30] 간행물 Zipf's law in Toki Pona https://exlingsociet[...] ExLing Society 2020-10-12
_[31] 서적 Handbook of Empirical Economics and Finance CRC Press
_[32] 보고서 Statistical metalinguistics and Zipf / Pareto / Mandelbrot http://www.csl.sri.c[...] SRI International 2022
_[33] 논문 Keywords and Co-Occurrence Patterns in the Voynich Manuscript: An Information-Theoretic Analysis 2013-06-21
_[34] 논문 Zipf's word frequency law in natural language: A critical review and future directions 2014-03-25
_[35] arXiv Scaling laws in human speech, decreasing emergence of new words, and a generalized model
_[36] 서적 2013 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB) 2013
_[37] 간행물 Test of two hypotheses explaining the size of populations in a system of cities 2015-12-02
_[38] conference Parallel Document Identification using Zipf's Law https://comparable.l[...] 2016
_[39] 간행물 Large-scale analysis of Zipf's Law in English texts
_[40] 간행물 Zipf's law and city size distribution: A survey of the literature and future research agenda https://openresearch[...] 2018-02
_[41] 웹사이트 Mystery text's language-like patterns may be an elaborate hoax https://www.newscien[...] 2022-02-25
_[42] 간행물 The growth equation of cities 2020-11-19
_[43] 간행물 Zipf's law for atlas models 2020-12
_[44] 간행물 Emergent statistical laws in single-cell transcriptomic data 2023-04-27
_[45] 간행물 E pluribus unum : From Complexity, Universality 2012-07
_[46] report Handling the Zipf distribution in computerized authorship attribution https://www.academia[...]
_[47] report An essential rephrasing of the Zipf-Mandelbrot law to solve authorship attribution applications by Gaussian statistics https://www.academia[...]
_[48] 간행물 Language as an evolving word web 2001-12-22
_[49] 간행물 Two Regimes in the Frequency of Words and the Origins of Complex Lexicons: Zipf's Law Revisited 2001-12
_[50] 간행물 Zipf Distribution of U.S. Firm Sizes 2001-09-07
_[51] conference Evaluation of the suitability of a Zipfian gap model for pairwise sequence alignment http://www.worldcomp[...]
_[52] 간행물 The Unity of Nature, Least-Action, and Natural Social Science https://www.jstor.or[...] 1942
_[53] 서적 Foundations of Statistical Natural Language Processing MIT Press 1999
_[54] 기타 Das Gesetz der Bevölkerungskonzentration 1913
_[55] 기타 Gibrat's law for (All) Cities 2004
_[56] 웹인용 Zipf, Power-laws, and Pareto - a ranking tutorial http://www.hpl.hp.co[...] 2007-10-26

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com