칸토어-베른슈타인 정리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 증명
4. 역사
- 4.1. 초기 역사
- 4.2. 명칭 문제
5. 전제 조건
6. 예시
- 6.1. [0, 1] → [0, 1) 전단사 함수
- 6.2. [0, 2) → [0, 1)² 전단사 함수
참조

1. 개요

칸토어-베른슈타인 정리는 두 집합 X와 Y 사이에 단사 함수 f: X → Y와 g: Y → X가 존재하면, 전단사 함수 h: X → Y가 존재한다는 정리이다. 이 정리는 선택 공리 없이 증명할 수 있으며, 기수의 관점에서 |X| ≤ |Y|이고 |Y| ≤ |X|이면 |X| = |Y|임을 의미한다. 칸토어-베른슈타인 정리는 여러 수학자에 의해 증명되었으며, 율리우스 쾨니히, 펠릭스 베른슈타인, 리하르트 데데킨트 등의 이름을 따서 불린다. 이 정리는 집합론에서 중요한 역할을 하며, [0, 1]에서 [0, 1)으로, 또는 [0, 2)에서 [0, 1)²으로의 전단사 함수를 구성하는 데 사용될 수 있다.

더 읽어볼만한 페이지

기수 - 초한수
초한수는 게오르크 칸토어가 도입한 무한 개념을 확장한 수로, 집합의 크기를 나타내는 기수와 정렬된 집합 내의 위치를 나타내는 서수로 나뉘며, 무한에도 여러 종류가 있음을 밝혀 현대 수학의 기초를 다졌다.
기수 - 칸토어의 정리
칸토어의 정리는 집합 X의 멱집합의 크기가 X의 크기보다 항상 크다는 것을 나타내며, 임의의 기수 κ에 대해 2^κ > κ가 성립한다는 내용으로, 칸토어의 대각선 논법으로 증명되고 집합론의 역설과 관련되어 전체 집합의 존재를 가정할 때 칸토어의 역설을 유발한다.
수학기초론 정리 - 괴델의 불완전성 정리
괴델의 불완전성 정리는 산술을 표현할 수 있는 무모순적 공리계는 그 안에서 증명하거나 반증할 수 없는 명제가 존재하며, 특히 체계 스스로의 무모순성을 증명할 수 없다는 수학적 논리 분야의 핵심 정리이다.
수학기초론 정리 - 칸토어의 정리
칸토어의 정리는 집합 X의 멱집합의 크기가 X의 크기보다 항상 크다는 것을 나타내며, 임의의 기수 κ에 대해 2^κ > κ가 성립한다는 내용으로, 칸토어의 대각선 논법으로 증명되고 집합론의 역설과 관련되어 전체 집합의 존재를 가정할 때 칸토어의 역설을 유발한다.

칸토어-베른슈타인 정리
개요
유형	집합론의 정리
관련 분야	수학, 논리학
다른 이름	칸토어-베른슈타인-슈뢰더 정리 슈뢰더-베른슈타인-칸토어 정리 쾨니히-베른슈타인 정리 (에른스트 체르멜로)
내용
가정	함수 f : A → B 가 존재 함수 g : B → A 가 존재
결론	A 와 B 사이에 전단사 함수 h : A → B 가 존재
의미	\|A\| ≤ \|B\| 이고 \|B\| ≤ \|A\| 이면 \|A\| = \|B\| 이다. 두 집합 A와 B 각각이 다른 집합의 부분집합과 대등하면, 두 집합은 대등하다.
증명
증명 방법	다양한 증명 방법 존재
일반적인 증명	구성적 증명 (집합 A를 분할하여 전단사 함수 h 구성)
역사
초기 증명 시도	칸토어 (1883): 오류 포함 슈뢰더 (1896): 오류 포함, 미발표
최초의 정확한 증명	베른슈타인 (1897): 칸토어에게 전달, 1898년 보렐에 의해 발표 체르멜로 (1901): 베른슈타인과는 독립적으로 증명
슈뢰더의 증명 발표	슈뢰더 (1898): 수정된 증명 발표 (여전히 오류 존재)
활용
집합의 크기 비교	두 집합의 크기 비교에 유용하게 사용
참고 자료
관련 항목	집합론, 기수 (수학)

2. 정의

'''칸토어-베른슈타인 정리'''는 두 집합의 크기를 비교하는 기본적인 정리로, 내용은 다음과 같다.^[29]

두 집합 $X$ 와 $Y$ 사이에 단사 함수 $f\colon X\to Y$ 와 $g\colon Y\to X$ 가 존재한다면, 전단사 함수 $h\colon X\to Y$ 가 존재한다.

이 정리는 선택 공리 없이 증명할 수 있다는 특징이 있다.

기수는 집합의 크기를 나타내는 개념으로, 같은 수의 원소를 가진 집합들을 하나의 동치류로 묶어 생각할 수 있다. 구체적으로, 두 집합

X

와

Y

사이에 전단사 함수가 존재하면 두 집합의 크기가 같다고 정의하고

|X|=|Y|

로 표기한다. 여기서

|X|

는 집합

X

의 크기를 나타내는 기수이다. 만약 단사 함수

X\to Y

가 존재한다면,

X

의 크기가

Y

의 크기보다 작거나 같다고 정의하고

|X|\le|Y|

로 표기한다. 이 기수의 순서 관계

\le

는 어떤 집합을 선택하든 상관없이 잘 정의된다. 이 순서는 자기 자신에 대해 항상 성립하는 반사 관계이며(항등 함수는 단사 함수이므로

|X|\le|X|

),

|X|\le|Y|

이고

|Y|\le|Z|

이면

|X|\le|Z|

가 성립하는 추이적 관계이다(단사 함수의 합성은 단사 함수).

칸토어-베른슈타인 정리는 기수의 관점에서 다음과 같이 표현할 수 있다.

만약 $|X|\le|Y|$ 이며 $|Y|\le|X|$ 라면, $|X|=|Y|$ 이다.

이는 기수의 순서 관계

\le

가

|X|\le|Y|

이고

|Y|\le|X|

이면

|X|=|Y|

가 성립하는 반대칭 관계임을 보여준다. 따라서 기수의 순서 관계는 부분 순서이다.

정렬 집합들 사이에서는 항상 크기를 비교할 수 있다. 만약 선택 공리를 가정한다면, 모든 집합은 어떤 정렬 집합과 크기가 같아지므로, 임의의 두 집합의 크기는 항상 비교 가능하게 된다. 즉, 선택 공리를 가정하면 기수의 순서는 전순서가 된다.

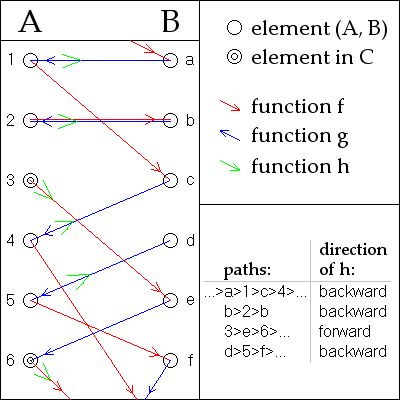
3. 증명

칸토어-베른슈타인 정리를 증명하는 방법은 여러 가지가 있다.^[1] 대부분의 증명은 집합 $A$ 와 $B$ 사이에 주어진 두 단사 함수 $f: A \to B$ 와 $g: B \to A$ 를 이용하여, $A$ 에서 $B$ 로 가는 전단사 함수 $h: A \to B$ 를 직접 구성하는 방식으로 이루어진다.

대표적인 방법 중 하나는 율리우스 쾨니히가 제시한 증명으로^[1], 각 원소에서 시작하여 $f$ 와 $g$ 및 그 부분 함수인 역함수 $g^{-1}$ , $f^{-1}$ 를 번갈아 적용하여 만들어지는 원소들의 열(sequence)을 분석하는 방식이다.

: '' $\cdots \rightarrow f^{-1}(g^{-1}(a)) \rightarrow g^{-1}(a) \rightarrow a \rightarrow f(a) \rightarrow g(f(a)) \rightarrow \cdots$ ''

이러한 열들은 각 원소가 속한 열의 시작점이나 형태(예: $A$ 에서 멈춤, $B$ 에서 멈춤, 양방향 무한, 순환)에 따라 분류될 수 있다. 각 분류에 따라 함수 $h$ 를 $f$ 또는 $g^{-1}$ 를 이용하여 정의함으로써 전체적으로 전단사 함수를 구성한다.

다른 접근 방식으로는 집합 $A$ 의 부분집합들을 귀납적으로 구성하여 전단사 함수 $h$ 를 정의하는 방법이 있다. 예를 들어, $A$ 를 특정 기준(예: $g$ 의 치역에 속하지 않는 원소에서 시작하여 $f$ 와 $g$ 를 반복 적용하여 도달할 수 있는 원소들의 집합 $C$ )에 따라 두 부분집합 $C$ 와 $A \setminus C$ 로 나누고, 다음과 같이 $h$ 를 정의하는 방식이다.

: $h(x) = \begin{cases}f(x)& \text{if }x \in C \\g^{-1}(x)& \text{if } x \notin C\end{cases}$

이 함수 $h$ 가 전단사 함수임을 보인다.

이 외에도 타르스키 고정점 정리를 이용하는 등 다양한 증명 방법이 존재한다. 각 증명의 구체적인 과정은 하위 섹션에서 자세히 다룬다.

3. 1. 표준적인 증명

칸토어-베른슈타인 정리의 표준적인 증명은 두 집합 사이에 각각 단사 함수가 존재하면 전단사 함수도 존재함을 보이는 방식으로, 주로 두 가지 접근법이 사용된다. 두 방법 모두 귀납적인 집합 구성을 통해 원하는 전단사 함수를 직접 만들어낸다.

=== 집합열을 이용한 증명 ===

두 집합

X

와

Y

사이에 두 단사 함수

f: X \to Y

와

g: Y \to X

가 주어졌다고 하자. 다음과 같이

X

의 부분 집합들의 열을 정의한다.^[29]

:

X_0=X

:

Y_0=g(Y)

:

X_{n+1}=g(f(X_n))

:

Y_{n+1}=g(f(Y_n))

여기서

f(X_n)

은

X_n

의

f

에 대한 상이고,

g(Y)

,

g(f(X_n))

,

g(f(Y_n))

도 마찬가지로

g

에 대한 상이다. 함수

f

와

g

가 단사이므로, 이들의 합성은

g \circ f: X \to X

역시 단사 함수이다.

이렇게 정의된 집합들은 다음 포함 관계를 만족한다.

:

X_0\supseteq Y_0\supseteq X_1\supseteq Y_1\supseteq X_2\supseteq Y_2\supseteq\cdots

이는 수학적 귀납법으로 증명할 수 있다.

기저 단계 (n=0): $X_0 = X \supseteq g(Y) = Y_0$ 는 정의상 성립한다. $f(X) \subseteq Y$ 이므로 $X_1 = g(f(X)) \subseteq g(Y) = Y_0$ 이다. 따라서 $X_0 \supseteq Y_0 \supseteq X_1$ 이다.
귀납 단계: 어떤 $k \ge 0$ 에 대해 $X_k \supseteq Y_k \supseteq X_{k+1}$ 이 성립한다고 가정하자. 함수 $g \circ f$ 는 단사이므로 집합의 포함 관계를 보존한다. 따라서 $g(f(X_k)) \supseteq g(f(Y_k)) \supseteq g(f(X_{k+1}))$$ 이 성립한다. 정의에 의해 이는 $X_{k+1} \supseteq Y_{k+1} \supseteq X_{k+2}$ 와 같다.

따라서 모든 자연수

n \ge 0

에 대해

X_n \supseteq Y_n \supseteq X_{n+1}

이 성립한다.

이제 함수

h\colon X\to Y

를 다음과 같이 정의하자.

:

h(x)=\begin{cases}f(x)& \text{만약 어떤 } n \ge 0 \text{에 대해 } x \in X_n \setminus Y_n \text{ 이면} \\g^{-1}(x)& \text{만약 모든 } n \ge 0 \text{에 대해 } x \notin X_n \setminus Y_n \text{ 이면}\end{cases}

여기서

g

는 단사 함수이므로, 치역

g(Y) = Y_0

로 공역을 제한하면 역함수

g^{-1}\colon Y_0 \to Y

를 정의할 수 있다.

x \notin \bigcup_{n=0}^\infty (X_n \setminus Y_n)

인 경우는

x

가 모든

n

에 대해

x \in Y_n

이거나 (

x \in \bigcap_{n=0}^\infty Y_n

), 어떤

k

에 대해

x \in Y_k \setminus X_{k+1}

인 경우이다. 두 경우 모두

x \in Y_0 = g(Y)

이므로

g^{-1}(x)

는 잘 정의된다.

이제

h

가 전단사 함수임을 보이자.

$h$ 는 단사 함수이다: $f$ 와 $g^{-1}$ 는 모두 단사 함수이므로, $h$ 는 각 정의 구간( $\bigcup_{n=0}^\infty (X_n \setminus Y_n)$ 와 그 여집합)에서 단사적이다. 서로 다른 구간에 속하는 $x_1 \in \bigcup_{n=0}^\infty (X_n \setminus Y_n)$ 와 $x_2 \notin \bigcup_{n=0}^\infty (X_n \setminus Y_n)$ 를 생각해보자. $x_1 \in X_k \setminus Y_k$ 인 $k \ge 0$ 가 존재한다. $h(x_1) = f(x_1)$ 이고 $h(x_2) = g^{-1}(x_2)$ 이다. 만약 $h(x_1) = h(x_2)$ 라면 $f(x_1) = g^{-1}(x_2)$ 이고, 양변에 $g$ 를 적용하면 $g(f(x_1)) = x_2$ 가 된다. $x_1 \in X_k \setminus Y_k$ 이므로 $x_2 = g(f(x_1)) \in g(f(X_k \setminus Y_k))$$ 이다. $g(f(X_k)) = X_{k+1}$ 이고 $g(f(Y_k)) = Y_{k+1}$ 이므로, $x_2 \in X_{k+1} \setminus Y_{k+1}$ 이다. 이는 $x_2 \notin \bigcup_{n=0}^\infty (X_n \setminus Y_n)$ 라는 가정에 모순이다. 따라서 $h(x_1) \neq h(x_2)$ 이고, $h$ 는 전체 정의역에서 단사 함수이다.

$h$ 는 전사 함수이다: 임의의 $y \in Y$ 를 생각하자. $g(y) \in X$ 이다.
만약 어떤 $n \ge 0$ 에 대해 $g(y) \in X_n \setminus Y_n$ 이라면, $g(y) \in g(Y) = Y_0$ 이므로 반드시 $n > 0$ 이다. $g(y) \in X_n \setminus Y_n = g(f(X_{n-1})) \setminus g(f(Y_{n-1}))$$ 이다. $g$ 는 단사이므로, $y \in f(X_{n-1}) \setminus f(Y_{n-1})$ 이다. 즉, $y = f(x)$ 를 만족하는 $x \in X_{n-1} \setminus Y_{n-1}$ 가 존재한다. 이 $x$ 는 $\bigcup_{n=0}^\infty (X_n \setminus Y_n)$ 에 속하므로, $h(x) = f(x) = y$ 이다.
만약 모든 $n \ge 0$ 에 대해 $g(y) \notin X_n \setminus Y_n$ 이라면, $h$ 의 정의에 따라 $x = g(y)$ 에 대해 $h(x) = h(g(y)) = g^{-1}(g(y)) = y$ 가 성립한다.

따라서 모든

y \in Y

에 대해

h(x) = y

인

x \in X

가 존재하므로,

h

는 전사 함수이다.

결론적으로

h

는 단사 함수이고 전사 함수이므로 전단사 함수이다.

=== 귀납적 집합 구성을 이용한 증명 ===

집합

A

와

B

사이에 단사 함수

f \colon A \to B

와

g \colon B \to A

가 주어졌다고 가정하자.

다음과 같이 집합족

\{ C_n \}_{n \in \mathbb{N}}

(

\mathbb{N} = \{0, 1, 2, \dots\}

) 를 귀납적으로 정의한다.

:

C_0 := A \setminus g(B)

(즉,

g

의 치역에 속하지 않는

A

의 원소들의 집합)

:

C_{n+1} := g(f(C_n))

(즉,

C_n

의 원소를

f

로 보내고 다시

g

로 보낸 집합)

이제 이 집합들의 합집합을

C

라고 하자.

:

C = \bigcup_{n=0}^\infty C_n = C_0 \cup C_1 \cup C_2 \cup \cdots

이제 함수

h \colon A \to B

를 다음과 같이 정의한다.

:

h(x) = \begin{cases}f(x)& \text{if }x \in C \\g^{-1}(x)& \text{if } x \notin C \text{ (즉, } x \in A \setminus C \text{)}\end{cases}

여기서

x \notin C

이면

x \notin C_0

이므로

x \in g(B)

이다.

g

는 단사이므로

g^{-1}(x)

는

B

의 원소로서 유일하게 정의된다. 이제 이 함수

h

가 전단사 함수임을 보이자.

$h$ 는 단사 함수이다:
만약 $x_1, x_2 \in C$ 이고 $h(x_1) = h(x_2)$ 이면, $f(x_1) = f(x_2)$ 이다. $f$ 는 단사이므로 $x_1 = x_2$ 이다.
만약 $x_1, x_2 \in A \setminus C$ 이고 $h(x_1) = h(x_2)$ 이면, $g^{-1}(x_1) = g^{-1}(x_2)$ 이다. 양변에 $g$ 를 적용하면 $x_1 = x_2$ 이다 ( $g^{-1}$ 도 단사).
만약 $x_1 \in C$ 이고 $x_2 \in A \setminus C$ 인데 $h(x_1) = h(x_2)$ 라고 가정하자. 그러면 $f(x_1) = g^{-1}(x_2)$ 이다. 양변에 $g$ 를 적용하면 $g(f(x_1)) = x_2$ 이다. $x_1 \in C = \bigcup_{n=0}^\infty C_n$ 이므로, 어떤 $n \ge 0$ 에 대해 $x_1 \in C_n$ 이다. 그러면 $x_2 = g(f(x_1)) \in g(f(C_n)) = C_{n+1}$ 이다. 그런데 $C_{n+1} \subseteq C$ 이므로 $x_2 \in C$ 가 된다. 이는 $x_2 \in A \setminus C$ 라는 가정에 모순이다. 따라서 $x_1 \in C$ 와 $x_2 \in A \setminus C$ 에 대해 $h(x_1) \neq h(x_2)$ 이다.

위 세 경우를 종합하면,

h

는 단사 함수이다.

$h$ 는 전사 함수이다: 임의의 $y \in B$ 를 생각하자. 우리는 $h(x) = y$ 인 $x \in A$ 를 찾아야 한다.

g(y) \in A

를 고려하자.

만약 $g(y) \in C$ 라면, $h$ 의 정의에 따라 $h(g(y))$ 는 정의되지 않는다 (정의역은 $A$ ). 대신 $g(y) \in C = \bigcup C_n$ 이므로 어떤 $n$ 에 대해 $g(y) \in C_n$ 이다.
만약 $n=0$ 이면 $g(y) \in C_0 = A \setminus g(B)$ 인데, 이는 $g(y)$ 가 $g$ 의 치역에 속한다는 사실에 모순이다. 따라서 $n > 0$ 이어야 한다.
$n > 0$ 이면 $g(y) \in C_n = g(f(C_{n-1}))$$ 이다. $g$ 는 단사이므로, $y \in f(C_{n-1})$$ 이다. 즉, $y = f(x)$ 를 만족하는 $x \in C_{n-1}$ 이 존재한다. $C_{n-1} \subseteq C$ 이므로 $x \in C$ 이다. 따라서 $h(x) = f(x) = y$ 이다.
만약 $g(y) \notin C$ (즉, $g(y) \in A \setminus C$ ) 라면, $h$ 의 정의에 따라 $x = g(y)$ 로 두면 $x \in A \setminus C$ 이므로 $h(x) = h(g(y)) = g^{-1}(g(y)) = y$ 이다.

따라서 모든

y \in B

에 대해

h(x) = y

인

x \in A

가 존재하므로,

h

는 전사 함수이다.

결론적으로

h

는 단사 함수이고 전사 함수이므로 전단사 함수이다. 이 증명은 다음과 같이 요약될 수 있다:

A

는

C

와

A \setminus C

로 분할되고,

B

는

f(C)

와

B \setminus f(C)

로 분할된다. 함수

h

는

C

에서

f(C)

로 가는 전단사 함수

f

와,

A \setminus C

에서

B \setminus f(C)

로 가는 전단사 함수

g^{-1}

를 조합한 것이다. 실제로

g^{-1}(A \setminus C) = g^{-1}(A) \setminus g^{-1}(C)

이고,

g^{-1}(A) = B

이며,

:

g^{-1}(C) = g^{-1}\left(\bigcup_{n=0}^\infty C_n\right) = g^{-1}(C_0) \cup g^{-1}\left(\bigcup_{n=1}^\infty C_n\right)

C_0 = A \setminus g(B)

이므로

g^{-1}(C_0)

는 공집합이다.

C_n = g(f(C_{n-1}))$

이므로,

:

g^{-1}\left(\bigcup_{n=1}^\infty C_n\right) = \bigcup_{n=1}^\infty g^{-1}(C_n) = \bigcup_{n=1}^\infty g^{-1}(g(f(C_{n-1}))) = \bigcup_{n=1}^\infty f(C_{n-1}) = \bigcup_{k=0}^\infty f(C_k) = f\left(\bigcup_{k=0}^\infty C_k\right) = f(C)

따라서

g^{-1}(A \setminus C) = B \setminus f(C)

이다. 즉,

h

는

A \setminus C

를

B \setminus f(C)

로 보내는 전단사 함수

g^{-1}

와 같다.

3. 2. 쾨니히의 증명

다음 증명은 율리우스 쾨니히에 의한 것이다.^[1]

일반성을 잃지 않으면서, 두 집합 ''A''와 ''B''가 상호소 집합이라고 가정한다. (만약 상호소가 아니라면, 크기가 같은 두 서로소 집합

\tilde A=\{(0,a)\colon a\in A\}

와

\tilde B=\{(1,b)\colon b\in B\}

로 대체할 수 있다.) 단사 함수

f\colon A\to B

와

g\colon B\to A

가 주어졌다고 하자. 이 함수들의 부분적인 역함수

f^{-1}\colon f(A)\to A

와

g^{-1}\colon g(B)\to B

를 정의한다. 이때

f^{-1}

와

g^{-1}

는 부분 함수이다. 즉, 정의역에 포함되지 않는 원소에 대해서는 함수값이 정의되지 않을 수 있다.

임의의 원소

a \in A

또는

b \in B

에 대해, 함수

f

와

g

, 그리고 그 역함수

f^{-1}

와

g^{-1}

를 반복적으로 적용하여 원소들의 열(sequence)을 만들 수 있다. 예를 들어,

a \in A

에서 시작하는 열은 다음과 같다.

:

\cdots \rightarrow f^{-1}(g^{-1}(a)) \rightarrow g^{-1}(a) \rightarrow a \rightarrow f(a) \rightarrow g(f(a)) \rightarrow \cdots

이 열은

A

의 원소와

B

의 원소가 번갈아 나타난다. 오른쪽으로는 함수

f

와

g

를 계속 적용하여 무한히 이어질 수 있다. 왼쪽으로는 역함수

f^{-1}

나

g^{-1}

를 적용하는데, 만약 어떤 원소에서 역함수가 정의되지 않으면(즉, 그 원소가 각각

g(B)

나

f(A)

에 속하지 않으면) 열은 그 지점에서 멈춘다.

함수

f

와

g

는 단사 함수이므로,

A \cup B

의 각 원소는 정확히 하나의 열에 속한다. 만약 두 열이 하나의 원소라도 공유한다면, 그 열은 완전히 동일해야 한다. 따라서 이러한 열들은

A \cup B

전체를 서로 겹치지 않는 부분집합들로 나누는 집합의 분할을 형성한다. 이제 각 열 안에서

A

의 원소들과

B

의 원소들 사이에 전단사 함수

h \colon A \to B

를 정의하면 된다.

각 열은 다음 네 가지 유형 중 하나로 분류될 수 있다.

A-스토퍼(A-stopper): 열이 왼쪽으로 진행하다가 $A$ 의 원소에서 멈추는 경우. 이는 $g^{-1}$ 가 정의되지 않는 $A$ 의 원소에서 시작하는 열이다. 이 열에 속하는 모든 $a \in A$ 에 대해 $h(a) = f(a)$ 로 정의한다. 그러면 $f$ 자체가 이 열의 $A$ 원소들과 $B$ 원소들 사이의 전단사 함수가 된다.
B-스토퍼(B-stopper): 열이 왼쪽으로 진행하다가 $B$ 의 원소에서 멈추는 경우. 이는 $f^{-1}$ 가 정의되지 않는 $B$ 의 원소에서 시작하는 열이다. 이 열에 속하는 모든 $a \in A$ 에 대해 $h(a) = g^{-1}(a)$ 로 정의한다. 즉, $g(h(a)) = a$ 가 성립한다. 그러면 $g^{-1}$ 가 이 열의 $A$ 원소들과 $B$ 원소들 사이의 전단사 함수가 된다.
양방향 무한대(Doubly infinite): 열이 양쪽 방향으로 무한히 계속되는 경우. 이 열에 속하는 $a \in A$ 에 대해 $h(a) = f(a)$ 로 정의하거나, $h(a) = g^{-1}(a)$ 로 정의할 수 있다. 어느 쪽이든 이 열의 $A$ 원소들과 $B$ 원소들 사이의 전단사 함수가 된다. (위 그림 예시에서는 $h(a) = g^{-1}(a)$ 를 사용했다.)
사이클(Cycle): 열의 원소들이 유한하게 반복되는 경우. 이 경우도 양방향 무한대와 마찬가지로 $h(a) = f(a)$ 또는 $h(a) = g^{-1}(a)$ 중 하나로 정의하면 전단사 함수가 된다. (위 그림 예시에서는 $h(a) = g^{-1}(a)$ 를 사용했다.)

이렇게 각 열마다 정의된 함수 조각들을 모두 합치면, 전체 집합

A

에서

B

로 가는 전단사 함수

h

가 구성된다. 따라서

A

와

B

의 크기(기수)는 같다.

3. 3. 타르스키 고정점 정리를 통한 증명

X

의 멱집합 격자

(\mathcal P(X),\subseteq)

는 완비 격자를 이룬다. 함수

:

\mathcal P(X)\to\mathcal P(X)

:

S\mapsto X\setminus g(Y\setminus f(S))

는 순서 보존 함수이므로, 타르스키 고정점 정리에 따라 고정점

S\subseteq X

를 갖는다. 즉,

:

X\setminus S=g(Y\setminus f(S))

이다. 따라서, 전단사 함수

:

X\to Y

:

x\mapsto\begin{cases}f(x)&x\in S\\g^{-1}(x)&x\in X\setminus S\end{cases}

가 존재한다.

4. 역사

'''칸토어-베른슈타인 정리'''의 명칭은 그 발견과 증명의 복잡한 역사를 반영한다. 전통적으로 "슈뢰더-베른슈타인 정리" 또는 "칸토어-베른슈타인 정리" 등으로 불리는데, 이는 1898년 슈뢰더와 베른슈타인이 각자 독립적으로 증명을 발표한 사실과 관련이 있다.^[22]^[23]

그러나 정리 자체는 1887년 칸토어가 처음 언급했으며^[3]^[2], 같은 해 데데킨트가 처음으로 증명했지만 발표하지는 않았다.^[4]^[25] 또한 슈뢰더가 발표한 증명에는 오류가 있었다는 점^[17]^[24] 등 여러 역사적 사실이 얽혀 있어, 정리의 이름에 누구를 포함해야 하는지에 대해서는 다양한 견해가 존재한다. 베른슈타인에 따르면 칸토어는 이 정리에 "동치 정리"(Äquivalenzsatz|애퀴발렌츠자츠^deu)라는 이름을 제안하기도 했다.^[2] 이처럼 수학 정리의 이름이 항상 최초 발견자나 증명자의 이름을 따르거나 역사적 경위를 정확히 반영하는 것은 아니며, 칸토어-베른슈타인 정리는 그러한 복잡한 과정을 보여주는 대표적인 사례 중 하나이다.

4. 1. 초기 역사

전통적인 명칭인 "슈뢰더-베른슈타인" 또는 "칸토어-베른슈타인"은 이 정리의 발견 및 증명 과정에 기여한 여러 수학자들의 이름을 반영하지만, 그 과정이 복잡하여 명칭에 대한 논란이 있다. 슈뢰더의 이름은 그의 증명에 오류가 있었기 때문에^[24] 제외되기도 하며, 정리를 처음 증명한 데데킨트의 이름은 보통 포함되지 않는다. 칸토어는 이 정리를 처음 언급했기 때문에 이름에 포함되기도 한다. 베른슈타인에 따르면, 칸토어는 이 정리에 "동치 정리"(Äquivalenzsatz)라는 이름을 제안했다.^[2]

정리의 발견과 증명 과정은 다음과 같이 요약할 수 있다.

연도	인물	내용
1887	칸토어	정리를 발표했지만, 증명은 포함하지 않았다.^[3]^[2]
1887	데데킨트	7월 11일, 선택 공리에 의존하지 않고 정리를 증명했다.^[4] 그러나 자신의 증명을 출판하거나 칸토어에게 알리지 않았다. 에른스트 체르멜로는 데데킨트의 증명을 발견했고, 1908년에^[5] 데데킨트의 논문 "Was sind und was sollen die Zahlen?"의 사슬 이론에 기반한 자신의 증명을 발표했다.^[2]^[6]
1895	칸토어	집합론과 초한수에 관한 첫 번째 논문에서 이 정리를 기수의 선형 순서의 쉬운 결과로 언급했다.^[7]^[8]^[9] 그러나 그는 후자의 정리를 증명할 수 없었고, 이는 1915년에 하르토그스에 의해 선택 공리와 동치임이 밝혀졌다.^[2]^[10]
1896	슈뢰더	(제본스의 정리의 따름 정리로) 증명을 발표했다.^[11]
1897	베른슈타인	칸토어의 세미나에 참여하던 19세 학생으로, 자신의 증명을 제시했다.^[12]^[13]
1897	슈뢰더	거의 동시에, 그러나 독립적으로 증명을 찾았다.^[12]^[13]
1897	데데킨트	베른슈타인의 방문 후, 독립적으로 두 번째 증명을 발견했다.
1898	베른슈타인	보렐의 함수에 관한 책^[14](1897년 취리히 국제 수학자 회의에서 칸토어에 의해 전달됨)과 자신의 학위 논문^[15]을 통해 증명을 발표했다(선택 공리에 의존하지 않음).^[2]
1898	슈뢰더	자신의 증명을 출판했다.^[16]
1902	코르셀트	슈뢰더의 증명에 결함이 있음을 발견했다(슈뢰더 사망 직전 확인).^[17]^[2]^[18] 코르셀트의 논문은 1911년에 출판되었다.

데데킨트의 두 증명은 모두 그의 유명한 1888년 논문 "Was sind und was sollen die Zahlen?"^[28]에 기반하며, 칸토어의 논문^[7]의 C 명제와 동치인 명제, 즉 "A ⊆ B ⊆ C 이고 |A| = |C| 이면 |A| = |B| = |C| 이다"라는 명제의 따름 정리로 이끌어냈다. 칸토어는 1882년 또는 1883년에 집합론과 초한수 연구 중에 이 속성을 관찰했으며, 따라서 (암묵적으로) 선택 공리에 의존하고 있었다.

4. 2. 명칭 문제

이 정리의 명칭은 역사적으로 여러 이름으로 불려왔다. 전통적으로는 "슈뢰더-베른슈타인 정리"라는 이름이 사용되었는데, 이는 1898년에 슈뢰더와 베른슈타인이 각각 독립적으로 증명을 발표한 것에 기인한다.^[22]^[23]

그러나 이 정리의 명칭에는 몇 가지 논쟁점이 있다. 칸토어는 1887년에 이 정리를 처음 언급했지만^[3]^[2] 증명을 제시하지는 않았다. 그럼에도 그의 선구적인 역할을 인정하여 "칸토어-베른슈타인 정리"라고 부르기도 한다. 베른슈타인에 따르면, 칸토어는 이 정리에 대해 "동치 정리"(Äquivalenzsatz|애퀴발렌츠자츠^deu)라는 이름을 제안했다고 한다.^[2]

한편, 슈뢰더의 이름이 포함되는 것에 대해서는 비판적인 시각이 존재한다. 그가 1898년에 발표한 증명은^[16] 1902년 코르셀트에 의해 오류가 있음이 밝혀졌기 때문이다.^[17]^[2]^[18]^[24] 슈뢰더 본인도 오류를 인정했다.^[2]

더욱 복잡한 점은, 이 정리를 역사상 처음으로 증명한 사람은 데데킨트라는 사실이다. 그는 1887년에 선택 공리에 의존하지 않는 증명에 성공했지만^[4]^[25], 이를 발표하거나 칸토어에게 알리지 않았다. 그의 증명은 나중에 체르멜로에 의해 발견되어 1908년에 알려졌다.^[5]^[2]^[6] 이처럼 최초 증명자임에도 불구하고 데데킨트의 이름은 이 정리의 명칭에 거의 포함되지 않는다.

수학 정리의 명칭이 항상 역사적 경위를 정확히 반영하는 것은 아니며, 칸토어-베른슈타인 정리 역시 그러한 사례 중 하나이다. 정리의 발견과 증명에 관련된 주요 인물과 시기는 다음과 같이 정리할 수 있다.

정리 증명 및 발표 관련 주요 연표
연도	인물	내용
1887	칸토어	정리를 발표했으나 증명은 포함하지 않음.^[3]^[2]
1887	데데킨트	선택 공리에 의존하지 않고 정리를 증명했으나 발표하지 않음.^[4]^[25]
1895	칸토어	첫 번째 집합론 논문에서 기수의 선형 순서(비교 가능성)의 결과로 정리를 언급.^[7]^[8]^[9]^[26] (선형 순서 자체는 증명 못함)^[2]^[10]
1896	슈뢰더	증명을 발표함.^[11]^[27]
1897	베른슈타인	칸토어 세미나에서 19세의 나이로 증명을 제시함.^[12]^[13]
1897	슈뢰더	베른슈타인과 거의 동시, 독립적으로 증명을 찾음.^[12]^[13]
1897	데데킨트	베른슈타인 방문 후 독립적으로 두 번째 증명을 발견함.
1898	베른슈타인	에밀 보렐의 저서^[14]^[23] 및 본인의 학위 논문^[15]을 통해 증명 발표.^[2]
1898	슈뢰더	자신의 증명을 출판함.^[16]
1902	코르셀트	슈뢰더의 1898년 증명에 결함이 있음을 발견 (1911년 발표).^[17]^[2]^[18]^[24]
1908	체르멜로	데데킨트의 미발표 증명을 발견하고, 이를 기반으로 자신의 증명을 발표.^[5]^[2]^[6]

데데킨트의 두 증명은 모두 그의 1888년 저서 "Was sind und was sollen die Zahlen?|바스 진트 운트 바스 졸렌 디 찰렌?^deu"에 나오는 '사슬 이론'에 기반하며^[2]^[6], 다음과 같은 명제의 따름정리로 유도된다.^[7]^[28]

: ''A'' ⊆ ''B'' ⊆ ''C'' 이고 |''A''| = |''C''| 이면 |''A''| = |''B''| = |''C''| 이다.

칸토어는 이와 동등한 속성을 1882년 또는 1883년경 집합론 연구 중에 발견했지만, 이는 암묵적으로 선택 공리에 의존하는 것이었다.^[7]

결론적으로, "칸토어-베른슈타인 정리", "슈뢰더-베른슈타인 정리", 혹은 단순히 "베른슈타인 정리" 등 다양한 명칭이 사용되는 것은 이러한 복잡한 역사적 배경 때문이다.

5. 전제 조건

칸토어의 1895년 증명은 사실상 선택 공리에 의존했는데, 이는 이 결과를 정렬 정리의 따름정리로 추론했기 때문이다.^[8]^[9] 하지만 율리우스 쾨니히가 제시한 증명을 포함한 다른 증명들은 선택 공리를 사용하지 않고도 이 정리를 증명할 수 있음을 보여준다.^[1]

만약 선택 공리를 가정한다면, 두 집합 사이에 각각 전사 함수가 존재할 경우, 그 역함수들로부터 단사 함수를 구성하고 칸토어-베른슈타인 정리를 적용하여 두 집합 사이에 전단사 함수가 존재함을 보일 수 있다.

한편, 쾨니히의 증명은 배중률을 사용한다. 배중률을 받아들이지 않는 구성주의 수학, 특히 직관주의 집합론( ${\mathsf{IZF}}$ )에서는 칸토어-베른슈타인 정리가 성립하지 않을 수 있다. 실제로 이러한 체계에서 칸토어-베른슈타인 정리를 가정하면 배중률이 따라 나온다는 것이 증명되었다.^[19] 따라서 직관주의자들은 칸토어-베른슈타인 정리의 명제를 일반적으로 받아들이지 않는다.^[20]

이 정리의 다른 증명 방법으로는 타르스키의 고정점 정리를 이용하는 것이 있다.^[21]

6. 예시

칸토어-베른슈타인 정리는 두 집합 사이에 각각 단사 함수가 존재하면, 두 집합 사이에 전단사 함수도 존재함을 보장하며 그 함수를 구성하는 방법을 제시한다. 이 정리를 이용하여 다양한 무한 집합들 사이의 크기가 같음을 보이고 구체적인 전단사 함수를 만들 수 있다.

아래는 칸토어-베른슈타인 정리를 이용한 전단사 함수 구성의 구체적인 예시들이다.

닫힌 구간 [0, 1]과 반열린 구간 [0, 1) 사이의 전단사 함수
반열린 구간 [0, 2)와 단위 정사각형 [0, 1)² 사이의 전단사 함수
반열린 구간 [0, ∞)과 열린 구간 (0, ∞) 사이의 전단사 함수

6. 1. [0, 1] → [0, 1) 전단사 함수

''참고:

[0, 1)

은 0을 포함하고 1을 제외하는 0에서 1까지의 반열린 구간이다.''

닫힌 구간

[0, 1]

에서 반열린 구간

[0, 1)

으로 가는 단사 함수

f: [0, 1]\to[0, 1)

를

f(x)=x/2

로 정의하고, 반대로

[0, 1)

에서

[0, 1]

로 가는 단사 함수

g: [0, 1 )\to [0, 1]

를

g(x)=x

로 정의할 수 있다.

칸토어-베른슈타인 정리의 구성적 증명 절차에 따라, 다음과 같이 집합

C

를 정의한다.

C_0=\{1\}

C_k=\{2^{-k}\}

(여기서

k=0, 1, 2, ...

)

C = \bigcup_{k=0}^\infty C_k = \{1, \tfrac{1}{2},  \tfrac{1}{4}, \tfrac{1}{8}, ... \}

이제

[0, 1]

에서

[0, 1)

로 가는 전단사 함수

h(x)

를 다음과 같이 정의할 수 있다.

h(x) = \begin{cases} f(x) = \frac{x}{2} , & x \in C \text{ 일 때} \\ x , & x \in [0, 1] \setminus C \text{ 일 때}\end{cases}

이 함수

h(x)

는

x

가 집합

C

(즉,

1, 1/2, 1/4, ...

)의 원소이면 그 값을

f(x)

에 따라 절반으로 만들고 (

1 \to 1/2, 1/2 \to 1/4, ...

),

C

의 원소가 아니면 그대로 둔다 (

g^{-1}(x)

에 해당하지만 여기서는

g

가 항등함수이므로

x

가 된다). 결과적으로

1

은

1/2

로,

1/2

은

1/4

등으로 이동하며

1

이 빠진 구간

[0, 1)

의 모든 원소와 일대일 대응을 이룬다.

6. 2. [0, 2) → [0, 1)² 전단사 함수

반열린 구간

[0, 2)

에서 열린 단위 정사각형

[0, 1 )^2

으로 가는 단사 함수

f

를 다음과 같이 정의할 수 있다.

f(x)=(x/2, 0)

반대로,

[0, 1 )^2

에서

[0, 2)

로 가는 단사 함수

g

도 정의할 수 있다.

(x, y) \in [0, 1 )^2

에 대해,

x

와

y

를 각각 십진법 소수로 다음과 같이 전개한다. (단, 소수 표현의 유일성을 위해 무한소수 표현을 사용한다고 가정한다. 예: 0.5 대신 0.499...)

x = \sum_{k=1}^\infty a_k \cdot 10^{-k} = 0.a_1 a_2 a_3 \dots

y = \sum_{k=1}^\infty b_k \cdot 10^{-k} = 0.b_1 b_2 b_3 \dots

여기서

a_k, b_k

는 0부터 9까지의 정수이다 (

a_k, b_k \in \{0, 1, ..., 9\}

).

이제 함수

g

를 다음과 같이 정의한다. 이는

x

와

y

의 소수점 아래 자릿수를 번갈아 배열하여 새로운 소수를 만드는 방식이다.

g(x, y) = \sum_{k=1}^\infty (10 \cdot a_k + b_k) \cdot 10^{-2k} = 0.(10a_1+b_1)(10a_2+b_2)\dots

(여기서 각

(10a_k+b_k)

는 두 자리 숫자로 간주)

이 함수

g

는

[0, 1 )^2

에서

[0, 1)

로 가는 단사 함수이다. (원본 소스에서는

[0, 2)

로 간다고 되어 있으나, 함수의 정의상 치역은

[0, 1)

이다.

[0, 2)

로 가는 단사 함수를 만들기 위해서는 예를 들어

g'(x,y) = g(x,y)

또는

g'(x,y) = g(x,y)+1

처럼 구간을 나누어 정의하거나, 아래의

g_2

와 같이 정의해야 한다. 여기서는 원본 소스의 설명을 따라

g

를 사용한 구성 과정을 설명한다.)

예를 들어,

g(\tfrac{1}{3}, \tfrac{2}{3}) = g(0.333..., 0.666...) = 0.(10 \cdot 3 + 6)(10 \cdot 3 + 6)... = 0.363636... = \tfrac{36}{99} = \tfrac{4}{11}

이다.

칸토어-베른슈타인 정리에 따르면, 두 집합 사이에 각각 단사 함수

f: [0, 2) \to [0, 1)^2

와

g: [0, 1)^2 \to [0, 2)

가 존재하므로 (여기서

g

는 위에서 정의한

[0, 1)^2 \to [0, 1)

함수를 이용하여

[0, 2)

로 가는 단사 함수로 확장 가능하다고 가정), 두 집합 사이에 전단사 함수

h: [0, 2) \to [0, 1)^2

가 존재한다. 이

h

는

f

와

g

(의 역함수

g^{-1}

)를 이용하여 구성할 수 있다.

구성 과정에서 사용되는 집합

C

는 다음과 같이 정의된다. (원본 소스의

C_0 = [1, 2)

정의는

g

의 치역이

[0, 1)

라고 가정할 때

[0, 2) \setminus g([0, 1)^2)

의 일부 또는 전부를 나타내는 것으로 해석될 수 있다.)

C_0 = [1, 2)

(원본 소스 표기)

C_1 = g(f(C_0)) = g(\{ (x/2, 0) \mid x \in [1, 2) \}) = g(\{ (x', 0) \mid x' \in [\tfrac{1}{2}, 1) \})

C_k = g(f(C_{k-1}))

for

k \ge 1

C = \bigcup_{k=0}^\infty C_k

전단사 함수

h

는 다음과 같이 정의된다.

h(x) = \begin{cases} f(x), & \text{if } x \in C \\ g^{-1}(x), & \text{if } x \notin C \text{ (즉, } x \in [0, 2) \setminus C \text{)} \end{cases}

이 구성 방법에서

C_0 = [1, 2)

는 비교적 간단하지만,

C_1 = g(\{ (x', 0) \mid x' \in [\tfrac{1}{2}, 1) \})

만 해도 그 형태가 상당히 복잡해진다.

참고로,

[0, 1)^2

에서

[0, 2)

로 가는 전단사 함수를 직접 정의하여 더 간단하게 전단사 함수

h

를 찾는 방법도 있다. 예를 들어 함수

g_2

를 다음과 같이 정의한다.

g_2(x, y) = 2 \cdot \sum_{k=1}^\infty (10 \cdot a_k + b_k) \cdot 10^{-2k}

이 함수

g_2

는 (십진법 표현의 유일성 문제를 해결한다는 가정 하에) 그 자체로

[0, 1)^2

에서

[0, 2)

로 가는 전단사 함수이다. 이

g_2

를 사용하면, 칸토어-베른슈타인 정리의 구성 과정에서 집합

C

는 공집합(

\emptyset

)이 되고, 결과적으로 모든

x \in [0, 2)

에 대해 전단사 함수는

h(x) = g_2^{-1}(x)

로 간단히 주어진다.

참조

_[1] 간행물 Sur la théorie des ensembles http://gallica.bnf.f[...]
_[2] 서적 Grundzüge der Mengenlehre https://books.google[...] Springer
_[3] 간행물 Mitteilungen zur Lehre vom Transfiniten
_[4] 서적 Gesammelte mathematische Werke http://gdz.sub.uni-g[...] Friedr. Vieweg & Sohn
_[5] 간행물 Untersuchungen über die Grundlagen der Mengenlehre I http://gdz.sub.uni-g[...]
_[6] 서적 Was sind und was sollen die Zahlen? http://echo.mpiwg-be[...] Friedr. Vieweg & Sohn
_[7] 서적 Gesammelte Abhandlungen mathematischen und philosophischen Inhalts http://gdz.sub.uni-g[...] Springer
_[8] 간행물 Beiträge zur Begründung der transfiniten Mengenlehre (1) http://www.digizeits[...]
_[9] 간행물 Beiträge zur Begründung der transfiniten Mengenlehre (2) http://www.digizeits[...]
_[10] 간행물 Über das Problem der Wohlordnung http://www.digizeits[...]
_[11] 간행물 Über G. Cantorsche Sätze http://gdz.sub.uni-g[...]
_[12] 서적 Einführung in die Mengenlehre – Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo Springer
_[13] 서적 Axiomatic Set Theory https://archive.org/[...] Dover Publications
_[14] 서적 Leçons sur la théorie des fonctions https://archive.org/[...] Gauthier-Villars et fils
_[15] 간행물 Untersuchungen aus der Mengenlehre https://archive.org/[...] Buchdruckerei des Waisenhauses
_[16] 간행물 Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze https://www.biodiver[...]
_[17] 간행물 Über einen Beweis des Äquivalenzsatzes http://gdz.sub.uni-g[...]
_[18] 문서 Korselt (1911), p.295
_[19] arXiv Cantor-Bernstein implies Excluded Middle
_[20] 서적 Mathematics and Logic in History and in Contemporary Thought Transaction Publishers
_[21] MathWorld Tarski's Fixed Point Theorem
_[22] 간행물 Über zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze
_[23] 서적 Leçons sur la théorie des fonctions Gauthier-Villars et fils
_[24] 간행물 Über einen Beweis des Äquivalenzsatzes
_[25] 서적 Gesammelte Werke III
_[26] 간행물 Beiträge zur Begründung der transfiniten Mengenlehre I
_[27] 간행물 Über G. Cantor'sche Sätze
_[28] 서적 Was sind und was sollen die Zahlen?
_[29] 서적 Set theory https://archive.org/[...] Springer 2003

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com