마름모육팔면체

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 기하학적 성질
3. 그래프
4. 한국에서의 마름모육팔면체
5. 예술 작품에서의 등장
6. 관련 다면체
- 6.1. 존슨의 다면체
참조

1. 개요

마름모육팔면체는 아르키메데스 다면체 중 하나로, 모든 꼭짓점이 동일한 형태로 구성되어 있다. 정육면체 또는 정팔면체의 면을 분리하고 밀어낸 후 그 사이에 정사각형과 정삼각형을 채워 넣는 방식으로 구성할 수 있다. 표면적은 약 $21.464a^2$ , 부피는 약 $8.714a^3$ 이며, 최적 쌓임 밀도는 $\frac{4}{3} \left( 4\sqrt{2} - 5 \right)$ 이다. 정육면체와 정팔면체와 같은 대칭성을 가지며, 팔면체 대칭을 갖는다. 벨라루스 국립 도서관의 건축물 형태로 사용되었으며, 루카 파치올리 초상화와 신성 비율 삽화 등 예술 작품에도 등장한다.

더 읽어볼만한 페이지

아르키메데스의 다면체 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다.
아르키메데스의 다면체 - 깎은 정이십면체
깎은 정이십면체는 정이십면체의 꼭짓점을 잘라낸 아르키메데스의 다면체로, 32개의 면, 90개의 변, 60개의 꼭짓점을 가지며, 축구공, 풀러렌 분자 등 다양한 분야에서 활용된다.

마름모육팔면체
개요
마름모육팔면체
종류	아르키메데스 균일 다면체
면	정삼각형: 8개 정사각형: 18개
변	48개
꼭짓점	24개
대칭	정팔면체군 O_h 오각십이면체군 T_h
슐레플리 기호	r{3, 4}
꼭짓점 도형	polyhedron small rhombi 6-8 vertfig.svg
꼭짓점 배열	24 (3 · 4³)
쌍대	델토이드 이십사면체
전개도	Polyhedron small rhombi 6-8 net.svg
다른 이름	작은 마름모육팔면체, 절단 마름모십이면체, 늘린 정사각형 직이각지붕
각도
정사각형-정사각형	135°
정사각형-정삼각형	144.7°

2. 기하학적 성질

마름모육팔면체는 정육면체(파란 면) 또는 정팔면체(빨간 면)를 팽창시킨 형태를 하고 있다.

마름모육팔면체는 아르키메데스 다면체 중 하나로, 모든 꼭짓점이 동일한 형태로 구성되어 있다. 한쪽을 45° 회전시켜도 꼭짓점 모양이 변하지 않으며, 이로 인해 만들어지는 입체는 미러의 입체라고 불린다. 균일 큰 마름모육팔면체도 이와 유사한 성질을 갖는다.^[2]

마름모육팔면체는 정육면체 및 정팔면체와 동일한 팔면체 대칭을 갖는다. 하지만 6개의 직사각형 면과 16개의 사다리꼴 면을 갖는 두 번째 변형 세트는 팔면체 대칭을 갖지 않고 사면체 대칭을 갖는다. 따라서 정사면체와 같은 회전에 대해서는 불변이지만 다른 반사를 갖는다. 이 도형은 점대칭이며, 키랄하지 않다.^[6]

성질	값
겉넓이	a^영어를 한 변의 길이로 할 때
부피	a^영어를 한 변의 길이로 할 때
외접구 반지름	한 변을 2로 할 때

겉넓이: a^영어를 한 변이라고 할때
부피: a^영어를 한 변이라고 할때
외접구 반지름: 한 변을 2로 하면

2. 1. 구성 방법

마름모육팔면체는 정육면체로부터 만들 수 있다. 각 면의 가운데에 원래 정육면체의 모서리에 평행한 작은 정육면체를 그리고, 정육면체의 모서리를 제거한 후, 정사각형 면들을 서로 인접한 정사각형들을 추가하여 연결하고, 꼭짓점은 정삼각형으로 채운다. 또는 두 개의 정사각뿔을 팔각 기둥의 밑면에 부착해서 마름모육팔면체를 만들 수 있다.^[2]

마름모육팔면체는 "확장된 팔면체" 또는 "확장된 정육면체"라고도 불린다. 정육면체 또는 정팔면체의 면들을 중심에서 분리하고 밀어낸 다음(애니메이션에서 각각 파란색 또는 빨간색으로 표시됨), 그 사이에 정사각형과 정삼각형을 채워 넣어 구성할 수 있기 때문이다. 이 구성 과정은 확장이라고 한다. 위의 모든 방법을 사용하여 마름모육팔면체는 8개의 정삼각형과 16개의 정사각형을 면으로 갖는다.^[3]

마름모육팔면체는 정육면체 또는 정팔면체의 모든 모서리와 꼭짓점을 잘라내어 만들 수도 있는데, 이 과정을 교정이라고 한다.

모서리 길이가 2인 마름모육팔면체의 데카르트 좌표는

\left(\pm \left(1 + \sqrt{2}\right), \pm 1, \pm 1 \right)

의 순열이다.

2. 2. 공식

한 모서리의 길이를 a^영어라고 할 때, 마름모육팔면체의 겉넓이(A^영어)와 부피(V^영어)는 다음과 같다.

:A^영어 = (18+2√3)a^영어² ≈ 21.464a^영어²

:V^영어 = (12+10√2)/3a^영어³ ≈ 8.714a^영어³

마름모육팔면체의 겉넓이 A^영어는 모든 면의 면적, 즉 8개의 정삼각형과 18개의 정사각형을 더하여 구할 수 있다. 마름모육팔면체의 부피 V^영어는 이를 두 개의 사각 돔과 하나의 팔각기둥으로 잘라서 구할 수 있다.^[4]

마름모육팔면체의 최적 쌓임 밀도는 다음과 같다.

:

이 최적 값은 브라베 격자에서 얻어진다는 것이 밝혀졌다. 마름모육팔면체는 마름모십이면체에 포함되어 있으며, 그 내접구는 마름모육팔면체의 내접구와 동일하므로 최적 쌓임 밀도의 값은 케플러 추측의 귀결이다. 즉, 마름모 십이면체 벌집의 각 셀에 마름모육팔면체를 넣음으로써 달성할 수 있으며, 그렇지 않으면 이를 초과하는 가상의 쌓기에 있는 각 마름모육팔면체에 구를 넣음으로써 구의 최적 쌓임 밀도를 초과할 수 있으므로 초과할 수 없다.

마름모육팔면체의 이각은 사각 돔과 팔각 기둥의 이각을 더하여 구할 수 있다.

상단과 하단의 두 인접한 정사각형 사이의 마름모육팔면체의 이각은 사각 돔의 이각인 135°이다. 두 인접한 정사각형 사이의 팔각 기둥의 이각은 정팔각형의 내부 각도 135°이다. 사각 돔이 팔각 기둥에 연결된 모서리에서 두 인접한 정사각형 사이의 이각은 사각 돔의 정사각형-팔각형 이각과 팔각 기둥의 정사각형-팔각형 이각의 합인 45° + 90° = 135°이다. 따라서, 모든 두 개의 인접한 정사각형에 대한 마름모육팔면체의 이각은 135°이다.
마름모육팔면체의 정사각형-삼각형 이각은 그 사이의 사각 돔의 이각인 144.7°이다. 사각 돔이 팔각 기둥에 연결된 모서리에서 정사각형-삼각형 사이의 이각은 사각 돔의 삼각형-팔각형 이각과 팔각 기둥의 정사각형-팔각형 이각의 합인 54.7° + 90° = 144.7°이다. 따라서, 모든 정사각형-삼각형에 대한 마름모육팔면체의 이각은 144.7°이다.

성질	값
겉넓이	한 변을 a^영어라고 할 때
부피	한 변을 a^영어라고 할 때
외접구 반지름	한 변을 2로 하면

2. 3. 대칭성

마름모육팔면체는 정육면체 및 정팔면체와 동일한 팔면체 대칭

\mathrm{O}_\mathrm{h}

을 갖는다.^[5] 그러나 마름모육팔면체는 6개의 직사각형 면과 16개의 사다리꼴 면을 갖는 두 번째 변형 세트를 가지는데, 이는 팔면체 대칭을 갖지 않고 사면체 대칭

\mathrm{T}_\mathrm{h}

을 갖는다. 따라서 정사면체와 같은 회전에 대해서는 불변이지만 다른 반사를 갖는다. 이 도형은 점대칭이며, 대칭성은 반전 중심의 출현에 의해 상호 교환이 가능하다는 것을 의미한다. 또한, 키랄하지 않다. 즉, 자신의 거울상과 합동이다.^[6]

마름모육팔면체는 아르키메데스 다면체인데, 이는 매우 대칭적이고 반정규 다면체임을 의미하며, 둘 이상의 서로 다른 정다각형 면이 한 꼭짓점에서 만난다. 모든 꼭짓점에서 만나는 다각형 면은 하나의 정삼각형과 세 개의 정사각형이며, 꼭짓점 도형은

3 \cdot 4^3

으로 표시된다. 이 도형의 쌍대다면체는 델토이드 이십사면체로, 카탈랑 다면체이며 마름모육팔면체와 동일한 대칭성을 공유한다.

3. 그래프

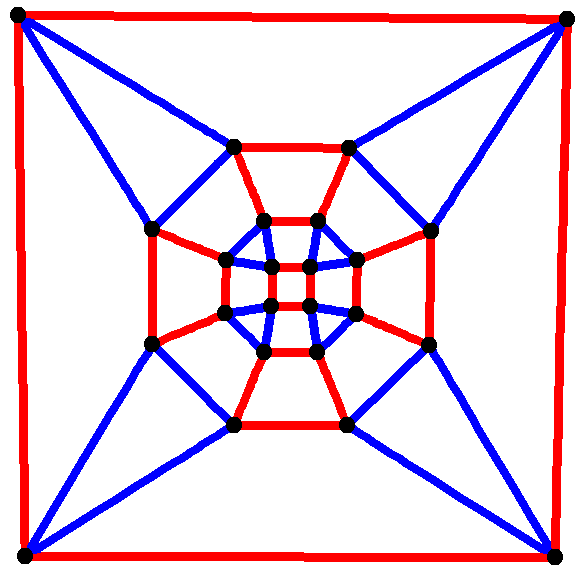
마름모육팔면체의 골격은 다면체 그래프로 나타낼 수 있으며, 이는 그래프가 평면 그래프이고 3-정점 연결임을 의미한다. 즉, 그래프의 가장자리는 그려지는 동안 교차하지 않으며, 임의의 두 정점을 제거해도 연결된 부분 그래프가 남는다.

마름모육팔면체 그래프는 24개의 정점과 48개의 변을 갖는다. 각 정점이 다른 4개와 연결되어 있으므로 사차 그래프이며, 아르키메데스 다면체의 그래프와 유사하여 아르키메데스 그래프로 분류된다.

4. 한국에서의 마름모육팔면체

민스크에 위치한 벨라루스 국립 도서관은 마름모육팔면체 형태의 건축물로 유명하다.^[8] 1980년대 큐브 열풍 당시, 마름모육팔면체 형태의 트위스트 퍼즐이 판매되었다.^[9]^[10]

5. 예술 작품에서의 등장

야코포 데 바르바리의 작품으로 알려진 ''루카 파치올리 초상화''. 물이 반쯤 채워진 유리 마름모육팔면체가 묘사되어 있다.

마름모육팔면체는 예술 작품에서도 나타난다. 1495년 야코포 데 바르바리의 작품으로 전통적으로 알려진 ''루카 파치올리 초상화''에는 물이 반쯤 채워진 유리 마름모육팔면체가 포함되어 있으며, 이는 레오나르도 다 빈치가 그렸을 수 있다.^[11] 레오나르도 다 빈치의 작품인 마름모육팔면체의 최초 인쇄 버전은 파치올리의 ''신성 비율''(1509)에 등장했다.

6. 관련 다면체

마름모육팔면체는 정육면체나 정팔면체의 면을 중심에서 분리하고 밀어낸 다음, 그 사이에 정사각형과 정삼각형을 채워 넣어 만들 수 있다. 이 때문에 "확장된 정육면체" 또는 "확장된 팔면체"라고도 불린다. 이러한 구성 과정은 확장이라고 한다. 정육면체나 정팔면체의 모든 모서리와 꼭짓점을 잘라내어 만드는 과정을 교정이라고 한다.

마름모육팔면체를 만드는 또 다른 방법은 두 개의 정정사각뿔을 정팔각 기둥의 밑면에 부착하는 것이다.^[2]

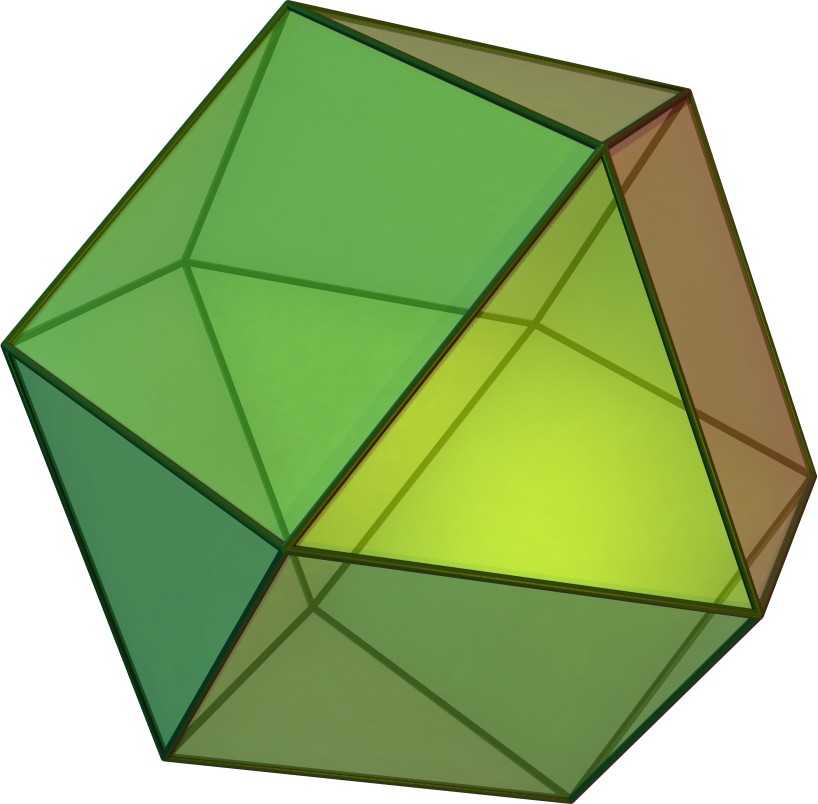
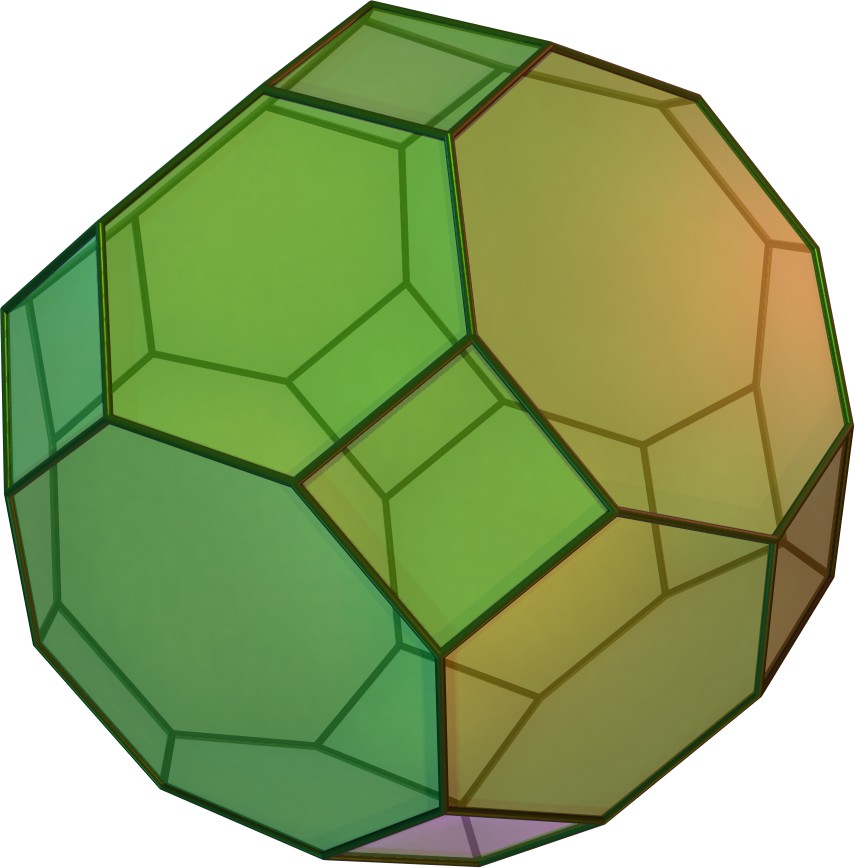
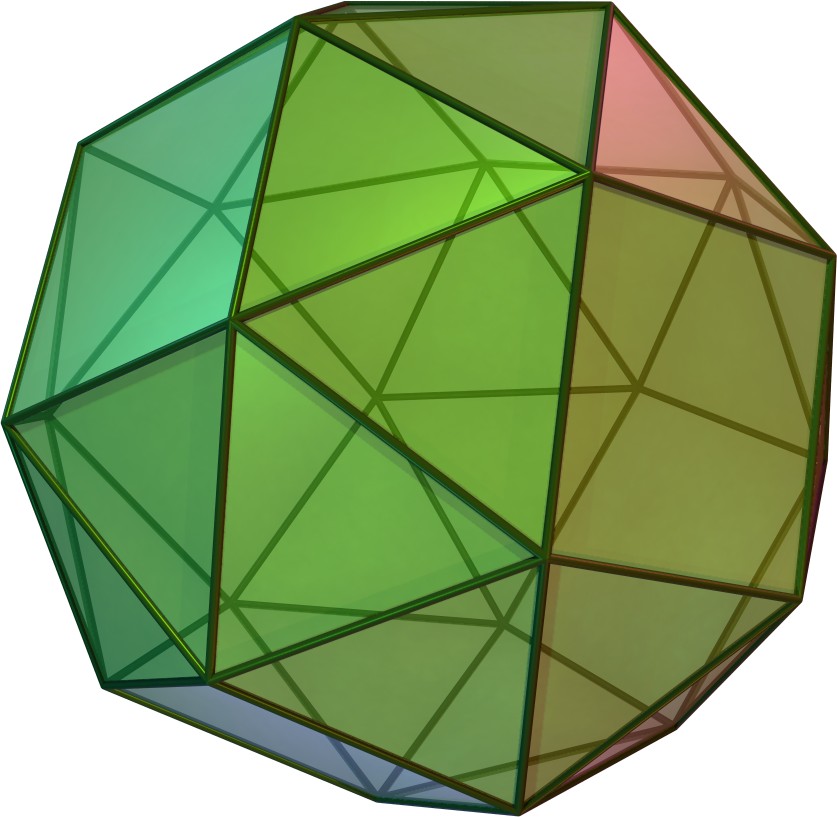
모서리 길이가 2인 마름모육팔면체의 데카르트 좌표는 $\left(\pm \left(1 + \sqrt{2}\right), \pm 1, \pm 1 \right)$ 의 순열이다.

6. 1. 존슨의 다면체

미러의 다면체는 한쪽을 45° 회전시킨 형태로 마름모육팔면체와 유사하다. 그 외에도 쌍사각대탑반기둥(22.5° 비틀기), 같은 방향 쌍사각대탑(각기둥 제거), 정사각대탑주(한쪽의 대탑 제거) 등도 마름모육팔면체와 관련 있는 존슨의 다면체이다.

참조

_[1] Harvp
_[2] Harvp
_[3] Harvp
_[4] Harvp
_[5] Harvp
_[6] Harvp
_[7] Harvp
_[8] Harvp
_[9] 웹사이트 Soviet Puzzle Ball http://twistypuzzles[...] 2015-12-23
_[10] 웹사이트 Diamond Style Puzzler https://www.jaapsch.[...] 2017-05-31
_[11] 간행물 The Portrait of Fra Luca Pacioli
_[12] 서적 プラトンとアルキメデスの立体三次元に浮かびあがる美の世界ランダムハウス講談社 2005-11
_[13] 문서 切稜立方体

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com