복잡계 네트워크

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
3. 현실 세계 네트워크의 주요 특징
4. 복잡계 네트워크 모델
5. 척도 없는 그래프의 강건성과 취약성
6. 한국 사회와 복잡계 네트워크
7. 분석 도구
참조

1. 개요

복잡계 네트워크는 그래프 이론을 기반으로 현실 세계의 다양한 네트워크 구조와 특성을 연구하는 학문 분야이다. 18세기 그래프 이론에서 시작하여, 20세기 후반 사회학, 심리학 연구를 통해 스몰 월드 현상과 약한 유대의 중요성이 밝혀지면서 발전했다. 1998년 와츠와 스트로가츠 모델의 등장으로 복잡계 네트워크 연구는 급격한 발전을 이루었고, 척도 없는 네트워크, 스몰 월드 네트워크, 클러스터성과 같은 특징들이 발견되었다. 이러한 특징들은 현실 세계의 다양한 네트워크, 예를 들어 인터넷, 생태계, 사회 연결망 등에서 나타나며, 와츠-스트로가츠 모델, 바라바시-알베르트 모델과 같은 수학적 모델을 통해 분석된다. 복잡계 네트워크 연구는 감염병 확산, 온라인 여론 형성, 마케팅 등 다양한 분야에 응용되고 있으며, 분석을 위해 다양한 소프트웨어가 활용된다.

더 읽어볼만한 페이지

네트워크 이론 - 사회 연결망
사회 연결망 분석은 개인이나 집단 간의 관계를 분석하여 사회적 구조와 행동을 이해하는 학제 간 연구 방법론으로, 다양한 이론적 틀을 활용하여 네트워크 내 위치와 정보 접근의 중요성을 분석하며 여러 분야에서 활용된다.
네트워크 이론 - 중심성
중심성은 그래프 이론에서 네트워크 내 노드의 중요성을 평가하기 위한 지표로, 차수 중심성, 근접 중심성 등 다양한 종류가 있으며 네트워크 흐름, 워크 구조 등 다양한 특징에 따라 분류된다.

복잡계 네트워크

2. 역사적 배경

소셜 네트워크, 생물 네트워크, 컴퓨터 네트워크 등은 규칙적이거나 무작위적이지 않은 연결 패턴을 가지는 비자명한 위상학적 특징을 보인다. 이러한 특징에는 차수 분포의 헤비 테일, 높은 클러스터링 계수, 동류성 또는 비동류성, 공동체 구조, 계층 구조 등이 포함된다.^[6]

과거에는 격자 그래프나 랜덤 그래프와 같은 네트워크 모델이 주로 연구되었으나, 이러한 모델들은 현실 세계의 복잡한 네트워크의 특징을 제대로 반영하지 못했다. 복잡계 네트워크의 대표적인 예시로는 척도 없는 네트워크^[7]와 스몰 월드 네트워크^[8]^[9]가 있으며, 전자는 멱함수 차수 분포를, 후자는 짧은 경로 길이와 높은 클러스터링 계수를 특징으로 한다.

1998년 덩컨 와츠와 Steven Strogatz|스티븐 스트로가츠^영어가 발표한 "와츠-스트로가츠 모델"은 스몰 월드 현상을 설명하는 수학적 모델로, 현실 세계의 네트워크와 유사한 성질을 단순한 알고리즘으로 생성하여 주목받았다. 이 연구는 인터넷, 생태계의 먹이 사슬, 논문의 인용 관계, 언어의 문법 구조 등 다양한 네트워크에서 공통된 성질을 발견하는 계기가 되었다.

복잡계 네트워크 연구는 수학, 물리학, 생물학, 컴퓨터 과학, 사회학 등 다양한 분야의 연구자들이 참여하여 빠르게 발전하고 있으며,^[11] 현실 세계의 다양한 현상을 설명하는 새로운 패러다임으로 자리 잡고 있다. 앞으로 네트워크 문제가 관련된 여러 분야에서 중요성이 더욱 커질 것으로 예상된다.

2. 1. 그래프 이론의 초기 발전

그래프 이론은 18세기 레온하르트 오일러가 창시한 학문으로, 그래프는 정점과 변의 집합으로 구성된다. 그래프 ''G''는 '''정점'''(노드, 사이트라고도 함)의 집합 ''V'' = {''v''₁, ''v''₂, ..., ''v''_n}과 '''변'''(가지, 링크, 에지, 본드, 타이라고도 함)의 집합 ''E'' = {''e''₁, ''e''₂, ..., ''e''_m}로 표현된다. 정점 ''i''에 연결된 변의 개수를 해당 정점의 '''차수''' ''k''_i라고 한다.

1959년 폴 에르되시와 알프레드 레니는 Random graph|랜덤 그래프^영어를 만드는 Erdős–Rényi model|에르되시-레니 모델^영어을 고안했다. 에르되시-레니 모델은 다양한 흥미로운 성질을 가지며 그래프의 해석적 발전을 크게 이끌었다. 그러나 그 후 그래프 이론 분야에서는 뚜렷한 진전이 거의 없었다.

2. 2. 사회학에서의 네트워크 연구

1960년대부터 70년대에 걸쳐 사회학에서는 두 가지 중요한 연구가 있었다. 첫 번째는 실험 사회 심리학자 스탠리 밀그램의 스몰 월드 현상(세상은 좁다는 현상)을 실증하려는 시도였다.^[12] 밀그램은 1967년에 고안한 실험에서 미국 내륙부 거주자에게 편지를 전달하고, 전혀 모르는 미국 동부 해안의 수취인에게 지인(이름으로 부르는 친밀한 관계)을 통해 편지를 전달하도록 의뢰하여, 도착하기까지 몇 명의 중개자가 필요한지를 조사했다.^[12] 그 결과, 평균 6명을 거치면 편지가 도착한다는 것을 확인했는데, 이는 여섯 단계 분리라는 표어로 알려져 있다.^[12]

두 번째는 사회학자 마크 그래노베터가 발견한 "약한 유대의 중요성"이다. 그래노베터는 1973년 논문에서 사람들이 직업을 구할 때, 친한 친구나 가족과 같은 "강한 유대" 관계보다 가끔 만나는 "약한 유대" 관계의 사람이 더 유효한 소개자가 된다는 것을 발견했다.

2. 3. 1990년대 이후의 발전

1998년, 코넬 대학교 박사 과정 학생이었던 덩컨 와츠와 지도 교수였던 Steven Strogatz|스티븐 스트로가츠^영어는 다수의 반딧불이의 깜빡임이나 귀뚜라미의 울음소리가 동조하는 현상을 규명하는 과정에서 스몰 월드 현상을 설명하는 "와츠-스트로가츠 모델"(WS 모델)이라는 수학 모델을 고안했다.^[18] 이들은 유사한 성질이 영화 배우의 공동 출연 관계, 전력 시스템, 선충의 신경 세포 등 현실 세계의 다양한 네트워크에도 공통적으로 존재한다는 것을 발견했다. 이들의 연구 성과는 『네이처』에 발표되었고,^[18] 이에 영감을 받은 연구를 통해 인터넷, 생태계의 먹이 사슬, 더 나아가 논문의 인용 관계 및 언어의 문법 구조와 같은 네트워크에서도 유사한 성질이 발견되었다. 이로써 사회학, 경제학, 정보 공학, 생물학 등 광범위한 분야에서 "복잡계 네트워크"라는 새로운 패러다임이 주목을 받게 되었다.

3. 현실 세계 네트워크의 주요 특징

소셜 네트워크, 생물 네트워크, 컴퓨터 네트워크 등 대부분의 현실 세계 네트워크는 규칙적이거나 무작위적이지 않은 연결 패턴을 보이며, 이는 비자명한 위상학적 특징으로 나타난다. 이러한 특징에는 차수 분포의 헤비 테일, 높은 클러스터링 계수, 정점 간의 동류성 또는 비동류성, 공동체 구조, 계층 구조 등이 포함된다.^[6] 방향성 네트워크의 경우에는 네트워크 상호성, 삼각 관계 중요도 프로파일 등의 특징이 추가된다.

이러한 특징들은 격자 그래프나 랜덤 그래프와 같은 과거에 연구된 네트워크 모델에서는 나타나지 않는다. 가장 복잡한 구조는 중간 정도의 상호 작용을 가진 네트워크에서 나타나며, 이는 최대 정보 내용(엔트로피)이 중간 확률에서 얻어진다는 사실과 관련이 있다.^[6]

현실 세계 네트워크의 대표적인 예시로는 척도 없는 네트워크^[7]와 스몰 월드 네트워크^[8]^[9]가 있다. 척도 없는 네트워크는 멱함수 차수 분포를 가지며, 스몰 월드 네트워크는 짧은 경로 길이와 높은 클러스터링 계수를 특징으로 한다.

복잡계 네트워크 연구는 수학, 물리학, 전력 시스템,^[10] 생물학, 기후, 컴퓨터 과학, 사회학, 역학 등 다양한 분야의 연구자들이 참여하면서 빠르게 발전하고 있다.^[11] 네트워크 과학 및 공학의 아이디어와 도구는 대사 및 유전자 조절 네트워크 분석, 생태계 안정성 및 강인성 연구,^[12] 임상 과학,^[13] 복잡한 무선 네트워크 모델링 및 설계,^[14] 등 광범위한 실용적인 문제에 적용되고 있다.

현실 세계 네트워크는 "척도 없는 성질"(차수 분포의 멱함수 법칙), "스몰 월드성", "클러스터성"이라는 공통적인 성질을 갖는다.^[23] 과거에는 이러한 사회적 네트워크의 성질이 주로 사회학의 연구 대상이었지만, 1998년 발표된 "와츠-스트로가츠 모델"이 주목받으면서 인터넷, 생태계 먹이 사슬, 논문의 피인용 관계, 언어의 문법 구조 등 다양한 네트워크에서도 공통된 성질이 발견되었다.

복잡계 네트워크 연구는 현실 세계의 다양한 현상을 설명하는 새로운 패러다임으로서 급속히 진전되고 있으며, 다른 연구 분야와의 상호 영향도 활발해지고 있다. 앞으로 복잡계 네트워크 과학은 네트워크 문제가 관련된 다수의 분야에서 보편성과 중요성을 더해갈 것으로 예상된다.

3. 1. 척도 없는 네트워크 (Scale-free networks)

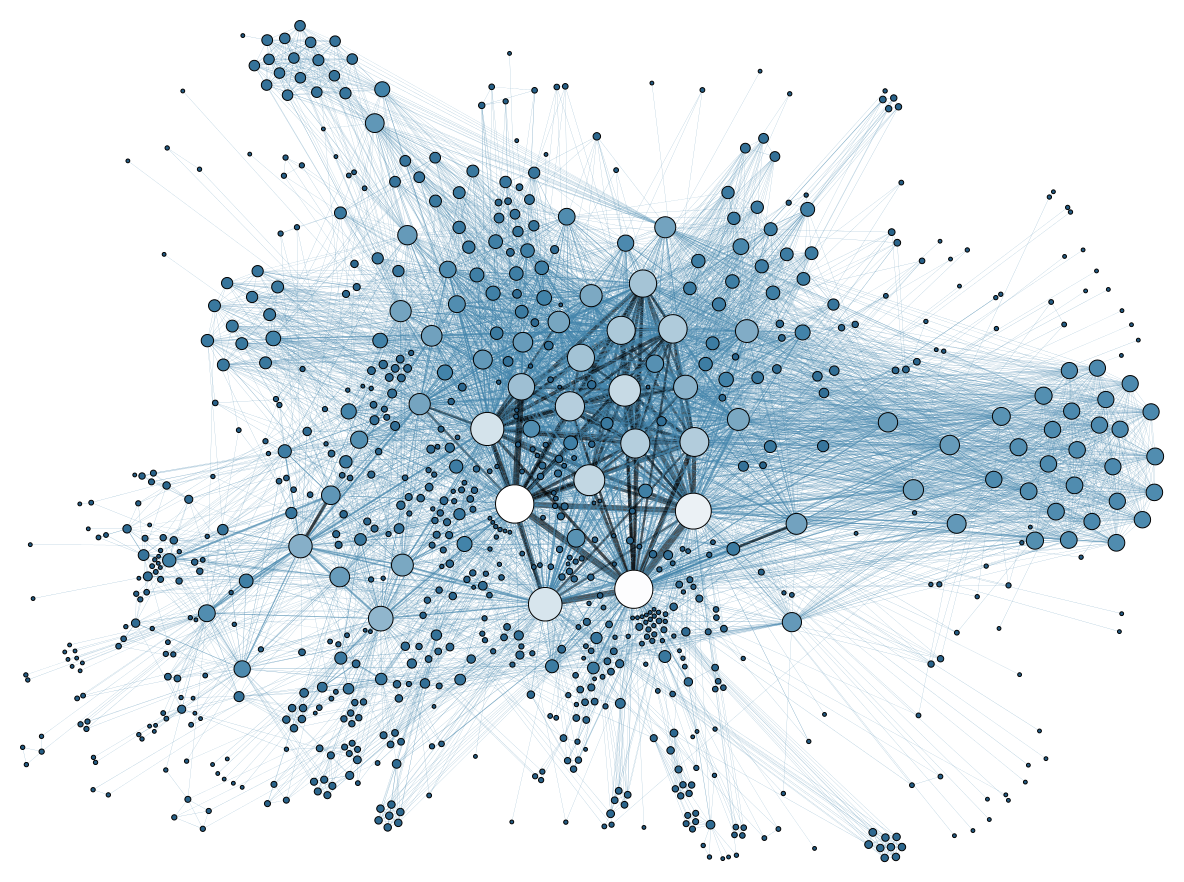
차수 분포가 멱법칙을 따르는 네트워크를 척도 없는 네트워크라고 한다.^[15] 이는 네트워크의 차수 분포에 특징적인 척도가 없음을 의미한다. 월드 와이드 웹, 자율 시스템(AS) 네트워크, 일부 인터넷 라우터 네트워크, 단백질 상호 작용 네트워크, 이메일 네트워크 등이 척도 없는 네트워크의 예시이다.

척도 없는 네트워크에서 평균보다 훨씬 큰 차수를 갖는 꼭짓점을 "허브"라고 부르기도 하지만, 고유한 임계값이 없으므로 오해의 소지가 있다.

바라바시-앨버트 모형, 적합성 모형은 척도 없는 차수 분포를 생성하는 성장형 네트워크 모델이다. 율 과정과 선호적 부착 역시 멱법칙 차수 분포를 따른다. 최근에는 쌍곡 기하학적 그래프가 척도 없는 네트워크 구성 방법으로 제안되기도 했다.

멱법칙 차수 분포를 갖는 네트워크는 꼭짓점의 무작위 삭제에 강하지만, 표적 공격에는 취약하여 네트워크가 빠르게 분열될 수 있다.

현실 세계의 네트워크는 "척도 없는 성질"(차수 분포의 멱함수 법칙)을 가진다. 예를 들어, 일부는 많은 지인을 갖지만 대다수는 적은 수의 지인을 갖는다. WWW에서는 극소수 유명 사이트가 수백만 링크를 모으지만, 대다수는 소수 링크 대상에서만 링크된다.

수학적으로 척도 없는 네트워크는 정점이 차수 ''k''를 가질 확률 ''p''(''k'')의 확률 분포 꼬리가

p(k) \propto k^{-\gamma}

의 멱법칙을 따른다고 표현된다.^[21] 이러한 차수 분포에는 형태를 특징짓는 크기(척도)가 없다.

반면, 단일 척도를 가진 네트워크는 모든 노드가 (대략) 동일한 차수를 갖는 격자 구조와 유사하다. 에르되시-레니(ER) 무작위 그래프, 무작위 정규 그래프, 정규 격자, 하이퍼큐브 등이 그 예시이다.

3. 2. 스몰 월드 네트워크 (Small-world networks)

스몰 월드 현상(일반적으로 6단계 분리로 알려짐)과 유사하게 네트워크는 스몰 월드 네트워크라고 불린다. 1998년, 덩컨 J. 와츠와 스티븐 스트로가츠는 처음으로 스몰 월드 네트워크 모델을 발표했는데, 이 모델은 단일 매개변수를 통해 무작위 그래프와 격자 사이를 부드럽게 보간한다. 그들의 모델은 단지 소수의 장거리 링크를 추가함으로써 지름이 네트워크 크기에 비례하는 정규 그래프를 "스몰 월드"로 변환할 수 있음을 보여주었다. 여기서 임의의 두 정점 사이의 평균 엣지 수는 매우 작고 (수학적으로는 네트워크 크기의 로그로 증가해야 함) 클러스터링 계수는 크게 유지된다.

랜덤 그래프와 척도 없는 네트워크와 같은 다양한 추상 그래프가 스몰 월드 속성을 나타내는 것으로 알려져 있다. 월드 와이드 웹 및 대사 네트워크와 같은 실제 네트워크도 이러한 속성을 나타낸다.

네트워크 지름의 크기를 언급하는 것 외에도, 작은 지름과 높은 클러스터링 계수의 동시 발생을 지칭할 수도 있다. 클러스터링 계수는 네트워크에서 삼각형의 밀도를 나타내는 메트릭이다. 예를 들어, 희소 무작위 그래프는 클러스터링 계수가 매우 작지만 실제 네트워크는 종종 상당히 큰 계수를 갖는다. 과학자들은 이러한 차이점이 실제 네트워크에서 엣지가 상관 관계가 있음을 시사한다고 지적한다.^[16]

현실 세계에 존재하는 네트워크는 다양하며, 거대하고 복잡한 구조를 가지고 있지만, "스몰 월드성"이라는 일정한 공통된 성질을 발견할 수 있다. "스몰 월드성"은, "세상은 좁다"라고 말해지는 것처럼, 겉보기에는 전혀 모르는 사람처럼 보여도, 실제로는 중간에 소수의 사람을 거치는 것만으로 연결되어 있다는 성질이다.

사회학에서 실험 사회 심리학자 스탠리 밀그램은 스몰 월드 현상을 실증하려는 시도를 하였다. 밀그램은 1967년에 고안한 실험에서, 미국 내륙부의 거주자에게 편지를 전달하고, 전혀 면식이 없는 동부 해안의 수취인에게 우편이 아닌 지인(이름으로 부르는 친밀한 관계)을 통해 전송하도록 의뢰하여, 도착하기까지 몇 명의 중개자가 필요한지를 조사했다. 그 결과는 평균 6명을 중개하는 것만으로 도착한다는 것이었다. 이 결과는 현재 표어적으로 여섯 단계 분리라고 불린다.

예시로 자주 언급되는 것은 "에르되시 수"이다. 에르되시 팔과 논문을 공동으로 집필한 경험이 있는 수학자의 에르되시 수를 1, 에르되시 수 ''e''의 수학자와 공저 관계에 있는 수학자의 에르되시 수를 ''e''+1로 한다. 전 세계 수학자들의 에르되시 수를 조사해 보면, 대부분은 에르되시 수 5에서 6 정도로 연결되어 있다. "베이컨 수"라는 놀이도 있다. 미국의 배우 케빈 베이컨 (시작점은 누구라도 상관없지만)과 영화에서 공동 출연한 적이 있는 배우의 베이컨 수를 1, 베이컨 수 ''b''의 배우와 공동 출연 관계에 있는 배우의 베이컨 수를 ''b''+1로 한다. 전 세계 배우들의 베이컨 수를 조사해 보면, 대다수가 베이컨 수 3에서 4 범위에 들어간다.

The Oracle of Bacon at Virginia - 베이컨 수를 알 수 있는 사이트

수학적으로 스몰 월드성은 그래프의 "평균 최단 거리"(고유 경로 길이 또는 지름이라고도 함)가 정점 수의 크기에 비해 작은 값을 가짐으로써 표현된다. 무방향, 가중치 없는 그래프에서 임의의 정점에서 정점까지 가기 위해 거쳐야 하는 변의 최소 개수를 "경로 길이"(거리라고도 함), 경로 길이 중에서 가장 짧은 것을 간의 "최단 거리"라고 부르는데, 의 평균값이 해당 그래프의 평균 최단 거리이다. 그래프에서 이 증가했을 때 이 기껏해야 에 비례하는 정도로 완만하게 증가할 때, 해당 그래프는 스몰 월드성을 만족한다고 정의된다.

2차원 격자를 생각하면, 그래프의 끝에서 끝까지 가기 위해서는 여러 정점을 거쳐야 한다. 즉 은 에 비례한다. 이 증가하면 도 상당히 증가해 버리므로, 스몰 월드성을 만족하지 못한다. 한편, 랜덤 그래프에서는 정점이 무작위로 연결되어 있으므로, 격자의 경우와 달리 지름길이 있을 것 같다. 실제로, 가지의 연결 확률 의 랜덤 그래프에서는

L = \frac{\log n}{\log (pn)} \propto \log n

이 된다. 이 점에서, 랜덤 그래프는 현실 세계의 네트워크에 가깝다고 할 수 있다.

3. 3. 클러스터성 (Clustering)

현실 세계의 네트워크는 "클러스터성"이라는 성질을 갖는다. 주변 지인 관계를 예로 들면, "나와 지인 A가 있을 때, 나와 A 모두를 아는 공통 지인 B가 한 명도 없다"는 상황은 소셜 데이팅 사이트를 이용하지 않는 한 거의 발생하지 않는다. 즉, 현실 세계의 네트워크에는 나, A, B로 구성된 삼각형 네트워크가 많이 포함되어 있다. 와츠와 스트로가츠는 이러한 성질을 "클러스터성"이라고 명명했다.^[23]

클러스터성은 그래프의 "클러스터 계수" ''C''로 표현된다. 그래프에서 임의의 정점 ''v''_''i''와 ''v''_''j'', ''v''_''i''와 ''v''_''k''가 모두 변으로 연결된 조합의 수를 ''N''₃, ''v''_''i'', ''v''_''j'', ''v''_''k''가 삼각형으로 연결된 조합의 수를 ''N''Δ라고 할 때, 그래프의 클러스터 계수는 ''C'' = 3''N''Δ / ''N''₃로 정의된다. 현실 세계의 네트워크에서 클러스터 계수는 0.1에서 0.7 정도로 측정된다.^[23]

클러스터성을 가진 그래프는 수학 모델로 표현할 수 있다. 랜덤 그래프는 모든 변이 무작위로 생성되므로 삼각형이 형성될 확률은 매우 낮다. 변 생성 확률 ''p''가 작으면 클러스터 계수는 거의 0이 되어 클러스터성을 만족하지 않는다. 반면, 2차원 삼각 격자는 삼각형이 많이 포함되어 있다. 2차원 삼각 격자의 클러스터 계수는 6 / ₆C₂ = 0.4이다. 따라서 격자의 클러스터 계수는 충분히 크며, 현실 세계 네트워크와 유사하다고 할 수 있다.

4. 복잡계 네트워크 모델

소셜 네트워크, 생물 네트워크, 컴퓨터 네트워크 등 현실 세계의 네트워크는 규칙적이거나 무작위적인 패턴이 아닌, 요소 간 연결에서 독특한 위상학적 특징을 보인다. 이러한 특징에는 차수 분포의 헤비 테일, 높은 클러스터링 계수, 동류성 또는 비동류성, 공동체 구조, 계층 구조 등이 포함된다. 방향성 네트워크의 경우에는 네트워크 상호성, 삼각 관계 중요도 프로파일 등이 추가적인 특징으로 나타난다.^[6]

이러한 특징들은 격자 그래프나 랜덤 그래프와 같은 기존의 네트워크 모델에서는 관찰되지 않는 현상이다. 복잡계 네트워크의 구조는 중간 정도의 상호작용을 가진 네트워크에서 가장 두드러지게 나타나는데, 이는 정보 내용(엔트로피)이 중간 정도의 확률에서 최대가 된다는 사실과 관련이 있다.^[6]

복잡계 네트워크 연구는 척도 없는 네트워크^[7]와 스몰 월드 네트워크^[8]^[9]의 발견과 정의를 통해 발전해왔다. 척도 없는 네트워크는 멱함수 차수 분포를 가지며, 스몰 월드 네트워크는 짧은 경로 길이와 높은 클러스터링 계수를 특징으로 한다.

그래프 이론에서 그래프는 정점(노드)과 변(가지, 링크)의 집합으로 표현된다. 정점 ''i''에 연결된 변의 개수를 차수 ''k''_i라고 한다. 1959년 폴 에르되시와 알프레드 레니는 Random graph|랜덤 그래프^영어를 만드는 Erdős–Rényi model|에르되시-레니 모델^영어을 고안했다.

1960년대부터 70년대에 걸쳐 사회학에서는 스몰 월드 현상("세상은 좁다")을 실험으로 증명하려는 스탠리 밀그램과, 사람들이 직업을 구할 때 친한 관계보다 드물게 접하는 "약한 유대" 관계가 더 중요하다는 것을 발견한 마크 그래노베터의 연구가 있었다.

이후, 1998년에 덩컨 와츠와 Steven Strogatz|스티븐 스트로가츠^영어는 와츠-스트로가츠 모델을 발표했다. 이들은 스몰 월드 현상을 설명하는 수학적 모델을 고안했으며, 이와 유사한 성질이 영화 배우의 공동 출연 관계, 전력 시스템, 선충의 신경 세포 등 다양한 네트워크에 존재함을 발견했다.^[18]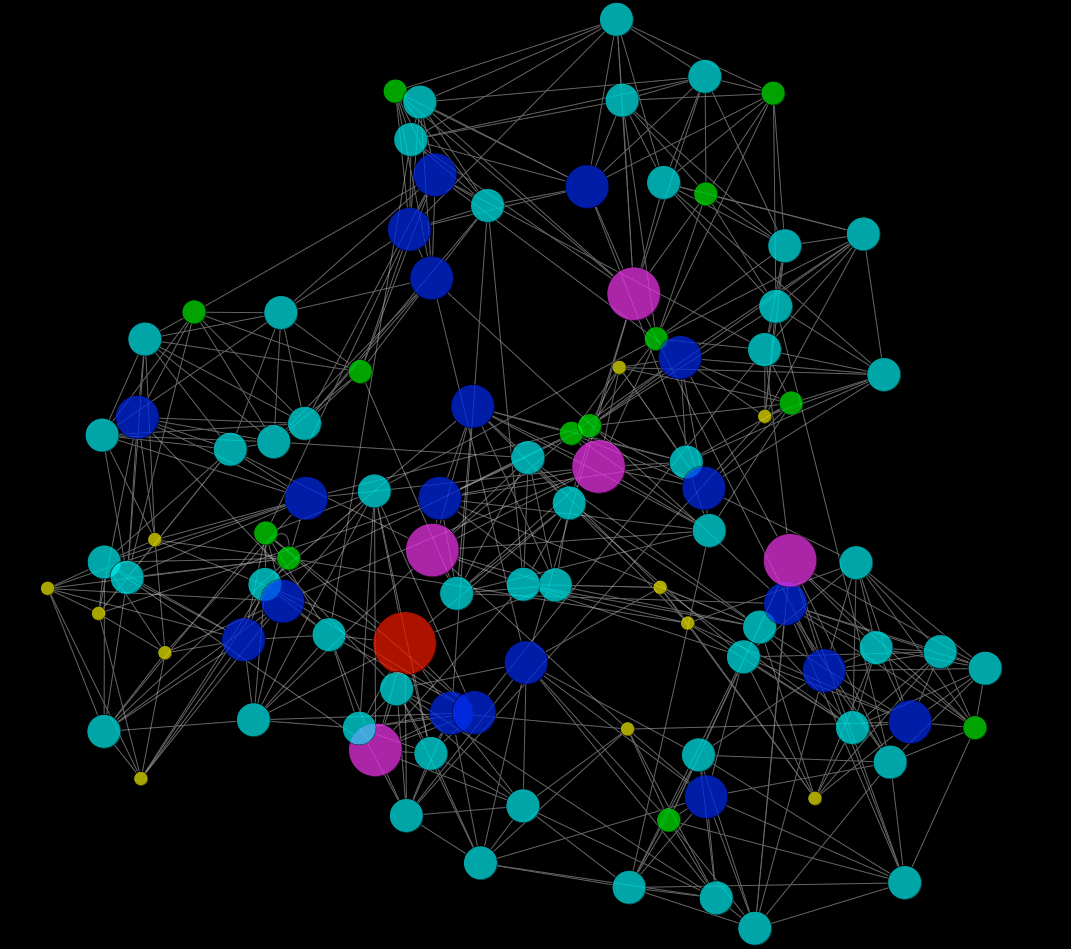

1999년에는 얼베르트 러슬로 바라바시^[24]와 Réka Albert|레카 알베르트^영어^[25]가 스케일 없는 성질을 갖는 바라바시-알베르트 모델을 고안했다. 이 모델에서는 기존 차수가 큰 정점에 새로운 변이 높은 확률로 추가되어 허브가 성장한다.

복잡계 네트워크 연구는 수학, 물리학, 생물학, 기후, 컴퓨터 과학, 사회학 등 다양한 분야로 확장되고 있다.^[11]

4. 1. 와츠-스트로가츠 모델 (Watts-Strogatz model)

와츠-스트로가츠 모델은 규칙적인 격자 그래프와 무작위 그래프의 중간 형태를 띠는 네트워크 모델이다. 1998년 덩컨 와츠와 Steven Strogatz|스티븐 스트로가츠^영어는 다수의 반딧불이 깜빡임이나 귀뚜라미 울음소리가 동조하는 현상을 연구하던 중 이 모델을 고안했다.^[18]

이 모델은 다음의 간단한 알고리즘으로 생성된다.

# 모든 정점을 1차원 격자 형태로 배열하고, 각 정점을 인접한 ''a''개의 정점과 엣지로 연결한다.

# 각 엣지를 확률 ''p''로 무작위하게 다른 위치에 재배치한다.

여기서 ''p''가 0이면 원래의 규칙적인 격자 구조가 유지되고, 1이면 완전히 무작위한 그래프가 된다. ''p'' 값을 0과 1 사이에서 조정하면, 규칙성과 무작위성이 혼합된 다양한 형태의 네트워크를 얻을 수 있다. 특히, ''p''를 0.1 근처로 설정하면, 현실 세계의 네트워크와 유사하게 스몰 월드 성과 높은 클러스터 성을 동시에 만족하는 그래프가 생성된다. 즉, "세상은 좁다"라는 현상처럼, 멀리 떨어진 정점 사이의 평균 거리가 짧으면서도, "친구의 친구는 친구일 가능성이 높다"라는 현상처럼, 서로 연결된 정점들이 군집을 이루는 경향이 강하게 나타난다.

그러나 와츠-스트로가츠 모델은 차수 분포가 스케일 프리 성을 만족하지 않는다는 한계가 있다. 그럼에도 불구하고, 이 모델은 단순하면서도 현실 세계 네트워크의 주요 특징들을 포착하여 사회적 네트워크를 포함하여, 영화 배우들의 공동 출연 관계, 전력 시스템, 선충의 신경 세포 연결 등 다양한 현상을 설명하는 데 중요한 역할을 했다.^[18]

4. 2. 바라바시-알베르트 모델 (Barabási-Albert model)

1999년, 얼베르트 러슬로 바라바시(Albert-László Barabási)^[24]와 Réka Albert^영어^[25]는 척도 없는 성질을 갖는 그래프의 수학적 모델을 고안했는데, 이를 "바라바시-알베르트 모델"(Barabási-Albert model; BA 모델)이라고 부른다. BA 모델은 다음 알고리즘으로 그래프를 생성한다.

# ''m''개의 정점으로 구성된 완전 그래프 ''K''_m에서 시작한다.

# 새로운 정점을 1개 추가한다. 이 정점에서 이미 존재하는 ''m''개의 정점에 변을 연결한다. 이때, 변이 연결될 확률은 각 정점의 해당 시점에서의 차수 ''k''에 비례한다.

# 2번 과정을 정점이 소정의 개수가 될 때까지 반복한다.

BA 모델에서는 기존 차수가 큰 정점에 새로운 변이 높은 확률로 추가되어 해당 정점이 허브로 성장해 간다. 이 모델에서 정점 차수 분포는 ''p''(''k'') = 2''m''(''m''+1) / [''k''(''k''+1)(''k''+2)] ∝ ''k''^-3 이 되며, γ = -3인 척도 없는 성질을 만족한다. 랜덤 그래프와 유사한 점도 있어 평균 최단 거리는 ''L'' ∝ ''log n''이 되어 스몰 월드 성질도 만족한다.

BA 모델의 약점은 클러스터 계수가 0에 가까운 작은 값이 되어 클러스터 성질을 만족하지 않는다는 것이다. 하지만 이후 연구를 통해 단순한 알고리즘이면서도 "척도 없는 성질", "스몰 월드 성질", "클러스터 성질"이라는 현실 세계 네트워크의 3가지 특징을 모두 만족하는 모델이 발표되었다.^[26]

4. 3. 공간 네트워크 (Spatial networks)

많은 실제 네트워크는 공간에 내재되어 있다. 교통, 기타 기반 시설 네트워크, 뇌 네트워크 등이 그 예시이다.^[3]^[4] 공간 네트워크에 대한 여러 모델이 개발되었다.^[17]

5. 척도 없는 그래프의 강건성과 취약성

척도 없는 네트워크는 무작위적인 고장에 매우 강하다. 예를 들어, 척도 없는 토폴로지를 가진 네트워크에서 전체 노드 중 무작위로 5%가 작동을 멈추더라도, 다른 경로가 존재하기 때문에 노드 간 연결이 유지되며, 시스템 전체의 평균 경로 길이(평균 최단 거리)는 거의 변하지 않는다.^[27] 이러한 강건성은 차수 분포의 지수와 관련이 있으며, 지수가 2 < γ < 3인 경우에 매우 높은 강건성을 가진다는 것이 모델을 통해 밝혀졌다.^[27]

하지만 이러한 강건성은 양날의 검과 같아서, 감염병이나 컴퓨터 바이러스가 네트워크 전체로 쉽게 확산될 수 있다는 것을 의미한다. 무작위 네트워크에서는 바이러스나 유행의 확산을 막는 임계값(threshold)이 존재하지만, 척도 없는 네트워크에서는 이러한 임계값이 존재하지 않아 확산이 쉽고, 막기도 어려우며 시간이 더 오래 걸린다.^[27]

반면, 척도 없는 네트워크는 특정 중요한 허브를 대상으로 하는 공격에는 취약하다. 차수가 집중된 상위 5%의 노드가 작동을 멈추면, 시스템 전체의 평균 경로 길이는 약 2배까지 증가한다.^[28]

이와 비슷한 특성은 자연계의 먹이 사슬 네트워크에서도 나타난다. 먹이 사슬 네트워크는 생물 종의 무작위적인 멸종에는 강하지만, 특정 중요한 종이 멸종하면 큰 영향을 받는다. 이러한 점은 생물 다양성을 논의할 때도 중요하다.^[29]

6. 한국 사회와 복잡계 네트워크

복잡계 네트워크 이론은 한국 사회의 다양한 현상을 설명하고 이해하는 데 유용하게 적용될 수 있다. 특히, 한국 사회는 고도의 정보통신기술 발달과 촘촘한 사회 연결망, 역동적인 사회 변화 등으로 인해 복잡계 네트워크의 특징이 두드러지게 나타난다.

7. 분석 도구

복잡계 네트워크를 분석할 때는 가시화, 통계 분석 등을 위해 컴퓨터를 사용하는 것이 필수적이다. 현재 다양한 분석 도구들이 프리웨어로 제공되고 있다.

http://vlado.fmf.uni-lj.si/pub/networks/pajek/ Pajek - 윈도우용 네트워크 분석 소프트웨어이다.
http://cneurocvs.rmki.kfki.hu/igraph/ igraph - 그래프 관련 알고리즘이 구현된 패키지이다. R에서도 구현되어 있다.
http://www.cytoscape.org/ Cytoscape - 멀티 플랫폼을 지원하는 네트워크 가시화/분석 소프트웨어이다. LGPL로 배포된다. (https://cytoscape.wordpress.com/ 한국어 사이트)

참조

_[1] 논문 Statistical mechanics of complex networks
_[2] 서적 Networks: An Introduction Oxford University Press
_[3] 논문 Network neuroscience 2017-02-23
_[4] 웹사이트 An Introduction to Network Neuroscience: How to build, model, and analyse connectomes - 0800-10:00 {{!}} OHBM https://www.pathlms.[...] 2020-03-11
_[5] 논문 Topological impact of negative links on the stability of resting-state brain network null 2021-01
_[6] 논문 What is a complex graph?
_[7] 논문 Scale-Free Networks 2003
_[8] 논문 Collective dynamics of 'small-world' networks
_[9] 논문 Classes of small-world networks
_[10] 논문 Applications of Complex Network Analysis in Electric Power Systems 2018-05-29
_[11] 논문 Networks in Motion http://www.physicsto[...]
_[12] 논문 Trophic coherence determines food-web stability
_[13] 논문 A complex network approach to clinical science
_[14] 학위논문 On the Fundamentals of Stochastic Spatial Modeling and Analysis of Wireless Networks and its Impact to Channel Losses http://spectrum.libr[...] Concordia University 2012-09-22
_[15] 논문 Statistical mechanics of complex networks
_[16] 논문 Generating correlated networks from uncorrelated ones 2003
_[17] 논문 Routing of multipoint connections 1988
_[18] 문서 Watts, D.J., and Strogatz, S.H. (1998)
_[19] 논문 The web of human sexual contacts https://arxiv.org/pd[...] 2001
_[20] 논문 Scale-Free Networks and Sexually Transmitted Diseases http://www.stdjourna[...] 2004
_[21] 문서 Amaral, L.A.N. et al (2000) によれば、現実世界の全てのネットワークが完全なべき乗則の次数分布となるわけではない。辺が集中することで混雑などのコストが発生する場合は集中は頭打ちとなる。典型例は航空路線のネットワークである。
_[22] 문서 「スモールワールド性」という用語の定義に関しては曖昧さがある。単にグラフの平均最短距離が小さい状態を指す場合もあれば、小さな平均最短距離と大きなクラスター係数とを共に満たす状態を指す場合もある。ランダムグラフは、前者の定義に従えばスモールワールドであり、後者に従えばスモールワールドではない。
_[23] 문서 Albert, R., and Barabási, A.-L. (2002)
_[24] 문서 "{{lang|hu|Barabási Albert László}} {{IPA|ˈbɒrabɑ̈ːʃi ˌɒrbɛrtˌlɑ̈ːsloː}}。バラバーシが姓、アルベルトとラースローが名（男性名）。[[セーケイ人]]（[[ハンガリー人]]の一派）。ルーマニア領トランシルヴァニアの[[:hu:Székelyföld|セーケイ地方]]の[[ハルギタ県]][[:hu:Karcfalva|カルツファルヴァ村またはカルツ村]]（ルーマニア語名 [[:ro:Cârța|クルツァ村]]）生まれ。国籍は[[ルーマニア]]と[[ハンガリー]]と[[米国]]の三重国籍。"
_[25] 문서 "{{lang|hu|Albert Réka}} {{IPA|ˈɒrbɛrt ˌre̝ːkɒ}}。アルベルトが姓、レーカが名（女性名）。[[セーケイ人]]（[[ハンガリー人]]の一派）。ルーマニア領トランシルヴァニアの[[:hu:Székelyföld|セーケイ地方]]の[[ムレシュ県|マロシュ県]][[:hu: Szászrégen |サースレーゲン市]]（ルーマニア語名 [[:ro:Reghin|レギン市]]）生まれ。国籍は[[ルーマニア]]と[[ハンガリー]]と[[米国]]の三重国籍。"
_[26] 문서 例えば Dorogovtsev, S.N. et al. (2002) や Klemm, K., and Eguíluz, V.M. (2002)
_[27] 서적 RobustComplex Networks: Structure,ness and Function http://www.cambridge[...] Cambridge University Press 2010-07
_[28] 문서 Albert, R. et al. (2000)
_[29] 문서 Solë, R.V., and Montoya, J.M. (2001)
_[30] 문서 Newman, M.E.J., and Girvan, M. (2004)
_[31] 문서 Costa, L.F. et al. (2005)
_[32] 논문 Network neuroscience 2017-02-23
_[33] 웹인용 An Introduction to Network Neuroscience: How to build, model, and analyse connectomes - 0800-10:00 {{!}} OHBM https://www.pathlms.[...] 2020-03-11
_[34] 논문 Topological impact of negative links on the stability of resting-state brain network null 2021-01
_[35] 논문 Statistical mechanics of complex networks
_[36] 서적 Networks: An Introduction https://archive.org/[...] Oxford University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com