야코비 타원함수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
야코비 타원 함수는 두 변수 (u, m)에 대한 함수 sn, cn, dn으로 정의되며, 여기서 0 ≤ m ≤ 1이다. 이 함수들은 타원 적분의 역함수를 통해 정의되며, 삼각 함수와 유사한 성질을 갖지만, 쌍곡선 함수로도 변환될 수 있다. 야코비 타원 함수는 주기성을 가지며, 삼각 함수와 쌍곡선 함수를 포함하는 다양한 특수값을 갖는다. 또한, 다른 타원 함수, 세타 함수, 네빌 세타 함수를 사용하여 정의할 수 있으며, 야코비 변환을 통해 다른 형태로 표현될 수 있다. 이 함수들은 미분, 덧셈 정리, 반각 공식 등 다양한 항등식을 만족하며, 비선형 상미분 방정식의 해로 나타낼 수 있다. 야코비 타원 함수는 지도 투영법 및 다양한 응용 분야에서 활용된다.
더 읽어볼만한 페이지
- 타원함수 - 바이어슈트라스 에타 함수
바이어슈트라스 에타 함수는 오메가 상수와의 관계를 통해 정의되고 바이어슈트라스 타원 함수 이론에서 중요한 역할을 하는, 바이어슈트라스 타원 함수와 관련된 특수 함수이다. - 타원함수 - 타원 적분
타원 적분은 불완전 타원 적분과 완전 타원 적적으로 나뉘며, 단진자의 주기나 타원의 호 길이 계산 등 물리적 현상 설명에 응용되는 특정한 형태의 적분이다.
2. 정의
야코비 타원 함수는 sn, cn, dn으로 표기하며, 두 개의 변수 와 ()에 대한 함수이다. 제1종 불완전 타원 적분을 이용하여 다음과 같이 정의할 수 있다.
타원 적분은 다음과 같이 정의한다.
:
이때, sn, cn, dn은 다음과 같이 정의된다.
:
:
:
여기서 는 '''야코비 진폭'''이라고 하며, 이다.
일부 저자들은 매개변수 ''m'' 대신 또는 을 사용하기도 한다. 이 경우 , 이다.
야코비 타원 함수는 로 표기하며, 여기서 와 는 , , , 중 하나이다. 는 인수이고 은 매개변수이며, 둘 다 복소수일 수 있다. 야코비 타원 함수는 와 모두에 대해 유형 함수이다.[2] 평면에서 영점과 극점의 분포는 잘 알려져 있지만, 평면에서의 분포는 아직 연구 중이다.[2]
인수 의 복소 평면에서 12개의 함수는 간단한 극점과 영점의 반복 격자를 형성한다.[3] 함수에 따라 하나의 반복 평행사변형(단위 세포)은 실수축에서 또는 , 허수축에서 또는 의 길이를 가진다. 여기서 및 는 4분 주기로 알려져 있으며, 는 제1종 타원 적분이다.
322px
보조 직사각형(단위 세포)의 네 모서리는 원점에서 시계 반대 방향으로 , , , 으로 명명된다. 함수 은 모서리에 영점을, 모서리에 극점을 갖는다.
이고 와 이 실수이면, 와 은 실수가 되고 야코비 타원 함수는 모두 실수선에서 실수 값을 갖는다. 야코비안 타원 함수는 에서 이중 주기적이므로 토러스를 통해 인수 분해된다. 각 함수는 토러스의 반대 위치에 두 개의 영점과 두 개의 극점을 갖는다.
야코비안 타원 함수는 다음과 같은 속성을 만족하는 이중 주기적 유형 함수이다.
- 모서리에는 단순한 영점이 있고 모서리에는 단순한 극점이 있다.
- 복소수 는 함수 의 주기의 절반과 같다. 즉, 함수 는 방향 에서 주기적이며, 주기는 이다.
- -|]]|thumb|독립 변수 ''u''와 모듈러스 ''k''의 함수로 나타낸 야코비 진폭(수직 축을 따라 측정)]
'''야코비 엡실론''' 함수는 다음과 같이 정의한다.
:
여기서 는 매개변수 을 갖는 제2종 불완전 타원 적분이다.
'''야코비 zn''' 함수는 다음과 같이 정의된다.
:
2. 1. 타원과의 관계
긴 반지름이 이고 짧은 반지름이 1인 타원을 생각하자. 이 타원은 데카르트 좌표계에서 다음과 같은 방정식으로 정의된다.:
이들을 극좌표계 로 변환하면, 다음과 같은 함수들을 얻는다.
:
:
:
또한, 다음과 같은 값을 정의할 수 있다.
:
그렇다면, 의 함수로서 , , 은 다음과 같이 야코비 타원함수로 주어진다.
:
:
:
이 경우, 은 타원의 이심률의 제곱이다.
:

는 단위 원에서 정의되며, 반지름은 ''r'' = 1이고 각도 는 양의 ''x''축에서 측정된 단위 원의 호 길이이다. 마찬가지로, 야코비 타원 함수는 단위 타원 ()에서 정의할 수 있다.
:
그렇다면:
:
각도 에 대해 매개변수
:
(제1종 완전 타원 적분)가 계산된다.
단위 원 ()에서 는 호의 길이가 된다.
를 타원 위의 점으로 하고, 를 단위 원이 와 원점 사이의 선과 교차하는 점이라고 하자.
그렇다면 단위 원에서 친숙한 관계:
:
타원에서는 다음과 같다.
:
따라서 원점 와 단위 원의 교차점 의 ''x''축 및 ''y''축에 대한 투영은 단순히 과 이다. 이러한 투영은 '삼각법으로서의 정의'로 해석될 수 있다. 요약하자면:
:
와 매개변수 을 갖는 점 의 및 값의 경우, 관계를 삽입한 후:
:
에:를 대입하면:
:
단위 타원 위의 점에 대한 ''x'' 및 ''y'' 좌표에 대한 후자의 관계는 단위 원 위의 점에 대한 좌표에 대한 관계 의 일반화로 간주될 수 있다.
다음 표는 모든 야코비 타원 함수 pq(u,m)에 대한 식을 변수 (''x'',''y'',''r'') 및 (''φ'',dn)에 대해 요약한다. 여기서
2. 2. 보조 야코비 타원함수
sn영어, cn영어, dn영어의 비를 이용하여 보조 야코비 타원 함수를 정의할 수 있다. 기본 야코비 타원함수들의 비는 다음과 같이 정의된다.[9]
야코비 타원함수는 타원 함수의 일종으로, 실수축과 허수축 방향으로 주기를 갖는 이중 주기 함수이다. 주요 성질은 다음과 같다.
3. 성질
3. 1. 주기성
야코비 타원함수는 타원 함수로, 실수축과 허수축 방향으로 각각 주기를 갖는 이중 주기 함수이다. 가 sn, cn, 또는 dn 함수를 나타낼 때, 다음과 같은 주기성을 갖는다.
:
여기서 은 '''실사분주기'''(real quarter period영어), 은 '''허사분주기'''(imaginary quarter period영어)를 나타내는 특수 함수이며, 다음과 같이 정의된다.[11]
:
:
즉, 야코비 타원함수는 타원 곡선 위에 정의된 유리형 함수이다.
야코비 타원 함수의 이중 주기는 다음과 같이 표현할 수 있다.
:
여기서 ''α''와 ''β''는 임의의 정수 쌍이고, ''K''(⋅)는 4분의 1 주기라고도 불리는 제1종 완전 타원 적분이다. 음의 단일성(''γ'')의 거듭제곱은 다음 표와 같다.
(−1)''γ''가 −1이면 준주기성을, 1이면 완전 주기성을 나타낸다. 예를 들어, α가 짝수일 때 α만 포함하는 함수는 4''K''(''m'')과 2''iK''(1 − ''m'')의 완전 주기를 갖는다. β만 포함하는 함수는 2K(m) 및 4''iK''(1 − ''m'')의 완전 주기를, α + β를 갖는 함수는 4''K''(''m'') 및 4''iK''(1 − ''m'')의 완전 주기를 갖는다.
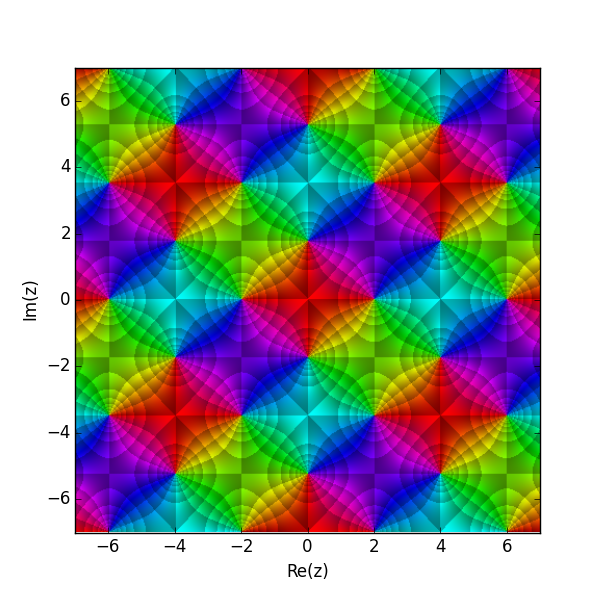
3. 2. 극점과 영점
sn, cn, dn 함수는 모두 에서 단순극을 가지며, 그 유수는 1이다.sn, cn, dn은 타원곡선 위에서 각각 하나의 영점을 가지며, 영점에서의 도함수는 1이다. 영점의 위치는 다음과 같다.
복소 평면에서 변수 ''u''에 대해 야코비 타원 함수는 극(및 영점)의 반복 패턴을 형성한다. 극의 잔류물은 모두 같은 절대값을 가지며 부호만 다릅니다. 각 함수 pq(''u'',''m'')은 극과 영점의 위치가 교환되는 "역함수"(곱셈적 의미) qp(''u'',''m'')을 갖는다.
야코비 타원 함수의 이중 주기는 다음과 같이 표현될 수 있다.
:
여기서 ''α''와 ''β''는 임의의 정수 쌍이다. ''K''(⋅)는 제1종 완전 타원 적분이며, 이는 4분의 1 주기로도 알려져 있다. 음의 단일성(''γ'')의 거듭제곱은 다음 표에 나와 있다.
인자 (−1)''γ''가 −1과 같을 때, 이 방정식은 준주기성을 나타낸다. 1과 같을 때는 완전 주기성을 나타낸다.
각 함수의 역은 대각선과 반대이며, 극과 영점이 교환된 동일한 크기의 단위 셀을 갖는다. (0,0), (''K'',0), (0,''K''′) 및 (''K'',''K''′)로 형성된 보조 사각형의 극과 영점 배치는 위에 설명된 극과 영점 배치 설명과 일치한다. 원점에 가장 가까운 극(즉, 보조 사각형 내)의 잔류물은 다음 표에 나열되어 있다.
2''K''만큼 위로 이동하거나 2''K''′만큼 오른쪽으로 이동한 극은 부호가 반전된 동일한 값을 가지며, 대각선 맞은편에 있는 극은 동일한 값을 갖는다.
극에 대한 정보는 야코비 타원 함수를 특성화하는 데 사용될 수 있다.[15]
- 함수 은 ()에서 의 잔류물을 갖는 유일한 타원 함수이며, 에서 의 값을 갖는다.
- 함수 은 ()에서 의 잔류물을 갖는 유일한 타원 함수이며, 에서 의 값을 갖는다.
- 함수 은 ()에서 의 잔류물을 갖는 유일한 타원 함수이며, 에서 의 값을 갖는다.
3. 3. 삼각함수·쌍곡함수와의 관계
일 때, 야코비 타원 함수는 삼각함수가 된다.[29]일 때, 야코비 타원 함수는 쌍곡함수가 된다.[29]
로 설정하면 뢴니스케이트 타원 함수 과 을 얻는다.
또는 일 때, 야코비 타원 함수는 타원 함수가 아닌 함수로 축소된다.
야코비 진폭의 경우, 이고 이며, 여기서 는 구데르만 함수이다.
일반적으로 p, q가 모두 d가 아니면 이다.
3. 4. 항등식
야코비 타원 함수들은 삼각함수와 유사한 다음 항등식들을 만족시킨다.:
:
야코비 타원 함수가 갖는 대수적인 관계식은 다음과 같다.
:
:
이들 방정식으로 정해지는 2개의 이차 곡면의 공통 부분은 타원 곡선이며, (cn, sn, dn)은 타원 곡선의 매개변수 표현을 제공한다. 야코비 타원 함수의 가법 정리에 의해, 이 타원 곡선의 점은 군을 이룬다.
:
3. 5. 합 공식
다음과 같은 합 공식이 존재한다. 여기서 매개변수 ''m''은 생략한다.:cn영어(''x''+''y'') = cn영어(''x'') cn영어(''y'') - sn영어(''x'') sn영어(''y'') dn영어(''x'') dn영어(''y'') / (1 - ''k''2 sn영어2(''x'') sn영어2(''y''))
:sn영어(''x''+''y'') = (sn영어(''x'') cn영어(''y'') dn영어(''y'') + sn영어(''y'') cn영어(''x'') dn영어(''x'')) / (1 - ''k''2 sn영어2(''x'') sn영어2(''y''))
:dn영어(''x''+''y'') = (dn영어(''x'') dn영어(''y'') - ''k''2 sn영어(''x'') sn영어(''y'') cn영어(''x'') cn영어(''y'')) / (1 - ''k''2 sn영어2(''x'') sn영어2(''y''))
cn영어, sn영어, dn영어은 다음 두 개의 제곱 관계를 만족한다(''m''에 대한 의존성은 생략).
:cn영어2(''u'') + sn영어2(''u'') = 1
:dn영어2(''u'') + ''m'' sn영어2(''u'') = 1
이로부터 (cn, sn, dn)이 위 두 방정식으로 정의된 두 이차 곡면의 교차점인 타원 곡선을 매개변수화한다는 것을 알 수 있다. 야코비 함수에 대한 덧셈 공식을 사용하여 이 곡선 위의 점들에 대한 군 법칙을 정의할 수 있다.
:cn영어(''x''+''y'') = (cn영어(''x'') cn영어(''y'') - sn영어(''x'') sn영어(''y'') dn영어(''x'') dn영어(''y'')) / (1 - ''m'' sn영어2(''x'') sn영어2(''y''))
:sn영어(''x''+''y'') = (sn영어(''x'') cn영어(''y'') dn영어(''y'') + sn영어(''y'') cn영어(''x'') dn영어(''x'')) / (1 - ''m'' sn영어2(''x'') sn영어2(''y''))
:dn영어(''x''+''y'') = (dn영어(''x'') dn영어(''y'') - ''m'' sn영어(''x'') sn영어(''y'') cn영어(''x'') cn영어(''y'')) / (1 - ''m'' sn영어2(''x'') sn영어2(''y''))
야코비 엡실론 함수와 zn 함수는 준 덧셈 정리를 만족한다.
:zn영어(''x''+''y'',''m'') = zn영어(''x'',''m'') + zn영어(''y'',''m'') - ''m''sn영어(''x'',''m'')sn영어(''y'',''m'')sn영어(''x''+''y'',''m'')
이중각 공식은 위 식에서 ''x'' = ''y''로 설정하여 쉽게 파생될 수 있다. 반각 공식은 모두 다음 형식을 취한다.
:pq영어(1/2''u'',''m'')2 = ''f''p / ''f''q
여기서:
:''f''c = cn영어(''u'',''m'') + dn영어(''u'',''m'')
:''f''s = 1 - cn영어(''u'',''m'')
:''f''n = 1 + dn영어(''u'',''m'')
:''f''d = (1 + dn영어(''u'',''m'')) - ''m''(1 - cn영어(''u'',''m''))
야코비 타원 함수가 갖는 대수적인 관계식으로
:cn영어2(''u'',''k'') + sn영어2(''u'',''k'') = 1
:dn영어2(''u'',''k'') + ''k''2 sn영어2(''u'',''k'') = 1
이 있다.
이들 방정식으로 정해지는 2개의 이차 곡면의 공통 부분은 타원 곡선이며, (cn, sn, dn)은 타원 곡선의 매개변수 표현을 제공한다는 것을 알 수 있다. 야코비 타원 함수의 가법 정리에 의해, 이 타원 곡선의 점은 군을 이룬다.
3. 6. 미분
세 가지 기본 야코비 타원 함수 sn(''z''), cn(''z''), dn(''z'')의 미분은 다음과 같이 표현된다. 여기서 매개변수 ''m''은 생략한다.[5]이것을 사용하여 다른 야코비 타원 함수 pq(''u, m'')의 미분()을 구할 수 있다. (인수 (u, m)은 생략)
또한, 타원 적분과 관련된 함수의 미분은 다음과 같다.
:
덧셈 정리를 통해, 0 < ''m'' < 1인 주어진 ''m''에 대해 주요 함수는 다음 비선형 상미분 방정식의 해가 된다.
- 는 다음 미분 방정식을 만족한다.
- *
- *
- 는 다음 미분 방정식을 만족한다.
- *
- *
- 는 다음 미분 방정식을 만족한다.
- *
- *
4. 역사
카를 구스타프 야코프 야코비가 1829년 저서 《타원함수론의 새로운 기반》(Fundamenta nova theoriae functionum ellipticarumla)에서 도입하였다.[33]
5. 표기법
타원 함수는 다양한 표기법으로 나타낼 수 있으며, 이는 혼란을 야기할 수 있다. 타원 함수는 두 변수의 함수이다. 첫 번째 변수는 '''진폭''' 로 표현될 수 있으며, 더 흔하게는 로 표현된다. 두 번째 변수는 '''매개변수''' 으로, 또는 인 '''타원 모듈러스''' 로, 또는 인 '''모듈 각도''' 로 표현될 수 있다.[2] 와 의 여원은 및 로 정의된다.
12개의 야코비 타원 함수는 일반적으로 로 표기되며, 여기서 와 는 , , , 중 임의의 문자이다. 형태의 함수는 표기 완성을 위해 자명하게 1로 설정된다. "주요" 함수는 일반적으로 , 및 으로 간주되며, 이들로부터 다른 모든 함수를 파생할 수 있다.
이 함수는 곱셈 규칙에 의해 서로 표기적으로 관련된다. (인수는 생략)
:
이로부터 다른 일반적으로 사용되는 관계를 파생할 수 있다.
:
:
:
곱셈 규칙은 타원 함수를 네빌 세타 함수로 식별하는 데서 바로 유래한다.[5]
:
6. 야코비 세타 함수를 이용한 정의
마찬가지로, 야코비 타원 함수는 세타 함수를 사용하여 정의할 수 있다.[10] 야코비 타원 함수는 야코비 세타 함수를 사용하여 정의할 수 있다.
이고 일 때, 야코비 세타 함수는 다음과 같다.
:
:
:
:
, , 로 놓으면, , , 및 에 대해, 야코비 타원 함수는 다음과 같이 표현된다.
:
야코비 zn 함수는 세타 함수로도 표현할 수 있다.
:
여기서 는 첫 번째 변수에 대한 편미분을 나타낸다.
야코비 타원 함수는 테타 함수를 사용하여 정의할 수도 있다. 를 로 줄여 쓰고, 도 각각 (테타 상수)로 줄여 쓴다. 이 때, 모수 ''k''는 가 된다. 로 놓으면,
:
:
:
가 된다.
이로써 야코비 함수가 모수 ''k''(τ)의 식으로 정의되었으므로, 이것을 반전하여 τ를 ''k''의 식으로 나타낼 필요가 있다. 먼저, ''여모수''를 생각한다. 이것은 τ의 함수로,
:
로 쓸 수 있다.
다음으로,
:
로 정한다.
그리고, 노름 ''q''를 로 정의하고, 노름 ''q''에 관하여 을 멱급수의 상으로 전개하면,
:
가 된다.
급수의 반전을 수행하면,
:
를 얻는다.
τ의 허수가 1/2 sqrt(3) 이상인 경우로 귀결시키면 되므로, ''q''의 절대값은 exp(-1/2 sqrt(3) π) ~ 0.0658 이하인 경우만 고려하면 된다. 이 값은 작기 때문에 위의 급수는 빠르게 수렴하여, 간단하게 ''q''의 값을 계산할 수 있다.
7. 네빌 세타 함수를 이용한 정의
야코비 타원 함수는 네빌 세타 함수를 사용하여 매우 간단하게 정의할 수 있다.[13]
:
야코비 타원 함수의 복잡한 곱셈을 단순화하는 것은 종종 이러한 항등식을 사용하여 더 쉽게 만들 수 있다.
8. 야코비 변환
야코비 타원 함수는 모듈러스(m)에 따라 다양한 형태로 변환될 수 있다. 이러한 변환은 야코비 허수 변환과 야코비 실수 변환으로 나뉜다.[5]
야코비 허수 변환은 허수 변수 ''i u''의 함수를 ''m'' 매개변수의 다른 값으로 표현하는 관계식이다.[12] 주요 함수에 대한 야코비 허수 변환은 다음과 같다.
- cn영어(u, m) = nc영어(i u, 1-m)
- sn영어(u, m) = -i sc영어(i u, 1-m)
- dn영어(u, m) = dc영어(i u, 1-m)
일반적으로 변환식은 와 같이 쓸 수 있다.
야코비 실수 변환과 허수 변환은 결합되어 더 간단한 세 가지 변환을 생성할 수 있다.[5] 실수 변환과 허수 변환은 6개의 변환 그룹(D3 또는 무조화군)에 속하는 두 가지 변환이다.
- : 실수 변환에서 파라미터 ''m''에 대한 변환
- : 허수 변환에서 ''m''의 변환
다른 변환들은 이 두 가지 기본 변환을 연속적으로 적용하여 구성할 수 있으며, 세 가지 가능성이 추가로 나타난다.
:
이 다섯 가지 변환은 항등 변환(''μ''''U''(''m'') = ''m'')과 함께 6개의 원소를 가진 그룹을 형성한다. 야코비 타원 함수와 관련하여 일반적인 변환은 단 세 개의 함수를 사용하여 표현할 수 있다.
:
:
:
여기서 ''i'' = U, I, IR, R, RI, 또는 RIR는 변환을 식별하며, γi는 이 세 함수에 공통적으로 적용되는 곱셈 계수이고, 프라임 기호는 변환된 함수를 나타낸다.
다음 표는 세 가지 ps 함수, 변환된 ''m''값, 그리고 여섯 가지 변환 각각에 대한 변환된 함수 이름을 나열한다.[5] (일반적으로, ''k''2 = ''m'', 1 − ''k''2 = ''k''12 = ''m''′ 이고 인자()는 생략)
야코비 변환의 가치는 임의의 실수 값 매개변수 ''m''을 가진 야코비 타원 함수 집합을
쌍곡선 함수는 허수 인수를 가진 원형 삼각함수에 비례하므로, 야코비 함수는 m=1일 때 쌍곡선 함수가 된다.[5]
8. 2. 야코비 실수 변환
야코비의 실수 변환과 허수 변환은 결합되어 더 간단한 세 가지 변환을 생성할 수 있다.[5] 실수 변환과 허수 변환은 6개의 변환 그룹(D3 또는 무조화군)에 속하는 두 가지 변환이다.실수 변환에서 파라미터 ''m''에 대한 변환을 μR(''m'') = 1/''m'', 허수 변환에서 ''m''의 변환을 μI(''m'') = 1-''m'' = ''m''′ 이라 하면, 다른 변환들은 이 두 가지 기본 변환을 연속적으로 적용하여 구성할 수 있으며, 세 가지 가능성이 추가로 나타난다.
:
\begin{align}
\mu_{IR}(m)&=&\mu_I(\mu_R(m))&=&-m'/m \\
\mu_{RI}(m)&=&\mu_R(\mu_I(m))&=&1/m' \\
\mu_{RIR}(m)&=&\mu_R(\mu_I(\mu_R(m)))&=&-m/m'
\end{align}
이 다섯 가지 변환은 항등 변환(''μ''''U''(''m'') = ''m'')과 함께 6개의 원소를 가진 그룹을 형성한다. 야코비 타원 함수와 관련하여 일반적인 변환은 단 세 개의 함수를 사용하여 표현할 수 있다.
:
:
:
여기서 ''i'' = U, I, IR, R, RI, 또는 RIR는 변환을 식별하며, γi는 이 세 함수에 공통적으로 적용되는 곱셈 계수이고, 프라임 기호는 변환된 함수를 나타낸다. 나머지 아홉 개의 변환된 함수는 위의 세 함수로부터 구성될 수 있다. cs, ns, ds 함수가 변환을 나타내도록 선택된 이유는 다른 함수들이 이 세 함수의 비율이 될 것이고(역수를 제외하고) 곱셈 계수가 상쇄되기 때문이다.
다음 표는 세 가지 ps 함수, 변환된 ''m''값, 그리고 여섯 가지 변환 각각에 대한 변환된 함수 이름을 나열한다.[5] (일반적으로, ''k''2 = ''m'', 1 − ''k''2 = ''k''12 = ''m''′ 이고 인자(
예를 들어 RIR 변환에 대한 표를 만들 수 있다.[13] 변환은 일반적으로
야코비 변환의 가치는 임의의 실수 값 매개변수 ''m''을 가진 야코비 타원 함수 집합을
8. 3. 기타 야코비 변환
야코비의 실수 변환과 허수 변환은 결합되어 더 간단한 세 가지 변환을 생성할 수 있다.[5] 실수 변환과 허수 변환은 6개의 변환 그룹(D3 또는 무조화군)에 속하는 두 가지 변환이다.
다른 변환들은 이 두 가지 기본 변환을 연속적으로 적용하여 구성할 수 있으며, 세 가지 가능성만 더 얻을 수 있다.
:
\begin{align}
\mu_{IR}(m)&=&\mu_I(\mu_R(m))&=&-m'/m \\
\mu_{RI}(m)&=&\mu_R(\mu_I(m))&=&1/m' \\
\mu_{RIR}(m)&=&\mu_R(\mu_I(\mu_R(m)))&=&-m/m'
\end{align}
이 다섯 가지 변환은 항등 변환(''μ''''U''(''m'') = ''m'')과 함께 6개의 원소를 가진 그룹을 형성한다. 야코비 타원 함수와 관련하여 일반적인 변환은 단 세 개의 함수를 사용하여 표현할 수 있다.
:
:
:
여기서 ''i'' = U, I, IR, R, RI, 또는 RIR는 변환을 식별하며, γi는 이 세 함수에 공통적으로 적용되는 곱셈 계수이고, 프라임 기호는 변환된 함수를 나타낸다. 다른 아홉 개의 변환된 함수는 위의 세 함수로부터 구성될 수 있다. cs, ns, ds 함수가 변환을 나타내도록 선택된 이유는 다른 함수들이 이 세 함수의 비율이 될 것이고(역수를 제외하고) 곱셈 계수가 상쇄되기 때문이다.
다음 표는 세 가지 ps 함수, 변환된 ''m''s, 그리고 여섯 가지 변환 각각에 대한 변환된 함수 이름을 나열한다.[5] (일반적으로, ''k''2 = ''m'', 1 − ''k''2 = ''k''12 = ''m''′ 이고 인자(
예를 들어 RIR 변환에 대한 표를 만들 수 있다.[13] 변환은 일반적으로
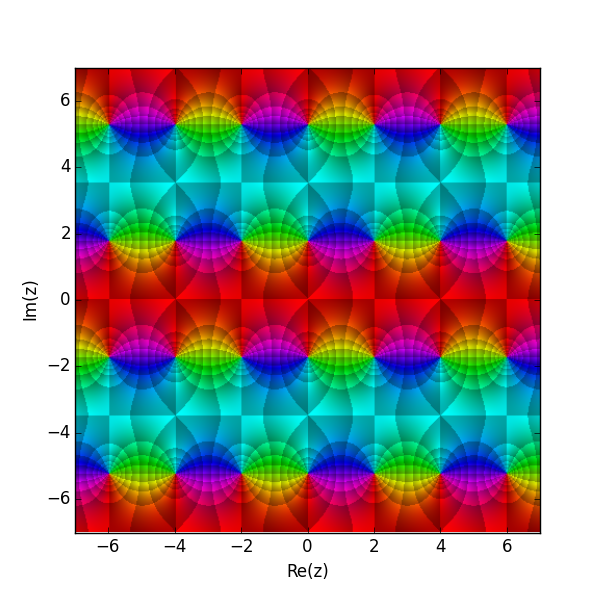
9. 야코비 쌍곡선
복소수를 도입하면, 타원은 연관된 쌍곡선을 갖는다. 아래의 표는 모든 야코비 타원 함수 pq(u,m)에 대한 식을 변수 (''x'',''y'',''r'') 및 (''φ'', dn)에 대해 요약한 것이다. 여기서
10. 소함수
기본 야코비 타원함수 sn, cn, dn의 비는 다음과 같이 정의한다.
함수 이름의 두 글자 순서를 바꾸면 위 세 함수의 역수가 된다.
:
\operatorname{ns}(u) = \frac{1}{\operatorname{sn}(u)}, \qquad \operatorname{nc}(u) = \frac{1}{\operatorname{cn}(u)}, \qquad
\operatorname{nd}(u) = \frac{1}{\operatorname{dn}(u)}.
마찬가지로, 세 개의 기본 함수의 비율은 분자의 첫 글자와 분모의 첫 글자를 차례로 나타낸다.
:
\operatorname{sc}(u) = \frac{\operatorname{sn}(u)}{\operatorname{cn}(u)}, \qquad
\operatorname{sd}(u) = \frac{\operatorname{sn}(u)}{\operatorname{dn}(u)}, \qquad \operatorname{dc}(u) = \frac{\operatorname{dn}(u)}{\operatorname{cn}(u)}, \qquad \operatorname{ds}(u) = \frac{\operatorname{dn}(u)}{\operatorname{sn}(u)}, \qquad \operatorname{cs}(u) = \frac{\operatorname{cn}(u)}{\operatorname{sn}(u)}, \qquad
\operatorname{cd}(u) = \frac{\operatorname{cn}(u)}{\operatorname{dn}(u)}.
더 간결하게 표현하면, 다음과 같다.
:
여기서 p와 q는 s, c, d 중 임의의 문자이다.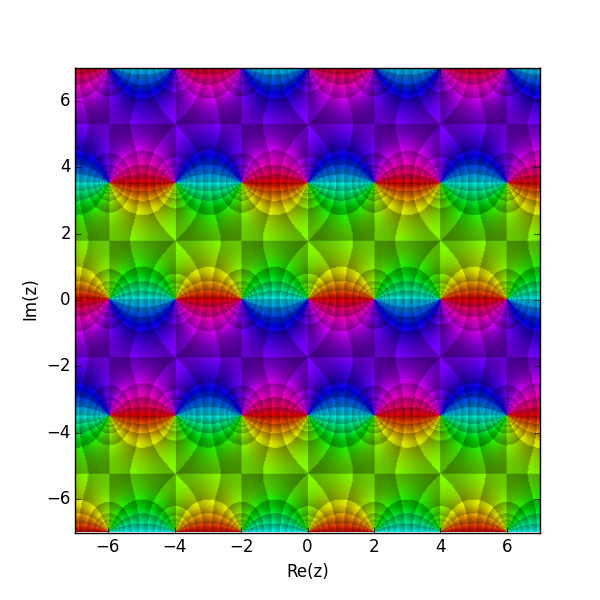
(이 표기법은 크리스토프 구더만과 글레이셔에 의한 것으로, 야코비의 원래 표기법에는 없다.)
11. 주기성, 극점, 유수
복소 평면에서 변수 ''u''에 대해 야코비 타원 함수는 극(및 영점)의 반복 패턴을 형성한다.[5] 각 함수 pq(''u'',''m'')는 극과 영점의 위치가 바뀌는 "역함수"(곱셈적 의미) qp(''u'',''m'')을 갖는다.[5] 반복 주기는 보통 실수 및 허수 방향에서 다르므로 "이중 주기"라는 용어를 사용하여 이를 설명한다.[5]
야코비 타원 함수의 이중 주기는 다음과 같이 표현할 수 있다.
:
여기서 ''α''와 ''β''는 임의의 정수 쌍이고, ''K''(⋅)는 사분의 일 주기라고도 불리는 제1종 완전 타원 적분이다. (−1)''γ''에서 음의 단일성(''γ'')의 거듭제곱은 다음 표와 같다.
인자 (−1)''γ''가 −1과 같으면, 위 방정식은 준주기성을 나타낸다. 1과 같으면 완전 주기성을 나타낸다. 예를 들어, α가 짝수일 때 α만 포함하는 항목의 경우 위 방정식은 완전 주기성을 나타내며, 함수는 4''K''(''m'')과 2''iK''(1 − ''m'')의 완전 주기를 갖는다. ''β''만 포함하는 항목이 있는 함수는 2K(m) 및 4''iK''(1 − ''m'')의 완전 주기를 가지며, α + β를 갖는 함수는 4''K''(''m'') 및 4''iK''(1 − ''m'')의 완전 주기를 갖는다.[5]
각 함수의 역은 대각선과 반대이며, 극과 영점이 교환된 동일한 크기의 단위 셀을 갖는다. (0,0), (''K'',0), (0,''K''′) 및 (''K'',''K''′)로 형성된 보조 사각형의 극과 영점 배치는 위에 설명된 극과 영점 배치 설명과 일치한다. 극을 나타내는 흰색 타원의 크기는 해당 극의 잔류물의 절대값의 대략적인 척도이다. 원점에 가장 가까운 극(즉, 보조 사각형 내)의 잔류물은 다음 표에 나열되어 있다.[5]
2''K''만큼 위로 이동하거나 2''K''′만큼 오른쪽으로 이동한 극은 부호가 반전된 동일한 값을 가지며, 대각선 맞은편에 있는 극은 동일한 값을 갖는다. 왼쪽 및 하단 모서리의 극과 영점은 단위 셀의 일부로 간주되지만, 상단 및 오른쪽 모서리의 극과 영점은 그렇지 않다.[5]
12. 특수값
:
야코비 진폭의 경우,
일반적으로 p, q가 모두 d가 아니면
13. 항등식
야코비 타원함수는 삼각함수와 유사하게 다음과 같은 항등식들을 만족시킨다.
:
:
이들 방정식으로 정해지는 두 이차 곡면의 공통 부분은 타원 곡선이며, (cn, sn, dn)은 타원 곡선의 매개변수 표현을 제공한다.
야코비 타원 함수가 갖는 대수적인 관계식은 다음과 같다.
:
:
13. 1. 반각 공식
야코비 타원 함수의 반각 공식은 다음과 같이 유도할 수 있다.:
:
:
13. 2. K 공식
'''K의 절반 공식''''''K의 삼분 공식'''
:
''x''3를 얻기 위해, 모듈러스의 아크탄젠트의 두 배의 탄젠트를 취한다.
또한 이 방정식은 K의 삼분의 sn-값을 생성한다.
:
:
이러한 방정식은 야코비 타원함수에 대한 다른 값을 생성한다.
:
:
'''K의 오분 공식'''
다음 방정식은 다음과 같은 해를 갖는다.
:
:
sn-값을 얻기 위해, 해 x를 다음 식으로 대입한다.
:
:
13. 3. 함수 제곱 간의 관계
야코비 타원함수는 삼각함수와 유사한, 다음과 같은 항등식들을 만족시킨다.:
:
두 가지 기본 관계식으로부터 함수 제곱 간의 관계를 유도할 수 있다. (인수(u, m)는 생략)
:
:
여기서 ''m + m' ''= 1이다. ''nq'' 형태의 함수를 곱하면 더 일반적인 방정식이 생성된다.
:
:
''q'' = ''d''일 때, 이는 삼각법적으로 단위 원(
:
- \operatorname{dn}^2{}+m'= -m\operatorname{cn}^2 = m\operatorname{sn}^2-m
:
- m'\operatorname{nd}^2{}+m'= -mm'\operatorname{sd}^2 = m\operatorname{cd}^2-m
:
m'\operatorname{sc}^2{}+m'= m'\operatorname{nc}^2 = \operatorname{dc}^2-m
:
\operatorname{cs}^2{}+m'=\operatorname{ds}^2=\operatorname{ns}^2-m
위 식에서,
:
- \operatorname{dn}^2(u)+m_1= -m\;\operatorname{cn}^2(u) = m\;\operatorname{sn}^2(u)-m
:
- m_1\;\operatorname{nd}^2(u)+m_1= -mm_1\;\operatorname{sd}^2(u) = m\;\operatorname{cd}^2(u)-m
:
m_1\;\operatorname{sc}^2(u)+m_1= m_1;\operatorname{nc}^2(u) = \operatorname{dc}^2(u)-m
:
\operatorname{cs}^2(u)+m_1=\operatorname{ds}^2(u)=\operatorname{ns}^2(u)-m
여기서, ''m'' + ''m''1 = 1 이고 ''m'' = ''k''2이다.
pq2 · qp2 = 1 및 pq = pr / qr을 사용하여 제곱에 대한 추가적인 관계식을 얻을 수 있다. 여기서 p, q, r은 s, c, d, n의 임의의 문자이며, ss = cc = dd = nn = 1로 한다.
13. 4. 덧셈 정리
매개변수 ''m''을 생략하면, 야코비 타원 함수에 대한 덧셈 공식은 다음과 같다.[1]:
\begin{align}
\operatorname{cn}(x+y) & =
{\operatorname{cn}(x)\;\operatorname{cn}(y)
- \operatorname{sn}(x)\;\operatorname{sn}(y)\;\operatorname{dn}(x)\;\operatorname{dn}(y)
\over {1 - k^2 \;\operatorname{sn}^2 (x) \;\operatorname{sn}^2 (y)}}, \\[8pt]
\operatorname{sn}(x+y) & =
{\operatorname{sn}(x)\;\operatorname{cn}(y)\;\operatorname{dn}(y) +
\operatorname{sn}(y)\;\operatorname{cn}(x)\;\operatorname{dn}(x)
\over {1 - k^2 \;\operatorname{sn}^2 (x)\; \operatorname{sn}^2 (y)}}, \\[8pt]
\operatorname{dn}(x+y) & =
{\operatorname{dn}(x)\;\operatorname{dn}(y)
- k^2 \;\operatorname{sn}(x)\;\operatorname{sn}(y)\;\operatorname{cn}(x)\;\operatorname{cn}(y)
\over {1 - k^2 \;\operatorname{sn}^2 (x)\; \operatorname{sn}^2 (y)}}.
\end{align}
이 공식들을 사용하여, 두 이차 곡면의 교차점인 타원 곡선 위의 점들에 대한 군법칙을 정의할 수 있다.[1]
야코비 엡실론 함수와 zn 함수는 다음과 같은 준 덧셈 정리를 만족한다.[1]
:
\operatorname{zn}(x+y,m)&=\operatorname{zn}(x,m)+\operatorname{zn}(y,m)-m\operatorname{sn}(x,m)\operatorname{sn}(y,m)\operatorname{sn}(x+y,m).\end{align}
이중각 공식은 위 식에서
:
여기서[1]
14. 비선형 상미분 방정식의 해로서의 야코비 타원 함수
야코비 타원 함수는 다음과 같은 비선형 상미분 방정식의 해로 나타낼 수 있다.[5]
\mathrm{sn}\,(x) 는 다음 미분 방정식의 해이다.
:
:또는
:
\mathrm{cn}\,(x) 는 다음 미분 방정식의 해이다.
:
:또는
:
\mathrm{dn}\,(x) 는 다음 미분 방정식의 해이다.
:
:또는
:
14. 1. 첫 번째 변수에 대한 미분
세 가지 기본 야코비 타원 함수 sn(''z''), cn(''z''), dn(''z'')의 미분 (첫 번째 변수에 대한 미분,:
:
:
이것들을 사용하여 다른 모든 함수의 미분을 도출할 수 있다. (인수 (u, m)은 생략)
위의 덧셈 정리를 사용하고 0 < ''m'' < 1인 주어진 ''m''에 대해, 주요 함수는 다음 비선형 상미분 방정식의 해이다.
\operatorname{sn}(x) 는 미분 방정식\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + (1+m) y - 2 m y^3 = 0 와\left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-m y^2) 를 푼다.\operatorname{cn}(x) 는 미분 방정식\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + (1-2m) y + 2 m y^3 = 0 와\left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-m + my^2) 를 푼다.\operatorname{dn}(x) 는 미분 방정식\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} - (2 - m) y + 2 y^3 = 0 와\left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (y^2 - 1) (1 - m - y^2) 를 푼다.
14. 2. 두 번째 변수에 대한 미분
첫 번째 변수:
\frac{\mathrm d}{\mathrm dm}\operatorname{cn}(z)&=\frac{\operatorname{sn}(z)\operatorname{dn}(z)((m-1)z+\mathcal{E}(z)-m\operatorname{sn}(z)\operatorname{cd}(z))}{2m(1-m)},\\
\frac{\mathrm d}{\mathrm dm}\operatorname{dn}(z)&=\frac{\operatorname{sn}(z)\operatorname{cn}(z)((m-1)z+\mathcal{E}(z)-\operatorname{dn}(z)\operatorname{sc}(z))}{2(1-m)},\\
\frac{\mathrm d}{\mathrm dm}\mathcal{E}(z)&=\frac{\operatorname{cn}(z)(\operatorname{sn}(z)\operatorname{dn}(z)-\operatorname{cn}(z)\mathcal{E}(z))}{2(1-m)}-\frac{z}{2}\operatorname{sn}(z)^2.\end{align}
15. 노름에 관한 전개
노메를
:
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1-q^{2n+1}} \sin ((2n+1)v),
:
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1+q^{2n+1}} \cos ((2n+1)v),
:
\sum_{n=1}^\infty \frac{q^{n}}{1+q^{2n}} \cos (2nv),
:
이때,
이변수 거듭제곱 급수 전개는 Schett에 의해 발표되었다.[16]
16. 고속 계산
세타 함수 비율은 야코비 타원 함수를 효율적으로 계산하는 방법을 제공한다. 산술-기하 평균과 란덴 변환을 기반으로 하는 다른 방법이 있다.[7]
야코비 진폭의 계산을 피하면서 산술-기하 평균을 통해 야코비 타원 함수를 빠르게 계산하는 방법은 허버트 E. 살저(Herbert E. Salzer)가 제시했다.[18]
다음과 같이 정의한다.
:
:
그리고 다음을 설정한다.
:
y_{N-1}&=y_N+\frac{a_Nc_N}{y_N}\\
y_{N-2}&=y_{N-1}+\frac{a_{N-1}c_{N-1}}{y_{N-1}}\\
\vdots&=\vdots\\
y_0&=y_1+\frac{m}{4y_1}.\end{align}
그러면 다음이 성립한다.
:
\operatorname{cn}(u,m)&=\sqrt{1-\frac{1}{y_0^2}}\\
\operatorname{dn}(u,m)&=\sqrt{1-\frac{m}{y_0^2}}\end{align}
(
문헌에서 발견된 야코비 타원 사인 함수를 빠르게 수렴하는 고속 계산을 위한 또 다른 방법은 다음과 같다.[19]
다음과 같이 정의한다.
:
&a_0 = u &b_0 = \frac{1-\sqrt{1-m}}{1+\sqrt{1-m}} \\
&a_1 = \frac{a_0}{1+b_0} &b_1 = \frac{1-\sqrt{1-b^2_0 }}{1+\sqrt{1-b^2_0}}\\
&\vdots = \vdots &\vdots = \vdots \\
&a_n = \frac{a_{n-1}}{1+b_{n-1}} &b_n = \frac{1-\sqrt{1-b^2_{n-1}}}{1+\sqrt{1-b^2_{n-1}}}\\
\end{align}
그리고 다음을 설정한다.
:
y_{n+1} &= \sin(a_n) \\
y_{n} &= \frac{y_{n+1}(1+b_n)}{1+y^2_{n+1}b_n} \\
\vdots &= \vdots\\
y_0 &= \frac{y_1(1+b_0)}{1+y^2_1b_0} \\
\end{align}
그러면 다음이 성립한다.
:
17. 쌍곡선 함수를 이용한 근사
- sn(''u''):
\operatorname{sn} (u,m)\approx \tanh (u)+\frac{1}{4}m'(\sinh (u)\cosh (u) -u)\operatorname{sech}^2 (u). - cn(''u''):
\operatorname{cn} (u,m)\approx \operatorname{sech} (u)-\frac{1}{4} m'(\sinh (u)\cosh (u) -u)\tanh (u) \operatorname{sech} (u). - dn(''u''):
\operatorname{dn} (u,m) \approx \operatorname{sech} (u)+\frac{1}{4} m'(\sinh (u)\cosh(u) +u)\tanh (u) \operatorname{sech} (u) .
야코비 진폭의 경우,
:
18. 연분수
실수
:
\begin{align}
&\frac{\textrm{dn}\left((p/2-a)\tau K\left[\frac{p\tau}{2}\right];k\left(\frac{p\tau}{2}\right)\right)}{\sqrt{k'\left(\frac{p\tau}{2}\right)}} = \frac{\sum^\infty_{n=-\infty}q^{p/2 n^2+(p/2-a)n}}{\sum^\infty_{n=-\infty}(-1)^nq^{p/2 n^2+(p/2-a)n}}\\[4pt]
={}&-1+\frac{2}{1-{}} \, \frac{q^a+q^{p-a}}{1-q^p+{}} \, \frac{(q^a+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}} \, \frac{q^p(q^a+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}} \, \frac{q^{2p}(q^a+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}\cdots
\end{align}
타원 모듈러스
:
:
:
:
:
19. 역함수
야코비 타원 함수의 역함수는 역삼각 함수와 유사하게 정의된다. 예를 들어,
\operatorname{arcsn}(x,m) = \int_0^x \frac{\mathrm{d}t}{\sqrt{(1-t^2)(1-mt^2)}} \operatorname{arccn}(x,m) =\int_x^1 \frac{\mathrm{d}t}{\sqrt{(1-t^2)(1-m+mt^2)}} \operatorname{arcdn}(x,m) = \int_x^1 \frac{\mathrm{d}t}{\sqrt{(1-t^2)(t^2+m-1)}}
20. 지도 투영법
퍼스 퀸컨셜 도법은 야코비 타원 함수를 사용하는 지도 투영법이다. 또한 각국에서 표준적으로 사용되는 가우스-크뤼거 도법에서도 투영식을 야코비 타원 함수로 나타낼 수 있다.
참조
[1]
서적
Elliptic Functions
Cambridge University Press
[2]
논문
The Analyticity of Jacobian Functions with Respect to the Parameter k
https://www.jstor.or[...]
2003
[3]
웹사이트
NIST Digital Library of Mathematical Functions (Release 1.0.17)
http://dlmf.nist.gov[...]
National Institute of Standards and Technology
2018-02-26
[4]
웹사이트
cplot, Python package for plotting complex-valued functions
https://github.com/n[...]
[5]
서적
Jacobian Elliptic Functions
https://archive.org/[...]
Oxford University Press
1944
[6]
문서
[7]
논문
Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean
https://epubs.siam.o[...]
1989-11
[8]
간행물
Jacobian Elliptic Functions
[9]
간행물
Elliptic Integrals
[10]
서적
A Course of Modern Analysis
Cambridge University Press
1927
[11]
논문
The Arithmetic-Geometric Mean of Gauss
https://www.research[...]
1984-01
[12]
서적
A Course in Modern Analysis
https://archive.org/[...]
The MacMillan Co.
1940
[13]
웹사이트
Introduction to the Jacobi elliptic functions
http://functions.wol[...]
Wolfram Research, Inc.
2018-01-07
[14]
웹사이트
Elliptic Functions: Complex Variables
https://paramanands.[...]
[15]
서적
A Course of Modern Analysis
Cambridge University Press
1927
[16]
논문
Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions
[17]
문서
[18]
논문
Quick calculation of Jacobian elliptic functions
1962-07
[19]
논문
The Even- and Odd-Mode Capacitance Parameters for Coupled Lines in Suspended Substrate
https://ieeexplore.i[...]
1971-05-05
[20]
간행물
Jacobian Elliptic Functions
[21]
간행물
Jacobian Elliptic Functions
[22]
간행물
Evaluations of series related to Jacobi elliptic functions
https://www.research[...]
2020
[23]
서적
Analytic Theory of Continued Fractions
Van Nostrand
1948
[24]
서적
Die Lehre von den Kettenbruchen
B.G. Teubner
1957
[25]
간행물
"§22.15 Inverse Functions"
[26]
웹사이트
The AMath and DAMath Special Functions: Reference Manual and Implementation Notes
http://www.wolfgang-[...]
2013-07-17
[27]
서적
Handbook of Elliptic Integrals for Engineers and Scientists
Springer-Verlag
1971
[28]
논문
Power series for inverse Jacobian elliptic functions
https://www.ams.org/[...]
2013-07-17
[29]
문서
http://nbviewer.ipyt[...]
[30]
간행물
"§22.15 Inverse Functions"
[31]
웹사이트
The AMath and DAMath Special Functions: Reference Manual and Implementation Notes
http://www.wolfgang-[...]
2013-07-17
[32]
논문
Power series for inverse Jacobian elliptic functions
http://www.ams.org/j[...]
2013-07-17
[33]
서적
http://archive.org/d[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
