유한요소법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 기본 개념
- 3.1. 주요 단계
4. 기술적 논의
5. 다양한 유한요소법
6. 유한차분법과의 비교
7. 응용 분야
8. 소프트웨어
9. 같이 보기
참조

1. 개요

유한요소법은 복잡한 공학 문제를 해결하기 위해 개발된 수치 해석 방법이다. 1940년대에 시작되어, 전체 영역을 작은 요소로 나누어 각 요소 내에서 해를 근사하는 방식으로 작동한다. 유한요소법은 구조 해석, 전산 유체 역학 등 다양한 분야에 적용되며, 복잡한 형상과 경계 조건을 다룰 수 있다는 장점이 있다. 다양한 요소 종류, 형상 함수, 행렬 표현을 사용하며, 상용 및 오픈 소스 소프트웨어가 개발되어 널리 사용된다.

더 읽어볼만한 페이지

순차 방정식 - 유한요소해석
유한요소해석은 대상물을 유한한 요소로 나누어 모델링하고 등가 방정식을 적용해 시스템 거동을 예측하는 수치해석 기법으로, 다양한 분야에 응용되며 컴퓨터 시뮬레이션을 통해 복잡한 시스템의 해법을 결정하는 데 사용된다.
유한요소법 - 유한요소해석
유한요소해석은 대상물을 유한한 요소로 나누어 모델링하고 등가 방정식을 적용해 시스템 거동을 예측하는 수치해석 기법으로, 다양한 분야에 응용되며 컴퓨터 시뮬레이션을 통해 복잡한 시스템의 해법을 결정하는 데 사용된다.
유한요소법 - 콤솔 멀티피직스
콤솔 멀티피직스는 전기, 기계, 유체, 화학 등 다양한 물리 현상을 유한 요소 해석으로 시뮬레이션하는 FEA 소프트웨어로, CAD, MATLAB, Excel 등과의 연동을 지원한다.
연속체역학 - 온도
온도는 물체의 뜨겁고 차가운 정도를 나타내는 물리량으로, 열역학적으로는 에너지 이동 방향으로 정의되며, 미시적으로는 분자 운동 에너지의 평균값으로 정의되고, 화학 반응 속도와 생명체에 큰 영향을 미친다.
연속체역학 - 밀도
밀도는 단위 부피당 질량을 나타내는 물리량으로 질량을 부피로 나눈 값으로 계산되며, 온도와 압력에 따라 변하고, 진밀도, 겉보기밀도, 부피밀도, 탭밀도 등 여러 종류가 있고, 고대 그리스 시대부터 발전해왔다.

유한요소법

2. 역사

알렉산드르 흐렌니코프(Хренников^ru)와 리하르트 쿠란트가 1940년대에 유한요소법의 초기 개발을 시작했다.^[5]^[6]^[7] 이들은 연속적인 범위를 가진 문제를 요소망(mesh^영어)이라는 세분화된 범위로 나누는 방식을 사용했다. 흐렌니코프는 범위를 격자로, 쿠란트는 타원 적분을 위한 편미분 방정식을 유한한 삼각형 영역으로 나누어 문제를 해결했다. 특히 쿠란트는 원기둥에서의 뒤틀림 문제를 해결하기 위해 이 방법을 사용했다.^[7]

1950년대 중후반부터 유한요소법은 항공 공학과 구조해석에 주로 사용되며 발전하기 시작했다.^[5] 1960년대에는 도시공학에 사용되었으며,^[5] 1973년에는 ''An Analysis of The Finite Element Method''^[12] 출판을 통해 물리적 시스템을 수치적으로 모델링하는 응용수학의 한 분야로 자리 잡았다.

슈투트가르트 대학교의 J. H. 아르기리스, 캘리포니아 대학교 버클리의 R. W. 클라우, 스완지 대학교의 O. C. 젠키에비츠 등의 연구를 통해 1960년대와 1970년대에 유한요소법은 더욱 발전했다. 이 시기에는 NASA가 NASTRAN의 최초 버전을 후원했고, 캘리포니아 대학교 버클리는 SAP IV^[10]를 공개하고, 이후 OpenSees를 널리 이용할 수 있게 했다. 노르웨이에서는 선박 분류 협회인 Det Norske Veritas (현재 DNV GL)가 1969년에 선박 분석을 위해 Sesam을 개발했다.^[11]

3. 기본 개념

유한요소법(FEM)은 복잡한 문제를 요소(element)라고 불리는 작은 부분으로 나누어 해결하는 방법이다. 전체 영역을 단순한 형태의 작은 요소로 나누고, 각 요소 내에서 해를 기저 함수들의 선형 결합으로 근사한다. 이렇게 근사된 요소 방정식들을 조합하여 전체 시스템에 대한 방정식을 구성하고, 이를 풀어 전체 문제의 해를 구한다.^[3]

전체 도메인을 더 간단한 부분으로 나누면 다음과 같은 장점이 있다.^[3]

복잡한 형상을 정확하게 표현할 수 있다.
서로 다른 재료의 특성을 쉽게 포함할 수 있다.
전체 해를 쉽게 표현할 수 있다.
국소적인 효과를 파악할 수 있다.

이산화를 위해서는 기저를 선택해야 한다. 1차원의 경우, 각 제어점

x_k

에 대해

x_k

에서 값이 1이고 나머지 모든 점에서는 0인 분할 선형 함수

v_k

를 선택한다. 2차원의 경우에도 각 정점

x_k

에 대해

x_k

에서 값이 1이고 나머지 모든 정점에서는 0인 기저 함수

v_k

를 선택한다.

"유한 요소법"에서 "요소"라는 단어는 도메인의 삼각형, 분할 선형 기저 함수, 또는 둘 다를 의미할 수 있다. 곡선 도메인에 관심이 있는 경우 삼각형을 곡선 요소로 바꾸고 요소를 곡선형으로 설명할 수도 있다.

고차 분할 다항식 기저 함수를 사용하는 방법에는 hp-FEM 및 스펙트럼 FEM이 있다. 더 발전된 구현(적응형 유한 요소 방법)은 결과의 품질을 평가하고, 해를 구하는 동안 메쉬를 수정하여 정확도를 높인다. 메쉬 적응성은 노드 이동, 요소 세분화, 기저 함수의 차수 변경 등 다양한 기술을 활용할 수 있다.

유한 요소법은 변분법을 사용하여 오차 함수를 최소화함으로써 해를 근사한다. 영역 전체를 더 단순한 부분으로 세분화하면 복잡한 형상 표현, 이종 재료 특성 부여, 전체 솔루션 표현 용이, 국소적 효과 파악 등의 이점이 있다.^[41]^[42]^[43]

계산을 위해 소영역으로 분할하는 것을 "메쉬를 생성한다"라고 하며, 메쉬의 적절성은 해석 결과의 정확성에 큰 영향을 미친다.

3. 1. 주요 단계

유한요소법의 일반적인 접근 방식은 다음과 같다.

1. 문제의 영역을 하위 도메인(요소)으로 나누고, 각 하위 도메인은 원래 문제에 대한 요소 방정식 집합으로 표현한다.

2. 모든 요소 방정식 집합을 최종 계산을 위한 전역 방정식 시스템으로 체계적으로 재결합한다.

전역 방정식 시스템은 알려진 해법 기술을 사용하며, 수치적 해답을 얻기 위해 원래 문제의 초기값에서 계산할 수 있다.^[3]

첫 번째 단계에서, 요소 방정식은 연구할 원래 복잡한 방정식(주로 편미분 방정식)을 국소적으로 근사하는 간단한 방정식이다. 이 근사는 갈레르킨 방법을 통해 이루어지는데, 이는 잔차와 가중 함수의 내적의 적분을 구성하고, 그 적분을 0으로 설정하는 과정이다. 이를 통해 PDE에서 모든 공간 미분을 제거하여, 정상 상태 문제에 대한 대수 방정식 집합이나 과도 문제에 대한 상미분 방정식 집합으로 근사한다.

두 번째 단계에서는 하위 도메인의 국소 노드에서 도메인의 전역 노드로 좌표를 변환하여 요소 방정식에서 전역 방정식 시스템을 생성한다. 이 공간 변환에는 참조 좌표계에 대한 방향 조정이 포함되며, 주로 FEM 소프트웨어를 사용하여 수행된다.

FEM의 실제 적용은 유한 요소 분석(FEA)이라고 불리며, 공학에서 공학 분석을 위한 계산 도구로 사용된다. FEA는 메쉬 생성 기술과 FEM 알고리즘으로 코딩된 소프트웨어를 사용하여 복잡한 문제를 더 작은 요소로 나누어 해석한다. FEA는 도메인이 복잡하거나, 변경될 때, 정밀도가 다를 때, 또는 솔루션에 매끄러움이 없을 때 유용하다.^[4]

유한 요소법은 변분법, 이산화 전략, 해법 알고리즘, 후처리 절차로 특징지어진다. 변분법에는 갈레르킨 방법, 불연속 갈레킨 방법, 혼합 방법 등이 있다. 이산화 전략은 유한 요소 메쉬 생성, 참조 요소에 대한 기저 함수 정의, 참조 요소를 메쉬의 요소에 매핑하는 절차를 포함하며, h-버전, p-버전, hp-버전, x-FEM, 등기하 해석 등이 있다. 수치적 해법 알고리즘은 직접 해법과 반복 해법으로 나뉘며, 후처리 절차는 유한 요소 해에서 관심 데이터를 추출하고 오차를 추정한다.

4. 기술적 논의

유한요소법(FEM)은 주어진 문제를 더 작은 요소로 나누어 해결하는 수치 해석 기법이다. 이 과정은 크게 두 단계로 나뉜다. 첫 번째 단계는 원래의 경계값 문제(BVP)를 변분법 형태로 바꾸는 것이다. 두 번째 단계는 이 변분법 형태를 이산화하여 유한 차원의 선형 문제로 만드는 것이다.

1차원 문제 P1과 2차원 문제 P2를 예로 들어 설명한다.
P1 (1차원 문제):: $\mbox{P1 }:\begin{cases}u''=f \mbox{ in } (0,1), \\u(0)=u(1)=0,\end{cases}$

여기서 $f$ 는 주어진 값이고, $u$ 는 $x$ 의 미지 함수이며, $u''$ 는 $x$ 에 대한 $u$ 의 2차 미분이다.
P2 (2차원 문제, 디리클레 문제):: $\mbox{P2 }:\begin{cases}u_{xx}+u_{yy}=f & \mbox{ in } \Omega, \\u=0 & \mbox{ on } \partial \Omega,\end{cases}$

여기서 $\Omega$ 는 $(x,y)$ 평면상의 영역이고, $\partial \Omega$ 는 그 경계이다. $u_{xx}$ 와 $u_{yy}$ 는 각각 $x$ 와 $y$ 에 대한 2차 미분을 나타낸다.

P1 문제는 부정적분을 통해 직접 풀 수 있지만, 이는 고차원 문제에는 적용하기 어렵다. 따라서 유한요소법을 사용하여 P1 문제를 해결하고, 이를 P2 문제로 확장한다.

첫 번째 단계는 P1과 P2를 변분법 평형 상태로 변환하는 것이다. 만약 $u$ 가 P1의 해이고, $v$ 가 경계 조건( $x=0,1$ 에서 $v=0$ )을 만족하는 매끄러운 함수라면, 다음 식이 성립한다.

(1) $\int_0^1 f(x)v(x) \, dx = \int_0^1 u''(x)v(x) \, dx.$

부분 적분을 사용하여 (1) 식의 우변을 정리하면 다음과 같다.

(2) $\begin{matrix}\int_0^1 f(x)v(x) \, dx & = & \int_0^1 u''(x)v(x) \, dx \\& = & u'(x)v(x)|_0^1-\int_0^1 u'(x)v'(x) \, dx \\& = & -\int_0^1 u'(x)v'(x) \, dx = -\phi (u,v).\end{matrix}$

위 식은 $v(0)=v(1)=0$ 이라는 전제를 바탕으로 한다.

유한 요소법은 변동 미분법을 사용하여 오차 함수를 최소화함으로써 해를 근사한다.^[49] 각 소영역 내를 1차 함수로 보간(근사 공간이 원래 해 공간의 부분 공간이 되는 경우에는 일종의 사영을 구하게 된다)한 경우, 전체 영역에서는 적절한 노름에 대해 최량 근사임이 나타난다.^[49]

유한 요소법은 선형 문제^[50]·비선형 문제^[51]^[52]·동적 해석^[53]^[54]^[55] 등, 다양한 문제에 대응할 수 있다. 이는 근사 방정식의 구성 방식 및 영역 형상에 대한 자유도가 높기 때문이다.^[41]^[42]^[43]

4. 1. 변분법 공식화

경계값 문제를 유한요소법으로 풀기 위해서는 우선 주어진 문제를 변분법 형태로 변환해야 한다. 이 단계는 수작업으로도 가능한데, 핵심은 원래의 미분 방정식에 시험 함수(test function)를 곱하고, 부분 적분을 통해 미분 차수를 낮추는 것이다.

예를 들어 다음 1차원 문제 P1을 생각해보자.

:

\mbox{P1 }:\begin{cases}u''=f \mbox{ in } (0,1), \\u(0)=u(1)=0,\end{cases}

여기서

f

는 주어진 함수,

u

는 미지 함수이며,

u''

는

u

의 2차 미분이다.

만약

u

가 P1의 해라면, 경계 조건 (

x=0, 1

에서

v=0

)을 만족하는 임의의 매끄러운 함수

v

에 대해 다음 식이 성립한다.

(1)

\int_0^1 f(x)v(x) \, dx = \int_0^1 u''(x)v(x) \, dx.

이제 (1) 식의 우변에 부분 적분을 적용하면 다음과 같이 정리할 수 있다.

(2)

\begin{matrix}\int_0^1 f(x)v(x) \, dx & = & \int_0^1 u''(x)v(x) \, dx \\& = & u'(x)v(x)|_0^1-\int_0^1 u'(x)v'(x) \, dx \\& = & -\int_0^1 u'(x)v'(x) \, dx = -\phi (u,v).\end{matrix}

여기서

v(0)=v(1)=0

(경계 조건)이라는 사실을 이용했다.

2차원 문제 P2의 경우에도 마찬가지로 그린 정리를 사용하여 부분 적분을 적용할 수 있다.

:

\int_{\Omega} fv\,ds = -\int_{\Omega} \nabla u \cdot \nabla v \, ds = -\phi(u,v),

여기서

\nabla

는 기울기를,

\cdot

는 벡터곱을 나타낸다.

이와 같이 원래의 미분 방정식을 적분 형태로 변환한 것을 약형식(Weak Formulation)이라고 한다. 약형식을 사용하면 미분 차수가 낮아져 해를 구하기가 더 쉬워진다.

리스 표현 정리를 이용하면 약형식 (2)를 만족하는 유일한 해

u

가 힐베르트 공간

H_0^1(0,1)

에 존재함을 보일 수 있다.

4. 2. 이산화

변분법으로 얻어진 약형식을 유한 차원 공간에서 근사하여 문제를 해결한다. 전체 영역을 유한 개의 요소로 나누고, 각 요소 내에서 해를 근사하는 함수(형상 함수)를 정의한다. 형상 함수는 일반적으로 다항식으로 표현되며, 요소의 종류와 차수에 따라 다양한 형태를 가진다.^[56] 갤러킨 방법(Galerkin method)은 유한요소법에서 널리 사용되는 이산화 방법 중 하나로, 시험 함수와 기저 함수를 동일하게 선택하는 방법이다.

해석 영역 내부를 작은 유한 범위의 요소로 분할한다. 일반적으로 요소는 그 경계에 절점이 배치되며, 요소 내부의 물리량은 각 절점에 대응하는 형상 함수와 절점 값의 곱의 합으로 표현된다.^[56] 유한 요소법에서는 많은 종류의 요소가 공식화되어 있으며, 문제에 따라 사용이 구분된다. 요소 종류의 차이는 요소의 형상, 요소 내에서 해의 근사에 사용하는 다항식의 차수, 인접한 요소 간의 경계에서의 근사 해의 연속성 등에 따른다.^[56]

4. 3. 요소

유한요소법에서는 문제의 형상, 요구되는 정확도, 계산 비용 등을 고려하여 다양한 종류의 요소를 선택한다.

영역을 더 단순한 부분, 즉 요소로 세분화하면 다음과 같은 이점이 있다.

복잡한 형상을 정확하게 표현할 수 있다.
이종 재료의 특성을 부여할 수 있다.
전체 솔루션의 표현이 용이하다.
국소적인 효과를 파악할 수 있다.

계산을 위해 소영역으로 분할하는 것을 "메쉬를 생성한다"라고 한다. 메쉬가 적절해야 해석 결과도 정확하다.

CAE 소프트웨어는 복잡한 기하 형상을 미소 요소로 분할하는 메쉬를 자동 생성하는 기능을 가진 경우가 많다. 다만, 이 경우에도 형상의 특이점 처리에 주의해야 한다.

자동차나 석유 파이프라인과 같이 복잡한 해석, 경계가 이동하는 고체 반응처럼 영역이 변화하는 경우, 필요한 정밀도가 영역 전체에서 변화하는 경우, 해가 매끄럽지 않은 경우 등에 유한요소법이 특히 적합하다. 메쉬의 거칠기를 조정하여 해석의 계산 비용을 줄일 수 있다. 변화가 크고 중요한 부분은 메쉬를 세밀하게 하여 예측 정밀도를 높이고, 변화가 작은 부분은 예측 정밀도를 높일 필요가 없으므로 메쉬를 거칠게 하여 계산량을 줄인다. 예를 들어 자동차 정면 충돌 시뮬레이션에서는 자동차 전면 등 중요한 영역은 메쉬를 세밀하게 하고, 후면은 메쉬를 거칠게 한다.

4. 4. 형상 함수

형상 함수는 요소 내에서 물리량(변위, 온도 등)을 보간하는 데 사용되는 함수이다. 각 절점에서의 물리량과 형상 함수의 곱을 합하여 요소 내의 임의의 점에서의 물리량을 계산한다.

예를 들어, 사면체 1차 요소의 경우 4개의 꼭짓점에 절점 ''i'' = 1, ..., 4가 설정된다. 절점 ''i''에 대한 형상 함수 ''N_i''와 각 점에서의 물리량 ''u_i''를 사용하여 요소 내의 임의의 점 ''p''에서의 물리량 ''u_p''는 형상 함수의 선형 결합으로 다음과 같이 표현된다.

:

u_p=\sum_{i=1}^{4}N_i u_i=\begin{pmatrix}N_1&N_2&N_3&N_4\end{pmatrix}\begin{pmatrix}u_1\\u_2\\u_3\\u_4\end{pmatrix}

형상 함수 ''N_i''는 다음과 같은 성질을 만족해야 한다.

절점 ''i''의 위치에서 ''N_i'' = 1
그 외의 절점 위치에서 ''N_i'' = 0

4. 5. 행렬 표현

Finite element method^영어은 최종적으로 연립 일차 방정식을 푸는 문제로 귀결된다.^[43] 각 요소에 대한 방정식을 조합하여 전체 시스템에 대한 행렬 방정식을 구성한다.

먼저, 각 요소의 절점에 있는 미지수에 적분을 적용하여 각 요소의 계수 행렬(연립 일차 방정식의 좌변 행렬)을 생성하는데, 이 계수 행렬을 '''요소 강성 행렬'''이라고 한다. 그런 다음, 각 요소의 계수 행렬(요소 계수 행렬)의 총합을 취하여 영역 전체의 계수 행렬('''전체 강성 행렬'''^[57])을 생성한다.

얻어지는 전체 계수 행렬은 일반적으로 희소 행렬이 된다.^[58] 이 희소 행렬 문제를 해결하기 위해 효율적인 솔버가 사용된다. 예를 들어, 직접법으로 푸는 경우 스카이라인법 등이 알려져 있다.^[58]

5. 다양한 유한요소법

응용요소법(Applied Element Method, AEM): 유한요소법(FEM)과 개별 요소법(Discrete element method, DEM)의 특징을 결합한 방법이다.

확장 유한요소법(eXtended Finite Element Method, XFEM): 일반화 유한요소법(GFEM)과 분할 단위 방법(PUM)을 기반으로 하는 수치 기법이다. 불연속 함수를 사용하여 미분 방정식의 해를 위한 해 공간을 풍부하게 함으로써 고전적인 유한 요소법을 확장한다. 불연속성을 포함하는 문제를 효과적으로 해석하는 방법이다.^[15]^[16]

일반화 유한요소법(Generalized Finite Element Method, GFEM): 알려지지 않은 해에 대한 가용 정보를 반영하는 함수(반드시 다항식일 필요는 없음)로 구성된 국소 공간을 사용하여 좋은 국소 근사를 보장한다. 분할 여부를 사용하여 이러한 공간을 "결합"하여 근사 부분 공간을 형성한다.^[17]

혼합 유한요소법(Mixed Finite Element Method): 편미분 방정식 문제의 이산화 과정에서 추가적인 독립 변수를 절점 변수로 도입하는 유한 요소법의 한 유형이다.

hp-유한요소법: 요소 크기(''h'')와 다항식 차수(''p'')를 적응적으로 조절하여 해의 정확도를 높이는 방법이다.^[18]

스펙트럼 요소법(Spectral Element Method): 유한 요소의 기하학적 유연성과 스펙트럼 방법의 정확성을 결합한 방법이다. 고차 라그랑주 보간법을 기반으로 하는 약 형식 편미분 방정식의 근사 해법이며, 특정 구적 규칙과 함께 사용된다.^[20]

메쉬프리 방법(Meshfree Methods): 격자(mesh)를 사용하지 않고 문제를 해석하는 방법이다.

불연속 갤러킨 방법(Discontinuous Galerkin Method, DGM)

유한 요소 극한 해석(Finite Element Limit Analysis)

늘어난 격자 방법(Stretched Grid Method)

루비냑 반복법(Loubignac iteration): 유한 요소법의 반복적인 방법 중 하나이다.

결정 소성 유한 요소법(Crystal Plasticity Finite Element Method, CPFEM): 프란츠 로터스(Franz Roters)가 개발한 고급 수치 해석 도구이다. 금속의 결정 구조를 고려하여 변형, 표면 거칠기, 파단 등의 수치적 연구에 적용된다.

가상 요소법(Virtual Element Method, VEM): Beirão da Veiga 외(2013)가 모방 유한 차분 (MFD) 방법의 확장으로 도입한 방법으로, 임의의 요소 형상에 대한 표준 유한 요소법의 일반화이다.^[21]

6. 유한차분법과의 비교

유한차분법(FDM)은 미분 방정식을 차분 방정식으로 근사하여 해를 구하는 방법이다. 유한요소법은 복잡한 형상과 경계 조건을 다루는 데 유리하며, 유한차분법은 구현이 간단하다는 장점이 있다.^[22] 구조해석 문제에서는 유한요소법이, 전산유체역학(CFD) 문제에서는 유한차분법 또는 유한체적법(FVM)이 주로 사용된다.

유한차분법과 유한요소법의 주요 차이점은 다음과 같다.

유한차분법은 미분 방정식 자체를 근사하는 반면, 유한요소법은 미분 방정식의 해공간을 근사한다.
유한요소법은 복잡한 형상을 다루기 쉽지만,^[3]^[22] 유한차분법은 기본적으로 직사각형 모양만 다룰 수 있어 형상 처리의 유연성이 떨어진다.^[22]
유한차분법은 구현이 쉽다는 장점이 있다.^[22]
일반적으로 불규칙한 CAD 형상에는 유한차분법을 사용하지 않고, 직사각형이나 블록 모양 모델에 주로 사용한다.^[23]
유한요소법은 메시 적응(mesh adaptation)에 더 유연하다.^[22]
경우에 따라 유한요소법이 유한차분법보다 더 높은 품질의 근사해를 제공하지만, 문제에 따라 결과가 달라질 수 있다.
구조 역학 문제에는 일반적으로 유한요소법이, 전산유체역학(CFD) 문제에는 유한차분법이나 유한체적법이 주로 사용된다. 특히 외부 유동 문제에서는 계산 비용을 줄이기 위해 각 셀 내에서 낮은 차수의 근사를 사용하는 유한차분법 또는 유한체적법이 선호된다.

7. 응용 분야

유한요소법(FEM)은 다양한 공학 분야에서 널리 사용되는 기술이다. 특히, 기계 공학 분야에서는 항공, 생체역학, 자동차 산업 등에서 제품 설계 및 개발에 필수적으로 활용된다.^[29] FEM 소프트웨어는 강성과 강도 시각화를 제공하고, 무게, 재료, 비용을 최소화하는 데 기여한다.^[29]

FEM 소프트웨어는 다양한 시뮬레이션 옵션을 제공하여 복잡한 모델링과 시스템 분석을 가능하게 한다.^[32] 이를 통해 엔지니어는 필요한 정확도와 계산 시간을 조절하여 대부분의 엔지니어링 문제를 해결할 수 있다. 또한, 가상 프로토타이핑을 통해 실제 제품 제작 전에 설계를 최적화할 수 있다.^[32]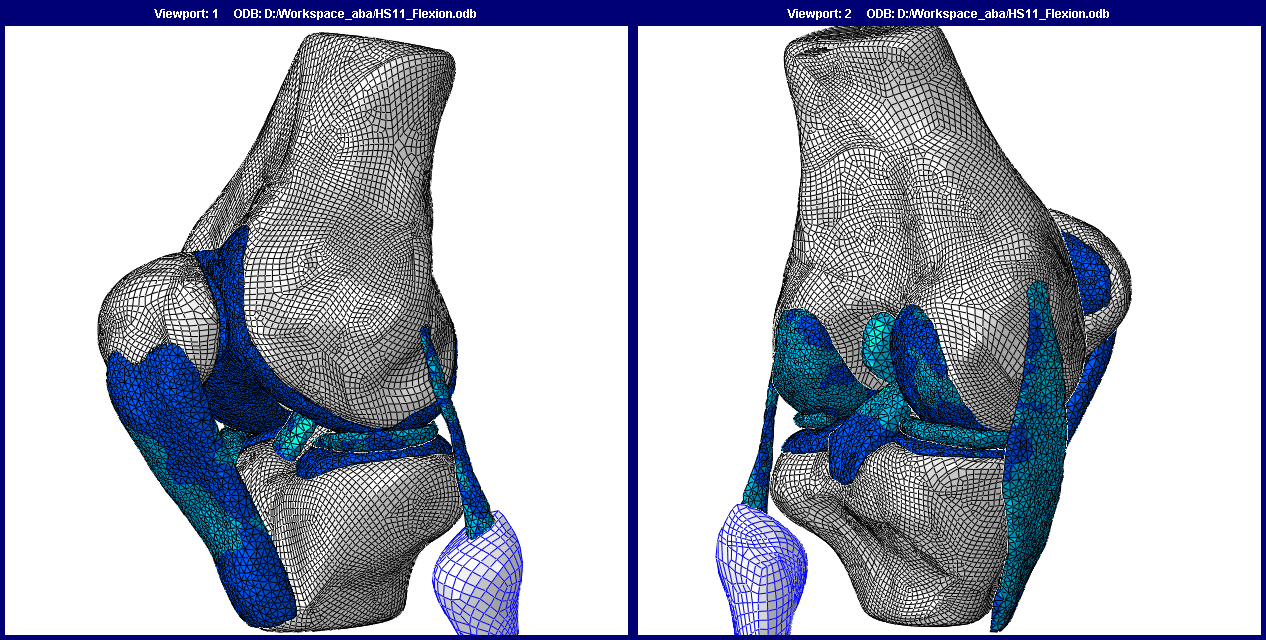

FEM의 도입은 제품 개발 시간을 단축시키고, 설계 개선을 가속화하며, 하드웨어 프로토타입 제작 횟수를 줄여 비용 절감에 기여한다.^[32] 결과적으로 생산성 향상과 수익 증가를 가져온다.^[32]

1990년대에는 FEM이 확률 모델링 및 신뢰성 평가에도 활용되기 시작했다.^[34]^[35] 최근에는 전산 유체 역학 분야에서 나비에-스토크스 방정식을 해결하는 데 FEM이 널리 사용되고 있다.^[36]^[37]^[38] 또한, 전산 플라즈마 연구에서도 자기유체역학, 블라소프 방정식, 슈뢰딩거 방정식 등에 FEM을 적용하여 좋은 결과를 얻고 있다.^[39]^[40]

전자 상태 계산(→실공간법^[60]), 전기 공학^[61], 전자기장 해석^[62], 유체 해석^[63]^[64]^[65] 등 다양한 분야에서 미분 방정식으로 표현되는 문제를 해결하는 데 FEM이 적용되고 있다. 더 나아가 유체 구조 연성, 전자기장 구조 해석과 같은 연성 해석 연구도 활발하게 진행되고 있다.^[66]

최근에는 4차 산업혁명 기술과의 융합을 통해 스마트 팩토리, 디지털 트윈, 인공지능 기반 설계 등 새로운 분야로 활용 영역을 확장하고 있다.

8. 소프트웨어

다양한 유한요소법 소프트웨어들이 개발되어 사용되고 있다.

GetFEM++^[70]
FreeFem++^[71]^[72]
FEniCS 프로젝트^[73]^[74]
MATLAB^[75]^[76]^[77]^[78]^[79]^[80]^[81]
MFEM

9. 같이 보기

유한차분법
경계 요소법
대용 전하법
입자법
FDTD법
변분법
메쉬 없는 방법

참조

_[1] 논문 High-dimensional finite elements for elliptic problems with multiple scales SIAM
_[2] 서적 A first course in the finite element method Cengage Learning
_[3] 서적 An Introduction to the Finite Element Method McGraw-Hill
_[4] 서적 The Finite Element Method for Engineers Wiley
_[5] 논문 Eighty Years of the Finite Element Method: Birth, Evolution, and Future 2022
_[6] 논문 Solution of problems of elasticity by the framework method
_[7] 논문 Variational methods for the solution of problems of equilibrium and vibrations
_[8] 웹사이트 СПб ЭМИ РАН http://emi.nw.ru/IND[...] 2018-03-17
_[9] 논문 Least squares smoothing of experimental data using finite elements 1968-07
_[10] 웹사이트 SAP-IV Software and Manuals http://nisee.berkele[...] 2013-01-24
_[11] 서적 Building Trust, The history of DNV 1864-2014 Dinamo Forlag A/S 2014
_[12] 서적 An Analysis of The Finite Element Method https://archive.org/[...] Prentice Hall
_[13] 서적 The Finite Element Method: Its Basis and Fundamentals https://books.google[...] Butterworth-Heinemann 2013-08-31
_[14] 서적 Finite Element Procedures Cambridge, MA: Klaus-Jürgen Bathe
_[15] 웹사이트 CutFEM: Discretizing Partial Differential Equations and Geometry https://ecmiindmath.[...] 2023-10-13
_[16] 논문 CutFEM: Discretizing geometry and partial differential equations 2015-11-16
_[17] 논문 Generalized Finite Element Methods: Main Ideas, Results, and Perspective 2004-06
_[18] 간행물 Higher-Order Finite Element Methods Chapman & Hall/CRC Press
_[19] 논문 The scaled boundary finite-element method – alias consistent infinitesimal finite-element cell method – for elastodynamics 1997-08-05
_[20] 웹사이트 Spectral Element Methods http://lsec.cc.ac.cn[...] 2017-07-28
_[21] 논문 Basic principles of Virtual Element Methods 2013
_[22] 논문 Option pricing with finite elements http://dx.doi.org/10[...] 2005-01
_[23] 뉴스 What's The Difference Between FEM, FDM, and FVM? http://www.machinede[...] 2017-07-28
_[24] 논문 Quantitative comparison between fast fourier transform and finite element method for micromechanical modeling of composite https://hal.science/[...] 2019-12
_[25] 논문 Simulation of micromechanical behavior of polycrystals: finite elements versus fast Fourier transforms https://iopscience.i[...] 2009-09-01
_[26] 논문 A variational fast Fourier transform method for phase-transforming materials https://iopscience.i[...] 2021-06-01
_[27] 논문 A Review of FE-FFT-Based Two-Scale Methods for Computational Modeling of Microstructure Evolution and Macroscopic Material Behavior 2022-10-01
_[28] 논문 A finite element perspective on nonlinear FFT-based micromechanical simulations: A FINITE ELEMENT PERSPECTIVE ON NONLINEAR FFT-BASED SIMULATIONS https://onlinelibrar[...] 2017-09-07
_[29] 논문 Engineering Asset Management 2009
_[30] 웹사이트 Finite Element Analysis: How to create a great model https://coventivecom[...] 2019-04-05
_[31] 논문 A comparison between dynamic implicit and explicit finite element simulations of the native knee joint https://ris.utwente.[...] 2019-09-19
_[32] 간행물 Accuracy and Economy of Finite Element Magnetic Analysis 1985-04
_[33] 웹사이트 McLaren Mercedes: Feature - Stress to impress http://www.mclaren.c[...] 2006-10-03
_[34] 논문 Methods with high accuracy for finite element probability computing 1995-05-19
_[35] 서적 Reliability Assessment Using Stochastic Finite Element Analysis John Wiley & Sons
_[36] 서적 Finite Element Approximation of the Navier-Stokes Equations Springer Berlin
_[37] 서적 Finite Element Methods and Navier-Stokes Equations Springer Science & Business Media
_[38] 서적 Finite Element Methods for Navier-Stokes Equations: Theory and Algorithms Springer Science & Business Media
_[39] 논문 A Space-Time Finite Element Method for the Nonlinear Schrödinger Equation: The Continuous Galerkin Method SIAM
_[40] 논문 Nonlinear Magnetohydrodynamics Simulation Using High-Order Finite Elements Elsevier
_[41] 서적 The mathematical theory of finite element methods (Vol. 15) Springer Science & Business Media
_[42] 서적 An introduction to the mathematical theory of finite elements Courier Corporation
_[43] 서적 数値解析入門サイエンス社 2003-06
_[44] 서적 The finite element method for elliptic problems (Vol. 40) SIAM
_[45] 논문 Stiffness and deflection analysis of complex structures
_[46] 서적 The finite element method for solid and structural mechanics Elsevier
_[47] 문서
_[48] 웹사이트 Poisson方程式に対する有限要素法の解析超特急 http://nalab.mind.me[...]
_[49] 문서
_[50] 논문 Finite element methods for linear hyperbolic problems
_[51] 서적 Nonlinear finite element methods Springer Science & Business Media
_[52] 논문 Solution of nonlinear problems of elastoplasticity by finite element method
_[53] 논문 Finite element formulations for large deformation dynamic analysis
_[54] 논문 A finite element dynamic analysis of flexible manipulators
_[55] 서적 The finite element method: linear static and dynamic finite element analysis Courier Corporation
_[56] 문서
_[57] 논문 全体剛性行列を用いた粒状要素解析
_[58] 논문 Skyline algorithms for multilevel substructure analysis
_[59] 논문 Adaptation of CAD model topology for finite element analysis
_[60] 논문 An efficient real space method for orbital-free density-functional theory
_[61] 논문 電気工学のための有限要素法
_[62] 서적 Finite element analysis of electrical machines (Vol. 101) Kluwer Academic Publishers
_[63] 서적 The finite element method in heat transfer and fluid dynamics CRC Press
_[64] 간행물 Finite element analysis in fluid dynamics NASA STI/Recon Technical Report A
_[65] 논문 A finite element method for analysis of fluid flow, heat transfer and free interfaces in Czochralski crystal growth
_[66] 논문 流体・構造連成有限要素解析における連成手法に関する検討
_[67] 서적 Meshfree methods: moving beyond the finite element method Taylor & Francis
_[68] 논문 Free mesh method: a new meshless finite element method
_[69] 논문 Meshfree and finite element nodal integration methods
_[70] 간행물 GetFEM: Automated FE modeling of multiphysics problems based on a generic weak form language
_[71] 서적 有限要素法で学ぶ現象と数理―FreeFem++ 数理思考プログラミング― 日本応用数理学会 2014
_[72] 논문 数理指向有限要素計算プログラミング言語 FreeFem++ 2001
_[73] 간행물 The fenics project Chalmers Finite Element Centre, Chalmers University of Technology 2003
_[74] 서적 Automated solution of differential equations by the finite element method: The FEniCS book Springer Science & Business Media 2012
_[75] 서적 The finite element method using MATLAB CRC Press 2018
_[76] 서적 The finite element method: basic concepts and applications with MATLAB, MAPLE, and COMSOL CRC Press 2017
_[77] 논문 Matlab implementation of the finite element method in elasticity 2002
_[78] 논문 MILAMIN: MATLAB‐based finite element method solver for large problems 2008
_[79] 간행물 iFEM: an innovative finite element methods package in MATLAB University of Maryland 2008
_[80] 논문 Remarks around 50 lines of Matlab: short finite element implementation 1999
_[81] 서적 MATLAB codes for finite element analysis: solids and structures Springer Science & Business Media 2008

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com