폴리감마 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 주요 성질
4. 표현
5. 특수값
6. 큐-폴리감마 함수 (q-Polygamma Function)
참조

1. 개요

폴리감마 함수는 감마 함수의 미분으로 정의되는 특수한 함수이다. 폴리감마 함수는 디감마 함수, 트리감마 함수, 테트라감마 함수 등으로 불리며, 복소 평면에서 해석적 성질을 갖는다. 주요 성질로는 점화식, 상반 공식, 곱셈 정리가 있으며, 급수 표현, 적분 표현, 점근 전개 등을 통해 나타낼 수 있다. 또한, 큐-폴리감마 함수와 같은 변형된 형태도 존재한다. 폴리감마 함수는 특수한 값들을 가지며, 오일러-마스케로니 상수, 조화수, 리만 제타 함수 등과 관련된다.

더 읽어볼만한 페이지

감마 함수 및 관련 함수 - 감마 분포
감마 분포는 형상 모수와 척도 모수로 정의되는 연속 확률 분포로, 확률 밀도 함수가 감마 함수로 표현되며, 베이즈 통계학에서 켤레 사전 분포로 활용되고, 형상 모수가 양의 정수일 때는 얼랑 분포를 나타낸다.
감마 함수 및 관련 함수 - 불완전 감마 함수
불완전 감마 함수는 감마 함수의 적분 구간을 나누어 정의되며 상부 불완전 감마 함수와 하부 불완전 감마 함수로 나뉘고, 확률론, 통계학, 물리학 등 다양한 분야에서 응용되는 함수이다.
특수 함수 - 람베르트 W 함수
람베르트 W 함수는 we^w = z를 만족하는 w를 찾는 람베르트 이름을 딴 역함수 관계를 가지며, 여러 분야에서 지수 함수 방정식을 푸는 데 응용되는 무한히 많은 가지를 가진 함수이다.
특수 함수 - 감마 함수
감마 함수는 양의 실수부를 갖는 복소수 z에 대해 오일러 적분으로 정의되고 해석적 연속을 통해 복소평면 전체로 확장된 팩토리얼 함수의 일반화로서, 수학, 물리학, 공학 등 다양한 분야에서 활용되며 여러 표현과 성질을 가진다.

폴리감마 함수
일반 정보
명칭	폴리감마 함수
다른 이름	체비쇼프 함수
유형	특수 함수
정의
정의	감마 함수의 로그 도함수
기호	ψ(m)(z)
수식	ψ(m)(z) = d(m+1)/dz(m+1) ln Γ(z)
다른 표현	ψ(m)(z) = (-1)(m+1) m! Σk=0→∞ (z + k)-(m+1)
성질
재귀 관계	ψ(m)(z+1) = ψ(m)(z) + (-1)(m) m! z-(m+1)
반사 공식	ψ(m)(1 − z) + (−1)(m+1) ψ(m)(z) = π d(m)/dz(m) cot(πz)
곱셈 정리	ψ(m)(kz) = ln(k) + k-(m+1) Σj=0→k-1 ψ(m)(z + j/k)
특수한 값
m = 0	ψ(0)(z) = 디감마 함수
m = 1	ψ(1)(z) = 트리감마 함수
관련 함수
관련 함수	감마 함수 Γ(z)
관련 함수	디감마 함수 ψ(0)(z)
관련 함수	트리감마 함수 ψ(1)(z)
관련 함수	후르비츠 제타 함수 ζ(s, q)

2. 정의

감마 함수의 로그 미분으로 정의되는 폴리감마 함수(polygamma function) $\psi_{n}(z)$ 는 다음과 같다.

: $\psi_n(z) = {d^{n+1}\over{d z^{n+1}} }\ln \Gamma(z) = {d^{n}\over{d z^{n}} } = {d^{n}\over{d z^{n}} } \psi_0(z)$

여기서 $\psi_0(z)$ 은 $\psi^{(0)}(z)$ 으로도 표기하며, 폴리감마 함수 중 첫 번째 함수인 디감마 함수이다.

디감마 함수는 감마 함수의 미분으로 정의된다.

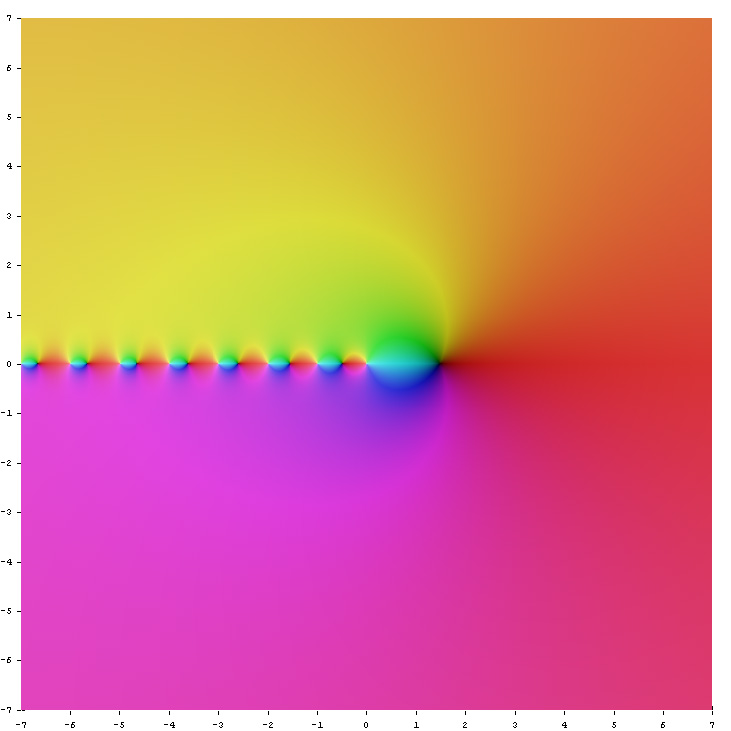
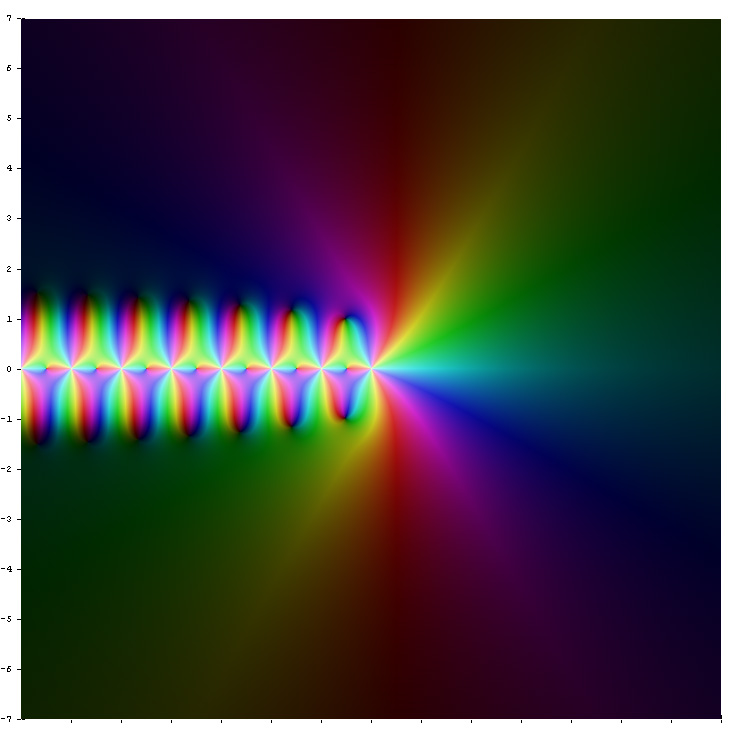
$\psi_{n}(z)$ 에서 $n=0$ 인 경우:
: $\psi_{0}(z) = \psi(z)$
$\psi_{n}(z)$ 에서 $n=1$ 인 경우:
: $\psi_{1}(z)$

감마 함수 Γ(''z'')에 대해,

:

\psi^{(n)}(z)= \frac{d^{n+1}}{dz^{n+1}} \ln{\Gamma(z)}  = \frac{d^n}{dz^n} \psi(z)

로 정의되는 함수를 '''폴리감마 함수'''라고 부른다.

ψ(''z''), ψ⁽¹⁾(''z''), ψ⁽²⁾(''z''), ψ⁽³⁾(''z''), ψ⁽⁴⁾(''z'')는 각각 '''디'''-, '''트리'''-, '''테트라'''-, '''펜타'''-, '''헥사''' -'''감마 함수'''라고 불린다.

폴리감마 함수 ψ^(''n'')(''z'')는 ''z'' = 0, −1, −2, ... 에서 ''n'' + 1 차 극점을 가지며, 그 점들을 제외한 모든 복소 평면에서는 해석적이다.

실수 x에 대한 ψ⁽ⁿ⁾(x). 주황색은 디감마 함수, 노란색은 트리감마 함수, 녹색은 테트라감마 함수, 빨간색은 펜타감마 함수, 파란색은 헥사감마 함수를 나타낸다.

3. 주요 성질

감마 함수의 로그 미분에서 시작하여, 폴리감마 함수는 다음과 같은 주요 성질들을 가진다.^[1]

m > 0에서 감마 함수의 미분은 다음과 같이 표현된다.

:

\Gamma'(m+1) = m!\cdot\left(  - \gamma + \sum_{k=1}^m \frac{1}{k} \right)

여기서 γ는 오일러-마스케로니 상수이다.

z ≠ 0, -1, -2, -3, ... 일 때, 폴리감마 함수는 다음과 같은 급수로 나타낼 수 있다.

:

\psi(z) = -\gamma -\sum_{n=0}^{\infty} \biggl (\frac{1}{z+n} - \frac{1}{n+1} \biggr )

:

\psi^{(n)}(z) = (-1)^{n+1} n! \sum_{k=0}^{\infty} \frac{1}{(z+k)^{n+1}}\qquad (n = 1,2,3, \cdots)

|z| < 1 인 영역에서 z = 0 일 때, 테일러 급수를 통해 다음과 같이 나타낼 수 있다.

:

\psi(z+1) = -\gamma +\sum_{k=2}^{\infty} (-1)^k\zeta(k) z^{k-1}

:

\psi^{(n)}(z+1) = (-1)^{n+1}  \sum_{k=1}^{\infty} \frac{(-1)^{k-1}(n+k-1)! \zeta(n+k) z^{k-1} }{(k-1)!}\qquad (n = 1,2,3, \cdots)

여기서 ζ(n)은 리만 제타 함수이다.

Re z > 0 일 때, 폴리감마 함수는 다음과 같은 적분 표현을 갖는다.

:

\psi(z) = -\gamma+ \int_{0}^{\infty} \frac{e^{-t}-e^{-zt}}{1-e^{-t}} dt

:

\psi^{(n)}(z) = (-1)^{n+1} \int_{0}^{\infty} \frac{t^ne^{-zt}}{1-e^{-t}} dt\quad (n=1,2,\cdots)

z → ∞ (|arg z| < π)일 때, 폴리감마 함수는 다음과 같은 점근 전개를 가진다.

:

\psi(z)  \sim \ln{z}- \frac{1}{2z}- \sum_{n=1}^{\infty} \frac{B_{2n}}{2nz^{2n}}

:

\psi^{(n)}(z)  \sim  (-1)^{(n-1)} \left( \frac{(n-1)!}{z^n}+ \frac{n!}{2z^{n+1}}+ \sum_{k=1}^{\infty} \frac{B_{2k}(2k+n-1)!}{(2k)!z^{2k+n}} \right )\quad (n=1,2,\cdots)

여기서 B_2k는 베르누이 수이다.

3. 1. 점화식

폴리감마 함수는 다음과 같은 점화식을 만족한다.^[1]

:

\psi^{(m)}(z+1)= \psi^{(m)}(z) + \frac{(-1)^m\,m!}{z^{m+1}}

이는 양의 정수 인수에 대해 고려하면 자연수의 거듭제곱의 역수의 합을 나타낸다.^[1]

:

\frac{\psi^{(m)}(n)}{(-1)^{m+1}\,m!} = \zeta(1+m) - \sum_{k=1}^{n-1} \frac{1}{k^{m+1}} = \sum_{k=n}^\infty \frac{1}{k^{m+1}} \qquad m \ge 1

그리고^[1]

:

\psi^{(0)}(n) = -\gamma\ + \sum_{k=1}^{n-1}\frac{1}{k}

여기서

\gamma

는 오일러-마스케로니 상수이다. 로그 감마 함수와 마찬가지로, 폴리감마 함수는

\mathbb{N}

의 영역에서 점화 관계와 주어진 함수 값(예: ''ψ''^(''m'')(1))에 의해서만 양의 실수로 유일하게 일반화될 수 있다. 단,

\mathbb{R}^{+}

에서 엄격한 단조성의 추가 조건이 필요한 ''m'' = 0인 경우는 제외한다. 이는

\mathbb{R}^{+}

에서 엄격한 로그 볼록성이 추가로 요구되는 감마 함수에 대한 보어-몰레럽 정리의 결과이다. ''m'' = 0의 경우, ''ψ''⁽⁰⁾은 무한대에서 정규화될 수 없기 때문에(역수의 합이 수렴하지 않음) 다르게 처리해야 한다.^[1]

3. 2. 상반 공식

Reflection formula^영어

:

(-1)^m \psi^{(m)} (1-z) - \psi^{(m)} (z) = \pi \frac{\mathrm{d}^m}{\mathrm{d} z^m} \cot{\pi z} = \pi^{m+1} \frac{P_m(\cos{\pi z})}{\sin^{m+1}(\pi z)}

여기서

P_m

은 정수 계수를 가지고 최고차항 계수가

(-1)^m \lceil 2^{m-1} \rceil

이며, 차수가

|m-1|

인 홀수 또는 짝수 다항식이다. 이들은 다음의 재귀 방정식을 따른다.

:

\begin{align} P_0(x) &= x \\ P_{m+1}(x) &= - \left( (m+1)xP_m(x)+\left(1-x^2\right)P'_m(x)\right).\end{align}

감마 함수의 상반 공식에 대해, 로그 미분을 취함으로써 다음 관계식을 유도할 수 있다.

:

(-1)^n\psi^{(n)}(1-z) - \psi^{(n)}(z) = \pi \frac{d^n}{dz^n} \operatorname{cot} \pi z

단,

\cot \pi z

는 코탄젠트 함수를 나타낸다.

3. 3. 곱셈 정리

곱셈 정리는 다음과 같다.^[1]

:

k^{m+1} \psi^{(m)}(kz) = \sum_{n=0}^{k-1} \psi^{(m)}\left(z+\frac{n}{k}\right)\qquad m \ge 1

디감마 함수에 대하여,

:

k \psi^{(0)}(kz) = k\ln{k} + \sum_{n=0}^{k-1}\psi^{(0)}\left(z+\frac{n}{k}\right)

이다.^[1]

3. 4. 부등식

쌍곡선 코탄젠트는 다음 부등식을 만족한다.

:

\frac{t}{2}\operatorname{coth}\frac{t}{2} \ge 1,

이는 다음 함수가

:

\frac{t^m}{1 - e^{-t}} - \left(t^{m-1} + \frac{t^m}{2}\right)

모든

m \ge 1

및

t \ge 0

에 대해 음수가 아님을 의미한다. 따라서 이 함수의 라플라스 변환은 완전히 단조롭다. 위의 적분 표현에 의해, 다음 식이

:

(-1)^{m+1}\psi^{(m)}(x) - \left(\frac{(m-1)!}{x^m} + \frac{m!}{2x^{m+1}}\right)

완전히 단조롭다고 결론 내릴 수 있다. 볼록성 부등식

e^t \ge 1 + t

는 다음 식이

:

\left(t^{m-1} + t^m\right) - \frac{t^m}{1 - e^{-t}}

모든

m \ge 1

및

t \ge 0

에 대해 음수가 아님을 의미하므로, 유사한 라플라스 변환 논증은 다음 식이 완전 단조성을 가짐을 보여준다.

:

\left(\frac{(m-1)!}{x^m} + \frac{m!}{x^{m+1}}\right) - (-1)^{m+1}\psi^{(m)}(x).

따라서 모든

m \ge 1

및

x > 0

에 대해, 다음 부등식이 성립한다.

:

\frac{(m-1)!}{x^m} + \frac{m!}{2x^{m+1}} \le (-1)^{m+1}\psi^{(m)}(x) \le \frac{(m-1)!}{x^m} + \frac{m!}{x^{m+1}}.

^[1]

4. 표현

감마 함수의 미분은 폴리감마 함수(polygamma function) $\psi_{n}(z)$ 로 주어지며, $\psi_0(z)$ 은 $\psi^{(0)}(z)$ 으로도 표기한다. 이것은 폴리감마 함수 중 첫번째 함수인 디감마 함수이다.

: $\psi_n(z) = {d^{n+1}\over{d z^{n+1}} }\ln \Gamma(z) = {d^{n}\over{d z^{n}} } = {d^{n}\over{d z^{n}} } \psi_0(z)$

: $\Gamma(z)=\lim_{n\to\infty}\frac{n^zn!}{\displaystyle\prod_{k=0}^n (z+k)} \!\;$

: $\Gamma(z)={1 \over z}\prod_{k=1}^{\infty} }$

: $\therefore \;\Gamma'(z)=\psi_0(z) \Gamma(z)$

: $\psi_0(z)=\psi(z) =$

$- \Gamma' (1)= \gamma = - \psi_0(1)$

:

\gamma = \lim_{n\to\infty } \left(\sum_{k=1}^n {1 \over k}  - \ln n \right)=\sum_{m=2}^{\infty} (-1)^m {{\zeta(m)}\over{m} }\;\; (\gamma \;

오일러-마스케로니 상수,

\zeta \;

리만 제타 함수)

:

\psi^{(0)}(z) = - \sum_{k=0}^\infty { {1} \over {(z+k)} }

:

\psi^{(0)}(1) = - \sum_{k=0}^\infty { {1} \over {(1+k)} }

:

\Gamma(1)=1

:

\;\Gamma'(1)=\psi_0(1)

후르비츠 제타 함수 표현

:

\psi^{(n)}(z) = (-1)^{n+1}\, n!\, \zeta (n+1,z)

* 오렌지색: 디감마 함수

노란색: 트리감마 함수
녹색: 테트라감마 함수
빨강: 펜타감마 함수
파랑: 헥사감마 함수]]

4. 1. 급수 표현

m이 정수이고 z가 음이 아닌 정수가 아닌 복소수일 때, 폴리감마 함수는 다음과 같은 급수 표현을 갖는다.^[1]

:

\psi^{(m)}(z) = (-1)^{m+1}\, m! \sum_{k=0}^\infty \frac{1}{(z+k)^{m+1}}

이는 후르비츠 제타 함수를 사용하여 다음과 같이 더 간결하게 표현할 수 있다.

:

\psi^{(m)}(z) = (-1)^{m+1}\, m!\, \zeta (m+1,z)

슐뢰밀히에 따르면, 폴리감마 함수에 대한 다음 급수 표현이 가능하다.

:

\frac{1}{\Gamma(z)} = z e^{\gamma z}  \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right) e^{-\frac{z}{n}}

이는 바이어슈트라스 인수분해 정리의 결과이다. 따라서 감마 함수는 다음과 같이 정의할 수 있다.

:

\Gamma(z) = \frac{e^{-\gamma z}}{z} \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^\frac{z}{n}

감마 함수의 자연 로그는 다음과 같이 표현된다.

:

\ln \Gamma(z) = -\gamma z - \ln(z) + \sum_{k=1}^\infty \left( \frac{z}{k} - \ln\left(1 + \frac{z}{k}\right) \right)

따라서 폴리감마 함수는 다음과 같은 합 표현을 갖는다.

:

\psi^{(n)}(z) = \frac{\mathrm{d}^{n+1}}{\mathrm{d}z^{n+1}}\ln \Gamma(z) = -\gamma \delta_{n0} - \frac{(-1)^n n!}{z^{n+1}} + \sum_{k=1}^{\infty} \left(\frac{1}{k} \delta_{n0} - \frac{(-1)^n n!}{(k+z)^{n+1}}\right)

여기서 δ_n0는 크로네커 델타이다.

또한, 레르흐 초월 함수는 다음과 같이 폴리감마 함수로 표현될 수 있다.

:

\Phi(-1, m+1, z)=\frac1{(-2)^{m+1}m!}\left(\psi^{(m)}\left(\frac{z}{2}\right)-\psi^{(m)}\left(\frac{z+1}{2}\right)\right)

''z'' ≠ 0, -1, -2, -3...일 때, 폴리감마 함수는 다음과 같은 급수로 표현된다.

:

\psi(z) = -\gamma -\sum_{n=0}^{\infty} \biggl (\frac{1}{z+n} - \frac{1}{n+1} \biggr )

:

\psi^{(n)}(z) = (-1)^{n+1} n! \sum_{k=0}^{\infty} \frac{1}{(z+k)^{n+1}}\qquad (n = 1,2,3, \cdots)

|''z''| < 1인 영역에서 ''z'' = 0에서의 테일러 전개를 통해 다음과 같이 표현할 수 있다.

:

\psi(z+1) = -\gamma +\sum_{k=2}^{\infty} (-1)^k\zeta(k) z^{k-1}

:

\psi^{(n)}(z+1) = (-1)^{n+1}  \sum_{k=1}^{\infty} \frac{(-1)^{k-1}(n+k-1)! \zeta(n+k) z^{k-1} }{(k-1)!}\qquad (n = 1,2,3, \cdots)

여기서 γ = 0.5772...는 오일러-마스케로니 상수이고, ''ζ''(''n'')은 리만 제타 함수이다.

4. 2. 적분 표현

Re^영어 z > 0일 때, 폴리감마 함수는 다음과 같은 적분 표현을 갖는다.

:

\begin{align}\psi^{(m)}(z)&= (-1)^{m+1}\int_0^\infty \frac{t^m e^{-zt}}{1-e^{-t}}\,\mathrm{d}t \\&= -\int_0^1 \frac{t^{z-1}}{1-t}(\ln t)^m\,\mathrm{d}t\\&= (-1)^{m+1}m!\zeta(m+1,z)\end{align}

여기서

\zeta(s,q)

는 후르비츠 제타 함수이다.

이는 폴리감마 함수를

\frac{(-1)^{m+1}t^m}{1-e^{-t}}

의 라플라스 변환으로 나타낸다. 베른슈타인의 단조 함수 정리에 따르면,

m>0

이고

x

가 실수이고 음수가 아닐 때,

(-1)^{m+1} \psi^{(m)}(x)

는 완전 단조 함수이다.

위 공식에서

m=0

으로 설정하면 디감마 함수의 적분 표현이 나오지 않는다. 디감마 함수는 가우스에 의해 제시된 적분 표현을 가지는데, 이는 위

m=0

의 경우와 유사하지만,

\frac{e^{-t}}{t}

라는 추가 항이 있다.

:

\psi(z) = -\gamma+ \int_{0}^{\infty} \frac{e^{-t}-e^{-zt}}{1-e^{-t}} dt

:

\psi^{(n)}(z) = (-1)^{n+1} \int_{0}^{\infty} \frac{t^ne^{-zt}}{1-e^{-t}} dt\quad (n=1,2,\cdots)

4. 3. 점근 전개

베르누이 수(B)에 대해,

:

\psi_1(z) = \frac{1}{z} + \frac{1}{2z^2} + \sum_{k=1}^{\infty}\frac{B_{2k}}{z^{2k+1}}  = \sum_{k=0}^{\infty}\frac{B_k}{z^{k+1}}

이러한 발산 급수는 큰 인수에 대해 특정 수치적 최소 정밀도를 갖는 근사값을 빠르게 얻는 데 사용할 수 있다.^[2]

:

\psi^{(m)}(z) \sim (-1)^{m+1}\sum_{k=0}^{\infty}\frac{(k+m-1)!}{k!}\frac{B_k}{z^{k+m}} \qquad m \ge 1

그리고

:

\psi^{(0)}(z) \sim \ln(z) - \sum_{k=1}^\infty \frac{B_k}{k z^k}

여기서 2nd Bernoulli numbers|2종 베르누이 수^영어를 선택했다. ''z'' → ∞ (|arg''z'' | < π)일 때, 폴리감마 함수는 다음의 점근 전개를 가진다.

:

\psi(z) \sim \ln{z}- \frac{1}{2z}- \sum_{n=1}^{\infty} \frac{B_{2n}}{2nz^{2n}}

:

\psi^{(n)}(z) \sim (-1)^{(n-1)} \left( \frac{(n-1)!}{z^n} + \frac{n!}{2z^{n+1}}+ \sum_{k=1}^{\infty} \frac{B_{2k}(2k+n-1)!}{(2k)!z^{2k+n}} \right ) \quad (n=1,2,\cdots)

단, ''B_2k''는 베르누이 수이다.

5. 특수값

폴리감마 함수는 m=1일 때 다음 값을 갖는다.

$\psi(1) = -\gamma$
$\psi^{(n)}(1) = (-1)^{n+1} n! \zeta(n+1) \quad (n=1,2,\cdots)$

폴리감마 함수는 m≧2의 양의 정수일 때 다음 값을 갖는다.

$\psi(m) = -\gamma + \sum_{k=1}^{m-1}\frac{1}{k} = -\gamma + H_{m-1} \qquad (m = 2,3,4, \cdots)$
$\psi^{(n)}(m) = (-1)^n n! \left \{ -\zeta(n+1) + \sum_{k=1}^{m-1}\frac{1}{k^{n+1}} \right \} \qquad (n = 1,2,3, \cdots,m = 2,3,4, \cdots)$

단, γ는 오일러-마스케로니 상수, ''H_m-1''는 조화수를 나타낸다.

6. 큐-폴리감마 함수 (q-Polygamma Function)

큐-폴리감마 함수는 폴리감마 함수의 큐-아날로그이다.

: $\psi_{q}^{(n)} (z)= }$

: $\psi_q(z) = \;\;\; , z>0$

큐 감마함수(q gamma function)

:

f(x+1) = f(x)

:

q \in \left( 0,1 \right)

구간

:

f(1) =1

:

\log f(x) ,x>0

:

f(x)= \Gamma_q (x)

:

\therefore  \Gamma_q(z)=  (1-q)^{1-z}\;\;\;

큐-포흐하머 기호

\; (q;q)\infty

참조

_[1] 논문 The polygamma function psi^k(x) for x=1/4 and x=3/4
_[2] 논문 Structural relations of harmonic sums and Mellin transforms up to weight w=5

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com