맨위로가기

하노이의 탑

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

하노이의 탑은 프랑스 수학자 에두아르 뤼카가 1883년에 발표한 퍼즐로, 인도 베나레스의 브라흐마 탑 전설을 바탕으로 고안되었다. 3개의 기둥과 크기가 다른 원반을 사용하여 원반을 다른 기둥으로 옮기는 방식으로 진행되며, 원반을 옮기는 규칙에 따라 최소 이동 횟수는 2n-1이다. 하노이의 탑은 재귀적 해법, 반복적 해법, 이진법 및 그레이 코드 해법 등 다양한 해결 방법을 가지고 있으며, 4개 이상의 기둥을 사용하는 변형도 존재한다. 문제 해결 능력, 심리학 연구, 프로그래밍 교육, 데이터 백업 등 다양한 분야에 응용되며, 대중문화에서도 소재로 활용된다.

더 읽어볼만한 페이지

  • 기계식 퍼즐 - 알렉산더의 별
    알렉산더의 별은 수학자 애덤 알렉산더가 고안하여 특허를 취득하고 판매된 3차원 퍼즐로, 조각들을 재배열하여 각 쌍의 평행 평면이 단일 색상으로 구성되도록 하는 것을 목표로 하며 100대 게임 중 하나로 선정되기도 했다.
  • 기계식 퍼즐 - 직소 퍼즐
    직소 퍼즐은 그림이 인쇄된 조각들을 맞춰 완성하는 퍼즐로, 교육용 지도에서 유래되어 대공황 시기에 인기를 얻었으며, 현재는 다양한 재료와 형태로 제작되고 사회적 의미도 지닌다.
하노이의 탑
기본 정보
하노이 탑
8개의 원반으로 이루어진 하노이 탑
종류수학 퍼즐
고안자에두아르 뤼카
발명 연도1883년
수학적 분석
최소 이동 횟수2n − 1 (n은 원반의 개수)

2. 유래

프랑스의 수학자 에두아르 뤼카( Édouard Lucas|에두아르 뤼카fra )가 1883년 '클라우스 교수'(professeur N. Claus)라는 필명으로 처음 발표하였다.[50] 이 필명은 뤼카(Lucas)의 애너그램이며, 뤼카는 게임과 함께 제공된 설명서에서 이 게임이 통킹에서 유래했다고 밝혔다. 설명서에는 'Li-sou-stian 대학 근무의 샴 출신 N. Claus 교수'라는 소개가 있었는데, 이 역시 뤼카가 근무했던 리세 생 루이(Saint-Louis)와 '아미앵 출신의 뤼카'(Lucas d'Amiens)의 애너그램으로, 실제로는 뤼카의 창작물로 여겨진다.[5][6][7] 1년 후 드 파르빌(Henri de Parville)은 이 사실을 밝히며 다음과 같은 브라흐마 탑 전설을 소개했다.[51]

>인도 베나레스(또는 바라나시)에 있는 한 사원에는 세상의 중심을 나타내는 큰 돔이 있고, 그 안에 세 개의 다이아몬드 바늘(또는 청동판 위의 바늘)이 세워져 있다. 바늘의 높이는 1 큐빗이고 굵기는 벌의 몸통만 하다. 그중 한 바늘에는 천지창조 때 신(브라흐마 또는 야훼)이 64개의 순금 원반을 끼워 놓았다. 가장 큰 원판이 바닥에 놓여 있고, 나머지 원판들이 점점 작아지며 꼭대기까지 쌓여 있다. 이것은 신성한 브라흐마의 탑이다. 브라흐마의 지시에 따라 승려(또는 사제)들은 밤낮으로 규칙에 따라 원판을 하나씩 다른 바늘로 옮긴다. 이 작업이 끝나면 탑은 무너지고 세상은 종말을 맞이하게 된다.[51][10]

이 전설은 뤼카가 게임의 신비로운 분위기를 더하기 위해 창작한 것으로 보이며, 패키지에는 '하노이의 탑'으로, 동봉된 리플릿에는 '브라흐마의 탑'으로 소개되었다. 하노이는 통킹의 중심 도시이며, 브라흐마는 힌두교나 불교의 창조신이다. 이 전설에는 사원이 수도원이고 승려가 수도승이라거나, 바늘이 대리석 기둥이라거나, 탑이 세상의 시작에 만들어졌다거나, 하루에 한 번만 원반을 옮길 수 있다는 등 다양한 변형이 존재한다.[5]

만약 전설대로 64개의 원반을 옮겨야 한다면, 최소 이동 횟수는 264 − 1회, 즉 18,446,744,073,709,551,615회(약 1844경 회)이다. 1초에 원반 하나를 옮긴다고 가정해도 약 5850억 년이 걸리는 계산인데,[11] 이는 현재 추정되는 우주의 나이(약 137억 년)보다 훨씬 긴 시간이다.

하노이의 탑은 이후 라우즈 볼, 가드너 등에 의해 소개되면서 널리 알려졌다. 일본에서는 1907년(메이지 40년)에 출판된 『세계 유희법 대전』이라는 책을 통해 소개되었으며, 이 책에는 원반 이동 횟수 계산 등 수학적인 분석도 포함되어 있었다. 이를 통해 한국에도 알려지게 된 것으로 보인다. 뤼카는 이후 자신의 본명을 밝히고 1889년 소책자를 출판했으며,[8] 사후 출판된 『수학 오락』에도 하노이의 탑이 실렸다.[9]

3. 규칙

6개의 원반 하노이의 탑 문제를 해결하는 반복 알고리즘의 애니메이션


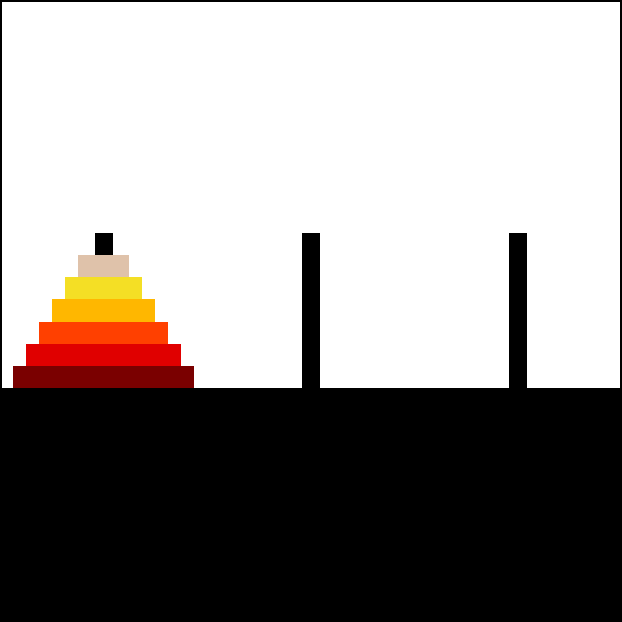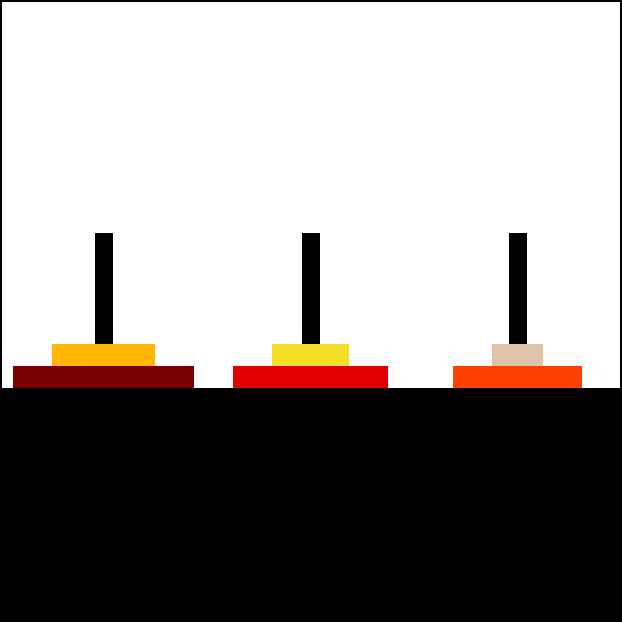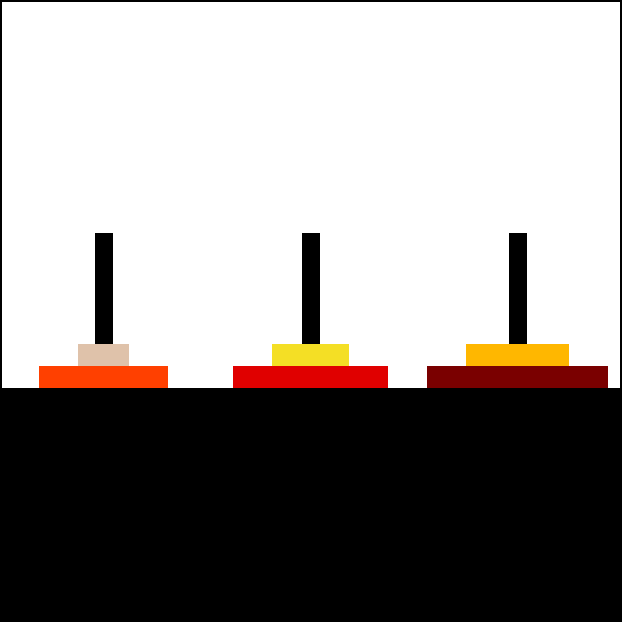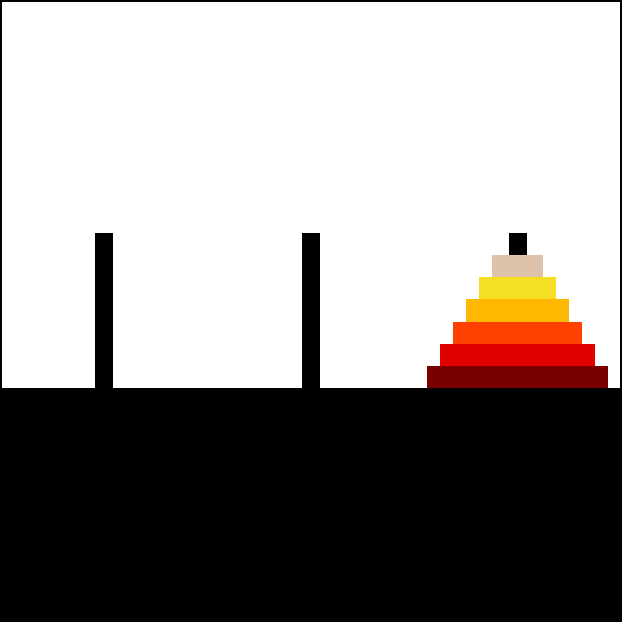
하노이의 탑은 다음 규칙에 따라 모든 원반을 시작 기둥이 아닌 다른 기둥으로 옮기면 완료된다.

  • 3개의 기둥과 가운데에 구멍이 뚫린, 크기가 다른 여러 개의 원반으로 구성된다.
  • 처음에는 모든 원반이 왼쪽 기둥에 작은 것이 위로 오도록 순서대로 쌓여 있다.
  • 원반은 한 번에 하나씩만 옮길 수 있으며, 어떤 기둥으로든 옮길 수 있다.
  • 작은 원반 위에 큰 원반을 올려놓을 수는 없다.


''n''개의 원반을 가진 하노이의 탑 퍼즐을 해결하는 데 필요한 최소 이동 횟수는 2''n'' − 1번이다.[12][48] 이는 ''n''번째 메르센 수 M''n''과 같다.

간단한 해법 중 하나는 가장 작은 원반과 그 외의 원반을 번갈아 옮기는 것이다. 가장 작은 원반을 옮길 때는 항상 정해진 방향(원반 개수가 짝수면 오른쪽, 홀수면 왼쪽)으로 다음 기둥으로 옮긴다. 만약 해당 방향에 기둥이 없다면 반대쪽 끝 기둥으로 옮긴 후, 다시 원래 정해진 방향으로 이동을 계속한다. 예를 들어 원반이 3개(홀수)라면, 가장 작은 원반을 목표 기둥으로 옮기고, 이후 왼쪽 방향으로 계속 옮긴다. 가장 작은 원반이 아닌 다른 원반을 옮길 차례에는 규칙에 맞는 이동 방법이 하나뿐이다. 이 방법을 따르면 최소 이동 횟수로 퍼즐을 완료할 수 있다.[13]

또한, 재귀적인 방법으로 해법을 생각할 수 있다. ''n''개의 원반을 옮기기 위해, 먼저 맨 아래의 가장 큰 원반을 제외한 ''n''-1개의 원반 묶음을 중간 기둥으로 옮긴다. 그 다음, 가장 큰 원반을 목표 기둥으로 옮긴다. 마지막으로 중간 기둥에 있는 ''n''-1개의 원반 묶음을 목표 기둥 위의 가장 큰 원반 위로 옮기면 된다.

이러한 재귀적인 구조 때문에 하노이의 탑 문제는 재귀를 설명하기 위한 컴퓨터 프로그래밍의 기초 예제로 자주 사용된다. 다만, 원반의 개수 ''n''이 커질수록 필요한 이동 횟수는 메르센 수처럼 급격히 증가한다.

4. 해법

하노이의 탑 문제는 재귀적인 사고방식을 통해 효과적으로 해결할 수 있다. 문제 해결의 핵심 원리는 주어진 문제를 해결 방법이 동일한 더 작은 크기의 여러 하위 문제로 나누는 것이다. 즉, ''n''개의 원반을 옮기는 전체 문제는 ''n''-1개의 원반을 옮기는 더 작은 문제로 축소될 수 있으며, 이 과정을 반복하여 결국 가장 간단한 문제(원반 1개 옮기기 또는 0개 옮기기)에 도달하게 된다.

이러한 재귀적 접근 방식은 수학적 귀납법을 이용해 그 정확성을 증명할 수 있으며, 프로그래밍 교육에서 재귀 개념을 설명하는 대표적인 예시로 자주 활용된다.[48] 하노이의 탑 문제에는 이러한 재귀적 해법 외에도, 규칙적인 패턴을 이용한 반복적 해법, 이진법이나 그레이 코드의 특성을 활용한 해법 등 다양한 해결 방법이 존재한다.

4. 1. 재귀적 해법

4개의 원반을 가진 하노이의 탑 퍼즐에 대한 재귀적 해결책 그림.


재귀적으로 문제를 해결하는 핵심 아이디어는 주어진 문제를 해결 방법이 동일한 더 작은 크기의 여러 하위 문제로 나누는 것이다. 각 하위 문제에 동일한 해결 절차를 반복 적용하면, 문제는 점점 작아져 결국 가장 간단한 형태인 '기본 사례'에 도달하게 된다. 하노이의 탑 문제에서 이 아이디어를 적용해 보자.

  • 세 개의 기둥을 각각 A(시작), B(보조), C(목표)라고 부른다.
  • 옮겨야 할 전체 원반의 개수를 ''n''개라고 한다.
  • 원반은 크기 순서대로 번호를 매기는데, 가장 작은 맨 위 원반을 1, 가장 큰 맨 아래 원반을 ''n''이라고 한다.


''n''개의 원반을 기둥 A에서 기둥 C로 옮기는 재귀적인 방법은 다음과 같다 (기둥 B를 보조 기둥으로 사용).

# '''1단계:''' 맨 위의 ''n''-1개 원반을 기둥 A에서 기둥 B로 옮긴다. 이때 기둥 C를 보조 기둥으로 사용한다. 이 과정은 원래 문제와 동일한 규칙을 따르는 더 작은 문제이다.

# '''2단계:''' 기둥 A에 남아있는 가장 큰 원반(''n''번 원반)을 기둥 A에서 기둥 C로 옮긴다. 이 이동은 항상 가능하다. 왜냐하면 ''n''-1개의 작은 원반들이 모두 기둥 B에 있기 때문이다.

# '''3단계:''' 기둥 B에 있는 ''n''-1개의 원반을 기둥 B에서 기둥 C로 옮긴다. 이때 기둥 A를 보조 기둥으로 사용한다. 이 과정 역시 더 작은 문제이다.

이 과정은 ''n''=1이 될 때까지 반복된다. 원반이 하나일 경우(n=1), 그냥 시작 기둥에서 목표 기둥으로 옮기면 된다. 원반이 없을 경우(n=0), 아무것도 하지 않는다. 이것이 재귀 호출이 멈추는 '기본 사례'이다.

이 방법은 시작 기둥, 목표 기둥, 보조 기둥이 어떤 것이든 동일하게 적용될 수 있다. 예를 들어 A에서 C로 옮기는 방법을 안다면, 기둥 이름만 바꿔서 A에서 B로 옮기거나 B에서 C로 옮기는 등 다른 모든 경우에도 적용할 수 있다. 이는 문제 자체가 기둥 이름의 순서와 관계없이 대칭적이기 때문이다.

수학적 귀납법을 사용하면 이 재귀적 해법이 항상 올바른 답을 제공하며, 동시에 필요한 최소 이동 횟수로 문제를 해결한다는 것을 증명할 수 있다. ''n''개의 원반을 옮기는 데 필요한 최소 이동 횟수 T_n은 점화 관계 T_n = 2T_{n-1} + 1 (단, T_0 = 0)으로 표현되며, 이를 풀면 T_n = 2^n - 1 이라는 결과를 얻는다. 즉, ''n''개의 원반을 옮기려면 최소 2^n - 1번의 이동이 필요하다.[48]

4. 2. 반복적 해법



하노이의 탑 문제는 재귀 호출 없이 반복적인 방식으로도 해결할 수 있다.

한 가지 간단한 해법은 가장 작은 원반과 가장 작은 원반이 아닌 다른 원반의 이동을 번갈아 수행하는 것이다.[13][48] 기둥을 왼쪽부터 A, B, C 순서로 놓았다고 가정한다.

1. 가장 작은 원반을 옮길 차례:

  • 원반의 총 개수(''n'')가 홀수이면, 가장 작은 원반을 항상 왼쪽 방향(A→C, C→B, B→A 순환)으로 다음 기둥으로 옮긴다. 즉, C→B→A→C 순서로 움직인다.[13][48]
  • 원반의 총 개수(''n'')가 짝수이면, 가장 작은 원반을 항상 오른쪽 방향(A→B, B→C, C→A 순환)으로 다음 기둥으로 옮긴다. 즉, B→C→A→B 순서로 움직인다.[13][48]
  • 만약 정해진 방향의 다음 기둥으로 옮길 수 없다면(예: 해당 위치에 기둥이 없거나 규칙에 어긋나는 경우), 가능한 다른 기둥(반대편 끝 기둥)으로 옮긴 후, 다음 이동 시에는 원래 정해진 방향 규칙을 계속 따른다.[13]

2. 가장 작은 원반이 아닌 다른 원반을 옮길 차례:

  • 이때는 옮길 수 있는 (가장 작은 원반이 아닌) 원반과 그 원반을 옮길 수 있는 기둥이 각각 하나뿐이다. 즉, 가장 작은 원반을 제외하고 규칙에 위반되지 않는 유일한 이동(작은 원반을 큰 원반 위로 옮기는 것)을 수행한다.[13][48]


이 과정을 반복하면 총 2''n'' − 1 번의 이동으로 퍼즐을 해결할 수 있다.[48]

또 다른 반복적 해법은 다음과 같은 세 가지 유형의 이동을 순서대로 반복하는 것이다. 단, 각 단계에서는 규칙에 맞는 유효한 이동만 수행한다.

  • 기둥 A와 기둥 B 사이에서 원반 하나를 옮긴다 (A→B 또는 B→A).
  • 기둥 A와 기둥 C 사이에서 원반 하나를 옮긴다 (A→C 또는 C→A).
  • 기둥 B와 기둥 C 사이에서 원반 하나를 옮긴다 (B→C 또는 C→B).


이 과정을 목표 상태에 도달할 때까지 반복한다. 이 방법을 따르면, 원반의 개수가 홀수이면 최종적으로 모든 원반이 목표 기둥(보통 C)이 아닌 기둥 B에 쌓이고, 짝수일 경우에는 목표 기둥인 기둥 C에 쌓이게 된다. (시작 기둥 A 기준)

4. 3. 이진법 및 그레이 코드 해법

원반의 위치는 이동 횟수를 이진수로 표현하여 더 직접적으로 결정할 수 있다. 이동 시작 상태를 0번 이동(모든 비트가 0)으로 하고, 최종 상태는 모든 비트가 1인 상태로 간주한다. 다음과 같은 규칙을 따른다.

  • 각 원반에 하나의 이진수 숫자(비트)가 할당된다.
  • 가장 왼쪽의 비트는 가장 큰 원반을 나타낸다. 0은 시작 기둥, 1은 최종 기둥에 있음을 의미한다. (원반 수가 홀수이면 오른쪽 기둥, 짝수이면 가운데 기둥이 최종 기둥이다.)
  • 비트열을 왼쪽에서 오른쪽으로 읽으며 각 비트로 해당 원반의 위치를 결정한다.
  • 어떤 비트가 바로 왼쪽(더 큰 원반의 비트)과 같은 값을 가지면, 해당 원반은 더 큰 원반과 같은 기둥 위에 쌓여 있다는 의미이다. 즉, 0이나 1이 연속되면 해당 원반들은 모두 같은 기둥에 있다.
  • 어떤 비트가 바로 왼쪽 비트와 다른 값을 가지면, 해당 원반은 더 큰 원반의 왼쪽 또는 오른쪽에 위치한다. 방향은 다음 규칙으로 결정된다.
  • 시작 기둥을 왼쪽으로 간주하고, 기둥은 순환한다고 가정한다 (오른쪽 기둥 옆은 왼쪽 기둥, 왼쪽 기둥 옆은 오른쪽 기둥).
  • 해당 원반보다 크면서 같은 기둥에 있는 원반의 수를 ''n''이라고 하자. 가장 큰 원반이 시작(왼쪽) 기둥에 있다면 ''n''에 1을 더한다.
  • ''n''이 짝수이면 원반은 오른쪽으로 한 칸 이동한 기둥에, ''n''이 홀수이면 왼쪽으로 한 칸 이동한 기둥에 위치한다. (단, 전체 원반 수가 짝수일 때는 방향이 반대이다.)


예를 들어 8개의 원반이 있는 경우:

  • 0번 이동: 이진수 00000000
  • 모든 비트가 0이므로 모든 원반이 시작(왼쪽) 기둥에 쌓여 있다.
  • 28 − 1번 이동: 이진수 11111111
  • 가장 큰 원반(첫 번째 비트)은 1이므로 최종(가운데) 기둥에 있다.
  • 다른 모든 원반의 비트도 1이므로, 모든 원반이 최종 기둥에 쌓여 퍼즐이 완료된다.
  • 216번 이동: 이진수 11011000 (8개 원반은 짝수이므로, 방향 규칙 반대 적용)
  • 원반 8 (가장 큰 원반, 첫 번째 비트 1): 최종(가운데) 기둥.
  • 원반 7 (두 번째 비트 1): 원반 8과 같은 값이므로 같은 기둥(가운데) 위에 있다.
  • 원반 6 (세 번째 비트 0): 이전 비트(1)와 다르다. ''n''=1 (원반 8이 최종 기둥에 있으므로 1을 더함)은 홀수. 원반 수가 짝수이므로 원래 왼쪽 이동 대신 오른쪽으로 한 칸 이동한 기둥(오른쪽 기둥)에 있다.
  • 원반 5 (네 번째 비트 1): 이전 비트(0)와 다르다. ''n''=0 (원반 6과 같은 기둥에 더 큰 원반 없음). 짝수. 원반 수가 짝수이므로 원래 오른쪽 이동 대신 왼쪽으로 한 칸 이동한 기둥(가운데 기둥)에 있다.
  • 원반 4 (다섯 번째 비트 1): 원반 5와 같은 값이므로 같은 기둥(가운데) 위에 있다.
  • 원반 3 (여섯 번째 비트 0): 이전 비트(1)와 다르다. ''n''=2 (원반 5, 4가 같은 기둥에 있음). 짝수. 원반 수가 짝수이므로 원래 오른쪽 이동 대신 왼쪽으로 한 칸 이동한 기둥(왼쪽 기둥)에 있다.
  • 원반 2 (일곱 번째 비트 0): 원반 3과 같은 값이므로 같은 기둥(왼쪽) 위에 있다.
  • 원반 1 (여덟 번째 비트 0): 원반 2와 같은 값이므로 같은 기둥(왼쪽) 위에 있다.


이동 횟수 ''m''의 이진수 표현과 비트 연산을 사용하면 ''m''번째 이동 시 원반이 이동하는 시작 기둥과 목표 기둥을 찾을 수도 있다. C 언어 표기법으로, ''m''번째 이동은 기둥 `(m & m - 1) % 3`에서 기둥 `((m | m - 1) + 1) % 3`으로 원반을 옮기는 것이다 (기둥 번호는 0, 1, 2). 시작 기둥은 0이고, 최종 기둥은 원반 수의 홀짝성에 따라 1 또는 2가 된다. 다른 공식으로는 기둥 `(m - (m & -m)) % 3`에서 기둥 `(m + (m & -m)) % 3`으로 이동하는 것이다.

또한, 이동할 원반은 이동 횟수 ''m''을 2로 몇 번 나눌 수 있는지(즉, ''m''의 이진수 표현에서 오른쪽 끝에 있는 0의 개수, 후행 0 세기)로 결정된다. 이동 횟수를 1부터 세고 원반 번호를 0(가장 작은 원반), 1, 2, ... 순서로 매기면, ''m''번째 이동에서 움직이는 원반 번호는 ''m''의 후행 0의 개수와 같다. 이를 이용하면 이전 상태 정보 없이 ''m''번째 이동 후 원반 위치를 빠르게 계산하는 비재귀적 컴퓨터 구현이 가능하다.[14]

그레이 코드는 이 퍼즐을 해결하는 또 다른 방법을 제공한다. 그레이 코드에서는 숫자를 이진수로 표현하지만, 인접한 숫자 간에는 단 하나의 비트만 다르다는 특징이 있다. 하노이 탑의 원반 수와 같은 비트 수의 그레이 코드를 0부터 순서대로 생성하면, 각 단계에서 변화하는 비트가 바로 이동해야 할 원반에 해당한다. 최하위 비트는 가장 작은 원반, 최상위 비트는 가장 큰 원반을 나타낸다.

이동 횟수를 1부터 세고 원반 번호를 0부터 매기면, ''m''번째 이동에서 움직일 원반의 번호는 ''m''을 2로 나눌 수 있는 횟수와 같다. 이는 이진법 해법에서 후행 0의 개수를 세는 것과 동일하다.

이 방법은 어떤 원반을 움직여야 하는지는 알려주지만, 어느 기둥으로 옮겨야 하는지는 직접 알려주지 않는다. 가장 작은 원반(0번 원반)의 경우 항상 두 가지 이동 가능성이 있다. 다른 원반들은 일반적으로 옮길 수 있는 기둥이 하나뿐이다 (단, 모든 원반이 한 기둥에 모여있는 경우는 제외). 가장 작은 원반의 이동 방향은 다음과 같은 규칙으로 결정된다.

  • ''f''를 시작 기둥, ''t''를 목표 기둥, ''r''을 나머지 기둥이라고 하자.
  • 원반 수가 홀수이면, 가장 작은 원반은 ''f'' → ''t'' → ''r'' → ''f'' → ... 순서로 기둥을 순환한다.
  • 원반 수가 짝수이면, 가장 작은 원반은 ''f'' → ''r'' → ''t'' → ''f'' → ... 순서로 기둥을 순환한다.[15]


그레이 코드 해법에서 각 단계별로 이동하는 원반의 크기(번호+1) 순서는 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1, ... 과 같은 수열을 이룬다. 이 수열은 자 함수(Ruler function)라고도 하며, 각 항은 해당 이동 횟수 ''m''을 인수분해했을 때 2의 거듭제곱 지수에 1을 더한 값과 같다.[16]

5. 수학적 분석

하노이의 탑 퍼즐은 3개의 기둥과 중앙에 구멍이 뚫린 크기가 다른 여러 개의 원반으로 구성된다. 처음에는 모든 원반이 한 기둥(보통 왼쪽)에 작은 것이 위로 오도록 순서대로 쌓여 있다. 목표는 다음 규칙에 따라 모든 원반을 다른 기둥(보통 오른쪽)으로 옮기는 것이다.


  • 원반은 한 번에 한 개씩만 옮길 수 있다.
  • 한 기둥에서 원반을 빼서 다른 기둥으로 바로 옮긴다.
  • 작은 원반 위에 큰 원반을 올려놓을 수 없다.


n개의 원반을 모두 옮기려면 최소 2^n - 1번의 이동이 필요하다.[48] 이 공식은 메르센 수 M_n의 정의식이기도 하며, 즉 주어진 원반 n개일 때 최소 이동 횟수는 n번째 메르센 수와 같다.

이 문제의 해결책은 재귀적으로 생각할 수 있다. 탑을 "가장 아래에 있는 원반"과 "나머지 n-1개의 원반군"으로 나눈다. 해결 과정은 다음과 같다.

1. 나머지 n-1개의 원반군을 시작 기둥에서 중간 기둥으로 옮긴다 (2^{n-1}-1번 이동).

2. 가장 아래에 있는 원반(가장 큰 원반)을 시작 기둥에서 목표 기둥으로 옮긴다 (1번 이동).

3. 나머지 n-1개의 원반군을 중간 기둥에서 목표 기둥으로 옮긴다 (2^{n-1}-1번 이동).

이 재귀적인 구조 때문에 하노이의 탑 문제는 재귀적 컴퓨터 프로그램의 간단한 예제로 자주 사용된다. 마찬가지로 재귀의 예제로 많이 사용되는 피보나치 수와 같이 n이 커지면 결과도 방대해진다.

퍼즐의 목표를 일반화하여, 모든 원반이 반드시 같은 기둥에 있지 않은 임의의 주어진 원반 배치에서 시작하여 최소 횟수의 이동으로 다른 주어진 배치에 도달하는 문제를 생각할 수 있다. 일반적으로 이 문제를 해결하기 위한 최단 이동 순서를 계산하는 것은 매우 어려울 수 있다. 안드레아스 힌츠(Andreas Hinz)는 최단 이동 순서에서 이동해야 하는 가장 큰 원반(초기 및 최종 배치 모두에서 같은 기둥을 차지하는 가장 큰 원반은 무시)이 정확히 한 번 또는 정확히 두 번 이동한다는 관찰에 기반한 해결책을 제시했다.

이 일반화된 문제와 관련된 수학은 임의로 선택된 두 개의 초기 및 최종 원반 배치 간의 최단 이동 순서에서 "평균" 이동 횟수를 고려할 때 더욱 흥미로운 수학적 논의로 이어진다. 힌츠와 찬 탓-훙(Chan Tat-Hung)은 독립적으로 발견했으며[26][27](또한 [28]) n개의 원반으로 이루어진 하노이의 탑에서 평균 이동 횟수는 다음의 정확한 공식으로 주어진다고 밝혔다.

: \frac{466}{885}\cdot 2^n - \frac{1}{3} - \frac{3}{5}\cdot \left(\frac{1}{3}\right)^n +

\left(\frac{12}{59} + \frac{18}{1003}\sqrt{17}\right)\left(\frac{5+\sqrt{17}}{18}\right)^n +

\left(\frac{12}{59} - \frac{18}{1003}\sqrt{17}\right)\left(\frac{5-\sqrt{17}}{18}\right)^n.

충분히 큰 ''n''에 대해서는 첫 번째와 두 번째 항만 0으로 수렴하지 않으므로, 점근적 표현 466/885\cdot 2^n - 1/3 + o(1)을 얻는다 (n \to \infty일 때). 따라서 직관적으로, 임의로 선택된 배치에서 다른 임의로 선택된 배치로 이동할 때 필요한 평균 이동 횟수는 모든 원반을 한 기둥에서 다른 기둥으로 옮기는 가장 어려운 경우(2^n - 1번 이동)의 약 466/885 \approx 52.6\% 정도임을 알 수 있다. 상수 466/885가 나타나는 것에 대한 또 다른 설명과 최단 경로를 계산하기 위한 새롭고 다소 개선된 알고리즘은 로믹(Romik)에 의해 제시되었다.[29]

6. 변형

자석 하노이 탑에서는 각 원반은 북쪽과 남쪽의 두 가지 면(일반적으로 "빨간색"과 "파란색")을 가진다. 같은 극끼리는 서로 닿을 수 없도록 각 원반의 자석이 방지하며, 원반을 움직일 때마다 뒤집어야 한다.

6. 1. 인접 기둥 이동 제한

원반을 인접한 기둥 사이에서만 움직일 수 있다면 (즉, 기둥 A, B, C가 주어졌을 때, A에서 C로 직접 이동할 수 없다면), n개의 원반을 기둥 A에서 기둥 C로 옮기는 데 3n - 1번의 이동이 필요하다. 이 해법은 모든 3n개의 유효한 위치를 사용하며, 항상 이전 이동을 취소하지 않는 고유한 이동을 수행한다. 모든 원반이 기둥 B에 있는 위치는 중간 지점, 즉 (3n - 1) / 2번 이동 후에 도달한다.

6. 2. 순환 하노이 탑

순환 하노이 탑(Cyclic Hanoieng)은 세 개의 기둥(A, B, C)이 원형으로 배열되어 있는 하노이의 탑 변형 문제이다. 기둥의 순서는 시계 방향으로 A → B → C → A, 반시계 방향으로 A → C → B → A로 정의된다. 이 문제의 핵심 규칙은 원반을 반드시 시계 방향으로만 한 칸씩 옮겨야 한다는 것이다.[19] 문제를 해결하기 위해서는 옮겨야 할 원반의 순서를 정하는 것으로 충분하며, 이는 두 개의 상호 재귀적인 절차를 통해 찾을 수 있다.

''n''개의 원반을 인접한 목표 기둥으로 '''반시계 방향'''으로 옮기는 절차는 다음과 같다.

# ''n'' − 1개의 원반을 '''반시계 방향'''으로 목표 기둥으로 옮긴다.

# ''n''번 원반을 시계 방향으로 한 단계 옮긴다.

# ''n'' − 1개의 원반을 '''시계 방향'''으로 시작 기둥으로 옮긴다.

# ''n''번 원반을 시계 방향으로 한 단계 옮긴다.

# ''n'' − 1개의 원반을 '''반시계 방향'''으로 목표 기둥으로 옮긴다.

''n''개의 원반을 인접한 목표 기둥으로 '''시계 방향'''으로 옮기는 절차는 다음과 같다.

# ''n'' − 1개의 원반을 '''반시계 방향'''으로 여분 기둥으로 옮긴다.

# ''n''번 원반을 시계 방향으로 한 단계 옮긴다.

# ''n'' − 1개의 원반을 '''반시계 방향'''으로 목표 기둥으로 옮긴다.

C(n)을 n개의 원반을 시계 방향으로 옮기는 이동 순서, A(n)을 반시계 방향으로 옮기는 이동 순서라고 할 때, 다음과 같은 관계식과 예시를 얻을 수 있다.

이동 방향공식예시 (n=1)예시 (n=2)
시계 방향 (C(n))A(n−1) n A(n−1)C(1) = 1C(2) = 1 1 2 1 1
반시계 방향 (A(n))A(n−1) n C(n−1) n A(n−1)A(1) = 1 1A(2) = 1 1 2 1 2 1 1



순환 하노이 탑 문제의 해법은 몇 가지 흥미로운 특징을 가진다.

# 한 기둥에서 다른 기둥으로 원반 탑 전체를 옮기는 이동 패턴은 중심점을 기준으로 대칭적이다.

# 가장 작은 원반(1번 원반)은 가장 먼저 옮겨지고, 모든 이동이 끝난 후 마지막으로 다시 옮겨진다.

# 가장 작은 원반의 이동과 다른 원반 하나의 이동이 번갈아 나타난다.

# 위에서 설명한 C(n)과 A(n) 절차로 계산된 원반 이동 횟수는 해당 방향으로 옮기는 데 필요한 최소 횟수이다.

6. 3. 4개 이상의 기둥

세 개의 말뚝을 사용하는 하노이의 탑 문제는 간단한 재귀 해법이 오래전부터 알려져 있었지만, 네 개의 말뚝을 사용하는 문제, 이른바 레브의 퍼즐(Reve's puzzle)에 대한 최적 해법은 2014년에 부쉬(Bousch)에 의해 증명되었다.[20]

하지만 네 개 이상의 말뚝을 사용하는 경우, 1941년에 제안된 프레임-스튜어트(Frame-Stewart) 알고리즘이 알려져 있으나, 이것이 최적의 해법인지는 아직 증명되지 않았다.[21] 프레임-스튜어트 알고리즘을 적용하여 문제를 해결하는 데 필요한 최소 이동 횟수를 구하는 공식에 대한 자세한 내용은 관련 논문에서 찾아볼 수 있다.[22] 네 개 말뚝 문제의 다른 변형에 대해서는 폴 스톡마이어(Paul Stockmeyer)의 조사 논문을 참고할 수 있다.[23]

소위 부쿠레슈티의 탑(Towers of Bucharest)과 클라겐푸르트의 탑(Towers of Klagenfurt) 게임 구성은 각각 삼진법과 오진법 그레이 코드를 생성하는 것과 관련이 있다.[47]

=== 프레임-스튜어트 알고리즘 ===

프레임-스튜어트 알고리즘은 다음과 같이 재귀적으로 설명할 수 있다.

  • n: 옮겨야 할 원반의 개수
  • r: 사용 가능한 말뚝의 개수
  • T(n,r): r개의 말뚝을 사용하여 n개의 원반을 옮기는 데 필요한 최소 이동 횟수


알고리즘 단계:

# 적절한 개수 k (1 \leq k < n)를 선택하여, 맨 위 k개의 원반을 출발 말뚝이나 도착 말뚝이 아닌 중간 말뚝 하나로 옮긴다. 이 과정은 T(k,r)번의 이동이 필요하다.

# 가장 큰 원반부터 n-k개의 원반을 남은 r-1개의 말뚝을 사용하여 도착 말뚝으로 옮긴다. 이때 k개의 원반이 놓인 말뚝은 사용하지 않는다. 이 과정은 T(n-k,r-1)번의 이동이 필요하다.

# 마지막으로, 중간 말뚝에 옮겨 놓았던 k개의 원반을 도착 말뚝으로 옮긴다. 이 과정은 다시 T(k,r)번의 이동이 필요하다.

전체 과정에 필요한 이동 횟수는 2T(k,r)+T(n-k,r-1)이다. 이 값이 최소가 되도록 중간 단계의 원반 개수 k를 선택해야 한다. 4개의 말뚝(r=4)의 경우, 최적의 k 값은 n - \left\lfloor\sqrt{2n+1}\right\rceil + 1로 주어진다. 여기서 \left\lfloor\cdot\right\rceil는 가장 가까운 정수 함수를 의미한다.[24] 예를 들어, 펜실베이니아 대학교(UPenn)의 CIS 194 강좌에서는 15개의 원반과 4개의 말뚝 문제의 최적 해가 129단계라고 제시하며, 이는 위 공식으로 계산된 k 값을 사용할 때 얻어진다.[25]

프레임-스튜어트 알고리즘은 임의의 말뚝 개수 r에 대해서도 최적의 해법일 것으로 추정된다. 이 알고리즘을 사용할 때 필요한 이동 횟수는 Θ(''n''1/(''r''−2)) 로 표현된다 (단, r은 고정된 값).

6. 4. 이색 하노이 탑

이 유명한 하노이의 탑 퍼즐의 변형은 1988년 7월에 열린 제2회 프랑스 수학 및 논리 게임 챔피언십에서 초등학교 3~6학년 학생들에게 제시되었다.[30]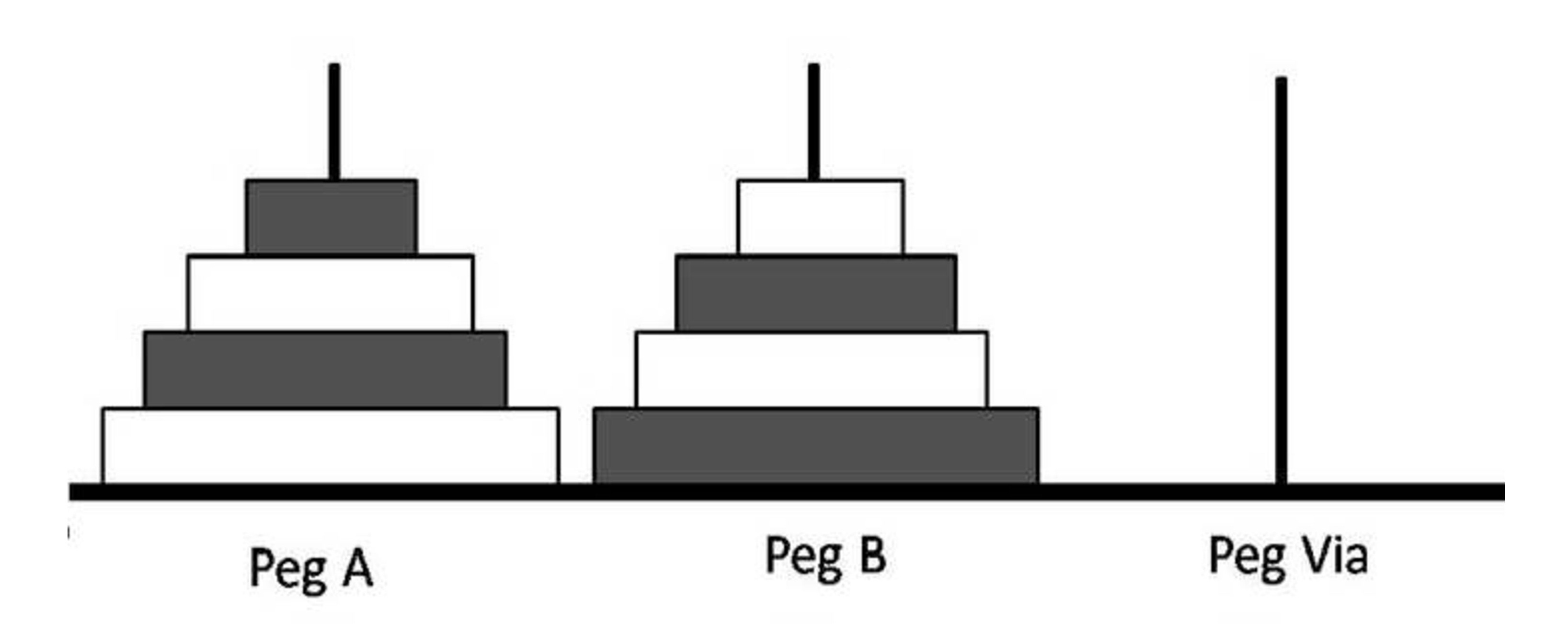





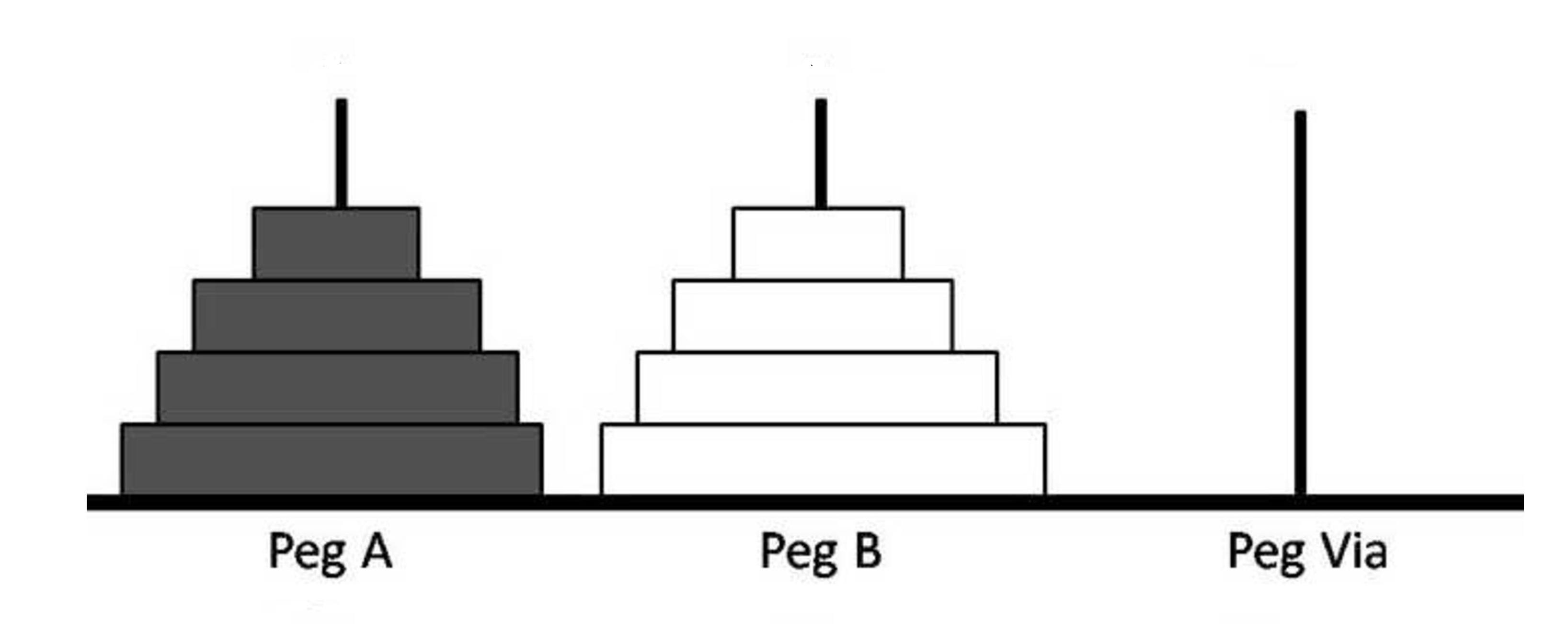
이 퍼즐의 규칙은 기본적으로 동일하다. 원반은 한 번에 하나씩 기둥 사이에서 옮겨진다. 더 큰 원반을 작은 원반 위에 올려놓을 수 없다. 차이점은 이제 모든 크기에 대해 검은색과 흰색 원반이 각각 하나씩 있다는 것이다. 또한, 초기 상태는 색상이 번갈아 가며 쌓인 두 개의 원반 탑이다. 퍼즐의 목표는 탑을 단색(같은 색상)으로 만드는 것이다. 탑의 맨 아래에 있는 가장 큰 원반은 위치를 바꾸는 것으로 간주한다.

7. 응용

하노이 탑은 문제 해결에 대한 심리학 연구에 자주 사용된다.[35] 또한 신경심리학적 진단 및 집행 기능 장애 치료를 위한 런던 탑 테스트라는 이 작업의 변형이 존재한다.[35] 전두엽 결함을 평가하려는 신경 심리학자들이 테스트로도 사용한다.[39]

장과 노먼[36]은 과제 설계에서 표현 효과의 영향을 연구하기 위해 이 게임의 몇 가지 동형(동등한) 표현을 사용했다. 그들은 게임 구성 요소의 물리적 설계를 변경하여 게임 규칙이 표현되는 방식을 변경함으로써 사용자 성능에 영향을 미친다는 것을 시연했다. 이 지식은 인간-컴퓨터 상호 작용의 표현을 위한 TURF 프레임워크[37] 개발에 영향을 미쳤다.

하노이 탑은 여러 테이프/미디어가 관련된 컴퓨터 데이터 백업을 수행할 때 백업 로테이션 방식으로도 사용된다.[38] 또한, 초보 프로그래밍 학생들에게 재귀 알고리즘을 가르치는 데 널리 사용된다. 이 퍼즐의 그림 버전은 emacs 편집기에 프로그래밍되어 있으며, M-x hanoi를 입력하여 액세스할 수 있다. Prolog로 작성된 샘플 알고리즘도 있다.

2010년, 연구자들은 개미 종 ''아르헨티나 개미''가 비선형 동역학과 페로몬 신호를 통해 하노이 탑 문제의 3디스크 버전을 성공적으로 해결할 수 있다는 실험 결과를 발표했다.[40]



2014년, 과학자들은 하노이 탑과 유사한 구조의 다층 팔라듐 나노시트를 합성했다.[34]

8. 대중문화 속 하노이의 탑

하노이의 탑 퍼즐은 다양한 형태의 대중문화 작품 속에서 소재로 활용되었다.


  • 9장의 카드를 사용하는 솔리테어 게임으로 각색되어 '타워 오브 하노이'(Tower of Hanoy)라는 이름으로 등장했다.[31][32] 원본 이름 'Hanoi'와 철자가 다른 'Hanoy'가 의도적인 변경인지 단순한 실수인지는 알려지지 않았다.[33]
  • 에릭 프랭크 러셀의 과학 소설 "Now Inhale"에서는, 주인공이 외계 행성의 포로가 되어 처형 전까지 게임을 해야 하는 상황에 놓인다. 주인공은 구조선 도착까지 1년 이상이 걸릴 것을 예상하고 64개의 원반으로 이루어진 하노이의 탑 게임을 선택한다. 이 소설은 세상의 종말까지 게임을 계속하는 불교 승려들의 전설을 언급하기도 한다.[41][42][43]
  • 1966년 방영된 영국의 SF 드라마 ''닥터 후''의 "천상의 장난감 제작자" 에피소드에서는 악당인 천상의 장난감 제작자가 주인공 닥터에게 10개의 조각으로 구성된 하노이의 탑 게임(총 1,023번 이동 필요)을 강요한다. 이 게임의 조각들은 쌓였을 때 피라미드 모양을 이룬다.[42][44]
  • 2007년에 출시된 게임 ''레이튼 교수와 악마의 상자''에서는 퍼즐 6번, 83번, 84번에서 하노이의 탑 개념이 사용되었다. 다만 원반 대신 팬케이크를 사용했으며, 식당 요리사가 팬케이크 더미를 한 접시에서 다른 접시로 옮기는 상황을 설정했다. 세 개의 접시를 사용하고, 큰 팬케이크 위에 작은 팬케이크만 놓을 수 있다는 기본 원칙은 동일하게 적용되었다.
  • 2011년 개봉한 영화 ''혹성 탈출: 진화의 시작''에서는 '루카스 타워'라는 이름으로 등장하며, 유인원의 지능을 측정하는 테스트 도구로 사용된다.[42]
  • 하노이의 탑 퍼즐은 구현이 간단하고 인지도가 높아 어드벤처 게임이나 컴퓨터 퍼즐 게임에서 자주 등장한다. ''스타워즈: 구 공화국의 기사''나 ''매스 이펙트'' 같은 게임에서도 퍼즐 요소로 활용되었다.[45] 직선형 원반 형태 외에도 다양한 모습으로 변형되어 나타나며, 세가에서 제작한 아케이드 게임 버전도 존재한다.[46]
  • 게임 ''선리스 씨''에서는 15개의 원반으로 구성된 버전(총 32,767번 이동 필요)이 무덤의 잠금 장치로 등장한다. 플레이어가 직접 퍼즐을 풀 수도 있지만, 게임 내 설명에 따르면 모든 과정을 완료해도 문은 열리지 않는다.
  • 미국의 리얼리티 TV 쇼 ''서바이버''에서는 여러 차례 챌린지 과제로 등장했다. 2002년 태국 시즌에서는 사원 모양의 조각을 사용했으며, 한 참가자가 해결법을 알면서도 팀 전략을 위해 일부러 챌린지에서 패배하기도 했다. 2011년 미국판 서바이버에서는 보상 챌린지의 일부로 등장했는데, 참가자 오지 루스와 벤자민 "코치" 웨이드 모두 퍼즐 해결에 어려움을 겪어 동료들의 도움을 받았다.
  • 게임 ''원신 임팩트''에서는 캐릭터 파루잔의 데이트 이벤트 퀘스트 중 하나인 "조기 학습 메커니즘"에서 이 퍼즐이 등장한다. 파루잔은 이를 일종의 메커니즘으로 간주하며 아이들을 위한 장난감 시제품 제작에 활용한다고 언급하고, '탑'이라고 부른다.

9. 소스 코드

하노이의 탑 문제는 재귀 호출을 이용하여 다양한 프로그래밍 언어로 구현할 수 있다. 다음은 여러 언어로 작성된 예시 코드이다.

'''OCaml'''



let rec move_tower n a b c = match n with

| 1 -> [(a,c)]

| _ -> (move_tower (n-1) a c b) @ (move_tower 1 a b c) @ (move_tower (n-1) b a c);;



'''Lisp'''



(defun hanoitowers (disc src aux dst)

(cond ((> disc 0)

(hanoitowers (- disc 1) src dst aux)

(princ (list "Move" disc "from" src "to" dst))



'''Pascal'''



procedure Hanoi(n: integer; from, dest, by: char);

Begin

if (n=1) then

writeln('Move the plate from ', from, ' to ', dest)

else begin

Hanoi(n-1, from, by, dest);

Hanoi(1, from, dest, by);

Hanoi(n-1, by, dest, from);

end;

End;



'''C++'''



#include

using namespace std;

void move(int from, int to)

{

cout << from << " -> " << to << '\n';

}

void hanoi(int n, int from, int by, int to)

{

if(n == 0) return;

hanoi(n - 1, from, to, by);

move(from, to);

hanoi(n - 1, by, from, to);

}



'''Python'''



def hanoi(number_of_disks_to_move, from_, to_, via_):

if number_of_disks_to_move == 1:

print(from_, "->", to_)

else:

hanoi(number_of_disks_to_move-1, from_, via_, to_)

print(from_, "->", to_)

hanoi(number_of_disks_to_move-1, via_, to_, from_)



'''Visual Prolog'''



class hanoi

predicates

hanoi : (unsigned N).

end class hanoi

implement hanoi

domains

pole = string.

clauses

hanoi(N) :- move(N, "left", "centre", "right").

class predicates

move : (unsigned N, pole A, pole B, pole C).

clauses

move(0, _, _, _) :- !.

move(N, A, B, C) :-

move(N-1, A, C, B),

stdio::writef("move a disc from % pole to the % pole\n", A, C),

move(N-1, B, A, C).

end implement hanoi

goal

console::init(),

hanoi::hanoi(4).



'''Swift'''



import Foundation

func hanoi(_ n: Int, from a: Int, to b: Int, by c: Int) {

if n==1 {

print("Move 1 from \(a) to \(b)")

}

else {

hanoi(n-1, from: a, to: b, by: c)

print("Move \(n) from\(a) to\(b)")

hanoi(n-1, from: c, to: b, by: a)

}

}


참조

[1] 웹사이트 A000225 - OEIS https://oeis.org/A00[...] 2021-09-03
[2] 서적 Metamagical Themas : Questing for the Essence of Mind and Pattern https://archive.org/[...] Basic Books
[3] 논문 A device for demonstrating some elementary properties of integers https://books.google[...] National Council of Teachers of Mathematics 2021-03-09
[4] 웹사이트 Tower of Hanoi https://mathworld.wo[...] 2023-10-20
[5] 서적 The Tower of Hanoi – Myths and Maths Springer 2013-01-31
[6] 웹사이트 The Tower of Hanoi: A Bibliography https://www.cs.wm.ed[...] 2024-02-21
[7] 뉴스 Revue des Sciences https://gallica.bnf.[...] 1883-12-27
[8] 서적 Jeux scientifiques pour servir à l'histoire, à l'enseignement et à la pratique du calcul et du dessin https://gallica.bnf.[...] Chambon et Baye 2024-01-27
[9] 서적 Récréations mathématiques https://gallica.bnf.[...] Librairie Albert Blanchard, 1979
[10] 웹사이트 Tower of Hanoi instructions in English, page 1 https://www.cs.wm.ed[...] 2024-02-21
[11] 서적 1000 playthinks: puzzles, paradoxes, illusions & games Workman
[12] 서적 Famous Puzzles of Great Mathematicians AMS Bookstore
[13] 논문 Doomsday Comes: A Nonrecursive Analysis of the Recursive Towers-of-Hanoi Problem
[14] 서적 Hacker's delight Addison-Wesley
[15] 서적 Mathematical Ideas http://occawlonline.[...] Addison Wesley Longman
[16] 서적 Théorie du Baguenodier Aimé Vingtrinier
[17] 웹사이트 Question Corner -- Generalizing the Towers of Hanoi Problem https://www.math.tor[...] 2023-07-28
[18] 서적 The Tower of Hanoi – Myths and Maths Springer Science+Business Media
[19] 논문 The Cyclic Towers of Hanoi: An Iterative Solution Produced by Transformation
[20] 논문 La quatrieme tour de Hanoi https://pdfs.semanti[...]
[21] 논문 Solution to advanced problem 3819 1941-03
[22] 논문 Variations on the Four-Post Tower of Hanoi Puzzle https://core.ac.uk/d[...]
[23] 논문 Variations on the Four-Post Tower of Hanoi Puzzle http://www.cs.wm.edu[...]
[24] 웹사이트 University of Toronto CSC148 Slog https://berkeycolort[...] 2015-07-22
[25] 웹사이트 UPenn CIS 194 Introduction to Haskell Assignment 1 http://www.seas.upen[...] 2016-01-31
[26] 논문 The Tower of Hanoi
[27] 논문 A statistical analysis of the towers of Hanoi problem
[28] 서적 Another Fine Math You've Got Me Into... Courier Dover
[29] 논문 Shortest paths in the Tower of Hanoi graph and finite automata
[30] 논문 A Recursive Solution to Bicolor Towers of Hanoi Problem http://rmm.ludus-opu[...] 2015
[31] 서적 Card Games for One https://books.google[...] Sterling Publishing Company 2003-05-28
[32] 서적 Everybody's Book of Hobbies https://books.google[...] Read Books Ltd 2018-03-06
[33] 웹사이트 Tower Of Hanoy Patience (AKA Tower Of Hanoi Patience) http://bbcmicro.co.u[...] 2020-10-17
[34] 논문 Hanoi Tower-like Multilayered Ultrathin Palladium Nanosheets 2014-11-04
[35] 논문 Specific impairments of planning https://royalsociety[...] 1982-06-25
[36] 학술지 Representations in distributed cognitive tasks http://wexler.free.f[...]
[37] 학술지 TURF: Toward a unified framework of EHR usability
[38] 보고서 Tower-Noticing Triggers Strategy-Change in the Tower of Hanoi: A Soar Model https://doi.org/10.2[...] Defense Technical Information Center 1989-06-01
[39] 학술지 Neuropsychological study of frontal lobe function in psychotropic-naive children with obsessive-compulsive disorder https://ajp.psychiat[...]
[40] 학술지 Optimisation in a natural system: Argentine ants solve the Towers of Hanoi 2011-01
[41] 잡지 Now Inhale https://archive.org/[...] 1959-04
[42] 서적 A Sampling of Remarkable Groups: Thompson's, Self-similar, Lamplighter, and Baumslag-Solitar Springer 2018
[43] 학술지 The coroutines of Hanoi 1985-01
[44] 웹사이트 The Fourth Dimension: The Celestial Toymaker https://www.bbc.co.u[...] BBC One 2021-04-02
[45] 웹사이트 Tower of Hanoi (video game concept) http://www.giantbomb[...] Giantbomb.com 2010-12-05
[46] 웹사이트 Tower of Hanoi / Andamiro http://www.segaarcad[...] Sega Amusements 2012-02-26
[47] 학술지 Loopless Gray Code Enumeration and the Tower of Bucharest https://page.mi.fu-b[...] 2020-12-16
[48] 서적 C言語による最新アルゴリズム事典 技術評論社
[49] 서적 1000 playthinks: puzzles, paradoxes, illusions & games Workman
[50] 서적 The Tower of Hanoi – Myths and Maths 2013-01-31
[51] 서적 Selected topics in mathematics https://archive.org/[...] Holt, Rinehart and Winston


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com