바이어슈트라스 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

바이어슈트라스 함수는 1872년 카를 바이어슈트라스가 제시한, 모든 점에서 연속이지만 미분 불가능한 대표적인 함수이다. 이 함수는 푸리에 급수를 이용하여 정의되며, 프랙탈의 일종으로 자기 유사성 및 하우스도르프 차원과 같은 특징을 갖는다. 바이어슈트라스 함수는 실해석학에서 유사한 성질을 가진 함수들을 지칭하는 데 사용되며, 이를 일반화한 바이어슈트라스-만델브로 함수도 존재한다. 위상수학 및 측도론 관점에서 볼 때, 모든 곳에서 미분 불능인 함수는 연속 함수의 일반적인 형태에 가깝다.

2. 정의

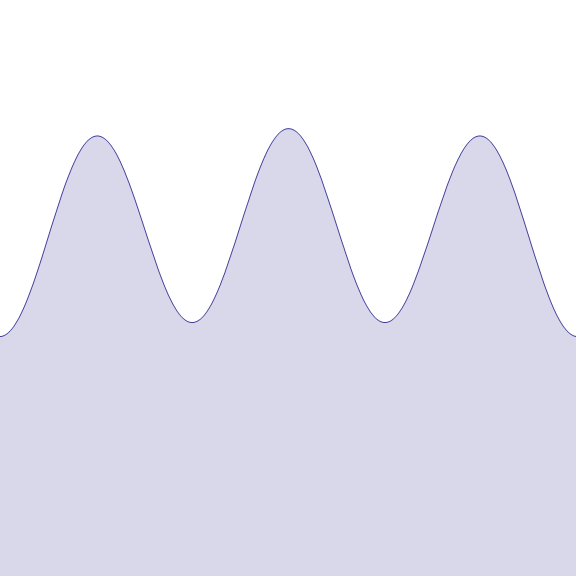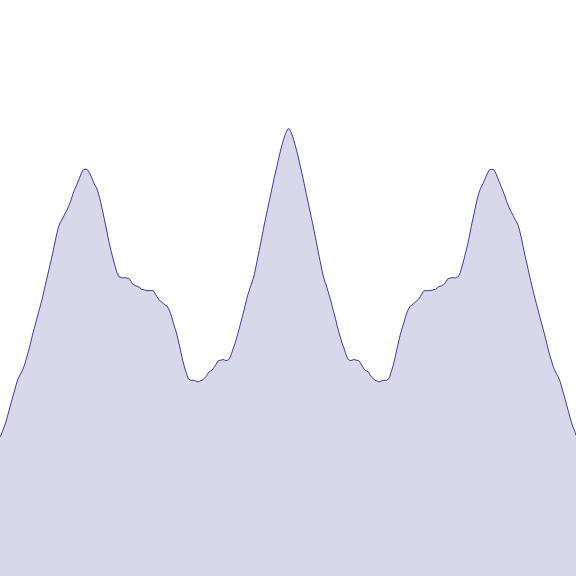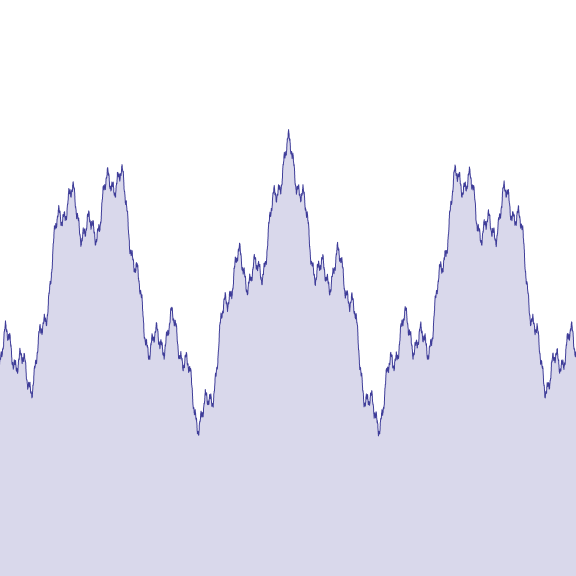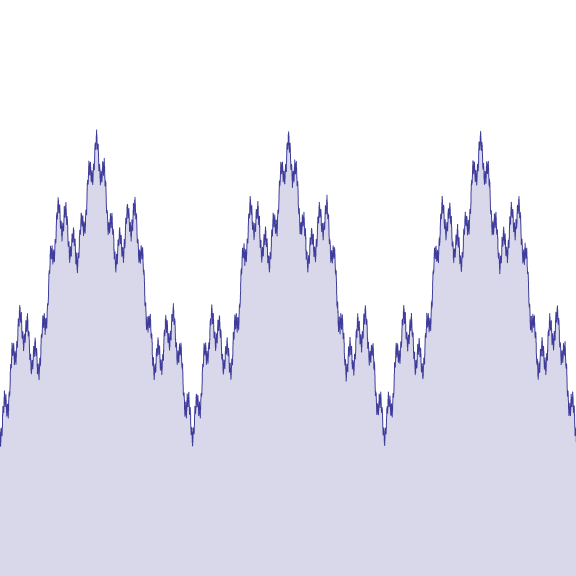
바이어슈트라스 함수는 어디에서도 미분 가능하지 않지만 연속 함수이다. 이 함수를 정의하는 무한 급수의 항들은

\pm a^n

으로 제한되며,

0 < a < 1

일 때 유한한 합을 가지므로, 바이어슈트라스 M-검정법에 의해 균등 수렴한다. 각 부분합이 연속이므로, 균등 극한 정리에 의해

f

는 연속이다. 또한, 각 부분합이 균등 연속이므로,

f

역시 균등 연속이다.

일반적으로 연속 함수는 미분 가능해야 하거나, 미분 불가능한 점이 유한하거나 가산 무한 집합이어야 한다고 생각하기 쉽다. 바이어슈트라스는 그의 논문에서 가우스를 포함한 이전의 수학자들이 종종 이것이 사실이라고 가정했다고 언급했다. 이는 미분 불가능한 점의 집합이 가산 집합이 아닌 연속 함수를 그리거나 시각화하기 어렵기 때문일 수 있다.

바이어슈트라스 함수는 처음 연구된 프랙탈 중 하나였지만, 이 용어는 훨씬 나중에 사용되었다. 이 함수는 모든 수준에서 세부 사항을 가지므로, 곡선의 일부를 확대해도 직선에 가까워지지 않는다. 오히려 아무리 가까운 두 점 사이에서도 함수는 단조적이지 않다.

2. 1. 바이어슈트라스 함수의 정의

바이어슈트라스 함수는 다음 푸리에 급수로 정의된다.

:

f(x)= \sum_{n=0}^\infty a^n\cos (b^n\pi x)

여기서

0 이고, b 는 양의 홀수 정수이며, 다음 조건을 만족한다.

:

ab>1+ \frac{3}{2}\pi

이 조건을 만족하는

b

의 최솟값은

b=7

이다.^[20]^[21]^[22] 이 함수의 정의와 모든 점에서 미분 불가능하다는 증명은 1872년 7월 18일 바이어슈트라스가 프로이센 과학 아카데미에 제출한 논문에서 처음 발표되었다.

실해석학에서 바이어슈트라스 함수는 종종 이와 유사한 정의 및 성질을 가진 함수를 가리키는 데 사용된다. 예를 들어, 무한급수 안의 코사인 함수를 삼각파로 대신한 함수가 있다. 고드프리 해럴드 하디는

0, ab\ge 1 조건을 만족하면 모든 점에서 미분 불가능함을 증명하였다.

^[23]

2. 2. 원 논문의 정의

바이어슈트라스가 원래 논문에서 제시한 함수는 다음과 같이 정의된다.

:

f(x)= \sum_{n=0}^\infty a^n\cos (b^n\pi x)

여기서

0, b 는 양의 홀수이고, ab>1+ \frac{3}{2}\pi 이다.

위 조건을 만족하는

b

의 최솟값은

b=7

이다. 이 함수의 정의와 모든 점에서 미분 불가능하다는 증명은 1872년 7월 18일 바이어슈트라스가 프로이센 과학 아카데미에 제출한 논문에서 처음 발표되었다.^[20]^[21]^[22]

3. 역사

카를 바이어슈트라스가 바이어슈트라스 함수를 발표하기 전과 후에 수학계에서 어떤 변화가 있었는지, 그리고 이 함수가 수학적으로 어떤 의미를 가지는지를 중심으로 설명한다.

바이어슈트라스의 원래 논문에서 함수는 다음과 같은 푸리에 급수로 정의되었다.^[3]^[4]^[5]

: $f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x),$

여기서 $0, b 는 양의 홀수 정수이고,$

: $ab > 1+\frac{3}{2} \pi.$

이러한 제약 조건을 만족하는 $0 이 존재하기 위한 b 의 최소값은 b=7 이다.$

바이어슈트라스 함수는 처음 연구된 프랙탈 중 하나였지만, 이 용어는 훨씬 나중에 사용되었다. 이 함수는 모든 수준에서 세부 사항을 가지므로, 곡선의 일부를 확대해도 점점 직선에 가까워지는 것을 보여주지 않는다. 오히려 두 점 사이, 아무리 가까워도 함수는 단조적이지 않을 것이다.

고전적인 바이어슈트라스 함수의 그래프의 하우스도르프 차원 $D$ 의 계산은 2018년까지 미해결 문제였으며, 일반적으로 $D = 2 + \log_b(a) < 2$ 라고 믿어졌다.^[6]^[7] ''D''가 2보다 작다는 것은 위에서 제시된 $a$ 와 $b$ 에 대한 조건에서 따른다. 30년이 넘어서야 이것이 엄밀하게 증명되었다.^[8]

바이어슈트라스 함수라는 용어는 종종 실해석학에서 바이어슈트라스의 원래 예와 유사한 속성과 구성을 가진 모든 함수를 지칭하는 데 사용된다. 예를 들어, 무한 급수에서 코사인 함수는 삼각파와 같은 조각적 선형 "지그재그" 함수로 대체될 수 있다. G. H. 하디는 위의 구성을 가진 함수가 $0 < a < 1, ab \geq 1$ 의 가정을 통해 어디에서도 미분 불가능하다는 것을 보였다.^[9]

3. 1. 발표 이전의 상황

연속 함수는 도함수를 가져야 하거나, 미분 불가능한 점의 집합이 가산 무한 또는 유한해야 한다고 예상할 수 있다. 바이어슈트라스는 그의 논문에서 가우스를 포함한 이전의 수학자들이 종종 이것이 사실이라고 가정했다고 언급했다.^[3] 이는 미분 불가능한 점의 집합이 가산 집합이 아닌 다른 집합인 연속 함수를 그리거나 시각화하는 것이 어렵기 때문일 수 있다. 더 나은 특성을 가진 연속 함수 클래스에 대한 유사한 결과가 존재하며, 예를 들어 미분 불가능한 점의 집합이 르베그 영집합이어야 하는 립시츠 함수가 있다 (라데마허의 정리). 일반적인 연속 함수를 그리려고 할 때, 우리는 일반적으로 립시츠 함수 또는 다른 잘 정의된 함수의 그래프를 그린다. 더욱이, 단조 함수에 대한 미분 불가능 점의 집합이 측도-0이라는 사실은 바이어슈트라스 함수의 급격한 진동이 어디에서도 미분 불가능하게 만들기 위해 필요함을 의미한다.

3. 2. 바이어슈트라스의 발표와 영향

카를 바이어슈트라스는 1872년 7월 18일 쾨니히리헤 아카데미 데어 비센샤프텐에 발표한 논문에서, 어디에서도 미분 불가능하지만 연속인 함수의 첫 번째 엄밀한 증명을 제시했다.^[3]^[4]^[5] 바이어슈트라스 함수는 다음의 푸리에 급수로 정의되었다.

f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x),

여기서

0, b 는 양의 홀수 정수이고,

ab > 1+\frac{3}{2} \pi.

이러한 조건을 만족하는

0 이 존재하기 위한 b 의 최소값은 b=7 이다.

이 발표 이전에는 연속 함수는 반드시 미분 가능하거나, 미분 불가능한 점이 유한하거나 가산 무한 집합일 것이라고 여겨졌다. 가우스를 포함한 많은 수학자들이 이러한 가정을 사실로 받아들였다. 이는 미분 불가능한 점의 집합이 가산 집합이 아닌 연속 함수를 시각화하기 어려웠기 때문으로 보인다.

바이어슈트라스의 발표는 수학계에 큰 충격을 주었다. 당시 수학자들은 직관에 의존하는 경향이 있었고, 바이어슈트라스 함수는 이러한 직관에 정면으로 배치되었기 때문이다. 바이어슈트라스 함수는 프랙탈의 초기 연구 사례 중 하나로 꼽히지만, '프랙탈'이라는 용어는 훨씬 후대에 등장했다.

바이어슈트라스 함수는 실해석학에서 유사한 속성을 가진 함수들을 통칭하는 용어로도 사용된다. G. H. 하디는

0 < a < 1, ab \geq 1

의 조건을 만족하는 함수가 어디에서도 미분 불가능함을 증명했다.^[9]

바이어슈트라스 함수는 미분 불가능하다고 알려진 초기 리만 함수를 바탕으로 한다. 리만 함수는 다음과 같다.^[10]

f(x) = \sum_{n = 1}^\infty \frac{\sin(n^2x)}{n^2}

베른하르트 리만은 이 함수가 미분 불가능하다고 주장했지만, 증거를 제시하지는 못했다. 1916년 G. H. 하디는 리만 함수가 특정 조건을 만족하는 점에서 미분 불가능함을 증명했다.^[9] 1969년과 1971년에 조셉 게르버는 리만 함수의 미분 가능성에 대한 연구를 완성했다.^[11]^[12] 리만 함수는 영집합의 점에서만 미분 가능하므로 거의 모든 곳에서 미분 불가능하다.

3. 3. 리만 함수와의 관계

바이어슈트라스 함수는 미분 불가능하다고 주장된 초기 리만 함수를 기반으로 한다. 이 함수는 때때로 바이어슈트라스 함수라고도 불린다.^[10]

:

f(x) = \sum_{n = 1}^\infty \frac{\sin(n^2x)}{n^2}

베른하르트 리만은 이 함수가 미분 불가능하다고 강력하게 주장했지만, 이에 대한 증거를 발표하지는 않았다. 바이어슈트라스는 리만의 논문이나 제자들의 구두 발표에서도 이 증거를 찾지 못했다고 언급했다.

1916년, G. H. 하디는 이 함수가

\pi x

의 값에서 유한한 도함수를 갖지 않는다는 것을 확인했는데, 여기서 ''x''는 무리수이거나

\frac{2A}{4B+1}

또는

\frac{2A+1}{2B}

형태의 유리수이며, ''A''와 ''B''는 정수이다.^[9] 1969년, 조셉 게르버는 리만 함수가 정수 ''A''와 ''B''를 사용하여

\frac{2A+1}{2B+1}\pi

의 형태로 표현될 수 있는 모든 ''x'' 값, 즉 홀수 분자와 분모를 가진 π의 유리수 배수에서 정의된 미분을 갖는다는 것을 발견했다. 이 점들에서 함수의 도함수는

-\frac{1}{2}

이다.^[11] 1971년, J. 게르버는 함수가

\frac{2A}{2B+1}\pi

형태로 표현될 수 있는 ''x'' 값에서 유한한 미분을 갖지 않는다는 것을 보여주어 리만 함수의 미분 가능성 문제를 완성했다.^[12]

리만 함수는 영집합의 점들에서만 미분 가능하므로 거의 모든 곳에서 미분 불가능하다.

4. 성질

바이어슈트라스 함수는 다음의 주요 성질들을 가진다.

연속성과 미분 불가능성: 모든 점에서 연속이지만, 모든 점에서 미분 불가능하다.
횔더 연속성: 횔더 연속이지만, 립시츠 연속은 아니다.
프랙탈 성질: 프랙탈의 초기 예시 중 하나이며, 자기 유사성을 보인다.

바이어슈트라스 함수는 원래 다음과 같은 푸리에 급수로 정의되었다.

:

f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x),

여기서

0, b 는 양의 홀수 정수이고,

:

ab > 1+\frac{3}{2} \pi.

이러한 조건을 만족하는

0 이 존재하기 위한 b 의 최소값은 b=7 이다. 1872년 7월 18일 쾨니히리헤 아카데미 데어 비센샤프텐 에 발표된 논문에서 바이어슈트라스는 이 함수가 어떤 구간에서도 미분 불가능하다는 것을 처음으로 증명했다.

^[3]^[4]^[5]

바이어슈트라스 함수는 프랙탈의 초기 예시 중 하나였지만, '프랙탈'이라는 용어는 훨씬 나중에 사용되었다. 이 함수는 모든 수준에서 세부 사항을 가지므로, 곡선의 일부를 확대해도 점점 직선에 가까워지는 것을 보여주지 않는다.

G. H. 하디는

0 < a < 1, ab \geq 1

의 조건을 만족하면, 위와 같은 구성을 가진 함수가 어디에서도 미분 불가능하다는 것을 보였다.^[9]

바이어슈트라스 함수는 종종 실해석학에서 바이어슈트라스의 원래 예와 유사한 속성 및 구성을 가진 모든 함수를 지칭하는 데 사용된다. 예를 들어, 무한 급수에서 코사인 함수는 삼각파와 같은 조각적 선형 "지그재그" 함수로 대체될 수 있다.

4. 1. 연속성과 미분 불가능성

바이어슈트라스 함수는 모든 점에서 연속이지만, 모든 점에서 미분 불가능하다.^[3]^[4]^[5]

모든 점에서 연속인 것은 바이어슈트라스 M-판정법을 통해 쉽게 증명된다.

M_n=a^n

을 사용하면 된다.

모든 점에서 미분 불가능함을 증명하는 것은 조금 더 복잡하다. 임의의 실수

x

에 대해, 두 수열

x_n

과

x_n'

을 구성하여 다음을 증명해야 한다.

:

\liminf_{n\to\infty}\frac{f(x_n)-f(x)}{x_n-x}>\limsup_{n\to\infty}\frac{f(x_n')-f(x)}{x_n'-x}

여기서

\liminf

와

\limsup

는 각각 하극한과 상극한을 의미한다.

과거에는 모든 연속함수가 대부분의 점에서 미분 가능하거나, 아주 적은 점에서만 미분 불가능하다고 생각했다. 바이어슈트라스의 논문에 따르면, 가우스를 포함한 초기 수학자들은 이를 당연하게 여기기도 했다. 하지만 바이어슈트라스 함수는 이러한 생각에 대한 반례를 제공한다. 실제로, 립시츠 연속성과 같이 더 강한 조건을 만족하는 연속함수는 거의 어디서나 미분 가능하다는 것이 증명되었다(레이드매처의 정리).

바이어슈트라스 함수는 다음과 같은 푸리에 급수로 정의된다.

:

f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x),

여기서

0, b 는 양의 홀수 정수이고,

:

ab > 1+\frac{3}{2} \pi.

이 조건을 만족하는

0 이 존재하기 위한 b 의 최소값은 b=7 이다.

이 함수는 어디에서도 미분 가능하지 않지만, 연속이다. 함수를 정의하는 무한 급수의 항들은

\pm a^n

으로 제한되며,

0 < a < 1

일 때 유한한 합을 가진다. 따라서 바이어슈트라스 M-검정법에 의해 균등 수렴한다. 각 부분합이 연속이므로, 균등 극한 정리에 의해

f

는 연속이다.

바이어슈트라스 함수는 초기에 연구된 프랙탈 중 하나이기도 하다. 이 함수는 모든 수준에서 세부적인 모습을 보여주며, 곡선의 어느 부분을 확대해도 직선에 가까워지지 않는다.

4. 2. 횔더 연속성

바이어슈트라스 함수는 다음과 같이 표현할 수 있다.

:

W_\alpha(x)=\sum_{n=0}^\infty b^{-n\alpha}\cos(b^nx)

여기서

\alpha

는

0<\alpha<1

를 만족한다.

W_\alpha(x)

는 α-횔더 연속성을 가진다. 즉, 상수

C

가 존재하여 임의의

x,y

에 대하여 다음이 성립한다.^[26]

:

|W_\alpha(x)-W_\alpha(y)|\le C|x-y|^\alpha

더 나아가

W_\alpha(x)

는 임의의

0\le\alpha<1

에 대해 α-횔더 연속이지만 립시츠 연속(즉 1-횔더 연속)은 아니다.

\alpha = -\frac{\ln(a)}{\ln(b)}

일 때,

W_\alpha(x)

는 지수 α를 갖는 횔더 연속 함수이며, 이는 어떤 상수 ''C''에 대하여

:

|W_\alpha(x)-W_\alpha(y)|\le C|x-y|^\alpha

가 모든

x

와

y

에 대해 성립한다는 의미이다.^[13] 게다가

W_1

은 모든 차수

\alpha < 1

에 대해 횔더 연속이지만, 립시츠 연속은 아니다.

4. 3. 립시츠 연속성

W_\alpha(x)

는 Hölder continuity|횔더 연속^영어 함수이며, 어떤 상수 ''C''에 대하여

|W_\alpha(x)-W_\alpha(y)|\le C|x-y|^\alpha

가 모든

x

와

y

에 대해 성립한다.^[13]

W_1

은 모든 차수

\alpha < 1

에 대해 횔더 연속이지만, 립시츠 연속은 아니다. 바이어슈트라스 함수의 립시츠 상수는 무한대이다.

4. 4. 프랙탈 성질

바이어슈트라스 함수는 프랙탈의 초기 예시 중 하나이며, 자기 유사성을 보인다. 하지만 엄밀한 의미에서 스케일 불변성을 가지는 것은 아니다.

이 함수는 곡선을 확대해도 직선에 가까워지지 않고, 임의의 두 점 사이에서 증가하거나 감소하는 단조성을 보이지 않는다.

4. 4. 1. 하우스도르프 차원

바이어슈트라스 함수는 최초의 프랙탈 중 하나로, 자기 유사성을 지닌다. 곡선을 확대해도 직선에 가까워지지 않으며 임의의 두 점 사이에서 단조성이 없다. 바이어슈트라스 함수의 하우스도르프 차원

D

는

2+\frac{\ln a}{\ln b}

를 상계로 갖는다. 일반적으로

D=2+\frac{\ln a}{\ln b}

라고 추측하나 아직 증명되지 않았다.^[24]^[25]

고전적인 바이어슈트라스 함수의 그래프의 하우스도르프 차원

D

의 계산은 2018년까지 미해결 문제였으며, 일반적으로

D = 2 + \log_b(a) < 2

라고 믿어졌다.^[6]^[7] ''D''가 2보다 작다는 것은 위에 제시된

a

와

b

에 대한 조건에서 따른다. 30년이 넘어서야 이것이 엄밀하게 증명되었다.^[8]

하우스도르프 차원은 다음과 같다.^[16]

:

D_{H} = 2 + \frac{\log{a}}{\log{b}}

4. 4. 2. 스케일 불변성

바이어슈트라스 함수에서는 합을

n \ge 0

에 대해서만 취하기 때문에 엄밀하게는 스케일 불변이 아니다.

:

\begin{align}w(bx) &= b^{-1} \sum_{n=0} ^\infty b^{n+1} \cos{(b^{n+1} \pi x)} \\&= b^{-1} \sum_{n=-1} ^\infty b^{n+1} \cos{(b^{n+1} \pi x)} - b^{-1} b^{0} \cos(b^{0} \pi x) \\&= b^{-1} \left[ w(x) - \cos \pi x \right] \\&\neq b^{-1} w(x)\end{align}

따라서 엄밀한 의미에서의 자기 유사성을 갖지 않는다.

5. 일반화

바이어슈트라스 함수는 여러 형태로 일반화되었다. 브누아 망델브로는 바이어슈트라스 함수를 일반화한 바이어슈트라스-만델브로 함수(Weierstrass-Mandelbrot function)를 제시했다.^[17]

이 외에도 다음과 같이 더욱 일반화된 바이어슈트라스-만델브로 함수가 있다.^[18]

: $W_{g}(t)= \sum_{n=-\infty}^{\infty} \lambda^{-nH} (g(0) - g(\lambda^{n} t)) e^{i\phi_n}$

여기서 ''H'' < 1이고, ''g''(t)는 ''t'' = 0에서 미분 가능한 주기 함수이다.

5. 1. 바이어슈트라스-만델브로 함수

브누아 망델브로는 바이어슈트라스 함수를 일반화한 바이어슈트라스-만델브로 함수(Weierstrass-Mandelbrot function)를 제시했다.^[17]

5. 1. 1. 정의

바이어슈트라스-만델브로 함수는 다음과 같이 정의된다.

:

W(t)= \sum_{n=-\infty}^{\infty} \frac{(1-e^{i \gamma^n t})e^{i\phi_n}}{\gamma^{(2-D)n}}

여기서 1 < ''D'' < 2, ''γ'' > 1 이다.

이 함수의 실수부를 취하고, ''φ'' = 0으로 두면 바이어슈트라스 함수를 얻을 수 있다.

:

\operatorname{Re} W(t) = \sum_{n=-\infty}^{\infty} \frac{1-\cos(\gamma^{n} t)}{\gamma^{(2-D) n}}

5. 1. 2. 프랙탈 차원

하우스도르프 차원은 ''D''로 여겨지지만, 엄밀한 증명은 이루어지지 않았다.

5. 1. 3. 스케일 불변성

''φ_n'' = ''μn''일 때 불변이 되는 것을 이산적 스케일 불변성(DSI)이라고 한다.

5. 1. 4. 통계적 성질

바이어슈트라스-만델브로 함수의 앙상블 평균은 0이다. 즉,

\langle W(t + \tau) - W(t) \rangle_e = 0

이다.

분산은

\gamma

에 대해서만 스케일 불변성을 가진다.

:

\begin{align}V(\tau) &= \langle W(t + \tau) - W(t) \rangle_e = 2 \sum_{n=-\infty}^{\infty} \frac{1 - \cos(\gamma^{n}\tau)}{\gamma^{(4-2D)n}}, \\V(\gamma \tau) &= \gamma^{4-2D} V(\tau)\end{align}

5. 1. 5. 파워 스펙트럼

파워 스펙트럼은 대략 다음 근사식으로 나타낼 수 있다.

:

S(\omega) \approx \frac{1}{\omega^{5-2D}\log{\gamma}}

즉, ''D'' → 2일 때 1/f 요동에 가까워진다.

5. 2. 추가 일반화

Weierstrass–Mandelbrot function|바이어슈트라스-만델브로 함수^영어(WMF)는 다음과 같이 더욱 일반화할 수 있다^[18]。

:

W_{g}(t)= \sum_{n=-\infty}^{\infty} \lambda^{-nH} (g(0) - g(\lambda^{n} t)) e^{i\phi_n}

여기서, ''H'' < 1, ''g''(t)는 ''t'' = 0에서 미분 가능한 주기 함수이다.

6. 모든 곳에서 미분 불능인 함수의 조밀성

바이어슈트라스 함수는 특이한 예시가 아니다. 병적이지만 연속함수에서는 일반적인 현상이다.

위상수학적 관점에서, 0,1 구간 위의 연속 실가 함수의 균등 수렴 위상을 가진 벡터 공간 $C([0,1];\mathbb{R})$ 에서, 0,1 위의 모든 곳에서 미분 불능인 함수의 집합은 나머지 집합을 이룬다.^[27]^[28]
측도론적 관점에서, 공간 $C([0,1];\mathbb{R})$ 에 고전적 위너 측도 $\gamma$ 를 부여했을 때, 적어도 한 점에서 미분 가능한 함수의 집합은 γ-영측도이다.

이는 바이어슈트라스 함수가 고립된 예시가 아니라는 것을 보여준다. "병리적"이지만, 연속 함수의 "전형"이기도 하다.

위상적 의미에서: [0, 1] 구간에서 미분 불가능한 실수 값 함수의 집합은 균등 수렴 위상을 가진 [0, 1] 구간의 모든 연속 실수 값 함수 벡터 공간 ''C''([0, 1]; '''R''')에서 코메이저이다.^[14]^[15]
측도론적 의미에서: 공간 ''C''([0, 1]; '''R''')에 고전적 비너 측도 ''γ''를 부여할 때, [0, 1]의 단 한 점에서도 미분 가능한 함수의 모음은 ''γ''-측도 영을 갖는다. 이는 ''C''([0, 1]; '''R''')의 유한 차원 "슬라이스"를 취하더라도 마찬가지이며, 미분 불가능한 함수가 ''C''([0, 1]; '''R''')의 우세 부분집합을 형성한다는 의미이다.

참조

_[1] 간행물 Note sur les principes fondamentaux de l'analyse https://books.google[...] Bulletin des sciences mathématiques 1890
_[2] 웹사이트 Math's Beautiful Monsters: How a destructive idea paved the way for modern math https://nautil.us/ma[...] 2017-10-26
_[3] 간행물 page 560 of the 1872 Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin https://books.google[...]
_[4] 서적 "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen" Königlich Preussichen Akademie der Wissenschaften 1895
_[5] 서적 Abhandlungen aus der Functionenlehre https://books.google[...] Julius Springer 1886
_[6] 서적 The Geometry of Fractal Sets Cambridge University Press 1985
_[7] 간행물 The Hausdorff dimension of graphs of Weierstrass functions http://www.ams.org/j[...] Proceedings of the American Mathematical Society 1998
_[8] 학술지 Hausdorff dimension of the graphs of the classical Weierstrass functions
_[9] 학술지 Weierstrass's nondifferentiable function 1916
_[10] 웹사이트 Weierstrass Function https://mathworld.wo[...]
_[11] 학술지 The Differentiability of the Riemann Function at Certain Rational Multiples of π 1969
_[12] 학술지 More on the Differentiability of the Riemann Function 1971
_[13] 서적 Trigonometric Series Cambridge University Press
_[14] 학술지 Sur les fonctions non-dérivables
_[15] 학술지 Über die Baire'sche Kategorie gewisser Funktionenmengen
_[16] 학술지 The Hausdorff dimension of graphs of Weierstrass functions https://doi.org/10.1[...] 1998-03
_[17] 간행물 On the Weierstrass-Mandelbrot Fractal Function http://www.jstor.org[...] Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences
_[18] 서적 Courbes et Dimension Fractale https://books.google[...] Springer 1993
_[19] 간행물 Note sur les principes fondamentaux de l'analyse http://books.google.[...] Bulletin des sciences mathématiques 1890
_[20] 간행물 page 560 of the 1872 Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin http://books.google.[...]
_[21] 서적 "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen," http://books.google.[...] Königlich Preussichen Akademie der Wissenschaften 1895
_[22] 서적 Abhandlungen aus der Functionenlehre http://books.google.[...] Julius Springer 1886
_[23] 학술지 Weierstrass's nondifferentiable function 1916
_[24] 서적 The Geometry of Fractal Sets Cambridge University Press 1985
_[25] 학술지 The Hausdorff dimension of graphs of Weierstrass functions http://www.ams.org/j[...] 1998
_[26] 인용 Trigonometric series. Vol. I, II http://matwbn.icm.ed[...] Cambridge University Press
_[27] 저널 인용 Sur les fonctions non dérivables
_[28] 저널 인용 Über die Baire'sche Kategorie gewisser Funktionenmengen

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com