양자 조화 진동자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 1차원 양자 조화 진동자
3. ''N''-차원 등방성 조화 진동자
- 3.1. 3차원 등방성 조화 진동자
4. 응용
- 4.1. 분자 진동
- 4.2. 고체 격자의 진동: 포논
참조

1. 개요

양자 조화 진동자는 양자역학적 시스템의 중요한 모델로, 고전적인 조화 진동자의 양자역학적 대응물이다. 1차원 양자 조화 진동자의 퍼텐셜은 용수철 상수와 질량에 의해 결정되며, 슈뢰딩거 방정식을 풀면 에너지 고유 상태와 에너지 준위를 얻을 수 있다. 에너지 준위는 양자화되어 있으며, 사다리 연산자 방법과 해석적인 풀이를 통해 파동 함수와 에너지 준위를 구할 수 있다. 또한 결맞는 상태는 최소 불확정성을 가지며, N차원 및 3차원 등방성 조화 진동자로 확장될 수 있다. 양자 조화 진동자는 분자 진동, 고체 격자의 진동(포논), 란다우 준위 등 다양한 물리적 현상을 설명하는 데 응용된다.

더 읽어볼만한 페이지

양자 모형 - 상자 속 입자
상자 속 입자는 양자역학에서 입자가 특정 영역에 갇혀 움직이는 이상적인 시스템으로, 슈뢰딩거 방정식을 통해 파동 함수와 양자화된 에너지 준위를 구할 수 있으며, 다양한 물리적 시스템을 이해하는 데 기초가 된다.
양자 모형 - 수소 분자 이온
수소 분자 이온은 수소 분자가 전자를 잃어 생성되는 분자 이온으로, 성간 물질 화학에서 중요한 역할을 하며, 1/2의 결합 차수를 가지는 일전자 결합으로 설명된다.
양자역학 - 광전 효과
광전 효과는 빛이 물질에 닿을 때 전자가 방출되는 현상으로, 빛 에너지가 광자라는 덩어리로 양자화되어 있고, 아인슈타인의 광양자 가설로 설명되며, 다양한 기술에 응용되지만 문제도 야기한다.
양자역학 - 진동수
진동수는 주기적인 현상이 단위 시간당 반복되는 횟수를 나타내는 물리량으로, 주기와 역수 관계를 가지며 소리의 높낮이, 빛의 색깔 등을 결정하는 중요한 요소이다.

양자 조화 진동자
양자 조화 진동자
양자 조화 진동자의 에너지 준위와 파동함수
모델 정보
유형	양자역학 모델
중요도	중요하고 잘 이해되는 모델
설명	양자역학에서 중요한 모델로, 양자화된 에너지 준위와 파동함수를 갖는 진동자를 설명
관련 개념
관련 분야	양자역학
관련 주제	조화 진동자, 슈뢰딩거 방정식
관련 방정식	슈뢰딩거 방정식
고전 조화 진동자와의 비교
고전 조화 진동자	고전역학에서의 조화 진동자
양자 조화 진동자	양자화된 에너지 준위를 갖는 조화 진동자
언어별 명칭
영어	Quantum harmonic oscillator
한국어	양자 조화 진동자

2. 1차원 양자 조화 진동자

1차원 양자 조화 진동자는 하나의 입자가 1차원 공간에서 특정 위치를 중심으로 진동하는 현상을 나타내는 기본적인 모델이다.

시간에 무관한 슈뢰딩거 방정식을 풀면 에너지 고유 상태와 에너지 준위를 구할 수 있다. 에너지 준위는 다음과 같이 불연속적인 값을 가진다.

: $E_n = \hbar \omega \left(n + {1 \over 2} \right)$ . (n=0,1,2,3,…)

이는 에너지 양자화의 대표적인 예시이다.

에너지 고유 상태는 에르미트 다항식과 가우스 함수를 곱한 형태로 나타나며, 다음과 같다.

: $\langle x|n\rangle=\psi_n(x) = \frac{1}{(2^n\,n!)^{1/2}} \left(\frac{\alpha}{\pi }\right)^{1/4} \cdot H_n\left(\sqrt{\alpha} x \right) \cdot e^{- \frac{\alpha x^2}{2 }}$

여기서,

: $H_n (x) \;$ : 에르미트 다항식

: $\alpha = \left( {mk \over \hbar^2} \right)^{1/2} = {m\omega \over \hbar}$

이다.

사다리 연산자 방법을 사용하면 미분 방정식을 풀지 않고도 에너지 고유값을 구할 수 있다.^[2] 이 방법은 양자장론 등 더 복잡한 문제에도 적용 가능하다.

가장 낮은 에너지 준위(n=0)는 영점 에너지라고 불리며, $\frac{\hbar\omega}{2}$이다. 하이젠베르크의 불확정성 원리에 따라 바닥 상태의 진동자는 위치와 운동량이 고정되지 않고 작은 범위의 분산을 가진다.

에너지가 증가함에 따라 확률 밀도는 고전적인 "전환점"에서 최고점에 이른다. 이는 고전적인 조화 진동자와 일치하며, 대응 원리가 만족됨을 보여준다.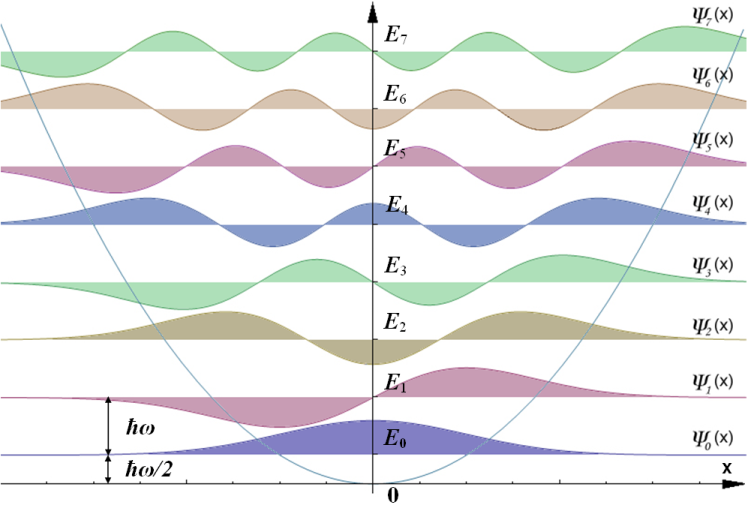

2. 1. 퍼텐셜

1차원 양자 조화 진동자의 퍼텐셜은 다음과 같다.

:

V(x) = \frac12kx^2 = \frac12m\omega^2 x^2

여기서

k

는 용수철 상수이고,

\omega

는 퍼텐셜에 갇힌 입자의 운동의 각진동수이다.

m

은 입자의 질량이다.

2. 2. 에너지 고유 상태

시간에 무관한 슈뢰딩거 방정식을 풀면 에너지 고유 상태와 에너지 준위를 구할 수 있다. 에너지 준위는 다음과 같이 불연속적인 값을 가진다.

:

E_n = \hbar \omega \left(n + {1 \over 2} \right)

. (n=0,1,2,3,…)

이는 에너지 양자화의 대표적인 예시이다.

에너지 고유 상태는 에르미트 다항식과 가우스 함수를 곱한 형태로 나타나며, 다음과 같다.

:

\langle x|n\rangle=\psi_n(x) =  \frac{1}{(2^n\,n!)^{1/2}}  \left(\frac{\alpha}{\pi }\right)^{1/4} \cdot H_n\left(\sqrt{\alpha} x \right) \cdot e^{- \frac{\alpha x^2}{2 }}

여기서,

:

H_n (x) \;

: 에르미트 다항식

:

\alpha = \left( {mk \over \hbar^2} \right)^{1/2} = {m\omega \over \hbar}

이다.

사다리 연산자 방법을 사용하면 미분 방정식을 풀지 않고도 에너지 고유값을 구할 수 있다.^[2] 이 방법은 양자장론 등 더 복잡한 문제에도 적용 가능하다.

가장 낮은 에너지 준위(n=0)는 영점 에너지라고 불리며, $\frac{\hbar\omega}{2}$이다. 하이젠베르크의 불확정성 원리에 따라 바닥 상태의 진동자는 위치와 운동량이 고정되지 않고 작은 범위의 분산을 가진다.

에너지가 증가함에 따라 확률 밀도는 고전적인 "전환점"에서 최고점에 이른다. 이는 고전적인 조화 진동자와 일치하며, 대응 원리가 만족됨을 보여준다.

2. 2. 1. 해석적인 풀이

1차원에서 시간에 무관한 슈뢰딩거 방정식은 다음과 같다.

:

-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} + {1 \over 2}m\omega^2x^2 \psi(x) = E \psi(x)

$\hbar$ : 디랙 상수 $h/2\pi$
$m$ : 진동자의 질량
$\psi(x)$ : 진동자의 파동함수
$E$ : 진동자의 에너지

다음과 같은 변수 변환

:

\epsilon = {2E \over \hbar \omega}

:

y = \sqrt x = \sqrt{\alpha} x

을 취하면 다음의 방정식을 얻는다. (이는 방정식에 나타난 물리량을 단위가 없는 양으로 바꾸기 위함이다.)

:

\frac{d^2 \psi(y)}{dy^2} + (\epsilon - y^2) \psi(y) = 0

이 형태는 풀기 어렵다. 따라서 평형점(x=0)으로부터 한없이 멀리 떨어진 곳에서의 파동함수의 거동을 살펴본다. (x → ∞ 이면 파동함수의 함수값이 0 이 되어야 한다는 양자역학의 통계적 해석에 관한 기본 조건이 풀이에 자연스럽게 이용된다.) 이 경우, 상수인 ''ε''에 비해 ''y''는 매우 커지므로(x → ∞ 이면 y → ∞), 위 식의 두 번째 항에서 ''ε''항을 무시할 수 있다. 그러면,

:

\frac{d^2 \psi_0(y)}{dy^2} - y^2 \psi_0(y) = 0

의 간단한 방정식을 얻는다. 이 방정식의 해는 실제 파동함수가 x → ∞ 일 때 원래의 해가 점근적으로 수렴해 가는 함수이다. 이 미분 방정식을 풀면

:

\psi_0(y) = e^{-{y^2 \over 2}}

를 얻는다. 그런데 이는 x 가 한없이 큰 곳에서의 해이므로, 실제 슈뢰딩거 방정식의 해는 특정 함수가 곱해진 형태인

:

\psi(y) = h(y) e^{-{y^2 \over 2}}

와 같은 형태의 함수일 것이라 생각해볼 수 있다.

따라서 이 함수를 시험해로 사용하여 슈뢰딩거 방정식에 대입하여 정리하면 다음과 같은 새로운 미분방정식을 얻는다.

:

\frac{d^2 h(y)}{dy^2} -2y \frac{d h(y)}{dy} + (\epsilon - 1 ) h(y)

위 방정식을 급수해 풀이법으로 풀면, 그 해로 에르미트 다항식 ''H(y)''를 얻는다.

:

h(y) = H(y) \;

이를 표준화하면 앞의 표준화 상수 N_n를 구할 수 있고, 다시 ''y''와 ''ε''을 역변환하면 아래의 양자 조화 진동자 파동함수를 얻는다.

:

\psi_n = N_n \cdot H_n\left(\sqrt{\alpha} x \right) \cdot e^{

\frac{\alpha x^2}{2 }}= \frac{1}{(2^n\,n!)^{1/2}} \left(\frac{\alpha}{\pi }\right)^{1/4} \cdot H_n\left(\sqrt{\alpha} x \right) \cdot e^{- \frac{\alpha x^2}{2 }} \,

앞서 제시된 해석은 생성 및 소멸 연산자 사이의 교환 관계만을 사용하는 대수적인 방법이다. 대수적 해석이 완료되면 해석적인 문제로 넘어가야 한다. 먼저 기저 상태, 즉 방정식

a\psi_0 = 0

의 해를 구해야 한다. 위치 표현에서 이것은 다음과 같은 1계 미분 방정식이다.

\left(x+\frac{\hbar}{m\omega}\frac{d}{dx}\right)\psi_0 = 0,

이 방정식의 해는 가우스 함수임을 쉽게 알 수 있다.^[3]

\psi_0(x)=Ce^{-\frac{m\omega x^2}{2\hbar}}.

개념적으로 이 방정식의 해가 하나뿐이라는 점이 중요하다. 만약 선형적으로 독립적인 기저 상태가 두 개 있다면, 조화 진동자에 대한 두 개의 독립적인 고유 벡터 사슬을 얻게 될 것이다. 기저 상태를 계산하면, 위치 표현에서 생성 연산자의 명시적 형태를 사용하여 들뜬 상태가 가우스 기저 상태에 에르미트 다항식을 곱한 것임을 귀납적으로 보일 수 있다. 또한 기저 상태의 유일성에서 예상되는 바와 같이, 사다리 방법으로 구성된 에르미트 함수 에너지 고유 상태

\psi_n

가 완전한 직교 함수 집합을 형성한다는 것을 증명할 수 있다.^[4]

이전 절과 명시적으로 연결하면, 위치 표현에서 기저 상태 |0⟩는

a| 0\rangle =0

에 의해 결정된다.

\left\langle x \mid a \mid 0 \right\rangle = 0 \qquad\Rightarrow \left(x + \frac{\hbar}{m\omega}\frac{d}{dx}\right)\left\langle x\mid 0\right\rangle = 0 \qquad\Rightarrow

\left\langle x\mid 0\right\rangle = \left(\frac{m\omega}{\pi\hbar}\right)^\frac{1}{4} \exp\left( -\frac{m\omega}{2\hbar}x^2 \right)= \psi_0  ~,

따라서

\langle x \mid a^\dagger \mid 0 \rangle = \psi_1 (x) ~,

그래서

\psi_1(x,t)=\langle x \mid e^{-3i\omega t/2} a^\dagger \mid 0 \rangle

이고, 이런 식으로 계속된다.

2. 2. 2. 대수적인 풀이

해밀토니언은 다음과 같이 인수분해할 수 있다.

:

H=(a^\dagger a+\frac12)\hbar\omega

.

여기서

:

a=\frac1{\sqrt2}\left(\omega\sqrt mx+ip/\sqrt m\right)

:

a^\dagger=\frac1{\sqrt2}\left(\omega\sqrt mx-ip/\sqrt m\right)

는 사다리 연산자이다. 이들은 에르미트 연산자가 아니므로, 관측 가능량이 아니다.

'''입자수 연산자'''(粒子數演算子, particle-number operator^영어)

N

은 다음과 같이 정의된다.

:

N=a^\dagger a

.

이 연산자는 에르미트 연산자이며, 그 고유 기저를

|n\rangle

이라고 하면,

:

N|n\rangle=n|n\rangle

이다.

N

의 고윳값은 음이 아닌 실수이다.

입자수 연산자와 사다리 연산자의 교환 관계는 다음과 같다.

:

[a,a^\dagger]=1

:

[a,N]=a

:

[a^\dagger,N]=-a^\dagger

.

따라서

:

a|n\rangle\propto|n-1\rangle

:

a^\dagger|n\rangle\propto|n+1\rangle

이다.

즉,

a

는

N

의 양자수를 1 감소시키고,

a^\dagger

는

N

의 양자수를 1 증가시킨다. 이 때문에

a^\dagger

를 '''생성 연산자'''(生成演算子, creation operator^영어),

a

를 '''소멸 연산자'''(消滅演算子,annihilation operator^영어)라고 부른다.^[2]

그리고,

:

a|n\rangle=\sqrt n|n-1\rangle

:

a^\dagger|n\rangle=\sqrt{n+1}|n+1\rangle

이다.

n

은 항상 정수이며,

N

의 고윳값은 항상 음이 아닌 정수이고, 바닥 상태

|0\rangle

로부터 다음과 같이 나타낼 수 있다.

:

|n\rangle=\frac{(a^\dagger)^n}{\sqrt{n!}}|0\rangle

.

해밀토니언

H=\hbar\omega(N+1/2)

의 고윳값(에너지 준위)

E_n

은 다음과 같다.

:

E_n=\hbar\omega(n+1/2)

.

2. 3. 결맞는 상태

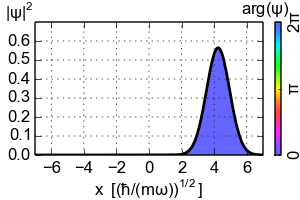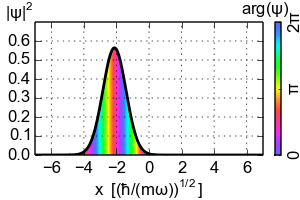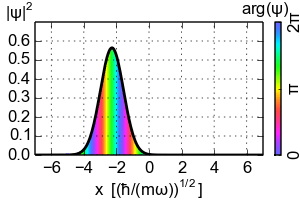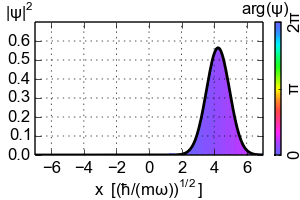
양자 조화 진동자의 코히어런트 상태(글라우버 상태라고도 함)는 최소 불확정성을 가지며, 그 물리량의 기댓값은 고전적인 계와 같이 진화하는 특별한 비분산 파동 패킷이다. 이들은 해밀토니안이 아닌 소멸 연산자의 고유 벡터이며, 결과적으로 직교성이 부족한 과잉 완비 기저를 형성한다.

코히어런트 상태는

\alpha \in \mathbb{C}

로 색인되며, 기저에서 다음과 같이 표현된다.

|\alpha\rangle = \sum_{n=0}^\infty |n\rangle \langle n | \alpha \rangle = e^{-\frac{1}{2} |\alpha|^2} \sum_{n=0}^\infty\frac{\alpha^n}{\sqrt{n!}} |n\rangle = e^{-\frac{1}{2} |\alpha|^2} e^{\alpha a^\dagger} e^{-{\alpha^* a}} |0\rangle.

코히어런트 상태는 에너지 고유 상태가 아니므로, 시간에 따른 진화는 파동 함수 위상의 단순한 이동이 아니다. 그러나 시간에 따라 진화된 상태는 위상 이동 매개변수

\alpha(t) = \alpha(0) e^{-i\omega t} = \alpha_0 e^{-i\omega t}

를 사용하는 코히어런트 상태이다.

|\alpha(t)\rangle = \sum_{n=0}^\infty e^{-i\left(n+\frac{1}{2}\right) \omega t}|n\rangle \langle n | \alpha \rangle =  e^{\frac{-i\omega t}{2}}e^{-\frac{1}{2} |\alpha|^2} \sum_{n=0}^\infty\frac{(\alpha e^{-i\omega t})^n}{\sqrt{n!}} |n\rangle = e^{-\frac{i\omega t}{2}}|\alpha e^{-i\omega t}\rangle

a \left| 0 \right\rangle = 0

이고 Kermack-McCrae 항등식을 통해, 마지막 형태는 기저 상태에 작용하는 유니터리 변위 연산자와 동일하다.

|\alpha\rangle=e^{\alpha \hat a^\dagger - \alpha^*\hat a}|0\rangle = D(\alpha)|0\rangle

. 기댓값은 다음과 같다.

\langle \hat{x} \rangle_{\alpha(t)} = \sqrt{\frac{2\hbar}{m\omega}}|\alpha_0|\cos{(\omega t - \phi)}

\langle \hat{p} \rangle_{\alpha(t)} = -\sqrt{2m\hbar \omega}|\alpha_0|\sin{(\omega t - \phi)}

여기서

\phi

는 복소수

\alpha

에 의해 기여되는 위상이다. 이 방정식은 입자의 진동 거동을 확인한다.

수치적 방법을 사용하여 계산된 불확정성은 다음과 같다.

\sigma_x(t)=\sqrt{\frac{\hbar}{2m\omega}}

\sigma_p(t) = \sqrt{\frac{m\hbar\omega}{2}}

이는

\sigma_x(t)\sigma_p(t) = \frac{\hbar}{2}

를 제공한다. 최저 위치-운동량 불확정성

\frac{\hbar}{2}

을 가질 수 있는 유일한 파동 함수는 가우스 파동 함수이며, 코히어런트 상태 파동 함수는 최소 위치-운동량 불확정성을 가지므로, 양자역학에서 일반적인 가우스 파동 함수는 다음 형태를 가진다.

\psi_\alpha(x')= \left(\frac{m\omega}{\pi\hbar}\right)^{\frac{1}{4}} e^{\frac{i}{\hbar} \langle\hat{p}\rangle_\alpha (x' - \frac{\langle\hat{x}\rangle_\alpha}{2}) - \frac{m\omega}{2\hbar}(x' - \langle\hat{x}\rangle_\alpha)^2} .

시간의 함수로 기댓값을 대입하면, 필요한 시간에 따라 변하는 파동 함수를 얻는다.

각 에너지 고유 상태의 확률을 계산하여 파동 함수의 에너지 분포를 구할 수 있다.

P(E_n)=|\langle n | \alpha \rangle|^2 =  \frac{e^{-|\alpha|^2}|\alpha|^{2n}}{n!}

이는 푸아송 분포에 해당한다.

3. ''N''-차원 등방성 조화 진동자

1차원 조화 진동자는 ''N''차원으로 쉽게 확장할 수 있다. 여기서 ''N''은 1, 2, 3, ... 과 같은 자연수이다. 1차원에서는 입자의 위치가 단일 좌표 ''x''로 결정되지만, ''N''차원에서는 ''N''개의 위치 좌표 $x_1, \dots, x_N$ 으로 표현된다. 각 위치 좌표에 대응하는 운동량 $p_1, \dots, p_N$ 이 존재하며, 이들 연산자 사이의 정준 교환 관계는 다음과 같다.^[5]^[6]

$\begin{align}{[}x_i , p_j{]} &= i\hbar\delta_{i,j} \\{[}x_i , x_j{]} &= 0 \\{[}p_i , p_j{]} &= 0\end{align}$

이 계의 해밀토니안은 다음과 같이 나타낼 수 있다.

$H = \sum_{i=1}^N \left( {p_i^2 \over 2m} + {1\over 2} m \omega^2 x_i^2 \right).$

이 식에서 볼 수 있듯이, ''N''차원 조화 진동자는 질량과 용수철 상수가 같은 ''N''개의 독립적인 1차원 조화 진동자와 동일하다. 이 때, $x_1, \dots, x_N$ 는 ''N''개 입자 각각의 위치를 나타낸다. 이러한 성질 덕분에 퍼텐셜 에너지를 각 좌표에 의존하는 항으로 분리할 수 있다.

이러한 관찰을 통해 양자수 집합 $\{n\}\equiv \{n_1, n_2, \dots, n_N\}$ 에 대해, ''N''차원 조화 진동자의 에너지 고유 함수는 1차원 고유 함수를 이용하여 다음과 같이 표현할 수 있다.

$\langle \mathbf{x}|\psi_{\{n\}}\rangle = \prod_{i=1}^N\langle x_i\mid \psi_{n_i}\rangle$

사다리 연산자 방법을 이용하면, ''N''개의 사다리 연산자 집합을 정의할 수 있다.

$\begin{align}a_i &= \sqrt{m\omega \over 2\hbar} \left(x_i + {i \over m \omega} p_i \right), \\a^{\dagger}_i &= \sqrt{m \omega \over 2\hbar} \left( x_i - {i \over m \omega} p_i \right).\end{align}$

1차원 경우와 유사하게, 각 $a_i$ 와 $a^{\dagger}_i$ 연산자는 각각 에너지를 $\hbar\omega$ 만큼 낮추거나 높인다. 해밀토니안은 다음과 같다.

$H = \hbar \omega \, \sum_{i=1}^N \left(a_i^\dagger \,a_i + \frac{1}{2}\right).$

이 해밀토니안은 동적 대칭군 $U(N)$ (''N''차원의 유니터리 군) 하에서 불변한다.

이 계의 에너지 준위는 다음과 같이 주어진다.

$E = \hbar \omega \left[(n_1 + \cdots + n_N) + {N\over 2}\right].$

$n_i = 0, 1, 2, \dots \quad (\text{차원 } i \text{의 에너지 준위}).$

1차원과 마찬가지로 에너지는 양자화되며, 바닥 상태 에너지는 ''N''개의 독립적인 1차원 조화 진동자의 바닥 상태 에너지의 합과 같다.

''N''차원에서는 바닥 상태를 제외한 에너지 준위는 축퇴되어 있는데, 이는 동일한 에너지를 갖는 여러 상태가 존재함을 의미한다. 축퇴도( $g_n$ )는 다음과 같은 공식으로 계산할 수 있다.

$g_n = \binom{N+n-1}{n}$

이 공식은 유니터리 군 $U(N)$ 의 대칭성에 관련된 표현의 차원과 같다.

3. 1. 3차원 등방성 조화 진동자

2차원 밀도 플롯으로 표현된 슈뢰딩거 3차원 구면 조화 진동자 궤도 함수 해

구면 대칭 3차원 조화 진동자 내 입자에 대한 슈뢰딩거 방정식은 변수 분리법으로 풀 수 있다. 이 과정은 수소-유사 원자 문제와 유사하지만, 다음과 같은 구면 대칭 퍼텐셜을 갖는다.^[7]

:

V(r) = {1\over 2} \mu \omega^2 r^2,

여기서 μ는 입자의 질량이다.

방정식의 해는 다음과 같다.^[7]

:

\psi_{klm}(r,\theta,\phi) = N_{kl} r^{l}e^{-\nu r^2}L_k^{\left(l+{1\over 2}\right)}(2\nu r^2) Y_{lm}(\theta,\phi)

여기서

:

N_{kl}=\sqrt{\sqrt{\frac{2\nu^3}{\pi }}\frac{2^{k+2l+3}\;k!\;\nu^l}{(2k+2l+1)!!}}~~

는 정규화 상수이다.;

\nu \equiv {\mu \omega \over 2 \hbar}~

;

:

{L_k}^{(l+{1\over 2})}(2\nu r^2)

는 일반화된 라게르 다항식이다. 다항식의 차수 k는 0 또는 양의 정수이다.;

$Y_{lm}(\theta,\phi)\,$ 는 구면 조화 함수이다.;
ħ는 환산 플랑크 상수이다.: $\hbar\equiv\frac{h}{2\pi}~.$

에너지 고유값은 다음과 같다.

:

E=\hbar \omega \left(2k + l + \frac{3}{2}\right) .

에너지는 일반적으로 단일 양자수

:

n\equiv 2k+l  \,.

로 표현된다.

k가 0 또는 양의 정수이기 때문에, 모든 짝수 n에 대해 ℓ = 0, 2, …, n − 2, n 이고, 모든 홀수 n에 대해 ℓ = 1, 3, …, n − 2, n 이다. 자기 양자수 m은 -ℓ ≤ m ≤ ℓ을 만족하는 정수이므로, 모든 n 및 ℓ에 대해 m으로 표시되는 2ℓ + 1개의 서로 다른 양자 상태가 있다. 따라서, n 레벨에서의 축퇴도는

:

\sum_{l=\ldots,n-2,n} (2l+1) = {(n+1)(n+2)\over 2} \,,

이다. 여기서 합은 n이 짝수인지 홀수인지에 따라 0 또는 1부터 시작한다.

이 결과는 위의 차원 공식과 일치하며, 관련 축퇴 군인 SU(3)의 대칭 표현의 차원과 같다.^[8]

4. 응용

양자 조화 진동자는 다양한 물리 현상을 설명하는 데 응용된다. 이원자 분자의 진동, 고체 격자의 진동인 포논 등이 그 예시이다.

4. 1. 분자 진동

이원자 분자의 진동은 양자 조화 진동자로 근사하여 다룰 수 있는 2체 문제의 한 예이다. 이 경우, 각진동수는 다음과 같이 주어진다.

:

\omega = \sqrt{\frac{k}{\mu}}

여기서

\mu = \frac{m_1 m_2}{m_1 + m_2}

는 환산 질량이고,

m_1

과

m_2

는 두 원자의 질량이다.^[10]

4. 2. 고체 격자의 진동: 포논

고체 내 원자들의 진동은 여러 개의 양자 조화 진동자가 연결된 문제로 볼 수 있다. 가장 간단한 형태인 1차원 양자 역학적 조화 사슬을 생각해보자. 이 사슬은 '''N'''개의 동일한 원자로 구성되어 있으며, 각 원자는 평형 위치에서 약간씩 벗어나 진동한다. 이러한 진동은 포논이라는 양자화된 단위로 나타난다.

이 시스템의 해밀토니안은 다음과 같이 표현된다.^[9]

\mathbf{H} = \sum_{i=1}^N {p_i^2 \over 2m} + {1\over 2} m \omega^2 \sum_{\{ij\} (nn)} (x_i - x_j)^2 \,,

여기서 m은 각 원자의 질량, x_i와 p_i는 ''i''번째 원자의 위치와 운동량 연산자이며, 합은 최근접 이웃(nn)에 대해 이루어진다.

파수 벡터의 정규 모드를 이용해 해밀토니안을 다시 작성하면, 푸리에 공간에서 문제를 더 쉽게 다룰 수 있다. 정규 좌표 Q_k와 켤레 운동량 Π_k를 도입하면 다음과 같다.

Q_k = {1\over\sqrt{N}} \sum_{l} e^{ikal} x_l

\Pi_{k} = {1\over\sqrt{N}} \sum_{l}  e^{-ikal} p_l \,.

여기서 k_n은 포논의 파수이며, 원자의 수가 유한하므로 양자화된 값을 갖는다.

이 변환을 통해 해밀토니안은 다음과 같이 단순화된다.

\mathbf{H} = {1\over {2m}}\sum_k \left({ \Pi_k\Pi_{-k} } + m^2 \omega_k^2 Q_k Q_{-k}\right) ~.

이는 N개의 결합되지 않은 조화 진동자를 나타낸다. 각 진동 모드 ω_k에 대한 에너지 준위는 다음과 같다.

E_n = \left({1\over2}+n\right)\hbar\omega_k   \quad\hbox{for}\quad n=0,1,2,3,\ldots

영점 에너지를 무시하면, 에너지 준위는

\tfrac32\hbar\omega , \ \tfrac52\hbar\omega ,\ \tfrac72\hbar\omega \ \cdots

와 같이 균일한 간격으로 나타난다. 즉, 격자를 다음 에너지 준위로 올리려면 정확히 ħω 만큼의 에너지가 필요하다. 이 에너지 양자가 바로 포논이다.^[9]

참조

_[1] 웹사이트 Transition amplitude for time-dependent linear harmonic oscillator with Linear time-dependent terms added to the Hamiltonian http://www.ncp.edu.p[...] National Center for Physics 2010-10-19
_[2] 서적 Mathematical Methods for Optical Physics and Engineering Cambridge University Press
_[3] 문서
_[4] 서적 Quantum Theory for Mathematicians Springer
_[5] 서적 Wave Mechanics: Volume 5 of Pauli Lectures on Physics Dover Books on Physics
_[6] 간행물 Immersion of the Fourier transform in a continuous group of functional transformations https://www.ncbi.nlm[...]
_[7] 서적 Quantum Mechanics https://archive.org/[...] North-Holland
_[8] 학술지 Three-dimensional isotropic harmonic oscillator and SU3.
_[9] 서적 Many particle physics Springer
_[10] 웹사이트 Quantum Harmonic Oscillator http://hyperphysics.[...] 2009-09-24

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com