오도권

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 오도권의 구조 및 원리
- 2.1. 조표와 관계조
- 2.2. 이명동음과 이론적 조
3. 오도권의 활용
- 3.1. 전조와 화성 진행
- 3.2. 음악 분석 및 작곡
4. 오도권의 역사
- 4.1. 초기 발전
- 4.2. 이후 발전
5. 오도권과 관련된 개념
- 5.1. 반음계 원
- 5.2. 온음계 오도권
6. 한국 대중음악에서의 오도권
참조

1. 개요

오도권은 음정 관계를 시각적으로 나타내는 음악 이론 개념으로, 완전 5도 간의 관계를 원형으로 배열하여 조성을 이해하는 데 도움을 준다. 12음 평균율과 같은 특정 조율 시스템에서는 완전 5도의 주파수 비율을 사용하여 음높이를 구성하지만, 순정 5도와는 미세한 차이가 발생한다. 오도권은 조표, 관계조, 이명동음과 같은 음악적 개념을 설명하는 데 사용되며, 화성 진행과 전조를 분석하고 작곡하는 데 활용된다. 바로크 시대에 이론화되었으며, 5도권 진행은 서양 음악에서 중요한 역할을 해왔고, 현대 대중음악에서도 널리 사용된다.

더 읽어볼만한 페이지

화성 (음악) - 세계의 조화
요하네스 케플러가 1619년에 발표한 "세계의 조화"는 천체의 운동, 음악, 기하학 간의 조화로운 관계를 탐구하며 행성 운동 제3법칙을 제시하고 다면체 연구를 포함하는 책이다.
화성 (음악) - 선율
선율은 음악의 핵심 요소로, 다양한 음악 양식에서 각기 다른 방식으로 활용되며 때로는 가사의 억양과 관계를 맺는 음악의 목표이자 주관적인 표현이다.
음악 이론 - 악보
악보는 음의 높낮이와 길이, 악기, 연주법 등을 시각적으로 표현하는 기호 체계로, 오선, 음표, 쉼표 등 다양한 기호를 사용하여 음악을 기록하고 전달하는 매체이다.
음악 이론 - 음이름
음이름은 조나 스케일과 관계없이 음의 높이를 나타내는 명칭으로, 서양 음악에서는 라틴 문자를 사용하여 표기하며, 각국별 표기법과 옥타브 구별법, 그리고 비서양 음악의 음이름 및 계명도 존재한다.

오도권
오도권
오도권
개요
정의	음악 이론에서 12개의 음높이류 사이의 관계를 보여주는 원
용도	조성 간의 관계, 음정, 화음 진행 등을 시각적으로 표현
관련 개념	딸림음, 버금딸림음, 조표
구조
배열 순서	완전5도 간격으로 배열 (시계 방향: 올림조, 반시계 방향: 내림조)
조표 변화	시계 방향으로 이동할 때마다 ♯이 하나씩 증가, 반시계 방향으로 이동할 때마다 ♭이 하나씩 증가
이명동음조	원의 특정 지점에서 이명동음조가 발생 (예: B♯ = C, G♯ = A♭, E♯ = F)
활용
조성 관계 파악	인접한 조들은 서로 밀접한 관계를 가짐 (예: C장조와 G장조, F장조)
전조 계획	곡의 흐름에 따라 자연스러운 전조 계획을 세울 수 있음
화성 분석	화성 진행의 경향을 파악하고, 대리 코드를 이해하는 데 도움
작곡 및 편곡	새로운 화성적 가능성을 탐색하고, 효과적인 음악적 아이디어를 구상
역사
기원	17세기 바로크 시대 (추정)
이론적 발전	요한 다비트 하이니헨, 니콜라이 딜레츠키 등의 음악 이론가에 의해 체계화
현대적 사용	음악 교육, 작곡, 화성 분석 등 다양한 분야에서 널리 활용
기타
관련 용어	Circle of fifths (영어) Quintenzirkel (독일어) Cercle des quintes (프랑스어)
참고 문헌	음악 이론 서적, 화성학 교재 등

2. 오도권의 구조 및 원리

오도권은 완전 5도 음정의 순서로 음고를 배열하며, 일반적으로 시계 방향으로 음고 및 해당 조가 원으로 표시된다. 이는 반시계 방향으로 4도권으로 볼 수 있다. 서양 음악의 화성 진행은 이 시스템에서 인접한 조를 일반적으로 사용하므로, 작곡 및 화성에 유용한 참조가 된다.^[1]

어떤 음고에서 시작하여 5도씩 상승하면 모든 음이 생성된 다음 시작하는 음고로 돌아간다. 음고 클래스는 옥타브에 관계없이 주어진 문자로 표시되는 모든 음표를 말한다. (예: 모든 "C"는 동일한 음고 클래스에 속한다.) 반시계 방향으로 이동하면 음고가 5도씩 하강하지만, 완전 4도로 상승하면 한 옥타브 높은 동일한 음표(따라서 동일한 음고 클래스)로 이어진다. C에서 반시계 방향으로 이동하는 것은 5도씩 하강하여 F로 가거나 4도씩 상승하여 F로 가는 것으로 생각할 수 있다.

2. 1. 조표와 관계조

오도권은 완전 5도 음정의 순서로 음고를 배열하며, 일반적으로 시계 방향으로 음고(및 해당 조)가 원으로 표시된다. 이는 반시계 방향으로 4도권으로 볼 수 있다. 서양 음악의 화성 진행은 이 시스템에서 인접한 조를 일반적으로 사용하므로, 작곡 및 화성에 유용한 참조가 된다.^[1]

원의 맨 위는 조 C 장조로, 올림표나 내림표가 없다. 시계 방향으로 진행하면 음고가 5도씩 상승하며, 해당 음고와 관련된 조표도 그에 따라 변경된다. G 장조는 올림표가 하나 있고, D 장조는 올림표가 2개 있는 식이다. 원의 위쪽에서 반시계 방향으로 진행하면 음표가 5도씩 하강하고 조표도 그에 따라 변경된다. F 장조는 내림표가 하나 있고, B♭|플랫^영어 장조는 내림표가 2개 있는 식이다. 일부 조(원의 맨 아래)는 올림표나 내림표로 표기할 수 있다.

어떤 음고에서 시작하여 5도씩 상승하면 모든 음이 생성된 다음 시작하는 음고로 돌아간다. (음고 클래스는 옥타브에 관계없이 주어진 문자로 표시되는 모든 음표로 구성된다. 예를 들어 모든 "C"는 동일한 음고 클래스에 속한다.) 반시계 방향으로 이동하면 음고가 5도씩 하강하지만, 완전 4도로 상승하면 한 옥타브 높은 동일한 음표(따라서 동일한 음고 클래스)로 이어진다. C에서 반시계 방향으로 이동하는 것은 5도씩 하강하여 F로 가거나 4도씩 상승하여 F로 가는 것으로 생각할 수 있다.

각 음은 장조 또는 단조의 으뜸음 역할을 할 수 있으며, 각 조에는 관련 온음계가 있다. 원형 다이어그램은 각 조표에 있는 올림표 또는 내림표의 수를 보여주며, 대문자는 장조를, 소문자는 단조를 나타낸다. 조표가 동일한 장조와 단조는 서로 ''딸림장조''와 ''딸림단조''라고 한다.

2. 2. 이명동음과 이론적 조

오도권은 완전 5도 음정의 순서로 음고를 배열하며, 일반적으로 시계 방향으로 음고(및 해당 조)가 원으로 표시된다. 이는 반시계 방향으로 4도권으로 볼 수 있다. 서양 음악의 화성 진행은 이 시스템에서 인접한 조를 일반적으로 사용하므로, 작곡 및 화성에 유용한 참조가 된다.^[1]

원의 맨 위는 조 C 장조로, 올림표나 내림표가 없다. 시계 방향으로 진행하면 음고가 5도씩 상승하고, 해당 음고와 관련된 조표도 그에 따라 변경된다. G 장조는 올림표가 하나 있고, D 장조는 올림표가 2개 있는 식이다. 반대로, 원의 위쪽에서 반시계 방향으로 진행하면 음표가 5도씩 하강하고 조표도 그에 따라 변경된다. F 장조는 내림표가 하나 있고, B♭^영어 장조는 내림표가 2개 있는 식이다. 일부 조(원의 맨 아래)는 올림표나 내림표로 표기할 수 있다.

어떤 음고에서 시작하여 5도씩 상승하면 모든 음이 생성된 다음 시작하는 음고로 돌아간다. (음고 클래스는 옥타브에 관계없이 주어진 문자로 표시되는 모든 음표로 구성된다. 예를 들어 모든 "C"는 동일한 음고 클래스에 속한다). 반시계 방향으로 이동하면 음고가 5도씩 하강하지만, 완전 4도로 상승하면 한 옥타브 높은 동일한 음표(따라서 동일한 음고 클래스)로 이어진다. C에서 반시계 방향으로 이동하는 것은 5도씩 하강하여 F로 가거나 4도씩 상승하여 F로 가는 것으로 생각할 수 있다.

완전 5도(3:2)의 정확한 주파수 비율을 사용하여 정의하는 것은, 5도권을 돌고 난 후 시작 음의 음높이 종류로 정확히 돌아오게 하지는 않는다. 12음 평균율 튜닝은 처음 음보다 정확히 7옥타브 위에 있는 음으로 되돌아가는 5도를 생성하며, 반음의 주파수 비율을 온음계적 반음의 주파수 비율과 동일하게 만든다. 표준 평균율 5도의 주파수 비율은 2^7/12:1(약 1.498307077:1)이며, 이는 순정 5도보다 약 2센트 좁다.

12개의 순정 5도로 상승하면 약 23.46센트의 초과분, 대략 반음의 1/4만큼 원이 닫히지 않는데, 이 간격을 피타고라스 콤마라고 한다. 옥타브당 12개의 음높이로 제한하면, 피타고라스 튜닝은 12개의 5도 중 하나의 폭을 현저히 줄여 심각하게 불협화음을 만든다. 이 비정상적인 5도를 울프 5도라고 하는데, 이는 음높이가 맞지 않는 음을 울부짖는 늑대를 해학적으로 표현한 것이다.

균등 분할 조율법은 완전 5도를 정의하는 정확한 3:2 주파수 비율을 사용하지 않는 반면, 순정 조율은 이 정확한 비율을 사용한다. 균등 분할 조율법에서 5도씩 상승하면 시작하는 음고로 돌아오지만, 정확한 3:2 비율을 사용하면(순정 조율) 이런 일이 일어나지 않는다. 균등 분할 조율법에서 이루어지는 조정은 피타고라스 콤마라고 한다. 이러한 차이로 인해 균등 분할 조율법에서 같은 음(예: 12음 균등 분할 조율법에서 C♯^영어와 D♭^영어 또는 19음 균등 분할 조율법에서 C♯^영어와 D♭♭^영어)은 순정 조율을 사용할 때는 같지 않다.

따라서 순정 조율에서 5도의 시퀀스는 원이 아닌 나선형으로 시각화할 수 있다. 즉, 12개의 5도 시퀀스는 피타고라스 콤마로 인해 "콤마 펌프"가 발생하여 나선형에서 한 단계 올라가는 것으로 시각화된다.

조표에 더블 샵 또는 더블 플랫이 있는 조는 이론적 조라고 한다. 12음 균등 분할 조율법에서는 중복되므로 사용이 극히 드물지만, 옥타브당 음의 수가 12의 배수가 아닌 경우 구분된다.

3. 오도권의 활용

바로크 음악 시대와 고전 시대 음악 시대의 음악 작품, 그리고 서양 대중음악, 전통 음악, 민속 음악에서 작품이나 노래가 새로운 조로 전조될 때, 이러한 전조는 종종 오도권과 관련이 있다.^[11]

실제로 작곡에서는 오도권 전체를 사용하는 경우가 드물다. 더 일반적으로 작곡가들은 "음악이 원이 추상적으로 나타내는 조적 구조의 더 작거나 큰 부분 전체를 일관되게 이동할 때 5도의 '사이클'이라는 작곡적 아이디어를 사용한다."^[11] 일반적인 관행은 완전한 12음계가 아닌, 온음계의 7음에서 오도 진행을 파생시키는 것이다. 이 온음계 버전의 원에서 5도 중 하나는 진정한 5도가 아니다. 그것은 F와 B 사이의 증 4도(또는 감 5도)이다. (예: "자연" 온음계에서(즉, 샤프나 플랫이 없는 경우).

오도권이 순열을 통해 온음계 장음계에서 파생되는 방식은 다음과 같다.

(자연) 단음계에서 파생되는 방식은 다음과 같다.

장조 베이스 라인 위에 구축할 수 있는 기본 화음 시퀀스는 다음과 같다.

단조 위에서 구축할 수 있는 기본 화음 시퀀스는 다음과 같다.

화음에 7음을 추가하면 하모니에 더욱 큰 전진감을 부여한다.

3. 1. 전조와 화성 진행

조성 음악은 원래의 조표와 단 하나만 다른, 밀접하게 관련된 조로 전조하는 경우가 많다. 이러한 조들은 서로 완전 5도 관계에 있어 오도권에서 인접해 있다. 화음 진행 또한 근음이 완전 5도 관계인 화음 사이를 이동하는 경우가 많아, 오도권은 화음 사이의 "화성적 거리"를 설명하는 데 유용하다.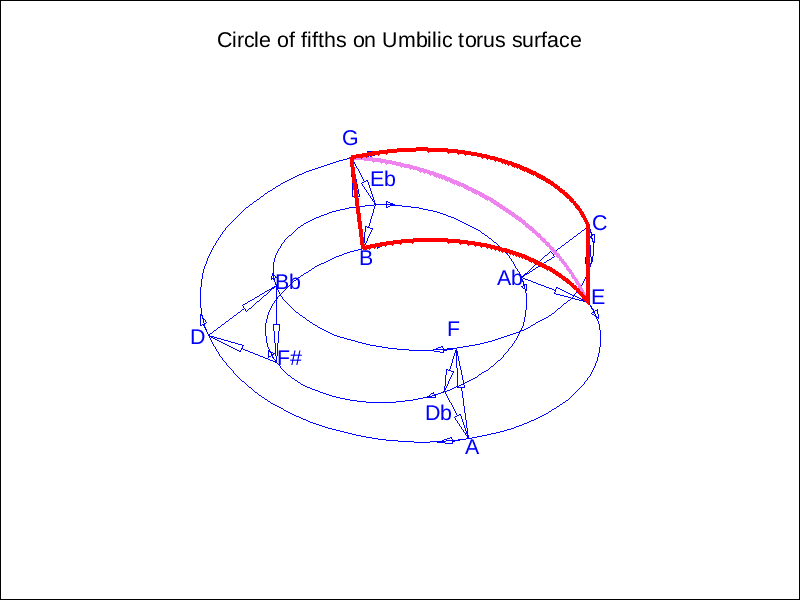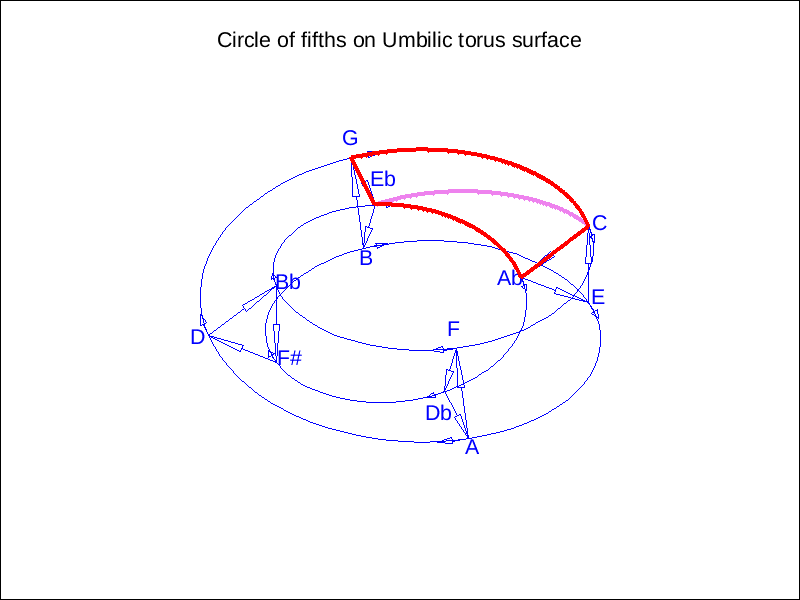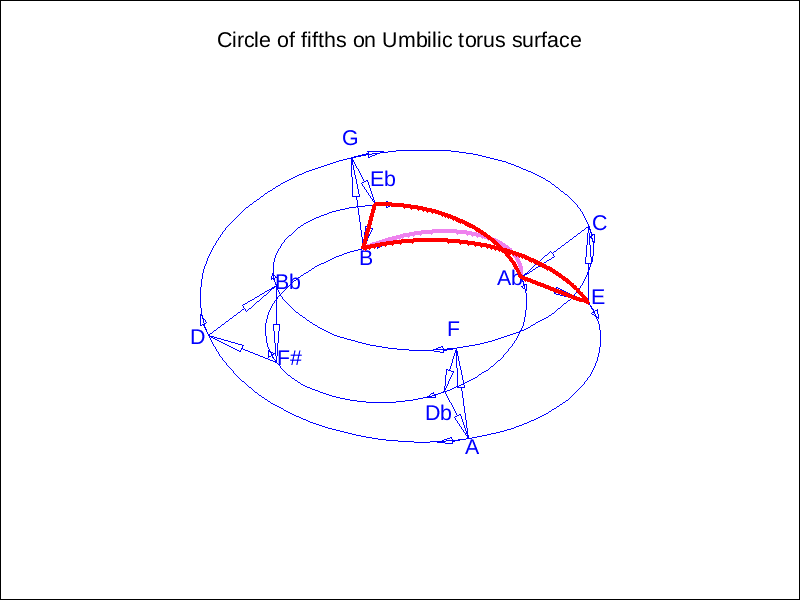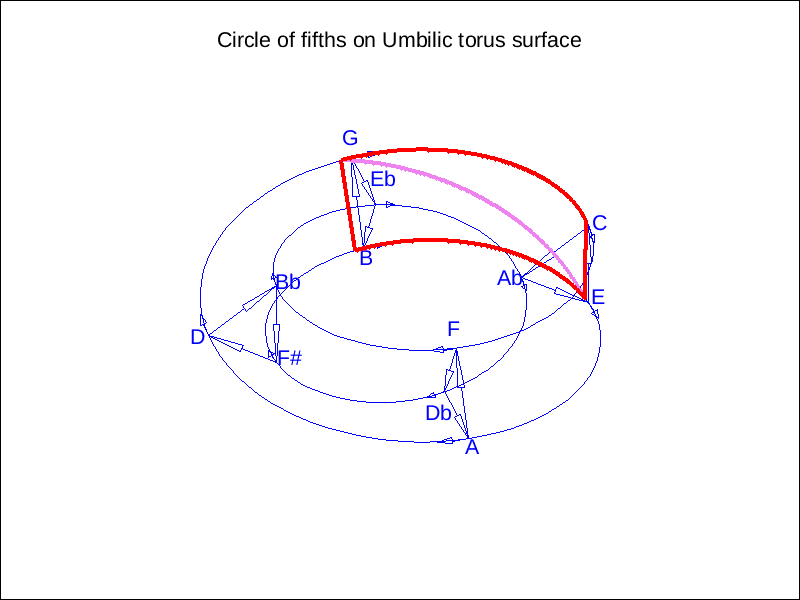

오도권은 화성 기능 또는 화음의 조성을 정리하고 설명하는 데 사용된다.^[2] 화음은 "기능적 연속"에서 오름차순 완전 4도(또는 내림차순 완전 5도)의 패턴으로 진행할 수 있다. 이때, 음계도 II는 딸림보다 음계도 IV에 더 가깝다고 할 수 있다. 이러한 관점에서 으뜸음(조성 중심)은 오도권에서 파생된 화음 진행의 종착점으로 간주된다.

리처드 프랑코 골드만은 ''서양 음악의 화성''에서 "4도 화음은 가장 간단한 유형의 음계 관계에서 으뜸음으로부터 가장 멀리 떨어져 있다. [하강하는] 오도권의 관점에서 볼 때, 으뜸음으로 향하기보다는 으뜸음에서 멀어진다."라고 하였다. 그는 I–ii–V–I 진행(정격 종지)이 I–IV–I (변격 종지)보다 더 최종적이거나 해결된 느낌을 줄 것이라고 말한다. 골드만은 "4도에 있는 화음은 II에 있는 화음보다 훨씬 먼저 나타나고, I–IV–vii^o–iii–vi–ii–V–I 진행에서 그 뒤에 최종적인 I이 나타난다"고 주장하며, 으뜸음에서 더 멀리 떨어진다고 주장하는 나티에와 동의한다. (대문자 로마 숫자는 장3화음, 소문자 로마 숫자는 단3화음을 나타낸다.)

바로크 음악 시대와 고전 시대 음악 시대의 음악 작품, 그리고 서양 대중음악, 전통 음악, 민속 음악에서 작품이나 노래가 새로운 조로 전조될 때, 이러한 전조는 종종 오도권과 관련이 있다.

실제 작곡에서는 오도권 전체를 사용하는 경우가 드물다. 더 일반적으로 작곡가들은 "음악이 원이 추상적으로 나타내는 조적 구조의 더 작거나 큰 부분 전체를 일관되게 이동할 때 5도의 '사이클'이라는 작곡적 아이디어를 사용한다."^[11] 일반적인 관행은 완전한 12음계가 아닌, 온음계의 7음에서 오도 진행을 파생시키는 것이다. 이 온음계 버전의 원에서 5도 중 하나는 진정한 5도가 아니다. 그것은 F와 B 사이의 증 4도(또는 감 5도)이다. (예: "자연" 온음계에서(즉, 샤프나 플랫이 없는 경우).

장조 베이스 라인 위에 구축할 수 있는 기본 화음 시퀀스는 다음과 같다.

단조 위에서는 다음과 같다.

화음에 7음을 추가하면 하모니에 더욱 큰 전진감을 부여한다.

3. 2. 음악 분석 및 작곡

조성 음악은 종종 원래의 조표와 단 하나만 다른 새로운 조성을 이루는 새로운 조성 중심으로 전조한다. 이러한 밀접하게 관련된 조는 서로 완전 5도 관계에 있으므로, 오도권에서 인접해 있다. 화음 진행 또한 종종 근음이 완전 5도 관계에 있는 화음 사이를 이동하며, 이는 오도권이 화음 사이의 "화성적 거리"를 설명하는 데 유용하게 한다.^[2] 화음은 "기능적 연속"에서 오름차순 완전 4도(또는 내림차순 완전 5도로 간주)의 패턴으로 진행할 수 있다. "...오도권으로 표시할 수 있으며, 여기에서 음계도 II는 딸림보다 음계도 IV에 더 가깝다"고 할 수 있다. 이 관점에서 으뜸음 또는 조성 중심은 오도권에서 파생된 화음 진행의 종착점으로 간주된다.

리처드 프랑코 골드만의 저서 ''서양 음악의 화성''에 따르면, "4도 화음은 가장 간단한 유형의 음계 관계에서 으뜸음으로부터 가장 멀리 떨어져 있다. [하강하는] 오도권의 관점에서 볼 때, 으뜸음으로 향하기보다는 으뜸음에서 멀어진다." 그는 I–ii–V–I 진행(정격 종지)이 I–IV–I (변격 종지)보다 더 최종적이거나 해결된 느낌을 줄 것이라고 말한다. 골드만은 "4도에 있는 화음은 II에 있는 화음보다 훨씬 먼저 나타나고, I–IV–vii^o–iii–vi–ii–V–I 진행에서 그 뒤에 최종적인 I이 나타난다"고 주장하며, 여기서도 으뜸음에서 더 멀리 떨어진다고 주장하는 나티에와 동의한다. (이 문서 및 관련 문서에서 대문자 로마 숫자는 장3화음을 나타내고 소문자 로마 숫자는 단3화음을 나타낸다.)

바로크 음악 시대와 고전 시대 음악 시대의 음악 작품, 그리고 서양 대중음악, 전통 음악, 민속 음악에서 작품이나 노래가 새로운 조로 전조될 때, 이러한 전조는 종종 오도권과 관련이 있다.

실제로 작곡에서는 오도권 전체를 사용하는 경우가 드물다. 더 일반적으로 작곡가들은 "음악이 원이 추상적으로 나타내는 조적 구조의 더 작거나 큰 부분 전체를 일관되게 이동할 때 5도의 '사이클'이라는 작곡적 아이디어를 사용한다."^[11] 일반적인 관행은 완전한 12음계가 아닌, 온음계의 7음에서 오도 진행을 파생시키는 것이다. 이 온음계 버전의 원에서 5도 중 하나는 진정한 5도가 아니다. 그것은 F와 B 사이의 증 4도(또는 감 5도)이다. (예: "자연" 온음계에서(즉, 샤프나 플랫이 없는 경우).

오도권이 순열을 통해 온음계 장음계에서 파생되는 방식, (자연) 단음계에서 파생되는 방식, 장조 베이스 라인 위에 구축할 수 있는 기본 화음 시퀀스, 단조 위에서 구축할 수 있는 기본 화음 시퀀스는 다음과 같다. (악보는 생략)

화음에 7음을 추가하면 하모니에 더욱 큰 전진감을 부여한다. (악보는 생략)

오도권이 형식 구성 장치이자 표현적인 음악적 트로프로서 지속적인 인기를 누리고 있다는 것은 20세기에 작곡된 수많은 "스탠다드" 팝송에서 분명하게 드러난다. 또한 재즈 음악가들이 즉흥 연주를 위한 수단으로 선호하는데, 오도권은 작곡가들이 음정, 화음 관계 및 진행을 이해하는 데 도움이 되기 때문이다.

바트 하워드, "플라이 미 투 더 문"
제롬 컨, "올 더 씽스 유 아"
레이 노블, "체로키". 많은 재즈 음악가들은 특히 중간 8마디가 오도권을 통해 빠르게 진행하면서, "여러 조성을 일시적으로 통과하는 일련의 II–V–I 진행을 만들어내기 때문에 이것을 매우 어렵게 생각한다."^[13]
코스마, 프레베르, 머서, "고엽"^[14]
비틀즈, "유 네버 기브 미 유어 머니"
마이크 올드필드, "인칸테이션"^[16]
카를로스 산타나, "유로파 (어스 크라이 헤븐스 스마일)"
글로리아 게이너, "아이 윌 서바이브"
펫 샵 보이즈, "잇츠 어 신"
도나 서머, "러브 투 러브 유, 베이비"

4. 오도권의 역사

오도권은 17세기 후반 아르칸젤로 코렐리에 의해 표준 화성 트로프로 패턴을 확립하는데 큰 영향을 주었다. 코렐리 시대에 5도권이 화성 운동의 주요 추진력으로 이론화되었고, 코렐리는 이 새로운 아이디어를 실질적으로 표현한 작곡가였다.^[3]

요한 제바스티안 바흐는 5도권 진행을 자신의 음악에 자주 사용했다. 예를 들어 ''모든 나라에서 하나님을 찬양하라'', BWV 51에서 솔로 베이스 라인은 코드 자체를 명시하기보다는 암시적으로 5도권 진행을 보여준다.

헨델은 G단조 하프시코드 모음곡 6번의 파사칼리아 악장에서 5도권 진행을 사용했다.

바로크 음악 작곡가들은 5도권에 의해 생성된 화성의 "추진력"을 향상시키기 위해 대부분의 구성 코드에 7음을 추가했다. 이 7음은 불협화음으로, 해결의 필요성을 만들어 각 진행을 화성적 긴장의 동시 해소제이자 재자극제로 만들어 표현 목적으로 활용했다. 헨델의 1715년 오페라 ''아마디지 디 가울라''의 아리아 "Pena tiranna"에서 7음의 사용을 보여주는 인상적인 구절이 나타난다.

바흐의 알레산드로 마르첼로의 오보에와 현을 위한 협주곡 건반악기 편곡에서도 7음 사용의 예시가 나타난다.

프란츠 슈베르트, 펠릭스 멘델스존, 로베르트 슈만등 여러 작곡가들이 5도권 혹은 수정된 딸림음관계를 사용하였다. 바그너의 오페라 ''신들의 황혼''에서, 딸림음 진행은 프롤로그의 끝에서 제1막의 첫 장면으로 전환되는 음악에서 발생하며, 부유한 기비충가의 인상적인 홀에서 설정된다. 기비충 가문의 수장인 "군터에게 할당된 모티프는 지위와 평판을 모두 보여준다".^[12]

4. 1. 초기 발전

오도권은 1600년대 후반과 1700년대 초반 바로크 시대의 조바꿈을 이론화하기 위해 발전했다.

최초의 오도권 도표는 작곡가이자 이론가인 니콜라이 딜레츠키의 Grammatika|그라마티카^ru (1677)에 등장하며, 그는 음악 이론을 작곡 도구로 제시하고자 했다.^[3] 이는 "서양식 다성 작곡을 러시아 청중에게 가르치기 위한 최초의 시도"였다.

독일 작곡가이자 이론가인 요한 다비트 하이니헨은 ''Neu erfundene und gründliche Anweisung|노이 에어푼데네 운트 그륀들리헤 안바이중^de'' (1711)에서 오도권 도표를 독립적으로 만들었으며,^[4] 이를 "오도권" (Musicalischer Circul|무지칼리셔 치르쿨^de)이라고 불렀다. 이 도표는 그의 ''Der General-Bass in der Composition|데어 게네랄바스 인 데어 콤포지치온^de'' (1728)에도 게재되었다.

하이니헨은 상대 단조를 장조 옆에 배치했는데, 이는 실제 조의 근접성을 반영하지 않았다. 요한 마테존(1735)과 다른 사람들은 이를 개선하려 시도했고, 다비드 켈너(1737)는 장조를 하나의 원에, 상대 단조를 두 번째, 안쪽 원에 배치할 것을 제안했다. 이는 이후 화음 공간으로 발전하여, 평행 단조를 포함하게 되었다.^[5]

일부 자료에서는 오도권이 피타고라스 시대에 고대부터 알려졌다고 암시한다.^[6]^[7]^[8] 이는 오해이며 시대착오이다.^[9] 오도에 의한 조율 (소위 피타고라스 조율)은 고대 메소포타미아 시대로 거슬러 올라간다.^[10] 음악 이론 참조. 그러나 그들은 이를 12음계로 확장하지 않고 7음에서 멈췄다. 피타고라스 콤마는 유클리드와 중국 수학자 (''회남자'')에 의해 계산되었다. 역사 참조. 따라서 12개의 오도의 주기가 거의 정확히 7옥타브라는 것은 고대부터 알려져 있었다 (더 실용적으로는, 오도를 올리고 4도를 내리는 것을 번갈아 하면 거의 정확히 1옥타브였다). 그러나 이것은 이론적인 지식이었으며, 반복되는 12음계 구성이나 조바꿈에 사용되지 않았다. 이는 나중에 평균율과 12음 평균율에서 이루어졌으며, 조율 상태에서 조바꿈을 허용했지만, 약 1500년까지 유럽에서 발전하지 않았다. 오도권으로 대중화되었지만, 그 앵글로색슨 어원적 기원은 "오도의 바퀴"라는 이름으로 거슬러 올라간다.

리처드 타루스킨에 따르면, 아르칸젤로 코렐리는 표준 화성 트로프로 패턴을 확립하는 데 가장 영향력 있는 작곡가였다. "17세기 후반인 코렐리의 시대에 정확히 5도권이 화성 운동의 주요 추진력으로 '이론화'되었으며, 그 새로운 아이디어를 실질적으로 표현한 작곡가는 누구보다도 코렐리였다."

5도권 진행은 요한 제바스티안 바흐의 음악에서 자주 나타난다. 다음은 ''모든 나라에서 하나님을 찬양하라'', BWV 51에서 솔로 베이스 라인이 코드 자체를 명시하기보다는 암시할 때에도 나타난다.

헨델은 G단조 하프시코드 모음곡 6번의 파사칼리아 악장의 기초로 5도권 진행을 사용했다.

바로크 음악 작곡가들은 5도권에 의해 생성된 화성의 "추진력"을 향상시키는 방법을 배웠으며, "대부분의 구성 코드에 7음을 추가"했다. "이 7음은 불협화음이므로 해결의 필요성을 만들어 각 진행을 화성적 긴장의 동시 해소제이자 재자극제로 만든다... 따라서 표현 목적으로 활용된다." 헨델의 1715년 오페라 ''아마디지 디 가울라''의 아리아 "Pena tiranna"에서 7음의 사용을 보여주는 인상적인 구절이 나타난다.

바흐의 알레산드로 마르첼로의 오보에와 현을 위한 협주곡 건반악기 편곡에서도 7음 사용의 예시가 나타난다.

4. 2. 이후 발전

오도권은 1600년대 후반과 1700년대 초반 바로크 시대의 조바꿈을 이론화하기 위해 발전했다.

최초의 오도권 도표는 작곡가이자 이론가인 니콜라이 딜레츠키의 ''Grammatika'' (1677)에 등장하며, 그는 음악 이론을 작곡 도구로 제시하고자 했다.^[3] 이는 "서양식 다성 작곡을 러시아 청중에게 가르치기 위한 최초의 시도"였다.

오도권 도표는 독일 작곡가이자 이론가인 요한 다비트 하이니헨에 의해 그의 ''Neu erfundene und gründliche Anweisung'' (1711)에서 독립적으로 만들어졌으며,^[4] 그는 이를 "오도권" (Musicalischer Circul^de)이라고 불렀다. 이 도표는 그의 ''Der General-Bass in der Composition'' (1728)에도 게재되었다.

하이니헨은 상대 단조를 장조 옆에 배치했는데, 이는 실제 조의 근접성을 반영하지 않았다. 요한 마테존(1735)과 다른 사람들은 이를 개선하려 시도했고, 다비드 켈너(1737)는 장조를 하나의 원에, 상대 단조를 두 번째, 안쪽 원에 배치할 것을 제안했다. 이는 이후 화음 공간으로 발전하여, 평행 단조를 포함하게 되었다.^[5]

일부 자료에서는 오도권이 피타고라스 시대에 고대부터 알려졌다고 암시한다.^[6]^[7]^[8] 이는 오해이며 시대착오이다.^[9] 오도에 의한 조율 (소위 피타고라스 조율)은 고대 메소포타미아 시대로 거슬러 올라간다.^[10] 그러나 그들은 이를 12음계로 확장하지 않고 7음에서 멈췄다. 피타고라스 콤마는 유클리드와 중국 수학자 (''회남자'')에 의해 계산되었다. 따라서 12개의 오도의 주기가 거의 정확히 7옥타브라는 것은 고대부터 알려져 있었다. 그러나 이것은 이론적인 지식이었으며, 반복되는 12음계 구성이나 조바꿈에 사용되지 않았다. 이는 나중에 평균율 템퍼먼트와 12음 평균율에서 이루어졌으며, 이는 조율 상태에서 조바꿈을 허용했지만, 약 1500년까지 유럽에서 발전하지 않았다. 오도권으로 대중화되었지만, 그 앵글로색슨 어원적 기원은 "오도의 바퀴"라는 이름으로 거슬러 올라간다.

프란츠 슈베르트의 내림 마장조 즉흥곡 D 899는 수정된 딸림음 관계로 진행되는 화음을 포함하고 있다.

멘델스존의 현악 사중주 2번의 간주곡 악장은 딸림음 진행의 짧은 부분을 가지고 있다.

로베르트 슈만의 "어린이의 잠" (''어린이 정경'')은 이 진행을 사용하며, 마지막 부분에서 변경된다. 곡은 예상되는 으뜸음 e단조 대신 A단조 화음으로 끝난다.

바그너의 오페라 ''신들의 황혼''에서, 딸림음 진행은 프롤로그의 끝에서 제1막의 첫 장면으로 전환되는 음악에서 발생하며, 부유한 기비충가의 인상적인 홀에서 설정된다. 기비충 가문의 수장인 "군터에게 할당된 모티프는 지위와 평판을 모두 보여준다".^[12]

5. 오도권과 관련된 개념

오도권은 반음계 원과 밀접하게 관련되어 있다. 반음계 원은 모든 음고 클래스를 원형으로 배열한 것이지만, 오도권은 이산적인 음정 구조를 가진다. 12음계에서 오도권은 완전 5도 또는 완전 4도를 생성하여 만들어진다. 31음 동일 조율과 같이 다른 음계를 사용하면 더 많은 음정을 생성기로 사용할 수 있어 다양한 원이 만들어진다.

5도권은 반음계에서 곱셈을 통해 만들어지며, 반대로도 가능하다. 12음 평균율에서 반음계 음들을 나타내는 12-튜플에 7을 곱하고 모듈로 12 감소를 적용하면 5도권을 얻을 수 있다.

온음계 5도권은 온음계 구성원만을 포함하며, C 장조에서는 B와 F 사이의 감5도를 포함한다. 화성 진행은 일반적으로 온음계 화음을 통해 5도권으로 진행되며, 하나의 감화음 코드를 포함한다.

5. 1. 반음계 원

오도권은 특정 조율의 동일 음정 음고 클래스를 원형으로 배열하는 반음계 원과 밀접하게 관련되어 있다. 반음계 원은 연속적인 공간으로 이해할 수 있으며, 원의 모든 점은 상상할 수 있는 음고 클래스에 해당하고, 상상할 수 있는 모든 음고 클래스는 원의 한 점에 해당한다. 반면 오도권은 근본적으로 뚜렷한 음정을 통해 배열된 '이산적' 구조이며, 각 점에 음고 클래스를 할당할 명확한 방법이 없다. 이러한 관점에서 두 원은 수학적으로 매우 다르다.

모든 양의 정수 ''N''에 대해, ''N'' 음정 동일 조율의 음고 클래스는 ''N''차 순환군 또는 잉여 클래스

\mathbb{Z}/N\mathbb{Z}

로 표현될 수 있다. 12음 동일 조율에서 그룹

\mathbb{Z}_{12}

는 네 개의 생성기를 가지며, 이는 상승 및 하강 반음과 상승 및 하강 완전 5도로 식별할 수 있다. 반음 생성기는 반음계 원을 생성하고, 완전 4도와 완전 5도는 오도권을 생성한다. 31음 동일 조율과 같은 대부분의 다른 조율에서는 훨씬 더 많은 음정을 생성기로 사용할 수 있으며, 그 결과 훨씬 더 많은 원이 가능하다.

5도권 또는 4도권은 반음계로부터 곱셈에 의해 매핑될 수 있으며, 그 반대도 마찬가지이다. 5도권과 반음계 사이를 매핑하려면 (정수 표기법으로) 7을 곱하고 (M7), 4도권의 경우에는 5 (P5)를 곱한다.

12음 평균율에서 정렬된 12-튜플 (음열) 정수부터 시작할 수 있다.

: (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)

이는 반음계의 음들을 나타낸다. 0 = 다, 2 = 라, 4 = 미, 5 = 파, 7 = 솔, 9 = 라, 11 = 시, 1 = 다, 3 = 라, 6 = 파, 8 = 솔, 10 = 라이다. 이제 전체 12-튜플에 7을 곱한다.

: (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)

그런 다음 각 숫자에 모듈로 12 감소를 적용한다 (숫자가 12보다 작아질 때까지 각 숫자에서 12를 필요한 만큼 뺀다).

: (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)

이는 다음과 같다.

: (다, 솔, 라, 가, 미, 시, 파, 다, 솔, 라, 가, 파)

이는 5도권이다.

이는 이명동음적으로 다음과 같다.

: (다, 솔, 라, 가, 미, 시, 솔, 라, 가, 미, 시, 파).

5. 2. 온음계 오도권

온음계 5도권은 온음계의 구성원만을 포함하는 5도권이다. 따라서 C 장조에서는 B와 F 사이의 감5도를 포함한다. 구조는 다양성을 내포한다를 참조하라.

화성 진행은 일반적으로 온음계 화음을 통한 5도권으로, 하나의 감화음 코드를 포함한다. C 장조에서 I-IV-vii^o-iii-vi-ii-V-I의 화성 진행은 다음과 같다.

6. 한국 대중음악에서의 오도권

(이전 출력이 없으므로, 수정할 내용이 없습니다. 원본 소스와 함께 섹션 제목, 요약 등을 제공해주시면 위키텍스트를 생성해 드립니다.)

참조

_[1] 웹사이트 The Circle of Fifths: A Brief History http://www.dummies.c[...] www.dummies.com 2009-02-23
_[2] 웹사이트 Wheel of Fifths – Harmonic Function https://www.wheelof5[...] 2023-10-05
_[3] 간행물
_[4] 서적 Neu erfundene und gründliche Anweisung https://books.google[...]
_[5] 서적 Tonal Pitch Space. https://books.google[...] Oxford University Press 2005
_[6] 웹사이트 The Circle of Fifths Complete Guide! https://jadebultitud[...] 2021-01-17
_[7] 웹사이트 The Circle of Fifths made clear https://www.linkedin[...]
_[8] 웹사이트 Dummies - Learning Made Easy https://www.dummies.[...]
_[9] 간행물 The Development of Musical Tuning Systems http://www.midicode.[...] 2020-05-24
_[10] 서적 The archaeomusicology of the Ancient Near East 2005
_[11] 서적 Circle of Fifths Oxford University Press
_[12] 서적 The Ring of Truth: The Wisdom of Wagner's Ring of the Nibelung Allen Lane
_[13] 서적 Chord Progressions for Songwriters Writers Club Press
_[14] 서적 Tonal Harmony with an Introduction to Twentieth-century Music McGraw-Hill
_[15] 악보 You Never Give Me Your Money Hal Leonard
_[16] 웹사이트 Mike Oldfield https://tubular.net/[...] 2021-02-19
_[17] 기타 I Will Survive Polygram International Publishing
_[18] 기타 It's a Sin. Sony/ATV Music Publishing (UK) Ltd
_[19] 기타 Love to Love you, Baby Bulle Music
_[20] 웹사이트 Foulds, John, ''A World Requiem'', Op. 60, pp. 153ff. https://imslp.org/wi[...]
_[21] 웹사이트 Ewald, Victor, ''Quintet No 4 in A{{music|b}}'', Op. 8 for Brass Quintet [211.01] https://www.hickeys.[...]
_[22] 기타 Circle of fifths Macmillan
_[23] 웹사이트 Pythagorean Tuning and Medieval Polyphony http://www.medieval.[...]
_[24] 기타 Temperaments Macmillan
_[25] 서적 A Folk Musicians Working Guide to Chords, Keys, Scales, and More Captain Fiddle Publications
_[26] 서적 Circle of fifths Oxford University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com