정칙 범주

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 정칙 논리
5. 예시
참조

1. 개요

정칙 범주는 범주론의 개념으로, 특정 조건을 만족하는 범주를 의미한다. 정칙 범주는 유한 완비 범주이며, 핵 쌍의 여균등화가 존재하고, 정칙 전사 사상의 당김은 정칙 전사 사상이다. 정칙 범주에는 정칙 사상, 유효 정칙 범주, 짧은 완전열 등의 개념이 존재하며, 집합 범주, 군 범주, 아벨 범주 등이 정칙 범주에 해당한다. 정칙 범주의 내부 논리는 정칙 논리이며, 정칙 범주는 수학의 여러 분야에서 활용된다.

더 읽어볼만한 페이지

범주론 - 작은 범주
그로텐디크 전체 $\mathcal{U}$ 가 주어졌을 때, $\mathcal{U}$ -작은 범주는 대상과 사상의 모임이 모두 $\mathcal{U}$ 의 원소인 범주를 의미하며, 이는 함자와 자연 변환과 함께 완비 범주이자 쌍대 완비 범주인 2-범주를 이룬다.
범주론 - 토포스
토포스는 유한 완비 범주이자 데카르트 닫힌 범주이며 부분 대상 분류자를 갖는 특정한 조건을 만족하는 범주로서, 일계 논리 또는 일계 정의가 있는 대상의 부분 대상 개념을 갖는 데카르트 닫힌 범주로 이해될 수 있고, 위상 공간의 일반화이자 집합론에 대한 범주론적 일반화로서 수학의 공리적 기초를 제공한다.

정칙 범주
정칙 범주
정의	유한 극한과 동등화 장치를 갖는 범주
추가 요구 사항	정칙 사상(regular morphism)은 안정적인 상(stable image)을 가져야 함 정칙 사상은 유효한 동등화 장치(effective coequalizer)여야 함
속성
모노사상	모노사상은 정칙 범주에서 안정적임
분할 모노사상	모든 모노사상은 분할 모노사상(split monomorphism)임
에피사상	모든 에피사상은 분할 에피사상(split epimorphism)임
정칙 에피사상	정칙 에피사상은 안정적임
예시
토포스	모든 토포스는 정칙 범주임
아벨 범주	모든 아벨 범주는 정칙 범주임
군의 범주	군의 범주는 정칙 범주임
환의 범주	환의 범주는 정칙 범주임
작은 범주의 범주	작은 범주의 범주는 정칙 범주임
대수적 격자	대수적 격자는 정칙 범주임

2. 정의

범주론에서, '''정칙 범주'''는 다음 조건들을 만족하는 범주 $\mathcal C$ 이다.

유한 완비 범주이다. 즉, 모든 유한 극한이 존재한다.
임의의 사상 $f\colon X\to Y$ 에 대해, 핵쌍 $\xleftarrow{\pi_1}XX\times_YX\xrightarrow{\pi_2}X$ 의 쌍대 동등자가 존재한다. 핵쌍은 대수 구조에서의 합동 관계의 일반화로 생각할 수 있다.
정칙 전사 사상의 당김은 정칙 전사 사상이다. 여기서 '''정칙 전사 사상'''은 어떤 두 사상의 쌍대 동등자로 나타낼 수 있는 사상이다.

두 정칙 범주 사이의 '''정칙 함자'''는 유한 극한과 핵쌍의 쌍대 동등자를 보존하는 함자이다. 작은 정칙 범주와 정칙 함자의 범주는

\operatorname{RegCat}

로 표기한다.

2. 1. 정칙 사상

범주론에서 사상(morphism)은 다양한 종류로 분류될 수 있다. 이 섹션에서는 정칙 사상, 유효 사상 등 주요 사상의 정의와 관계를 간략하게 설명한다.

임의의 범주 속 사상에 대해 다음 세 조건은 서로 동치이다.^[1]

정칙 전사 사상이자 단사 사상이다.
전사 사상이자 정칙 단사 사상이다.
동형 사상이다.

(하지만, 임의의 범주에서는 전사 사상이자 단사 사상이지만 동형 사상이 아닌 사상이 존재할 수 있다.)

다음과 같은 포함 관계가 성립한다.

:동형 사상 ⊆ 유효 단사 사상 ⊆ 정칙 단사 사상 ⊆ 강한 단사 사상 ⊆ 극단 단사 사상 ⊆ 단사 사상

:동형 사상 ⊆ 분할 단사 사상 ⊆ 정칙 단사 사상 ⊆ 강한 단사 사상 ⊆ 극단 단사 사상 ⊆ 단사 사상

:동형 사상 ⊆ 유효 전사 사상 ⊆ 정칙 전사 사상 ⊆ 강한 전사 사상 ⊆ 극단 전사 사상 ⊆ 전사 사상

:동형 사상 ⊆ 분할 전사 사상 ⊆ 정칙 전사 사상 ⊆ 강한 전사 사상 ⊆ 극단 전사 사상 ⊆ 전사 사상

분할 단사 사상이 정칙 단사 사상인 이유는 분할 단사 사상

f\colon X\to Y

및 그 왼쪽 역사상

r\colon Y\to X

이 주어졌을 때

f=\operatorname{eq}\{f\circ r,\operatorname{id}_Y\}

이기 때문이다. 마찬가지로, 분할 전사 사상이 정칙 전사 사상인 이유는 분할 전사 사상

f\colon X\to Y

및 그 오른쪽 역사상

s\colon Y\to X

이 주어졌을 때

f=\operatorname{eq}\{s\circ f,\operatorname{id}_X\}

이기 때문이다.

어떤 범주에서 모든 사상

f\colon X\to Y

의 스스로와의 당김

X\times_YX

이 존재한다면, 이 범주에서 정칙 전사 사상의 개념과 유효 전사 사상의 개념이 일치한다. 토포스(또는 더 일반적으로 준토포스)에서, 다음이 성립한다.

모든 전사 사상은 정칙 전사 사상이자 유효 전사 사상이다.
모든 단사 사상은 정칙 단사 사상이다.

아벨 범주에서, 모든 단사 사상은 정칙 단사 사상이다.

2. 1. 1. 정칙 전사 사상

범주

\mathcal C

에서, 어떤 두 사상

f,g\colon X\to Y

의 쌍대 동등자

:

\operatorname{coeq}\{f,g\}\colon Y\to Q

로 나타낼 수 있는 사상을 '''정칙 전사 사상'''(regular epimorphism^영어)이라고 한다. 정칙 단사 사상은 (쌍대 극한이므로) 항상 단사 사상이다.

2. 1. 2. 정칙 단사 사상

범주

\mathcal C

에서, 어떤 두 사상

f,g\colon X\to Y

의 동등자

:

\operatorname{eq}\{f,g\}\colon K\to X

로 나타낼 수 있는 사상을 '''정칙 단사 사상'''(regular monomorphism^영어)이라고 한다. 정칙 단사 사상은 (극한이므로) 항상 단사 사상이다.

2. 1. 3. 유효 사상

사상

f\colon X\to Y

가 스스로와의 당김

:

\pi_1,\pi_2\colon X\times_YX\to X

을 가지며,

\pi_1,\pi_2

의 쌍대 동등자가

f

와 같다면,

f

를 '''유효 전사 사상'''(effective epimorphism^영어)이라고 한다. 유효 전사 사상은 정의에 따라 정칙 전사 사상이다. 이와 같은 스스로와의 당김은 '''핵쌍'''(kernel pair^영어)이라고 하며, 대략 대수 구조에서의 합동 관계의 일반화로 생각할 수 있다. 즉, 유효 전사 사상은 "합동 관계"에 대한 "몫"으로의 사영 사상으로 생각할 수 있다.

사상

f\colon X\to Y

가 스스로와의 밂

:

\iota_1,\iota_2\colon Y\to Y\sqcup_XY

을 가지며,

\iota_1,\iota_2

의 동등자가

f

와 같다면,

f

를 '''유효 단사 사상'''(effective monomorphism^영어)이라고 한다. 유효 단사 사상은 정의에 따라 정칙 단사 사상이다. 이 정의에서,

\iota_1,\iota_2

의 동등자는

f

의 "치역"으로 생각할 수 있다. 즉, 유효 단사 사상은 정의역과 치역 사이의 동형을 정의하는 단사 사상으로 생각할 수 있다.

동치 관계 이론은 정칙 이론이다. 정칙 범주 내의 대상

X

에 대한 동치 관계는 반사성, 대칭성, 추이성에 대한 조건을 만족하는 단사 사상

X \times X

이다.

모든 커널 쌍

p_0, p_1: R \rightarrow X

는 동치 관계

R \rightarrow X \times X

를 정의한다. 반대로, 동치 관계는 커널 쌍으로 나타날 때 '''유효'''하다고 한다.^[3] 동치 관계는 코이퀄라이저를 가지고, 그것이 이 코이퀄라이저의 커널 쌍일 때 유효하다.

2. 2. 정칙 범주

범주

\mathcal C

가 다음 조건들을 만족시킨다면 '''정칙 범주'''라고 한다.

유한 완비 범주이다.
임의의 사상 $f\colon X\to Y$ 의 스스로에 대한 당김 $\xleftarrow{\pi_1}XX\times_YX\xrightarrow{\pi_2}X$ 에 대하여, $\pi_0,\pi_1\colon X\times_YX\to X$ 의 쌍대 동등자가 존재한다. 이는 $f$ 의 '''핵쌍'''이라고 한다.
정칙 전사 사상의 당김은 정칙 전사 사상이다.

두 정칙 범주 사이의 '''정칙 함자'''

F\colon\mathcal C\to\mathcal D

는 다음 조건을 만족시키는 함자이다.

유한 연속 함자이다. 즉, 유한 극한을 보존한다.
핵쌍의 쌍대 동등자를 보존한다.

작은 정칙 범주와 정칙 함자의 범주를

\operatorname{RegCat}

라고 한다.

범주 ''C''가 다음 세 가지 속성을 만족하면 '''정칙'''이라고 한다.^[1]

''C''는 유한 완비이다.
''f'' : ''X'' → ''Y''가 ''C''의 사상이고,

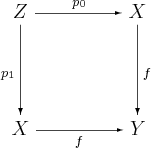
:가 당김이면, ''p''₀, ''p''₁의 여균등화가 존재한다. 쌍 (''p''₀, ''p''₁)은 ''f''의 '''핵 쌍'''이라고 한다. 당김이므로 핵 쌍은 유일한 동형사상까지 유일하다.

''f'' : ''X'' → ''Y''가 ''C''의 사상이고,

:가 당김이고, ''f''가 정칙 전사 사상이면 ''g''도 정칙 전사 사상이다. '''정칙 전사 사상'''은 어떤 쌍의 사상의 여균등화로 나타나는 전사 사상이다.

2. 3. 유효 정칙 범주 (바 완전 범주)

정칙 범주

\mathcal C

가 다음 조건을 만족시킨다면, '''유효 정칙 범주'''(effective regular category^영어) 또는 '''바 완전 범주'''(Barr-exact category^영어)라고 한다. (이는 퀼런 완전 범주와 관계없는 개념이다.)^[3]

임의의 대상 $X$ 가 주어졌으며, $X\times X$ 의 부분 대상 $r\colon Y\hookrightarrow X\times X$ 가 동치 관계를 이룰 때, $r$ 는 핵쌍으로부터 유도된다.

동치 관계 이론은 정칙 이론이다. 정칙 범주 내의 대상

X

에 대한 동치 관계는 반사성, 대칭성, 추이성에 대한 조건을 만족하는 단사 사상

X \times X

이다.

모든 커널 쌍

p_0, p_1: R \rightarrow X

는 동치 관계

R \rightarrow X \times X

를 정의한다. 반대로, 동치 관계는 커널 쌍으로 나타날 때 '''유효'''하다고 한다.^[3] 동치 관계는 코이퀄라이저를 가지고, 그것이 이 코이퀄라이저의 커널 쌍일 때 유효하다.

정칙 범주는 모든 동치 관계가 유효할 경우 '''정확'''하거나, '''바의 의미에서 정확'''하거나, '''유효 정칙'''이라고 한다.^[4]

3. 성질

정칙 범주 $\mathcal{C}$에서, 모든 정칙 전사 사상들의 모임 $\operatorname{RegEpi}(\mathcal{C})$과 단사 사상들의 모임 $\operatorname{Mono}(\mathcal{C})$은 분해계를 이룬다. 즉, 임의의 사상 $f\colon X\to Y$에 대하여, 정칙 전사 사상 $e\colon X\to Y'$과 단사 사상 $m\colon Y'\to Y$이 존재하여 $f = m \circ e$를 만족한다. 이때 $Y$의 부분 대상 $m$을 $f$의 '''치역'''이라고 한다.

1차 논리에서 '''정칙 공식'''(regular formula^영어)은 명제 변수 $P_1, P_2, \dots$, 논리곱 $\land$, 존재 기호 $\exists$만으로 구성된다. '''정칙 논리'''는 $\forall x\colon(\phi(x)\to\phi'(x))$ 꼴의 명제들만을 다룰 수 있는, 1차 논리를 약화시킨 논리이다.

정칙 범주의 내부 논리는 정칙 논리이다. 구체적으로, 정칙 범주 $\mathcal{C}$의 끝 대상 $1\in\mathcal{C}$을 골랐을 때, 다음과 같은 대응이 존재한다.

정칙 논리	정칙 범주
종류(sort^영어)	$\mathcal{C}$의 대상 $X\in\mathcal{C}$
$\forall(x:X),(x:X)\colon x=x$인 종류 $X$	끝 대상 $1\in\mathcal{C}$
종류 $X$의 상수 $c$	사상 $c\colon1\to X$
종류 $X\to Y$의 함수 $f$	사상 $f\colon X\to Y$
함수의 합성 $f\circ g$	사상의 합성 $f\circ g$
$\forall(x\colon X),(x\colon X)\colon f(x)=f(x)\implies x=x'$가 성립하는 함수 $f$	단사 사상 $f\colon X\hookrightarrow Y$
종류 $Y$에 대한 술어 $R(y)\iff\exists x\in X\colon f(x)=y$	부분 대상 $f\colon X\hookrightarrow Y$
$\forall(y\colon Y)\exists(x\colon X)\colon f(x)=y$가 성립하는 함수 $f$	정칙 전사 사상 $f\colon X\twoheadrightarrow Y$
$\forall(z,z\colon X\times Y)\colon\pi_X(z)=\pi_X(z)\land\pi_Y(z)=\pi_Y(z)\implies z=z$, $\forall(x\colon X)\forall(y\colon Y)\exists(z\colon X\times Y)\colon(\pi_X(z)=x\land\pi_Y(z)=y)$	곱 $X\overset{\pi_X}\leftarrow X\times Y\overset{\pi_Y}\to Y$
$\forall(x\colon X)\colon f(x)=g(x)\implies\exists(y:Y)\colon h(y)=x$	동등자 $h\colon Y\hookrightarrow X\overset f{\underset g\rightrightarrows}Y$

정칙 범주에서의 짧은 완전열, 완전열, Epi-mono factorization에 관한 내용은 하위 섹션에 자세히 설명되어 있으므로 여기서는 생략한다.

3. 1. 정칙 사상

범주

\mathcal C

에서, 어떤 두 사상

f,g\colon X\to Y

의 쌍대 동등자

:

\operatorname{coeq}\{f,g\}\colon Y\to Q

로 나타낼 수 있는 사상을 '''정칙 전사 사상'''(regular epimorphism^영어)이라고 한다. 정칙 단사 사상은 (쌍대 극한이므로) 항상 단사 사상이다.

마찬가지로, 범주

\mathcal C

에서, 어떤 두 사상

f,g\colon X\to Y

의 동등자

:

\operatorname{eq}\{f,g\}\colon K\to X

로 나타낼 수 있는 사상을 '''정칙 단사 사상'''(regular monomorphism^영어)이라고 한다. 정칙 단사 사상은 (극한이므로) 항상 단사 사상이다.

임의의 범주 속의 사상에 대하여, 다음 세 조건은 서로 동치이다.

정칙 전사 사상이자 단사 사상이다.
전사 사상이자 정칙 단사 사상이다.
동형 사상이다.

(반면, 임의의 범주에서는 전사 사상이자 단사 사상이지만 동형 사상이 아닌 사상이 존재할 수 있다.)

다음과 같은 포함 관계가 성립한다.

:동형 사상 ⊆ 유효 단사 사상 ⊆ 정칙 단사 사상 ⊆ 강한 단사 사상 ⊆ 극단 단사 사상 ⊆ 단사 사상

:동형 사상 ⊆ 분할 단사 사상 ⊆ 정칙 단사 사상 ⊆ 강한 단사 사상 ⊆ 극단 단사 사상 ⊆ 단사 사상

:동형 사상 ⊆ 유효 전사 사상 ⊆ 정칙 전사 사상 ⊆ 강한 전사 사상 ⊆ 극단 전사 사상 ⊆ 전사 사상

:동형 사상 ⊆ 분할 전사 사상 ⊆ 정칙 전사 사상 ⊆ 강한 전사 사상 ⊆ 극단 전사 사상 ⊆ 전사 사상

분할 단사 사상이 정칙 단사 사상인 이유는 분할 단사 사상

f\colon X\to Y

및 그 왼쪽 역사상

r\colon Y\to X

이 주어졌을 때

f=\operatorname{eq}\{f\circ r,\operatorname{id}_Y\}

이기 때문이다. 마찬가지로, 분할 전사 사상이 정칙 전사 사상인 이유는 분할 전사 사상

f\colon X\to Y

및 그 오른쪽 역사상

s\colon Y\to X

이 주어졌을 때

f=\operatorname{eq}\{s\circ f,\operatorname{id}_X\}

이기 때문이다.

3. 2. 완전열

정칙 범주

\mathcal C

에서 '''짧은 완전열'''은 다음과 같은 꼴이다.

:

N\overset{\iota}{\underset{\iota'}\rightrightarrows}X\overset q\to Q

여기서

\{\iota,\iota'\}

는

q

의 핵쌍이다.

만약

\mathcal C

가 아벨 범주이기도 하다면,

N\overset{\iota}{\underset{\iota'}\rightrightarrows}X\overset q\to Q

가 (정칙 범주의) 짧은 완전열인 것은

:

0\to N\overset{\iota-\iota'}\to X\overset q\to Q\to0

가 (아벨 범주의) 완전열인 것과 같다.

정칙 범주에서

R\rightrightarrows X\to Y

형태의 그림은 코이퀄라이저이자 커널 쌍일 때 '''완전열'''이라고 한다. 이는 호몰로지 대수학에서의 완전열을 일반화한 것이다. 아벨 범주에서 다음 그림

:

R\;\overset r{\underset s\rightrightarrows}\; X\xrightarrow{f} Y

은

0\to R\xrightarrow{(r,s)}X\oplus X\xrightarrow{(f,-f)} Y\to 0

이 통상적인 의미에서 짧은 완전열인 경우와 같은 의미에서 완전하다.

3. 3. Epi-mono factorization

정칙 범주

\mathcal C

에서 모든 정칙 전사 사상들의 모임

\operatorname{RegEpi}(\mathcal C)

과 단사 사상들의 모임

\operatorname{Mono}(\mathcal C)

은 분해계를 이룬다. 즉, 임의의 사상

f\colon X\to Y

에 대하여, 정칙 전사 사상

e\colon X\to Y'

과 단사 사상

m\colon Y'\to Y

이 존재하여

f=m\circ e

를 만족한다. 이때

Y

의 부분 대상

m

을

f

의 '''치역'''이라고 한다.

정칙 범주에서 정칙 전사와 단사는 인수분해계를 이룬다. 모든 사상 ''f:X→Y''는 정칙 전사 ''e:X→E''와 단사 ''m:E→Y''의 합성으로 인수분해될 수 있으며, 즉 ''f=me''이다. 이러한 인수분해는 유일하다. 다시 말해, ''e':X→E' ''가 다른 정칙 전사이고 ''m':E'→Y''가 다른 단사이며 ''f=m'e''라고 하면, ''he=e' ''및 ''m'h=m''을 만족하는 동형 사상 ''h:E→E' ''가 존재한다. 이때 단사 ''m''을 ''f''의 '''상'''이라고 한다.

4. 정칙 논리

1차 논리에서 '''정칙 공식'''(regular formula^영어)은 명제 변수 $P_1, P_2, \dots$ , 논리곱 $\land$ , 존재 기호 $\exists$ 만으로 나타낼 수 있는 공식이다. '''정칙 논리'''는 $\forall x \colon (\phi(x) \to \phi'(x))$ 꼴의 명제들만을 다룰 수 있는, 1차 논리를 약화시킨 논리이다.

정칙 범주의 내부 논리는 정칙 논리이다. 구체적으로, 정칙 범주 $\mathcal C$ 의 끝 대상 $1 \in \mathcal C$ 을 골랐을 때, 다음과 같은 대응이 존재한다.

정칙 논리	정칙 범주
종류(sort^영어)	$\mathcal C$ 의 대상 $X \in \mathcal C$
$\forall(x \colon X), (x$ \colon X) \colon x = x인 종류 $X$	끝 대상 $1 \in \mathcal C$
종류 $X$ 의 상수 $c$	사상 $c \colon 1 \to X$
종류 $X \to Y$ 의 함수 $f$	사상 $f \colon X \to Y$
함수의 합성 $f \circ g$	사상의 합성 $f \circ g$
$\forall(x \colon X), (x$ \colon X) \colon f(x) = f(x) \implies x = x'가 성립하는 함수 $f$	단사 사상 $f \colon X \hookrightarrow Y$
종류 $Y$ 에 대한 술어 $R(y) \iff \exists x \in X \colon f(x) = y$	부분 대상 $f \colon X \hookrightarrow Y$
$\forall(y \colon Y) \exists(x \colon X) \colon f(x) = y$ 가 성립하는 함수 $f$	정칙 전사 사상 $f \colon X \twoheadrightarrow Y$
$\forall(z, z$ \colon X \times Y) \colon \pi_X(z) = \pi_X(z) \land \pi_Y(z) = \pi_Y(z) \implies z = z, $\forall(x \colon X) \forall(y \colon Y) \exists(z \colon X \times Y) \colon (\pi_X(z) = x \land \pi_Y(z) = y)$	곱 $X \overset{\pi_X}\leftarrow X \times Y \overset{\pi_Y}\to Y$
$\forall(x \colon X) \colon f(x) = g(x) \implies \exists(y \colon Y) \colon h(y) = x$	동등자 $h \colon Y \hookrightarrow X \overset f{\underset g\rightrightarrows} Y$

5. 예시

정칙 범주의 예시는 다음과 같다.

범주	설명
Set	집합과 집합 간의 함수로 구성된 범주이다.
기본 토포스	모든 기본 토포스
Grp	군과 군 준동형사상으로 구성된 범주이다.
환과 환 준동형사상으로 구성된 범주
다양체의 모형	모든 다양체의 모형으로 구성된 범주
유계 만남 반격자	순서 관계에 의해 사상이 주어지는 모든 유계 만남 반격자
아벨 범주	모든 아벨 범주

집합의 범주, 모든 기본 토포스, 모든 아벨 범주, 모나드 범주 등은 유효 정칙 범주이다. 모든 동치 관계가 유효할 경우 이 범주는 '정확'하거나, 바의 의미에서 정확하거나, 유효 정칙이라고 한다.^[3]^[4]

정칙 범주가 '''아닌''' 예시는 다음과 같다.

'''Top'''는 위상 공간과 연속 함수로 구성된 범주이다.^[1]
'''Cat'''는 작은 범주와 함자로 구성된 범주이다.^[1]

5. 1. 정칙 범주의 예시

'''Set'''는 집합과 집합 간의 함수로 구성된 범주이다.
더 일반적으로는, 모든 기본 토포스가 정칙 범주이다.
'''Grp'''는 군과 군 준동형사상으로 구성된 범주이다.
환과 환 준동형사상으로 구성된 범주도 정칙 범주이다.
더 일반적으로는, 모든 다양체의 모형으로 구성된 범주가 정칙 범주에 해당한다.
순서 관계에 의해 사상이 주어지는 모든 유계 만남 반격자도 정칙 범주이다.
모든 아벨 범주 역시 정칙 범주이다.

5. 2. 유효 정칙 범주의 예시

집합의 범주, 모든 기본 토포스, 모든 아벨 범주, 모나드 범주 등은 유효 정칙 범주이다. 모든 동치 관계가 유효할 경우 이 범주는 '정확'하거나, 바의 의미에서 정확하거나, 유효 정칙이라고 한다.^[3]^[4]

5. 3. 정칙 범주가 아닌 예시

'''Top'''는 위상 공간과 연속 함수로 구성된 범주이다.^[1]
'''Cat'''는 작은 범주와 함자로 구성된 범주이다.^[1]

참조

_[1] 서적
_[2] 웹사이트 Regular Categories and Regular Logic http://www.brics.dk/[...] 1998
_[3] 서적
_[4] 서적

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com

정칙 논리	정칙 범주
종류(sort^영어)	\(\mathcal{C}\)의 대상 \(X\in\mathcal{C}\)
\(\forall(x:X),(x:X)\colon x=x\)인 종류 \(X\)	끝 대상 \(1\in\mathcal{C}\)
종류 \(X\)의 상수 \(c\)	사상 \(c\colon1\to X\)
종류 \(X\to Y\)의 함수 \(f\)	사상 \(f\colon X\to Y\)
함수의 합성 \(f\circ g\)	사상의 합성 \(f\circ g\)
\(\forall(x\colon X),(x\colon X)\colon f(x)=f(x)\implies x=x'\)가 성립하는 함수 \(f\)	단사 사상 \(f\colon X\hookrightarrow Y\)
종류 \(Y\)에 대한 술어 \(R(y)\iff\exists x\in X\colon f(x)=y\)	부분 대상 \(f\colon X\hookrightarrow Y\)
\(\forall(y\colon Y)\exists(x\colon X)\colon f(x)=y\)가 성립하는 함수 \(f\)	정칙 전사 사상 \(f\colon X\twoheadrightarrow Y\)
\(\forall(z,z\colon X\times Y)\colon\pi_X(z)=\pi_X(z)\land\pi_Y(z)=\pi_Y(z)\implies z=z\), \(\forall(x\colon X)\forall(y\colon Y)\exists(z\colon X\times Y)\colon(\pi_X(z)=x\land\pi_Y(z)=y)\)	곱 \(X\overset{\pi_X}\leftarrow X\times Y\overset{\pi_Y}\to Y\)
\(\forall(x\colon X)\colon f(x)=g(x)\implies\exists(y:Y)\colon h(y)=x\)	동등자 \(h\colon Y\hookrightarrow X\overset f{\underset g\rightrightarrows}Y\)