궤도 이심률
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
궤도 이심률은 역제곱 법칙이 적용되는 이체 문제에서 궤도의 찌그러진 정도를 나타내는 0 이상의 값이다. 궤도 이심률 값에 따라 원 궤도(e=0), 타원 궤도(0
더 읽어볼만한 페이지
- 궤도 - 궤도면
궤도면은 인공위성과 발사체의 궤도를 결정하는 중요 요소로, 지구 중력의 비구형성으로 인해 회전하며, 발사 시점은 목표 궤도면과 발사 기지의 교차 시간에 따라 결정된다. - 궤도 - 다체 문제
다체 문제는 상호작용하는 여러 물체의 운동을 다루는 문제로, 특히 중력적으로 상호작용하는 천체들의 운동을 예측하는 문제가 대표적이며, 삼체 문제부터는 해석적 해를 구하기 어려워 섭동 이론이나 수치 해석 등의 방법이 활용된다. - 천체물리학 - 천문학
천문학은 우주 공간에서 일어나는 현상들을 연구하는 자연과학으로, 별, 행성, 은하 등을 연구하며 고대부터 발전해 왔고 현대에는 첨단 기술을 이용해 우주를 관측하고 이론적으로 탐구하는 학문이다. - 천체물리학 - 우주
우주는 모든 공간과 시간, 에너지, 물질, 천체 등을 포함하며 물리 법칙의 지배를 받는 "존재의 총체"로, 천문학, 항공우주공학, 철학, 종교 등 다양한 분야에서 정의되며 빅뱅 이론으로 설명되는 기원과 진화, 암흑 물질과 암흑 에너지로 구성된 요소, 그리고 외계 생명체 가능성이 연구되는 공간이다.
2. 정의
궤도 이심률은 역제곱 법칙이 적용되는 이체 문제에서 케플러 궤도의 모양을 정의하는 음이 아닌 수이다. 기하학적으로 초점과 준선 사이의 거리 비율로 정의될 수 있다.
원뿔 곡선의 이심률 는 초점 F, 준선 L상의 점 P', 곡선상의 점 P의 거리의 비로 정의된다.
:
이심률이 변하지 않는 곡선상의 어떤 점 P에 대해서도 이심률이 변하지 않는 곡선이 원뿔 곡선이다.
타원 궤도의 경우, 이심률 는 궤도 긴반지름 a, 궤도 짧은반지름 b를 이용하여 다음과 같이 나타낼 수 있다.[28]
:
궤도 이심률은 총 궤도 에너지, 각운동량, 환산 질량, 중심력의 계수 등을 이용하여 표현할 수도 있다.
수성의 이심률은 ''e'' = 0.2056인데, 아크사인 값을 찾아 투영 각도가 11.86°임을 알 수 있다. 둥그런 물체를 이 각도만큼 기울여 보았을 때 보이는(눈에 투영되는) 타원의 이심률은 0.2056으로 동일하다.
2. 1. 궤도 이심률의 값에 따른 궤도 종류
역제곱 법칙이 적용되는 이체 문제에서, 모든 궤도는 케플러 궤도이다. 이 케플러 궤도의 이심률은 음수가 아닌 값으로 정의된다.궤도 이심률 값은 다음과 같은 네 가지 경우가 있을 수 있다.
궤도 이심률 ''e''는 다음과 같이 주어진다.
:
여기서 ''E''는 총 궤도 에너지, ''L''은 각운동량, ''m''red은 환산 질량을 나타내며, ''α''는 역제곱 법칙 중심력(중력이나 전자기력 등)의 계수이고 다음과 같이 주어진다.
:
:(''α''는 인력일 때 음수이고, 척력일 때 양수이다.)
중력의 경우에는 다음과 같이 표현할 수 있다.
:
여기서 ''ε''는 고유 궤도 에너지(총 에너지를 환산 질량으로 나눈 값)이고, ''μ''는 총 질량에 비례하는 표준 중력 변수이며, ''h''는 특정 상대 각운동량(각운동량을 환산 질량으로 나눈 값)이다.
''e''의 값이 0에서 1까지 증가함에 따라 궤도의 형태는 가늘고 긴 타원이 되고, ''e''의 값이 1에서 무한대까지 증가함에 따라 쌍곡선 모양 궤도는 쌍곡선의 분점이 접힌 정도를 나타내며, 그 범위는 180° ~ 0°이다. 타원과 쌍곡선의 경계, 즉 ''e''=1일 때는 포물선이 된다.
방사형 궤도는 이심률이 아닌 궤도의 에너지에 따라 타원, 포물선, 쌍곡선으로 나뉜다. 방사형 궤도는 각운동량이 0이므로 이심률은 항상 1이다. 에너지를 유지한 상태에서 각운동량을 줄이면, 타원, 포물선, 쌍곡선 궤도는 각각 ''e''=1인 상태에서 해당 방사형 궤도의 유형 중 하나로 나타나게 된다.
쌍곡선 궤도에서의 척력(방사형 포함) 또한 이에 적용될 수 있다.
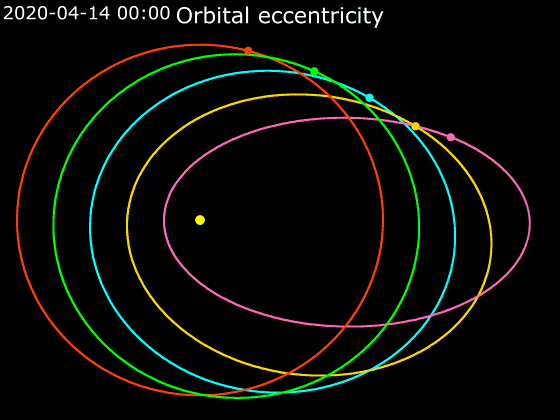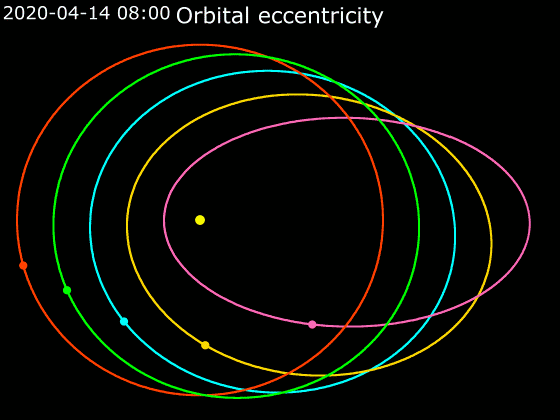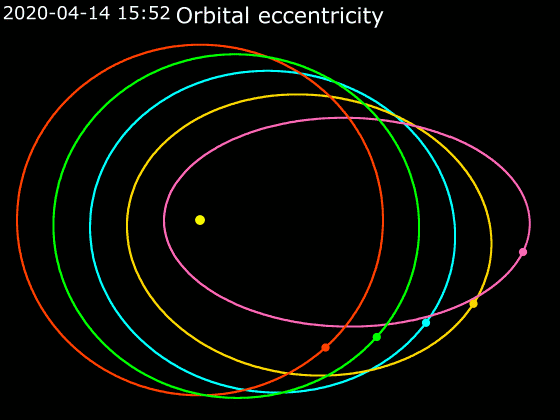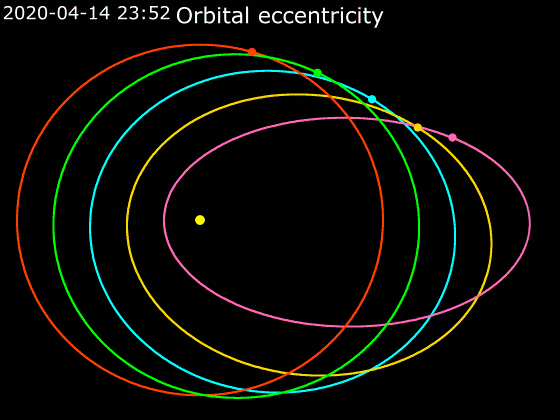
[[파일:Legend_red_ball.svg|15px]] 0.0 [[파일:Legend_lime_ball.svg|15px]] 0.2 [[파일:Legend_cyan_ball.svg|15px]] 0.4 [[파일:Legend_gold_ball.svg|15px]] 0.6 [[파일:Legend_pink_ball.svg|15px]] 0.8
3. 계산
궤도 이심률은 이심률 벡터의 크기로 계산할 수 있다.[1]
:
- '''e'''는 이심률 벡터이다.
타원 궤도에서는 궤도 근지점()과 원지점()을 통해서도 계산할 수 있는데, 여기서 ''a''는 궤도 긴반지름이다.[1]
:
- ''r''a는 원지점까지의 거리이다. (타원의 초점에서 가장 먼 거리)
- ''r''p는 근지점까지의 거리이다. (타원의 초점에서 가장 가까운 거리)
타원 궤도의 이심률은 근지점과 원지점 간의 비율을 얻는 데 사용될 수 있다.[1]
:
지구의 경우, 궤도 이심률 ≈ 0.0167 이고, 원지점 = 원일점, 근지점 = 근일점이므로, 원지점과 근지점 간의 비율 ra/rp ≈ 1.034이다.
4. 예시
지구의 궤도 이심률은 현재 약 0.0167로 거의 원형이다. 금성과 해왕성은 이보다 더 낮은 값을 가진다. 수백 수천만 년 동안, 지구의 궤도 이심률은 다른 행성들의 영향으로 0.0034에서 0.058 사이에서 변화해 왔다.[33] 수성은 태양계 행성 중 가장 큰 궤도 이심률(0.2056)을 가지며, 근일점에서 원일점보다 두 배 정도의 태양 복사를 받는다.
태양계 소행성들은 대부분 0 ~ 0.35 사이의 값을 가지며, 평균값은 0.17이다.[34] 비교적 큰 이심률 값은 과거 충돌이나 목성의 영향 때문이다. 달의 이심률은 0.0549이다. 해왕성의 위성 트리톤의 이심률은 0.000016으로 매우 작다.[35] 반면 작은 위성들은 비교적 큰 이심률을 가지는데, 네레이드는 0.75이다.
혜성들의 이심률은 매우 다양하다. 주기 혜성들은 대체로 0.2 ~ 0.7 사이이며,[36] 핼리 혜성은 0.967이다. 주기를 갖지 않는 혜성들은 1에 더 가깝다. 헤일-밥 혜성은 0.995,[38] C/2006 P1(맥나우트)은 1.000019이다.[37] 알려진 혜성 중 가장 이심률이 큰 혜성은 C/1980 E1으로, 1.057이다.[40]
항성간 천체인 오무아무아는 1.20, 보리소프 혜성은 약 3.3으로 매우 큰 쌍곡선 궤도 이심률을 갖는다.
대한민국 천문우주연구원은 백색 왜성과 쌍성을 이루는 펄서 PSR J1909-3744의 이심률이 0.000000135로, 관측된 천체 중 가장 작은 값임을 밝혀냈다.
4. 1. 태양계 천체들의 궤도 이심률 (표)
5. 평균 이심률
평균 이심률은 오랜 시간 동안 일어난 섭동의 영향으로 나타나는 이심률 변화의 평균값이다. 해왕성의 현재 이심률은 0.0113이지만,[41] 1800년부터 2050년까지의 평균 이심률은 0.00859이다.[42]
6. 기후적 영향
궤도물리학에 따르면 계절의 지속 기간은 지구의 궤도가 지점과 분점 사이의 공간을 휩쓸고 지나가는 면적이 클수록 길어지며, 따라서 만약 이심률이 극단적으로 커진다면 원일점 쪽에서 나타나는 계절이 오래 지속될 것이라고 예측한다. 현재 지구에서는 지구가 근일점에 접근할수록(태양에 가까워질수록) 북반구는 가을을 지나 겨울로 향하고, 한편 남반구에서는 반대되는 계절이 나타나고 있다. 결과적으로 북반구에서는 가을과 겨울이 봄과 여름보다 살짝 짧다. 하지만 전 지구적으로 보았을 때는 남반구는 오히려 봄과 여름이 살짝 짧음으로서 균형이 맞는다. 2006년에는 밀란코비치 주기에 따라 북반구의 여름이 겨울보다 4.66일 더 길었고, 봄은 가을보다 2.9일 더 길었다.[43][44]
장축단선의 세차운동은 지구의 지점과 분점의 위치를 느리게 바꾸고 있다. 이 움직임은 지구의 "궤도"를 바꾸는 것이지 지구의 자전축을 바꾸는 것이 아니다(자전축 변화는 자전축의 세차운동 참조). 다음 1만 년 동안, 북반구의 겨울은 조금씩 길어질 것이고 여름은 조금씩 짧아질 것이다. 하지만 한쪽이 차가워짐에 따라 반대쪽은 따뜻해지는 것처럼 어떠한 영향도 반대의 영향을 받을 것이다.[45] 이러한 변화의 기후적 영향은 밀란코비치 주기의 일부이다.
7. 외계 행성
발견된 많은 외계 행성은 태양계 행성보다 큰 궤도 이심률을 갖는다.[46][16] 궤도 이심률이 낮은 외계 행성은 항성에 가까워 조석 고정되어 있을 가능성이 높다.[46][16] 태양계처럼 낮은 궤도 이심률을 가진 행성계는 드물다.[46][16] 대전이 가설은 태양계 행성이 원에 가까운 궤도를 가지는 이유를 설명하는 가설 중 하나이다.[48][49][50][51][52][53][54][55][56][20][21][22][23][24][25][26][27]
참조
[1]
서적
Foundations of mechanics
AMS Chelsea Pub./American Mathematical Society
2008
[2]
서적
Fundamentals of Astrodynamics
https://books.google[...]
Courier Dover
2020
[3]
웹사이트
Graph of the eccentricity of the Earth's orbit
http://www.museum.st[...]
Illinois State Museum (Insolation values for the climate of the last 10 million years)
1991
[4]
웹사이트
Neptunian Satellite Fact Sheet
http://nssdc.gsfc.na[...]
NASA
2008-01-22
[5]
웹사이트
Asteroids
https://web.archive.[...]
2007-03-04
[6]
서적
Physics and Chemistry of the Solar System
https://books.google[...]
Academic Press
2012-12-02
[7]
웹사이트
JPL Small-Body Database Browser: C/2006 P1 (McNaught)
http://ssd.jpl.nasa.[...]
2009-12-17
[8]
웹사이트
JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)
http://ssd.jpl.nasa.[...]
2008-12-05
[9]
웹사이트
Comet C/2006 P1 (McNaught) – facts and figures
http://www.perthobse[...]
Perth Observatory in Australia
2007-01-22
[10]
웹사이트
JPL Small-Body Database Browser: C/1980 E1 (Bowell)
http://ssd.jpl.nasa.[...]
2010-03-22
[11]
웹사이트
Neptune Fact Sheet
http://nssdc.gsfc.na[...]
NASA
2007-11-29
[12]
웹사이트
Keplerian elements for 1800 A.D. to 2050 A.D.
http://ssd.jpl.nasa.[...]
JPL Solar System Dynamics
2009-12-17
[13]
웹사이트
United States Naval Observatory
https://web.archive.[...]
2007-10-13
[14]
간행물
Equatorial insolation: from precession harmonics to eccentricity frequencies
http://www.clim-past[...]
[15]
웹사이트
Long Term Climate
http://ircamera.as.a[...]
2016-09-01
[16]
웹사이트
ECCENTRICITY
http://exoplanets.or[...]
[17]
서적
Rare Earth: Why Complex Life is Uncommon in the Universe
Springer
[18]
간행물
Exoplanet orbital eccentricity: multiplicity relation and the Solar System
[19]
간행물
Planetesimals in Debris Disks
2015-12-15
[20]
웹사이트
Jupiter's Youthful Travels Redefined Solar System
http://www.nasa.gov/[...]
NASA
2015-11-04
[21]
웹사이트
How Did Jupiter Shape Our Solar System?
http://www.universet[...]
2011-08-23
[22]
웹사이트
Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System
http://www.space.com[...]
Space.com
2015-03-23
[23]
웹사이트
Mysteries of the asteroid belt
https://thehistoryof[...]
2014-03-09
[24]
웹사이트
The Grand Tack
http://planetplanet.[...]
2013-08-02
[25]
간행물
Water delivery and giant impacts in the 'Grand Tack' scenario
[26]
간행물
Relative Likelihood for Life as a Function of Cosmic Time
2016-08
[27]
웹사이트
Is Earthly Life Premature from a Cosmic Perspective?
https://www.cfa.harv[...]
Harvard-Smithsonian Center for Astrophysics
2016-08-01
[28]
웹사이트
離心率 天文学辞典
https://astro-dic.jp[...]
2024-03-08
[29]
웹사이트
Earth Fact Sheet
https://nssdc.gsfc.n[...]
アメリカ航空宇宙局
2019-10-02
[30]
웹사이트
Moon Fact Sheet
https://nssdc.gsfc.n[...]
アメリカ航空宇宙局
2019-10-02
[31]
웹사이트
Mercury Fact Sheet
https://nssdc.gsfc.n[...]
アメリカ航空宇宙局
2019-10-02
[32]
웹사이트
Pluto Fact Sheet
https://nssdc.gsfc.n[...]
アメリカ航空宇宙局
2019-10-02
[33]
웹인용
Graph of the eccentricity of the Earth's orbit
http://www.museum.st[...]
Illinois State Museum (Insolation values for the climate of the last 10 million years)
1991
[34]
웹인용
Asteroids
http://filer.case.ed[...]
2007-01-13
[35]
웹인용
Neptunian Satellite Fact Sheet
http://nssdc.gsfc.na[...]
NASA
2008-01-22
[36]
서적
Physics and Chemistry of the Solar System
https://books.google[...]
Academic Press
2012-12-02
[37]
웹인용
JPL Small-Body Database Browser: C/2006 P1 (McNaught)
http://ssd.jpl.nasa.[...]
2009-12-17
[38]
웹인용
JPL Small-Body Database Browser: C/1995 O1 (Hale-Bopp)
http://ssd.jpl.nasa.[...]
2008-12-05
[39]
웹인용
Comet C/2006 P1 (McNaught) - facts and figures
http://www.perthobse[...]
Perth Observatory in Australia
2011-02-01
[40]
웹인용
JPL Small-Body Database Browser: C/1980 E1 (Bowell)
http://ssd.jpl.nasa.[...]
2010-03-22
[41]
웹인용
Neptune Fact Sheet
http://nssdc.gsfc.na[...]
NASA
2009-12-17
[42]
웹인용
Keplerian elements for 1800 A.D. to 2050 A.D.
http://ssd.jpl.nasa.[...]
JPL Solar System Dynamics
2009-12-17
[43]
웹사이트
United States Naval Observatory
http://aa.usno.navy.[...]
2007-10-13
[44]
논문
Equatorial insolation: from precession harmonics to eccentricity frequencies
http://www.clim-past[...]
2017-04-27
[45]
웹인용
Arizona U., Long Term Climate
http://ircamera.as.a[...]
2017-04-27
[46]
웹사이트
ORBITAL ECCENTRICITES
http://exoplanets.or[...]
2003-09-20
[47]
서적
Rare Earth: Why Complex Life is Uncommon in the Universe
https://archive.org/[...]
Springer
[48]
웹인용
Jupiter's Youthful Travels Redefined Solar System
http://www.nasa.gov/[...]
NASA
2015-11-04
[49]
웹인용
How Did Jupiter Shape Our Solar System?
http://www.universet[...]
2015-11-04
[50]
웹인용
Jupiter's 'Smashing' Migration May Explain Our Oddball Solar System
http://www.space.com[...]
Space.com
2015-11-04
[51]
웹인용
Mysteries of the asteroid belt
https://thehistoryof[...]
2015-11-07
[52]
웹인용
The Grand Tack
http://planetplanet.[...]
2015-11-07
[53]
논문
Water delivery and giant impacts in the 'Grand Tack' scenario
http://www.sciencedi[...]
2014
[54]
간행물
Relative Likelihood for Life as a Function of Cosmic Time
http://iopscience.io[...]
2016-08
[55]
뉴스
Is Earthly Life Premature from a Cosmic Perspective?
https://www.cfa.harv[...]
Harvard-Smithsonian Center for Astrophysics
2016-08-01
[56]
문서
Relative Likelihood, by Loeb, Batista, and Sloan
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com