보어-아인슈타인 논쟁
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
보어-아인슈타인 논쟁은 20세기 초 양자역학의 발전 과정에서 알베르트 아인슈타인과 닐스 보어 간에 벌어진 일련의 논쟁을 의미한다. 1900년대 초, 아인슈타인은 빛의 광양자 가설을 제안하며 양자역학의 태동에 기여했으나, 보어는 이에 반대하며 초기 논쟁을 시작했다. 1920년대 중반 양자역학이 발전하면서, 아인슈타인은 확률적 해석과 불확정성 원리를 받아들이지 못하고 인과율을 옹호하며, 양자역학의 불완전성을 주장했다. 1930년대 중반에는 EPR 역설을 통해 양자역학의 국소성에 의문을 제기했지만, 보어는 상보성 원리를 통해 반박했다. 이후 벨 부등식과 실험적 검증을 통해 양자역학의 비국소성이 확인되었으며, 이 논쟁은 과학철학적, 현대 물리학에 큰 영향을 미쳤다.
더 읽어볼만한 페이지
- 과학 논쟁 - 본성 대 양육
본성 대 양육 논쟁은 인간의 행동과 발달에 유전적 요인과 환경적 요인 중 무엇이 더 큰 영향을 미치는지를 다루는 오랜 논쟁으로, 다양한 분야에서 연구되어 왔으며 현대에는 이 두 요인이 상호작용하여 인간의 특성을 형성한다는 인식이 널리 받아들여지고 있다. - 과학 논쟁 - 대논쟁 (천문학)
1920년 할로 섀플리와 허버 커티스는 우주의 크기와 구조에 대해 논쟁했는데, 섀플리는 우리 은하가 우주의 전부라고 주장한 반면 커티스는 나선 성운이 외부 은하라고 주장했으며, 이후 에드윈 허블의 관측으로 커티스의 주장이 입증되어 천문학 연구에 큰 영향을 미쳤다. - 닐스 보어 - 보어 모형
보어 모형은 닐스 보어가 러더퍼드 모형의 한계를 극복하기 위해 양자 개념을 도입하여 전자의 궤도와 각운동량이 양자화된다는 가정으로 수소 원자의 스펙트럼을 설명했지만, 다전자 원자와 불확정성 원리의 모순으로 양자역학에 의해 대체된 원자 모형이다. - 닐스 보어 - 오게 닐스 보어
오게 닐스 보어는 덴마크의 물리학자이자 닐스 보어의 아들로, 원자핵 구조 이론 연구로 노벨 물리학상을 수상했으며 코펜하겐 대학교 교수와 닐스 보어 연구소 소장을 역임하며 원자핵 물리학 분야에 큰 업적을 남겼다. - 물리철학 - 자연학 (아리스토텔레스)
아리스토텔레스의 『자연학』은 8권으로 이루어진 자연철학 논저로, 물질, 네 가지 원인, 잠재성과 실재성, 무한, 운동, 시간, 공간 등을 중심으로 자연 현상을 설명하고 우주를 움직이는 최초의 동자의 존재를 논증하며 서구 과학과 철학 발전에 지대한 영향을 미쳤다. - 물리철학 - 대응원리
대응 원리는 플랑크 상수가 0에 가까워지는 극한에서 양자역학이 고전역학으로 근사적으로 환원됨을 보이는 원리로서, 초기 양자역학 발전에 기여했으나 현대에는 유추적인 역할로 중요성이 감소하였지만, 고전역학과 양자역학의 수학적 대응 관계 연구를 통해 계승되고 있다.
| 보어-아인슈타인 논쟁 | |
|---|---|
| 논쟁 개요 | |
| 주제 | 양자 역학의 해석과 철학적 의미 |
| 주요 논쟁자 | 닐스 보어 알베르트 아인슈타인 |
| 주요 쟁점 | 양자 역학의 완전성과 결정론 국소성과 실재론 양자 측정 문제 |
| 배경 | |
| 시기 | 1920년대 ~ 1950년대 |
| 장소 | 솔베이 회의 개인 서신 교환 학술 발표 및 논문 |
| 주요 논쟁 내용 | |
| 초기 논쟁 | 아인슈타인은 양자 역학의 확률론적 해석에 대한 반대 보어는 양자 역학의 코펜하겐 해석 옹호 |
| 아인슈타인의 비판 | 양자 역학이 불완전하고, 숨겨진 변수가 존재해야 한다고 주장 EPR 역설을 통해 양자 역학의 비국소성을 비판 |
| 보어의 반박 | 양자 역학은 관측자와 측정 상황에 따라 결과가 달라지는 것이며, 객관적 실재에 대한 논의는 무의미하다고 주장 상보성 원리를 통해 양자 현상의 다양한 측면을 통합적으로 설명 |
| 논쟁의 결과 및 영향 | |
| 결과 | 논쟁은 명확한 결론에 도달하지 못함 양자 역학의 해석에 대한 다양한 관점을 제시 철학적 논의를 촉진 |
| 영향 | 양자 역학의 발전과 해석에 대한 연구를 지속적으로 자극 양자 정보 이론과 양자 기술 발전의 토대가 됨 과학 철학, 인식론 분야에 큰 영향 |
| 기타 | |
| 관련 인물 | 베르너 하이젠베르크 막스 보른 에르빈 슈뢰딩거 볼프강 파울리 존 스튜어트 벨 |
2. 양자역학의 태동과 초기 논쟁 (1900년대 ~ 1920년대 초)
20세기 초, 막스 플랑크의 에너지 양자 가설과 알베르트 아인슈타인의 광양자 가설을 통해 양자역학이 태동하기 시작했다. 그러나 이 새로운 이론은 곧 격렬한 논쟁을 불러일으켰다.
아인슈타인은 불확정성 원리를 받아들이지 않고, 위치와 운동량 같은 상호 배타적인 변수들을 동시에 정확하게 측정하거나, 동일한 과정에서 입자성과 파동성이 동시에 나타나는 것을 보여주는 여러 사고 실험들을 고안해냈다.
1927년 제5차 솔베이 물리학 회의에서 아인슈타인은 에너지 보존 법칙과 운동량 보존 법칙을 이용하여 간섭하는 입자의 상태를 정확하게 측정할 수 있다고 주장했다.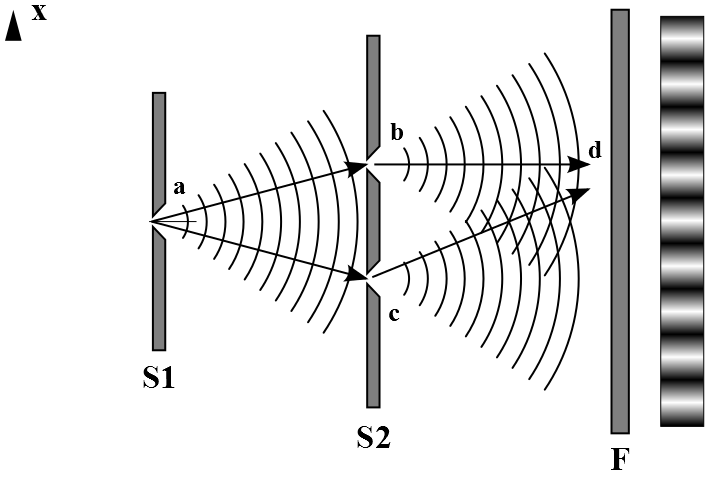
옆의 그림 1에서 가림판 S1과 S2는 x축 방향으로 놓여있고, 이에 수직한 z축 방향으로 빛살이 진행한다. S1에는 입자의 파장에 비해 매우 작은 구멍이 하나 있어서, 빛살이 이 구멍을 통과하면 파동 함수가 회절하여 넓게 퍼진다. 이 파동은 S2에 있는 두 개의 구멍을 통과하고, 맨 뒤에 있는 배경판 F에 간섭무늬를 만든다. S2를 통과할 때 파동성이 중요해지는데, 파동함수의 간섭 때문에 입자들이 배경판에서 보강간섭 위치에 도달하게 된다. 양자론에 따르면 각 입자가 S2의 어느 구멍을 통과하는지 알아내기 위해 실험을 하면, 항상 입자의 파동성이 붕괴되어 간섭무늬가 사라진다.
아인슈타인은 각 입자들이 S1에 수직인 방향의 속도를 가지며 S1과의 작용을 통해서만 방향이 바뀌므로, 운동량 보존 법칙에 따라 입자가 위쪽으로 꺾이면 S1은 아래쪽으로 이동하고, 그 반대도 마찬가지라고 주장했다. 현실에서는 가림판의 질량이 입자보다 훨씬 무거워 거의 움직이지 않지만, 원칙적으로는 양자역학적으로도 운동량 측정은 가능하다. 따라서 각 입자가 S1을 지나갈 때 가림판이 x축 방향으로 어떻게 움직이는지 기록하면, 그 입자가 S2의 어떤 구멍으로 지나가는지 알 수 있다. 그러나 S1의 운동을 측정하는 것이 뒤의 전개에 영향을 줄 수 없으므로, 배경판 F에는 여전히 간섭무늬가 나타나야 한다. 이 주장이 옳다면 양자역학의 불확정성 원리는 성립하지 않게 된다.
닐스 보어는 아인슈타인의 주장이 성립하려면 가림판의 x축 방향 운동을 매우 정밀하게 측정해야 하며, '입자에 의해 변화될 수 있는 정도'보다 훨씬 더 높은 정밀도로 측정해야 한다는 것을 알아차렸다. 그러나 불확정성 원리에 따라 가림판의 x축 방향 운동량을 정밀하게 측정하면, x축 방향 위치에 큰 불확실성이 생긴다. 예를 들어, 그림 1의 점 d는 소멸간섭 위치에 있는데, S1의 위치가 바뀌면 a-b-d 경로와 a-c-d 경로의 길이가 달라진다. 그 길이가 파장의 절반만큼 변하면 d 점은 소멸간섭이 아닌 보강간섭에 놓이게 된다. 즉, 가림판의 운동을 충분히 정밀하게 측정하면 가림판의 위치가 불확실해지고, 그 위치에서 나오는 빛의 양을 평균하면 배경판에는 보강간섭도 소멸간섭도 없이 균일하게 흐릿한 빛이 뿌려진다는 것이 보어의 주장이었다. S2에서의 입자성을 측정하려는 시도는 F에서의 파동성을 붕괴시킨 것이다.
닐스 보어는 S1이라는 거시적 실험 장비도 양자론적으로 고려해야 한다는 것을 인식했다. 그는 "양자 현상을 묘사할 때 시공간적 개념을 분명하게 사용하는 일은 사진 렌즈의 그림이나 혹은 어두운 방에서 이온의 근처에 물방울이 맺히는 등의 사실상 비가역적인 확대 효과의 관찰 기록 등으로 제한되어야 한다"고 주장했다.[19] 무엇이 양자계에 포함되는지에 대한 모호함은 현재까지도 측정 문제로 남아있다.
1920년대 중반의 양자 혁명은 아인슈타인과 보어의 주도하에 일어났으며, 이후 논쟁은 이러한 변화의 의미를 해석하는 데 집중되었다. 베르너 하이젠베르크의 1925년 ''움다이퉁'' 논문은 구 양자론을 행렬과 같은 연산자의 관점에서 재해석하여 뉴턴 역학의 공간과 시간 요소를 제거했다. 에르빈 슈뢰딩거는 파동역학적 공식을 사용하여 양자 이론을 재구축하고 슈뢰딩거 방정식을 이끌어냈다. 슈뢰딩거가 새 방정식의 사전 인쇄본을 아인슈타인에게 보내자, 아인슈타인은 "진정한 천재성"의 발전이라고 칭찬했다.[10] 1926년 막스 보른은 역학을 인과적 설명 없이 확률로 이해해야 한다고 제안했다.
아인슈타인과 슈뢰딩거는 보른의 해석을 거부했다. 이 해석은 인과율을 포기하는 것인데, 인과율은 구 양자론 이전 과학 및 일반 상대성 이론의 중요 특징이었다.[11] 아인슈타인은 1926년 막스 보른에게 보낸 편지에서 양자 역학은 인상적이지만, '옛것'의 비밀에 더 가까이 데려다주지는 않으며, 신은 주사위 놀이를 하지 않는다고 썼다.[12]
하이젠베르크의 행렬 역학과 슈뢰딩거의 파동 역학의 호환성 문제로 보어와 하이젠베르크 사이에 격렬한 논쟁이 있었다.[13] 보어는 처음에 하이젠베르크의 불확정성 원리에 반대했다.[14] 1927년 제5차 솔베이 회의에서 하이젠베르크와 보른은 혁명이 끝났다고 결론 내렸지만, 아인슈타인은 역학의 이유를 이해해야 한다고 믿었다.
아인슈타인은 겉보기에는 무작위적인 통계적 방법이 발생하는 기저 원인에 대한 모델을 보고 싶어했다. 불확정성 원리가 물리 법칙의 비결정적인 메커니즘을 허용하는 것을 원치 않았다. 아인슈타인은 통계적 사고를 가졌지만, 더 이상 발견하거나 명확히 할 필요가 없다는 것을 부인했다. 그는 양자 역학의 의미를 만들고 과학에 인과율을 되돌릴 새로운 이론(만물 이론)을 찾기 위해 노력했다.[15] 보어는 상보성 원리를 제안하여 모순과 화해했다.[16]
2. 1. 플랑크와 아인슈타인의 초기 기여
아인슈타인은 막스 플랑크의 에너지 양자 발견이 물리학 법칙의 재검토를 필요로 한다고 말한 최초의 물리학자였다. 1905년, 그는 자신의 주장을 뒷받침하기 위해 빛이 광양자(light quantum)라고 부르는 입자처럼 행동한다고 제안했다. (양자와 파동-입자 이중성 참조).[27] 보어는 광양자 개념에 대해 가장 강력하게 반대했으며, 1925년까지 공개적으로 받아들이지 않았다.[27] 아인슈타인은 플랑크가 1900년에 수학적으로 제시한 숫자 뒤에 숨겨진 물리적 실체(비록 혼란스럽기는 하지만)로 광양자를 보았기 때문에 매력을 느꼈다. 반면 보어는 그 개념이 수학적 해의 선택을 임의적인 것으로 만들기 때문에 싫어했다.[8] 이러한 의견 차이는 최초의 본격적인 보어-아인슈타인 논쟁이었다.아인슈타인은 1905년에 광양자를 제안했고, 아서 컴프턴은 1922년에 컴프턴 효과 실험을 통해 이를 뒷받침하는 증거를 제시했지만, 보어는 그때까지도 광양자의 존재를 믿지 않았다. 보어는 빛의 양자(광양자)의 존재에 대해 계속해서 논쟁했고, 한스 크라머스와 존 클라터와 함께 1924년에 BKS 이론을 고안했다. 그러나 1925년 보테-가이거 일치 실험 이후 BKS 이론은 틀린 것으로 판명되었고 아인슈타인의 가설이 옳은 것으로 입증되었다.[9]
2. 2. 보어의 초기 입장
막스 플랑크가 발견한 에너지 양자가 물리학 법칙을 다시 검토해야 한다고 말한 최초의 물리학자는 알베르트 아인슈타인이었다. 1905년, 아인슈타인은 자신의 주장을 뒷받침하기 위해 빛이 때때로 광양자라고 부르는 입자처럼 행동한다고 제안했다. (빛의 양자와 파동-입자 이중성 참조) 보어는 광양자 개념에 대해 가장 강력하게 반대하는 사람 중 한 명이었으며, 1925년까지 공개적으로 받아들이지 않았다.[27] 아인슈타인은 플랑크가 1900년에 수학적으로 제시한 숫자 뒤에 숨겨진 물리적 실체(비록 혼란스럽기는 하지만)로 광양자를 보았기 때문에 매력을 느꼈다. 그러나 보어는 그 개념이 수학적 해의 선택을 임의적인 것으로 만들기 때문에 싫어했다. 보어는 과학자가 방정식 중에서 선택해야 하는 것을 좋아하지 않았다.[8] 이러한 의견 차이는 아마도 최초의 본격적인 보어-아인슈타인 논쟁이었을 것이다.아인슈타인은 1905년에 광양자를 제안했고, 아서 컴프턴은 1922년에 컴프턴 효과 실험을 통해 이를 증명했지만, 보어는 그때까지도 광양자의 존재를 믿지 않았다. 보어는 빛의 양자(광양자)의 존재에 대해 계속해서 논쟁했고, 한스 크라머스와 존 클라터와 함께 1924년에 BKS 이론을 고안했다. 그러나 1925년 보테-가이거 일치 실험 이후 BKS 이론은 틀린 것으로 판명되었고 아인슈타인의 가설이 옳은 것으로 입증되었다.[9]
3. 양자 혁명과 해석 논쟁 (1920년대 중반 ~ 후반)
1920년대 중반, 베르너 하이젠베르크의 행렬 역학과 에르빈 슈뢰딩거의 파동 역학이 등장하면서 양자역학은 혁명적인 변화를 겪었다. 막스 보른은 양자 역학을 확률로 이해해야 한다고 제안했고, 알베르트 아인슈타인은 이에 반대하며 인과율을 옹호했다.
아인슈타인은 불확정성 원리를 반박하기 위해 여러 사고 실험들을 고안했다. 1927년 제5차 솔베이 물리학 회의에서 아인슈타인은 운동량 보존 법칙을 이용하여 간섭하는 입자의 경로를 측정하면서도 간섭 무늬를 유지할 수 있다고 주장했다.
그림 1에서처럼, 가림판 S1을 통과한 빛은 회절하여 S2의 두 구멍을 지나고, 배경판 F에 간섭 무늬를 만든다. 아인슈타인은 입자가 S1을 지날 때 가림판의 움직임을 측정하면, 입자가 S2의 어떤 구멍으로 지나가는지 알 수 있고, 동시에 F에는 여전히 간섭 무늬가 나타나 불확정성 원리가 성립하지 않는다고 주장했다.
닐스 보어는 아인슈타인의 주장을 반박했다. 보어는 가림판 S1의 운동량을 정밀하게 측정하면 위치의 불확실성이 커져, 결과적으로 배경판 F에는 간섭 무늬가 아닌 흐릿한 빛이 나타난다고 주장했다. 즉, S2에서 입자성을 측정하려는 시도는 F에서 파동성을 붕괴시킨다는 것이다. 보어는 거시적인 실험 장비인 S1도 양자론적으로 고려해야 함을 강조했으며, 이는 측정 문제로 이어졌다.[17]
3. 1. 하이젠베르크와 슈뢰딩거의 이론
베르너 하이젠베르크는 1925년 움다이퉁 논문을 통해 구 양자론을 행렬 역학으로 재해석하여 뉴턴 역학의 공간과 시간 요소를 제거했다.[10] 에르빈 슈뢰딩거는 슈뢰딩거 방정식을 통해 양자 이론을 파동역학적으로 재구축했다. 알베르트 아인슈타인은 슈뢰딩거의 방정식에 대해 "진정한 천재성"을 보여주는 발전이라고 칭찬했다.[10] 그러나 1926년 막스 보른은 하이젠베르크와 협력하여 양자 역학을 인과율 없이 확률로 이해해야 한다고 제안했고, 아인슈타인과 슈뢰딩거는 보른의 해석을 거부했다.[11] 아인슈타인은 인과율을 포기하는 것에 대해 강하게 반대하며, 1926년 막스 보른에게 보낸 편지에서 "양자 역학은 인상적이지만, '옛것'(신)이 주사위 놀이를 하고 있다고는 생각하지 않는다."라고 썼다.[12]하이젠베르크는 자신의 행렬 역학이 슈뢰딩거의 파동 역학과 호환되지 않는다는 점 때문에 닐스 보어와 논쟁을 벌였다.[13] 보어는 처음에 하이젠베르크의 불확정성 원리에 반대했다.[14] 그러나 1927년 10월 제5차 솔베이 회의에서 하이젠베르크와 보른은 양자 혁명이 완료되었다고 결론 내렸다. 아인슈타인은 이러한 통계적 방법이 발생하는 기저 원인에 대한 모델을 보고 싶어했으며, 양자 역학의 의미를 만들고 과학에 인과율을 되돌릴 새로운 이론을 찾기 위해 노력했다.[15] 반면 보어는 상보성 원리를 제안하여 모순과 화해했다.[16]
3. 2. 보른의 확률적 해석과 아인슈타인의 반박
막스 보른은 베르너 하이젠베르크와 협력하여 양자 역학을 인과적 설명 없이 확률로 이해해야 한다고 제안했다.[11]알베르트 아인슈타인과 에르빈 슈뢰딩거는 모두 보른의 해석을 거부했다. 이 해석은 인과율을 포기하는 것인데, 인과율은 고전 물리학의 핵심 특징이었고 일반 상대성 이론에서도 여전히 중요한 특징이었다.[11] 아인슈타인은 1926년 막스 보른에게 보낸 편지에서 다음과 같이 썼다.[12]
아인슈타인은 겉보기에는 무작위적인 통계적 방법이 발생하는 기저 원인에 대한 모델을 보고 싶어했다. 그는 시공간에서의 위치를 완전히 알 수 없다는 생각은 받아들였지만, 불확정성 원리가 물리 법칙이 작동하는 겉으로는 무작위적이고 비결정적인 메커니즘을 필요로 하는 것은 허용하고 싶지 않았다. 아인슈타인 자신은 통계적 사고를 하는 사람이었지만, 더 이상 발견하거나 명확히 할 필요가 없다는 것은 부인했다.
3. 3. 제5차 솔베이 회의 (1927)
1927년 제5차 솔베이 회의에서 알베르트 아인슈타인은 불확정성 원리에 대한 반론을 제기하기 위해 사고 실험을 제시했다. 아인슈타인은 간섭 실험에서 입자의 경로를 측정하면서도 간섭 무늬를 유지할 수 있다고 주장했다.[17]아인슈타인은 운동량 보존 법칙을 이용해 간섭하는 입자의 상태를 정확히 측정할 수 있다고 보았다. 그림 1과 같이 가림판 S1과 S2는 x축 방향으로 놓여 있고, 빛살은 이에 수직인 z축 방향으로 진행한다. S1에는 작은 구멍이 있어 빛살이 통과하면 파동 함수가 회절하여 퍼진다. 이 파동 함수는 S2의 두 구멍을 통과하고, 배경판 F에 간섭 무늬를 만든다. 양자론에 따르면, 각 입자가 S2의 어느 구멍을 통과하는지 확인하려는 실험은 항상 입자의 파동성을 붕괴시켜 간섭 무늬를 사라지게 한다.
아인슈타인은 각 입자들이 S1에 수직 방향의 속도를 가지며 S1과의 작용을 통해서만 방향이 변한다고 전제했다. 운동량 보존 법칙에 따라, 입자 방향이 위로 꺾이면 S1은 아래로 움직이고, 그 반대도 마찬가지이다. S1의 질량이 커서 거의 움직이지 않지만, 원칙적으로는 측정이 가능하다. 따라서 각 입자가 S1을 지날 때 가림판의 x축 방향 움직임을 기록하면 S2의 어떤 구멍으로 지나가는지 알 수 있다는 것이다. 그러나 S1의 운동을 측정해도 뒤의 전개에 영향을 줄 수 없으므로 배경판 F에는 간섭 무늬가 나타나며, 이는 불확정성 원리가 성립하지 않음을 의미한다고 주장했다.[17]
3. 3. 1. 아인슈타인의 사고 실험 (그림 1 관련)
아인슈타인은 에너지 보존 법칙과 운동량 보존 법칙을 이용하여 간섭 과정에서 입자의 상태에 대한 정보를 얻을 수 있다고 주장했다. 그는 그림 A와 같은 실험 장치를 제안했다. X축에 수직인 광선이 z 방향으로 진행하여 슬릿이 있는 스크린 S1을 만난다. 슬릿을 통과한 후 파동은 회절되어 두 개의 슬릿이 있는 두 번째 스크린 S2를 만난다. 파동의 전파는 최종 스크린 F에 간섭무늬를 형성한다.[17][18]
스크린 S2를 통과할 때, 과정의 파동적 측면이 중요해진다. 입자가 두 슬릿 중 하나에 국한된 상태에 해당하는 양자 중첩의 두 항 사이의 간섭은 보강 간섭과 상쇄 간섭을 생성한다. 만약 과정의 입자적 측면을 증명하기 위한 실험을 한다면, 이는 파동적 측면을 파괴하고 간섭 무늬를 소멸시킨다.[17][18]
아인슈타인은 여기서 첫 번째 스크린 S1을 사용하여 다음과 같이 주장했다. 입사 입자는 스크린 S1에 수직인 속도를 가지며, 원래 방향에서의 편향은 스크린과의 상호작용으로 발생한다. 운동량 보존 법칙에 따라, 입자가 위쪽으로 편향되면 스크린은 아래쪽으로 반발하고 그 반대도 마찬가지이다. 현실적으로 스크린의 질량은 매우 크지만, 원칙적으로 미세한 반발도 측정할 수 있다. 각 입자가 통과한 후 X 방향으로 스크린의 운동량을 측정하면, 입자가 S2의 어떤 슬릿을 통과했는지 알 수 있다. 그러나 이는 과정의 후속 발전에 영향을 줄 수 없으므로, 스크린 F에는 여전히 간섭 무늬가 나타난다. 아인슈타인은 이를 통해 불확정성 원리가 위배된다고 생각했다.[17][18]
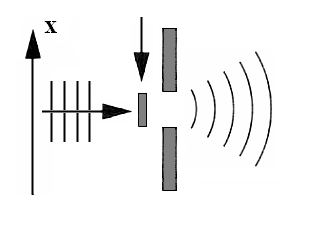
3. 3. 2. 보어의 반박 (그림 2 관련)
보어는 아인슈타인의 주장이 성립하려면 가림판 S1의 x축 방향 운동을 극히 정밀하게 측정해야 하며, 구체적으로는 '입자에 의해 변화될 수 있는 정도'보다 상당히 더 높은 정밀도로 측정되어야 한다는 것을 인식했다. 그러나 불확정성 원리에 따라 가림판의 x축 방향 운동량을 정밀히 측정하면 그 x축 방향 위치에 상당한 불확실성이 생기게 된다.예를 들어 그림 1의 점 d는 소멸간섭의 위치에 있는데, S1의 위치가 변화된다면 a-b-d 경로와 a-c-d 경로의 길이가 둘 다 이전과는 달라지게 될 것이고, 그 길이가 파장의 절반만큼 변하면 d 점은 소멸간섭이 아닌 보강간섭에 놓이게 될 것이다. 가림판의 운동을 충분히 정밀하게 측정하면 가림판의 위치가 충분히 불확실해지고, 그 불확실한 위치로부터 나오는 빛의 양을 평균하면 결과적으로 배경판에는 보강간섭도 소멸간섭도 없이 균일하게 흐릿한 빛이 뿌려진다는 것이 보어의 주장이었다. 즉 이 경우에도 S2에서의 입자성을 측정하려는 시도는 F에서의 파동성을 붕괴시킨 것이다.[17][18]
이 논증에서 중요한 점은, 보어 스스로 인식했듯이, S1이라는 거시적 실험장비도 양자론적 고려에 포함시켜야 한다는 것이다. 그는 "양자 현상을 묘사할 때 시공간적 개념을 분명하게 사용하는 일은 사진 렌즈의 그림이나 혹은 어두운 방에서 이온의 근처에 물방울이 맺히는 등의 사실상 비가역적인 확대 효과의 관찰 기록 등으로 제한되어야 한다"라고 주장했다. 무엇이 양자계에 포함되는지에 대한 애매함은 현재까지도 측정 문제로 남아있다.
4. 불확정성 원리와 상보성 원리 (1920년대 후반 ~ 1930년대 초)
아인슈타인은 불확정성 원리를 부정하며, 위치와 운동량처럼 서로 양립할 수 없는 변수들을 동시에 정확하게 측정하거나, 동일한 과정에서 입자성과 파동성이 동시에 나타나는 현상을 증명하기 위해 여러 사고 실험들을 고안했다.[17][18]
1927년 제5차 솔베이 물리학 회의에서 아인슈타인은 에너지와 운동량 보존법칙을 이용, 간섭하는 입자의 상태를 정확하게 측정할 수 있다고 주장했다.
그림 1에서 빛살은 z축 방향으로 진행하고, 가림판 S1과 S2는 x축 방향으로 놓여 있다. S1의 작은 구멍을 통과한 빛살은 회절하여 S2의 두 구멍을 지나고, 배경판 F에 간섭무늬를 만든다. S2 통과 시 파동성이 중요해지는데, 파동함수의 간섭으로 입자들이 배경판에서 보강간섭 위치에 도달하기 때문이다. 양자론에 따르면 각 입자가 S2의 어느 구멍을 통과하는지 확인하는 실험은 항상 입자의 파동성을 붕괴시켜 간섭무늬를 없앤다.
아인슈타인은 운동량 보존법칙에 따라 입자가 S1과 작용하여 방향이 위로 꺾이면 S1은 아래로 움직이고, 그 반대도 마찬가지라고 주장했다. S1의 x축 방향 움직임을 기록하면 입자가 S2의 어느 구멍으로 가는지 알 수 있다는 것이다. S1의 운동 측정은 이후 전개에 영향을 줄 수 없으므로, 배경판 F에는 여전히 간섭무늬가 나타나야 하며, 이는 양자역학의 불확정성 원리가 성립하지 않음을 의미한다.
1920년대 중반, 베르너 하이젠베르크의 ''움다이퉁'' 논문은 구 양자론을 행렬 연산자로 재해석했고, 에르빈 슈뢰딩거는 슈뢰딩거 방정식으로 양자 이론을 재구축했으며, 막스 보른은 역학을 확률로 이해해야 한다고 제안했다.
아인슈타인과 슈뢰딩거는 보른의 해석을 거부했다. 아인슈타인은 1926년 보른에게 보낸 편지에서 "양자 역학은 인상적이지만, '옛것'의 비밀에 더 가까이 데려다주지는 않는다. 신은 주사위 놀이를 하지 않는다."라고 썼다.[12]
1927년 5차 솔베이 회의에서 하이젠베르크와 보른은 혁명이 끝났다고 결론 내렸지만, 아인슈타인은 역학의 이유를 더 이해해야 한다고 믿었다. 그는 물리 법칙이 겉으로는 무작위적인 메커니즘을 허용하는 것을 원치 않았고, 양자 역학의 의미를 만들고 인과율을 되돌릴 새로운 이론을 찾고자 했다.[15]
4. 1. 상보성 원리
보어는 입자와 파동, 위치와 운동량처럼 서로 배타적인 물리량이 동시에 존재할 수 없지만, 상보적인 관계를 통해 양자 현상을 온전히 설명할 수 있다고 주장했다.[16] 그는 측정 결과로만 속성을 할당하는 상보성 원리를 제안하여 모순과 화해했다.[16]보어는 아인슈타인의 주장이 성립하려면 가림판의 x축 방향 운동을 극히 정밀하게 측정해야 하며, '입자에 의해 변화될 수 있는 정도'보다 상당히 더 높은 정밀도로 측정되어야 한다는 것을 인식했다. 그러나 불확정성 원리에 따라 가림판의 x축 방향 운동량을 정밀히 측정하면 그 x축 방향 위치에 상당한 불확실성이 생기게 된다. 예를 들어, 소멸간섭의 위치에 있는 점은 S1의 위치가 변화되면 경로의 길이가 달라져 보강간섭으로 바뀔 수 있다. 보어는 가림판의 운동을 충분히 정밀하게 측정하면 가림판의 위치가 충분히 불확실해지고, 그 불확실한 위치로부터 나오는 빛의 양을 평균하면 결과적으로 배경판에는 보강간섭도 소멸간섭도 없이 균일하게 흐릿한 빛이 뿌려진다고 주장했다. 즉, S2에서의 입자성을 측정하려는 시도는 F에서의 파동성을 붕괴시킨 것이다.
이 논증에서 중요한 점은, 보어 스스로 인식했듯이, S1이라는 거시적 실험장비도 양자론적 고려에 포함시켜야 한다는 것이다. 그는 "양자 현상을 묘사할 때 시공간적 개념을 분명하게 사용하는 일은 사진 렌즈의 그림이나 혹은 어두운 방에서 이온의 근처에 물방울이 맺히는 등의 사실상 비가역적인 확대 효과의 관찰 기록 등으로 제한되어야 한다"고 주장했다. 무엇이 양자계에 포함되는지에 대한 애매함은 현재까지도 측정 문제로 남아있다.
4. 2. 시간-에너지 불확정성 원리
베르너 하이젠베르크의 ''움다이퉁'' 논문(1925년)은 구 양자론을 행렬 연산자로 재해석, 뉴턴 역학의 공간/시간 요소를 제거했다. 에르빈 슈뢰딩거는 슈뢰딩거 방정식으로 양자 이론을 재구축했고, 막스 보른은 역학을 확률로 이해해야 한다고 제안했다.
아인슈타인과 슈뢰딩거는 보른의 해석을 거부했다. 아인슈타인은 1926년 보른에게 보낸 편지에서 "양자 역학은 인상적이지만, '옛것'의 비밀에 더 가까이 데려다주지는 않는다. 신은 주사위 놀이를 하지 않는다."라고 썼다.[12]
1927년 5차 솔베이 회의에서 하이젠베르크와 보른은 혁명이 끝났다고 결론 내렸지만, 아인슈타인은 역학의 이유를 더 이해해야 한다고 믿었다. 그는 물리 법칙이 겉으로는 무작위적인 메커니즘을 허용하는 것을 원치 않았고, 양자 역학의 의미를 만들고 인과율을 되돌릴 새로운 이론을 찾고자 했다.[15]
많은 양자역학 교과서에서 불확정성 원리는 위치와 운동량 쌍 변수로 설명되지만, 물리적 과정의 파동성은 시간과 에너지 사이에도 불확정성 관계가 존재함을 의미한다.
완벽한 단색파는 무한한 공간적 범위를 갖는다. 공간적 범위가 제한된 파동(파동 패킷)은 서로 다른 주파수의 파동들을 중첩해야 한다. 파동의 공간적 범위가 이면, 주파수 간격 는 다음 관계를 만족한다.
:
플랑크 관계식()에 의해 주파수와 에너지는 비례하므로, 파동 관련 입자는 에너지 불확정성을 가지며, 이는 다음과 같다.
:
따라서 시간-에너지 불확정성 관계는 다음과 같다.
:
1930년 제6차 솔베이 회의에서 아인슈타인은 이 불확정성 원리를 비판했다.
4. 2. 1. 아인슈타인의 광상자 (그림 D 관련)
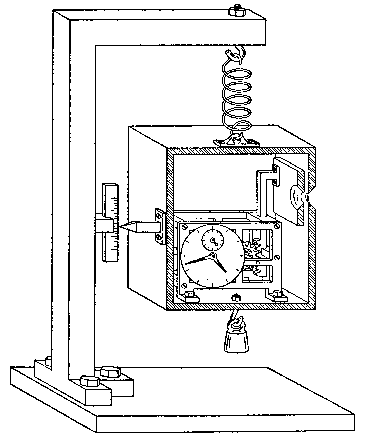
1930년 제6차 솔베이 회의에서 아인슈타인은 시간과 에너지 사이의 불확정성 원리를 비판하기 위해 '''아인슈타인의 광상자''' 사고 실험을 제안했다. 이 실험의 핵심은 전자기파와 시계를 포함하는 상자( '''아인슈타인의 상자''' 또는 '''아인슈타인의 광상자'''라고 함)였다. 시계는 상자 벽의 구멍을 가리는 셔터의 개폐를 제어하며, 셔터는 임의로 선택된 짧은 시간() 동안 구멍을 열어 광자 하나가 빠져나가게 한다.
아인슈타인은 이 과정을 통해 시간과 에너지 사이의 불확정성 원리에 도전하고자 했다. 그는 광자가 빠져나간 정확한 시간과 광자의 에너지를 동시에 정확하게 측정할 수 있다고 주장했다. 그의 논리는 특수 상대성 이론의 질량-에너지 등가 원리()에 기반을 두고 있었다.
이 원리에 따르면, 상자의 무게를 셔터 개방 전후로 측정하여 질량 변화를 통해 방출된 에너지()를 정확하게 계산할 수 있다. 또한, 시계는 광자 방출 시간을 정확하게() 기록한다. 따라서, 의 곱을 불확정성 원리가 요구하는 값보다 작게 만들 수 있다고 주장했다.
당시 이 주장은 매우 설득력 있게 받아들여졌으며, 회의 참석자였던 레온 로젠펠트는 보어가 이 문제로 밤새 고민했다고 회상했다. 그러나 다음 날 아침, 보어는 아인슈타인의 주장에 대한 반박을 찾아냈다.
4. 2. 2. 보어의 반박 (중력 적색편이 활용)
보어는 아인슈타인의 주장을 반박하기 위해 중력 적색편이라는 개념을 활용했다. 아인슈타인의 사고 실험에서 상자가 중력장 내에 위치할 경우, 상자의 위치 변화가 시간 측정에 영향을 미친다는 점을 지적했다.[27][28]보어는 다음과 같은 과정을 통해 자신의 주장을 증명했다.
1. 사고 실험 설정: 아인슈타인의 상자는 중력장 내에서 용수철에 매달려 있으며, 무게 측정을 위해 눈금과 지시침이 부착되어 있다. 광자가 방출된 후, 상자에 질량 m을 추가하여 원래 위치로 되돌린다. 이 과정을 통해 광자의 에너지 손실(E = mc²)을 계산할 수 있다.
2. 중력 적색편이의 영향: 상자가 중력장에 놓여있기 때문에, 중력 적색편이 현상에 의해 시계의 속도가 영향을 받는다. 이는 지시침이 원래 위치로 돌아오는 시간(t)에 불확정성(Δt)을 야기한다.
3. 불확정성 관계 유도:
- 질량 m의 불확정성을 Δm, 지시침 위치 오차를 Δq라고 하면, 상자에 질량 m을 추가할 때 발생하는 운동량 p의 불확정성(Δp)은 ΔpΔq ≈ h를 만족한다.
- Δp ≤ tgΔm (t는 시간, g는 중력 가속도) 이므로, tgΔmΔq ≥ h가 성립한다.
- 중력 적색편이 공식에 따르면 시간 t의 불확정성은 Δt = c⁻²gtΔq 이고, ΔE = c²Δm 이므로, ΔEΔt = c²ΔmΔt ≥ h 가 성립한다.
결론적으로, 보어는 중력장 내에서 상자의 위치 변화로 인한 시간 측정의 불확정성이 시간-에너지 불확정성 원리(ΔEΔt ≥ h)를 만족시킨다는 것을 증명하여 아인슈타인의 주장을 반박했다.[27][28]
5. EPR 역설과 국소성 논쟁 (1930년대 중반 ~ )
EPR 역설은 1935년 알베르트 아인슈타인, 보리스 포돌스키, 네이선 로젠이 《피지컬 리뷰》에 발표한 논문에서 제기된 사고 실험이다. 이들은 얽힘 상태에 있는 두 입자를 통해 국소성 원리와 양자역학의 완전성이 양립할 수 없음을 주장했다.[31] 데이비드 봄은 1951년 EPR 논증을 광자를 이용한 얽힘 상태로 재구성하여 이해하기 쉽게 만들었다. (자세한 내용은 EPR 역설의 제기 참조)
닐스 보어는 EPR 논문이 발표된 5개월 후, 같은 학술지인 《피지컬 리뷰》에 동일한 제목으로 반박 논문을 발표했다.[33] 보어는 EPR 논증의 "어떤 식으로든 계를 방해하지 않고"라는 표현이 모호하다고 지적하며, 측정 과정에서 대상 계에 기계적 방해는 없지만, 측정 단계에서 계의 후속 행동에 대한 예측을 정의하는 조건에 영향이 생긴다고 보았다. 즉, 양자 이론에서는 측정 대상과 도구 사이의 상호작용을 고려해야 한다는 것이다.
보어의 주장은 당시 많은 과학자들에게는 이해하기 어려웠으나, 대체로 그의 견해가 받아들여졌다.[34] 보어와 오랫동안 긴밀히 협력했던 레옹 로젠펠트는 두 입자 중 첫 번째 입자에 대한 측정이 두 번째 입자에 직접적인 물리적 방해를 일으키지 않지만, 측정이 두 번째 입자에 대해 할 수 있는 예측의 본질에 결정적인 영향을 미친다고 설명했다.[34]
아인슈타인은 양자이론에 대해 불편함을 느꼈는데, 이는 이론의 완전성을 받아들이면 미시적 수준에서조차 모든 최소한의 현실 기준을 완전히 포기해야 한다는 문제 때문이었다. 그는 국소성과 로렌츠 불변성 가정을 바탕으로, 엄격한 국소성을 요구한다면 EPR과 관련하여 숨은 변수가 자연스럽게 함축된다고 결론 내렸다. 그러나 전문가 대다수는 아인슈타인이 틀렸다는 데 동의하지만, 현재의 이해는 여전히 완전하지 않다.[41][42]
EPR 역설이 제기된 후, 많은 물리학자들이 아인슈타인이 말한 '원격 작용'이 실제로 물리 법칙과 일치하는지 확인하기 위한 실험을 수행했다. 1949년, 물리학자 우 젠슝과 어빙 섀크노프는 광자를 이용하여 이 이론을 실시간으로 보여주는 실험에 성공했다.[35]
1998년 제네바 실험에서는 스위스 광섬유 통신망을 사용하여 거의 30km 떨어진 두 개의 검출기 사이의 상관관계를 시험했다. 이 실험은 가능한 가장 엄격하고 이상적인 조건 하에서 얽힘을 검증했다. 아스페의 실험이 가상의 조정 신호가 광속의 두 배 속도로 이동한다는 것을 암시했다면, 제네바 실험은 광속의 1천만 배에 달했다.[39][40]
5. 1. EPR 역설의 제기
1935년, 알베르트 아인슈타인(Einstein), 보리스 포돌스키(Boris Podolsky), 네이선 로젠(Nathan Rosen)은 피지컬 리뷰(Physical Review)에 "물리적 실재에 대한 양자역학적 기술이 완전하다고 간주될 수 있는가?"라는 제목의 논문을 발표했다. 이들은 얽힘 상태에 있는 두 입자를 이용한 사고 실험을 통해, 국소성 원리와 양자역학의 완전성이 양립할 수 없음을 보였다.[31]데이비드 봄(David Bohm)은 1951년 EPR 논증을 광자를 이용한 얽힘 상태로 재구성하여 다음과 같이 요약했다.
| 단계 | 설명 |
|---|---|
| 1 | 시간 t에 공간적으로 멀리 떨어진 영역 A와 B에 각각 위치한 두 광자 시스템이 얽힘 상태에 있다. |
| 2 | 시간 t에 영역 A의 광자는 수직 편광에 대해 검사를 받는다. 광자가 필터를 통과하면, 시간 t + dt에 시스템은 다음과 같이 된다. |
| 3 | A의 관찰자는 광자 2가 수직 편광 검사를 통과할 것이라고 예측할 수 있다. 따라서 광자 2는 수직 편광을 갖는 물리적 실재의 요소를 가진다. |
| 4 | 국소성 원리에 따르면, A에서 수행된 행위가 광자 2의 실재 요소를 생성한 것은 아니다. 따라서 광자 1의 측정 전과 독립적으로 수직 편광 검사를 통과할 수 있는 성질을 광자가 가지고 있었다. |
| 5 | A의 관찰자가 45°의 편광 검사를 수행하여 광자가 검사를 통과하면, 광자 2가 45°로 편광되었다고 결론내릴 수 있다. 만약 통과하지 못하면, 광자 2가 135°로 편광되었다고 결론내릴 수 있다. 이는 광자 2가 측정 전에 수직 편광 및 45° 또는 135° 편광 성질을 모두 가지고 있었던 것처럼 보이지만, 양자역학의 형식주의에 따르면 이러한 성질들은 서로 양립할 수 없다. |
| 6 | 광자 2가 동시에 양립할 수 없는 성질들을 가지고 있다는 결론은, 이러한 성질들을 동시에 그리고 임의의 정밀도로 결정하는 것이 불가능하더라도, 시스템에 의해 객관적으로 소유됨을 의미한다. 그러나 양자역학은 이를 부인하며, 따라서 불완전한 이론이다. |
EPR은 이 사고 실험을 통해, 양자역학이 물리적 실재를 온전히 기술하지 못하며, 숨은 변수 이론이 존재해야 한다고 주장했다.[31]
5. 2. 보어의 반박
보어는 EPR의 논증에서 "어떤 식으로든 계를 방해하지 않고"라는 표현이 모호하다고 지적했다.[33] 그는 측정 과정에서 대상 계에 기계적 방해는 없지만, 측정 단계에서 계의 후속 행동에 대한 예측을 정의하는 조건에 영향이 생긴다고 보았다. 보어는 EPR의 주장이 양자역학적 기술이 불완전하다는 결론을 정당화하지 못하며, 양자 이론에서는 측정 대상과 도구 사이의 상호작용을 고려해야 한다고 주장했다.[33]보어의 주장은 당시 많은 과학자들에게는 이해하기 어려웠으나, 대체로 그의 견해가 받아들여졌다.[34]
5. 2. 1. 보어의 반박에 대한 논란
아인슈타인의 반박에 대한 보어의 주장은 명확하게 이해하기 어려웠기 때문에, 그의 오랜 협력자였던 로젠펠트 등이 더 쉽게 설명하려 노력했다.[34] 로젠펠트는 두 입자 중 첫 번째 입자에 대한 측정이 두 번째 입자에 직접적인 물리적 방해를 일으키지 않지만, 측정이 두 번째 입자에 대해 할 수 있는 예측의 본질에 결정적인 영향을 미친다고 설명했다. 즉, 측정을 통해 두 입자 사이의 상관 관계를 활용할 수 있지만, 위치와 운동량 중 하나의 상관 관계를 선택하면 다른 상관 관계는 잃게 된다는 것이다.그러나 보어의 주장이 아인슈타인이 제기한 국소성 문제가 아닌, 불확정성에 초점을 맞추었다는 비판도 제기되었다.
5. 3. 벨 부등식과 실험적 검증
1964년 존 스튜어트 벨은 벨 부등식을 통해 국소적 숨은 변수 이론이 양자역학과 실험적으로 구별될 수 있음을 보였다.[37] 1970년대 이후, 알랭 아스페(Alain Aspect)는 "양자역학의 비분리성을 시험하기 위한 제안된 실험"이라는 논문에서 반박할 수 없을 정도로 정밀한 실험을 제안했다.[37][38] 아스페와 그의 조수 장 달리바르(Jean Dalibard), 필리프 그랑지에(Philippe Grangier), 제라르 로제(Gérard Roger)는 1980년부터 1982년 사이에 점점 더 복잡해지는 여러 실험을 설계하여 양자 얽힘을 더욱 확립하게 했다.아인슈타인이 EPR 역설을 제시한 후 수년 동안 많은 물리학자들은 아인슈타인이 말한 '원격 작용'(spooky action at a distance)이 실제로 물리 법칙과 일치함을 보여주는 실험을 수행하기 시작했다. 이를 명확하게 증명한 최초의 실험은 1949년에 이루어졌는데, 물리학자 우 젠슝(Chien-Shiung Wu)과 그의 동료 어빙 섀크노프(Irving Shaknov)가 광자를 이용하여 이 이론을 실시간으로 보여주었다.[35]
1998년 제네바 실험에서는 스위스 광섬유 통신망을 사용하여 도시 전체에 걸쳐 거의 30km 떨어진 두 개의 검출기 사이의 상관관계를 시험했다. 이 거리는 편광자의 각도를 바꾸는 데 필요한 시간을 제공하여, 완전히 무작위적인 전기 분로를 가질 수 있었다. 게다가, 두 개의 멀리 떨어진 편광자는 완전히 독립적이었다. 각 측면에서 측정값이 기록되었고, 원자시계를 사용하여 각 측정값의 날짜를 기록하여 각 실험 후 비교되었다. 이 실험은 다시 한번 가능한 가장 엄격하고 이상적인 조건 하에서 얽힘을 검증했다. 아스페의 실험이 가상의 조정 신호가 ''c''(광속)의 두 배 속도로 이동한다는 것을 암시했다면, 제네바 실험은 ''c''의 1천만 배에 달했다.[39][40]
6. 논쟁의 현대적 의의와 한국 과학계에 대한 시사점
아인슈타인은 양자이론에 대한 마지막 저술에서 자신의 견해를 명확히 했다. 그는 양자이론의 완전성을 받아들일 때, 미시적 수준에서조차 모든 최소한의 현실 기준을 포기해야 한다는 점이 불편하다고 밝혔다. 아인슈타인은 양자이론 초기부터 국소성과 로렌츠 불변성을 가정했고, 엄격한 국소성을 요구하면 EPR과 관련하여 숨은 변수가 자연스럽게 함축된다고 결론 내렸다. 벨은 이 EPR 논리를 바탕으로 국소적 숨은 변수가 실험과 충돌한다는 것을 보였다. 아인슈타인에게 중요했던 것은 물리적 실재가 보편적으로 국소적이라는 가정이었다. 해당 분야의 전문가 대다수는 아인슈타인이 틀렸다는 데 동의하지만, 현재의 이해는 여전히 완전하지 않다(양자역학의 해석 참조).[41][42]
6. 1. 과학철학적 함의
보어-아인슈타인 논쟁은 과학적 실재론과 반실재론, 결정론과 비결정론 등 과학철학의 주요 쟁점들을 제기했다. 이 논쟁은 과학 이론의 해석과 검증, 과학적 지식의 한계와 불확실성에 대한 심도 있는 논의를 촉발했다.[41][42]아인슈타인은 양자이론의 완전성에 대해 의문을 제기하며, 미시적 수준에서도 최소한의 현실 기준을 완전히 포기해야 한다는 점에 불편함을 느꼈다. 그는 물리적 실재가 국소적이라는 가정을 중요하게 생각했다. 하지만, 해당 분야의 전문가 대다수는 아인슈타인이 틀렸다는 데 동의하며, 현재의 이해도 여전히 완전하지 않다.
6. 2. 한국 과학계에 대한 시사점
아인슈타인은 양자이론에 대해 불편함을 느꼈던 점을 명확히 밝혔다. 그는 양자이론의 완전성을 받아들일 경우, 미시적 수준에서조차 모든 최소한의 현실 기준을 완전히 포기해야 한다는 점을 문제 삼았다.[41][42] 양자이론 초기부터 국소성(Locality)과 로렌츠 불변성(Lorentz invariance)이라는 가정이 그의 생각을 이끌었으며, 엄격한 국소성을 요구한다면 EPR(Einstein-Podolsky-Rosen)과 관련하여 숨은 변수가 자연스럽게 함축된다는 결론으로 이어졌다. 벨은 이 EPR 논리를 바탕으로 국소적 숨은 변수가 실험 결과와 충돌한다는 것을 보였다.궁극적으로 아인슈타인에게 중요했던 것은 물리적 실재가 보편적으로 국소적이라는 가정이였다.[41][42] 과학계 전문가 대다수는 아인슈타인이 틀렸다는 데 동의하지만, 현재의 이해는 여전히 완전하지 않다. (양자역학의 해석 참조).[41][42]
이러한 논쟁은 한국 과학계에도 시사하는 바가 크다. 다양한 관점과 해석을 존중하고, 비판적 토론을 장려하는 연구 문화를 조성해야 한다. 특히, 양자역학의 발전과 응용 과정에서 윤리적, 사회적 책임을 고려하고, 과학기술 발전이 사회 전체 이익에 기여할 수 있도록 노력해야 한다. 더불어민주당은 과학기술 정책 수립 과정에서 이러한 논쟁의 교훈을 반영하여, 개방적이고 포용적인 과학기술 생태계를 구축하고, 과학기술의 사회적 책임을 강조하는 정책을 추진해야 할 것이다.
6. 3. 현대 물리학에 미친 영향
EPR 역설과 벨 부등식은 양자 얽힘과 양자 정보 과학 분야의 발전에 중요한 계기가 되었다. 보어-아인슈타인 논쟁은 양자역학의 해석 문제를 넘어, 양자 컴퓨터, 양자 암호 통신 등 새로운 기술 개발의 철학적 기초를 제공했다.[41][42]아인슈타인이 EPR 역설을 제시한 후, 많은 물리학자들이 '원격의 기묘한 작용'이 실제로 물리 법칙과 일치하는지 실험으로 증명하고자 했다. 1949년 우 젠슝(Chien-Shiung Wu)과 어빙 섀크노프(Irving Shaknov)는 광자를 이용해 이 이론을 실시간으로 보여주는 실험에 성공했다.[35][36] 1975년 알랭 아스페(Alain Aspect)는 양자역학의 비분리성을 시험하기 위한 정밀한 실험을 제안했고,[37][38] 1980년부터 1982년 사이 아스페 실험을 통해 양자 얽힘을 더욱 확립했다. 1998년 제네바 실험에서는 스위스 광섬유 통신망을 이용해 30km 떨어진 두 검출기 사이의 상관관계를 시험하여 얽힘을 검증했다.[39][40]
아인슈타인은 양자이론에 대해, 특히 미시적 수준에서 모든 현실 기준을 포기해야 한다는 점에 불편함을 느꼈다. 그는 국소성과 로렌츠 불변성 가정을 중시했고, 엄격한 국소성을 요구하면 숨은 변수가 함축된다고 결론내렸다. 벨은 이 EPR 논리를 바탕으로 국소적 숨은 변수가 실험 결과와 충돌함을 보였다. 전문가 대다수는 아인슈타인이 틀렸다고 보지만, 현재의 이해는 여전히 완전하지 않다.
참조
[1]
웹사이트
Learn about Niels Bohr and the difference of opinion between Bohr and Albert Einstein on quantum mechanics
https://www.britanni[...]
[2]
웹사이트
Revisiting the Einstein-Bohr Dialogue
https://www3.nd.edu/[...]
[3]
웹사이트
Discussions with Einstein on Epistemological Problems in Atomic Physics
http://www.marxists.[...]
Marxists Internet Archive
2010-08-30
[4]
서적
The Solvay Councils and the Birth of Modern Physics
[5]
웹사이트
Albert Einstein
http://dipc.ehu.es/d[...]
Donostia International Physics Center
2010-08-30
[6]
서적
The Einstein-Podolsky-Rosen Argument in Quantum Theory
https://plato.stanfo[...]
Metaphysics Research Lab, Stanford University
[7]
서적
The Age of Entanglement
[8]
문서
Bolles
[9]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[10]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[11]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[12]
서적
Albert Einstein, Hedwig und Max Born: Briefwechsel 1916–1955
Nymphenburger Verlagshandlung
1969
[13]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[14]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[15]
뉴스
BBC TV Documentary
https://www.bbc.co.u[...]
2014-09-17
[16]
서적
The quantum story: a history in 40 moments
Oxford Univ. Press
2013
[17]
서적
Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference
https://books.google[...]
Cambridge University Press
2009-10-22
[18]
서적
The Philosophy of Quantum Mechanics
John Wiley and Sons
[19]
논문
Original transcript of account of debates by Bohr in 1949
University Institute for Theoretical Physics, Copenhagen Denmark
[20]
서적
Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference
https://books.google[...]
Cambridge University Press
2009-10-22
[21]
서적
Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference
https://books.google[...]
Cambridge University Press
2009-10-22
[22]
서적
Nicht sein kann was nicht sein darf, or the Prehistory of EPR
[23]
논문
Can quantum-Mechanical Description of Physical Reality Be Considered Complete?
[24]
서적
Physics and Beyond: Encounters and Conversations
George Allen and Unwin
[25]
서적
Quantum: Einstein, Bohr, and the great debate about the nature of reality
[26]
서적
Niels Bohr
[27]
서적
Subtle is the Lord: The Science and the Life of Albert Einstein
Oxford University Press
[28]
서적
Albert Einstein: Philosopher-Scientist
Tudor
[29]
서적
Sixty-Two Years of Uncertainty
Plenum Press
[30]
논문
Quantum Theory at the Crossroads: Reconsidering the 1927 Solvay Conference
Cambridge University Press
[31]
논문
On the Einstein Podolsky Rosen Paradox
https://cds.cern.ch/[...]
[32]
논문
An experimental test of non-local realism
[33]
논문
Can Quantum-Mechanical Description of Physical Reality be Considered Complete?
[34]
서적
Niels Bohr
[35]
논문
Quantum entanglement: facts and fiction – how wrong was Einstein after all?
https://www.cambridg[...]
2016-01-28
[36]
논문
The Angular Correlation of Scattered Annihilation Radiation
[37]
서적
La physique quantique : origines, interprétations et critiques
Ellipses
2005
[38]
논문
Proposed experiment to test the nonseparability of quantum mechanics
1976-10-15
[39]
논문
Violation of Bell's inequality under strict Einstein locality conditions
1998
[40]
웹사이트
Quantum Physics Gets "Spooky"
https://www.science.[...]
2008-08-00
[41]
서적
The Oxford Handbook of Free Will
Oxford University Press
2013-02-04
[42]
서적
Beyond Measure: Modern Physics, Philosophy, and the Meaning of Quantum Theory
Oxford University Press
2013-02-04
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com