지수 적분 함수

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

지수 적분 함수는 0이 아닌 실수 x에 대해 정의되는 특수 함수로, 적분 형태로 표현된다. 이 함수는 실수 및 복소수 영역에서 정의되며, 초등 함수로 표현되지 않는다. 지수 적분 함수는 수렴 및 발산 급수, 초등 함수와의 관계, 그리고 다른 특수 함수들과의 관계를 가지며, 열전달, 지하수 흐름, 복사 전달, 중성자 수송 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

특수 초기하함수 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = a^x* 형태의 함수이며, 특히 자연로그의 역함수인 *e^x*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다.
특수 초기하함수 - 르장드르 다항식
르장드르 다항식은 르장드르 미분 방정식의 해로 정의되는 직교 다항식 계열로, 생성 함수, 로드리게스 공식, 또는 점화식을 통해 정의될 수 있으며, 물리학, 공학, 수치해석 등 다양한 분야에서 응용된다.
적분 - 가우스 적분
가우스 적분은 특정한 정적분의 값으로 정의되며, 확률론, 통계학, 물리학 등 여러 분야에서 중요한 역할을 수행하고 정규분포와 관련된 계산에서 핵심적인 역할을 한다.
적분 - 적분표
적분표는 다양한 함수들의 부정적분과 정적분 예시를 모아 놓은 목록으로, 유리 함수, 무리 함수, 삼각 함수, 지수 함수, 로그 함수 등 여러 함수와 닫힌 형식으로 표현되지 않는 함수의 정적분 값, 절댓값 함수, 곱으로 이루어진 함수를 포함하며, 마이어 히르슈의 적분 목록집에서 시작하여 그라드슈테인과 르지크의 표로 발전했다.
거듭제곱 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = a^x* 형태의 함수이며, 특히 자연로그의 역함수인 *e^x*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다.
거듭제곱 - 반감기
반감기는 어떤 양이 원래 값의 절반으로 줄어드는 데 걸리는 시간을 의미하며, 방사성 붕괴, 화학 반응 등 다양한 분야에서 활용되고 방사성 동위원소의 안정성을 나타내는 지표이다.

지수 적분 함수
개요
유형	특수 함수
분야	수학
정의	Ei(x) = -∫(-x, ∞) (e^(-t) / t) dt
함수 정보
다른 이름	적분 지수 함수
기호	Ei
수학적 성질
미분	d/dx Ei(x) = e^x / x
특이점	x = 0 (로그 분기점)
정의역	실수 전체
치역	실수 전체

2. 정의

지수 적분 함수는 실수 및 복소수 영역에서 여러 가지 형태로 정의된다. 핵심은 적분 경로 및 분지 절단(branch cut)을 어떻게 설정하는지에 따라 달라진다.^[1] 실수 영역과 복소수 영역에서의 정의는 각각 하위 섹션을 참고하면 된다.

2. 1. 실수 영역에서의 정의

0이 아닌 실수

x

에 대하여, '''지수 적분 함수'''

\operatorname{Ei}(x)

는 코시 주요값을 이용하여 다음과 같이 정의된다.^[1]

:

\operatorname{Ei}(x) = -\operatorname{p.\!v.}\int_{-x}^{\infty}\frac{e^{-t}}{t}\,\operatorname{d}\!t = \operatorname{p.\!v.}\int_{-\infty}^{x}\frac{e^{t}}{t}\,\operatorname{d}\!t

이 함수는 초등 함수가 아님이 리쉬 알고리즘에 의해 증명되었다.

이후 내용에서는

\operatorname(x)

로 나타낸다.

:

\begin{align}\operatorname(x) &= \lim_{\epsilon\to+0}\left(-\int_{-x}^{-\epsilon}\frac{e^{-t}}{t}\,\operatorname{d}\!t-\int_{\epsilon}^{\infty}\frac{e^{-t}}{t}\,\operatorname{d}\!t\right)\quad &(x>0)\\\operatorname(x) &= -\int_{-x}^{\infty}\frac{e^{-t}}{t}\,\operatorname{d}\!t\quad &(x<0)\end{align}

2. 2. 복소수 영역에서의 정의

임의의 복소수

x

에 대하여 이 함수를 해석적 연속으로 정의할 수 있다. 그러나 이 경우 음의 실수에서 분지절단이 생긴다.^[1] 복소수

z

에 대한 지수 적분

\operatorname{Ei}(z)

는 다음과 같이 정의된다.

:

\operatorname{Ei}(z) = -\pi i + \int_{-\infty-0i}^{1-0i}\frac{e^{t}}{t}\,\operatorname{d}\!t + \int_{1}^{z}\frac{e^{t}}{t}\,\operatorname{d}\!t

이것은 다중값 함수이지만, 음의 실수축에서 분지 절단을 수행하고 양의 실수축에서 실수값을 취하도록 한다.^[18]^[19] (문헌에 따라 정의가 다르다)

:

\operatorname{Ei}(x\pm 0i) = \operatorname{Ei}^{real}(x)\pm\pi i \quad(x<0), \quad \operatorname{Ei}(x) = \operatorname{Ei}^{real}(x) \quad(x>0)

3. 성질

지수 적분 함수 $\operatorname{Ei}(z)$ 는 음의 실수에서 분지절단을 갖고, 다른 곳에서는 정칙함수이다. 다음 함수는 전해석 함수이다.

: $\operatorname{Ei}(z)-\ln z$

부분 적분을 사용하면 다음 공식을 얻을 수 있다.^[5]

: $\operatorname{Ei}(z) = \frac{e^{z}} {z} \left (\sum _{k=0}^{n} \frac{k!} {z^{k}} + e_{n}(z)\right), \quad e_{n}(z) \equiv (n + 1)!\ ze^{-z}\int _{ -\infty }^{z} \frac{e^{t}} {t^{n+2}}\,dt$

고정된 $z$ 에 대해, 오차항 $|e_n(z)|$ 의 절댓값은 감소하다가 증가한다. 최솟값은 $n\sim |z|$ 에서 발생하며, 이 때 $\vert e_{n}(z)\vert \leq \sqrt{\frac{2\pi } {\vert z\vert }}e^{-\vert z\vert }$ 이다.

복소 함수 $\operatorname{Ein}(z)$ 는 다음과 같이 정의된다.

: $\operatorname{Ein}(z) = \int_{0}^{z} \frac{1-e^{-t}}{t}\,\operatorname{d}\!t$

이는 복소 평면 전체에서 정칙이며, 오일러-마스케로니 상수 $\gamma$ 에 대해 다음이 성립한다.

: $\operatorname{Ein}(z) - E_1(z) - \log z = \gamma$

$E_1(z)$ 와 $\operatorname{Ei}(z)$ 는 다음과 같이 표현할 수 있다.

: $\begin{align}E_1(z) &= -\gamma-\log z+\operatorname{Ein}(z) \\\operatorname{Ei}(z) &= \gamma+\log z-\operatorname{Ein}(-z)\end{align}$

이 표현을 통해 지수 적분 함수의 다가성(多價性) 문제를 복소 로그 함수 $\log z$ 에 가둘 수 있다.

지수 적분 함수는 합류 초월기하 함수와 밀접하게 관련되어 있으며, 다음과 같이 표현할 수 있다.

: $E_1(z)=e^{-z}U(1,1,z)$

또한, 로그 적분 함수 li(''x'')와는 다음 공식으로 관련되어 있다.^[1]

: $\operatorname{li}(e^x) = \operatorname{Ei}(x)$ (단, $x$ 는 0이 아닌 실수)

일반화된 지수 적분 함수는 상부 불완전 감마 함수의 특수한 경우로 표현할 수 있다.^[8]

: $E_n(x) =x^{n-1}\Gamma(1-n,x).$

3. 1. 수렴 급수

오일러-마스케로니 상수 (

\gamma

)를 포함하는 지수 적분 함수의 테일러 급수는 다음과 같이 표현될 수 있다.^[2]

:

E_1(z) = -\gamma - \ln z - \sum_{k=1}^{\infty} \frac{(-z)^k}{k\; k!} \qquad (\left| \operatorname{Arg}(z) \right| < \pi)

이 급수는 모든 복소수

z

에 대해 수렴하며, 음의 실수축을 따라 절단선을 갖는 복소 로그의 일반적인 값을 사용한다. 이 공식은 0과 2.5 사이의 실수

x

에 대한 부동 소수점 연산을 사용하여

E_1(x)

를 계산하는 데 사용될 수 있다.

x > 2.5

의 경우 파국적 소거로 인해 결과가 부정확하다.

스리니바사 라마누잔은 더 빠르게 수렴하는 급수를 발견했다.

:

{\rm Ei} (x) = \gamma + \ln x + \exp{(x/2)} \sum_{n=1}^\infty \frac{ (-1)^{n-1} x^n} {n! \, 2^{n-1}} \sum_{k=0}^{\lfloor (n-1)/2 \rfloor} \frac{1}{2k+1}

3. 2. 점근 급수 (발산 급수)

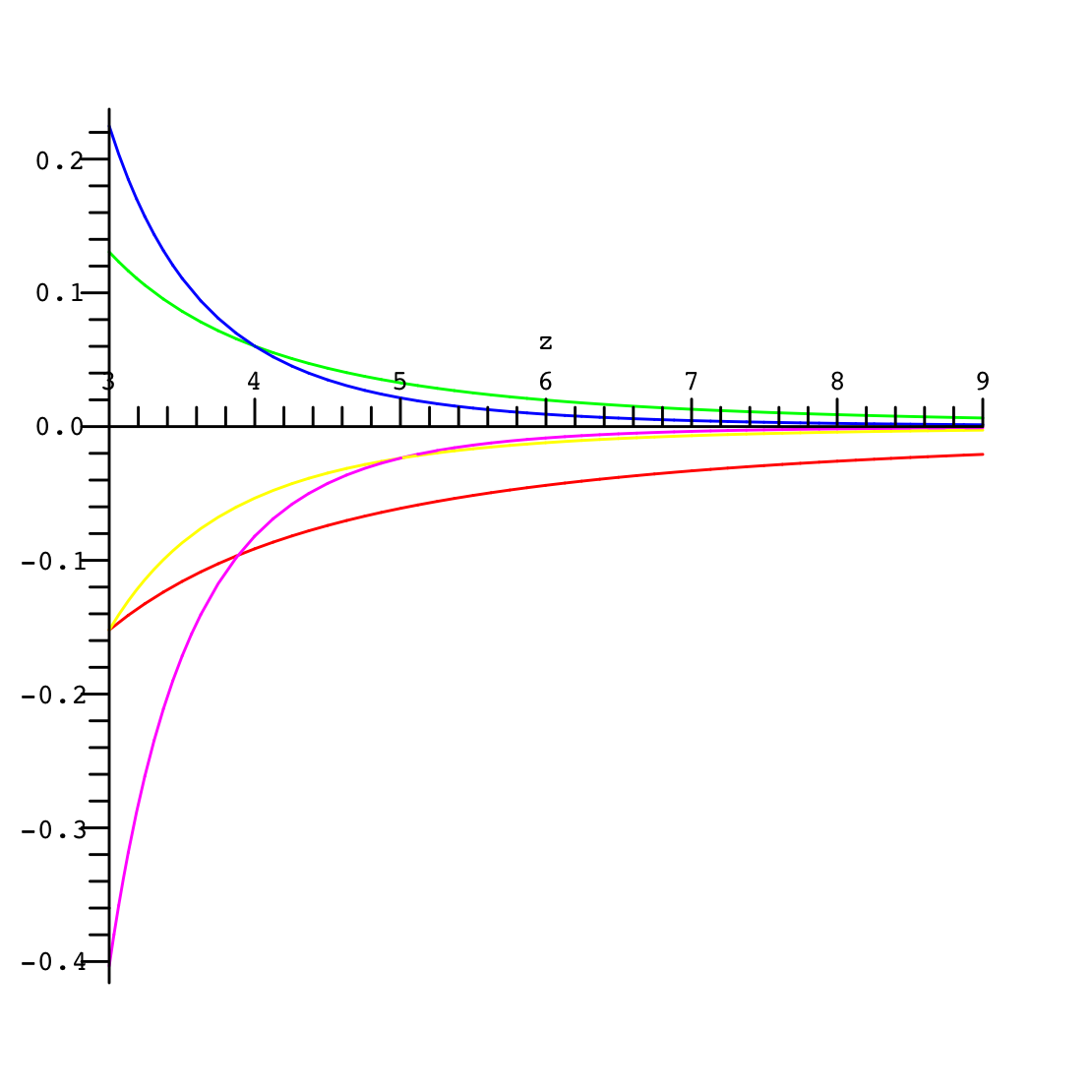
불행하게도, 위의 급수는 큰 모듈러스의 인수에 대해 수렴 속도가 느리다. 예를 들어, E₁(10)에 대해 유효 숫자 3자리까지 정확한 답을 얻으려면 40개 이상의 항이 필요하다.^[3] 그러나 x의 양의 값에 대해, 부분 적분을 통해

x e^x E_1(x)

를 적분하여 얻을 수 있는 발산 급수 근사가 있다:^[4]

:

E_1(x)=\frac{\exp(-x)} x \left(\sum_{n=0}^{N-1} \frac{n!}{(-x)^n} +O(N!x^{-N}) \right)

위 근사의 상대 오차는 잘린 합의 항의 수인

N

의 다양한 값에 대해 그림 오른쪽에 표시된다(

N=1

은 빨간색,

N=5

는 분홍색).

잘린 합에서 서로 다른 수 $~N~$ 개의 항에 대한 점근 근사의 상대 오차

z|^영어의 절댓값이 충분히 클 때 E₁|^영어은 다음과 같이 근사할 수 있다.

:

E_1(z) = -e^{-z}\left\{\sum_{k=1}^{n}(k-1)!\left(-\frac{1}{z}\right)^k + O\left(\frac{1}{z^{n+1}}\right)\right\}

우변은

n \to \infty

에서 발산하므로 적당한 항에서 잘라서 사용한다.

3. 3. 초등 함수와의 관계

E_1

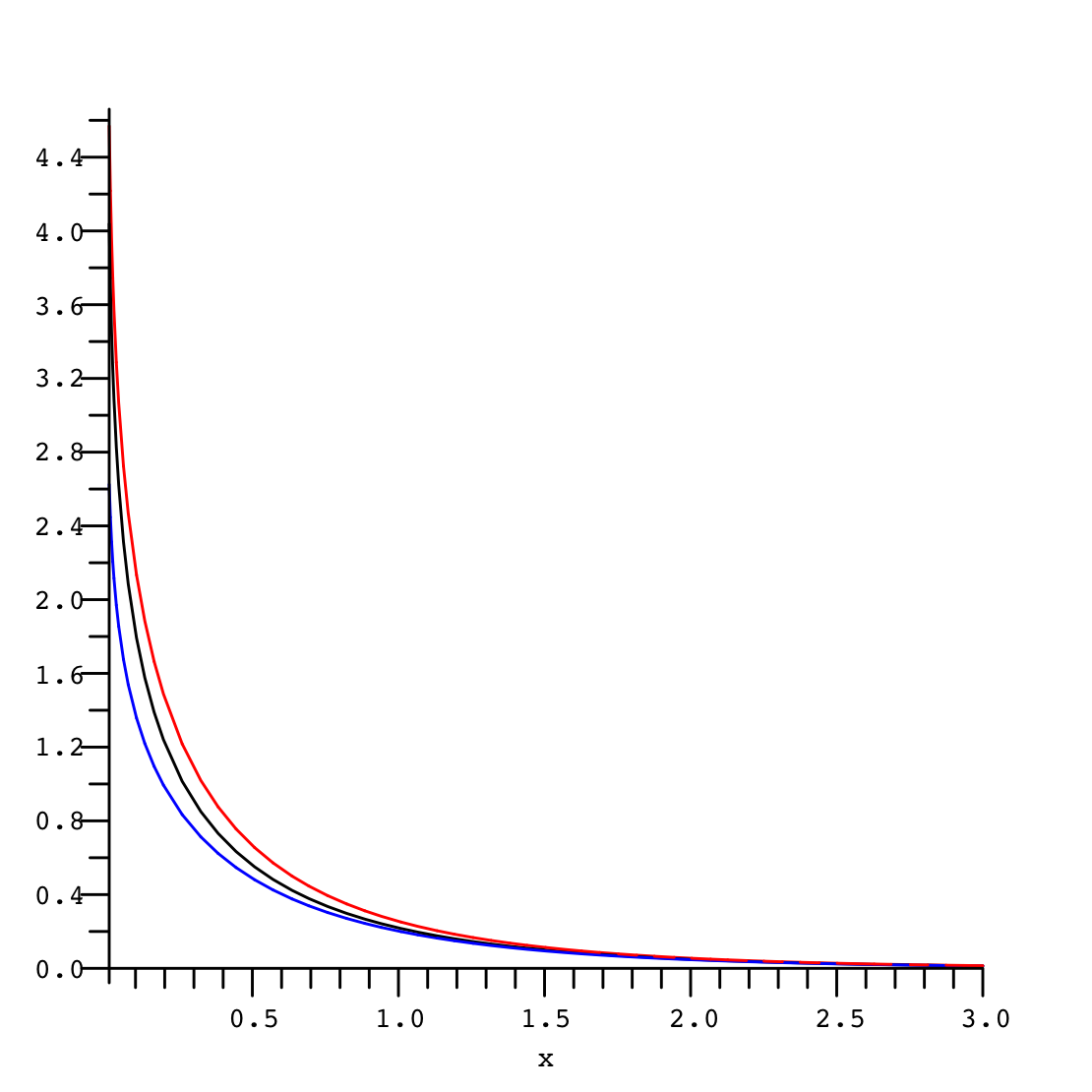
은 인수가 클 때는 음의 지수 함수처럼, 인수가 작을 때는 로그 함수처럼 동작한다. 인수가 양의 실수일 경우,

E_1

은 다음과 같이 초등 함수에 의해 범위를 제한할 수 있다.^[6]

:

\frac 1 2 e^{-x}\,\ln\!\left( 1+\frac 2 x \right)< E_1(x) < e^{-x}\,\ln\!\left( 1+\frac 1 x \right)\qquad x>0

이 부등식의 왼쪽 부분은 왼쪽 그래프에서 파란색으로 표시되어 있으며, 중앙 부분

E_1(x)

는 검은색으로, 오른쪽 부분은 빨간색으로 표시되어 있다.

3. 4. Ein 함수를 이용한 표현

\operatorname{Ein}

은 다음과 같이 정의되는 전해석 함수이다.^[7]

:

\operatorname{Ein}(z)= \int_0^z (1-e^{-t})\frac{dt}{t}= \sum_{k=1}^\infty \frac{(-1)^{k+1}z^k}{k\; k!}

이를 이용하면, 다음과 같이 쓸 수 있다.

:

E_1(z) \,=\, -\gamma-\ln z + {\rm Ein}(z)\qquad \left| \operatorname{Arg}(z) \right| < \pi

:

\operatorname{Ei}(x) \,=\, \gamma+\ln{x} - \operatorname{Ein}(-x)\qquad x \neq 0

여기서

\gamma

는 오일러-마스케로니 상수이다.

\operatorname{Ein}(z)

는 복소평면 전체에서 정칙이며,

E_1(z)

와

\operatorname{Ei}(z)

는 다음과 같이 표현할 수 있다.

:

\begin{align}E_1(z) &= -\gamma-\log z+\operatorname{Ein}(z) \\\operatorname{Ei}(z) &= \gamma+\log z-\operatorname{Ein}(-z)\end{align}

이 표현을 통해 지수 적분 함수의 다가성(多價性) 문제를 복소 로그 함수

\log z

에 가둘 수 있다.

3. 5. 다른 함수와의 관계

지수 적분 함수는 합류 초월기하 함수와 밀접한 관련이 있다. 쿠머 방정식은 일반적으로 합류적 초기하 함수

M(a,b,z)

및

U(a,b,z)

로 풀리지만,

a=0

및

b=1

인 경우에는 두 번째 해가

E_1(-z)

로 주어진다.

E_1(z)

는 지수 함수와 함수

U(1,1,z)

의 곱으로 표현할 수 있다.

:

E_1(z)=e^{-z}U(1,1,z)

3. 5. 1. 로그 적분 함수와의 관계

지수 적분은 다음 공식을 통해 로그 적분 함수 li(''x'')와 밀접하게 관련되어 있다.^[1]

:

\operatorname{li}(e^x) = \operatorname{Ei}(x)

여기서

x

는 0이 아닌 실수 값이다.

로그 적분은 로그 함수의 역수의 적분으로 정의되는 함수이다. 로그 적분은 소수의 분포를 나타내는 공식(소수 정리)에 나타난다.^[1]

3. 5. 2. 불완전 감마 함수와의 관계

일반화된 지수 적분 함수는 상부 불완전 감마 함수의 특수한 경우로 표현할 수 있다.^[8]

:

E_n(x) =x^{n-1}\Gamma(1-n,x).

일반화된 형태는 때때로 Misra 함수^[9]

\varphi_m(x)

라고 불리며, 다음과 같이 정의된다.

:

\varphi_m(x)=E_{-m}(x).

4. 삼각 적분

:

z

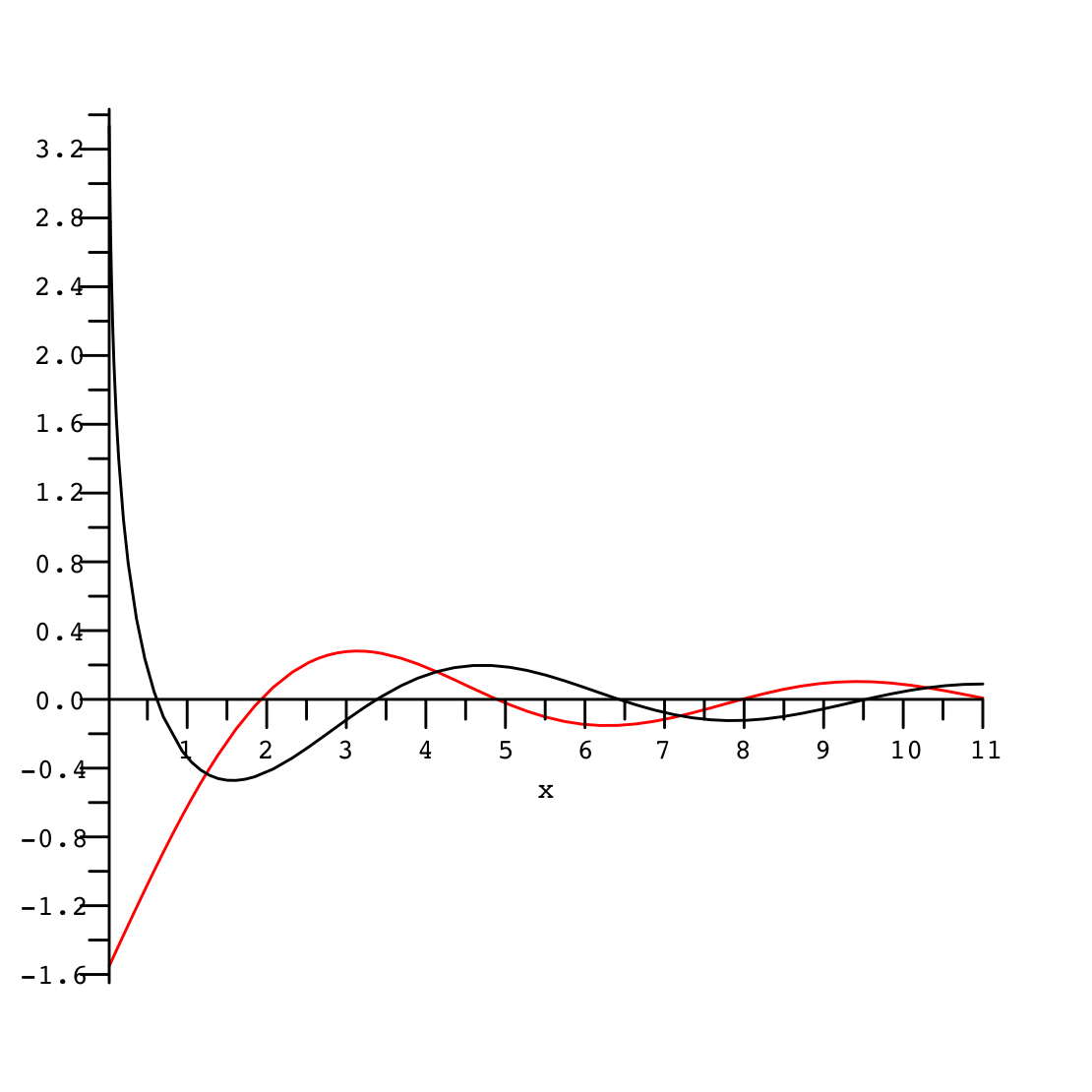
가 허수이고, 음이 아닌 실수부를 가지는 경우, 다음 공식을 사용하여 삼각 적분

\operatorname{Si}

와

\operatorname{Ci}

의 관계를 얻을 수 있다.

:

E_1(z) = \int_1^\infty\frac{e^{-tz}} t \, dt

:

E_1(ix) = i\left[ -\tfrac{1}{2}\pi + \operatorname{Si}(x)\right] - \operatorname{Ci}(x)\qquad (x > 0)

\mathrm{E}_1(ix)

의 실수부와 허수부는 오른쪽 그림에서 검정색과 빨간색 곡선으로 나타내었다.

삼각 적분 함수는 다음과 같이 정의된다.

'''사인 적분''' (sine integral^영어)은 사인 함수를 포함하는 적분에 의해 정의되는 함수이다. 피적분 함수는 비정규화 sinc 함수이다.

:

\operatorname{Si}(z)=\int_{0}^{z}\frac{\sin{t}}{t}\,\operatorname{d}\!t

:

\operatorname{si}(z)=-\int_{z}^{\infty}\frac{\sin{t}}{t}\,\operatorname{d}\!t=\operatorname{Si}(z)-\frac{\pi}{2}

'''코사인 적분''' (cosine integral^영어)은 코사인 함수를 포함하는 적분에 의해 정의되는 함수이다.

:

\operatorname{Ci}(z)=-\int_{z}^{z+\infty}\frac{\cos{t}}{t}\,\operatorname{d}\!t

복소 함수로서의 코사인 적분은 다가 함수이지만, 다음과 같이 복소 로그 함수와 정칙 함수의 합으로 나타낼 수 있다.

:

\operatorname{Ci}(z) = \gamma+\log{z}-\operatorname{Cin}(z)

:

\operatorname{Cin}(z) = \int_{0}^{z}\frac{1-\cos{t}}{t}\,\operatorname{d}\!t

임의의 복소수

z

에 대해 다음 관계가 성립한다.

:

\operatorname{Ein}(\pm iz) = \operatorname{Cin}(z)\pm i\operatorname{Si}(z)

5. 근사

지수 적분 함수는 여러 가지 방법으로 근사할 수 있다. 대표적으로 Swamee와 Ohija, Allen과 Hastings가 제안한 근사식이 있으며,^[13] 연분수 전개^[14]를 이용하거나 Barry ''et al.''^[15]이 제시한 공식을 사용할 수도 있다.

5. 1. Swamee와 Ohija의 근사

Swamee와 Ohija는 다음 근사식을 제안했다.^[13]

:

E_1(x)=(A^{-7.7}+B)^{-0.13}

여기서,

:

\begin{align}A &= \ln\left [\left (\frac{0.56146}{x}+0.65\right)(1+x)\right] \\B &= x^4e^{7.7x}(2+x)^{3.7}\end{align}

5. 2. Allen과 Hastings의 근사

Allen과 Hastings의 근사식은 다음과 같다.^[13]^[14]

:

E_1(x) = \begin{cases} - \ln x +\textbf{a}^T\textbf{x}_5,&x\leq1 \\ \frac{e^{-x}} x \frac{\textbf{b}^T \textbf{x}_3}{\textbf{c}^T\textbf{x}_3},&x\geq1 \end{cases}

여기서,

:

\begin{align}\textbf{a} & \triangleq [-0.57722, 0.99999, -0.24991, 0.05519, -0.00976, 0.00108]^T \\\textbf{b} & \triangleq[0.26777,8.63476, 18.05902, 8.57333]^T \\\textbf{c} & \triangleq[3.95850, 21.09965, 25.63296, 9.57332]^T \\\textbf{x}_k &\triangleq[x^0,x^1,\dots, x^k]^T\end{align}

5. 3. 연분수 전개

지수 적분 함수는 다음과 같은 연분수 형태로 표현될 수 있다.^[14]

:

E_1(x) = \cfrac{e^{-x}}{x+\cfrac{1}{1+\cfrac{1}{x+\cfrac{2}{1+\cfrac{2}{x+\cfrac{3}{\ddots}}}}}}.

5. 4. Barry 등의 근사

Barry ''et al.''의 근사식은 다음과 같다.^[15]

:

E_1(x) = \frac{e^{-x}}{G+(1-G)e^{-\frac{x}{1-G}}}\ln\left[1+\frac G x -\frac{1-G}{(h+bx)^2}\right],

여기서 각 문자의 값은 다음과 같다.

:

\begin{align}h &= \frac{1}{1+x\sqrt{x}}+\frac{h_{\infty}q}{1+q} \\q &=\frac{20}{47}x^{\sqrt{\frac{31}{26}}} \\h_{\infty} &= \frac{(1-G)(G^2-6G+12)}{3G(2-G)^2b} \\b &=\sqrt{\frac{2(1-G)}{G(2-G)}} \\G &= e^{-\gamma}\end{align}

\gamma

는 오일러-마스케로니 상수이다.

6. 지수 적분 함수의 역함수

지수 적분 함수의 역함수는 다음과 같은 멱급수 형태로 나타낼 수 있다.^[16]

: $\forall |x| < \frac{\mu}{\ln(\mu)},\quad \mathrm{Ei}^{-1}(x) = \sum_{n=0}^\infty \frac{x^n}{n!} \frac{P_n(\ln(\mu))}{\mu^n}$

여기서 $\mu$ 는 라마누잔-졸드너 상수이고, $(P_n)$ 는 다음의 점화 관계로 정의되는 다항식 수열이다.

: $P_0(x) = x,\ P_{n+1}(x) = x(P_n'(x) - nP_n(x)).$

$n > 0$ 에 대해, $\deg P_n = n$ 이며, 다음 공식을 얻는다.

: $P_n(x) = \left.\left(\frac{\mathrm d}{\mathrm dt}\right)^{n-1} \left(\frac{te^x}{\mathrm{Ei}(t+x)-\mathrm{Ei}(x)}\right)^n\right|_{t=0}.$

7. 응용

지수 적분 함수는 다음과 같은 분야에서 응용된다.^[17]

선형 공급원 및 싱크가 있는 과도 상태 또는 비정상 상태 흐름에 대한 방사형 확산 방정식
단순화된 1차원 기하학에서의 중성자 수송 방정식 해

(참고: 하위 섹션에서 이미 시간 의존적 열전달, 지하수 흐름, 복사 전달은 구체적으로 다루고 있으므로, 여기서는 간단하게 언급만 함)

7. 1. 시간 의존적 열전달

시간에 따라 변하는 열전달 문제를 해결하는 데 지수 적분 함수가 사용된다.^[17]

7. 2. 지하수 흐름

대수층에서의 비평형 지하수 흐름을 분석하고 모델링하는 데 지수 적분 함수가 사용된다. 특히, Theis 해법은 지수 적분 함수를 기반으로 한다.^[17]

7. 3. 복사 전달

별과 행성 대기에서의 복사 전달 과정에 사용된다.^[17]

7. 4. 중성자 수송

원자로 등에서 중성자의 이동 및 반응을 기술하는 중성자 수송 방정식의 해를 구하는 데 지수 적분 함수가 사용된다.^[17]

참조

_[1] 서적 Abramowitz and Stegun
_[2] 서적 Abramowitz and Stegun
_[3] 서적 Bleistein and Handelsman
_[4] 서적 Bleistein and Handelsman
_[5] 간행물 Asymptotic Approximations https://doi.org/10.1[...] Springer International Publishing 2023-05-04
_[6] 서적 Abramowitz and Stegun
_[7] 서적 Abramowitz and Stegun
_[8] 서적 Abramowitz and Stegun
_[9] 기타 After Misra (1940)
_[10] 기타 Milgram (1985)
_[11] 서적 Abramowitz and Stegun
_[12] 서적 Abramowitz and Stegun
_[13] 논문 Revisit of Well Function Approximation and An Easy Graphical Curve Matching Technique for Theis' Solution 2003-05-01
_[14] 논문 Numerical evaluation of exponential integral: Theis well function approximation 1998-02-26
_[15] 논문 Approximation for the exponential integral (Theis well function) 2000-01-31
_[16] 웹사이트 Inverse function of the Exponential Integral Ei-1(x) https://math.stackex[...] 2024-04-24
_[17] 서적 Nuclear Reactor Theory Van Nostrand Reinhold Company
_[18] 웹사이트 Wolfram Mathworld: Exponential Integral http://mathworld.wol[...]
_[19] 웹사이트 SpringerLink: Integral exponential function http://eom.springer.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com