지수 함수
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
지수 함수는 자연로그의 역함수로, 로 표기하며, 실수의 함수로 항상 양수 값을 갖는다. 지수 함수는 여러 가지 방법으로 정의할 수 있으며, 극한, 거듭제곱 급수, 함수 방정식 등을 통해 정의될 수 있다. 지수 함수는 미분 가능하며, 도함수는 자기 자신과 같고, 로그 함수를 사용하여 정의할 수도 있다. 복소 지수 함수는 삼각 함수와 관련이 있으며, 행렬 지수 함수는 리 군과 리 대수 이론에서 중요한 역할을 한다. 지수 함수는 초월 함수이며, 계산 시에는 expm1 함수를 사용하여 정확도를 높일 수 있다.
를 양의 상수, 를 모든 실수 값을 취하는 변수로 할 때, 로 주어지는 함수를 지수함수라고 한다. 예를 들어, 함수 는 지수함수이다. 자연로그의 역함수로 주어지는 지수함수는 또는 와 같이 쓴다. 이때 는 '자연로그의 밑'이라 한다. 지수함수 역시 그래프로 나타낼 수 있으며, 실수 의 함수로서 그래프는 항상 양수이고, 왼쪽에서 오른쪽으로 증가한다. 이때 그래프는 축과 만나지 않지만, 축에 점점 접근해간다.
함수 에서,
2. 정의
''a''가 양의 실수, ''x''가 임의의 실수일 때, ''a''를 밑, ''x''를 지수로 하는 지수함수를 ''a''''x'' 로 쓴다. 특별히 지수가 자연수(혹은 유리수)일 때, 이 함수는 ''a''의 거듭제곱과 일치한다. 지수함수는 다음의 공리에 의해 정의된다.
지수 함수는 여러 가지로 정의할 수 있으며, 서로 다른 본질을 가지고 있지만 모두 동등하다.
가장 간단한 정의 중 하나는 다음과 같다. 지수 함수는 자기 자신과 같은 미분 가능한 함수이며, 변수의 값이 0일 때 값이 1인 유일한 함수이다.
지수 함수는 자연로그의 역함수이다. 역함수 정리에 따르면 자연로그는 위 정의를 만족하는 역함수를 갖는다. 따라서 다음이 성립한다.
:
여기서 는 모든 실수이고 는 모든 양의 실수이다.
지수 함수는 거듭제곱 급수의 합이다.:[20][2]
여기서 는 의 팩토리얼(처음 개의 양의 정수의 곱)이다.
지수 함수는 다음과 같은 함수 방정식을 만족한다.:
양의 실수 밑으로의 거듭제곱의 확장: 를 양의 실수라고 하자. 지수 함수와 자연로그는 서로의 역함수이므로 이다. 이 정수라면, 로그의 함수 방정식은 다음을 의미한다.
가장 오른쪽의 식은 이 임의의 실수일 때 정의되므로, 이것은 모든 양의 실수 와 모든 실수 에 대해 를 정의할 수 있게 해준다.
특히, 가 오일러의 수 이면 (역함수)이고 따라서 이다. 이것은 지수 함수에 대한 두 가지 표기법의 동등성을 보여준다.
여기서 은 정수값만 취한다.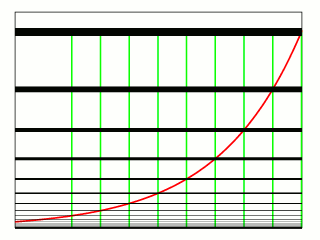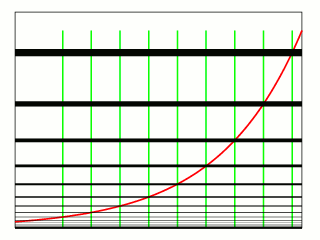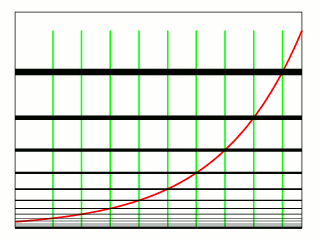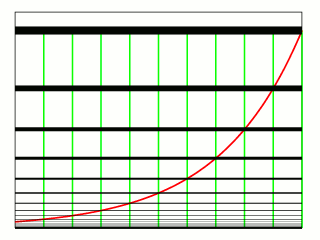
지수 함수는 어떤 양이 현재 값에 비례하는 비율로 성장하거나 감소할 때마다 나타난다. 그러한 상황 중 하나가 복리이며, 사실 바로 이러한 관찰을 통해 1683년 야코프 베르누이가[22] 이제는 로 알려진 수
를 발견했다.
지수 함수의 도함수(변화율)는 지수 함수 자체이다. 더 일반적으로, 변화율이 함수 자체에 ''비례하는'' 함수는 지수 함수로 표현될 수 있다. 이 도함수 특성은 지수 성장 또는 지수 감소를 야기한다.
지수 함수는 복소 평면에서 정함수로 확장된다. 오일러의 공식은 순허수 인수에서의 값을 삼각 함수와 관련짓는다. 지수 함수는 인수가 행렬이거나, 심지어 바나흐 대수 또는 리 대수의 원소인 경우에도 유사체를 갖는다.
3. 극한
::,
::,
::,
밑 의 지수 함수의 극한은 와 1 의 위치 관계에 따라 결정된다.
4. 미분
e를 밑으로 하는 지수 함수 ''e''''x''의 도함수는 ''e''''x'' 자신이 된다. 미분방정식 의 특수해는 이다. 일반적인 지수함수 ''a''''x''의 도함수는 가 된다.[22]
수학 및 과학에서 지수 함수의 중요성은 주로 그 자체의 도함수와 같고, x=0일 때 1과 같은 유일한 함수라는 성질에서 비롯된다. 즉,
이다.
일반적으로, 변화율이 함수 자체에 ''비례하는'' 함수는 지수 함수로 표현될 수 있다. 이 도함수 특성은 지수 성장 또는 지수 감소를 야기한다. 임의의 미분 가능한 함수 f에 대해 연쇄 법칙에 따라 다음이 성립한다.
밑 a의 지수 함수는 실수 전체 집합 R에서 무한히 미분 가능하며, 도함수는 다음과 같다.
4. 1. 음함수 미분을 이용한 지수함수의 미분
라 하면, 이다. 양변을 에 대해 미분하면, 이다.5. 로그함수의 역함수로서의 정의
로그함수를 정적분으로 정의할 경우, 지수함수는 거듭제곱이 아닌 로그함수의 역함수로 정의된다.
자연로그는 다음과 같이 정의한다.
:
이때 는 강한 증가 함수이며 치역이 실수 전체이므로 역함수가 존재한다. 이 역함수를 라고 표기한다.
이 함수의 도함수는 역함수의 미분법에 의해
:
즉, 이다. 또한, 이므로, 이다.
그리고 로그함수와의 역함수 관계를 이용하여 다음 등식이 성립함을 보일 수 있다.
:
:로 놓으면
:이므로 로그의 성질에 의하여 이다.
:따라서 가 성립한다.
로그함수 는 정의역 전체에서 연속 함수이므로 중간값 정리에 의하여 방정식 을 만족하는 해 가 존재하며, 단사함수이므로 실수 는 단 하나만 존재한다. 방정식 의 해를 라 한다.
:
이제 로 놓고 이것을 '''지수함수'''로 정의한다.
6. 그래프
함수의 그래프 는 위로 향하고 있으며, 가 증가함에 따라 더욱 빠르게 증가한다.[1] 그래프는 항상 축 위에 있지만, 가 크게 음수가 될수록 축에 임의로 가까워진다. 따라서 축은 수평 점근선이다. 방정식 는 각 점에서 그래프의 접선의 기울기가 그 점에서의 높이(즉, 좌표)와 같다는 것을 의미한다.
밑 의 지수 함수는 실수 전체 집합 R에서 무한히 미분 가능하며, 도함수는 를 만족한다.
지수 함수는 항상 양수이므로, 그 도함수의 부호는 의 부호에 의해서만 결정된다. 따라서 지수 함수는 밑 가 보다 클 때 엄밀히 단조 증가하고, 보다 작을 때는 엄밀히 단조 감소하며, 일 때는 상수 함수 이다.
밑 의 지수 함수의 극한은 와 의 위치 관계에 따라 결정된다:
- 이면 ;
- 이면
지수 함수는 멱함수에 대해 로 가는 극한에서 지수 함수가 더 빠르게 발산한다는 예측 가능한 거동을 보인다:
; 극한 비교 정리:
: 임의의 실수 와 에 대해 가 성립한다.
지수 함수는 로그 볼록 함수(따라서 볼록)이면서 로그 오목 함수이다.
7. 지수 함수의 다양한 표현
지수 함수 f의 인수 x(실수 또는 복소수) 값은 a≡f(0), b≡f(1)/f(0), k≡f'(0)/f(0)일 때 다음과 같이 표현할 수 있다.
- abx
- aekx (k=ln b, b=ek)
지수 함수는 어떤 양이 현재 값에 비례하는 비율로 성장하거나 감소할 때 나타난다. 복리는 이러한 상황의 한 예시이며, 1683년 야코프 베르누이는[22] 다음 수식을 발견했다.
이 수는 현재 e로 알려져 있다. 이후 1697년 요한 베르누이는 지수 함수의 미적분을 연구했다.[22]
원금 1이 연이율 x로 매월 복리로 이자가 발생하면, 매달 발생하는 이자는 현재 값의 x/12배이므로, 매달 총액은 (1 + x/12)배가 된다. 연말의 값은 (1 + x/12)12가 된다. 이자가 매일 복리로 발생한다면, (1 + x/365)365가 된다. 1년 동안의 기간 수를 무한대로 늘리면 다음의 지수 함수의 극한 정의가 나타난다.
이는 레온하르트 오일러가 처음 제시했다.[21]
지수 함수는 기본적인 거듭제곱 항등식을 따른다.
이는 exp x에 대한 지수 표기법 ex를 정당화한다.
지수 함수의 도함수(변화율)는 지수 함수 자체이다. 변화율이 함수 자체에 비례하는 함수는 지수 함수로 표현될 수 있으며, 이는 지수 성장 또는 지수 감소를 야기한다.
지수 함수는 복소 평면에서 정함수로 확장된다. 오일러의 공식은 순허수 인수에서의 값을 삼각 함수와 관련짓는다. 지수 함수는 인수가 행렬이거나 바나흐 대수 또는 리 대수의 원소인 경우에도 유사체를 갖는다.
7. 1. 미분 가능한 함수
- 모든 , 에 대해 를 만족하는 지수 함수 (덧셈을 곱셈으로 변환; 로그 함수의 주요 성질과 반대: 곱셈을 덧셈으로 변환)는 이라는 조건과 동등하며, 일반적인 형태는 이다. 때때로 의 값을 의 ''역로그'' 또는 ''역로그함수 값''이라고 한다.[13]
- (함수가 자체 도함수와 동일)를 만족하는 지수 함수 의 일반적인 형태는 이다.
- 과 를 만족하는 유일한 지수 함수를 '''지수 함수'''라고 하며, ''자연 지수 함수'' 또는 ''자연 역로그 함수''라고도 한다. 기호는 이고, 일반적인 형태는 또는 이다.
7. 2. 자연로그의 역함수
자연로그의 역함수로 주어지는 지수함수는 또는 와 같이 쓴다. 이때 를 '자연로그의 밑'이라 한다. 지수함수 는 그래프로 나타낼 수 있으며, 실변수 의 함수로서 그래프는 항상 양수이고, 왼쪽에서 오른쪽으로 증가한다. 이때 그래프는 축과 만나지 않지만, 축에 점점 접근해간다.[2]자연로그는 다음과 같이 정의한다.
이때 는 강한 증가 함수이며 치역이 실수 전체이므로 역함수가 존재한다. 이때의 역함수를 라고 표기한다.
이 함수의 도함수는 역함수의 미분에 의하여
즉, 이다. 또한, 이므로, 이다.
로그함수와의 역함수 관계를 이용하면 다음 등식이 성립함을 보일 수 있다.
:로 놓으면
:이므로 로그의 성질에 의하여
:따라서 가 성립한다.
로그함수 는 정의역 전체에서 연속 함수이므로 중간값 정리에 의하여 방정식 을 만족하는 해 가 존재하며, 단사함수이므로 실수 는 단 하나만 존재한다. 방정식 의 해를 라 한다.
이제 로 놓고 이것을 '''지수함수'''로 정의한다.
수학적 귀납법을 이용하면 가 자연수일 때 임을 보일 수 있다.
역함수 정리에 따르면 자연로그는 위 정의를 만족하는 역함수를 갖는다. 이것이 존재성을 증명하는 첫 번째 방법이다. 따라서 다음이 성립한다.[2]
:
여기서 는 모든 실수이고 는 모든 양의 실수이다.
7. 3. 거듭제곱 급수
지수 함수는 다음과 같은 거듭제곱 급수의 합으로 나타낼 수 있다.[20][2]
:
여기서 는 의 팩토리얼(처음 개의 양의 정수의 곱)이다. 이 급수는 비율 검정에 따라 모든 에 대해 절대 수렴한다. 따라서 합의 도함수는 항별 미분으로 계산할 수 있으며, 이것은 급수의 합이 지수함수의 정의를 만족함을 보여준다. 이것은 존재성을 증명하는 두 번째 방법이며, 부산물로 지수 함수가 모든 에 대해 정의되고 모든 곳에서 매클로린 급수의 합임을 보여준다.
7. 4. 극한
함수 에서일 때 위 지수함수의 극한은 다음과 같다.
:,
8. 일반 지수 함수
때때로 '지수 함수'는 지수에 인수가 포함된 모든 함수를 가리키는 이름으로 사용되기도 한다. 예를 들어
일반적인 지수 함수
- 모든
u ,v ,d 에 대해:f(u+d)/f(u) = f(v+d)/f(v) (정의역에서 '차이가 같은' 인수 쌍은 공역에서 '비율이 같은' 값 쌍에 매핑된다). 즉, 모든d 에 대해f(x+d)/f(x) 의 값은x 에 무관하다.[5][6][7][8] - 모든
u ,v 에 대해:f'(u)/f(u) = f'(v)/f(v) . 즉,f'(x)/f(x) 의 값은x 에 무관하다. 이 상수 값을 때때로 함수f 의 '속도 상수'라고 하며, 기호k 로 나타낸다.[9][10][11] (f(u)/f(v))^{1/(u-v)} 의 값은u 와v 에 무관하다. 즉,(f(x+d)/f(x))^{1/d} 의 값은x 와d 에 무관하다. 이 상수 값을 함수f 의 '밑'이라고 한다.[12]
좁은 의미의 양의 실수
:
\exp_a(n) = a^n := \underset{n \text{ factors}}{\underbrace{a\times a\times \cdots \times a}}
또한
이러한 구성은 지수 함수적 성장 또는 지수 함수적 감쇠 현상에 자연스럽게 대응된다.
등비수열의 예시는 다음과 같다.
- 예 1: 인구가 10년마다 30% 증가하는 상황을 가정하면, 1900년의 인구가
N 일 때, 1910년, 1920년, … 의 인구는N \times 1.3 ,N \times 1.3^2 , … 와 같이 계산할 수 있으며,n 10년 후에는N \times 1.3^n 이 된다. 1890년, 1880년, … 의 인구는N \times 1.3^{-1} ,N \times 1.3^{-2} , … 가 된다. - 예 2: 탄소-14는 방사성 붕괴의 반감기
T = 5730년을 갖는다(즉,T 년마다 방사성 입자의 수가 절반이 된다). 어떤 시점에서 측정한 방사성 입자의 수가N 이라면,n 주기 후에는 방사성 입자의 수는N \times (1/2)^n 밖에 없다.
2개의 측정 시점 "사이"에서의 인구나 방사성 입자의 수를 결정하는 것은 -제곱근을 통해 가능하다. 예를 들어 인구가 10년에 1.3배가 될 때, 1년마다 몇 배가 되는지를 결정하려면,
비정수(유리수)
실수
- 함수이다.
- 항등식
a^{x + y} = a^x \cdot a^y 을 만족한다. 즉 합이 곱으로 사상된다. - 연속이다.
- 로그 함수(이는 곱을 합으로 사상한다)의 역함수이다.
- 미분 가능하며, 또한 도함수가 원함수에 비례한다.
지수 함수의 정의에는 여러 관점이 있으며, 합을 곱으로 매핑하는 대수적 성질, 도함수가 자신에 비례하는 미분적 성질, 지수 함수와 로그 함수의 관계 등에 기반한다.
9. 복소 지수 함수
복소 지수 함수는 실수 인수에 대한 멱급수 정의에서 실수 변수를 복소수로 대체하여 정의할 수 있다.
:
또는, 실수 변수가 복소수로 대체된 실수 인수에 대한 극한 정의를 모델링하여 복소 지수 함수를 정의할 수도 있다.
:
멱급수 정의를 이용하면, 코시 곱을 통해 지수 함수의 곱셈 성질이 모든 복소수에 대해서도 성립함을 보일 수 있다.
:
복소 지수 함수의 정의는 삼각 함수를 복소 인수로 확장하는 정의로 이어진다. t영어가 실수일 때, 급수 정의는 다음과 같이 전개된다.
:
여기서 실수 부분과 허수 부분은 각각 cos t영어와 sin t영어의 급수 전개와 일치한다.
이러한 관계를 바탕으로 복소수 z에 대한 코사인 함수와 사인 함수는 다음과 같이 정의된다.[19]
:
& \cos z:= \frac{\exp(iz)+\exp(-iz)}{2} = \sum_{k=0}^\infty (-1)^k \frac{z^{2k}}{(2k)!}, \\[5pt]
\text{and } \quad & \sin z := \frac{\exp(iz)-\exp(-iz)}{2i} =\sum_{k=0}^\infty (-1)^k\frac{z^{2k+1}}{(2k+1)!}
\end{align}
이렇게 정의된 지수 함수, 코사인 함수, 사인 함수는 비율 판정법에 의해 무한한 수렴 반지름을 가지므로 정함수(즉, 복소 평면 전체에서 정칙)이다.
오일러 공식은 복소 지수 함수와 삼각 함수 사이의 관계를 나타낸다.
:
복소 지수 함수는 주기 를 가지는 주기 함수이며, 다음 식이 성립한다.
:
10. 행렬 지수 함수
행렬 지수 함수는 정사각 행렬에 대해 지수 함수의 멱급수 정의를 적용하여 정의한다.[21] 이는 리 군과 리 대수 이론에서 중요한 역할을 한다.
지수 함수의 멱급수 정의는 정방 행렬(이 경우 함수는 행렬 지수 함수라고 함)에 대해서, 그리고 더 일반적으로는 모든 단위를 갖는 바나흐 대수에서 의미가 있다. 이러한 설정에서
몇 가지 대안적인 정의가 같은 함수를 이끌어낸다. 예를 들어,
또는
리 군
11. 초월성
함수 e|e영어''z''는 유리 함수환
a|a영어1, ..., a|a영어''n''이 서로 다른 복소수일 때, e|e영어a|a영어1z|z영어, ..., e|e영어a|a영어''n''z|z영어는
12. 계산
x영어=0 근처의 인수를 계산할 때, 의 값을 직접 계산하는 expm1 함수를 사용하는 것이 유용할 수 있다. 이는 윌리엄 카한이 제안했다.[27][28] 예를 들어, 다음과 같은 테일러 급수를 사용할 수 있다.
이 함수는 1979년 휴렛 패커드(Hewlett-Packard) HP-41C 계산기에 처음 구현되었으며, 여러 계산기, 운영 체제(예: 버클리 유닉스 4.3BSD[26]), 컴퓨터 대수 시스템, 프로그래밍 언어(예: C99) 등에서 제공된다.[25]
기저 외에도, IEEE 754-2008 표준은 2와 10을 기저로 하는 0 근처의 유사한 지수 함수로 과 을 정의한다.
로그에도 유사한 방법이 사용되었다(lnp1 참조).[18]
쌍곡선 탄젠트 항등식,
은 를 구현하지 않는 시스템에서 작은 값에 대해 고정밀도 값을 제공한다.
참조
[1]
웹사이트
Exponential Function Reference
https://www.mathsisf[...]
2020-08-28
[2]
웹사이트
Exponential Function
https://mathworld.wo[...]
2020-08-28
[3]
서적
Lehrbuch der Differential- und Integralrechnung
https://archive.org/[...]
1900
[4]
문서
(1) Every (positive) function f is exponential, for it can be written as x↦e^(ln f(x)). (2) The function x↦Σ_(i=0)^∞ x^n/n! is not exponential.
[5]
서적
Calculus 1
1998
[6]
웹사이트
What is the base of an exponential function?
2020
[7]
웹사이트
What makes exponential functions unique
https://www.math.ksu[...]
[8]
웹사이트
Exponentialfunktionen
https://www.mathebib[...]
[9]
서적
An Elementary Course of Infinitesimal Calculus
https://archive.org/[...]
1919
[10]
서적
Differential Equations and Historical Notes
https://horizons-200[...]
1972
[11]
웹사이트
Exponential growth and decay
https://www.math.wpi[...]
[12]
문서
This defining condition is derivable from the usual way to describe an exponential function
[13]
서적
Plane and Spherical Trigonometry
https://archive.org/[...]
1911
[14]
서적
Calculus 1
1998
[15]
서적
Divine Proportion
2005
[16]
서적
Cours d'Analyse Infinitésimale
https://archive.org/[...]
1914
[17]
웹사이트
How to find the exponential curve between two generic points
https://math.stackex[...]
2019
[18]
문서
A similar approach to reduce round-off errors of calculations for certain input values of trigonometric functions
[19]
서적
Principles of Mathematical Analysis
https://archive.org/[...]
McGraw-Hill
1976
[20]
서적
Real and complex analysis
https://archive.org/[...]
McGraw-Hill
1987
[21]
서적
e: the Story of a Number
[22]
웹사이트
The number e
http://www-history.m[...]
University of St Andrews, Scotland
2001-09
[23]
서적
Continued Fractions
2008
[24]
서적
Mathematical Analysis
https://archive.org/[...]
Addison Wesley
1974
[25]
웹사이트
Computation of expm1 = exp(x)−1
http://www.math.utah[...]
Department of Mathematics, Center for Scientific Computing, University of Utah
2002-07-09
[26]
서적
The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library
Springer International Publishing AG
2017-08-22
[27]
서적
HP 48G Series – Advanced User's Reference Manual (AUR)
http://www.hpcalc.or[...]
Hewlett-Packard
1994-12
[28]
서적
HP 50g / 49g+ / 48gII graphing calculator advanced user's reference manual (AUR)
http://www.hpcalc.or[...]
Hewlett-Packard
2009-07-14
[29]
백과사전
McGraw-Hill Encyclopedia of Science & Technology
McGraw-Hill
2007
[30]
서적
Modern Physics
Harcourt Brace Jovanovich
1989
[31]
서적
Differential Equations with Applications and Historical Notes
McGraw-Hill
1972
[32]
웹사이트
Intégrer pour mieux dériver
http://megamaths.per[...]
[33]
웹사이트
exp(x)
http://www.wolframal[...]
2018-05-07
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

