페르미-디랙 통계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 개념
4. 페르미-디랙 분포
- 4.1. 에너지에 따른 입자 분포
5. 양자 및 고전 영역
6. 유도
7. 응용
참조

1. 개요

페르미-디랙 통계는 엔리코 페르미와 폴 디랙이 1926년에 독립적으로 개발한 양자 통계로, 파울리 배타 원리를 따르는 구별 불가능한 입자인 페르미 입자의 통계적 분포를 설명한다. 이 통계는 금속 내 전자, 백색 왜성 붕괴 등, 고전적인 맥스웰-볼츠만 통계로는 설명하기 어려운 현상을 이해하는 데 기여했다. 페르미-디랙 분포 함수는 페르미 입자가 특정 에너지 준위를 점유할 확률을 나타내며, 절대 영도에서 페르미 에너지는 페르미온의 최대 에너지 준위와 같다.

더 읽어볼만한 페이지

통계역학 - 볼츠만 상수
볼츠만 상수 k는 온도와 에너지를 연결하는 상수이며, 기체 상수와 아보가드로 상수의 비로 정의되고, SI 단위계에서 1.380649×10⁻²³ J/K의 값을 가지며, 거시 물리학과 미시 물리학을 연결하는 중요한 역할을 한다.
통계역학 - 상태 밀도
상태 밀도는 계에서 특정 에너지 준위에 존재할 수 있는 상태의 수를 나타내는 물리량으로, 계의 종류, 차원, 분산 관계 등에 따라 달라지며, 고체 물리학과 양자역학적 계에서 중요한 역할을 한다.
양자장론 - 양자 색역학
양자 색역학은 색 전하를 국소 대칭으로 정의한 SU(3) 게이지 군의 비아벨 게이지 이론으로, 쿼크와 글루온을 기본 입자로 하여 쿼크 사이의 강한 상호작용을 매개하며, 점근적 자유성과 색 가둠의 특징을 가지는 이론이다.
양자장론 - 양자화 (물리학)
양자화는 물리량의 불연속성을 의미하며, 흑체 복사, 광전 효과, 수소 원자 스펙트럼 등을 설명하는 데 사용되고, 정준 양자화, 경로 적분 양자화 등 다양한 방법이 존재한다.
물리학에 관한 - 전력
전력은 전압과 전류의 곱으로 계산되며, 발전소에서 생산되어 송전 및 배전을 통해 소비자에게 공급되고, 에너지 저장 기술을 통해 안정적으로 공급될 수 있으며, 산업, 상업, 가정 등 다양한 분야에서 소비된다.
물리학에 관한 - N형 반도체
N형 반도체는 전자를 주된 전하 운반체로 사용하는 반도체이다.

페르미-디랙 통계
페르미-디랙 통계
다양한 온도에서 페르미-디랙 분포 함수의 그래프
종류	입자 통계
적용 대상	페르미온
개발자	엔리코 페르미, 폴 디랙
에너지 분포	페르미 분포 함수
기본 정보
관련 항목	보스-아인슈타인 통계 맥스웰-볼츠만 통계
통계 종류	양자 통계
입자 종류	동일한 페르미온
입자 특성	반정수 스핀
점유수	각 양자 상태는 최대 하나의 입자만 가질 수 있음 (파울리 배타 원리)
페르미 분포 함수
함수 형태	f(ε) = 1 / (exp((ε - μ) / kT) + 1)
변수	ε: 입자의 에너지 μ: 화학 퍼텐셜 (페르미 에너지) k: 볼츠만 상수 T: 절대 온도
특징	저온에서 페르미 에너지 이하의 상태는 거의 모두 채워짐 고온에서는 맥스웰-볼츠만 분포에 접근
응용
주요 응용 분야	금속 내 전자의 행동 연구 반도체 내 전자 및 정공의 분포 백색 왜성과 중성자별의 안정성 연구

2. 역사

엔리코 페르미와 폴 디랙은 1926년에 페르미-디랙 통계를 독자적으로 개발하였다.^[2]^[3] 막스 보른에 따르면, 파스쿠알 요르단도 1925년에 '파울리 통계'라는 이름으로 같은 통계를 개발했지만, 논문 발표가 늦어졌다.^[4]^[5]^[6] 디랙은 페르미가 처음으로 이 통계를 연구했기 때문에 "페르미 통계"라 부르고 해당 입자를 "페르미온"이라 명명했다.^[7]

페르미-디랙 통계 발표 전에는 전자의 행동 양상을 이해하기 어려웠다. 예를 들어, 상온에서 금속의 전자 열용량이 전류에 기여하는 전자보다 훨씬 적은 것처럼 보이는 현상^[1]과, 금속에 높은 전압을 가했을 때 발생하는 전계 방출 전류가 온도에 거의 영향을 받지 않는 이유를 설명하기 힘들었다. 당시 금속 전자 이론이었던 드루드 모형은 모든 전자가 동등하다고 가정하여 이러한 문제에 직면했다. 즉, 각 전자가 볼츠만 상수 ''k''_B 만큼 비열에 기여한다고 보았다. 페르미-디랙 통계는 이러한 문제를 해결하였다.

1926년 랄프 파울러는 페르미-디랙 통계를 사용하여 별이 백색왜성으로 붕괴하는 현상을 설명했다.^[8] 1927년 아르놀트 조머펠트는 이 통계를 금속 내 전자에 적용하여 자유 전자 모형을 개발했고,^[9] 1928년 파울러와 로타어 노르트하임은 금속의 전계 방출 현상에 적용했다.^[10] 이후 페르미-디랙 통계는 물리학의 중요한 부분으로 자리 잡았다.

3. 개념

페르미 입자들은 구별 불가능한 입자이며 파울리 배타 원리를 따른다. 즉, 두 개 이상의 입자가 같은 양자 상태에 동시에 존재할 수 없다. 양자역학적으로, 이러한 배타 원리는 입자의 교환 연산자 아래 계의 파동 함수가 -1의 고윳값을 갖는 것을 의미한다. 서로 상호작용하지 않는 페르미 입자로 이루어진 계를 페르미 기체라고 한다.^[1]

파울리 배타 원리에 의하여, 페르미 기체의 통계적 분포는 맥스웰-볼츠만 분포를 따르는 고전적 이상 기체와 차이를 보인다. 이러한 페르미 기체의 통계를 '''페르미-디랙 통계'''라 한다.^[1] 1926년 페르미-디랙 통계가 도입되기 전에는, 서로 모순되는 현상으로 인해 전자의 특정 행동 양상을 이해하는 것이 어려웠다. 예를 들어, 상온에서 금속의 전자 열용량은 전류에 기여하는 전자 수보다 100배 적은 전자에서 비롯되는 것처럼 보였다. 또한 상온에서 금속에 고전압을 가했을 때 생성되는 전계 방출 전류가 온도에 거의 무관한 이유도 이해하기 어려웠다.^[1]

당시 금속의 전자 이론이었던 드루드 모형이 직면한 어려움은 전자들이 (고전 통계 이론에 따르면) 모두 동등하다고 간주했기 때문이었다. 다시 말해, 각 전자는 볼츠만 상수 ''k''_B 정도의 크기로 비열에 기여한다고 믿었다.^[1] 이 문제는 페르미-디랙 통계가 개발될 때까지 해결되지 않았다.

페르미-디랙 통계는 1926년 엔리코 페르미^[2]와 폴 디랙^[3]에 의해 처음 발표되었다. 막스 보른에 따르면, 파스쿠알 조르단은 1925년에 '파울리 통계'라고 부르는 동일한 통계를 개발했지만, 적시에 발표되지 않았다.^[4]^[5]^[6] 디랙에 따르면, 이는 페르미가 처음 연구했으며, 디랙은 이를 "페르미 통계"라고 부르고 해당 입자를 "페르미온"이라고 불렀다.^[7]

열역학적 평형 상태에 있는 동일한 페르미온 시스템에서 단일 입자 상태 i의 평균 페르미온 수는 '''페르미-디랙(F-D) 분포'''로 주어진다.^[11]

: $\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1},$

여기서 k_B는 볼츠만 상수, T는 절대 온도, ε_i는 단일 입자 상태 i의 에너지, μ는 총 화학 포텐셜이다.

절대 영도에서, μ는 페르미온 당 포텐셜 에너지를 더한 페르미 에너지와 같다. 단, 양의 스펙트럼 밀도의 근방에 있는 경우이다. 반도체 내 전자와 같이 스펙트럼 갭이 있는 경우, 대칭점 μ는 일반적으로 페르미 준위 또는 전자의 경우 전기화학적 포텐셜이라고 하며 갭의 중간에 위치한다.^[13]^[14]

페르미-디랙 분포는 시스템의 페르미온 수가 충분히 커서 시스템에 페르미온 하나를 더 추가해도 μ에 미치는 영향이 무시할 수 있을 때만 유효하다.^[15] 페르미-디랙 분포는 최대 하나의 페르미온만이 각 가능한 상태를 점유할 수 있도록 허용하는 파울리 배타 원리를 사용하여 유도되었기 때문에, 결과적으로 $0 < \bar{n}_i < 1$ 이 된다.

상태 ''i''의 입자 수의 분산은 $\bar{n}_i$ 에 대한 위의 식으로부터 계산할 수 있다.^[17]^[18]

: $V(n_i) = k_\text{B}T \frac{\partial}{\partial \mu} \bar{n}_i = \bar{n}_i(1 - \bar{n}_i).$

이상적인 페르미 기체의 역온도(β), 화학퍼텐셜(μ), 연속 변수로서의 에너지 ε를 사용하여

: $f(\epsilon) = \frac{1}{\mathrm{e}^{\beta(\epsilon-\mu)} +1}$

와 같이 정의되는 함수를 '''페르미-디랙 분포 함수'''라고 한다. 페르미-디랙 분포 함수는 0부터 1사이의 값을 갖는다.

4. 페르미-디랙 분포

파울리 배타 원리에 따라, 페르미 기체의 통계적 분포는 맥스웰-볼츠만 분포를 따르는 고전적 이상 기체와 차이를 보인다. 이러한 페르미 기체의 통계를 '''페르미-디랙 통계'''라 한다.

상태 $i$ 에 놓여 있는 입자의 점유수는 다음과 같다.^[11]

: $n_i = \frac{g_i}{e^{(\epsilon_i-\mu) / k T} + 1}$

$n_i$ : 상태 $i$ 에 놓인 입자의 점유수
$g_i$ : 상태 $i$ 에서의 겹침
$\scriptstyle \epsilon_i$ : 상태 $i$ 에서의 에너지
$\scriptstyle \mu$ : 화학 퍼텐셜 (때때로 페르미 에너지라 불리며, $E_F$ 로 표시한다)
$k$ : 볼츠만 상수
$T$ : 절대온도

\scriptstyle \mu

가 페르미 에너지

E_F

이고

\scriptstyle g_i = 1

이면,

:

F(E) = \frac 1 {1 + e^{(E-E_F) / kT}} = \left(1 + e^{(E-E_F) / kT}\right)^{-1}

가 된다.

위의 수식을 '''페르미 함수'''라 부른다.

열역학적 평형 상태에 있는 동일한 페르미온 시스템에서 단일 입자 상태 의 평균 페르미온 수는 '''페르미-디랙(F-D) 분포'''로 주어진다.

:

\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1}

여기서 는 볼츠만 상수, 는 절대 온도, 는 단일 입자 상태 의 에너지, 그리고 는 총 화학 포텐셜이다.

절대 영도에서, 는 페르미온 당 포텐셜 에너지를 더한 페르미 에너지와 같다. 페르미-디랙 분포는 시스템의 페르미온 수가 충분히 커서 시스템에 페르미온 하나를 더 추가해도 에 미치는 영향이 무시할 수 있을 때만 유효하다.^[15] 페르미-디랙 분포는 최대 하나의 페르미온만이 각 가능한 상태를 점유할 수 있도록 허용하는 파울리 배타 원리를 사용하여 유도되었기 때문에, 결과적으로

0 < \bar{n}_i < 1

이 된다.

상태 ''i''의 입자 수의 분산은

\bar{n}_i

에 대한 위의 식으로부터 계산할 수 있다.^[17]^[18]

:

V(n_i) = k_\text{B}T \frac{\partial}{\partial \mu} \bar{n}_i = \bar{n}_i(1 - \bar{n}_i).

페르미-디랙 분포는 높은 온도와 낮은 입자 밀도의 극한에서 맥스웰-볼츠만 통계에 접근한다.

4. 1. 에너지에 따른 입자 분포

에너지에 따른 입자 분포는 페르미-디랙 분포에 상태 밀도를 곱하여 구할 수 있다. 단위 에너지 범위, 단위 부피당 페르미온의 평균 개수는 다음과 같다.^[20]^[21]

:

\bar{\mathcal{N}}(\varepsilon) = \frac{g(\varepsilon)}{e^{(\varepsilon - \mu) / k_\text{B} T} + 1}.

여기서

g(\varepsilon)

는 상태 밀도(단위 에너지 범위당 단위 부피당 상태의 수),

k_\text{B}

는 볼츠만 상수,

T

는 절대 온도,

\mu

는 총 화학 포텐셜이다.

이 식은 다음과 같이 유도된다. 에너지

\varepsilon_i

를 가진 페르미온의 평균 개수는 페르미-디랙 분포

\bar{n}_i

에 축퇴도(degeneracy)

g_i

(즉, 에너지

\varepsilon_i

를 갖는 상태의 수)를 곱하여 구할 수 있다.^[19]

:

\bar{n}(\varepsilon_i) =  \frac{g_i}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1}.

g_i \ge 2

일 때, 에너지

\varepsilon_i

가 같은 페르미온이 차지할 수 있는 상태가 하나 이상이므로

\bar{n}(\v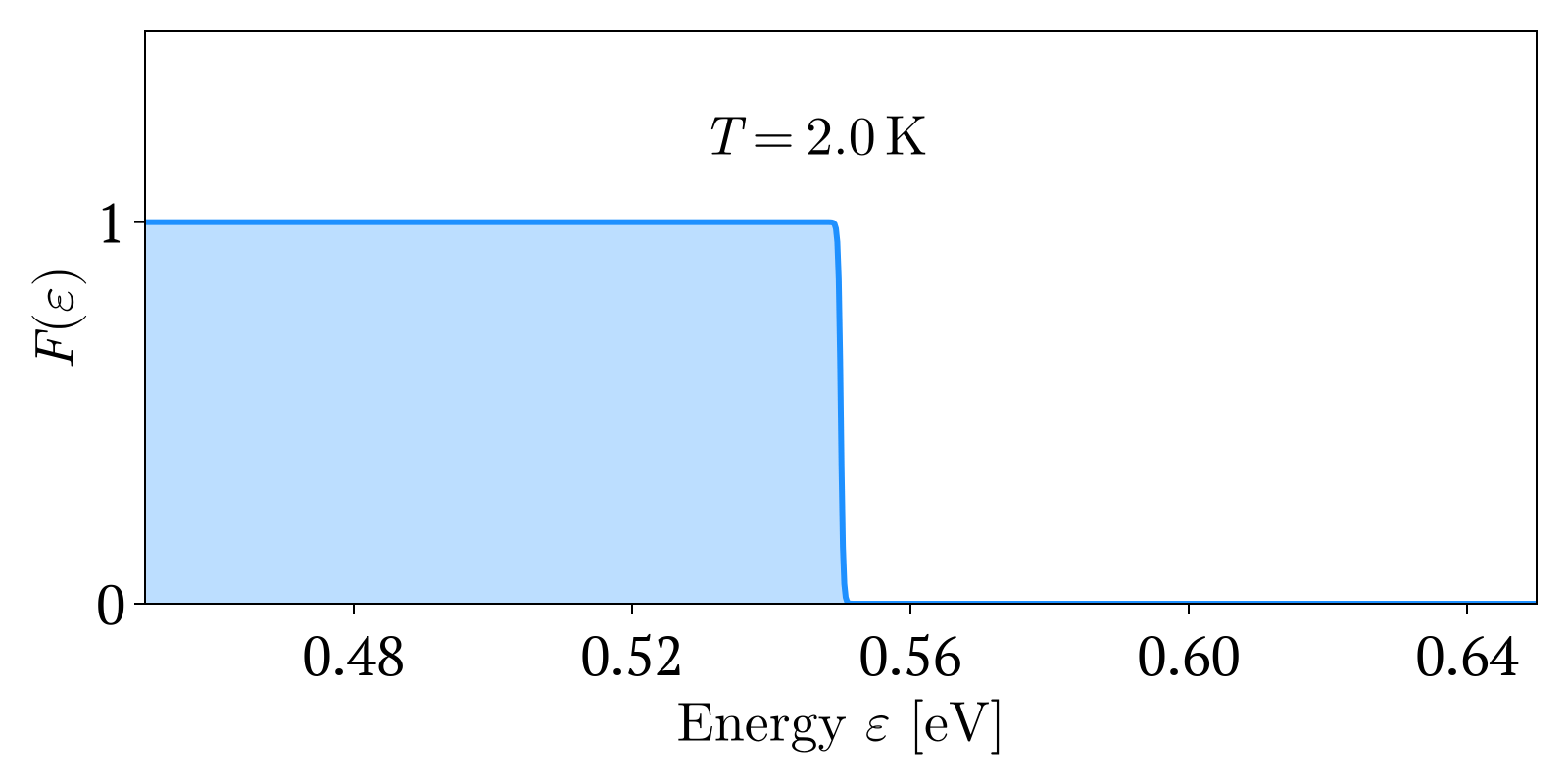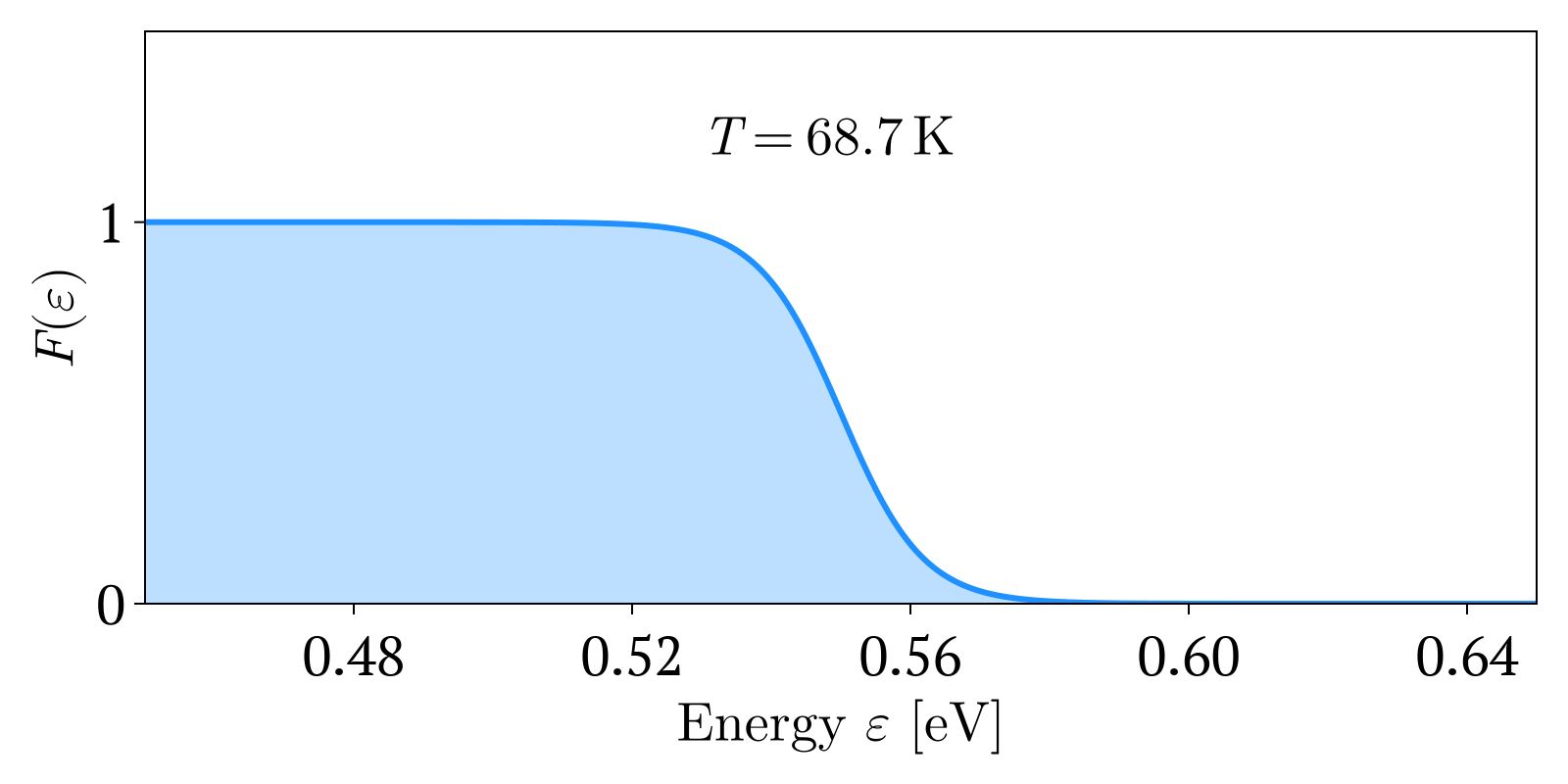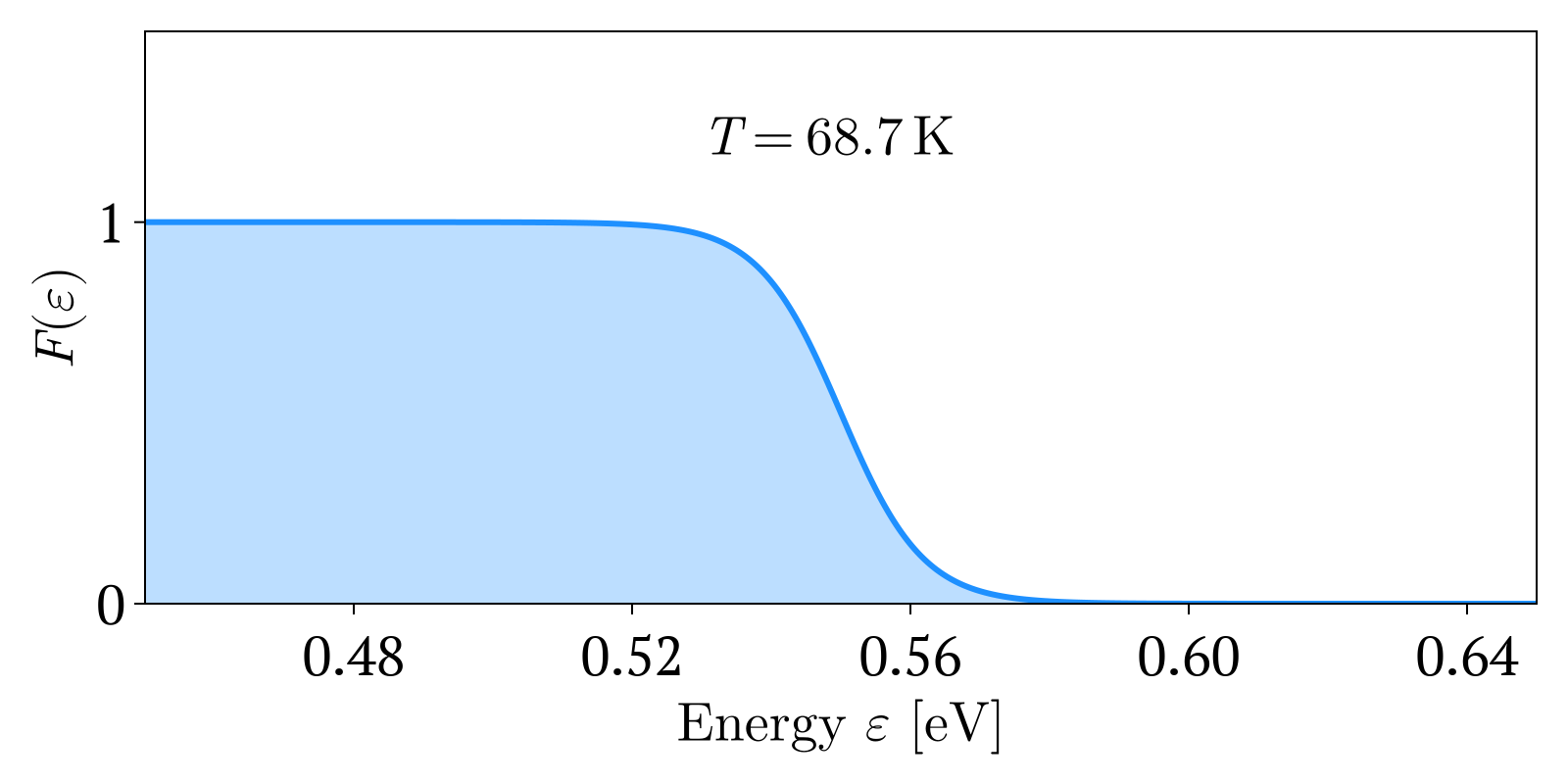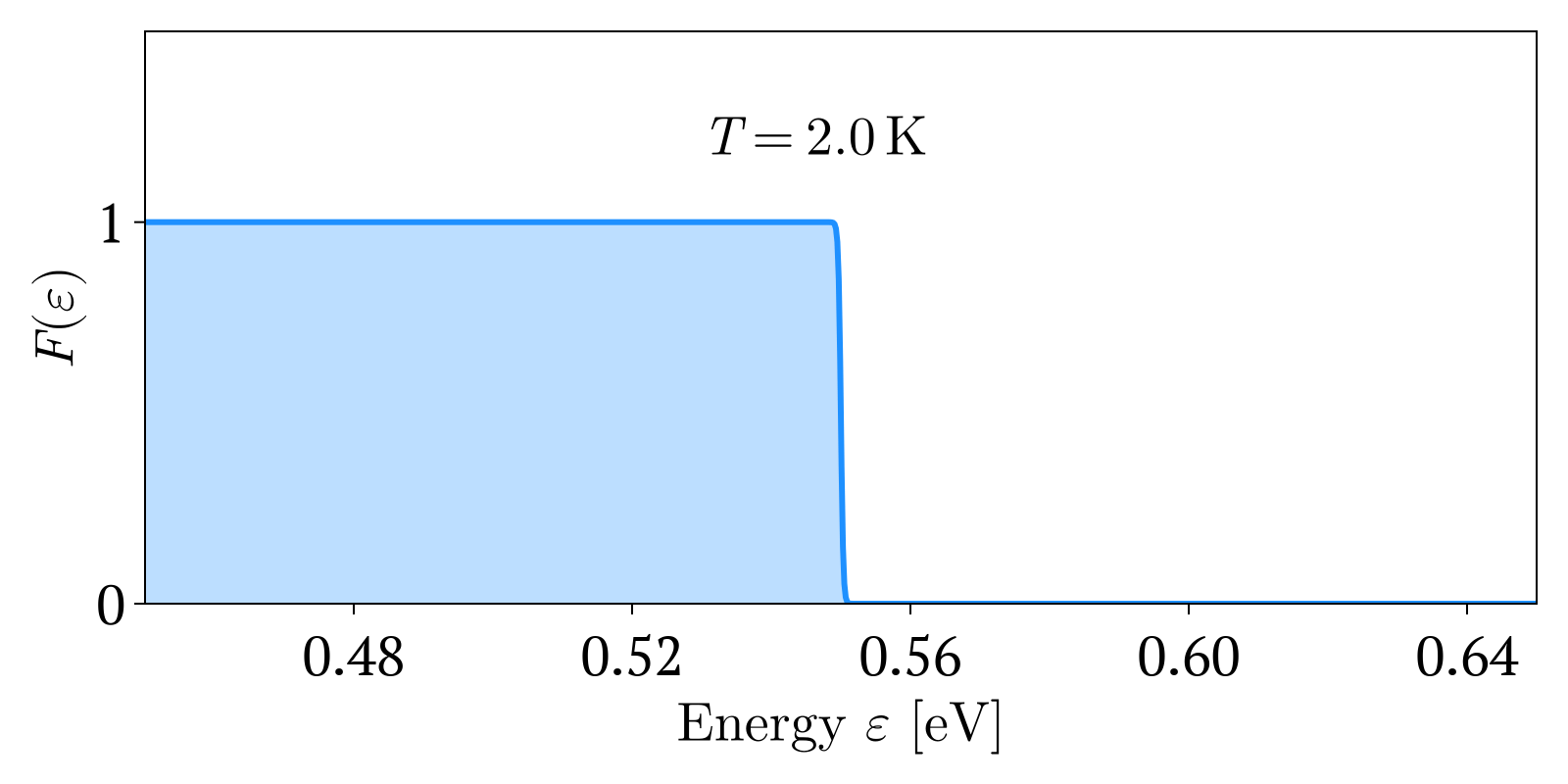arepsilon_i) > 1

이 될 수 있다.

양자수

\nu

로 지정되는 에너지 준위

\epsilon_\nu

를 점유하고 있는 페르미 입자의 개수

n_\nu

의 통계적 기댓값

\langle n_\nu \rangle

은 다음과 같다.^[32]^[33]

:

\langle n_\nu \rangle =f(\epsilon_\nu)\equiv \frac{1}{\mathrm{e}^{\beta(\epsilon_\nu-\mu)} +1}

이는 페르미 입자가 하나의 준위에 하나까지만 점유할 수 있다는 파울리의 배타 원리와 일치한다.

5. 양자 및 고전 영역

페르미-디랙 통계는 높은 온도와 낮은 입자 밀도의 극한에서 맥스웰-볼츠만 통계로 접근한다.^[11] 고전 영역은 입자의 농도가 평균 입자 간 간격 $\bar{R}$ 에 해당하고 이것이 입자의 평균 드 브로이 파장 $\bar{\lambda}$ 보다 훨씬 클 때 성립한다.

: $\bar{R} \gg \bar{\lambda} \approx \frac{h}{\sqrt{3mk_{\rm B}T}},$

여기서 $h$ 는 플랑크 상수이고, $m$ 은 입자의 질량이다.

일반적인 금속의 전도 전자는 T^영어 = 300 K(약 실온)에서 $\bar{R} \approx \bar{\lambda}/25$ 이기 때문에 고전 영역에 있지 않다. 이는 전자의 질량이 작고 금속 내 전도 전자의 농도가 높기 때문이다. 따라서 일반적인 금속의 전도 전자에는 페르미-디랙 통계가 필요하다.^[1]

백색왜성의 전자 또한 높은 온도(표면에서 일반적으로 T^영어 = ^[23])와 높은 전자 농도로 인해 고전적인 근사를 사용할 수 없으며, 페르미-디랙 통계가 필요하다.^[1]

6. 유도

페르미-디랙 분포는 큰 바른틀 앙상블, 바른틀 앙상블, 미시정준 앙상블을 사용하여 유도할 수 있다. 세 가지 앙상블 모두에서 유도된 페르미-디랙 분포는 다음과 같다.^[11]

: $\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1}$

여기서 $\bar{n}_i$ 는 상태 ''i''의 평균 입자 수, $\varepsilon_i$ 는 상태 ''i''의 에너지, $\mu$ 는 화학 퍼텐셜, $k_\text{B}$ 는 볼츠만 상수, ''T''는 절대 온도이다.

큰 바른틀 앙상블: 상호작용하지 않는 페르미온으로 구성된 양자계를 고려한다.^[24] 이 앙상블에서 계는 에너지와 입자를 저장소와 교환할 수 있으며, 온도와 화학 퍼텐셜은 저장소에 의해 고정된다. 각 단일 입자 준위는 저장소와 접촉하는 별도의 열역학적 계를 형성하며, 파울리 배타 원리에 의해 각 준위는 비어 있거나 하나의 입자로 채워질 수 있다.
바른틀 앙상블: 상호작용이 없는 N개의 동일한 페르미온으로 구성된 다체계를 고려한다. 페르미온 사이의 상호작용이 무시할 만큼 작기 때문에, 다체계의 에너지는 단일 입자 에너지의 합으로 표현될 수 있다. 파울리 배타 원리와 총 입자 수 제약 조건을 고려하여 점유수의 평균값을 계산하면 페르미-디랙 분포를 얻을 수 있다.
미시정준 앙상블: 라그랑주 승수를 사용하여 주어진 에너지와 입자 수 제약 조건 하에서 가능한 배열의 수를 최대화한다. 스털링 근사를 사용하면 페르미-디랙 점유수를 얻을 수 있다.

이 식에서 알 수 있듯이, 페르미-디랙 분포는 파울리 배타 원리에 따라 한 상태에 최대 하나의 페르미온만 존재할 수 있으므로,

0 < \bar{n}_i < 1

을 만족한다.

6. 1. 큰 바른틀 앙상블

상호작용하지 않는 페르미온 시스템에서, 각 단일 입자 준위는 저장소와 접촉하는 별도의 열역학적 계를 형성한다. 파울리 배타 원리에 의해 각 준위는 비어 있거나 하나의 입자로 채워질 수 있다.

페르미 기체의 큰 분배 함수는 다음과 같다.

:

Z _G ^{FD} = \prod _{k=1} ^\infty (1 + ze ^{-\beta \epsilon_k})

(

z =\exp(\beta\mu)

.

이에 따라, 상태

i

에 놓여 있는 입자의 점유수는 다음과 같다.

:

n_i = \frac{g_i}{e^{\epsilon_i-\mu \over k T} + 1}

$n_i$ : 상태 $i$ 에 놓인 입자의 점유수
$g_i$ : 상태 $i$ 에서의 겹침
$\scriptstyle \epsilon_i$ : 상태 $i$ 에서의 에너지
$\scriptstyle \mu$ : 화학 퍼텐셜(때때로 페르미 에너지라 불리며, $E_F$ 로 표시한다)
$k$ : 볼츠만 상수
$T$ : 절대온도

이 경우에

\scriptstyle \mu

가 페르미 에너지

E_F

이고

\scriptstyle g_i = 1

이면,

:

F(E) = \frac 1 {1 + e^ = \left(1 + e^{{E-E_F} \over kT}\right)^{-1}

가 된다.

위의 수식을 '''페르미 함수'''라 부른다.

열역학적 평형 상태에 있는 동일한 페르미온 시스템에서 단일 입자 상태 의 평균 페르미온 수는 '''페르미-디랙(F-D) 분포'''로 주어진다.^[11]

:

\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1}

여기서 는 볼츠만 상수, 는 절대 온도, 는 단일 입자 상태 의 에너지, 그리고 는 총 화학 포텐셜이다.

페르미-디랙 분포는 시스템의 페르미온 수가 충분히 커서 시스템에 페르미온 하나를 더 추가해도 에 미치는 영향이 무시할 수 있을 때만 유효하다.^[15] 페르미-디랙 분포는 최대 하나의 페르미온만이 각 가능한 상태를 점유할 수 있도록 허용하는 파울리 배타 원리를 사용하여 유도되었기 때문에, 결과적으로

0 < \bar{n}_i < 1

이 된다.

상태 ''i''의 입자 수의 분산은

\bar{n}_i

에 대한 위의 식으로부터 계산할 수 있다.^[17]^[18]

:

V(n_i) = k_\text{B}T \frac{\partial}{\partial \mu} \bar{n}_i = \bar{n}_i(1 - \bar{n}_i).

페르미-디랙 분포는 서로 상호작용하지 않는 페르미온의 양자계에만 적용되며, 그랜드 정준 앙상블에서 쉽게 유도할 수 있다.^[24] 이 앙상블에서 계는 에너지와 입자를 저장소(온도 ''T''와 화학 포텐셜 ''μ''는 저장소에 의해 고정됨)와 교환할 수 있다.

상호 작용하지 않는다는 특성 때문에, 각각의 이용 가능한 단일 입자 준위(에너지 준위 ''ϵ'')는 저장소와 접촉하는 별도의 열역학적 계를 형성한다. 다시 말해, 각 단일 입자 준위는 별도의 아주 작은 그랜드 정준 앙상블이다. 파울리 배타 원리에 의해, 단일 입자 준위에는 두 가지의 미시 상태만 존재한다. 입자가 없는 경우(에너지 ''E'' = 0) 또는 입자가 하나 있는 경우(에너지 ''E'' = ''ε'')이다. 따라서 그 단일 입자 준위에 대한 분배 함수는 단 두 개의 항만을 가진다.

:

\begin{align}\mathcal Z &= \exp\big(0(\mu - \varepsilon)/k_{\rm B} T\big) + \exp\big(1(\mu - \varepsilon)/k_{\rm B} T\big) \\&= 1 + \exp\big((\mu - \varepsilon)/k_{\rm B} T\big),\end{align}

그리고 그 단일 입자 준위 하위 상태에 대한 평균 입자 수는 다음과 같이 주어진다.

:

\langle N\rangle = k_{\rm B} T \frac{1}{\mathcal Z} \left(\frac{\partial \mathcal Z}{\partial \mu}\right)_{V,T} = \frac{1}{\exp\big((\varepsilon-\mu)/k_{\rm B} T\big) + 1}.

이 결과는 각 단일 입자 준위에 적용되므로, 계의 전체 상태에 대한 페르미-디랙 분포를 제공한다.^[24]

입자 수의 분산(열적 요동)도 유도할 수 있다(입자 수는 간단한 베르누이 분포를 따른다).

:

\big\langle (\Delta N)^2 \big\rangle = k_{\rm B} T \left(\frac{d\langle N\rangle}{d\mu}\right)_{V,T} = \langle N\rangle \big(1 - \langle N\rangle\big).

양자수 로 지정되는 에너지 준위 }}를 점유하고 있는 페르미 입자의 개수 }}의 통계적 기댓값 ⟩}}을 생각하자. 점유수는 거시적인 관측량이 아니지만, 기댓값을 구해두면 양자 이상 기체 등의 해석에 편리하다.^[32] ⟩}}을 그랜드 카노니컬 분포로 구하면 다음과 같다.^[33]

:

\langle n_\nu \rangle =f(\epsilon_\nu)\equiv \frac{1}{\mathrm{e}^{\beta(\epsilon_\nu-\mu)} +1}

6. 2. 바른틀 앙상블

상호 작용이 없는 N개의 동일한 페르미온으로 구성된 다체계를 고려한다. 페르미온 사이의 상호 작용이 무시할 만큼 작기 때문에, 다체계의 상태 R의 에너지

E_R

는 단일 입자 에너지의 합으로 표현될 수 있다.

:

E_R = \sum_{r} n_r \varepsilon_r,

여기서

n_r

은 점유수이며, 에너지

\varepsilon_r

를 갖는 단일 입자 상태

r

에 있는 입자의 수이다. 합은 모든 가능한 단일 입자 상태

r

에 대해 이루어진다.

다체계가 상태

R

에 있을 확률은 정규화된 정준 분포에 의해 주어진다.^[26]

:

P_R = \frac{e^{-\beta E_R}}{\displaystyle\sum_{R'} e^{-\beta E_{R'}}},

여기서

\beta = 1/k_\text{B}T

,

e^{-\beta E_R}

는 볼츠만 인자이며, 합은 다체계의 모든 가능한 상태

R'

에 대해 이루어진다. 점유수

n_i

의 평균값은 다음과 같다.^[1]

:

\bar{n}_i = \sum_R n_i P_R.

다체계의 상태

R

는 단일 입자 상태의 입자 점유, 즉

n_1, n_2, \ldots

를 지정함으로써 지정될 수 있다.

:

P_R = P_{n_1, n_2, \ldots} = \frac{e^{-\beta(n_1 \varepsilon_1 + n_2 \varepsilon_2 + \cdots)}}{\displaystyle\sum_{n_1',n_2',\ldots} e^{-\beta(n_1' \varepsilon_1 + n_2' \varepsilon_2 + \cdots)}},

\bar{n}_i

에 대한 방정식은 다음과 같다.

:

\begin{align}\bar{n}_i &= \sum_{n_1,n_2,\dots} n_i P_{n_1, n_2, \dots} \\&= \frac{\displaystyle\sum_{n_1,n_2,\dots} n_i e^{-\beta(n_1\varepsilon_1 + n_2\varepsilon_2 + \cdots + n_i\varepsilon_i + \cdots)}}{\displaystyle\sum_{n_1,n_2,\dots} e^{-\beta(n_1\varepsilon_1 + n_2\varepsilon_2 + \cdots + n_i\varepsilon_i + \cdots)}},\end{align}

위 식에서 합은 파울리 배타 원리를 따르는

n_1, n_2, \ldots

값의 모든 조합에 대해 이루어지며, 각

r

에 대해

n_r = 0

또는

1

이다. 또한,

n_1, n_2, \ldots

값의 각 조합은 입자의 총 수가

N

이라는 제약 조건을 만족한다.

:

\sum_r n_r = N.

합을 재배열하면 다음과 같다.

:

\bar{n}_i = \frac{\displaystyle\sum_{n_i=0}^1 n_i e^{-\beta(n_i\varepsilon_i)} \sideset{}{^{(i)}}\sum_{n_1,n_2,\dots} e^{-\beta(n_1\varepsilon_1+n_2\varepsilon_2+\cdots)}}{\displaystyle\sum_{n_i=0}^1 e^{-\beta(n_i\varepsilon_i)} \sideset{}{^{(i)}}\sum_{n_1,n_2,\dots} e^{-\beta(n_1\varepsilon_1 + n_2\varepsilon_2 + \cdots)}},

여기서 합 기호의 위첨자

(i)

는 합이

n_i

에 대해 이루어지지 않으며, 합과 관련된 입자의 총 수가

N_i = N - n_i

라는 제약 조건을 따른다는 것을 나타낸다.

\textstyle\sum^{(i)}

가

N_i

제약 조건을 통해 여전히

n_i

에 의존하므로,

n_i = 0

이면

\textstyle\sum^{(i)}

는

N_i = N

으로 평가되고,

n_i = 1

이면

\textstyle\sum^{(i)}

는

N_i = N - 1

으로 평가된다. 표기법을 단순화하고,

\textstyle\sum^{(i)}

가

N - n_i

를 통해 여전히

n_i

에 의존한다는 것을 명확히 하기 위해 다음과 같이 정의한다.

:

Z_i(N - n_i) \equiv \sideset{}{^{(i)}}\sum_{n_1,n_2,\ldots} e^{-\beta(n_1\varepsilon_1+n_2\varepsilon_2+\cdots)},

그러면

\bar{n}_i

에 대한 이전 식은

Z_i

로 다시 작성하고 평가할 수 있다.

:

\begin{align}\bar{n}_i &= \frac{\displaystyle\sum_{n_i=0}^1 n_i e^{-\beta(n_i\varepsilon_i)} \, Z_i(N - n_i)}{\displaystyle\sum_{n_i=0}^1 e^{-\beta(n_i\varepsilon_i)} \, Z_i(N - n_i)} \\&= \frac{0 + e^{-\beta\varepsilon_i} \, Z_i(N - 1)}{Z_i(N) + e^{-\beta\varepsilon_i} \, Z_i(N - 1)} \\&= \frac{1}{[Z_i(N)/Z_i(N - 1)] \, e^{\beta\varepsilon_i}+1}.\end{align}

Z_i(N)/Z_i(N - 1)

를 대체할 식을 찾기 위해 다음 근사를 사용한다.^[27]

:

\begin{align}\ln Z_i(N - 1) &\simeq \ln Z_i(N) - \frac{\partial \ln Z_i(N)}{\partial N } \\&= \ln Z_i(N) - \alpha_i,\end{align}

여기서

\alpha_i \equiv \frac{\partial \ln Z_i(N)}{\partial N}

이다.

입자의 수

N

가 충분히 커서 계에 입자가 추가될 때 화학 퍼텐셜

\mu

의 변화가 매우 작다면,

\alpha_i \simeq - \mu / k_\text{B}T

이다.^[28] 양변에 지수 함수를 적용하고,

\alpha_i

를 대입하고 재배열하면,

:

Z_i(N) / Z_i(N - 1) =  e^{-\mu / k_\text{B}T}.

위의 식을

\bar{n}_i

에 대한 방정식에 대입하고,

1/k_\text{B}T

를

\beta

로 대체하기 위해 이전에 정의된

\beta

를 사용하면 페르미-디랙 분포를 얻는다.

:

\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu)/k_\text{B}T} + 1}.

6. 3. 미시정준 앙상블

Fermi–Dirac distribution^영어는 라그랑주 승수를 사용하여 주어진 에너지와 입자 수 제약 조건 하에서 가능한 배열의 수를 최대화하여 유도할 수 있다. 스털링 근사를 사용하면, 다음과 같은 페르미-디랙 점유수를 얻을 수 있다.^[11]

:

\bar{n}_i = \frac{1}{e^{(\varepsilon_i - \mu) / k_\text{B} T} + 1}

여기서 는 볼츠만 상수, 는 절대 온도, 는 단일 입자 상태 의 에너지, 는 총 화학 포텐셜이다.

이 식에서 알 수 있듯이, 페르미-디랙 분포는 파울리 배타 원리에 따라 한 상태에 최대 하나의 페르미온만 존재할 수 있으므로,

0 < \bar{n}_i < 1

을 만족한다.

양자수 로 지정되는 에너지 준위 를 점유하고 있는 페르미 입자의 개수 의 통계적 기댓값 은 다음과 같이 그랜드 카노니컬 분포로 구할 수 있다.^[32]^[33]

:

\langle n_\nu \rangle =f(\epsilon_\nu)\equiv \frac{1}{\mathrm{e}^{\beta(\epsilon_\nu-\mu)} +1}

이는 페르미 분포 함수에 해당 준위의 에너지 를 대입하면 점유수의 기댓값을 얻을 수 있음을 의미한다. 페르미 분포 함수가 0부터 1 사이의 값만 가질 수 있다는 점은, 파울리 배타 원리에 따라 페르미 입자가 하나의 준위에 하나까지만 점유할 수 있다는 사실과 일치한다.

7. 응용

페르미-디랙 분포 함수는 준위가 존재하지 않는 에너지에서도 고려될 수 있다. 하지만 이 경우, 페르미-디랙 분포 함수의 값은 점유수로서의 의미를 가지지 않는다.

예를 들어, 반도체나 절연체 내 전자의 경우, 페르미 에너지가 에너지 갭 내에 존재하기 때문에 에너지 갭까지 확장한 페르미-디랙 분포 함수를 고려하는 경우가 많다.^[1]

참조

_[1] 서적 (제목 없음)
_[2] 논문 Sulla quantizzazione del gas perfetto monoatomico
_[3] 논문 On the Theory of Quantum Mechanics
_[4] 논문 History of Science: The Puzzle of the Bohr–Heisenberg Copenhagen Meeting https://web.archive.[...] 2000-05-19
_[5] 논문 Jordan, Pauli, Politics, Brecht and a variable gravitational constant
_[6] 논문 Aber Jordan war der Erste
_[7] 서적 Principles of Quantum Mechanics https://books.google[...] Oxford University Press
_[8] 논문 On dense matter 1926-12
_[9] 논문 Zur Elektronentheorie der Metalle 1927-10-14
_[10] 논문 Electron Emission in Intense Electric Fields 1928-05-01
_[11] harvnb
_[12] 서적 Statistical Physics: Volume 5 Elsevier
_[13] harvnb
_[14] 서적 Thermal Physics https://books.google[...] W. H. Freeman
_[15] harvnb
_[16] harvnb
_[17] 서적 Quantum Photonics, 2nd edition https://www.springer[...] Springer 2020
_[18] harv
_[19] 서적 Principles of Modern Physics https://archive.org/[...] McGraw-Hill
_[20] harvnb
_[21] 논문
_[22] 논문
_[23] 웹사이트 Ask an Astrophysicist http://imagine.gsfc.[...] NASA Goddard Space Flight Center
_[24] 서적 Statistical Mechanics PHI Learning Pvt. Ltd.
_[25] 저널 Observation of Anderson Localization in an Electron Gas
_[26] 논문
_[27] 웹사이트 #추정 Derivative#Definition via difference quotients
_[28] 논문
_[29] 서적 Basics of Statistical Physics World Scientific
_[30] 논문
_[31] 웹사이트 物性物理学入門 (進化する教科書 Wiki) http://utht.t.u-toky[...] 東京大学　知の構造化センター 2019-11
_[32] 서적 統計力学II 培風館
_[33] 웹사이트 確率論及統計論第IX章量子統計力学 §75. Fermi統計法，Bose統計法 http://ebsa.ism.ac.j[...] 2019-11

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com