특수 상대성이론

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

특수 상대성 이론은 1905년 알베르트 아인슈타인이 발표한 이론으로, 시간과 공간의 상대성을 다룬다. 이 이론은 빛의 속도가 모든 관찰자에게 일정하다는 가정과 상대성 원리에 기반하며, 이를 통해 시간 팽창, 길이 수축, 질량-에너지 등가성 등의 예측을 한다. 특수 상대성 이론은 고전 역학의 한계를 극복하고, 전자기학 및 다른 물리학 분야와 조화를 이루며, 로렌츠 변환, 민코프스키 시공간, 4차원 벡터 등의 수학적 도구를 사용한다. 실험적으로도 여러 차례 검증되었으며, 현대 물리학의 중요한 기반이 된다.

더 읽어볼만한 페이지

특수 상대성이론 - 상대론적 양자화학
상대론적 양자화학은 상대성이론을 적용하여 원자와 분자의 구조 및 성질을 연구하는 화학 분야로, 특히 무거운 원소에서 전자의 속도가 빨라 상대론적 효과가 두드러지게 나타나 원자 크기, 결합 에너지, 스펙트럼 등에 영향을 미치며, 금의 색, 수은의 낮은 녹는점 등 여러 현상을 설명하는 데 필요하다.
특수 상대성이론 - 동시성의 상대성
동시성의 상대성은 상대적으로 움직이는 기준계에서 공간적으로 분리된 두 사건의 시간 판단이 달라지는 현상으로, 아인슈타인의 특수 상대성 이론에서 절대적인 동시성이 존재하지 않음을 나타내는 핵심 개념이다.
알베르트 아인슈타인 - 광전 효과
광전 효과는 빛이 물질에 닿을 때 전자가 방출되는 현상으로, 빛 에너지가 광자라는 덩어리로 양자화되어 있고, 아인슈타인의 광양자 가설로 설명되며, 다양한 기술에 응용되지만 문제도 야기한다.
알베르트 아인슈타인 - 보스-아인슈타인 응축
보스-아인슈타인 응축은 극저온에서 보존 입자들이 가장 낮은 에너지 상태로 응축되어 새로운 물질 상을 형성하는 현상으로, 1995년 실험적으로 관측되어 노벨 물리학상을 수상했으며, 초유체 현상과 같은 특이한 양자 현상을 보이며 다양한 분야에서 응용 가능성을 가진다.
물리학 개념 - 절연체
절연체는 전기 전도성을 막아 전기의 흐름을 제어하고 안전을 확보하며, 밴드 이론에 따라 큰 띠틈을 가져 외부 전압이 띠틈을 넘어서면 절연 파괴가 발생하며, 유리에서 세라믹, 고분자 복합 재료 등으로 제작되어 전선, 케이블 등 다양한 분야에 사용된다.
물리학 개념 - 전기 전도체
전기 전도체는 전기를 잘 통하는 물질로, 금속, 전해질, 초전도체, 반도체 등이 있으며, 구리, 은, 알루미늄 등 다양한 재료가 전선 등에 사용된다.

특수 상대성이론
일반 정보
시공간을 도표로 나타낸 세계선
주제
분야	물리학
하위 분야	상대성이론
역사
발표	1905년
발표자	알베르트 아인슈타인
주요 내용
핵심 개념	상대성 원리 광속 불변의 원리
기본 가정	모든 물리 법칙은 모든 관성 기준계에서 동일하다. 진공에서의 광속은 광원의 운동 상태와 무관하게 모든 관성 기준계에서 동일하다.
주요 결과	시간 지연 길이 수축 질량-에너지 등가
관련 개념	시공간
관련 인물
주요 인물	알베르트 아인슈타인 헨드릭 로런츠 앙리 푸앵카레 헤르만 민코프스키
관련 이론
선행 이론	고전역학
후속 이론	일반 상대성이론
응용
활용 분야	입자물리학 핵물리학 천체물리학 GPS

2. 역사적 배경

전자기학이 설명하는 바에 따르면, 관측자 또는 관측 대상의 관성 운동을 수반하는 실험 결과는 뉴턴 역학과 모순될 수 있다. 알베르트 아인슈타인은 1905년에 발표한 논문에서 특수 상대성 이론을 발표하고, 전자기적 현상까지 포함한 관성계 사이의 등가성을 공리로 하여 다음과 같은 결과를 보였다.

어떤 관측자에 대한 시간 경과와 공간 이동 속도의 관계, 상대 운동하는 좌표계에서의 시간 경과, 상대 운동하는 좌표계에서의 "로렌츠 수축"이 공간 형태에 미치는 효과
질량과 에너지의 등가성

특수 상대성 이론은 뉴턴 역학으로 설명할 수 없었던 사항들을 모두 설명하며, 특히 빛의 속도에 가까운 물체의 역학적 거동에 대한 실험 사실과 잘 부합한다. 이로 인해 상대성 이론은 현대 물리학에서 중요한 체계로 지지받고 있다. 정성적으로는 물체의 에너지 방출·흡수에 따른 질량 감소·증가가 확인된다.

특수 상대성 이론은 일반 상대성 이론의 특수한 경우이다. 일반 상대성 이론은 중력 등 외력(또는 관성력)이 있는 비관성계를 포함하는 반면, 특수 상대성 이론은 관성력이 작용하지 않는 관성계를 다룬다. 관성계는 모든 좌표계의 특수한 경우이므로, "특수" 상대성 이론이라고 부른다.

2. 1. 특수 상대성 이론의 등장 배경

맥스웰 방정식에 따르면, 전자기파는 특정한 속도를 지닌다. 1905년 이전 학자들은 전자기파가 에테르라는 매질 위에서 전파되며, 전자기파의 속도는 에테르에 대한 상대적인 속도라고 해석하였다.^[162] 그러나 1887년 마이컬슨-몰리 실험을 통해 에테르의 존재를 증명하지 못하였다. 1889년 조지 프랜시스 피츠제럴드는 이를 설명하기 위해 물체가 높은 속도로 움직일 때 그 길이가 축소된다고 제안하였고,^[162] 헨드릭 로런츠^[163]^[164]^[165]와 조지프 라모어^[166]는 이에 기반하여 오늘날 로런츠 변환이라 불리는 변환을 도입하였다. 그러나 이들은 이 효과를 에테르에 의한 전기적 효과로 취급하였다.

1902년 앙리 푸앵카레는 《과학과 가설》에서 공간, 시간, 동시성의 상대성에 대한 고찰을 하였고, 상대성 원리의 반례는 관찰될 수 없으며 "에테르가 존재하지 않을 수도 있다"는 의견을 펼쳤다. 하지만 동시에 비유클리드 기하학과 관련된 여러 언급과 함께 "에테르 개념을 뒷받침하는 몇 가지 주장"도 하였다.

1905년 6월 앙리 푸앵카레는 로런츠의 작업에 존재하던 논리상의 간극을 없애는 논문을 제출하였다. 그는 로런츠의 전기동역학 방정식이 완전히 로런츠-공변이 아님을 보였다. 그는 그 변환의 군론적 성질을 밝혔고, 전하 밀도와 전류 밀도에 대한 로런츠 변환 공식을 수정하였다. 푸앵카레는 이때 "로런츠 변환"이라는 용어를 처음으로 사용하였고, 오늘날 사용되는 대칭적 형식을 제시하였다. 그는 길이 수축을 설명하고 전자의 안정성을 보장하는, "푸앵카레 응력"이라 부른 비-전기적 결합력을 도입하였다. 그는 비-전기적 힘에까지 로런츠-불변성을 확장하여 중력파를 포함한 로런츠-불변 중력 모델을 묘사하였다.

결국 푸앵카레는 (아인슈타인과는 독립적으로) 6월 논문을 상당히 확장하였다. 그는 이 변환들이 최소 작용의 원리에서 도출됨을 보였고 푸앵카레 응력의 몇 가지 성질을 밝혔다. 로런츠 군이라는 용어를 만들었으며, 로런츠 변환의 군론적 성질을 더욱 자세히 증명하여,

\scriptstyle{x^2+y^2+z^2-c^2t^2}

값이 로런츠 변환에 대해 불변임을 보였다. 중력 이론을 개발하는 과정에서, 로런츠 변환이 단지 사차원 공간에서의 회전에 불과하다는 것을 보였으며, 사차원 벡터를 사용하였다.

알베르트 아인슈타인은 1905년 논문 〈움직이는 물체의 전기역학에 대하여〉(Zur Elektrodynamik bewegter Körper^de)^[167]에서 로런츠 변환 및 관련 공식들이 시공간의 근본적인 성질임을 두 개의 기본 가정 아래 증명하였다. 같은 해 아인슈타인은 질량-에너지 등가성에 대한 논문 《물체의 관성이 그 에너지 함량에 관계있는가?》^[168]를 발표하였다. 이 두 논문은 오늘날 특수 상대성 이론의 시초로 평가된다.

이후 독일의 수학자 헤르만 민코프스키는 물리적 장소를 나타내는 3차원과 시간을 나타내는 1차원을 통합하여 비유클리드 기하학적 4차원 공간인 민코프스키 시공간을 제안하였고, 세계선(world line), 고유시간(proper time) 등을 도입하였다. 민코프스키는 앞으로 시간과 장소를 따로 보는 기존 관점은 사라지고 오직 4차원 통일체만이 본질적으로 남을 것이라고 하였다. 민코프스키의 주장이 알려진 초창기에, 알베르트 아인슈타인은 민코프스키 공간이라는 추상적 구조를 시공간 묘사에 쓰는 것에 대해 회의적이었으나, 일반 상대성 이론을 연구하며 결국 일반 상대성 이론의 시공간은 휘어진 민코프스키 공간으로 묘사됨을 알고는 민코프스키의 생각이 필수적임을 깨달았다고 한다. 민코프스키 시공간은 양자장론이 발달할 수 있는 초석 가운데 하나가 되었다.

2. 2. 주요 기여자들

알베르트 아인슈타인은 1905년 논문 〈움직이는 물체의 전기역학에 대하여〉(Zur Elektrodynamik bewegter Körper^de)^[167]에서 로런츠 변환 및 관련된 공식들이 시공간의 근본적인 성질임을 두 개의 기본 가정 아래 증명하였다. 같은 해에 질량-에너지 등가성에 대한 논문 《물체의 관성이 그 에너지 함량에 관계있는가?》^[168]를 발표하였다. 이 두 논문은 오늘날 특수 상대성 이론의 시초로 평가된다.

헨드릭 로런츠^[163]^[164]^[165]는 오늘날 로런츠 변환이라고 불리는 변환을 도입하였다. 그러나 로런츠는 이 효과들을 에테르에 의한 전기적 효과라고 취급하였다.

앙리 푸앵카레는 1902년 《과학과 가설》에서 공간, 시간, 동시성의 상대성에 대한 고찰을 하였고, 상대성 원리의 반례는 관찰될 수 없으며 "에테르가 존재하지 않을 수도 있다"는 의견을 펼쳤다. 하지만 비유클리드 기하학과 관련된 언급과 함께 "에테르 개념을 뒷받침하는 주장"도 하였다. 1905년 6월, 푸앵카레는 로런츠의 작업에 존재하던 논리상의 간극을 없애는 논문을 제출하였다. 그는 로런츠의 전기동역학 방정식이 완전히 로런츠-공변이 아님을 보이고, 변환의 군론적 성질을 밝혔다. 또한 전하 밀도와 전류 밀도에 대한 로런츠 변환 공식을 수정하였으며, "로런츠 변환"이라는 용어를 처음으로 사용하고 오늘날 사용되는 대칭적 형식을 제시하였다.

헤르만 민코프스키는 물리적 장소를 나타내는 3차원과 시간을 나타내는 1차원을 통합하여 비유클리드 기하학적 4차원 공간인 민코프스키 시공간을 제안하고, 세계선(world line), 고유시간(proper time) 등을 도입하였다.

3. 특수 상대성 이론의 기본 원리

특수 상대성 이론은 기본적으로 다음 두 가지 가정을 바탕으로 한다.^[27]

1. 관성계는 동등하다.

2. 진공에서의 빛의 속력은 어느 관성계에서나 일정하다.

첫 번째 가정은 어느 관성계(속도가 일정한 계)에서든 물리 법칙은 동등하게 적용된다는 뜻이다. 예를 들어 땅에서 볼 때 시속 100km로 가는 차가 같은 방향으로 시속 50km로 가는 기차 안에서는 시속 50km로 이동하는 것처럼 보이지만, 이 구체적인 값의 차이와는 달리 두 관성계 모두에서 관성의 법칙, 운동량 보존의 법칙, 에너지 보존의 법칙 등 물리 법칙은 동등하게 적용된다. 모든 관성계에 적용되는 물리 법칙이 같으므로 물리 법칙의 차이를 이용해서 두 관성계를 구분할 수 없다. 따라서 두 관성계는 동등하고 어느 하나가 다른 하나에 비해 더 '진정한 기준관성계'에 가깝지 않다.

두 번째 가정은 어느 관성계에서 관측하든지 빛의 속도는 동일하게 관측된다는 것이다. 기존의 갈릴레오 변환에서는 관성계 A에 대해 ''u''의 속도로 움직이는 관성계 B에서 관측한 어느 물체의 속도가 ''v''일 때 관성계 A에서 관측한 물체의 속도는 ''u''+''v''이다. 하지만 이 변환은 빛에 대해서는 적용되지 않는다. 즉, 관성계 A에 대해 ''u''의 속도로 움직이는 관성계 B에서 관측한 빛의 속력이 ''c''일 때 관성계 A에서 관측한 빛의 속력은 ''u''+''c''가 아닌 ''c''이다.

상대성 원리는 물리 법칙이 각 관성 좌표계에서 동일한 형태를 갖는다는 것을 나타낸다. 19세기 후반, 전자기파의 존재는 일부 물리학자들로 하여금 우주가 "에테르"라는 물질로 가득 차 있다고 가정하게 했다. 그들은 이 물질이 파동 또는 진동이 전파되는 매체 역할을 할 것이라고 생각했다. 에테르는 모든 속도를 측정할 수 있는 절대적인 기준 틀로 여겨졌으며, 지구 또는 다른 고정된 기준점에 대해 고정되고 움직이지 않는 것으로 간주될 수 있었다. 에테르는 전자기파를 지원할 만큼 충분히 탄성이 있어야 하는 동시에, 그러한 파동이 물질과 상호 작용할 수 있지만, 그 속을 통과하는 물체에는 저항을 제공하지 않아야 했다. 1887년 마이컬슨-몰리 실험을 포함한 다양한 실험 결과는 에테르가 존재하지 않는다는 것을 보여줌으로써 특수 상대성 이론으로 이어졌다.^[27] 아인슈타인의 해결책은 에테르와 절대적인 정지 상태 개념을 폐기하는 것이었다. 상대성 이론에서, 균일한 운동을 하는 모든 기준 틀은 동일한 물리 법칙을 관찰할 것이다. 특히, 진공에서의 빛의 속도는 서로 다른 (하지만 일정한) 속도로 움직이는 여러 시스템에 의해 측정되는 경우에도 항상 ''c''로 측정된다.

아인슈타인의 원래 논문에서는 다음 두 가지 사항을 지도 원리(전제 조건, 공리)로 하여 특수 상대성 이론의 물리학적 틀이 전개되었다.

특수 상대성 원리: 물리 법칙에 관해 모든 관성계는 대등하다. 즉, 모든 관성계에서 물리 법칙을 기술하는 운동 방정식은 그 형식이 불변하다.
광속 불변의 원리: 진공 중의 빛의 속도는 광원의 운동 상태와 무관하다.

광속 불변의 원리는 상대성 이론 구축에 필요한 최소한의 요건을 맥스웰 이론에서 추출한 것이며, 물리적으로 새로운 주장을 포함하는 것은 특수 상대성 원리뿐이다.

현대에는 광속 불변의 원리를 다음과 같이 표현하기도 한다.

> "진공 중의 빛의 속도는 일정하며, 어떤 관성계에서 측정해도 같은 값을 가진다."

하지만, 이것은 원래 특수 상대성 원리와 (원 논문의) 광속 불변의 원리에서 연역되는 내용이다. 어떤 관성계 S와, S에 대해 일정 방향으로 속도 v로 운동하는 관성계 S'을 생각할 때, 광속 불변의 원리에 따르면 관성계 S에서는 모든 빛의 속도가 광원의 운동 상태에 관계없이 일정한 값 c를 가진다. 마찬가지로, 관성계 S'에서는 모든 빛의 속도가 c'로 관측된다고 한다. 이때, 관성계 간의 등가성을 주장하는 특수 상대성 원리에 따르면, c' = c임을 알 수 있다.^[136] 즉, "모든 관성계에서, 모든 광원으로부터의 빛의 속도는 일정값 c이다"라는 주장은, 아인슈타인의 원 논문의 두 지도 원리로부터 유도 가능하다. 이처럼, 빛의 속도와 같은 물리 상수^[137]는 모든 관성계에서 동일한 값을 가진다는 것을 특수 상대성 원리는 함의하고 있다.

4. 로런츠 변환

로런츠 변환은 특수 상대성 이론에서 서로 다른 관성 좌표계 간의 좌표 변환을 나타내는 수학적 도구이다. 갈릴레이 변환과 달리, 로런츠 변환은 시간과 공간을 서로 얽혀 있는 것으로 취급하며, 광속 불변 원리를 만족시킨다.

그림 2–1. 소성계(primed system)는 소성되지 않은 계(unprimed system)에 대해 ''x'' 축을 따라 일정한 속도 ''v''로 움직이고 있으며, 소성되지 않은 계에 정지해 있는 관찰자의 관점에서 본 그림이다. 상대성 원리에 따르면, 소성계에 정지해 있는 관찰자는 기록하는 속도가 −''v''가 된다는 점을 제외하면 이와 유사한 구성을 보게 된다.

관성 좌표계는 3개의 공간 축을 따라 위치를 측정할 수 있으며 (따라서 정지 또는 일정한 속도) 운동(가속도)의 변화를 겪지 않는 공간에서의 관찰 관점을 의미한다. 또한, 관성 좌표계는 "시계"(균일한 주기를 가진 모든 기준 장치)를 사용하여 사건의 시간을 측정할 수 있다.

사건은 관성 좌표계에 따라 공간에서 단일하고 고유한 순간과 위치를 할당할 수 있는 발생을 의미한다. 즉, 시공간의 "점"이다. 상대성 이론에서 빛의 속도는 관성 좌표계에 관계없이 일정하므로 빛의 펄스를 사용하여 거리를 명확하게 측정하고 사건이 발생한 시간을 시계에 참조할 수 있다. 사건이 발생한 후 빛이 시계에 도달하는 데 시간이 걸리더라도 가능하다.

마이컬슨-몰리 실험에서 두 사람은 지구의 공전에 주목하여 실험을 하였으나, 빛의 속도에 유의미한 차이는 인정되지 않았고, 두 사람이 기대했던 관측자 이동 속도의 영향("에테르의 바람"의 효과)은 실험적으로 지지되지 않았다.^[131]

헤르츠, 피츠제럴드, 로렌츠, 푸앵카레 등^[132]의 학자들은 에테르 설에 덧붙여, 앞뒤를 맞추기 위한 가정을 부여함으로써 실험 사실과 이론을 일치시키려 시도했다.

로렌츠와 피츠제럴드는 각자 독립적으로, 운동하는 물체가 "에테르의 바람"을 받아 수축하는 '''피츠제럴드-로렌츠 수축'''을 제시했다.

로렌츠와 푸앵카레는 시간의 흐름이 관측자에 따라 다르다고 하는 "국소 시간"이라는 상대성 이론의 싹이라고 할 수 있는 사색을 제기했다.^[134]

어떤 사건이

S \,

계에서

(x,y,z,t) \,

의 시공간 좌표를 갖고,

S \,

에 대해

u \,

의 상대속도를 가지는

S' \,

계에서

(x',y',z',t') \,

의 좌표를 갖는다면, 이 두 좌표들 간의 관계는 다음과 같다.

:

x' = \gamma (x - ut) \,

:

y' = y \,

:

z' = z \,

:

t' = \gamma \left(t - \frac{u x}{c^{2}} \right) \,

이 변환의 특징은 변환 후에도 빛의 속도는

c \,

로 일정하다는 것이다. 이는 맥스웰 방정식에서 빛의 속도가 좌표계에 관계없이 일정하다고 예측한 사실과 일치한다. 따라서 고전역학의 갈릴레오 변환과 전자기학의 맥스웰 방정식을 모순 없이 결합시켜주는 변환으로 평가된다.

뉴턴은 역학을 기술하면서 "절대 시간과 절대 공간"을 정의하였는데, 시간과 공간은 거기에 있는 물체의 존재나 운동에 영향을 받지 않는다고 가정했다.

'''로런츠 변환'''이란 민코프스키 공간 상의 선형 변환으로 민코프스키 계량을 불변하게 유지하는 것이다. 즉 임의의 4차원 벡터에 대해,

:

\eta(\varphi(\vec{a}),\varphi(\vec{b}))=\eta(\vec{a},\vec{b})

가 성립하는 것을 말한다.

로런츠 변환와 4차원 벡터를 사용하여

:

의 형태로 나타낼 수 있는 선형 변환을 '''푸앵카레 변환'''이라고 한다.

필요하다면 공간 방향의 좌표축을 회전시킴으로써, 로런츠 변환은

:

\left(\begin{array}{c}ct'\\x'\\y'\\z'\end{array}\right)=\left(\begin{array}{c}ct\cosh\zeta-x\sinh\zeta\\-ct\sinh\zeta+x\cosh\zeta\\y\\z\end{array}\right)

로 나타낼 수 있다.^[144]

이 값 는 정규 직교 기저의 선택에 의존하지 않고, 로런츠 변환 의 고유값에 의해서만 결정되며, 를 의 '''래피디티'''라고 한다.

관측자 에서 본 관측자 의 상대 속도를 라고 하면,

:

v=c\tanh\zeta

가 된다.^[145]

따라서,

:

\cosh\zeta=\frac{1}{\sqrt{1-\tanh^2\zeta}}=\frac{1}{\sqrt{1-(v/c)^2}},

:

\sinh\zeta=\frac{\tanh\zeta}{\sqrt{1-\tanh^2\zeta}}=\frac{(v/c)}{\sqrt{1-(v/c)^2}}

이다. 여기서 '''로렌츠 인자''' 를

:

\gamma:=\frac{1}{\sqrt{1-(v/c)^2}}

로 정의하면, 다음과 같은 결과가 유도된다.

관측자 A에서 본 관측자 B의 상대 속도를 라고 할 때, 필요하다면 공간 방향의 좌표축을 회전시켜 로렌츠 변환은

:

\left(\begin{array}{c}ct'\\x'\\y'\\z'\end{array}\right)=\left(\begin{array}{c}(ct-x\cdot(v/c))\gamma\\(x-vt)\gamma\\y\\z\end{array}\right)

로 쓸 수 있다.

로런츠 변환의 식에서, (0에 근사)라고 하면, 식은,

:

\left(\begin{array}{c}ct'\\x'\\y'\\z'\end{array}\right)=\left(\begin{array}{c}ct\\x-vt\\y\\z\end{array}\right)

가 되어, 갈릴레이 변환과 일치한다. 즉, "뉴턴 역학 근사"란 관성 좌표계 간의 상대 속도 가 광속 에 비해 충분히 작은 경우의 이론이라고 말할 수 있다.

5. 특수 상대성 이론의 주요 결과

특수 상대성 이론의 결과는 로렌츠 변환 방정식을 통해 도출될 수 있다.^[36] 이 변환식과 특수 상대성 이론은 모든 상대 속도에서 뉴턴 역학과 다른 물리적 예측을 하며, 상대 속도가 빛의 속도에 근접할 때 가장 두드러진다. 빛의 속도는 대부분의 인간이 접하는 속도보다 훨씬 크기 때문에 상대성 이론이 예측하는 일부 효과는 처음에는 직관에 반하는 것으로 여겨진다.

특수 상대성 이론의 주요 결과는 다음과 같다.

시간 지연: 서로 상대 운동하는 두 관측자 A, B가 있을 때, A가 관측한 B의 시계는 B가 관측한 A의 시계보다 느리게 간다. 이 지연의 크기는 상대 운동 속도에 따라 달라진다.(#시간 지연 (Time Dilation))
길이 수축: 상대 운동하는 물체는 서로에게서 길이가 줄어들어 보인다.(#길이 수축 (Length Contraction))
질량-에너지 등가성: 에너지와 질량은 상호 변환 가능하며, 관측자와 관측 대상의 운동 상태에 따라 서로 변환된다.
상대론적 속도 덧셈: 속도 합성 법칙은 비선형적이다.(#상대론적 속도 덧셈)
운동하는 물체^[147]는 속도가 빠를수록 가속하기 어려워지며, 빛의 속도에 도달할 수 없다.

아인슈타인은 로렌츠 불변성(특수 상대성 이론의 본질)을 상대성 및 빛의 속도 불변성이라는 두 가지 기본 원칙에 기반하여 유도했다.

뉴턴은 역학을 기술하면서 '절대 시간과 절대 공간'을 정의했는데, 이는 물체의 존재나 운동에 영향을 받지 않는다고 가정했다.

5. 1. 시간 지연 (Time Dilation)

시간 지연(Time dilation)은 상대속도를 가진 다른 관성계를 관측할 때 시간이 팽창되어 보이는 현상이다. 즉, 관성계 A에서 움직이는 다른 관성계 B를 보면 B의 시간이 상대적으로 느리게 가는 것으로 관측된다. 모든 관성계는 동등하므로, 반대로 B에서 A를 관측하면 A의 시간이 상대적으로 느리게 가는 것으로 보인다.

A에서 관측한 B의 시간은 다음과 같이 나타난다.

:

\Delta t' = \gamma  \Delta t = \frac{\Delta t}{\sqrt{1-v^2/c^2}} \,

여기서

:

\Delta t \,

는 관찰자의 좌표계에 대해 이동하는 좌표계에서 측정한 두 사건 사이의 시간 간격,

:

\Delta t' \,

는 관찰자의 좌표계에서 측정한 두 사건 사이의 시간 간격,

:

v \,

는 관찰자와 이동하는 좌표계 간의 상대속도,

:

c \,

는 진공 중에서의 빛의 속도,

:

\gamma = \frac{1}{\sqrt{1-v^2/c^2}} \,

는 로런츠 인자이다.

이 두 관측 결과는 모순처럼 보이지만 그렇지 않다. A에서 B의 시간을 측정하려면 시작 시각과 끝 시각을 측정해 차이를 구해야 한다. B는 움직이므로 시작 시각의 B의 위치와 끝 시각의 위치에 각각 시계를 놓아야 한다. 이때 측정 전에 두 시계가 가리키는 시각이 같아야 한다. 이를 '''동기화'''(synchronization^영어)라 한다. 그러나 A에서 두 시계를 동기화해도 B가 관측했을 때는 동시성의 상대성에 의해 두 시계가 다른 시각을 가리키는 것으로 보인다. 따라서 B가 보기에는 A가 잘못된 실험을 하는 것으로 보이고, B의 시간이 A보다 느리게 간다는 A의 관측 결과는 B에게 맞지 않다.

B에서 A를 관측하는 경우에는 B에 동기화된 2개의 시계와 A에 하나의 시계를 사용해 실험한다. 즉 A와 B는 서로 다른 실험을 하는 것이고, 따라서 두 결과는 상호 모순적이지 않다.^[48]

시간 지연은 쌍둥이 역설로 설명하기도 한다.^[57] 지구에 있는 쌍둥이 중 한 명이 우주선을 타고 빠른 속도로 여행을 하고 지구로 돌아올 경우, 지구에 있는 쌍둥이 보다 우주선을 타고 여행을 다녀온 쌍둥이의 시간이 느리게 간다.

구체적인 예시를 들어 설명하자면, 여행하는 쌍둥이가 떨어진 별까지 의 속도로 왕복하는 시나리오를 생각해 보자. 여행하는 동안 각 쌍둥이는 서로에게 매년 시간 신호(자신의 고유 시간으로 측정)를 보낸다. 여행 후, 누적된 카운트를 비교한다. 여행의 외출 단계에서 각 쌍둥이는 다른 쌍둥이의 신호를 의 낮은 속도로 받는다. 처음에는 상황이 완벽하게 대칭적이다. 각 쌍둥이가 자신의 시계로 측정할 때 2년 만에 다른 쌍둥이의 1년 신호를 받는다는 점에 주목하라. 여행하는 쌍둥이가 자신의 시계로 측정하여 4년째에 돌아서면서 대칭성은 깨진다. 그녀의 여행의 남은 4년 동안, 그녀는 의 향상된 속도로 신호를 받는다. 상황은 정지해 있는 쌍둥이와는 매우 다르다. 빛의 속도 지연으로 인해 그는 여동생이 자신의 시계로 8년이 지나서야 돌아서는 것을 본다. 따라서 그는 비교적 짧은 기간 동안 여동생으로부터 향상된 속도 신호를 받는다. 비록 쌍둥이들은 총 시간에 대한 각자의 측정에서 동의하지 않지만, 각 쌍둥이는 다른 쌍둥이로부터 보낸 신호의 총 개수에 대해 완전히 동의한다는 것을 알 수 있다. 따라서 역설은 없다.^[48]

항목	정지해 있는 쌍둥이가 측정한 값	그림 4-4	여행하는 쌍둥이가 측정한 값	그림 4-4
총 여행 시간	$T = \frac{2L}{v}$		$T' = \frac{2L}{\gamma v}$
보낸 펄스의 총 개수	$fT = \frac{2fL}{v}$	10	$fT' = \frac{2fL}{\gamma v}$	8
여행하는 쌍둥이의 턴어라운드가 감지된 시간	$t_1 = \frac{L}{v} + \frac{L}{c}$		$t_1' = \frac{L}{\gamma v}$
초기 $f'$ 속도로 수신된 펄스 수	$f't_1$ $= \frac{fL}{v}(1 + \beta)\left(\frac{1-\beta}{1+\beta}\right)^{1/2}$ $= \frac{fL}{v}(1 - \beta ^2)^{1/2}$	4	$f$ t_1 $= \frac{fL}{v}(1 - \beta^2)^{1/2}\left(\frac{1-\beta}{1+\beta}\right)^{1/2}$ $= \frac{fL}{v}(1 - \beta )$	2
여행의 나머지 시간	$t_2 = \frac{L}{v} - \frac{L}{c}$		$t_2' = \frac{L}{\gamma v}$
최종 $f''$ 속도로 수신된 신호 수	$f''t_2$ $= \frac{fL}{v}(1 - \beta)\left( \frac{1 + \beta}{1 - \beta} \right)^{1/2}$ $= \frac{fL}{v}(1 - \beta ^2)^{1/2}$	4	$f$ 't_2 $= \frac{fL}{v}(1 - \beta^2)^{1/2}\left( \frac{1 + \beta}{1 - \beta} \right)^{1/2}$ $= \frac{fL}{v}(1 + \beta)$	8
수신된 펄스의 총 개수	$\frac{2fL}{v}(1 - \beta ^2)^{1/2}$ $= \frac{2fL}{\gamma v}$	8	$\frac{2fL}{v}$	10
쌍둥이가 '다른' 쌍둥이가 얼마나 늙었는지에 대해 계산한 값	$T' = \frac{2L}{\gamma v}$		$T = \frac{2L}{v}$

5. 2. 길이 수축 (Length Contraction)

길이 수축(Length contraction)은 어떤 관성계에서 상대속도를 가지는 다른 관성계를 관측할 때 길이가 수축된 것으로 관측되는 현상이다. 즉, 관성계 A에서 움직이는 다른 관성계 B를 보면 B의 길이가 상대적으로 짧아진 것으로 관측된다. 모든 관성계는 동등하기 때문에, 반대로 관성계 B에서 관성계 A를 관측하면 A의 길이가 상대적으로 짧아진 것으로 관측된다.

A에서 관측한 B의 길이는 다음과 같이 나타낼 수 있다.

:

L'\ =  \frac{L}{\gamma}= L \sqrt{1-v^2/c^2} \,

여기서

:

L \,

는 이동하는 물체의 좌표계에서 측정한 물체의 길이(고유 길이)이고,

:

L' \,

는 물체에 대해 이동하는 관찰자의 좌표계에서 측정한 물체의 길이이다.

이 두 관측 결과는 서로 모순되는 것처럼 보이지만 그렇지 않다. 길이를 측정하기 위해서는 물체의 양 끝 지점의 위치를 동시에 측정해서 그 차를 구해야 한다. 그러나 A에서 두 지점을 동시에 측정했더라도, B가 관측했을 때는 동시성의 상대성에 의해 양 끝을 다른 시각에 측정한 것으로 관측된다. 따라서 B가 관측하기에는 A가 잘못된 실험을 하는 것으로 보이고, B의 길이가 짧아졌다는 A의 관측 결과는 B에게 맞지 않는 것이다.

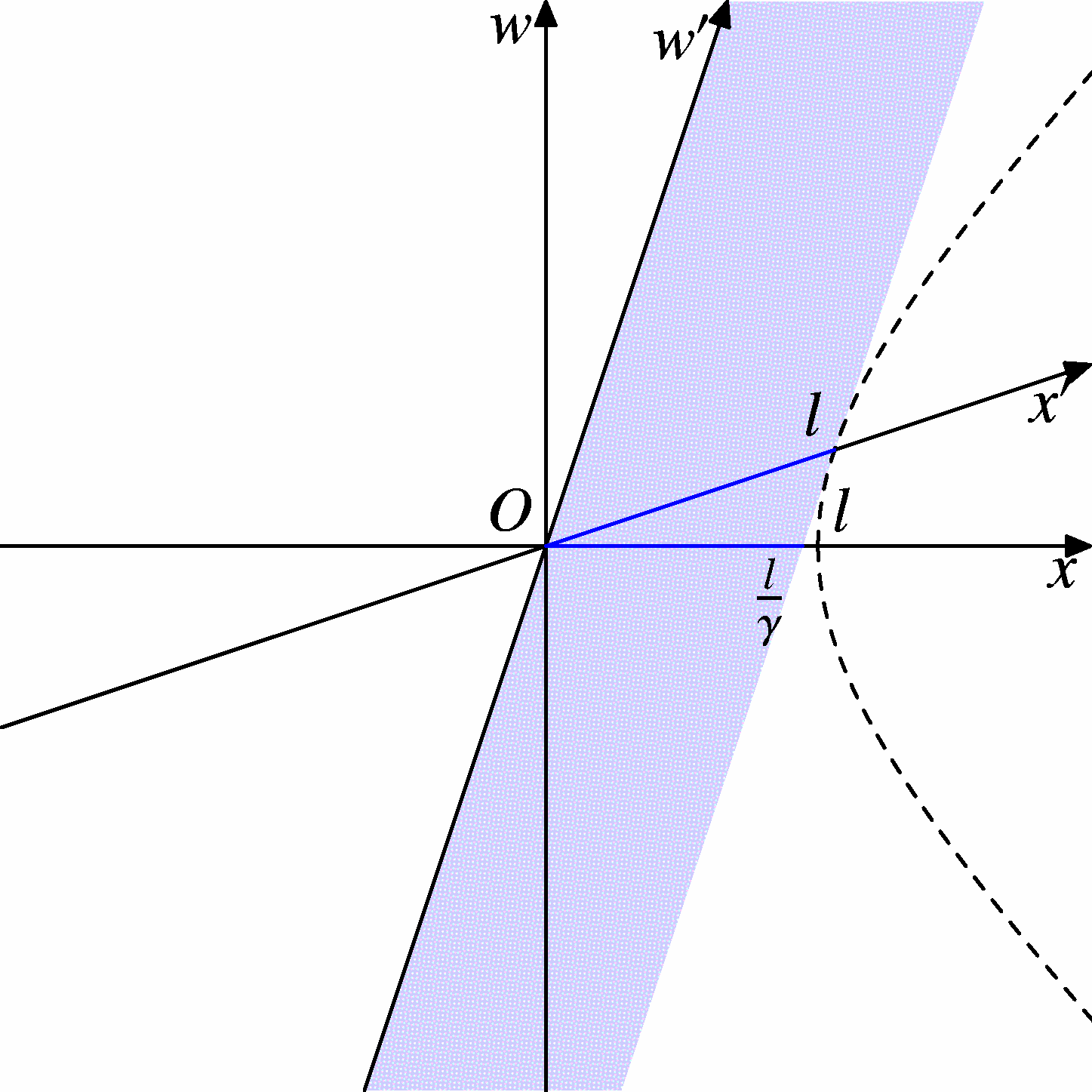
로렌츠 수축. 그림에서는 시간 을 로 나타낸다. 관성계 에 고유 길이가 인 막대(축의 짙은 보라색)가 있으며, 이 막대의 시공간상의 궤적이 옅은 보라색이다. 이것을 다른 관성계 에서 측정하면 길이가 로 줄어든 것처럼 보인다. 여기서 는 로렌츠 인자 이다. 관성계 와 관성계 에서는 막대의 측정 지점이 다르다는 것에 주의한다.

지상에서 (지면에 대해) 정지해 있는 관측자 입장에서 볼 때, 고속으로 비행하는 로켓은 (지상에) 정지해 있을 때보다 진행 방향으로 수축되어 짧게 보인다.

지상에서 상공으로 향하는 로켓을 관측할 때, 로켓 후단에 설치된 시계는 로켓 전단에 설치된 시계보다 시간 차이가 크다. 이때, 로켓에 탑승한 관측자 입장에서 보면 로켓의 속도에서의 운동 좌표계에서 로켓 후단과 전단의 시계가 나타내는 시각은 동시에 보인다.

실제 로켓이 관측자에게 어떻게 보이는지에 대해서는 특수 상대성 이론에 의한 시각 및 좌표의 시간 차이 외에, 로켓 각 부분에서 오는 빛의 도달 시간을 고려해야 한다. 이를 고려하면 더욱 왜곡된 모습으로 보일 수 있다.

로렌츠 수축은 아인슈타인이 특수 상대성 이론을 제안하기 전에 로렌츠와 피츠제럴드가 독립적으로 제안한 것이다.

사다리 역설에서, 길이 의 사다리와 깊이 인 차고가 있고, 사다리가 고속으로 차고에 접근한다고 가정하자. 차고가 정지해 보이는 관성계에서 보면 사다리가 로렌츠 수축하기 때문에 사다리는 차고에 들어갈 것이다. 반면, 사다리가 정지해 보이는 관성계에서 보면, 반대로 차고가 로렌츠 수축하기 때문에 사다리는 차고에 들어가지 않을 것이다. 어느 쪽이 정답일까?

결론부터 말하면, 둘 다 정답이며, 차고의 계에서 보면 사다리는 차고에 들어가는 것처럼 보이고, 사다리의 계에서 보면 사다리는 차고에 들어가지 않는 것처럼 보인다. 즉, 사다리의 앞쪽 끝과 뒤쪽 끝에 관한 사건을 구분하여 말하면, 차고의 정지계에서는 사다리의 뒤쪽 끝이 차고에 완전히 들어간 '''후''', 사다리의 앞쪽 끝이 차고의 뒷벽에 부딪치는 반면, 사다리의 정지계에서는 사다리가 차고에 완전히 들어가지 않고, 사다리의 뒤쪽 끝이 차고에 들어오기 '''전'''에 사다리의 앞쪽 끝이 차고의 뒷벽에 부딪힌다.^[150] 사다리의 앞쪽 끝이 차고의 뒷벽에 부딪치는 사건과 사다리의 뒤쪽 끝이 차고에 들어가는 사건 사이에는 인과 관계가 없으므로, 어느 쪽이 먼저 일어나는지는 관성계에 따라 변화하는 것이다.

5. 3. 상대론적 속도 덧셈

상대론적 속도 덧셈은 특수 상대성 이론에서 속도가 어떻게 더해지는지를 나타낸다. 고전 역학에서는 단순히 두 속도를 더하면 되지만, 특수 상대성 이론에서는 로렌츠 변환을 사용하여 속도를 계산해야 한다.^[36]

표준 배치를 갖는 두 관성 좌표계 ''S''와 ''S′''를 생각해보자. ''S''에서 입자가 속도 벡터 u = (''u''_x, ''u''_y, ''u''_z)로 움직일 때, ''S′''에서의 속도 u′ = (''u′''_x, ''u′''_y, ''u′''_z)는 다음과 같이 주어진다.^[17]

''u′''_x = (''u''_x - ''v'') / (1 - ''u''_x''v''/''c''²)
''u′''_y = ''u''_y / (γ(1 - ''u''_x''v''/''c''²))
''u′''_z = ''u''_z / (γ(1 - ''u''_x''v''/''c''²))

여기서 ''v''는 ''S''에 대한 ''S′''의 상대 속도이고, ''c''는 광속, γ = 1 / √(1 - ''v''²/''c''²)는 로렌츠 인자이다.

역변환은 다음과 같다.

''u''_x = (''u′''_x + ''v'') / (1 + ''u′''_x''v''/''c''²)
''u''_y = ''u′''_y / (γ(1 + ''u′''_x''v''/''c''²))
''u''_z = ''u′''_z / (γ(1 + ''u′''_x''v''/''c''²))

이 공식은 두 속도 v와 u′의 ''결과'' u를 제공하며, 갈릴레이 상대성 이론에서의 속도 덧셈 공식 u = u′ + v를 대체한다.

어떤 물체(예: 광자)가 한 좌표계에서 빛의 속도로 움직인다면(즉, ''u'' = ±''c'' 또는 ''u′'' = ±''c''), 다른 어떤 좌표계에서도 빛의 속도로 움직인다. 또한, 크기가 ''c''보다 작은 두 속도의 결과 속도는 항상 크기가 ''c''보다 작다.

이처럼 특수 상대성 이론에서는 어떤 물체의 속도도 빛의 속도를 초과할 수 없다.

5. 4. 질량-에너지 등가성 (Mass-energy Equivalence)

정지 에너지라 불리는

E = mc^{2} \,

는 물체가 정지 상태에서 가지는 에너지를 나타낸다. 여기서 m은 정지 질량을 의미하며, 이는 어느 관성계에서나 일정하다. 오늘날 상대성 이론에서 "질량"이라고 하면 일반적으로 정지 질량을 가리킨다.^[93]

질량과 에너지는 자유롭게 변환될 수 있다는 의미는 아니지만, 완전히 동등하다는 의미를 가진다. 즉, 질량

m \,

의 정의에 가깝다.

질량-에너지 등가성은 특수 상대성 이론의 중요한 결과 중 하나이다. 에너지 보존 법칙에 따라, 어떤 반응에서 입자 질량의 합이 감소하면, 반응 후 입자의 운동 에너지는 증가해야 한다. 마찬가지로, 물체가 운동 에너지를 흡수하면 질량이 증가한다.

아인슈타인은

E=mc^2

를 위한 질량과 에너지의 등가성(및 변환 가능성)에 대한 경험적 논거를 제시하는 적어도 4편의 논문을 작성했다.

질량

m \,

을 갖는 것과 에너지

mc^2 \,

를 갖는 것은 등가이며, 질량 결손이나 핵반응·쌍소멸에 따른 에너지 방출·흡수로부터 확인되고 있다.

예를 들어, 핵분열 반응에서 우라늄 원자핵이 분열될 때 질량이 감소하고, 이 감소한 질량만큼 에너지가 방출된다. 핵융합 반응에서는 수소 원자핵들이 융합하여 헬륨 원자핵이 될 때 질량이 감소하고, 이 역시 에너지 방출로 이어진다.

한국의 원자력 발전은 핵분열 반응을 이용하며, 이 과정에서 발생하는 질량 결손이 에너지로 변환되어 전기를 생산한다.

5. 5. 상대론적 운동량과 에너지

고전 역학에서 운동량은

\vec p = m\vec v \,

로 정의되지만, 상대론적 속도에서는 보존되지 않는다. 상대론적 운동량은 다음과 같이 정의된다.

:

\vec p = \gamma m \vec v \,

이 식에서

v << c \,

(속도가 광속보다 매우 작은 경우)이면, 고전적인 운동량

\vec p = m\vec v \,

와 같아진다.

고전적인 운동 에너지

K = \frac{1}{2} m v^{2} \,

역시 상대론적 속도에서는 성립하지 않고, 다음과 같이 정의된다.

:

K = (\gamma - 1) m c^{2} \,

이 식 역시

v << c \,

일 때 고전적인 운동 에너지

K = \frac{1}{2} m v^{2} \,

와 같아진다.

입자의 상대론적 운동량과 총 상대론적 에너지는 다음과 같이 주어진다.^[102]

사차원 운동량의 불변 크기는 에너지-운동량 관계를 생성한다.

\mathbf{P}^2 = \eta^{\mu\nu}P_\mu P_\nu = -\left (\frac{E}{c} \right )^2 + p^2 .

이 불변량이 무엇인지 알아내기 위해, 스칼라이므로 어느 기준틀에서 계산해도 상관없다는 점을 이용해 총 운동량이 0인 기준틀에서 계산하면,

\mathbf{P}^2 = - \left (\frac{E_\text{rest}}{c} \right )^2 = - (m c)^2 .

를 얻는다.

여기서 정지 에너지(

E_\text{rest}

)는 독립적인 불변량임을 알 수 있다. 정지 에너지는 운동하는 입자나 계에 대해서도 운동량이 0인 기준틀로 변환하여 계산할 수 있다. 정지 에너지는 아래의 유명한 방정식에 따라 질량과 관련이 있다.

E_\text{rest} = m c^2.

6. 특수 상대성 이론과 전자기학

고전 전자기학의 이론적 연구는 파동 전파의 발견으로 이어졌다. 전자기적 효과를 일반화하는 방정식은 '''E''' 및 '''B''' 장의 유한한 전파 속도가 하전 입자에 대한 특정 거동을 요구한다는 것을 발견했다. 움직이는 전하에 대한 일반적인 연구는 리에나르-비헤르트 전위를 형성하며, 이는 특수 상대성 이론으로 가는 단계이다.

움직이는 전하의 전기장에 대한 로렌츠 변환을 정지 관찰자의 기준 틀로 변환하면 일반적으로 자기장이라고 하는 수학적 항이 나타난다. 반대로, 움직이는 전하에 의해 생성된 "자기"장은 사라지고, 공통 운동 기준 틀에서는 순수하게 "정전기"장이 된다. 따라서 맥스웰 방정식은 고전적 우주 모델에서 특수 상대성 효과에 대한 경험적 적합일 뿐이다. 전기장과 자기장은 기준 틀에 따라 달라지므로 얽혀 있으며, 이를 "전자기"장이라고 한다. 특수 상대성 이론은 한 관성 좌표계의 전자기장이 다른 관성 좌표계에서 어떻게 나타나는지에 대한 변환 규칙을 제공한다.

3차원 형태의 맥스웰 방정식은 이미 특수 상대성 이론의 물리적 내용과 일치하지만, 텐서 미적분학의 언어로 표현되는 명백히 공변적인 형태로 조작하기가 더 쉽다.^[109]

이미 운동량의 개념을 4차원 벡터화했으므로, 힘의 개념을 4차원 벡터화한 '''4차원 힘'''이 정의되면, 뉴턴에 의한 질점의 운동 방정식을 로렌츠 변환에 불변하게 만든 특수 상대성 이론의 운동 방정식

: $\vec{f}=m\frac{\mathrm{d}\vec{p}}{\mathrm{d}t}$

을 정식화할 수 있다.

현재 알려진 4종류의 힘 중, 전자기력, 강력, 약력의 3가지는 4차원 힘으로 표현 가능하다는 것이 알려져 있다. 이 중 전자기력을 4차원 힘으로 표현하는 방법은 아래에서 설명한다.

한편, 중력은 특수 상대성 이론의 범위 내에서 4차원 벡터화하려고 해도 로렌츠 변환에 대해 불변하지 않으므로 잘 되지 않는다. 중력을 다루기 위해서는 일반 상대성 이론이 필요하다.

여기서는 전자기학의 기본적인 개념과 방정식을 특수 상대성 이론에 부합하는 형태로 다시 쓴다.

관성계

: $(x^0,x^1,x^2,x^3),~x^0=ct$

를 하나 고정하고, 이 관성계에서 전자기학을 기술한다. 자세한 내용은 생략하지만, 이 기술은 다른 관성계에서 전자기학을 기술한 것과 로렌츠 변환으로 서로 옮겨갈 수 있음을 확인할 수 있으므로, 특수 상대성 이론에 부합한다.

국제단위계를 사용하는 경우에 대해 기술했지만, Gaussian units|가우스 단위계|preserve=1^영어를 사용하고 있는 서적에서의 정의와는 광속도 가 걸리는 위치가 다른 등의 차이가 있으므로 주의가 필요하다.^[151]

전하 밀도 와 전류 밀도 를 사용하여, '''4차원 전류 밀도'''를,

: $(j^0,j^1,j^2,j^3):=(c\rho,j_x,j_y,j_z)$

로 정의한다.

그러면 연속 방정식

: $\frac{\partial\rho}{\partial t}+\nabla\cdot\boldsymbol{j}=0$

는, 4차원 전류 밀도와 '''4차원 기울기(four-gradient)''' 를 사용하여

: $\partial_\nu j^\nu=0$

로 표현할 수 있다. 여기서 는 의 약기이다.

진공의 유전율, 투자율을 각각 라고 하면, 맥스웰 방정식에 의해 유도되는 전자기파의 속도 가 진공 중의 광속과 일치한다는 것이 실험·관측에 의해 확인되었으므로, 빛의 정체는 전자기파라고 생각하게 되었다. 이 사실로부터,

: $c=\frac{1}{\sqrt{\mu_0\varepsilon_0}}$

이다.

전장 와 자기 선속 밀도 를 사용하여 '''전자기 텐서'''를

: $(F^{\alpha\beta})_{\alpha\beta}:=\begin{pmatrix}0&-E_x/c&-E_y/c&-E_z/c\\E_x/c&0&-B_z&B_y\\E_y/c&B_z&0&-B_x\\E_z/c&-B_y&B_x&0\end{pmatrix}$

에 의해 정의한다.

전자기장을 다른 관성계에서 보았을 경우, 전장과 자기 선속 밀도가 각각 와 였다고 하고, 이들로부터 만든 전자기 텐서를 라고 한다.

와 가 로렌츠 부스트식으로 이동하는 필요 충분 조건은,

: $\begin{align}(E'_x,B'_x)&=(E_x,B_x),\\(E'_y,B'_y)&=\gamma(E_y- |\boldsymbol{v}| B_z,B_y+ |\boldsymbol{v}| E_z /c^2 ),\\(E'_z,B'_z)&=\gamma(E_z+ |\boldsymbol{v}| B_y,B_z- |\boldsymbol{v}| E_y /c^2 ) \end{align}$

가 성립하는 것임을 간단한 계산으로 확인할 수 있다. 여기서 는 두 관성계 사이의 상대 속도이고, 는 로렌츠 인자이다.

비상대론적 극한 에서는 이므로, 상술한 조건식은 고전 전자기학에서 알려져 있는 관성계 간의 변환 공식

: $\begin{array}{l}\boldsymbol{E}'=\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B},\\\boldsymbol{B}'=\boldsymbol{B}- \boldsymbol{v}\times\boldsymbol{E}/c^2\end{array}$

와 일치한다.

따라서 전자기 텐서는 로렌츠 변환에 대해 공변이라고 결론 내릴 수 있다.

특수 상대성 이론 이전의 맥스웰 방정식 해석에는 비대칭성이 있었다. 예를 들어 자석을 고정된 코일에 가까이 가져가면 전자기 유도에 의해 전류가 흐르는 것으로 해석되지만, 반대로 코일을 고정된 자석에 가까이 가져가면 로렌츠 힘으로 전자가 움직여 전류가 흐르는 것으로 해석되었다. 오늘날의 시점에서 보면, 이 두 경우는 단순한 관성계의 교환에 불과함에도 불구하고, 두 해석이 다른 것은 부자연스럽다. 사실, 흐르는 전류의 양은 어느 경우든 동일하며, 자석과 코일의 상대 속도에 의해서만 결정된다.

이러한 비대칭적인 해석이 된 것은, 당시에는 전장과 자기 선속 밀도가 완전히 별개의 개념이었기 때문이다. 위의 식도, 오늘날의 시각으로 보면 전장과 자기 선속 밀도를 전자기 텐서라는 동일한 텐서로 묶어야 함을 시사하는 것처럼 보이지만, 당시에는 위의 식의 두 번째 항은 어디까지나 "가상적인" 전장이나 자기 선속 밀도의 효과로 여겨졌다.

이러한 이론의 비대칭성 해소에 관심을 가졌던 아인슈타인은 특수 상대성 이론을 통해 이 비대칭성을 해소했다.

전자기 텐서가 로렌츠 변환에 대해 공변임을 이미 보였으므로, 맥스웰 방정식을 전자기장 텐서로 나타내면, 맥스웰 방정식도 로렌츠 변환에 대해 공변임을 보일 수 있다.

전자기 텐서와 4원 전류 밀도를 사용하면 맥스웰 방정식의 2식

: $\begin{align}\nabla\cdot\boldsymbol{E}&=\frac{\rho}{\epsilon_0}\\\nabla\times\boldsymbol{B}-\frac{1}{c^2}\frac{\partial\boldsymbol{E}}{\partial t}&=\mu_0\boldsymbol{j}\end{align}$

은 모두

: $\partial_{\alpha} F^{\alpha\beta}=\mu_0 j^{\beta}$

와 동일한 형태로 표현할 수 있으며, 나머지 2식

: $\begin{align}\nabla\cdot\boldsymbol{B}&=0\\\frac{\partial\boldsymbol{B}}{\partial t}+\nabla\times\boldsymbol{E}&=0\end{align}$

은 모두

: $\partial_\gamma F_{\alpha\beta}+\partial_\alpha F_{\beta\gamma}+\partial_\beta F_{\gamma\alpha}=0$ (는 서로 다름)

과 동일한 형태로 표현할 수 있다. 또한, 리치 계산의 표기법을 사용하면 위의 식은

: $\partial_{[\alpha}F_{\beta\gamma]}=0$

으로도 표기할 수 있다.

맥스웰 방정식은 미분 형식과 외미분을 사용하면 더욱 간결하게 표현할 수 있다는 것이 알려져 있지만, 여기서는 생략한다.

전자기장에는 반드시 다음 조건을 만족하는 짝 ('''전자기 퍼텐셜''')가 존재한다는 것이 알려져 있다.

: $\boldsymbol{B}=\operatorname{rot} \boldsymbol{A}$ 、 $\boldsymbol{E}=-\operatorname{grad}\phi-\frac{\partial \boldsymbol{A}}{\partial t}$

여기서는 전자기 퍼텐셜의 4원 벡터 버전인 '''4원 퍼텐셜'''

를 사용하여 맥스웰 방정식을 표현한다.

하나의 전자기장에 대해 위의 식을 만족하는 전자기 퍼텐셜은 유일하지 않다는 것이 알려져 있다. 그래서 로렌츠 공변성을 해치지 않는 형태로 전자기 퍼텐셜을 제한하기 위해 4원 기울기를 사용한 다음 조건 ('''로렌츠 게이지''')을 부과한다.

이때, 맥스웰 방정식은 4원 전류 밀도를 사용하여

라는 한 개의 식으로 쓸 수 있다. 여기서

: $\Box:=\frac{1}{c^2}\frac{\partial^2}{\partial t^2}-\frac{\partial^2}{\partial x^2}-\frac{\partial^2}{\partial y^2}-\frac{\partial^2}{\partial z^2}$

는 달랑베르시안이다.

전하 를 가진 질점이 있고, 이 질점의 4차원 속도를 라고 하며, 의 반변 성분을 라고 하자. 이 때, 이 질점이 전자기장으로부터 받는 4차원 힘을 전자기장 텐서 를 사용하여

로 정의하면, 이 4차원 힘으로부터 만들어지는 질점의 운동 방정식은

: $\frac{\mathrm{d}p^{\alpha}}{\mathrm{d}\tau}=qF^{\alpha\beta}u_{\beta}$

이다. 여기서 는 질점의 4차원 운동량의 성분이고, 는 질점의 고유 시간이다.

위의 운동 방정식은 에 대해 정의되어 있지만, 4차원 운동량과 4차원 속도의 공간 성분(의 공변 표현) 에 주목하면, 전자기장 텐서의 정의로부터, 운동 방정식의 공간 성분은

: 좌변의 공간 성분 $=\gamma\frac{\mathrm{d}\boldsymbol{p}}{\mathrm{d}t}$

: 우변의 공간 성분 $=\gamma q(\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B})$

가 됨을 알 수 있다. 여기서 는 로렌츠 인자 이다.

즉 상대론에서의 운동 방정식의 공간 성분은, 로렌츠 힘에 관한 운동 방정식

: $\frac{\mathrm{d}\boldsymbol{p}}{\mathrm{d}t}=q(\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B})$

과 완전히 일치한다.

운동 방정식의 시간 성분에 관해서는, 가 질점의 에너지 를 나타낸다는 점에 주목하면,

: 좌변의 시간 성분 $=\frac{\gamma}{c}\frac{\mathrm{d}E}{\mathrm{d}t}$

: 우변의 시간 성분 $=\frac{\gamma}{c}(q\boldsymbol{E}\cdot\boldsymbol{v})$

이므로, 다음 식이 성립한다.

: $\frac{\mathrm{d}E}{\mathrm{d}t}=q\boldsymbol{E}\cdot\boldsymbol{v}=q(\boldsymbol{E}+\boldsymbol{v}\times\boldsymbol{B})\cdot\boldsymbol{v}.$

우변은 단위 시간당 전자기장의 로렌츠 힘이 질점에 한 일이기 때문에, 이 식은 로렌츠 힘에 의한 일이 에너지로 변환된다는 것을 의미한다. 즉, 이것은 '''에너지 보존 법칙'''에 해당하는 식이다.

7. 특수 상대성 이론의 실험적 검증

민코프스키 시공간에서 특수 상대성 이론은 관심 영역에서 중력 퍼텐셜의 절댓값이 ''c''²보다 훨씬 작을 때만 정확하다.^[118] 강한 중력장에서는 일반 상대성 이론을 사용해야 한다. 일반 상대성 이론은 약한 장의 극한에서 특수 상대성 이론이 된다. 플랑크 길이 이하와 같은 매우 작은 규모에서는 양자 중력을 초래하는 양자 효과를 고려해야 한다. 그러나 거시적 규모와 강한 중력장이 없는 경우, 특수 상대성 이론은 매우 높은 정확도(10⁻²⁰)로 실험적으로 검증되었으며,^[119] 따라서 물리학계에서 받아들여지고 있다. 이에 모순되는 것처럼 보이는 실험 결과는 재현할 수 없으며, 따라서 실험 오류로 널리 여겨진다.^[120]

특수 상대성 이론은 수학적으로 자기 모순이 없으며, 모든 현대 물리학 이론, 특히 양자장론, 끈 이론, 그리고 (무시할 수 있는 중력장의 극한의 경우) 일반 상대성 이론의 유기적인 부분이다.

뉴턴 역학은 작은 속도(빛의 속도에 비해)에서 특수 상대성 이론으로부터 수학적으로 도출된다. 따라서 뉴턴 역학은 느리게 움직이는 물체의 특수 상대성 이론으로 간주될 수 있다. 더 자세한 내용은 ''고전 역학''을 참조하십시오.

아인슈타인의 1905년 논문 이전에 수행된 여러 실험은 현재 상대성 이론의 증거로 해석된다. 이 중 아인슈타인이 1905년 이전에 피조 실험을 알고 있었던 것으로 알려져 있으며,^[121] 역사학자들은 아인슈타인이 자신의 이론 개발에 아무런 역할을 하지 않았다고 후년에 주장했음에도 불구하고, 적어도 1899년 이전에 마이컬슨-몰리 실험을 알고 있었다고 결론지었다.^[122]

피조 실험 (1851, 1886년 마이컬슨과 몰리에 의해 반복 수행)은 움직이는 매질에서 빛의 속도를 측정했으며, 결과는 상대론적 선형 속도 합산과 일치한다.
유명한 마이컬슨-몰리 실험(1881, 1887)은 절대적인 기준 속도를 감지하는 것이 불가능하다는 가설을 더욱 뒷받침했다. 여기서 많은 다른 주장과는 달리, 이 실험은 빛의 속도가 광원과 관찰자의 속도에 대해 불변이라는 것에 대해 거의 언급하지 않았다. 광원과 관찰자 모두 항상 같은 속도로 함께 이동했기 때문이다.
트루턴-노블 실험 (1903)은 축전기의 토크가 위치와 관성 기준틀에 독립적임을 보여주었다.
레일리-브레이스 실험 (1902, 1904)은 길이 수축이 상대성 원리에 따라 동반 이동하는 관찰자에게 복굴절을 초래하지 않는다는 것을 보여주었다.

입자 가속기는 빛의 속도에 가까운 속도로 움직이는 입자의 특성을 가속하고 측정하며, 여기서 입자의 행동은 상대성 이론과 일치하고 이전의 뉴턴 역학과 일치하지 않는다. 이러한 기계는 상대론적 원리에 따라 설계되지 않으면 작동하지 않을 것이다. 또한, 특수 상대성 이론을 검증하기 위해 상당수의 현대적인 실험이 수행되었다. 몇 가지 예는 다음과 같다.

실험	설명
상대론적 에너지와 운동량 검증	입자의 한계 속도 검증
아이브스-스틸웰 실험	상대론적 도플러 효과 및 시간 지연 검증
시간 지연의 실험적 검증	빠르게 움직이는 입자의 반감기에 대한 상대론적 효과
케네디-손다이크 실험	로렌츠 변환에 따른 시간 지연
휴즈-드레버 실험	공간 및 질량의 등방성 검증
로렌츠 위반에 대한 현대적 탐색	다양한 현대적 검증
방출 이론을 검증하기 위한 실험	빛의 속도가 방출체의 속도에 독립적임을 입증
에테르 끌림 가설을 검증하기 위한 실험	"에테르 흐름 방해" 없음

특수 상대성 이론은 다음과 같은 현상으로도 검증되었다.

전장과 자장의 통일 이론으로서의 특수 상대성 이론 검증^[152]: 전류가 흐르는 전선 주위에 자장이 발생한다.
시계 지연 검증
횡방향 도플러 효과 측정: 뫼스바우어 효과를 일으키는 방사선원과 그 흡수체에 대해, 방사선원을 회전하는 원반의 중심에, 흡수체를 원주에 배치하여 회전시키면 뫼스바우어 효과가 발생하지 않는다.
하펠-케이팅 실험: 항공기로 운반한 원자 시계와 지상에서 정지한 채로 있는 원자 시계 사이에 발생하는 오차가 이론과 오차 (불확정성 원리도 포함) 범위 내에서 일치한다.^[155] 이 실험에서의 상대론 효과는 특수 상대성 이론에서의 운동에 의한 시계 지연, 일반 상대성 이론에서의 중력 편이에 의한 시계 지연, 사냐크 효과의 3가지가 복합적으로 나타난다.
입자의 평균 수명 연장: 우주선의 충돌로 발생하는 매우 수명이 짧은 입자가, 단순하게 광속 정도로 이동한다고 생각해도 수백 미터 정도밖에 이동할 수 없어야 하는데, 지상에서 관측할 수 있다. 또한, 입자 가속기에서 입자를 광속 근처까지 가속하면, 붕괴될 때까지의 수명이 연장된다. 이 수명 연장은 엄밀히 특수 상대성 이론에 의한 예측을 따른다.
질량과 에너지의 등가성: 오토 한은 핵분열 반응을 발견했지만, 이 반응 시의 질량 결손으로 인해, 대량의 에너지가 방출되었다. 이 방출은 특수 상대성 이론의 귀결 중 하나인 질량-에너지 동등성에서 결손에 상당하는 질량으로 환산되는 원자핵 내부의 핵자의 결합 에너지이다.
기타: 광속 근처까지 가속된 전자 등의 하전 입자를 자기장에 의해 구부리면, 방사광이라고 불리는 빛이 발생한다. 이 빛은 특수 상대성 이론의 효과에 의해 전방에 집중되어, 입자 궤도의 접선 방향으로 매우 높은 지향성을 가진 빛이 된다.

8. 추가 논의

랑제뱅 광시계 설명에서 정지/운동 상태의 관찰자 지정은 임의적이다. 관찰자 B가 광시계를 가지고 왼쪽으로 v의 속도로 움직일 때, 관찰자 A는 B의 시계가 자신의 국소 시계보다 느리게 작동한다고 인식한다.

여기에는 역설이 없는데, A와 B 모두에게 동의하는 독립적인 관찰자 C가 없기 때문이다. 관찰자 C는 자신의 기준 틀에서 측정을 수행하며, 그 기준 틀에 따라 A 또는 B의 시간 측정에 동의하거나 모두와 일치하지 않을 수 있다.

8. 1. 4차원 벡터와 텐서

4-벡터는 에너지-운동량 4-벡터의 맥락에서 언급되었지만, 크게 강조되지는 않았다. 실제로, 특수 상대성 이론의 기본적인 유도 과정에서는 4-벡터가 필요하지 않다. 하지만 4-벡터, 더 일반적으로는 텐서를 이해하면 특수 상대성 이론의 수학적, 개념적 이해를 크게 단순화할 수 있다. 이러한 객체만 사용하여 작업하면 "명백하게" 상대론적 불변인 공식을 얻을 수 있으며, 이는 사소하지 않은 맥락에서 상당한 이점을 제공한다. 예를 들어, 일반적인 형태의 맥스웰 방정식의 상대론적 불변성을 증명하는 것은 쉽지 않지만, 전자기장 텐서를 사용하면 이는 일상적인 계산, 사실 관찰에 지나지 않는다.^[109]

반면에 일반 상대성 이론은 처음부터 물리적으로 관련된 객체를 나타내는 4-벡터, 더 일반적으로는 텐서에 크게 의존한다. 특정 좌표에 의존하지 않는 방정식을 통해 이를 연결하려면, 특수 상대성 이론에서와 같이 "평평한" 시공간뿐만 아니라 "곡선" 시공간에서도 이러한 4-벡터를 연결할 수 있는 텐서가 필요하다.

4-튜플 는 그 성분 ''A_i''가 로렌츠 변환에 따라 프레임 간에 변환되면 "4-벡터"이다.

만약 (ct, x, y, z)^영어 좌표를 사용한다면, ''A''는 (''x''-방향^영어) 다음과 같이 변환될 때 4–벡터이다.

:

\begin{align}A_0' &= \gamma \left( A_0 - (v/c) A_1 \right)  \\A_1' &= \gamma \left( A_1 - (v/c) A_0 \right)\\A_2' &= A_2 \\A_3' &= A_3\end{align} ,

이것은 앞서 제시된 로렌츠 변환에서 단순히 ''ct''를 ''A''₀로, ''x''를 ''A''₁로 대체함으로써 얻어진다.

4-벡터의 마지막 세 성분은 3차원 공간에서 표준 벡터여야 한다. 그러므로 4-벡터는 로렌츠 변환뿐만 아니라 회전 아래에서도 (c \Delta t, \Delta x, \Delta y, \Delta z)^영어와 같이 변환되어야 한다.^[110]

4-벡터의 성질은 다음과 같다.

선형 결합에 대한 닫힘: ''A''와 ''B''가 4-벡터라면, C = aA + aB^영어 역시 4-벡터이다.
내적 불변성: ''A''와 ''B''가 4-벡터라면, 이들의 내적(스칼라 곱)은 불변량이다. 즉, 내적 값은 계산되는 좌표계에 관계없이 동일하다. 내적 계산 방식이 3-벡터의 내적 계산 방식과 다르다는 점에 주목해야 한다. 다음에서, $\vec{A}$ 와 $\vec{B}$ 는 3-벡터이다.
: $A \cdot B \equiv$ $A_0 B_0 - A_1 B_1 - A_2 B_2 - A_3 B_3 \equiv$ $A_0 B_0 - \vec{A} \cdot \vec{B}$

: 로렌츠 변환에 대한 불변성 외에도, 위 내적은 3차원 공간에서의 회전에 대해서도 불변이다.

: 두 벡터는 A \cdot B = 0 ^영어일 때 ''직교''한다고 한다. 3-벡터와 달리, 직교하는 4-벡터는 서로 수직일 필요는 없다. 규칙은 두 4-벡터가 45° 선, 즉 광선의 세계선으로부터 동일하고 반대 방향의 각도로 벗어날 때 직교한다는 것이다. 이는 광원과 같은 4-벡터가 ''자신''과 직교한다는 것을 의미한다.

벡터 크기의 불변성: 벡터의 크기는 4-벡터와 자기 자신의 내적이며, 좌표계에 무관한 성질이다. 간격과 마찬가지로, 크기는 양수, 음수 또는 0이 될 수 있으며, 이에 따라 벡터는 시간꼴, 공간꼴 또는 영(광원꼴)으로 지칭된다. 영 벡터는 영 벡터와 같지 않다는 점에 유의해야 한다. 영 벡터는 A \cdot A = 0 ^영어인 벡터이고, 영 벡터는 모든 성분이 0인 벡터이다. 노름의 불변성을 보여주는 특수한 경우로는 불변 간격 $c^2 t^2 - x^2$ 과 상대론적 운동량 벡터의 불변 길이 E^2 - p^2 c^2 ^영어가 있다.^[29]^[110]

4-벡터의 종류는 다음과 같다.

변위 4-벡터: ''시공간 간격''이라고도 하며, (''Δt, Δx, Δy, Δz''),^영어 또는 무한소 간격의 경우 (''dt'', ''dx'', ''dy'', ''dz'')^영어로 표현된다.
: $dS \equiv (dt, dx, dy, dz)$
속도 4-벡터: 변위 4-벡터를 $d \tau$ 로 나눈 결과로, 여기서 $d \tau$ 는 ''dt'', ''dx'', ''dy'', ''dz''를 생성하는 두 사건 사이의 고유 시간이다.
: $V \equiv \frac{dS}{d \tau} = \frac{(dt, dx, dy, dz)}{dt/\gamma} =$ $\gamma \left(1, \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt} \right) =$ $(\gamma, \gamma \vec{v} )$

: 4-속도는 입자의 세계선에 접하며, 입자 좌표계에서 시간 1단위와 같은 길이를 갖는다.

: 가속 입자는 항상 정지해 있는 관성 좌표계를 갖지 않는다. 그러나 입자와 순간적으로 동행하는 관성 좌표계를 항상 찾을 수 있다. 이 좌표계, 즉 ''순간 동행 좌표계''(MCRF)는 특수 상대성 이론을 가속 입자 분석에 적용할 수 있게 한다.

: 광자는 널선을 따라 움직이므로, 광자의 경우

d \tau = 0

이며, 4-속도는 정의될 수 없다. 광자가 정지해 있는 좌표계는 없으며, 광자의 경로를 따라 MCRF를 설정할 수 없다.

에너지-운동량 4-벡터:
: $P \equiv (E/c, \vec{p}) = (E/c, p_x, p_y, p_z)$

: 앞서 언급했듯이, 에너지-운동량 4-벡터에 대한 다양한 처리 방식이 있어,

(E, \vec{p})

또는 로도 표현될 수 있다. 첫 번째 성분은 주어진 좌표계에서 입자(또는 입자계)의 총 에너지(질량 포함)이고, 나머지 성분은 공간 운동량이다. 에너지-운동량 4-벡터는 보존되는 양이다.

가속도 4-벡터: 이는 속도 4-벡터를 \tau ^영어에 대해 미분한 결과이다.
: $A \equiv \frac{dV}{d \tau} =$ $\frac{d}{d \tau} (\gamma, \gamma \vec{v}) =$ $\gamma \left( \frac{d \gamma}{dt}, \frac{d(\gamma \vec{v})}{dt} \right)$
힘 4-벡터: 이는 운동량 4-벡터를 $\tau .$ 에 대해 미분한 것이다.
: $F \equiv \frac{dP}{d \tau} =$ $\gamma \left(\frac{dE}{dt}, \frac{d \vec{p}}{dt} \right) =$ $\gamma \left( \frac{dE}{dt},\vec{f} \right)$

예상대로, 위의 4-벡터의 최종 성분은 모두 공간 3-운동량, 3-힘 등에 해당하는 표준 3-벡터이다.^[29]^[110]

특수 상대성 이론의 첫 번째 가정은 모든 관성 좌표계의 등가성을 선언한다. 한 좌표계에서 성립하는 물리 법칙은 모든 좌표계에 적용되어야 한다. 그렇지 않으면 좌표계를 구별하는 것이 가능해지기 때문이다. 뉴턴 역학 운동량은 로렌츠 변환에 따라 제대로 작동하지 않으며, 아인슈타인은 운동량 보존을 포기하는 대신 운동량의 정의를 4-벡터를 포함하는 것으로 변경하는 것을 선호했다.

물리 법칙은 좌표계에 독립적인 구성 요소를 기반으로 해야 한다. 즉, 물리 법칙은 항상 좌표계에 독립적인 스칼라를 연결하는 방정식의 형태를 취할 수 있다. 그러나 4-벡터를 포함하는 방정식은 적절한 랭크의 텐서를 사용해야 하며, 텐서 자체는 4-벡터로 구성된 것으로 생각할 수 있다.^[29]

특수 상대성 이론은 "평평한" 4차원 민코프스키 공간 – 시공간의 한 예시 –을 사용한다. 민코프스키 시공간은 표준 3차원 유클리드 공간과 매우 유사해 보이지만, 시간에 관해서는 중요한 차이점이 있다.

3차원 공간에서 거리(선분 요소) ''ds''의 미분은 다음과 같이 정의된다.

ds^2 = d\mathbf{x} \cdot d\mathbf{x} = dx_1^2 + dx_2^2 + dx_3^2,

여기서 ''d'''''x''' = (''dx''₁, ''dx''₂, ''dx''₃)^영어는 세 개의 공간 차원의 미분이다. 민코프스키 기하학에서는 시간에서 파생된 좌표 ''X''⁰를 가진 추가 차원이 있어 거리 미분이 다음을 충족한다.

ds^2 = -dX_0^2 + dX_1^2 + dX_2^2 + dX_3^2,

여기서 ''d'''''X''' = (''dX''₀, ''dX''₁, ''dX''₂, ''dX''₃)^영어는 네 개의 시공간 차원의 미분이다. 이것은 깊은 이론적 통찰력을 시사한다. 특수 상대성 이론은 유클리드 공간의 회전 대칭과 유사한 시공간의 회전 대칭이다.^[124] 유클리드 공간이 유클리드 메트릭을 사용하는 것처럼, 시공간은 민코프스키 메트릭을 사용한다. 기본적으로, 특수 상대성 이론은 ''어떤 관성 기준틀''에서 보더라도 ''모든 시공간 간격'' (즉, 두 사건 사이의 4차원 거리)의 ''불변성''으로 표현될 수 있다. 특수 상대성 이론의 모든 방정식과 효과는 민코프스키 시공간의 이러한 회전 대칭(푸앵카레 군)에서 파생될 수 있다.

위의 ''ds''의 실제 형태는 메트릭과 ''X''⁰ 좌표의 선택에 따라 달라진다.

시간 좌표를 공간 좌표처럼 보이게 하려면 허수로 처리할 수 있다. ''X''₀ = ''ict''^영어 (이것을 윅 회전이라고 한다).

일부 저자는 ''X''⁰ = ''t''^영어를 사용하고, 다른 곳에서는 ''c''의 인자를 사용한다. 예를 들어, 공간 좌표는 ''c''로 나누어지거나, 계량 텐서에 ''c''^±2의 인자가 포함된다.^[125]

이러한 많은 관례는 ''c'' = 1^영어인 자연 단위를 사용함으로써 대체될 수 있다. 그러면 공간과 시간은 동등한 단위를 가지며, ''c''의 인자는 어디에도 나타나지 않는다.

위에서 시간 좌표와 세 개의 공간 좌표에 대한 로렌츠 변환은 이들이 서로 얽혀 있음을 보여준다. 이는 더 일반적으로 사실이다. 즉, 특정 쌍의 "시간과 같은" 수량과 "공간과 같은" 수량은 동일한 로렌츠 변환에 따라 자연스럽게 결합된다.

위에서 표준 구성, 즉 ''x'' 방향의 부스트에 대한 로렌츠 변환은 다음과 같이 행렬 형태로 다시 표현될 수 있다.

\begin{pmatrix}ct'\\ x'\\ y'\\ z'\end{pmatrix} = \begin{pmatrix}\gamma & -\beta\gamma & 0 & 0\\

\beta\gamma & \gamma & 0 & 0\\

0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}ct\\ x\\ y\\ z\end{pmatrix} =\begin{pmatrix}\gamma ct- \gamma\beta x\\\gamma x - \beta \gamma ct \\ y\\ z\end{pmatrix}.

뉴턴 역학에서 크기와 방향을 갖는 양은 수학적으로 유클리드 공간에서 3차원 벡터로 설명되며, 일반적으로 시간으로 매개변수화된다. 특수 상대성 이론에서 이러한 개념은 공간과 같은 벡터 수량에 적절한 시간과 같은 수량을 추가하여 확장되며, 우리는 민코프스키 시공간에서 4차원 벡터 또는 "4차원 벡터"를 갖게 된다. 벡터의 성분은 텐서 지수 표기법을 사용하여 작성되는데, 이는 많은 장점을 가지고 있기 때문이다. 이 표기법은 방정식이 명백한 공변성을 갖도록 하며 푸앵카레 군에 따라, 따라서 이 사실을 확인하기 위한 지루한 계산을 거치지 않아도 된다. 이러한 방정식을 구성할 때, 이전에 관련이 없는 것으로 생각되었던 방정식이 실제로 동일한 텐서 방정식의 일부이므로 밀접하게 연결되어 있음을 자주 발견한다. 다른 물리량을 텐서로 인식하면 변환 법칙이 단순화된다. 전체적으로, 위쪽 지수(윗첨자)는 제곱을 나타내는 경우를 제외하고(이것은 문맥에서 명확해야 함) 공변 벡터를 나타내는 지수이며, 아래쪽 지수(아랫첨자)는 반공변 벡터를 나타내는 지수이다. 단순성과 이전 방정식과의 일관성을 위해 데카르트 좌표가 사용될 것이다.

4차원 벡터의 가장 간단한 예는 시공간에서 사건의 위치이며, 이는 반공변 위치 벡터 4차원 벡터에서 시간과 같은 성분 ''ct''와 공간과 같은 성분 '''x''' = (''x'', ''y'', ''z'')^영어로 구성되며, 다음과 같은 성분을 갖는다.

X^\nu = (X^0, X^1, X^2, X^3)= (ct, x, y, z) = (ct, \mathbf{x} ).

여기서 ''X''⁰ = ''ct''^영어를 정의하여 시간 좌표가 다른 공간 차원과 동일한 거리의 차원을 갖도록 한다. 즉, 공간과 시간을 동일하게 처리한다.^[126]^[127]^[128] 이제 위치 4차원 벡터의 반공변 성분의 변환은 다음과 같이 간결하게 작성할 수 있다.

X^{\mu'}=\Lambda^{\mu'}{}_\nu X^\nu

여기서

\nu

에 대한 암시적 합산이 0에서 3까지 있으며,

\Lambda^{\mu'}{}_{\nu}

는 행렬이다.

더 일반적으로, 4차원 벡터

T^\nu

의 모든 반공변 성분은 한 프레임에서 다른 프레임으로 로렌츠 변환에 의해 변환된다.

T^{\mu'} = \Lambda^{\mu'}{}_{\nu} T^\nu

다른 4차원 벡터의 예로는 고유 시간에 대한 위치 4차원 벡터의 도함수로 정의된 4차원 속도 U^\mu ^영어가 있다.

U^\mu = \frac{dX^\mu}{d\tau} = \gamma(v)( c , v_x , v_y, v_z ) = \gamma(v) (c, \mathbf{v} ).

여기서 로렌츠 인자는 다음과 같다.

\gamma(v)= \frac{1}{\sqrt{1 - v^2/c^2 }} \qquad v^2 = v_x^2 + v_y^2 + v_z^2.

물체의 상대론적 에너지

E = \gamma(v)mc^2

과 상대론적 운동량

\mathbf{p} = \gamma(v)m \mathbf{v}

는 각각 반공변 4차원 운동량 벡터의 시간과 같은 성분과 공간과 같은 성분이다.

P^\mu = m U^\mu = m\gamma(v)(c,v_x,v_y,v_z)= \left (\frac{E}{c},p_x,p_y,p_z \right ) = \left (\frac{E}{c}, \mathbf{p} \right ).

여기서 ''m''은 불변 질량이다.

4차원 가속도는 4차원 속도의 고유 시간 도함수이다.

A^\mu = \frac{d U^\mu}{d\tau}.

''3''차원 속도와 가속도에 대한 변환 규칙은 매우 어색하다. 표준 구성에서조차 속도 방정식은 비선형성으로 인해 매우 복잡하다. 반면에 ''4''차원 속도와 ''4''차원 가속도의 변환은 로렌츠 변환 행렬을 통해 더 간단하다.

스칼라장 φ의 4차원 기울기는 반공변적이 아니라 공변적으로 변환된다.

\begin{pmatrix}\dfrac{1}{c} \dfrac{\partial \phi}{\partial t'} &\dfrac{\partial \phi}{\partial x'} &\dfrac{\partial \phi}{\partial y'} &\dfrac{\partial \phi}{\partial z'}\end{pmatrix}= \begin{pmatrix}\dfrac{1}{c} \dfrac{\partial \phi}{\partial t} &\dfrac{\partial \phi}{\partial x} &\dfrac{\partial \phi}{\partial y} &\dfrac{\partial \phi}{\partial z}\end{pmatrix}\begin{pmatrix}\gamma & +\beta\gamma & 0 & 0\\+\beta\gamma & \gamma & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix} ,

이는 다음과 같은 전치 행렬이다.

(\partial_{\mu'} \phi) = \Lambda_{\mu'}{}^{\nu} (\partial_\nu \phi)\qquad \partial_{\mu} \equiv \frac{\partial}{\partial x^{\mu}}.

이는 데카르트 좌표에서만 해당된다. 이것이 부분 도함수로 축소되는 것은 데카르트 좌표에서 공변 미분이며, 다른 좌표에서는 그렇지 않다.

더 일반적으로, 4차원 벡터의 ''공''변 성분은 ''역'' 로렌츠 변환에 따라 변환된다.

T_{\mu'} = \Lambda_{\mu'}{}^{\nu} T_\nu,

여기서

\Lambda_{\mu'}{}^{\nu}

는 의 역행렬이다.

특수 상대성 이론의 공준은 로렌츠 변환 행렬이 취하는 정확한 형태를 제한한다.

더 일반적으로, 대부분의 물리량은 (성분으로) 텐서로 가장 잘 설명된다. 따라서 한 프레임에서 다른 프레임으로 변환하기 위해 잘 알려진 텐서 변환 법칙^[129]을 사용한다.

T^{\alpha' \beta' \cdots \zeta'}_{\theta' \iota' \cdots \kappa'} = \Lambda^{\alpha'}{}_{\mu} \Lambda^{\beta'}{}_{\nu} \cdots \Lambda^{\zeta'}{}_{\rho} \Lambda_{\theta'}{}^{\sigma} \Lambda_{\iota'}{}^{\upsilon} \cdots \Lambda_{\kappa'}{}^{\phi} T^{\mu \nu \cdots \rho}_{\sigma \upsilon \cdots \phi}

여기서

\Lambda_{\chi'}{}^{\psi}

는 의 역행렬이다. 모든 텐서는 이 규칙에 따라 변환된다.

4차원 2차 반대칭 텐서의 예로는 상대론적 각운동량이 있으며, 6개의 성분을 갖는다. 세 개는 고전적인 각운동량이고, 다른 세 개는 시스템의 질량 중심의 부스트와 관련이 있다. 고유 시간에 대한 상대론적 각운동량의 도함수는 상대론적 토크이며, 또한 2차 반대칭 텐서이다.

전자기장 텐서는 또 다른 2차 반대칭 텐서장으로, 6개의 성분을 갖는다. 세 개는 전기장이고, 다른 세 개는 자기장이다. 또한 전자기 응력-에너지 텐서 즉, 전자기 응력-에너지 텐서가 있다.

계량 텐서는 두 벡터의 내적을 정의할 수 있게 해주며, 이를 통해 벡터의 크기를 할당할 수 있다. 시공간의 4차원적 특성을 고려할 때, 민코프스키 계량 ''η''는 (적절히 선택된 좌표계에서 유효한) 다음과 같은 성분을 가진다. 이는 4 × 4^영어 행렬로 배열될 수 있다.

\eta_{\alpha\beta} = \begin{pmatrix}

1 & 0 & 0 & 0\\

0 & 1 & 0 & 0\\0 & 0 & 1 & 0\\0 & 0 & 0 & 1\end{pmatrix} ,

이 계량은 해당 좌표계에서 역수 와 같다. 우리는 위와 같은 부호를 사용하며, 다른 저자들은 다른 부호 체계를 사용한다. - 민코프스키 계량 대체 부호 참조.

푸앵카레 군은 민코프스키 계량을 보존하는 가장 일반적인 변환 군이다.

\eta_{\alpha\beta} = \eta_{\mu'\nu'} \Lambda^{\mu'}{}_\alpha \Lambda^{\nu'}{}_\beta

이는 특수 상대성 이론의 근본적인 물리적 대칭이다.

계량은 벡터와 텐서의 지수 올리고 내리기에 사용될 수 있다. 불변량은 계량을 사용하여 구성될 수 있으며, 4-벡터 ''T''와 다른 4-벡터 ''S''의 내적은 다음과 같다.

T^{\alpha}S_{\alpha}=T^{\alpha}\eta_{\alpha\beta}S^{\beta} = T_{\alpha}\eta^{\alpha\beta}S_{\beta} = \text{불변 스칼라}

불변이라는 것은 모든 관성 좌표계에서 동일한 값을 갖는다는 것을 의미한다. 왜냐하면 이는 스칼라(0차 텐서)이므로, 사소한 변환에서 Λ가 나타나지 않기 때문이다. 4-벡터 ''T''의 크기는 자기 자신과의 내적의 양의 제곱근이다.

|\mathbf{T}| = \sqrt{T^{\alpha}T_{\alpha}}

이 아이디어를 고차 텐서로 확장할 수 있다. 2차 텐서의 경우, 다음과 같은 불변량을 형성할 수 있다.

T^{\alpha}{}_{\alpha},T^{\alpha}{}_{\beta}T^{\beta}{}_{\alpha},T^{\alpha}{}_{\beta}T^{\beta}{}_{\gamma}T^{\gamma}{}_{\alpha} = \text{불변 스칼라},

마찬가지로 고차 텐서에서도 적용된다. 불변 표현식, 특히 4-벡터의 자기 자신과의 내적은 계산에 유용한 방정식을 제공한다. 왜냐하면 로렌츠 변환을 수행하지 않고도 불변량을 결정할 수 있기 때문이다.

좌표 미분은 반변적으로 변환된다.

dX^{\mu'}=\Lambda^{\mu'}{}_\nu dX^\nu

따라서 다음과 같이 구성된 위치 사차원 벡터의 미분 ''dX^μ''의 제곱 길이는

d\mathbf{X}^2 = dX^\mu \,dX_\mu = \eta_{\mu\nu}\,dX^\mu \,dX^\nu = -(c\,dt)^2+(dx)^2+(dy)^2+(dz)^2

불변량이다. 선 요소 ''d'''''X'''²가 음수일 때는 고유 시간의 미분이고, ''d'''''X'''²가 양수일 때는 고유 거리의 미분이다.

4-속도 ''U''^μ는 불변 형식을 갖는다.

\mathbf U^2 = \eta_{\nu\mu} U^\nu U^\mu = -c^2 \,,

이는 모든 속도 사차원 벡터가 크기 ''c''를 갖는다는 것을 의미한다. 이것은 상대성 이론에서 좌표 정지 상태라는 것은 없다는 사실을 나타내는 표현이다. 최소한 항상 시간을 통해 앞으로 이동하고 있다. 위의 방정식을 ''τ''로 미분하면 다음과 같다.

2\eta_{\mu\nu}A^\mu U^\nu = 0.

따라서 특수 상대성 이론에서 가속도 사차원 벡터와 속도 사차원 벡터는 직교한다.

운동량 4-벡터의 불변 크기는 에너지-운동량 관계를 생성한다.

\mathbf{P}^2 = \eta^{\mu\nu}P_\mu P_\nu = -\left (\frac{E}{c} \right )^2 + p^2 .

이 불변량이 무엇인지 알아내기 위해 먼저 이것이 스칼라이므로, 우리가 그것을 계산하는 기준틀에 상관없이, 총 운동량이 0인 기준틀로 변환하여 계산해도 된다.

\mathbf{P}^2 = - \left (\frac{E_\text{rest}}{c} \right )^2 = - (m c)^2 .

정지 에너지는 독립적인 불변량임을 알 수 있다. 정지 에너지는 운동하는 입자나 계에 대해서도, 운동량이 0인 기준틀로 변환하여 계산할 수 있다.

정지 에너지는 위에서 논의한 유명한 방정식에 따라 질량과 관련이 있다.

E_\text{rest} = m c^2.

운동량 중심틀(총 운동량이 0인 곳)에서 측정된 계의 질량은 이 틀에서 계의 총 에너지로 주어진다. 다른 틀에서 측정된 개별 계 질량의 합과 같지 않을 수 있다.

뉴턴 운동 제3법칙을 사용하려면, 두 힘 모두 동일한 시간 좌표에 대한 운동량의 변화율로 정의되어야 한다. 즉, 위에 정의된 3차원 힘이 필요하다. 불행히도 3차원 힘 벡터의 성분을 포함하는 4차원 텐서는 없다.

입자가 ''c''로 움직이지 않는 경우, 3차원 힘을 입자의 동행 기준틀에서 관찰자의 기준틀로 변환할 수 있다. 이것은 사차원 힘이라고 하는 4-벡터를 생성한다. 이것은 고유 시간에 대한 위 에너지-운동량 4-벡터의 변화율이다. 사차원 힘의 공변 버전은 다음과 같다.

F_\nu = \frac{d P_{\nu}}{d \tau} = m A_\nu

물체의 정지틀에서, 사차원 힘의 시간 성분은 물체의 "불변 질량"이 변하지 않는 한 0이다(이것은 에너지/질량이 물체에 직접 추가되거나 제거되는 비닫힌 계를 필요로 한다). 이 경우, 그것은 질량 변화율에 ''c''를 곱한 값의 음수이다. 그러나 일반적으로 사차원 힘의 성분은 삼차원 힘의 성분과 같지 않다. 왜냐하면 삼차원 힘은 좌표 시간에 대한 운동량의 변화율, 즉 ''dp''/''dt''로 정의되는 반면, 사차원 힘은 고유 시간에 대한 운동량의 변화율, 즉 ''dp''/''dτ''로 정의되기 때문이다.

연속 매질에서 3차원 ''힘 밀도''는 ''일률 밀도''와 결합하여 공변 4-벡터를 형성한다. 공간 부분은 작은 셀(3차원 공간에서)에 가해지는 힘을 해당 셀의 부피로 나눈 결과이다. 시간 성분은 −1/''c'' 곱하기 해당 셀에 전달된 일률을 해당 셀의 부피로 나눈 값이다. 이것은 아래 전자기학 섹션에서 사용될 것이다.

8. 2. 가속 좌표계

특수 상대성 이론은 관성 좌표계뿐만 아니라 가속 좌표계도 다룰 수 있다. 가속 좌표계에서는 등가 원리에 따라 중력과 유사한 효과가 나타난다.

'''벨의 우주선 역설'''

벨의 우주선 역설은 가속하는 두 우주선 사이의 거리가 변하는 현상을 설명하는 사고 실험이다.

그림 7-4와 같이 두 개의 동일한 우주선이 우주 공간에 떠 있고 서로에 대해 정지해 있다. 이들은 끊어지기 전까지 제한된 양만 늘어날 수 있는 끈으로 연결되어 있다. 주어진 순간에 두 우주선은 같은 방향으로 동일한 상수 고유 가속도로 가속한다.^[112] 이때 끈은 끊어질까?

그림 7-5의 시공간 도표를 통해 이 역설에 대한 올바른 해결책을 확인할 수 있다. 민코프스키 시공간에서 두 관찰자는 고유 시간

\sigma

동안 상수 크기

k

가속도로 가속한다. 이 단계 전후에는 함께 움직이며 관성적이다. 민코프스키 기하학에서 동시성 선

A'B''

을 따른 길이는 동시성 선

AB

를 따른 길이보다 크다.

길이 증가는 로렌츠 변환을 통해 계산할 수 있다. 가속이 완료되면, 우주선은 어떤 틀

S'

에서 일정한 오프셋을 유지한다.

x_{A}

와

x_{B}=x_{A}+L

이 틀

S

에서 우주선의 위치라면, 틀

S'

에서의 위치는 다음과 같다.^[113]

:

\begin{align}x'_{A}& = \gamma\left(x_{A}-vt\right)\\x'_{B}& = \gamma\left(x_{A}+L-vt\right)\\L'& = x'_{B}-x'_{A} =\gamma L\end{align}

'''사상의 지평선'''

사상의 지평선은 가속하는 관찰자에게 특정 영역 너머의 사건을 관측할 수 없는 현상이다.

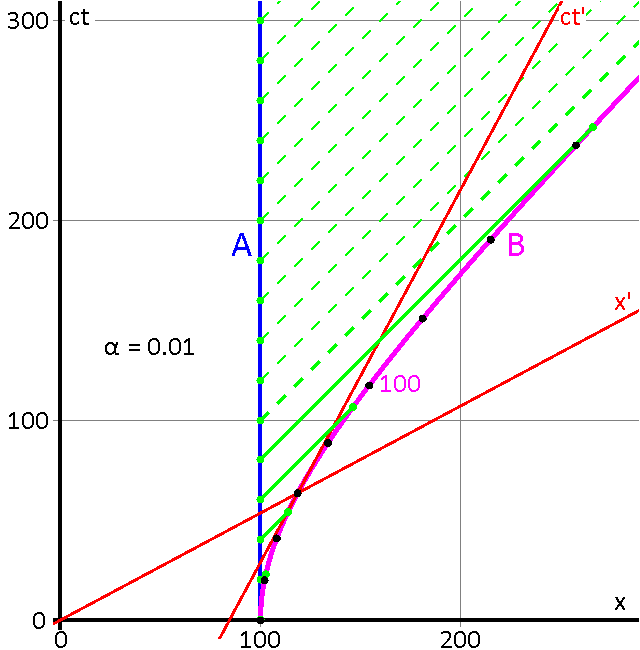
그림 7-6과 같이, 임의의 순간에 가속하는 관찰자의 공간 축은 원점을 통과하고 쌍곡선에서 현재 위치를 통과하는 선으로 형성되며, 시간 축은 위치에서 쌍곡선에 접선이다. 속도 매개변수

\beta

는

ct

가 증가함에 따라 1의 한계에 접근한다. 마찬가지로,

\gamma

는 무한대에 접근한다.

9. 참고 문헌

Relativitätstheorie: Spezielle und allgemeine Relativitätstheorie|상대성 이론: 특수 상대성 이론과 일반 상대성 이론^de, 알베르트 아인슈타인 (1920).
The Meaning of Relativity|상대성의 의미^영어, 알베르트 아인슈타인 (1996). 파인 커뮤니케이션즈.
Анри Пуанкаре и теория относительности|앙리 푸앵카레와 상대성 이론^ru, 아나톨리 A. 로구노프 (2005). 나우카, 모스크바.
Gravity|중력^영어, 찰스 미스너, 킵 손, 존 아치볼드 휠러 (1971). W. H. 프리먼 & Co.
Formal Structure of Electromagnetics: General Covariance and Electromagnetics|전자기학의 형식 구조: 일반 공변성과 전자기학^영어, E.J. 포스트 (1997). 도버 간행물.
Introduction to Special Relativity|특수 상대성이론 입문^영어 (2판), 볼프강 린들러 (1991). 옥스퍼드 대학교 출판부.
Physical Relativity: Space-time Structure from a Dynamical Perspective|물리적 상대성 이론: 역학적 관점에서의 시공간 구조^영어, 하비 R. 브라운 (2005). 옥스퍼드 대학교 출판부.
Relativity: An Introduction to the Special Theory|상대성 이론: 특수 이론 입문^영어, 아스가르 카디르 (1989). 월드 사이언티픽 출판.
Special Relativity (M.I.T. Introductory Physics)|특수 상대성 이론 (M.I.T. 입문 물리학)^영어, A. P. French (1968). W. W. 노턴 & 컴퍼니.
The Theory of Relativity|상대성 이론^영어, 루드비크 실버스타인 (1914).
Space, Time, and Spacetime|공간, 시간 및 시공간^영어, 로렌스 스클라 (1977). 캘리포니아 대학교 출판부.
Philosophy of Physics|물리학의 철학^영어, 로렌스 스클라 (1992). 웨스트뷰 출판사.
Relativistic World|상대론적 세계^영어, 세르게이 스테파노프 (2018). 데 그루이터.
Spacetime Physics|시공간 물리학^영어 (2판), 에드윈 테일러, 존 아치볼드 휠러 (1992). W. H. 프리먼 & Co.
Modern Physics|현대 물리학^영어 (4판), 폴 티플러, 랄프 럴린 (2002). W. H. 프리먼 & Co.
Test of the Second Postulate of Special Relativity in the GeV Region|GeV 영역에서의 특수 상대성 이론 제2 공준 검증^영어, T. Alvager et al. (1964). ''Physics Letters''.
The Mysterios Connection Between Henri Poincaré and Albert Einstein|앙리 푸앵카레-알베르트 아인슈타인 연결의 미스터리^영어, 올리비에 다리고 (2004). ''Isis''.
Satellite Test of Special Relativity Using the Global Positioning System|GPS를 이용한 특수 상대성 이론의 위성 시험^영어, 피터 볼프, 제라드 프티 (1997). ''Physical Review A''.
Special relativity|특수 상대성 이론^영어, 스콜라피디아.
Special relativity: kinematics|특수 상대성 이론: 운동학^영어, 볼프강 린들러 (2011). 스콜라피디아.
Zur Elektrodynamik bewegter Körper|운동하는 물체의 전기역학에 관하여^de, 알베르트 아인슈타인 (1905). 안날렌 데어 피지크, 베른.
On the Electrodynamics of Moving Bodies|운동하는 물체의 전기역학에 관하여^영어 (1923). ''상대성 원리''에 출판된 영어 번역본.
相対性理論|상대성 이론^일본어, 알베르트 아인슈타인, 우치야마 타츠오 번역 (1988). 이와나미 문고, 이와나미 서점.
Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?|물체의 관성은 그 에너지의 크기에 의존하는가^de, A. 아인슈타인 (1905). 안날렌 데어 피지크, 라이프치히.
Über die Grundgleichungen der Electrodynamik für bewegte Körper|운동 물체에 대한 전기역학의 기본 방정식에 관하여^de, 하인리히 헤르츠 (1890). 안날렌 데어 피지크, 라이프치히.
相対性理論|상대성 이론^일본어, 사토 가츠히코 (1996). 이와나미 쇼텐.
特殊相対論|특수 상대론^일본어, 슈츠, 에리구치 료지・후타마세 토시후미 번역 (2010). 마루젠.
場の古典論 = 전기역학, 특수 및 일반 상대성 이론=|장의 고전론 = 전기역학, 특수 및 일반 상대성 이론=^일본어, 란다우, 리프시츠, 츠네토 토시히코・히로시게 토오루 번역 (1978). 도쿄도서출판.
The Classical Theory of Fields|장의 고전론^영어, L.D. 란다우, E.M. 리프시츠 (1971).
線形代数と特殊相対論|선형대수와 특수 상대론^일본어, 마에하라 쇼지 (1993). 니혼 효론샤.
ローレンツ電子論|로렌츠 전자론^일본어, H.A. 로렌츠, 히로시게 토오루 번역 (1973).
アインシュタインの相対性原理|아인슈타인의 상대성 원리^일본어, M. 본, W. 빔, 세야 마사오 번역 (1971). 코단샤.
相対性理論|상대성 이론^일본어, 멜러, 나가타 츠네오, 이토 다이스케 번역 (1959). 미스즈 서방.
アインシュタイン|아인슈타인^일본어, 야노 켄타로 (1991). 코단샤.
相対論の意味|상대론의 의미^일본어, 알베르트 아인슈타인, 야노 켄타로 번역 (1958). 이와나미 서점.
理論電磁気学|이론 전자기학^일본어, 스나가와 시게노부 (1999). 키노쿠니야 서점.
電磁気学|전자기학^일본어, 스나가와 시게노부 (1987). 이와나미 서점.
詳解電磁気学演習|상세 전자기학 연 습^일본어, 고토 켄이치 (1970).
相対論はどこから生まれたか|상대론은 어디에서 태어났는가^일본어, 히로시게 토오루 (1971). 일본 물리학회.
ファインマン物理学〈3〉電磁気学|파인만 물리학〈3〉전자기학^일본어, 파인만, 미야지마 류오 번역 (1986). 이와나미 서점.
電磁気学初めて学ぶ電磁場理論|전자기학 처음 배우는 전자기장 이론^일본어, 엔도 마사모리 (2013). 모리키타 출판.
史上最強図解これならわかる! 電磁気学|사상 최강 그림해설 이것만 알면 돼! 전자기학^일본어, 엔도 마사모리 (2014). 나츠메사.
物理学史Ⅱ|물리학사Ⅱ^일본어, 히로시게 토오루 (1968). 바이후칸.
一般相対性理論|일반 상대성 이론^일본어, 노무라 키요히데 (2019). 큐슈 대학.
相対性理論|상대성 이론^일본어, 우치야마 타츠오 (1977). 이와나미 서점.
相対性理論(上)|상대성 이론(상)^일본어, W. 파울리 (2007). 치쿠마 서방.
趣味で相対論|취미로 상대론^일본어, 히로에 카츠히코 (2008). 리코 도서.
相対性理論と量子力学の誕生|상대성 이론과 양자역학의 탄생^일본어, 알베르트 아인슈타인, 슈뢰딩거 외, 타니카와 야스타카, 나카무라 세이타로, 아오키 쇼조 번역 (1972).
原子時計を測る -300億分の1秒物語|원자 시계를 측정한다 -300억 분의 1초 이야기^일본어, 토니 존스, 마츠우라 슌스케 번역 (2001). 아오토사.
電波測距儀|전파 거리 측정기^일본어, 스다 교아키 (1976). 모리키타 출판.
On the Relative Motion of the Earth and the Luminiferous Ether|지구와 빛을 전달하는 에테르의 상대 운동에 관하여^영어, 마이컬슨, 몰리 (1887). ''아메리칸 저널 오브 사이언스''.
電波時計のしくみ|전파 시계의 구조^일본어, 이와마 츠카사 (2011). 전자 정보 통신 학회.
理科年表|이과 연표^일본어, 국립 천문대 (2012).
弾性体と流体|탄성체와 유체^일본어, 츠네후지 토시히코 (1983). 이와나미 서점.
質量の起源|질량의 기원^일본어, 막스 얀머, 오오츠키 요시히코, 하타노 요시카즈, 사이토 타케시 번역 (1977). 고단샤.
Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern|운동하는 물체에서의 전자기적·광학적 현상을 이론화하려는 시도^de, 헨드릭 로렌츠 (1895).
Electromagnetic phenomena in a system moving with any velocity smaller than that of light|광속 이하의 속도로 운동하는 계에서의 전자기 현상^영어, 헨드릭 로렌츠 (1904). 네덜란드 왕립 학술원.
Sur la dynamique de l'électron|전자의 동역학에 대하여^프랑스어, 앙리 푸앵카레 (1905). ''Rendiconti del Circolo matematico di Palermo''.
The principle of relativity; original papers|상대성 원리; 원본 논문^영어, 알베르트 아인슈타인, 헤르만 민코프스키 (1920).
Measurement of the Red Shift in an Accelerated System Using the Mössbauer Effect in Fe, H. J. Hay et al. (1960). ''Phys. Rev. Lett.''.

10. 같이 보기

쌍둥이 역설^[57], 벨의 우주선 역설

참조

_[1] 서적 Introduction to Electrodynamics Pearson
_[2] 서적 Classical Electrodynamics John Wiley & Sons
_[3] 논문 Zur Elektrodynamik bewegter Körper https://web.archive.[...] Annalen der Physik 1905
_[4] 서적 Classical Mechanics Addison-Wesley Publishing Company
_[5] 서적 The Variational Principles of Mechanics Dover Publications
_[6] 웹사이트 What is the experimental basis of Special Relativity? http://www.edu-obser[...] 2008-09-17
_[7] 서적 Relativity: The Special and the General Theory https://books.google[...] Routledge 2001
_[8] 웹사이트 The Feynman Lectures on Physics Vol. I Ch. 15-9: Equivalence of mass and energy https://feynmanlectu[...]
_[9] 간행물 Science and Common Sense The Scientific Monthly 1954-07
_[10] 간행물 The Electromagnetic Mass and Momentum of a Spinning Electron Proceedings of the National Academy of Sciences 1926
_[11] 간행물 Kinematics of an electron with an axis Phil. Mag.
_[12] 문서 Einstein himself, in The Foundations of the General Theory of Relativity, Ann. Phys. 49 (1916), writes "The word 'special' is meant to intimate that the principle is restricted to the case ...". See p. 111 of The Principle of Relativity, A. Einstein, H. A. Lorentz, H. Weyl, H. Minkowski, Dover reprint of 1923 translation by Methuen and Company.
_[13] 웹사이트 Lecture Notes on General Relativity http://ned.ipac.calt[...]
_[14] 문서 Wald, General Relativity, p. 60: "... the special theory of relativity asserts that spacetime is the manifold $\mathbb{R}^4$ with a flat metric of Lorentz signature defined on it. Conversely, the entire content of special relativity ... is contained in this statement ..."
_[15] 서적 Explorations in Mathematical Physics: The Concepts Behind an Elegant Language https://books.google[...] Springer Science & Business Media
_[16] 서적 Relativity Made Relatively Easy https://books.google[...] OUP Oxford
_[17] 서적 Essential Relativity: Special, General, and Cosmological https://books.google[...] Springer Science & Business Media 1977
_[18] 문서 Autobiographical Notes 1949
_[19] 웹사이트 James Clerk Maxwell: a force for physics https://physicsworld[...] 2024-03-22
_[20] 웹사이트 November 1887: Michelson and Morley report their failure to detect the luminiferous ether http://www.aps.org/p[...] 2024-03-22
_[21] 문서 Personal Knowledge: Towards a Post-Critical Philosophy https://books.google[...] 1974
_[22] 문서 Fundamental Ideas and Methods of the Theory of Relativity 1920
_[23] 문서 Spacetime and Electromagnetism 1990
_[24] 서적 The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity https://books.google[...] Courier Dover Publications 1952
_[25] 문서 Einstein, On the Relativity Principle and the Conclusions Drawn from It, 1907; "The Principle of Relativity and Its Consequences in Modern Physics", 1910; "The Theory of Relativity", 1911; Manuscript on the Special Theory of Relativity, 1912; Theory of Relativity, 1913; Einstein, Relativity, the Special and General Theory, 1916; The Principal Ideas of the Theory of Relativity, 1916; What Is The Theory of Relativity?, 1919; The Principle of Relativity (Princeton Lectures), 1921; Physics and Reality, 1936; The Theory of Relativity, 1949.
_[26] 서적 A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity Incomprehensible Books
_[27] 서적 Einstein's generation. The origins of the relativity revolution University of Chicago Press 2009
_[28] 서적 Physical Applications of Homogeneous Balls 2004
_[29] 서적 Introduction to Classical Mechanics Cambridge University Press 2007
_[30] 서적 The Special Theory of Relativity, A Mathematical Exposition Springer 1993
_[31] 서적 Independent Axioms for Minkowski Spacetime Addison Wesley Longman Limited 1997
_[32] 간행물 A constructive approach to the special theory of relativity
_[33] 서적 The Geometry of Spacetime: An Introduction to Special and General Relativity Springer 2011
_[34] 서적 Introduction to the Theory of Relativity Dover edition 1976
_[35] 서적 Space and Time in Special Relativity https://archive.org/[...] McGraw-Hill 1968
_[36] 서적 Introduction to special relativity https://books.google[...] Wiley 1968
_[37] 서적 Albert Einstein's Special Theory of Relativity: Emergence (1905) and Early Interpretation (1905–1911) Springer-Verlag 1998
_[38] 간행물 The rotation of the plane of polarization in moving media http://www.dwc.knaw.[...] 2018-11-15
_[39] 간행물 Electromagnetic phenomena in a system moving with any velocity smaller than that of light http://www.dwc.knaw.[...] 2018-11-15
_[40] 서적 Attempt at a Theory of Electrical and Optical Phenomena in Moving Bodies (Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern) https://en.wikisourc[...] E. J. Brill 1895
_[41] 서적 Secrets of the Old One: Einstein, 1905 Copernicus Books (imprint of Springer Science + Business Media) 2006
_[42] 간행물 The Genesis of the Theory of Relativity http://www.bourbaphy[...] 2018-11-15
_[43] 문서 This concept is counterintuitive at least for the fact that, in contrast to usual concepts of [[distance]], it may assume ''negative'' values (is not [[Positive-definite bilinear form|positive definite]] for non-coinciding events), and that the ''square''-denotation is misleading. This ''negative square'' lead to, now not broadly used, concepts of [[Minkowski space#History|''imaginary time'']]. It is immediate that the negative of Δ''s''² is also an invariant, generated by a variant of the [[metric signature]] of spacetime.
_[44] 서적 Essential Relativity Springer-Verlag 1977
_[45] 간행물 Relativity in the Global Positioning System
_[46] 간행물 Sensitivity analysis of the Sagnac-effect optical-fiber ring interferometer 1979
_[47] 서적 An Introduction to Mechanics https://archive.org/[...] McGraw-Hill 1973
_[48] 서적 Special Relativity W. W. Norton & Company 1968
_[49] 간행물 The Principle of Relativity, and Non-Newtonian Mechanics https://en.wikisourc[...] 2023-08-22
_[50] 간행물 Paul Langeyin and the Theory of Relativity http://www.isc.meiji[...] 2023-06-12
_[51] 서적 Understanding Physics https://books.google[...] Springer-Verlag
_[52] 서적 Astronomy, A Physical Perspective https://books.google[...] Cambridge University Press
_[53] 서적 Flat and Curved Space-times https://books.google[...] Oxford University Press
_[54] 서적 The feynman lectures on physics; vol I: The new millennium edition https://www.feynmanl[...] Basic Books 2023-06-12
_[55] 서적 Fundamental Physics: Extended Third Edition John Wiley & sons 1988
_[56] 서적 Relativity: An introduction to space-time physics https://books.google[...] CRC Press
_[57] 간행물 L'Évolution de l'espace et du temps https://en.wikisourc[...] 2023-06-20
_[58] 간행물 The twin "paradox" and the conventionality of simultaneity
_[59] 서적 Spacetime Physics https://archive.org/[...] W. H. Freeman and Company 1966
_[60] 간행물 Length Contraction Paradox 1962
_[61] 서적 The Theory of the Relativity of Motion https://books.google[...] University of California Press 1917
_[62] 간행물 The Tachyonic Antitelephone 1970
_[63] 웹사이트 Special Relativity Lecture Notes – Section 10 https://www1.phys.vt[...] Virginia Tech 2018-10-31
_[64] 서적 Special Relativity for the Enthusiastic Beginner CreateSpace Independent Publishing Platform 2017
_[65] 웹사이트 Is Faster-Than-Light Travel or Communication Possible? http://math.ucr.edu/[...] Department of Mathematics, University of California, Riverside 2018-10-31
_[66] 서적 Applications of Electrodynamics in Theoretical Physics and Astrophysics https://books.google[...] CRC Press
_[67] 서적 Four Decades of Scientific Explanation https://books.google[...] University of Pittsburgh 2006
_[68] 간행물 Measuring Speed of Light: Why? Speed of what? http://sci-ed.org/do[...] 2015-07-03
_[69] 간행물 Fresnel's coefficient for light of different colours. (First part) https://archive.org/[...]
_[70] 간행물 Fresnel's coefficient for light of different colours. (Second part) https://archive.org/[...]
_[71] 서적 The universe of general relativity Birkhäuser 2012-04-17
_[72] 서적 Basic Relativity https://books.google[...] Springer 2001
_[73] 서적 Explanatory Supplement to the Astronomical Almanac https://archive.org/[...] University Science Books 1992
_[74] 논문 European Physical Society logo Arago (1810): the first experimental result against the ether
_[75] 웹사이트 Airy's Water Telescope (1870) http://www.royalobse[...] The Royal Observatory Greenwich 2018-11-20
_[76] 논문 Airy's water telescope http://adsbit.harvar[...] 2018-11-20
_[77] 서적 Going Critical Springer 2004
_[78] 논문 The Relativistic Doppler Effect http://adsbit.harvar[...] 2018-10-11
_[79] 서적 The Doppler Effect Logos Press Limited 1965
_[80] 서적 The Feynman Lectures on Physics: Volume 1 Addison-Wesley 1977-02
_[81] 논문 Invisibility of the Lorentz Contraction 1959-11-15
_[82] 논문 The Apparent Shape of a Relativistically Moving Sphere 2008-10-24
_[83] 웹사이트 Relativistic Distortion http://www.math.ubc.[...] Mathematics Department, University of British Columbia 2017-04-12
_[84] 웹사이트 Appearances at Relativistic Speeds https://web.archive.[...] Michigan State University, East Lansing, MI 2017-04-12
_[85] 웹사이트 The Ball is Round https://web.archive.[...] Institut für Physik Universität Hildesheim 2017-04-16
_[86] 논문 Apparent Shape of Large Objects at Relativistic Speeds 1961
_[87] 논문 Visual appearance of wireframe objects in special relativity 2014
_[88] 문서
_[89] 서적 Superluminal Radio Sources Cambridge University Press 1987
_[90] 웹사이트 Apparent Superluminal Velocity of Galaxies http://math.ucr.edu/[...] Department of Mathematics, University of California, Riverside 2017-04-12
_[91] 웹사이트 "Superluminal" motions in astronomical sources https://web.archive.[...] School of Physics and Astronomy, Rochester Institute of Technology 2017-04-20
_[92] 웹사이트 Jets, Superluminal Motion, and Gamma-Ray Bursts https://web.archive.[...] Department of Physics and Astronomy, University of Alabama 2017-04-29
_[93] 간행물 Does the inertia of a body depend upon its energy content? http://www.fourmilab[...]
_[94] 서적 Concepts of Mass in Classical and Modern Physics https://books.google[...] Courier Dover Publications 1997
_[95] 서적 Einstein from ''B'' to ''Z'' https://books.google[...] Springer 2002
_[96] 간행물 "On the Inertia of Energy Required by the Relativity Principle'" https://archive.toda[...]
_[97] 문서
_[98] 서적 Einstein's Mass–Energy Equation, Volume I: Early History and Philosophical Foundations Momentum Pres 2018
_[99] 웹사이트 Acceleration in special relativity: What is the meaning of "uniformly accelerated movement" ? http://www.normalesu[...] Physics Department, ENS Cachan 2016-01-22
_[100] 웹사이트 The Relativistic Rocket http://math.ucr.edu/[...] 2012-08-30
_[101] 웹사이트 The special theory of relativity shows that time and space are affected by motion http://library.think[...]
_[102] 웹사이트 "Mechanics and Relativity. Chapter 14: Relativistic Collisions" https://phys.librete[...] California State University Affordable Learning Solutions Program 2023-01-02
_[103] 논문 The elementary process of bremsstrahlung 1994
_[104] 서적 The Two-Body Force in Nuclei Springer 1972
_[105] 논문 On some close collisions of fast β-particles with electrons, photographed by the expansion method. The Royal Society Publishing
_[106] 서적 Thomas' Calculus: Early Transcendentals Pearson Education, Inc. 2008
_[107] 서적 Spacetime Physics https://archive.org/[...] W. H. Freeman 1992
_[108] 문서
_[109] 서적 Formal Structure of Electromagnetics: General Covariance and Electromagnetics Dover Publications Inc. 1962
_[110] 서적 A first course in general relativity Cambridge University Press 1985
_[111] 웹사이트 Can Special Relativity Handle Acceleration? http://math.ucr.edu/[...] math.ucr.edu 2017-05-28
_[112] 문서
_[113] 간행물 Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity
_[114] 서적 Very Special Relativity: An Illustrated Guide https://archive.org/[...] Harvard University Press 2007
_[115] 서적 Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles https://archive.org/[...] John Wiley & Sons 1985
_[116] 간행물 A Theory of Electrons and Protons 1930
_[117] 간행물 The Positive Electron 1933
_[118] 서적 Einstein's general theory of relativity: with modern applications in cosmology https://books.google[...] Springer 2007
_[119] 간행물
_[120] 웹사이트 Experiments that Apparently are NOT Consistent with SR/GR https://math.ucr.edu[...] University of California at Riverside 2024-07-10
_[121] 간행물 Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905 http://philsci-archi[...] 2004
_[122] 간행물 On the role of the Michelson–Morley experiment: Einstein in Chicago 2009
_[123] 서적 Gravitation W.H. Freeman & Co 1973
_[124] 서적 Dynamics and Relativity Wiley 2009
_[125] 서적 The Road to Reality Vintage books 2007
_[126] 서적 Quantum Field Theory
_[127] 서적 Gravitation
_[128] 서적 An Introduction to Quantum Field Theory
_[129] 서적 Spacetime and Geometry: An Introduction to General Relativity https://books.google[...] Addison Wesley 2004
_[130] 문서
_[131] 문서
_[132] 문서
_[133] 문서
_[134] 문서
_[135] 문서
_[136] 문서
_[137] 문서
_[138] 문서
_[139] 웹사이트 Derivations of the Lorentz transformations - Wikipedia https://en.wikipedia[...]
_[140] 문서
_[141] 문서
_[142] 문서
_[143] 문서
_[144] 문서
_[145] 문서
_[146] 문서
_[147] 문서
_[148] Kotobank ローレンツ収縮
_[149] Kotobank フィッツジェラルド‐ローレンツ短縮
_[150] 웹사이트 相対論2009年度第14回 http://www.phys.u-ry[...] 琉球大学 2015-12-24
_[151] 문서
_[152] 문서
_[153] 문서
_[154] 문서
_[155] Youtube 当時の映像 gdRmCqylsME
_[156] 문서
_[157] 문서
_[158] 문서
_[159] 서적 Spacetime Physics: Introduction to Special Relativity https://archive.org/[...] W. H. Freeman 1992
_[160] 웹사이트 Experimental Basis of Special Relativity http://www.edu-obser[...]
_[161] 논문 La théorie de Lorentz et le principe de réaction 1900
_[162] 저널 The Ether and the Earth’s Atmosphere 1889-05-17
_[163] 저널 La Théorie electromagnétique de Maxwell et son application aux corps mouvants 1892
_[164] 저널 The Relative Motion of the Earth and the Aether 1892
_[165] 서적 Attempt of a Theory of Electrical and Optical Phenomena in Moving Bodies E.J. Brill 1895
_[166] 저널 A Dynamical Theory of the Electric and Luminiferous Medium. Part III. Relations with Material Media 1897
_[167] 저널 Zur Elektrodynamik bewegter Körper http://wikilivres.ca[...] 2012-11-05
_[168] 저널 Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com