반응 속도식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

반응 속도식은 화학 반응의 속도를 반응물의 농도 변화로 나타내는 식이다. 반응 속도식은 반응 차수와 반응 속도 상수를 포함하며, 실험을 통해 결정된다. 반응 속도식은 초기 속도 방법, 적분 방법, 넘침 방법 등을 통해 결정될 수 있으며, 0차, 1차, 2차 반응 등 다양한 형태를 가진다. 반응 속도에 영향을 미치는 요인으로는 농도, 온도, 촉매, 용매 등이 있으며, 복잡한 반응 메커니즘과 평형 반응, 연속 반응, 병렬 반응 등 다양한 반응 유형을 설명하는 데 활용된다. 반응 속도론은 화학 공학, 약학, 환경 과학 등 다양한 분야에 응용된다.

더 읽어볼만한 페이지

화학반응속도론 - 반응 속도
반응 속도는 닫힌 계에서 화학 반응의 진행 속도를 나타내는 물리량으로, 반응물과 생성물의 농도 변화율을 화학량론 계수로 나눈 값이며 다양한 요인에 영향을 받고 반응 메커니즘 연구에 필수적이다.
화학반응속도론 - 연쇄반응
연쇄 반응은 분자 반응으로 생성물과 불안정한 분자가 생성되어 추가 반응을 촉발하는 과정으로, 화학, 핵반응, 기체 내 전자 사태, 반도체 항복, 생명체 내 반응 등에서 관찰되며 개시, 성장, 종결 단계를 거친다.

반응 속도식
반응 속도식
정의	화학 반응의 속도를 반응물 또는 생성물의 농도와 관련시키는 방정식
형태	반응 속도 = k[A]^x[B]^y
설명	여기서 k는 반응 속도 상수, [A]와 [B]는 반응물의 농도, x와 y는 각 반응물의 부분 반응 차수이다.
반응 차수
정의	속도식에서 농도 항의 지수의 합
예시	위의 식에서 전체 반응 차수는 x + y이다.
속도 상수 (k)
정의	특정 온도에서 반응 속도와 반응물 농도 간의 비례 상수
단위	반응 차수에 따라 달라짐
반응 속도 결정 단계
정의	다단계 반응에서 가장 느린 단계
중요성	전체 반응 속도를 결정함
예시
반응	2NO(g) + O2(g) → 2NO2(g)
속도식	반응 속도 = k[NO]^2[O2]
설명	이 반응은 NO에 대해 2차, O2에 대해 1차, 전체적으로 3차 반응이다.
영향 요인
농도	일반적으로 반응물의 농도가 증가하면 반응 속도도 증가함
온도	일반적으로 온도가 증가하면 반응 속도 상수 k가 증가하여 반응 속도가 증가함. 아레니우스 방정식 참조.
촉매	촉매는 활성화 에너지를 낮추어 반응 속도를 증가시킴

2. 정의

두 반응물 A와 B가 결합해 생성물 C를 만드는 일반적인 화학 반응을 가정해 보자.

: $\mathrm{A} + 2\mathrm{B} \rightarrow 3\mathrm{C}.$

이는 다음과 같이 표현할 수 있다.

: $0 = -\mathrm{A} - 2\mathrm{B} + 3\mathrm{C}.$

주어진 계수 -1, -2, 3 (반응물은 소비되기 때문에 음의 부호)들은 화학양론 계수로, 하나의 A 분자가 2개의 B와 결합하여 3개의 C를 생성하는 반응이다. 그러므로, 기호 [X]를 반응하는 물질 X의 몰 농도라 정의하면 다음과 같이 나타낼 수 있다.^[3]

: $-\frac{d[\mathrm{A}]}{dt} = - \frac{1}{2} \frac{d[\mathrm{B}]}{dt} = \frac{1}{3} \frac{d[\mathrm{C}]}{dt}.$

만약 반응이 반응 중간체를 생성하지 않고, 일정한 온도와 부피를 가진 닫힌계에서 일어난다면, ''반응 속도''는 다음과 같이 정의된다.

: $v = \frac{1}{\nu_i} \frac{d[\mathrm{X}_i]}{dt},$

이 식에서 $\nu_i$ 는 X_''i''에 대한 화학양론 계수이다.^[4]

3. 반응 차수와 반응 속도

반응 속도식은 일반적으로 멱법칙(Power laws)으로 표현되며, 반응 차수는 실험적으로 결정된다.^[56] 반응 차수는 각 반응물의 농도가 반응 속도에 미치는 영향을 나타내는 지수이다.

묽은 용액에서 단일단계반응은 경험적으로 질량작용의 법칙을 따르며, 반응 속도는 화학양론계수에서 얻어진 차수와 반응물의 농도에만 의존한다.^[58]

반응 속도식의 일반적인 형태는 다음과 같다:^[6]

: $v_0 = k[\ce A]^x[\ce B]^y \cdots$

여기서,

''k''는 속도 상수이다.
''x'', ''y''는 각 반응물의 부분 반응 차수이며, 분수일 수도 있다.
전체 반응 차수는 부분 반응 차수의 합이다.^[7]

단일 반응 (단일 전이상태를 가진 단일 단계 반응)은 질량 작용의 법칙을 따르며, 반응 속도는 반응물의 농도에만 의존하고, 농도는 화학량론적 계수의 거듭제곱으로 표현된다고 예측한다.^[8]

수학적 곱셈 표기법을 사용한 단일 반응에 대한 미분 반응 속도식은 다음과 같다.

:

-{d\over dt}[\text{반응물}] = k \prod_i [\text{반응물}_i]

여기서,

$-{d\over dt}[\text{반응물}]$ 은 시간에 따른 반응물 농도 변화의 속도이다.
''k''는 반응의 속도 상수이다.
$\prod_i [\text{반응물}_i]$ 는 반응물의 농도를 화학량론적 계수의 거듭제곱으로 표현하여 모두 곱한 것을 나타낸다.

3차 반응 이상은 기본적인 반응에서는 거의 일어나지 않지만, 반응 전체에서는 정수가 아닌 것을 포함하여 어떤 차수 반응이라도 일어날 수 있다.

반응 차수에 따른 반응 속도식, 적분형 반응 속도식, 속도 상수 단위, 직선 플롯, 반감기
반응 차수	반응 속도식	적분형 반응 속도식	속도 상수(k)의 단위	k를 결정할 때의 직선 플롯	반감기
0차 반응	$-{d[A]}/{dt} = k$	$\ [A] = [A]_0 - kt$	$\rm\frac{M}{s}$	$[A] \ \mbox{vs.} \ t$	$t_{1/2} = \frac{[A]_0}{2k}$
1차 반응	$-{d[A]}/{dt} = k[A]$	$\ [A] = [A]_0 e^{-kt}$	$\rm\frac{1}{s}$	$\ln ([A]) \ \mbox{vs.} \ t$	$t_{1/2} = \frac{\ln (2)}{k}$
2차 반응	$-{d[A]}/{dt} = k[A]^2$ ^[45]	$\frac{1}{[A]} = \frac{1}{[A]_0} + kt$ ^[45]	$\rm\frac{1}{M \cdot s}$	$\frac{1}{[A]} \ \mbox{vs.} \ t$	$t_{1/2} = \frac{1}{k[A]_0}$ ^[45]
n차 반응 (n≧2)	$-{d[A]}/{dt} = k[A]^n$	$\frac{1}{[A]^{n-1}} = \frac{1} + (n-1)kt$	$\frac{1} \ \mbox{vs.} \ t$	$t_{1/2} = \frac{2^{n-1}-1}{(n-1)k{[A]_0}^{n-1}}$

위 표에서 M은 몰 농도(mol·L^-1), ''t''는 시간, ''k''는 속도 상수를 나타낸다.

3. 1. 초기 속도 방법

초기 속도 방법은 반응 초기에 농도 변화를 측정하여 반응 차수를 결정하는 방법이다.^[59]^[60] 어떤 반응물에 대한 반응 차수는 반응물의 농도가 달라질 때의 초기 속도를 다음 반응 속도식의 자연 로그를 사용해서 추정할 수 있다.

:

\ln r = \ln k + x\ln[A] + y\ln[B] + ...

예를 들어, 반응물 A의 초기 농도를 다르게 하고 다른 농도 [B], [C], ...를 일정하게 한 일련의 실험에서 초기 속도를 측정해서 다음을 만들 수 있다.

:

\ln r = x\ln[A] + \textrm{constant}

그러면,

\ln [A]

에 대한

\ln r

의 그래프의 기울기는 반응물 A의 반응 차수 x에 대응한다.^[9]^[10]

하지만, 이 방법은 항상 신뢰할 수 있는 것은 아니다.

# 초기 속도의 측정은 (반감기에 비해서) 짧은 시간 동안의 농도의 작은 변화를 정확히 결정해야 하며, 오차가 민감하다.

# 반응 속도식은 중간물이나 생성물 같이 반응 속도가 반응이 시작할 때 존재하지 않는 물질에 의존할 경우에는 완전히 결정되지 않는다.

3. 2. 적분 방법

적분 방법은 시간에 따른 농도 변화를 측정하여 반응 속도식의 적분형과 비교하여 반응 차수를 결정하는 방법이다. 초기 속도 방법으로 결정된 잠정적 반응 속도식은 일반적으로 긴 시간(여러 번의 반감기)동안 측정된 농도를 반응 속도식의 적분형과 비교해서 검증된다.^[61]^[62]

예를 들어, 일차 반응의 적분된 반응 속도 법칙은 다음과 같다.

:

\ \ln{[A]} = -kt + \ln{[A]_0}

이 때, [A]는 시간 t일 때 농도이고 [A]₀은 시간이 0일 때의 초기 농도이다. 일차 반응 속도 법칙은

\ln{[A]}

가 시간에 관한 선형 함수일 때 검증된다. 이 경우, 반응 상수

k

는 기울기에 부호가 거꾸로 된 것이다.^[61]^[62]

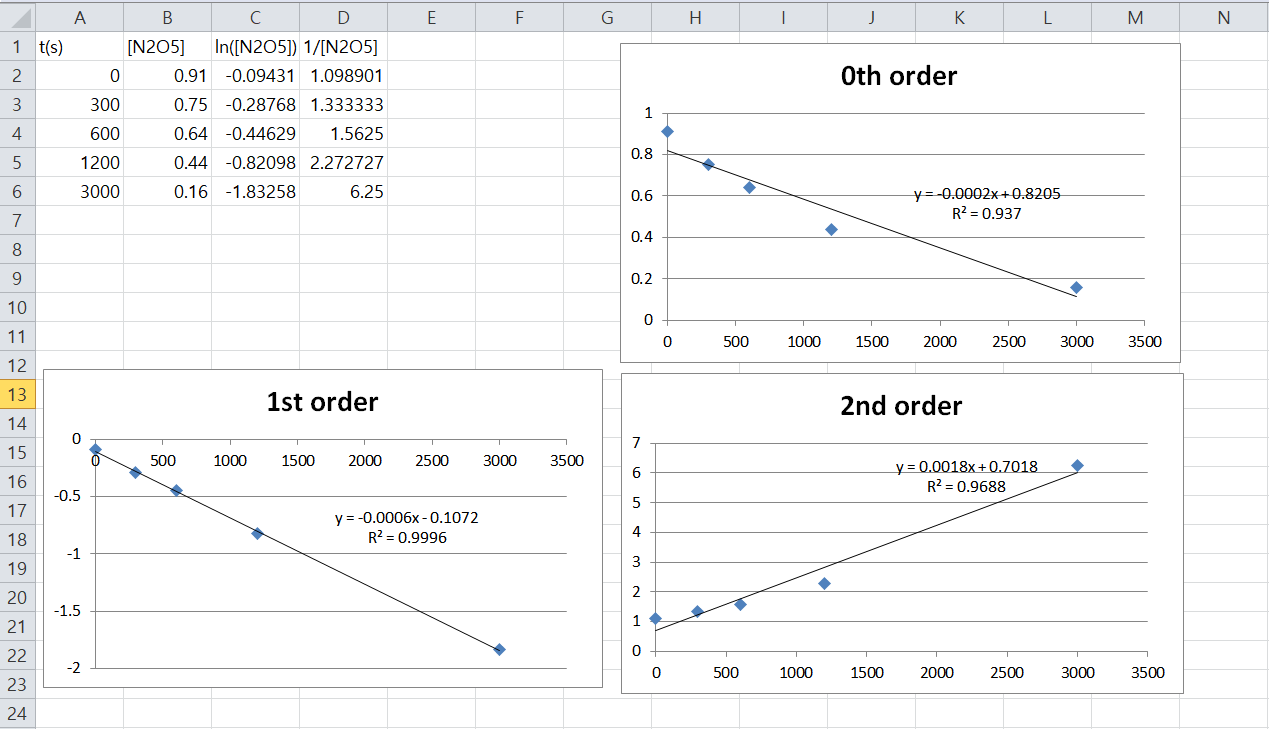
위 적분 방법의 적용 방법으로는 데이터 플로팅(data plotting)이 있다. 주어진 시간에 따른 농도를 그래프를 그려서 플로팅을 한 후에 시간과

[A]

,

ln[A]

, 또는

1/[A]

의 선형관계를 통해 각각 0차, 1차, 또는 2차에서의 속도 법칙을 검증할 수 있다. 이때 상관분석을 통해서 r² 값이 1에 제일 가까운 관계인 것(즉, 선형에 제일 가까운 것)이 해당 차수가 되는 것이다. 예를 들어 시간과

[A]

,

ln[A]

, 또는

1/[A]

사이의 r² 값 중에 시간과

ln[A]

사이의 r² 값이 1에 제일 가까우면 해당 반응은 1차 반응이 된다.

간단한 예시로 45°C에서 오산화 이질소(N₂O₅)가 사염화 탄소(CCl₄) 용매 안에서 분해되는 반응의 반응 차수와 속도 상수를 그래프를 이용하여 구하면 다음과 같다.^[71]

:2N₂O₅(CCl₄) → 4NO₂(g)+O₂(g)

다음 표는 시간에 따른 N₂O₅의 농도 변화 값을 보여준다.

시간에 따른 N₂O₅ 농도 변화
t (s)	[N₂O₅] (M)
0	0.91
300	0.75
600	0.64
1200	0.44
3000	0.16

위의 값을 이용하여 시간에 따른 $[N_2O_5]$ , $ln[N_2O_5]$ , $1/[N_2O_5]$ 의 값을 계산하고 그래프를 그린 후에 r² 값, 추세선 방정식을 엑셀 프로그램과 같은 데이터 플로팅이 가능한 플로터 프로그램을 이용하여 구한다. 우측 상단의 그림에서 알 수 있듯이 시간과 $ln[N_2O_5]$ 사이의 r² 값이 1에 제일 가까우므로, 이 반응은 1차 반응이다. 다음으로, 시간에 대한 $ln[N_2O_5]$ 의 그래프 직선 위에 있는 임의의 두 실험값으로부터 기울기를 구함으로써 속도 상수를 결정할 수 있다. 즉, 그 점들의 y값( $ln[N_2O_5]$ 값)과 x값(시간)의 차이에 대한 비로부터 기울기를 구할 수 있다. 이 때, 속도 상수 k에 대하여 $k=-m$ 이다. 이를 통해 위의 반응의 속도 상수를 구하면 $k=5.7\times10^{-4}s^{-1}$ 이다.^[72]

3. 3. 넘침 방법 (오스트발트 방법)

오스트발트의 넘침 방법(혹은 고립 방법)은 주어진 반응물에 대한 부분적 반응 차수를 계산하는 방법이다. 이 방법에서는 한 반응물의 농도를 다른 모든 반응물에 비해 매우 높게 유지하여 농도가 사실상 일정하게 만든다.^[73]

예를 들어 반응 속도 법칙이

r = k \cdot [{\rm A}]^\alpha \cdot [{\rm B}]^\beta

인 반응 a·A + b·B → c·C에서, A에 대한 부분적 반응 차수 α는 다량의 B를 이용하여 결정된다. 이 경우, 반응 속도식은 다음과 같이 단순화된다.^[73]

:

r = k' \cdot [{\rm A}]^\alpha

(여기서

k' = k  \cdot [{\rm B}]^\beta

)

단순화된 식에서 α는 적분 방법을 통해 결정할 수 있다. 같은 조건에서 B에 관한 반응 차수 β는 초기 농도 [B]₀를 변화시키면서 일련의 유사한 실험을 수행하여 k'의 변화를 측정함으로써 결정할 수 있다.^[73]

3. 4. 0차 반응

0차 반응은 반응 속도가 반응물의 농도에 영향을 받지 않는 반응이다. 이는 반응이 효소 또는 촉매 표면과의 접촉을 필요로 하고, 동시에 반응할 수 있는 반응물 분자의 수를 제한하는 병목 현상이 있을 때 발생할 수 있다.^[63]

많은 효소 촉매 반응은 반응물의 농도가 속도를 조절하는 효소 농도보다 훨씬 높아서 효소가 포화되는 경우 0차 반응이다. 예를 들어, 효소 간 알코올 탈수소효소(LADH)에 의해 일어나는 아세탈알데히드에 대한 에탄올의 생물학적 산화 작용은 에탄올의 0차 반응이다.^[64]

유사하게 촉매 표면이 포화 상태일 경우 불균일 촉매와의 반응이 0차 반응이 될 수 있다. 예를 들어, 고온의 텅스텐 표면에서의 포스핀(PH₃)의 분해는 일정한 속도로 분해되는 포스핀의 0차 반응이다.^[63]

균질 촉매에서는 가역적 억제로부터 0차 반응 양상이 나타날 수 있다. 예를 들어 3세대 그럽스 촉매를 이용한 개환복분해중합은 피리딘과 루테늄 중심 사이에서 발생하는 가역적 억제로 촉매에서 0차 반응의 양상을 나타낸다.^[65]

0차 반응의 속도식은 다음과 같다.

:

-{d[A] \over dt} = k[A]^0 = k,

'''''k'''''의 단위는 '''''mol dm^-3 s^-1''''이다.^[14]

0차 반응
반응 속도식	$-{d[A]}/{dt} = k$
적분된 반응 속도식	$[A] = [A]_0 - kt$
반응 속도 상수 (k)의 단위	$\rm\frac{M}{s}$
k를 결정하기 위한 선형 그래프	vs.
반감기	$t_{1/2} = \frac{[A]_0}{2k}$

3. 5. 1차 반응

1차 반응은 반응 속도가 한 가지 반응물의 농도에만 비례하는 반응이다. S_N1 반응, 방사성 붕괴 등이 이에 해당한다.^[66]

1차 반응의 반응 속도식은 다음과 같다.

:

-\frac{d[\ce A]}{dt} = k[\ce A],

여기서 ''k''는 반응 속도 상수(단위는 s^-1)이며, [A]는 반응물의 농도이다.^[18]

1차 반응의 반감기는 초기 농도와 무관하며, 다음 식으로 주어진다.^[19]

:

t_{1/2} = \frac{\ln{(2)}}{k}

1차 반응의 예시는 다음과 같다.^[20]^[21]^[22]

H2O2 (l) -> H2O (l) + 1/2O2 (g)
SO2Cl2 (l) -> SO2 (g) + Cl2 (g)
2N2O5 (g) -> 4NO2 (g) + O2 (g)

유기화학에서 S_N1 반응은 1차 반응으로, 친핵체와 다이아조늄 염 이온의 반응 속도 방정식은 다음과 같다.^[25]

:

v_0 = k[\ce{ArN2+}],

(Ar은 아릴기)

1차 반응 속도식을 적분하면 다음과 같다.^[43]

:

\ \ln{[A]} = -kt + \ln{[A]_0}

이는 지수 감소 함수로도 표현 가능하다.

:

A=A_0e^{-kt}\,

1차 반응
항목	내용
반응 속도식	$-{d[\ce A]}/{dt} = k[\ce A]$
적분된 반응 속도식	$\ce{[A] = [A]0} e^{-kt}$
반응 속도 상수 (k)의 단위	$\rm\frac{1}{s}$
k를 결정하기 위한 선형 그래프	$\ln ([A]) \ \mbox{vs.} \ t$
반감기	$t_\frac{1}{2} = \frac{\ln (2)}{k}$

3. 6. 2차 반응

2차 반응은 반응 속도가 두 가지 반응물의 농도 곱에 비례하거나, 한 반응물의 농도 제곱에 비례하는 반응이다.^[67] 예시로는 SN2 반응, 알칼리 가수 분해 반응이 있다.

$v= k [A]^2\,$ (반응물 A의 농도 제곱에 비례)
$v= k[A][B]\,$ (두 반응물 A, B의 농도 곱에 비례)

첫 번째 유형의 예로, NO₂ + CO → NO + CO₂ 반응에서 반응물 NO₂에 대해 2차 반응이고, 반응물 CO에 대해 0차 반응이다. 따라서 이 반응에서 관찰된 속도는

v= k [NO_2]^2

이고, CO의 농도와 무관하다.^[67]

단일 반응물의 농도 제곱에 비례하는 반응 속도의 경우, 반응물의 농도와 시간 사이의 상관성은 다음과 같다.

:

\frac{1}{\ce{[A]}} = \frac{1}{\ce{[A]0}} + kt

두 반응물의 농도의 곱에 비례하는 속도에 대하여 시간의 상관성은 다음과 같다.

:

\frac{\ce{[A]}}{\ce{[B]}} = \frac{\ce{[A]0}}{\ce{[B]0}} e^{(\ce{[A]0} - \ce{[B]0}) kt}

만약 두 반응물의 농도가 같다면, 전자의 방정식을 만족한다.

두 번째 유형은 에틸 아세테이트의 알칼리 가수 분해와 같은 친핵 첨가-제거 반응을 포함한다.^[66]

:CH3COOC2H5 + OH- -> CH3COO- + C2H5OH

이 반응은 각각의 반응물에 대해 1차 반응이고, 전체적으로 2차 반응이다 : r=k[CH3COOC2H5][OH]

만약 이미다졸(imidazole)이 위의 가수 분해 반응을 촉매한다면, 반응 속도식은 v= k [imidazole] [CH3COOC2H5]가 된다.^[66] 반응 속도는 한 반응물(에틸 아세테이트)에 대하여 1차 반응이고, 이미다졸에 대하여도 1차 반응인데, 이미다졸은 촉매로서 전체 화학 방정식에 나타나지 않는다.

잘 알려진 또 다른 종류의 이차 반응은 아세톤에서의 n-부틸 브로민과 아이오딘화 나트륨의 반응과 같은 S_N2 반응(이분자 친핵성 치환 반응)이다.

:CH3CH2CH2CH2Br + NaI -> CH3CH2CH2CH2I + NaBr(v)

요오드화 나트륨과 아세톤이 각각 염으로서 소듐터트부톡사이드(sodium tert-butoxide)과 용매로서 터트부탄올(tert-butanol)로 대체되는 경우, 동일한 화합물이 다른 일반적인 유형의 2차 반응인 이분자(E2) 제거 반응을 겪을 수 있다.

:CH3CH2CH2CH2Br + NaOt-Bu -> CH3CH2CH=CH2 + NaBr + HOt-Bu

2차 반응의 적분형 반응 속도식은 다음과 같다.

:

\frac{1}{[\mathrm{A}]} = \frac{1}{[\mathrm{A}]_0} + kt

또는

:

\frac{[A]}{[B]} = \frac{[A]_0}{[B]_0} \exp \left(([\mathrm{A}]_0 - [\mathrm{B}]_0)kt \right)

([A]₀와 [B]₀는 반드시 다른 값이다.)

2차 반응의 반감기를 나타내는 식은 다음과 같다.

:

t_{1/2} = 1/k[\ce A]_0

이러한 반응에서는 반응물의 농도가 초기 농도의 절반이 되면, 그 다음 반감기는 2배가 된다.

3. 7. 유사 1차 반응

어떤 반응물의 농도가 매우 커서 상수처럼 취급될 수 있을 때, 2차 반응이 1차 반응처럼 보이는 현상을 유사 1차 반응이라고 한다.^[26]

일반적으로 반응 속도식이

v = k[A][B]

인 2차 반응에서, 반응물 B의 농도가 일정하다면,

v = k[A][B] = k'[A]

로 나타낼 수 있다. 이때 유사 1차 반응의 속도 상수

k' = k[B]

이다. 이처럼 2차 반응 속도식을 유사 1차 반응 속도식으로 차수를 낮추면, 통합된 반응 속도식을 구하기가 더 쉬워진다.

유사 1차 반응을 얻는 한 가지 방법은 한 반응물의 농도를 다른 반응물에 비해 훨씬 과량으로 만드는 것이다. (즉,

[B]\gg[A]

) 이렇게 하면 반응이 진행되어도 과량으로 존재하는 반응물 B는 소량만 반응하므로, B의 농도는 일정하다고 간주할 수 있다.

예를 들어, 희석된 무기산에 의한 에스터의 가수분해는 물의 농도가 매우 과량으로 존재하기 때문에 유사 1차 반응 속도론을 따른다.

:CH₃COOCH₃ + H₂O → CH₃COOH + CH₃OH

또한 산 수용액에서 수크로스(설탕)의 가수분해는 종종

r = k[sucrose]

인 1차 반응으로 인용되지만, 실제로는

r = k[sucrose][H^+][H2O]

인 3차 반응이다. 그러나 촉매인 H⁺와 용매인 H₂O의 농도는 일반적으로 일정하므로, 이 반응은 유사 1차 반응으로 나타난다.^[68]

반응물이 A와 B 두 가지일 때, 두 반응물의 농도를 동시에 조사하기는 어렵다. 한 반응물의 농도를 조사하고 거기에서 다른 농도를 계산하면 오차가 커질 수 있다. 이 문제를 해결하기 위해 오스트발트의 분리법(유사 1차 반응 근사)이 사용된다.

4. 반응 속도에 영향을 미치는 요인

반응 속도는 여러 요인에 의해 영향을 받는다. 주요 요인은 다음과 같다.

농도: 반응물의 농도는 반응 속도에 큰 영향을 미친다. 일반적으로 농도가 높을수록 반응 속도가 빨라진다.
온도: 온도가 높아지면 분자 운동이 활발해져 반응 속도가 증가한다.
촉매: 촉매는 반응의 활성화 에너지를 낮춰 반응 속도를 빠르게 한다. 하버-보슈 공정의 역반응은 촉매 표면에서 반응이 일어나기 때문에 영차 반응의 예시이다.^[40]
용매: 용매의 종류 및 극성 등 용매의 특성은 반응 속도에 영향을 줄 수 있다. (주어진 원본 소스에는 용매에 대한 직접적인 언급은 없지만, 요약에 언급되어 있으므로 포함함)

이 외에도 반응물의 종류, 표면적 등 다양한 요인이 반응 속도에 영향을 미칠 수 있다.

4. 1. 농도

Reaction orders^영어에서 반응물의 농도는 반응 속도에 큰 영향을 준다. 일반적으로 반응물의 농도가 높을수록 반응 속도가 증가하는 경향이 있다.

영차 반응: 반응 속도가 반응물의 농도에 의존하지 않는다. 반응물의 농도가 증가해도 반응 속도는 일정하다.^[40]
일차 반응: 반응 속도가 하나의 반응물의 농도에만 의존한다.
이차 반응: 반응 속도가 하나의 반응물의 농도의 제곱에 비례하거나, 두 반응물의 농도의 곱에 비례한다.

오스트발트의 분리법(의사 1차 반응 근사)을 통해 복잡한 반응을 단순화할 수 있다. 한 반응물의 농도가 매우 크고 변화가 적을 경우, 그 농도를 상수로 간주하여 반응을 1차 반응처럼 취급할 수 있다.^[44]

4. 2. 온도

온도가 높을수록 반응 속도는 증가한다. 아레니우스 식을 통해 온도와 반응 속도 상수 간의 관계를 설명할 수 있다.

4. 3. 촉매

촉매는 반응 속도를 증가시키지만, 자신은 소모되지 않는 물질이다. 균일 촉매와 불균일 촉매로 구분된다. 영차 반응은 반응이 일어나는 촉매나 표면이 반응물에 의해 채워진 경우에 나타난다.^[40]

5. 복잡한 반응 메커니즘

복잡한 속도식은 관련된 화학 종의 다양한 농도에서 하나 이상의 차수에 대한 법칙에 근사하면 "혼합 차수"로 설명된다. 예를 들어, $v_0 = k_1[A]+k_2[A]^2$ 형태의 속도식은 동시 1차 및 2차 반응(또는 더 흔하게는 동시 유사 1차 및 2차) 반응을 나타내며, 혼합 1차 및 2차로 설명할 수 있다.^[31] [A]의 값이 충분히 크면 이러한 반응은 2차 반응 속도에 근사하지만, [A]가 작을수록 반응 속도는 1차(또는 유사 1차)에 근사한다. 반응이 진행됨에 따라 반응물 소모에 따라 반응이 2차에서 1차로 바뀔 수 있다.

또 다른 유형의 혼합 차수 속도식은 분모에 두 개 이상의 항이 있는데, 이는 종종 속도 결정 단계의 정체가 농도 값에 따라 달라지기 때문이다. 한 예는 알코올을 헥사시아노철산(III) 이온 [Fe(CN)₆³⁻]에 의해 케톤으로 산화시키는 것으로, 루테네이트 (VI) 이온(RuO₄²⁻)을 촉매로 사용한다.^[32] 이 반응에서 헥사시아노철산(III)의 소실 속도는 $v_0 = \frac{\ce{[Fe(CN)6]^2-}}{k_\alpha + k_\beta\ce{[Fe(CN)6]^2-}}$ 이다.

이것은 반응 시작 시(농도가 높고 루테늄 촉매가 빠르게 재생될 때) 헥사시아노철산(III)에 대해 0차이지만, 농도가 감소하고 촉매 재생이 속도 결정 단계가 되면 1차로 바뀐다.

두 항 분모를 가진 혼합 차수 속도식을 갖는 주목할 만한 메커니즘은 다음과 같다.

효소 촉매 작용에 대한 미카엘리스-멘텐 반응 속도론: 기질 농도가 낮을 때는 기질에 대해 1차(전체적으로 2차), 기질 농도가 높을 때는 기질에 대해 0차(전체적으로 1차)이다.
단분자 반응에 대한 린데만 메커니즘: 저압에서는 2차, 고압에서는 1차이다.

5. 1. 연쇄 반응

5. 2. 평형 반응 (가역 반응)

정반응과 역반응이 비슷한 속도로 동시에 일어나는 반응을 평형 반응 (가역 반응)이라고 한다. 일반적인 반응식은 다음과 같다.^[34]

: {\mathit{a}A} + {\mathit{b}B} <=> {\mathit{p}P} + {\mathit{q}Q}

위 반응에 대한 반응 속도식은 다음과 같이 쓸 수 있다. (각 반응이 기본 반응이라고 가정)^[34]

:

v = k_1 [\ce A]^a[\ce B]^b - k_{-1} [\ce P]^p[\ce Q]^q

여기서,

''k''₁은 A와 B가 반응하여 P와 Q를 생성하는 정반응의 속도 상수이다.
''k''₋₁는 P와 Q가 반응하여 A와 B를 생성하는 역반응의 속도 상수이다.

평형 상태(''v''=0)에서, 평형 상수(K)는 다음과 같이 정의된다.^[34]

:

K =  \frac{[\ce P]^p[\ce Q]^q}{[\ce A]^a[\ce B]^b} = \frac{k_1}{k_{-1}}

간단한 평형 반응의 예시는 다음과 같다.

: A <=> P

반응물 A의 초기 농도를 [A]0, 생성물 P의 초기 농도를 0이라고 할 때, 평형 상수 ''K''는 다음과 같다.

:

K \ \stackrel{\mathrm{def}}{=}\  \frac{k_{1}}{k_{-1}} = \frac{\left[\ce P\right]_e} {\left[\ce A\right]_e}

(

[\ce A]_e

와

[\ce P]_e

는 각각 평형 상태에서 A와 P의 농도)

시간 ''t''에서 A의 농도

[\ce A]_t

는 P의 농도

[\ce P]_t

와 다음 관계를 갖는다.

: [A]_\mathit{t} = [A]0 - [P]_\mathit{t}

평형 상태에서는 다음과 같다.

: [A]_\mathit{e} = [A]0 - [P]_\mathit{e}

''K''의 정의에 따라,

:

[\ce P]_e = \frac{k_{1}}{k_1+k_{-1}}\ce{[A]0}

:

\ [\ce A]_e = \ce{[A]0} - [\ce P]_e = \frac{k_{-1}}{k_1+k_{-1}}\ce{[A]0}

이 식들을 통해 연립 방정식을 풀면 A의 농도만으로 표현할 수 있다.^[34]

반응 속도식은 다음과 같이 주어졌다.

:

v = k_1 [\ce A]^a[\ce B]^b - k_{-1} [\ce P]^p[\ce Q]^q

A <=> P 의 경우,

:

-\frac{d[\ce A]}{dt} = k_1 [\ce A]_t - k_{-1} [\ce P]_t

(미분은 A에서 P로 가는 반응 속도이며, A의 농도가 감소하므로 음수이다.)

''x''를 시간 ''t''에서 A의 농도

[\ce A]_t

,

x_e

를 평형 상태에서 A의 농도로 정의하면,

:

\begin{align}

\frac{d[\ce A]}{dt} &= {k_1 [\ce A]_t} - {k_{-1} [\ce P]_t}\\[8pt]
\frac{dx}{dt} &= {k_1 x} - {k_{-1} [\ce P]_t}\\[8pt]

&= {k_1 x} - {k_{-1} (\ce{[A]0} - x)}\\[8pt]&= {(k_1 + k_{-1})x} - {k_{-1} \ce{[A]0}}\end{align}

:

k_1 + k_{-1} = k_{-1} \frac{\ce{[A]0}}{x_e}

이므로,

반응 속도는 다음과 같다.

:

\frac{dx}{dt} = \frac{k_{-1}\ce{[A]0}}{x_e} (x_e - x)

최종적으로,

:

\ln \left(\frac{\ce{[A]0} - [\ce A]_e}{[\ce A]_t-[\ce A]_e}\right) = (k_1 + k_{-1})t

시간에 따른 A의 농도에서 평형 상태에서의 농도를 뺀 값의 음의 자연 로그를 시간 ''t''에 대해 그래프로 나타내면 기울기가 ''k₁'' + ''k₋₁''인 직선이 된다. [A]_''e''와 [P]_''e''를 측정하면 ''K''와 두 개의 반응 속도 상수 값을 알 수 있다.^[34]

시간 ''t'' = 0에서의 농도가 위와 다른 경우, 위와 같은 단순화는 불가능하며, 미분 방정식 시스템을 풀어야 한다. 일반화된 표현식은 다음과 같다.^[46]

:

\begin{align}& \left[ \ce A \right]=\ce{[A]0}\frac{1}{k_{1}+k_{-1}}\left( k_{-1}+k_{1}e^{-\left( k_{1}+k_{-1} \right)t} \right)+\ce{[P]0}\frac{k_{-1}}{k_{1}+k_{-1}}\left( 1-e^{-\left( k_{1}+k_{-1} \right)t} \right) \\[8pt]& \left[ \ce P \right]=\ce{[A]0}\frac{k_{1}}{k_{1}+k_{-1}}\left( 1-e^{-\left( k_{1}+k_{-1} \right)t} \right)+\ce{[P]0}\frac{1}{k_{1}+k_{-1}}\left( k_{1}+k_{-1}e^{-\left( k_{1}+k_{-1} \right)t} \right)\end{align}

평형 상수가 1에 가깝고 반응 속도가 매우 빠른 경우 (예: 분자의 입체 이성질체 분석), 핵자기 공명 분광법에서 완전 선형 분석과 같은 다른 방법으로 속도 상수를 결정해야 한다.^[46]

5. 3. 연속 반응

한 반응의 생성물이 다른 반응의 반응물로 작용하는 반응이다.^[1]

반응 속도 상수

k_1

과

k_2

를 갖는 다음 반응 A -> B -> C 의 속도식은 다음과 같다.

반응물 A에 대해: $\frac{d[\ce A]}{dt} = -k_1 [\ce A]$
반응물 B에 대해: $\frac{d[\ce B]}{dt} = k_1 [\ce A] - k_2 [\ce B]$
생성물 C에 대해: $\frac{d[\ce C]}{dt} = k_2 [\ce B]$

개별 농도를 반응물의 총 개체수로 조정하여 확률이 되도록 하면, 이러한 선형 미분 방정식 시스템은 마스터 방정식으로 공식화될 수 있다. 미분 방정식은 해석적으로 풀 수 있으며, 적분된 속도 방정식은 다음과 같다.

:

[\ce A]=\ce{[A]0} e^{-k_1 t}

:

\left[ \ce B \right]= \begin{cases}\ce{[A]0}\frac{k_{1}}{k_{2}-k_{1}}\left( e^{-k_{1}t}-e^{-k_{2}t} \right)+\ce{[B]0}e^{-k_{2}t}& k_{1}\ne k_{2}  \\\ce{[A]0}k_{1}te^{-k_{1}t}+\ce{[B]0}e^{-k_{1}t} & \text{그 외}  \\\end{cases}

:

\left[ \ce C \right]= \begin{cases}\ce{[A]0}\left( 1+\frac{k_{1}e^{-k_{2}t}-k_{2}e^{-k_{1}t}}{k_{2}-k_{1}} \right)+\ce{[B]0}\left( 1-e^{-k_{2}t} \right)+\ce{[C]0} & k_{1}\ne k_{2}  \\\ce{[A]0}\left( 1-e^{-k_{1}t}-k_{1}te^{-k_{1}t} \right)+\ce{[B]0}\left( 1-e^{-k_{1}t} \right)+\ce{[C]0} & \text{그 외}  \\\end{cases}

정상 상태 근사는 더 쉬운 방법으로 매우 유사한 결과를 도출한다.^[1]

5. 4. 병렬 반응 (경쟁 반응)

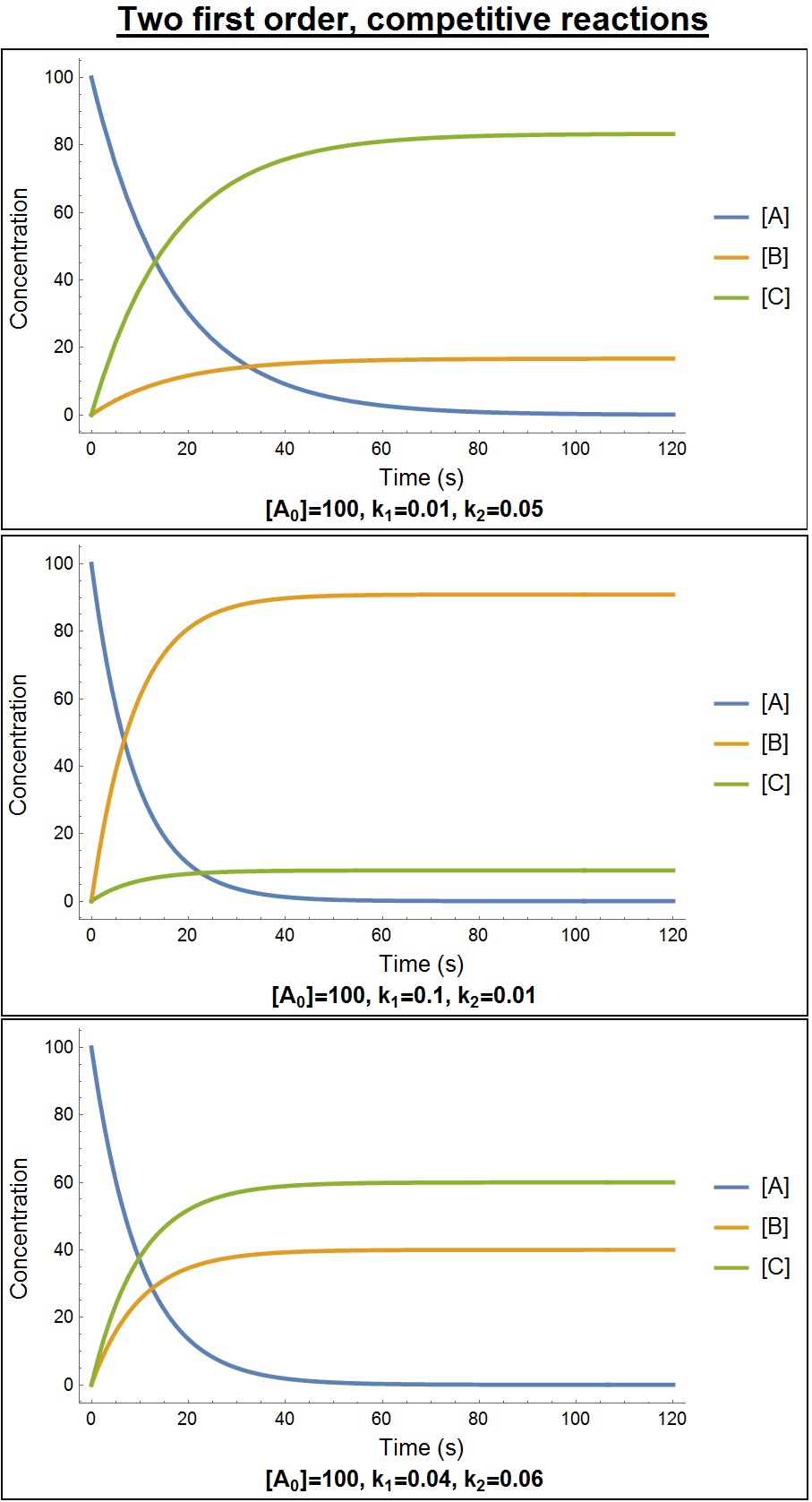
어떤 물질이 동시에 반응하여 두 가지 다른 생성물을 생성할 때, 병렬 반응 또는 경쟁 반응이 일어난다고 한다.

; 두 개의 1차 반응이 일어나는 경우

반응 A -> B 와 A -> C 의 속도 상수가 각각

k_1

과

k_2

라고 한다. 이 때 각 농도의 시간 변화 식은 다음과 같다.

:

-\frac{d[\ce A]}{dt}=(k_1+k_2)[\ce A]

:

\frac{d[\ce B]}{dt}=k_1[\ce A]

:

\frac{d[\ce C]}{dt}=k_2[\ce A]

적분형 반응 속도식은 다음과 같다.

:

\ [\ce A] = [A]_0 e^{-(k_1+k_2)t}

:

[\ce B] = \frac{k_1}{k_1+k_2}[\ce A]_0 (1-e^{-(k_1+k_2)t})

:

[\ce C] = \frac{k_2}{k_1+k_2}[\ce A]_0 (1-e^{-(k_1+k_2)t})

이 경우, 다음 관계식이 중요하다.

:

\frac{\ce{[B]}}{\ce{[C]}}=\frac{k_1}{k_2}

; 1차 반응과 2차 반응이 하나씩 일어나는 경우^[47]

이는 이분자 반응과, 유사 1차 반응으로 간주할 수 있는 가수 분해가 동시에 일어나는 경우에 적용할 수 있다. 병행 반응에 의해 반응물이 일부 소비되므로, 가수 분해의 반응 속도를 조사하는 것은 어렵다. 예를 들어, A와 R이 반응하여 C가 생성되지만, 동시에 가수 분해가 진행되어 A가 B로 변한다고 하는 경우이다. 반응식으로 나타내면, {A} + H2O -> B 와 {A} + R -> C 가 된다. 반응 속도식은 다음과 같다.

:

\frac{d[\ce B]}{dt}=k_1\ce{[A][H2O]}=k_1'[\ce A]

:

\frac{d[\ce C]}{dt}=k_2\ce{[A][R]}

(단,

k_1'

은 유사 1차 속도 상수이다.)

주 생성물 C의 농도에 대해 적분하면, 다음 식이 얻어진다.

:

[C]=[R]_0 \left [ 1-e^{-\frac{k_2}{k_1'}[\ce A]_0(1-e^{-k_1't})} \right ]

이는 다음과 등가이다.

:

ln \frac{\ce{[R]_0}}{\ce{[R]_0-[C]}}=\frac{k_2[\ce A]_0}{k_1'}(1-e^{-k_1't})

[B]와 [C]의 농도 관계는 다음과 같다.

:

[\ce B]=-\frac{k_1'}{k_2} ln \left ( 1 - \frac{\ce{[C]}}{[R]_0} \right )

이는 해석적으로 얻어진 해이지만, 다음 근사가 사용되고 있다.

:{[A]_0}-[C]\approx [A]_0

그 때문에, 앞의 식에서의 [C]는 [C]가 [A]₀에 비해 매우 작을 때만 사용할 수 있다.

6. 반응 속도론의 응용

(원문 소스가 제공되지 않았고, 이전 단계에서 결과물이 없었으므로, 수정할 내용이 없습니다. 따라서 아무것도 출력할 수 없습니다.)

참조

_[1] 서적 The IUPAC Compendium of Chemical Terminology: The Gold Book https://goldbook.iup[...] International Union of Pure and Applied Chemistry (IUPAC) 2019
_[2] 웹사이트 14.3: Effect of Concentration on Reaction Rates: The Rate Law https://chem.librete[...] 2015-01-18
_[3] 서적 2006
_[4] 웹사이트 Rate of reaction
_[5] 서적 2006
_[6] 서적 2006
_[7] 서적 1990
_[8] 서적 1990
_[9] 서적 2006
_[10] 서적 1987
_[11] 서적 2006
_[12] 서적 1987
_[13] 서적 1987
_[14] 서적 A Textbook of physical chemistry. Vol. 5: Dynamics of chemical reactions, statistical thermodynamics and macromolecules Macmillan India Ltd 2007
_[15] 서적 2006
_[16] 서적 1995
_[17] 간행물 Kinetic Study of Living Ring-Opening Metathesis Polymerization with Third-Generation Grubbs Catalysts 2017-09-25
_[18] 서적 A Textbook of physical chemistry. Vol. 5: Dynamics of chemical reactions, statistical thermodynamics and macromolecules Macmillan India Ltd 2007
_[19] 서적 Chemical Kinetics and Reaction Mechanisms McGraw-Hill 1981
_[20] 서적 2006
_[21] 서적 Chemical Kinetics Harper & Row 1987
_[22] 서적 General Chemistry Prentice-Hall 2002
_[23] 서적 General Chemistry Saunders 1992
_[24] 서적 A Textbook of physical chemistry. Vol. 5: Dynamics of chemical reactions, statistical thermodynamics and macromolecules Macmillan India Ltd 2007
_[25] 서적 1990
_[26] 서적 1995
_[27] 웹사이트 NDRL Radiation Chemistry Data Center https://web.archive.[...]
_[28] 서적 2006
_[29] 서적 1987
_[30] 서적 1987
_[31] 서적 1987
_[32] 간행물 Ruthenium(VI)-Catalyzed Oxidation of Alcohols by Hexacyanoferrate(III): An Example of Mixed Order http://jchemed.chem.[...] 2006-11
_[33] 서적 1987
_[34] 간행물 Determination of the Rotational Barrier for Kinetically Stable Conformational Isomers via NMR and 2D TLC http://jchemed.chem.[...] 2007-09
_[35] 간행물 A Kinetic Approach to the Alkylating Potential of Carcinogenic Lactones
_[36] 서적 The Regulation of Cellular Systems Springer Science & Business Media 2012
_[37] 서적 Modeling Biomolecular Networks in Cells
_[38] 문서 System modeling in cell biology: from concepts to nuts and bolts MIT Press Cambridge 2006
_[39] 서적 Control theory and systems biology MIT Press 2010
_[40] 서적 アトキンス一般化学（下）東京化学同人
_[41] 웹사이트 IUPAC Gold Book definition of rate law http://goldbook.iupa[...] IUPAC
_[42] 서적 アトキンス基礎物理化学（下）―分子론적アプローチ― 東京化学同人
_[43] 문서 『アトキンス基礎物理化学（下）―分子론적アプローチ―』p.661
_[44] 간행물 A method to describe enzyme-catalyzed reactions by combining steady state and time course enzyme kinetic parameters... 2010-01
_[45] 웹사이트 NDRL Radiation Chemistry Data Center http://www.rcdc.nd.e[...]
_[46] 뉴스 Determination of the Rotational Barrier for Kinetically Stable Conformational Isomers via NMR and 2D TLC An Introductory Organic Chemistry Experiment http://jchemed.chem.[...] 2007
_[47] 간행물 A Kinetic Approach to the Alkylating Potential of Carcinogenic Lactones 2005
_[48] 서적 The regulation of cellular systems Chapman & Hall 1996
_[49] 서적 Modeling biomolecular networks in cells: structures and dynamics 슈プリンガー・サイエンス・アンド・ビジネス・メディア 2010
_[50] 문서 System modeling in cell biology: from concepts to nuts and bolts MIT Press Cambridge 2006
_[51] 문서 Control theory and systems biology MIT Press Cambridge 2010
_[52] 웹사이트 IUPAC Gold Book definition of rate law http://goldbook.iupa[...] IUPAC
_[53] 문서 2006
_[54] 웹사이트 Rate of reaction
_[55] 문서 2006
_[56] 문서 2006
_[57] 문서 1990
_[58] 문서 1990
_[59] 서적 Physical Chemistry W. H. Freeman 2006
_[60] 서적 Chemical Kinetics and Reaction Mechanisms McGraw-Hill 2002
_[61] 문서
_[62] 문서
_[63] 문서 2006
_[64] 문서 1995
_[65] 간행물 Kinetic Study of Living Ring-Opening Metathesis Polymerization with Third-Generation Grubbs Catalysts 2017-09-25
_[66] 서적 Chemical kinetics : the study of reaction rates in solution https://www.worldcat[...] VCH 1990
_[67] 서적 General chemistry https://www.worldcat[...] Saunders College Pub 1992
_[68] 서적 Physical chemistry : principles and applications in biological sciences https://www.worldcat[...] Prentice Hall 1995
_[69] 웹인용 Aliphatic Carbon-Centered Radical Reaction Rates http://www.rcdc.nd.e[...] 1998-12-05
_[70] 서적 Kinetic systems: mathematical description of chemical kinetics in solution https://www.worldcat[...] Wiley-Interscience 1972
_[71] 서적 Reimeondeu Chang ui ilban hwahak. https://www.worldcat[...] Sai Peulleoseu 2018
_[72] 서적 Reimeondeu Chang ui ilban hwahak. https://www.worldcat[...] Sai Peulleoseu 2018
_[73] 서적 Espenson

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com