삼차원의 점군

1. 개요

삼차원의 점군은 3차원 공간에서 원점을 고정하는 등거리 변환들의 대칭군을 의미한다. 이러한 점군은 회전, 반사, 반전 등의 연산을 포함하며, 유한군과 무한군으로 분류된다. 유한 점군은 결정학적 제한 정리에 따라 32개로 제한되며, 7개의 무한 축군과 7개의 다면체군으로 구성된다. 이항 정다면체군은 점군의 이중 피복으로, 스핀 군의 부분군으로 표현된다. 점군은 추상 군의 유형에 따라 분류되며, 순환군, 이면체군, 그리고 다면체군으로 세분화된다.

2. 3차원 등거리 변환

대칭군(대칭 연산) 연산은 원점을 고정하는 3차원 공간 R³의 등거리 변환으로, O(3) 군을 형성한다. 이러한 연산은 다음과 같이 분류할 수 있다.

* 직접(방향 보존) 대칭 연산은 SO(3) 군을 형성한다.
항등 연산은 E 또는 항등 행렬 I로 표시된다.
원점을 통과하는 축을 중심으로 θ 각도로 회전한다. 임의의 양의 정수 n에 대해 θ = 360°/n로 회전하는 것은 C_n으로 표시된다(C_n 군에 대한 쇼엔플리스 표기법에서, 이 군은 생성된다). 항등 연산은 C₁으로도 표기되며, 회전 연산자의 특수한 경우이다.
* 간접(방향 반전) 연산:
반전은 i 또는 C_i로 표시되며, 이는 좌표축을 중심으로 180° 회전한 후 직교 좌표 평면에서 반사하는 것이다. 행렬 표기법은 −I이다.
원점을 통과하는 평면에서의 반사는 σ로 표시된다.
** 부정 회전은 회전-반사라고도 하며, 축을 중심으로 θ 각도로 회전하고 축에 수직인 원점을 통과하는 평면에서 반사하는 것이다. 임의의 양의 정수 n에 대해 θ = 360°/n로 회전-반사하는 것은 S_n으로 표시된다(S_n 군에 대한 쇼엔플리스 표기법에서, n이 짝수일 경우 생성된다).
반전은 회전-반사의 특수한 경우(i = S₂)이며, 반사도 특수한 경우(σ = S₁)이므로, 이러한 연산은 종종 부정 회전으로 간주된다.

원뿔 기호는 때때로 Ĉ_n 및 Ŝ_n과 같이 연산자를 나타내기 위해 기호에 추가된다.

2.1. 직접 등거리 변환 (회전 변환)

대칭군(대칭 연산) 연산은 원점을 고정하는 3차원 공간 R³의 직접 등거리 변환으로, SO(3) 군을 형성한다. 이러한 연산은 항등 연산과 회전 연산으로 분류할 수 있다.

* 항등 연산: E 또는 항등 행렬 I로 표시된다.
* 회전 연산: 원점을 통과하는 축을 중심으로 θ 각도로 회전한다. 임의의 양의 정수 n에 대해 θ = 360°/n로 회전하는 것은 C_n으로 표시된다(C_n 군에 대한 쇼엔플리스 표기법에서, 이 군은 생성된다). 항등 연산은 C₁으로도 표기되며, 회전 연산자의 특수한 경우이다.

회전군, 즉 SO(3)의 유한 부분군은 다음과 같다. 순환군 C_n (정규 피라미드의 회전군), 이면체군 D_n (정규 각기둥 또는 정규 쌍뿔의 회전군), 정 사면체, 정팔면체/정육면체 및 정이십면체/정십이면체의 회전군 T, O 및 I이다.

특히, 이면체군 D₃, D₄ 등은 3차원 공간에 임베디드된 평면 정다각형의 회전군이며, 이러한 도형은 퇴화된 정각기둥으로 간주될 수 있다. 따라서, 이것은 또한 이면체(그리스어: 두 면을 가진 입체)라고 불리며, 이것이 이면체군이라는 이름을 설명한다.

쇤플리스 표기법, 콕세터 표기법, (오비폴드 표기법)으로 주어진 회전 부분군은 다음과 같다.

회전군 SO(3)는 3차원 유클리드 공간의 전체 점 회전군인 O(3)의 부분군이다. 따라서 O(3)는 SO(3)와 군의 직접곱과 반사군 C_i (여기서 반사는 그 행렬 −I로 표시됩니다)의 직접곱이다.
:O(3) = SO(3) × { I , −I }

따라서 반사를 통해 모든 직접 등거리 변환과 모든 간접 등거리 변환 사이에 1대 1 대응이 있다. 또한 SO(3)의 모든 직접 등거리 변환 그룹 H와 반사를 포함하는 O(3)의 모든 등거리 변환 그룹 K 사이에 1대 1 대응이 있다.
:K = H × { I , −I }
:H = K ∩ SO(3)
여기서 등거리 변환 ( A, I )는 A와 동일시된다.

유한군의 경우, 대응 관계는 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

회전군 H	n의 패리티	반사를 포함하는 군 K
Cn	짝수	Cnh
	홀수	S2n
Dn	짝수	Dnh
	홀수	Dnd
T		Th
O		Oh
I		Ih

2.2. 간접 등거리 변환

대칭군(대칭 연산) 연산은 원점을 고정하는 3차원 공간 R³의 등거리 변환으로, O(3) 군을 형성한다. 이 연산 중 간접(방향 반전) 연산은 다음과 같다.

* 반전은 i 또는 C_i로 표시되며, 이는 좌표축을 중심으로 180° 회전한 후 직교 좌표 평면에서 반사하는 것이다. 행렬 표기법은 −I이다.
* 원점을 통과하는 평면에서의 반사는 σ로 표시된다.
* 부정 회전은 회전-반사라고도 하며, 축을 중심으로 θ 각도로 회전하고 축에 수직인 원점을 통과하는 평면에서 반사하는 것이다. 임의의 양의 정수 n에 대해 θ = 360°/n로 회전-반사하는 것은 S_n으로 표시된다(S_n 군에 대한 쇼엔플리스 표기법에서, n이 짝수일 경우 생성된다).

반전은 회전-반사의 특수한 경우(i = S₂)이며, 반사도 특수한 경우(σ = S₁)이므로, 이러한 연산은 종종 부정 회전으로 간주된다.

원뿔 기호는 때때로 Ĉ_n 및 Ŝ_n과 같이 연산자를 나타내기 위해 기호에 추가된다.

회전군 SO(3)는 3차원 유클리드 공간의 전체 점 회전군인 O(3)의 부분군이다. 따라서 O(3)는 SO(3)와 군의 직접곱과 반사군 C_i (여기서 반사는 그 행렬 −I로 표시됩니다)의 직접곱이다.

:O(3) = SO(3) × { I , −I }

따라서 반사를 통해 모든 직접 등거리 변환과 모든 간접 등거리 변환 사이에 1대 1 대응이 있다. 또한 SO(3)의 모든 직접 등거리 변환 그룹 H와 반사를 포함하는 O(3)의 모든 등거리 변환 그룹 K 사이에 1대 1 대응이 있다.

:K = H × { I , −I }
:H = K ∩ SO(3)

여기서 등거리 변환 ( A, I )는 A와 동일시된다.

유한군의 경우, 대응 관계는 다음과 같다.

직접 등거리 변환군 H가 지표 2의 부분군 L을 가지면, 간접 등거리 변환을 포함하지만 반전은 없는 해당 그룹이 존재한다.
:$M\; =\; L\; \backslash cup\; (\; (H\; \backslash setminus\; L)\; \backslash times\; \backslash \{\; -I\; \backslash \})$

예를 들어, H = C₄는 M = S₄에 해당한다.

따라서 M은 $H\; \backslash setminus\; L$의 등거리 변환을 반전시켜 H에서 얻어진다. 이 그룹 M은 추상 군으로 간주될 때 H와 동형이다. 반대로, 간접 등거리 변환을 포함하지만 반전은 없는 모든 점군 M에 대해, 간접 등거리 변환을 반전시켜 회전군 H를 얻을 수 있다.

유한 군의 경우, 대응 관계는 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

회전군 H	지표-2 부분군 L	n의 패리티	간접 등거리 변환을 포함하는 군 M
C2n	Cn	짝수	S2n
		홀수	Cnh
D2n	Dn	짝수	Dnh
		홀수	Dnd
Dn	Cn	임의	Cnv
O	T		Td

3. 켤레류

두 객체의 대칭 유형을 비교할 때, 각 객체에 대해 원점을 개별적으로 선택하며, 동일한 중심을 가질 필요는 없다. 또한, 두 객체의 대칭군이 O(3)의 켤레 부분군이면 동일한 대칭 유형을 갖는 것으로 간주된다. 그룹 G의 두 부분군 H₁, H₂는 g ∈ G가 존재하여 H₁ = g⁻¹H₂g이면 켤레라고 한다.

예를 들어, 두 개의 3차원 객체는 다음과 같은 경우 동일한 대칭 유형을 가진다.
* 두 객체 모두 서로 다른 거울면에 대한 거울 대칭을 갖는 경우
* 두 객체 모두 서로 다른 축에 대한 3회 회전 대칭을 갖는 경우.

여러 거울면 및/또는 회전축의 경우, 두 대칭군은 첫 번째 대칭군의 전체 구조를 두 번째 대칭군의 구조에 매핑하는 회전이 있는 경우에만 동일한 대칭 유형을 갖는다. 켤레 정의는 구조의 거울상을 허용하지만, 이것은 필요하지 않으며, 구조 자체는 비키랄이다. 예를 들어, 대칭군이 3회 회전축을 포함하는 경우, 두 반대 방향으로의 회전을 포함한다. 구조는 나선축을 가진 11쌍의 공간군에 대해 키랄하다.

4. 무한 등거리 변환군

다양한 무한 등거리 변환군이 존재한다. 예를 들어, 축을 중심으로 회전하는 무리수 회전에 의해 생성되는 "순환군"(하나의 원소로 생성된다는 의미이며, 꼬임군과 혼동해서는 안 된다)이 있다. 같은 축을 중심으로 더 많은 회전을 추가하여 비순환 아벨 군을 만들 수 있다. 원을 중심으로 유리수의 각도에 위치한 원 위의 점 집합은 무한 개의 생성원을 필요로 하는 점군을 보여준다. 또한 다른 축을 중심으로 회전하여 생성되는 비아벨 군도 있다. 이것들은 일반적으로 자유군이다. 회전이 특별히 선택되지 않는 한 무한하다.

지금까지 언급된 모든 무한군은 O(3)의 폐포로서 위상군이 아니다. 이제 O(3)의 위상적으로 닫힌 부분군에 대해 논의한다.

전체 O(3)은 구 대칭의 대칭군이며, SO(3)는 해당 회전군이다. 다른 무한 등거리 변환군은 원점을 통과하는 축을 중심으로 한 모든 회전과 축을 통과하는 평면에서의 반사, 그리고/또는 축에 수직인 원점을 통과하는 평면에서의 반사를 추가로 포함한다. 축을 통과하는 평면에서의 반사를 갖는 군(축에 수직인 원점을 통과하는 평면에서의 반사가 있거나 없는 경우)은 두 가지 유형의 원통 대칭에 대한 대칭군이다. 무한 회전 대칭을 갖는 모든 3차원 형상(R³의 부분 집합)은 축을 통과하는 모든 평면에 대한 거울 대칭도 가져야 한다. 무한 회전 대칭을 갖는 물리적 객체는 축을 통과하는 거울 평면의 대칭도 가지지만, 예를 들어 축을 중심으로 회전하는 원뿔의 속도 벡터나 전선 주위의 자기장과 같은 벡터장은 그렇지 않을 수 있다.

유한 등거리 변환군의 모든 의미에서 한계가 있는 7개의 연속적인 군이 있다. 이러한 소위 제한 점군 또는 퀴리 제한군은 이를 처음 연구한 피에르 퀴리의 이름을 따서 명명되었다. 7개의 무한 일련의 축군이 5개의 제한군(그 중 2개는 중복)을 생성하고, 나머지 7개의 점군은 2개의 추가 연속군을 생성한다. 국제 표기법에서 목록은 ∞, ∞2, ∞/m, ∞mm, ∞/mm, ∞∞, ∞∞m이다. 이들 모두가 물리적 객체에 가능한 것은 아니며, 예를 들어 ∞∞ 대칭을 가진 객체는 ∞∞m 대칭도 갖는다.

5. 유한 등거리 변환군

3차원에서 원점을 고정하는 대칭은 원점을 중심으로 하는 구에서의 대칭으로 완전히 특징지어진다. 유한 3차원 점군에 대해서는 구 대칭군을 참조한다.

공액 관계까지 고려하면, 유한 3차원 점군의 집합은 다음과 같다.

* 7개의 무한한 축군 시리즈: 최대 1개의 2-겹 이상의 회전축을 가진다. 이들은 무한한 원기둥 상의 유한 대칭군, 또는 유한 원기둥 상의 대칭군이다. 이들은 때때로 축 또는 각주 점군이라고 불린다.
* 나머지 7개의 점군: 여러 개의 3-겹 이상의 회전축을 가진다. 이 그룹은 여러 개의 3-겹 회전축을 가진 점군으로도 특징지을 수 있다. 가능한 조합은 다음과 같다.
* 4개의 3-겹 축 (정사면체 대칭 T, T_h, T_d)
* 4개의 3-겹 축과 3개의 4-겹 축 (정팔면체 대칭 O 및 O_h)
* 10개의 3-겹 축과 6개의 5-겹 축 (이십면체 대칭 I 및 I_h)

결정학 제한 정리에 따르면, 제한된 수의 점군만이 이산 병진 대칭과 호환된다: 7개의 무한 시리즈에서 27개, 나머지 7개 중 5개이다. 이들을 함께 32개의 소위 결정학적 점군을 이룬다.

최대 대칭성을 갖는 이산 점군에는 두 가지가 있는데, 이들은 어떤 이산 점군도 자신을 진부분군으로 가질 수 없다. 이들은 O_h와 I_h이다. 이 두 그룹의 최대 공통 부분군은 T_h이다. 이 두 그룹은 각각 2회 회전 대칭을 4회로 변경하고, 5회 대칭을 추가하여 얻을 수 있다.

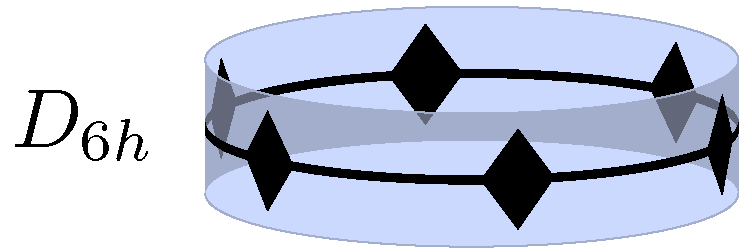
결정학적 점군 중 어떤 결정학적 점군도 자신을 진부분군으로 가질 수 없는 것은 O_h와 D_6h 두 가지이다. 이들의 최대 공통 부분군은 방향에 따라 D_3d와 D_2h이다.

5.1. 축군 (7개의 무한 시리즈)

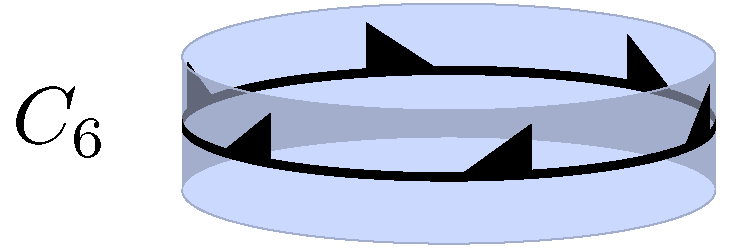
7개의 무한 축군 계열은 임의의 정수 n을 지수로 가지며, 각 계열에서 n번째 대칭군은 축을 중심으로 한 n겹의 회전 대칭을 포함한다. 즉, 360°/n 각도로의 회전에 대한 대칭이다. n=1은 회전 대칭이 전혀 없는 경우를 포함한다. 다른 회전 대칭 축이 없는 네 개의 계열(순환 대칭)과 2겹 대칭 축이 추가된 세 개의 계열(이이각형 대칭)이 있다. 이들은 축 좌표와 그 축에서의 반사를 통해 확장된 2차원 점군으로 이해할 수 있다. 이들은 프리즈 군과 관련이 있으며, 실린더 주위에 n번 반복되는 프리즈 군 패턴으로 해석할 수 있다.

점군에 대한 여러 표기법으로는 헤르만-모갱 표기법(결정학에서 사용), 쇤플라이스 표기법(분자 대칭을 설명하는 데 사용), 오비폴드 표기법, 콕세터 표기법이 있다. 오비폴드 표기법은 벽지 군 및 프리즈 군에도 적용할 수 있는 통일된 표기법이다. 결정학적 군은 n이 1, 2, 3, 4 및 6으로 제한되며, 결정학적 제한을 제거하면 모든 양의 정수가 허용된다.

계열은 다음과 같다.

홀수 n의 경우 Z_2n = Z_n × Z₂이고 Dih_2n = Dih_n × Z₂이다.

군 C_n (사소한 C₁ 포함) 및 D_n은 카이랄이며, 나머지는 비카이랄이다. 수평(h) 및 수직(v) 용어와 해당 아래첨자는 추가 거울면에 해당하며, 이는 회전 축에 평행(수직)하거나 회전 축에 수직(수평)할 수 있다.

가장 간단한 비자명 축군은 추상군 Z₂와 동일하다.

*C_i (S₂와 동일) – 점에서의 반전 대칭
*C₂ – 2겹 회전 대칭
*C_s (C_1h 및 C_1v와 동일) – 반사 대칭, 양측 대칭이라고도 함.

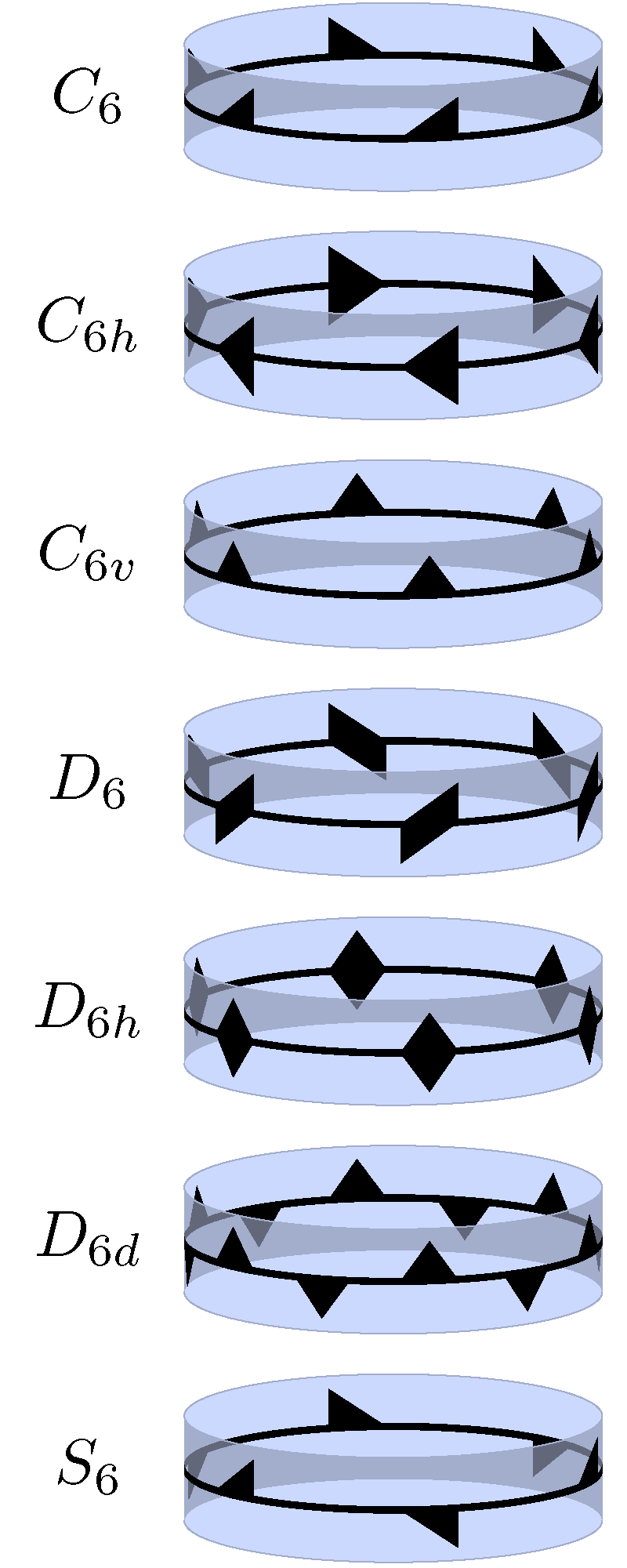
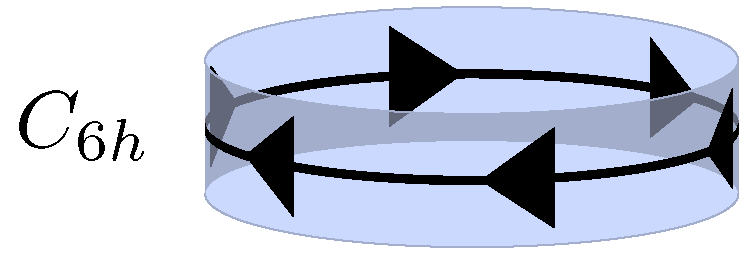
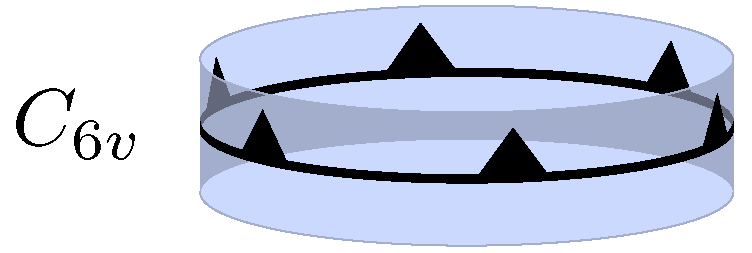
이 중 C_n은 차수 n인 단축 군(순환군)이며, 360°/n 각도의 단일 회전에 의해 생성된다. C_nh는 차수 2n인 군으로 축에 수직인 거울면을 추가하여 얻어지며, C_nv는 차수 2n인 군으로 축을 포함하는 일련의 n 거울면을 추가하여 얻어진다. C_nv는 정규 n면 피라미드의 대칭군이다. 대칭군이 C_n 또는 D_n인 일반적인 물체는 프로펠러이다.

D_nh는 수평 및 수직 반사면이 모두 추가된 차수 4n인 군이다. 회전의 하위 군은 차수 2n인 이이각형 군 D_n이며, 주 회전축에 수직인 2겹 회전축은 여전히 있지만 거울면은 없다. 2D에서 D_n에는 반사가 포함되지만, 3D에서는 두 연산이 구별된다. D_n은 "뒤집기"를 포함하지만 반사는 포함하지 않는다.

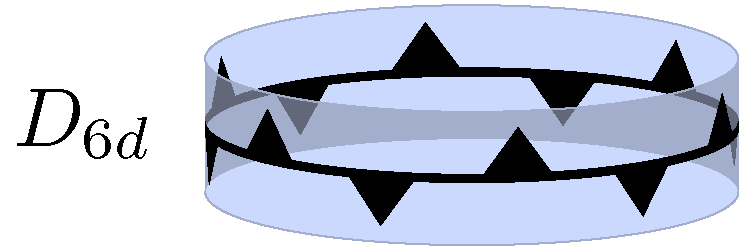
D_nd(또는 D_nv)는 주 회전축을 포함하는 수직 거울면이 있지만 수평 거울면이 있는 대신 수평면에서의 반사와 180°/n 각도로의 회전을 결합하는 등각변환이 있는 군이다. D_nh는 "정규" n각 각기둥과 "정규" n각 쌍각뿔의 대칭군이다. D_nd는 "정규" n각 역각기둥, 그리고 "정규" n각 사다리꼴 다면체의 대칭군이다. D_n은 부분적으로 회전된 ("꼬인") 각기둥의 대칭군이다.

군 D₂와 D_2h는 특별한 회전축이 없다는 점에서 주목할 만하다. 대신 세 개의 수직 2겹 축이 있다. D₂는 모든 다면체 대칭의 하위 군이고, D_2h는 다면체 군 T_h 및 O_h의 하위 군이다. D₂는 트위스테인과 같은 분자 및 호모테트라머인 Concanavalin A에 나타난다. D₂의 원소는 단위 립시츠 사원수에 의해 주어진 회전과 1대2의 관계에 있다.

군 S_n은 수평면에서의 반사와 360°/n 각도로의 회전의 조합에 의해 생성된다. 홀수 n의 경우 이는 두 개를 별도로 생성된 군, 차수 2n인 C_nh와 같으므로 S_n 표기법이 필요하지 않지만, 짝수 n의 경우 별개이고 차수가 n이다. D_nd와 마찬가지로 해당 회전을 포함하지 않고도 여러 부적절한 회전을 포함한다.

7개의 무한 계열의 모든 대칭군은 서로 다르지만, 다음과 같은 4쌍의 상호 동일한 군을 제외한다.

*C_1h 및 C_1v: 단일 반사(C_s )가 있는 차수 2의 군
*D₁ 및 C₂: 단일 180° 회전이 있는 차수 2의 군
*D_1h 및 C_2v: 평면에서의 반사와 해당 평면의 선을 통한 180° 회전이 있는 차수 4의 군
*D_1d 및 C_2h: 평면에서의 반사와 해당 평면에 수직인 선을 통한 180° 회전이 있는 차수 4의 군.

S₂는 단일 반전(C_i )이 있는 차수 2의 군이다.

군은 다음과 같이 구성할 수 있다.

* C_n: 축을 중심으로 2π/n 각도로 회전하는 회전에 해당하는 요소인 C_n이라고도 하는 요소에 의해 생성된다. 그 원소는 E(항등원), C_n, C_n², ..., C_nⁿ⁻¹이다.
* S_2n: 요소 C_2nσ_h에 의해 생성되며, 여기서 σ_h는 축 방향의 반사이다. 그 원소는 C_n의 원소와 C_2nσ_h, C_2n³σ_h, ..., C_2n²ⁿ⁻¹σ_h가 추가된다.
* C_nh: 요소 C_n과 반사 σ_h에 의해 생성된다. 그 원소는 군 C_n의 원소이며, 원소 σ_h, C_nσ_h, C_n²σ_h, ..., C_nⁿ⁻¹σ_h가 추가된다.
* C_nv: 축에 수직인 평면의 방향의 요소 C_n과 반사 σ_v에 의해 생성된다. 그 원소는 군 C_n의 원소이며, 원소 σ_v, C_nσ_v, C_n²σ_v, ..., C_nⁿ⁻¹σ_v가 추가된다.
* D_n: 요소 C_n과 축에 수직인 평면의 방향을 중심으로 한 180° 회전 U = σ_hσ_v에 의해 생성된다. 그 원소는 군 C_n의 원소이며, 원소 U, C_nU, C_n²U, ..., C_n^n − 1U가 추가된다.
* D_nd: 요소 C_2nσ_h 및 σ_v에 의해 생성된다. 그 원소는 군 C_n의 원소와 S_2n 및 C_nv의 추가 원소이며, 원소 C_2nσ_hσ_v, C_2n³σ_hσ_v, ..., C_2n^2n − 1σ_hσ_v가 추가된다.
* D_nh: 요소 C_n, σ_h 및 σ_v에 의해 생성된다. 그 원소는 군 C_n의 원소와 C_nh, C_nv 및 D_n의 추가 원소이다.

5.2. 다면체군 (7개의 점군)

다면체군은 2보다 큰 차수의 회전축이 2개 이상인 점군을 말하며, 매우 높거나 다면체 대칭이라고 불린다. 여기에는 다음이 포함된다.

* T (332), [3,3]⁺, 23, 차수 12: 키랄 사면체 대칭
* 4개의 C₃ 축 (정육면체의 두 꼭지점 또는 정사면체의 한 꼭지점을 통과)과 3개의 C₂ 축 (정육면체의 면 중심 또는 사면체의 모서리 중간점을 통과)을 갖는다.
* 정사면체의 회전군이며, 교대군 A₄와 동형이다.
* T_d, T_h 및 팔면체 대칭의 정규 부분군이다.
* 이진 사면체 군에 의해 주어진 회전에 1대2로 대응된다.

* T_d (*332), [3,3], 3m, 차수 24: 전체 사면체 대칭
* T와 동일한 회전축을 가지지만, C₂ 축은 D_2d 축이 되고, 4개의 3회전축은 4개의 C 부분군을 생성한다.
* 6개의 거울면 (각각 정육면체의 두 모서리 또는 사면체의 한 모서리를 포함)을 가지며, 단일 S₄ 축과 2개의 C₃ 축을 갖는다.
* 대칭군 S₄와 동형이다.
* O_h의 정규 부분군이다.

* T_h (3*2), [3⁺,4], 2/m, m, 차수 24: 피라이토헤드럴 대칭
* T와 동일한 회전축을 갖지만, 정육면체 면과 평행한 거울면을 갖는다.
* C₃ 축은 S₆ 축이 되고, 반전 대칭이 있다.
* A₄ × Z₂와 동형이며, 대칭군 S₄와는 동형이 아니다.
* 피라이토헤드론의 대칭이다.
* O_h의 정규 부분군이다.

* O (432), [4,3]⁺, 432, 차수 24: 키랄 팔면체 대칭
* T와 같지만, C₂ 축은 C₄ 축이 되며, 정육면체의 모서리 중간점을 통과하는 2회전축이 있어 3개의 D₂ 부분군을 생성한다.
* 정육면체와 팔면체의 회전군이다.
* S₄와 동형이다.

* O_h (*432), [4,3], 4/m2/m, mm, 차수 48: 전체 팔면체 대칭
* O와 동일한 회전축을 갖지만, T_d와 T_h의 거울면을 모두 포함하는 거울면을 갖는다.
* S₄ × Z₂와 동형이며, 정육면체와 팔면체의 대칭군이다.

* I (532), [5,3]⁺, 532, 차수 60: 키랄 이십면체 대칭
* 이십면체와 십이면체의 회전군이다.
* 전체 대칭군 I_h에서 지표 2의 정규 부분군이다.
* 5개의 문자에 대한 교대군인 A₅와 동형이다.

* I_h (*532), [5,3], 2/m, m, 차수 120: 전체 이십면체 대칭
* 이십면체와 십이면체의 대칭군이다.
* A₅ × Z''₂와 동형이다.

6. 결정학적 점군

최대 대칭성을 갖는 이산 점군에는 O_h와 I_h 두 가지가 있으며, 이들은 어떤 이산 점군도 자신을 진부분군으로 가질 수 없다. 이 두 그룹의 최대 공통 부분군은 T_h이다. O_h와 I_h는 각각 2회 회전 대칭을 4회로 변경하고, 5회 대칭을 추가하여 얻을 수 있다.

결정학적 점군 중 어떤 결정학적 점군도 자신을 진부분군으로 가질 수 없는 것은 O_h와 D_6h 두 가지이다. 이들의 최대 공통 부분군은 방향에 따라 D_3d와 D_2h이다.

7. 이항 정다면체군

Spin(3) → SO(3) 맵은 3차원 스핀 군에 의한 회전 군의 이중 피복이다. 격자 정리에 의해 Spin(3)의 부분군과 SO(3)의 부분군(회전점군) 사이에는 갈루아 연결이 존재한다. Spin(3)의 부분군의 이미지는 회전점군이고, 점군의 역상은 Spin(3)의 부분군이다.

유한 점군의 역상은 ⟨l,n,m⟩으로 표현되는 이항 정다면체군이라고 불린다. 이는 관련 다면체 군 (l,m,n)의 두 배의 차수를 가진다. 예를 들어, 이코사헤드랄 군 (2,3,5)의 역상은 이진 이코사헤드랄 군 ⟨2,3,5⟩이다.

이진 다면체 군은 다음과 같다:
*$A\_n$: ('n' + 1)-각형의 이진 순환 군, 차수 2n
*$D\_n$: n-각형의 이진 이면체 군, ⟨2,2,n⟩, 차수 4n
*$E\_6$: 이진 사면체 군, ⟨2,3,3⟩, 차수 24
*$E\_7$: 이진 팔면체 군, ⟨2,3,4⟩, 차수 48
*$E\_8$: 이진 이코사헤드랄 군, ⟨2,3,5⟩, 차수 120
이들은 ADE 분류에 의해 분류되며, C²를 이진 다면체 군의 작용으로 나눈 몫은 듀 발 특이점이다.

방향을 반전시키는 점군의 경우, 두 개의 핀 군이 있기 때문에 상황이 더 복잡해지며, 주어진 점군에 해당하는 두 개의 가능한 이진 군이 있다.

이는 공간의 피복이 아닌 군의 피복에 해당한다는 점에 유의해야 한다. 구는 단순 연결되어 있으므로 피복 공간이 없다. 따라서 3차원 다면체를 덮는 "이진 다면체"라는 개념은 없다. 이진 다면체 군은 스핀 군의 이산 부분군이며, 스핀 군의 표현 하에서 벡터 공간에서 작용하며, 이 표현에서 다면체를 안정화시킬 수 있다. Spin(3) → SO(3) 맵 아래에서 그들은 기본 (비이진) 군이 작용하는 동일한 다면체에 작용하는 반면, 스핀 표현 또는 다른 표현 하에서 다른 다면체를 안정화시킬 수 있다.

8. 추상군 유형에 따른 분류

3차원에서의 임의의 대칭군이 아닌 가장 작은 추상 군은 사원수군 (8차수), Z₃ × Z₃ (9차수), 이면체 군 Dic₃ (12차수), 그리고 16차수 군 14개 중 10개이다.

다음 표의 "# 2차 원소의 개수" 열은 C₂, C_i, C_s 유형의 등거리 변환 부분군의 총 개수를 나타낸다. 이 총 개수는 다양한 추상 군 유형을 구별하는 데 도움이 되는 특성 중 하나이며, 해당 등거리 변환 유형은 동일한 추상 군의 다양한 등거리 변환 군을 구별하는 데 도움이 된다.

3차원에서의 등거리 변환 군의 가능성 내에서, 2차 원소가 0, 1, 3개인 무한히 많은 추상 군 유형이 있으며, 2차 원소가 4n + 1개인 두 개, 2차 원소가 4n + 3개인 세 개가 있다 (각각 n ≥ 8). 2차 원소의 양의 짝수 개수는 결코 존재하지 않는다.

== 순환군 ==
n겹 회전 대칭군의 대칭은 C_n이며, 추상적 군 유형은 순환군 Z_n으로, 이는 C_n으로도 표기된다. 그러나 이 추상적 군 유형을 가진 대칭군에는 두 개의 무한한 계열이 더 있다.

짝수 차수 2n에 대해, 축을 중심으로 180°/n 각도로 회전하는 것과 축에 수직인 평면에서의 반사를 결합하여 생성되는 S_2n (쇼엔플리스 표기법) 그룹이 있다. S₂의 경우 C_i 표기법이 사용되며, 이는 반전에 의해 생성된다.
홀수인 n에 대해 임의의 차수 2n에 대해, C_nh가 있으며; 이는 n겹 회전축과 수직인 반사면을 가지고 있다. 이는 축을 중심으로 360°/n 각도로 회전하는 것과 반사를 결합하여 생성된다. C_1h의 경우 C_s 표기법이 사용되며, 이는 평면에서의 반사에 의해 생성된다.

따라서 결정학적 제한이 적용되는 10개의 순환 결정학적 점군은 다음과 같다.

== 이면체군 ==
2차원 이각형군 D_n에는 반사가 포함되어 있지만, 3차원에서는 D_n으로 표시되는 대칭군은 반사가 아닌 n개의 회전축에 수직인 n개의 2중 축을 포함한다. D_n은 정규 밑면을 가진 n각 각기둥과 정규 밑면을 가진 n각 쌍뿔의 회전군이며, 정규 n각 엇각기둥과 정규 n각 사다리꼴 다면체의 회전군이기도 하다. 이 군은 또한 모든 면에 동일한 키랄 표시 또는 모양의 일부 수정을 통해 키랄성을 갖게 한 후 그러한 객체의 전체 대칭군이기도 하다.

추상적인 군 유형은 이각형군 Dih_n이며, D_n으로도 표시된다. 그러나, 이 추상적인 군 유형을 가진 세 가지 더 많은 무한 시리즈의 대칭군이 있는데, 차수가 2n인 C_nv (정규 n각 각뿔의 대칭군), 차수가 4n인 D_nd (정규 n각 엇각기둥의 대칭군), 홀수 n에 대한 차수가 4n인 D_nh 등이 그것이다.

Dih_4n+2 $\backslash cong$ Dih_2n+1 × Z₂라는 속성을 참고하여, 12개의 결정학적 점군을 표로 나타내면 다음과 같다. (D_1d는 C_2h와 동일)

👆

좌우로 밀어서 보기

📌 열 고정 해제

차수	등거리 변환군	추상적 군	|주기 다이어그램
4	D2, C2v, C2h	Dih2 = Z2 × Z2	3
6	D3, C3v	Dih3	3
8	D4, C4v, D2d	Dih4	5
10	D5, C5v	Dih5	5
12	D6, C6v, D3d, D3h	Dih6 = Dih3 × Z2	7
14	D7, C7v	Dih7	7
16	D8, C8v, D4d	Dih8	9
18	D9, C9v	Dih9	9
20	D10, C10v, D5h, D5d	Dih10 = D5 × Z2	11

== 기타 ==
C_2n,h (차수 4n)는 추상적인 군 유형 Z_2n × Z₂이다. n = 1의 경우 Dih₂를 얻으므로 n ≥ 2이다.

2개의 순환 결정학적 점군은 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

차수	등거리 변환군	추상군	2차 원소 개수	사이클 다이어그램
8	C4h	Z4 × Z2	3
12	C6h	Z6 × Z2 = Z3 × Z22 = Z3 × Dih2	3
16	C8h	Z8 × Z2	3
20	C10h	Z10 × Z2 = Z5 × Z22 = Z5 × Dih2	3

D_nh (차수 4n)는 추상적인 군 유형 Dih_n × Z₂이다. 홀수 n의 경우는 이미 다루었으므로, 차수가 8n인 D_2nh가 있으며, 이는 추상적인 군 유형 Dih_2n × Z₂ (n≥1)이다.

3개의 이면각 결정학적 점군은 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

차수	등거리 변환군	추상군	2차 원소 개수	사이클 다이어그램
8	D2h	Z23	7
16	D4h	Dih4 × Z2	11
24	D6h	Dih6 × Z2 = Dih3 × Z22	15
32	D8h	Dih8 × Z2	19

나머지 7개는 5개의 결정학적 점군을 굵게 표시하여 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

|등거리 변환군 || 추상군 || 2차 원소 개수	사이클 다이어그램
12	T	A4	3
24	Td, O	S4	9
24	Th	A4 × Z2	7
48	Oh	S4 × Z2	19
60	I	A5	15
120	Ih	A5 × Z2	31

8.1. 순환군

n겹 회전 대칭군의 대칭은 C_n이며, 추상적 군 유형은 순환군 Z_n으로, 이는 C_n으로도 표기된다. 그러나 이 추상적 군 유형을 가진 대칭군에는 두 개의 무한한 계열이 더 있다.

짝수 차수 2n에 대해, 축을 중심으로 180°/n 각도로 회전하는 것과 축에 수직인 평면에서의 반사를 결합하여 생성되는 S_2n (쇼엔플리스 표기법) 그룹이 있다. S₂의 경우 C_i 표기법이 사용되며, 이는 반전에 의해 생성된다.
홀수인 n에 대해 임의의 차수 2n에 대해, C_nh가 있으며; 이는 n겹 회전축과 수직인 반사면을 가지고 있다. 이는 축을 중심으로 360°/n 각도로 회전하는 것과 반사를 결합하여 생성된다. C_1h의 경우 C_s 표기법이 사용되며, 이는 평면에서의 반사에 의해 생성된다.

따라서 결정학적 제한이 적용되는 10개의 순환 결정학적 점군은 다음과 같다.

8.2. 이면체군

2차원 이각형군 D_n에는 반사가 포함되어 있지만, 3차원에서는 D_n으로 표시되는 대칭군은 반사가 아닌 n개의 회전축에 수직인 n개의 2중 축을 포함한다. D_n은 정규 밑면을 가진 n각 각기둥과 정규 밑면을 가진 n각 쌍뿔의 회전군이며, 정규 n각 엇각기둥과 정규 n각 사다리꼴 다면체의 회전군이기도 하다. 이 군은 또한 모든 면에 동일한 키랄 표시 또는 모양의 일부 수정을 통해 키랄성을 갖게 한 후 그러한 객체의 전체 대칭군이기도 하다.

추상적인 군 유형은 이각형군 Dih_n이며, D_n으로도 표시된다. 그러나, 이 추상적인 군 유형을 가진 세 가지 더 많은 무한 시리즈의 대칭군이 있는데, 차수가 2n인 C_nv (정규 n각 각뿔의 대칭군), 차수가 4n인 D_nd (정규 n각 엇각기둥의 대칭군), 홀수 n에 대한 차수가 4n인 D_nh 등이 그것이다.

Dih_4n+2 $\backslash cong$ Dih_2n+1 × Z₂라는 속성을 참고하여, 12개의 결정학적 점군을 표로 나타내면 다음과 같다. (D_1d는 C_2h와 동일)

8.3. 기타

C_2n,h (차수 4n)는 추상적인 군 유형 Z_2n × Z₂이다. n = 1의 경우 Dih₂를 얻으므로 n ≥ 2이다.

2개의 순환 결정학적 점군은 다음과 같다.

D_nh (차수 4n)는 추상적인 군 유형 Dih_n × Z₂이다. 홀수 n의 경우는 이미 다루었으므로, 차수가 8n인 D_2nh가 있으며, 이는 추상적인 군 유형 Dih_2n × Z₂ (n≥1)이다.

3개의 이면각 결정학적 점군은 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

차수	등거리 변환군	추상군	2차 원소 개수	사이클 다이어그램
8	D2h	Z23	7
16	D4h	Dih4 × Z2	11
24	D6h	Dih6 × Z2 = Dih3 × Z22	15
32	D8h	Dih8 × Z2	19

나머지 7개는 5개의 결정학적 점군을 굵게 표시하여 다음과 같다.

👆

좌우로 밀어서 보기

📌 열 고정 해제

|등거리 변환군 || 추상군 || 2차 원소 개수	사이클 다이어그램
12	T	A4	3
24	Td, O	S4	9
24	Th	A4 × Z2	7
48	Oh	S4 × Z2	19
60	I	A5	15
120	Ih	A5 × Z2	31